
This question tests your understanding of the formula to solve for the average, or arithmetic mean, of a group of values. In this case, you are told the average (x + y) and are asked to solve for a missing term (x).
The answer choices are algebraic expressions, not numerical values, so you can infer that the question must not supply enough information to solve for the actual value of x. Rather, what you will solve for is x “in terms of y.” All this means is that the actual value of x will vary depending on the value of y.
From the format of the answer choices, you can glean that your task on this question is to set up the average formula, plug in the information provided by the question stem into the appropriate positions in the formula, and use what you know about solving algebraic equations to isolate the variable x on one side and everything else on the other.
The GMAT assumes that you have a working knowledge of several classic formulas. You should be comfortable using these so that you don’t have to waste time trying to remember them on Test Day.
The GMAT tests these formulas by giving you some information that relates to a known formula and asking you for a different, missing piece of information that can be solved for using that formula.
Many of the formulas commonly tested on the GMAT have three parts. For example:

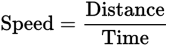
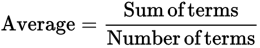
This chapter will cover the formulas listed above, plus others. The important thing to remember is that when you are given two parts of any three-part formula, you can always solve for the missing part. Keep this in mind when you encounter a question that seems to have you stumped. Always start by figuring out what formula is at issue; then figure out what parts of the given information can be substituted into that formula. At this point, the path to the solution will usually become clear.
As with all questions that hinge on standard mathematical formulas, you must first use your Pattern Recognition skills to identify the relevant formula. Once you’ve done so, Critical Thinking becomes important as you determine how the given information applies to the formula at hand. The GMAT often presents information in a less-than-intuitive way, forcing you to decode the meaning and relevance of that information to the solution.
Here are the main topics we’ll cover in this chapter:
Now let’s apply the Kaplan Method to the math formulas question you saw earlier:
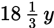




This question gives you a lot of information. You are told that the average of the four terms, x, 25, y, and 30, is x + y. A quick glance at the answer choices reveals that you are being asked to solve for x in terms of y.
You’ll need to set up the average formula and then isolate x. But don’t rush to the conclusion that you have to do a lot of algebra here.
Think critically about how you can approach this problem to save time. Picking numbers
is almost always a simple way to handle problems in which you need to solve for one
variable in terms of another. Once you put the terms in the average formula, you can
pick a number for x, solve the problem for y, and then plug that number into the answer choices to get the one that matches your
choice for x. The average formula is the sum of terms divided by the number of terms. Here, that
would look like this:
 . Multiplying both sides by 4 results in x + 25 + y + 30 = 4 (x + y). Distribute the 4 and you have x + 25 + y + 30 = 4x + 4y.
. Multiplying both sides by 4 results in x + 25 + y + 30 = 4 (x + y). Distribute the 4 and you have x + 25 + y + 30 = 4x + 4y.
Now pick an easy number to substitute for x. Let’s have x = 1. That gives you 1 + 25 + y + 30 = 4 + 4y. Combine like terms, and you have 56 + y = 4 + 4y. Doing the subtraction necessary to get y and the numbers on different sides of the equation leaves you with 52 = 3y. Divide each side by 3, and you find that y = 17
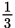 . Since you chose 1 to stand in for x, all you need to do is substitute 17
. Since you chose 1 to stand in for x, all you need to do is substitute 17
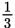 in for y and find the answer choice that equals 1. That’s choice (E).
in for y and find the answer choice that equals 1. That’s choice (E).
You could also have solved algebraically. Taking the equation above, x + 25 + y + 30 = 4x + 4y, you can continue to simplify by combining like terms until you get 55 = 3x + 3y. Factoring out a 3 from the right side gives you 55 = 3(x + y), and dividing both sides by 3 results in
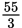 . Isolating x and converting
. Isolating x and converting
 to a mixed number results in
to a mixed number results in
 , which corresponds to choice (E).
, which corresponds to choice (E).
Using picking numbers can save you valuable time on this problem. You can also solve it with pure algebra, of course, and that approach can be used to confirm your answer if you initially solve by picking numbers.
Now let’s look at each of the common math formulas that show up on the GMAT Quantitative section, starting with averages.