Per saperne di piùMatematica e geometria
La novità della geometria analitica
Nel corso del Seicento l’introduzione della geometria analitica, frutto delle ricerche indipendenti di Descartes e di Pierre Fermat, imprime una importante svolta al pensiero matematico anche a livello teorico: offre, infatti, alla geometria una metodologia d’indagine del tutto nuova, che permette di ridurre qualsiasi problema di tipo geometrico a un problema di algebra, utilizzando le formule o, in generale, i metodi propri di questa scienza. Traducendo, infatti, in termini algebrici le nozioni classiche di punto, retta, piano, e le relazioni intercorrenti tra essi, la geometria analitica consente di rendere uniforme la trattazione di tutti i problemi geometrici. La geometria classica, al contrario, sebbene guidata da un’unica metodologia deduttiva – quella della logica tradizionale – non possiede una procedura unitaria per la risoluzione dei vari problemi, che può differire da caso a caso. Con l’introduzione della geometria analitica, invece, la deduzione viene affidata esclusivamente agli algoritmi algebrici.
La traduzione delle relazioni geometriche in relazioni tra enti algebrici, oltre a provocare un ampliamento di metodi, consente pure l’esplorazione di nuovi rapporti e di nuove proprietà esistenti tra gli enti geometrici. Quando una curva corrisponde a una certa equazione algebrica, semplici passaggi di tipo algebrico o computi numerici possono rivelare anche le più nascoste proprietà della curva stessa; semplici variazioni di questo o quel coefficiente possono far apparire relazioni prima insospettate. Vediamo un caso paradigmatico per illustrare i principi di base della geometria analitica. Dato un sistema di assi cartesiani x e y, la retta r è il luogo dei punti geometrici di coordinate x=1, y=1; x=2, y=2; x=3, y=3 ecc.; per cui l’equazione algebrica y=x descrive esattamente la retta da noi esaminata. La retta di equazione y=2x dà invece y=1, x=2; y=2, x=4; y=3, x=6. Per cui il coefficiente 2 fornisce un parametro che, graficamente, si traduce in una retta di differente inclinazione rispetto alla retta r.
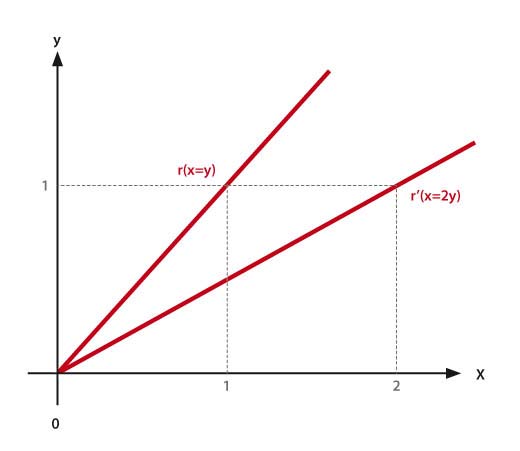

La retta e le coordinate cartesiane
Non si ha più, in sostanza, un mondo di enti geometrici chiusi in sé, astrattamente isolati nello spazio euclideo, come entità immobili disgiunte l’una dall’altra. Questo aspetto è di grande rilevanza, in quanto la geometria analitica getta le basi per un insieme di ricerche che permettono di porre in modo nuovo e rigoroso determinati problemi di geometria classica, sui quali la matematica greca ha lungamente meditato senza trovare risposte precise e definite.
La geometria analitica si presenta dunque come uno dei nuclei centrali e più fecondi della moderna indagine matematica. Questa posizione centrale le permetterà di influire sullo sviluppo di tutte le più importanti ricerche matematiche del XVII secolo, in primo luogo sull’analisi infinitesimale. Infatti molti concetti fondamentali del nuovo calcolo devono la loro origine alla necessità di risolvere problemi geometrici impostati con i metodi propri della geometria analitica.
Geometria proiettiva
Se la geometria analitica conosce importanti sviluppi, specie nella seconda metà del XVII secolo, non altrettanto può dirsi per la geometria proiettiva, che pure ha origine nel corso del Seicento. I suoi concetti fondamentali sono fissati dall’artista e matematico francese Girard Desargues (1593-1662) in un libro stampato in poche copie nel 1639 dal titolo Bozza di un saggio sul tentativo di studiare gli effetti dell’incontro di un cono con un piano. L’autore riprende e sviluppa idee maturate in seno alle ricerche rinascimentali sulla prospettiva. Com’è noto, un cerchio, se guardato di sbieco, ha l’aspetto di un’ellisse; oppure un fascio di luce uscente da un paralume cilindrico può tracciare su un muro una figura a forma di cerchio o di iperbole, a seconda dell’inclinazione che noi diamo al paralume stesso. Dunque forme e dimensioni mutano in relazione al piano di incidenza che taglia il cono dei raggi luminosi. Tuttavia, alcune proprietà restano immutate attraverso questi cambiamenti, ed è su queste proprietà invarianti che Desargues concentra la propria attenzione. Un solo esempio: una sezione conica rimane sempre una sezione conica qualunque sia il numero di proiezioni alle quali viene sottoposta. Le ricerche di Desargues rimangono un fatto unico e isolato nel corso del XVII secolo. La lettura del suo testo suscita non poche perplessità tra i matematici del suo tempo, ma lo scarso interesse per la geometria proiettiva è dovuto proprio ai grandi successi che si stanno allora conseguendo in altri campi della geometria, specialmente in quello della geometria analitica.
Calcolo delle probabilità

Frontespizio di Christiaan Huygens, “Libellus de ratiociniis in ludo aleae” in un’edizione del 1714
Il calcolo delle probabilità è un’altra creazione dei matematici del Seicento. Pierre Fermat e Blaise Pascal ne sono i fondatori. Per la verità essi non sono i primi ad affrontare l’argomento. Già Luca Pacioli e poi Girolamo Cardano, tra XV e XVI secolo, se ne sono occupati in alcuni dei loro lavori, ma i fondamenti teorici di questa disciplina si devono essenzialmente alle riflessioni compiute dai due matematici francesi. Il graduale emergere di un interesse per problemi connessi al calcolo delle probabilità è sostenuto, in primo luogo, dallo sviluppo delle compagnie di assicurazioni, ma uno stimolo altrettanto influente viene dall’analisi e dalla soluzione di problemi specifici posti da giocatori di carte o di dadi. Nel 1654 Antoine Gombaud, cavaliere di Méré, un nobile di notevole erudizione con la passione per il gioco, pone a Pascal questioni riguardanti la probabilità nel gioco dei dadi. Su questi quesiti Pascal mantiene una fitta corrispondenza con Fermat, ed è proprio in questo scambio di lettere che i due matematici francesi sviluppano alcuni concetti basilari della teoria della probabilità. Entrambi, però, non danno una stesura sistematica ai loro risultati. Tuttavia, le loro ricerche ispirano un lavoro pubblicato nel 1657 dall’olandese Christiaan Huygens (1629-1695), dal titolo Libellus de ratiociniis in ludo aleae (Breve libro sui ragionamenti nel gioco dei dadi), che rappresenta il primo trattato sistematico sulla probabilità, nel quale si introduce il concetto di “valore atteso”. Nel 1671, sempre in Olanda, il politico e matematico Johan de Witt (1625-1672), nell’opera intitolata Trattato delle rendite vitalizie (Waerdye van Lijfrenten, naer proportie van Lof-Renten), introduce quella nozione che oggi viene definita come “speranza matematica” e costruisce tavole per i premi annuali delle assicurazioni basate sulla conoscenza delle probabilità di vita alle varie età. I tassi di mortalità sono oggetto di studio anche da parte del fisico e matematico inglese Edmond Halley (1656-1743).
Logaritmi
L’atto di nascita del calcolo logaritmico è dato dalla pubblicazione, nel 1614, dell’opera intitolata Mirifici logarithmorum canonis descriptio (Descrizione della regola meravigliosa dei logaritmi). Esce a firma del matematico scozzese John Napier (1550-1617), che sviluppa l’idea di utilizzare funzioni inverse di funzioni esponenziali allo scopo di semplificare e velocizzare calcoli molto complessi. Anche il matematico svizzero Joost Bürgi (1552-1632) giunge ai medesimi risultati di Napier, in modo del tutto indipendente da quest’ultimo, ma egli pubblica il suo lavoro intitolato Arithmetische und geometrische Progress Tabulen (Tavole di progressioni aritmetiche e geometriche) solo nel 1620, su insistenza di Keplero, di cui è assistente. L’opera di Napier ha una grande influenza sui matematici del Seicento, soprattutto grazie all’influente opera di diffusione del calcolo logaritmico operata dal matematico inglese Henry Briggs (1556?-1630), autore di importanti lavori, tra i quali l’Arithmetica Logarithmica del 1624. I calcoli mediante logaritmi si diffondono soprattutto nel mondo degli astronomi, che possono beneficiare di un potente strumento per ridurre i tempi necessari a sviluppare i loro calcoli lunghi e complessi.
Teoria dei numeri interi
Come abbiamo avuto modo di dire all’inizio, nel Seicento non solo si creano campi di ricerca matematica completamente nuovi, ma si arricchiscono di nuovi risultati settori già sviluppatisi nei secoli precedenti. Uno di questi è la teoria dei numeri interi: qui domina incontrastata la figura di Pierre Fermat. Le ricerche di Fermat vengono pubblicate postume solo nel 1670, quando viene ristampata la copia di una traduzione latina dell’Arithmetica di Diofanto di Alessandria, uscita nel 1621 e appartenente al matematico francese. È proprio su questa copia che Fermat annota, in margine alle pagine del libro, la maggior parte dei suoi risultati. Dei molti teoremi enunciati, però, non si trova mai alcuna dimostrazione. Saranno i matematici del Settecento a trovare queste dimostrazioni, eccetto una: quella relativa al cosiddetto “ultimo (o grande) teorema di Fermat”, che è rimasto una sfida per più di tre secoli, fino al lavoro del matematico britannico Andrew Wiles del 1994. Questo teorema dice che non è possibile trovare quattro numeri interi positivi a, b, c, n (con n maggiore di 2) che diano soluzioni intere dell’equazione:
xn + yn = zn
“Della qual cosa – scrive Fermat – ho scoperto una dimostrazione veramente mirabile, che non può essere contenuta nel margine troppo stretto della pagina”. Tra gli storici della matematica è ormai convinzione diffusa che la presunta dimostrazione trovata da Fermat sia sbagliata. Infatti, quella trovata da Andrew Wiles ha richiesto conoscenze e apparati matematici impensabili per un matematico del XVII secolo.
Algebra

Edizione del 1670 dell’”Arithmetica” di Diofanto con in basso il commento di Fermat, in latino, che espone il teorema (Observatio Domini Petri de Fermat)
Per quanto riguarda gli sviluppi dell’algebra nel Seicento, va ricordato che i contributi più importanti vengono prodotti principalmente nella prima metà del secolo, poiché, dopo la nascita della geometria analitica, gli studi di algebra rimangono strettamente collegati a quelli della nuova disciplina fondata da Descartes e da Fermat. Tuttavia, in tale periodo, i matematici impostano nuovi problemi, individuano nuove regole e provvedono anche a migliorare le notazioni algebriche.
Importanti sono le ricerche dell’inglese Thomas Harriot (1560-1621). Nell’opera del 1631 intitolata Artis analyticae praxis ad aequationes algebraicas resolvendas (Pratica dell’arte analitica per la soluzione di equazioni algebriche), egli mette in evidenza le relazioni tra i coefficienti e le radici, ma non tiene conto delle radici negative e immaginarie. A lui si deve l’introduzione di segni come maggiore e minore.
Il suo connazionale William Oughtred (1575-1660), nella sua Clavis Mathematicae (Chiave della matematica) del 1631, introduce il segno x per indicare il prodotto. Il francese Albert Girard (1595?-1632), nella sua Nuova invenzione in algebra del 1629, fa delle relazioni tra radici e coefficienti il fondamento stesso della teoria algebrica e, per conferire ad esse la massima generalità, accoglie i numeri immaginari. Giunge così a enunciare il principio che un’equazione ha un numero di radici uguale al suo grado e a dimostrare la regola sulla somma delle potenze n-esime delle radici. Anche René Descartes, avvalendosi di nuove notazioni, formula importanti regole operazionali concernenti la soluzione e la trasformazione di equazioni algebriche, come ad esempio la regola dei segni, che ancora oggi porta il suo nome.
Infine, Isaac Newton nella sua Arithmetica universalis del 1707 descrive, anche se non dimostra, un metodo per determinare il massimo numero di radici reali positive o negative e quindi anche il minimo numero possibile di radici complesse.