Appendix F
Technical Issues in Estimating the Market Risk Premium

In its simplest form, the historical market risk premium can be measured by subtracting the return on government bonds from the return (total return to shareholders) on a large sample of companies over some time frame. But this requires many choices that will affect the results. For the best measurement of the risk premium using historical data, follow these guidelines:

Calculate the premium relative to long-term government bonds. When calculating the market risk premium, compare historical market returns with the return on 10-year government bonds. Long-term government bonds match the duration of a company's cash flows better than short-term bonds.

Use the longest period possible. How far back should you look when using historical observations to predict future results? If the market risk premium is stable, a longer history will reduce estimation error. Alternatively, if the premium changes and estimation error is small, a shorter period is better. To determine the appropriate historical period, search for any trends in the market risk premium compared with the imprecision associated with short-term estimates.

To test for the presence of a long-term trend, we regress the U.S. market risk premium against time. Over the past 114 years, no statistically significant trend is observable.1 Based on regression results, the average excess return has fallen by two basis points a year, but this result cannot be statistically distinguished from zero. Premiums calculated over shorter periods are too volatile to be meaningful. For instance, U.S. stocks outperformed bonds by 18 percent in the 1950s but offered no premium in the 1970s. Given the lack of any discernible trend and the significant volatility of shorter periods, use the longest time series possible.

Use an arithmetic average of longer-dated intervals (such as 10 years). When reporting market risk premiums, most data providers report an annual number, such as 6.4 percent per year. But how do they convert a century of data into an annual number? And is the annualized number even relevant?

Annual returns can be calculated using either an arithmetic average or a geometric average. An arithmetic (simple) average sums each year's observed premium and divides by the number of observations:

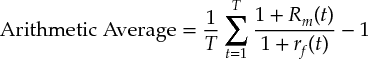
where

T	=	number of observations
Rm(t)	=	the market return in year t
rf(t)	=	the risk-free rate in year t

A geometric average compounds each year's excess return and takes the root of the resulting product:

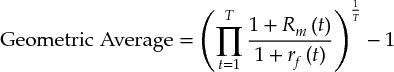
The choice of averaging methodology will affect the results. For instance, between 1900 and 2014, U.S. stocks outperformed long-term government bonds by 6.4 percent per year when averaged arithmetically. Using a geometric average, the number drops to 4.2 percent. This difference is not random; arithmetic averages always exceed geometric averages when returns are volatile.

So which averaging method on historical data best estimates the expected rate of return? Well-accepted statistical principles dictate that the best unbiased estimator of the mean (expectation) for any random variable is the arithmetic average. Therefore, to determine a security's expected return for one period, the best unbiased predictor is the arithmetic average of many one-period returns. A one-period risk premium, however, can't value a company with many years of cash flow. Instead, long-dated cash flows must be discounted using a compounded rate of return. But when compounded, the arithmetic average will generate a discount factor that is biased upward (too high).

The cause of the bias is quite technical, so we provide only a summary here. There are two reasons why compounding the historical arithmetic average leads to a biased discount factor. First, the arithmetic average may be measured with error. Although this estimation error will not affect a one-period forecast (the error has an expectation of zero), squaring the estimate (as you do in compounding) in effect squares the measurement error, causing the error to be positive. This positive error leads to a multiyear expected return that is too high. Second, a number of researchers have argued that stock market returns are negatively autocorrelated over time. If positive returns are typically followed by negative returns (and vice versa), then squaring the average will lead to a discount factor that overestimates the actual two-period return, again causing an upward bias.

We have two choices to correct for the bias caused by estimation error and negative autocorrelation in returns. First, we can calculate multiyear returns directly from the data, rather than compound single-year averages. Using this method, a cash flow received in 10 years will be discounted by the average 10-year market risk premium, not by the annual market risk premium compounded 10 times.² From 1900 through 2014, the average one-year excess return equaled 6.1 percent. The average 10-year cumulative excess return equaled 69.1 percent,³ which translates to an annual rate of 5.5 percent. Alternatively, researchers have used simulation to show that an estimator proposed by Marshall Blume best adjusts for problems caused by estimation error and autocorrelation of returns:⁴

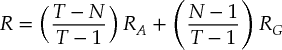
where

T	=	number of historical observations in the sample
N	=	forecast period being discounted
RA	=	arithmetic average of the historical sample
RG	=	geometric average of the historical sample

Blume's estimator depends on the length of time for which you plan to discount. The first year's cash flow should be discounted using the arithmetic average (T = 130, N = 1), whereas the tenth year's cash flow should discounted based on a return constructed with a 91.7 percent weighting on the arithmetic average and an 8.3 percent weighting on the long-term geometric average (T = 130, N = 10). The resulting estimator for the 10-year cash flow equals 6.2 percent.

Even with the best statistical techniques, however, these estimates are probably too high, because our sample includes only U.S. data, representing the best-performing market over the last century. Since it is unlikely that the U.S. stock market will replicate its performance over the next century, we adjust downward the historical market risk premium. Research shows that the U.S. arithmetic annual return exceeded a 17-country composite return by 0.8 percent in real terms.⁵ If we subtract an 0.8 percent survivorship premium from our range presented earlier, this leads to an expected return between 5.0 percent and 5.5 percent.

Notes

1 Some authors, such as Jonathan Lewellen, argue that the market risk premium does change over time—and can be measured using financial ratios, such as the dividend yield. We address these models separately. J. Lewellen, “Predicting Returns with Financial Ratios,” Journal of Financial Economics 74, no. 2 (2004): 209–235.

2 Jay Ritter writes, “There is no theoretical reason why one year is the appropriate holding period. People are used to thinking of interest rates as a rate per year, so reporting annualized numbers makes it easy for people to focus on the numbers. But I can think of no reason other than convenience for the use of annual returns.” J. Ritter, “The Biggest Mistakes We Teach,” Journal of Financial Research 25 (2002): 159–168.

3 To compute the average 10-year cumulative return, we use overlapping 10-year periods. To avoid underweighting early and late observations (for instance, the first observation would be included only once, whereas a middle observation would be included in 10 separate samples), we create a synthetic 10-year period by combining the most recent observations with the oldest observations. Nonoverlapping windows lead to similar results but are highly dependent on the starting year.

4 D. C. Indro and W. Y. Lee, “Biases in Arithmetic and Geometric Averages as Estimates of Long-Run Expected Returns and Risk Premia,” Financial Management 26, no. 4 (Winter 1997): 81–90; and M. E. Blume, “Unbiased Estimators of Long-Run Expected Rates of Return,” Journal of the American Statistical Association 69, no. 347 (September 1974): 634–638.

5 E. Dimson, P. Marsh, and M. Staunton, “The Worldwide Equity Premium: A Smaller Puzzle,” in Handbook of Investments: Equity Risk Premium, ed. R. Mehra (Amsterdam: Elsevier Science, 2007).