4

Accurate Predictions

The original Parsonnet paper had achieved a respectable amount of impact, and my paper on the trial of the model in a British hospital had been well received. I was coming to the end of my specialty training, but there was still some more work to do before I would be ready to seek appointment as an independent surgeon, and that had to be something truly special, as the competition for the coveted posts of senior or consultant heart surgeon was (and still is) fierce. It was the last year of my training, and I had to choose an exceptional location in which truly special skills could be obtained. In those days, many senior medical trainees in the United Kingdom added the final lustre to the polish on their credentials by going to the United States to do research or some other attachment in their chosen specialty. In fact, so common was this practice that it acquired the unofficial status of a kind of additional qualification:

Mr Joe Hacker-Forceps
MB BS FRCS BTA
(Medical Bachelor, Bachelor of Surgery, Fellow of the Royal College of Surgeons, Been To America)

I did not fancy seeking a BTA, largely because working in a laboratory and being told what research I could or could not do left me cold. I wanted an attachment with a bit more freedom, and with a focus on clinical work. The university hospitals of Bordeaux in France offered specialist areas in cardio-thoracic surgery and transplantation that were unique — on top of which, I already had some French connections, could speak the language, and was partial to a nice Margaux wine. So Bordeaux it was. It lived up to expectations. The pay was terrible, the work was hard, and the impact on my young family severe, but, in terms of the value of the clinical attachment, the place was unbeatable. Some of the best surgery I had ever seen took place there, and I made the most of the experience, not just by learning from the precise and meticulous way French surgeons did everything both in and out of the operating theatre, but also from the rich pickings that their advanced surgery offered for scientific publication. Many French doctors had a poor command of the English language and found it difficult to publish in the predominantly English-speaking medical world, and so I was able to offer my services as a medical writer and translator to get their work the recognition it so richly deserved in the mainstream Anglophone medical literature, while, at the same time, becoming a co-author on some innovative and high-profile clinical papers.

I therefore operated, learned, and wrote in Bordeaux, but I also befriended François Roques, an ambitious, intelligent, but somewhat surly senior trainee heart surgeon who was desperately looking to improve his own curriculum vitae by publishing something. ‘So publish something’, I said. ‘Yes, it is easy for you to say, but what? It’s all been done before’, said François, and so I suggested risk modelling applied to French cardiac surgery, along the same lines of my then recent paper from Manchester on the Parsonnet score. At first, I was met with a blank stare. The concept of quality monitoring and risk assessment was not, at that time, common currency in France. After a few brief words of explanation, François’s eyes lit up. He saw the value of such work, and decided to do it.

In fact, François Roques did a lot more than simply apply Parsonnet in France. He and his collaborators also modified the Parsonnet model to fit the French patient population, thus effectively creating their own French risk model, compared the two, and found that theirs was better. The paper describing this ‘French score’ was published in 1997. It had relatively little impact, because its appeal to the profession outside France was necessarily limited. By then, I was back in Britain, having achieved my career ambition and secured a consultant post. I was working at Papworth Hospital in Cambridge, one of the world’s greatest institutions for cardiac surgery, when François unexpectedly got in touch. He, too, had become a consultant (praticien hospitalier), and was now working in Martinique in the French West Indies, but the balmy Caribbean environment had done nothing to dampen his newfound enthusiasm for risk modelling.

‘I think you and I can do better’, he said.

‘Better than what?’

‘Better than Parsonnet, better than the French score, better than everything. We should create our own risk model.’

I liked the sound of that, and the two of us agreed to go ahead.

Email was still not widely available at the time, so, over the next couple of years, the fax lines between Cambridge and Martinique were, we like to think, glowing red hot on the ocean bed with the enormous amount of data travelling through them, back and forth, as we argued over which risk factors to study, and over the shape and strategy of the project. We decided to collect data from all over Europe. I belonged to the European Club of Young Cardiac Surgeons, which met annually in a different European city, and I was able to recruit my fellow club members to co-ordinate the exercise in their own country. François and I picked out every risk factor known or suspected to influence outcome. We designed a user-friendly, single-sided A4 form to collect the data, with carefully designed wording and explanations. We asked for data on risk factors, the operation performed, and the outcome: was the patient alive or dead afterwards? We even designed a logo (dismissively described by my then secretary as looking like a cheap shoe for a deformed foot):

We printed out tens of thousands of these forms, packaged them, and sent them to individual hospitals in eight European countries, and recruited one of the best biostatisticians in France, Philippe Michel, of the University of Bordeaux, to do the analysis. After all the data were gathered, some 20,000 patients from 128 hospitals in eight European countries were studied, and information collected on 97 risk factors in all the patients. The data were laboriously transcribed into a computer database at the University of Bordeaux. We therefore knew the risk profile of the patients, and we knew which had survived. We then flew to Bordeaux to create the risk model. For days, Francois, Philippe, and I studied and validated data, and designed and discarded models, and the university computers churned the data and tested and tweaked each successive version of the possible models. Finally, at about two in the morning on 2 May 1997, we had a model that worked very well and was simple to use, intuitive, and credible. We named it the European System for Cardiac Operative Risk Evaluation (EuroSCORE), and, feeling chuffed with the elegant acronym, went to bed.*

[* That’s not strictly true. François and Philippe went to bed, and I went to my hotel room and switched on the BBC news to watch the gradual unfolding of the landslide that brought Tony Blair to power after nearly two decades of Conservative Party rule.]

The paper describing EuroSCORE was accepted for presentation at the plenary session of the next meeting of the European Association for Cardio-Thoracic Surgery in Brussels, and I had the privilege of reading the paper to a packed house. A few weeks later, the full paper was published in the association’s journal (Nashef 1999).

The success of EuroSCORE exceeded our wildest expectations. The model has been used globally, in every continent and in almost every country with cardiac surgery. The paper alone has been cited in more than 2,300 scientific publications, and the term EuroSCORE has entered the medical vocabulary. The risk model that it refers to has been used for decision-making about the risk of surgery, for evaluating the quality of care, for predicting death (which it was designed to do), for comparing the results of surgery, for predicting complications (which it was not designed to do), and for estimating the cost and length of hospitalisation. In some countries, it has even entered the legal system, so that the family of a heart surgery patient with a low EuroSCORE is automatically compensated if he or she dies.

Now that we have a risk model, how do we put it into practice?

When a risk model allows us to predict the likely outcome, we immediately have a benchmark against which we can compare the actual outcome. The easiest and most basic use of this tool is for the monitoring of surgical performance using hospital mortality (death from the operation).

Most patients admitted to hospital for a heart operation, or any other kind of operation, are alive when they enter hospital. Very rarely, a patient arrives ‘dead but warm’, and is brought back to life by a heart operation, but this is extremely rare. We can therefore safely assume that virtually all patients having a heart operation are alive when they come in to hospital, and most will be alive when they leave hospital after operation. The difference between the number coming in alive and the number leaving alive is the hospital mortality. This is an objective measure, difficult to falsify, and available in the data of almost any hospital, no matter how rudimentary the hospital information system. Thus the hospital mortality can be expressed as a percentage: if 100 patients enter the hospital alive, and 98 leave the hospital alive, then the actual mortality is 2 per cent.

A risk model such as EuroSCORE allows us to predict what that mortality should be on average, taking into account the risk profile of the patients. By adding up the EuroSCOREs for all 100 patients together, and dividing by 100, we have another percentage, and that is the average predicted mortality.

The next step is to compare the two. If a particular hospital’s actual mortality is 1 per cent and its predicted mortality is 2 per cent, can we conclude that this hospital is doing better than predicted? No, we can’t. We can be pretty sure that the hospital is doing no worse than predicted, but, to be able to say that it is actually doing better than predicted, we need to be confident that the result isn’t likely to be due to chance.

When we look at data, we very rarely look at the entire data from the population that interests us. Most of the time, we collect a sample of data, and hope that the findings in that sample reflect those in the whole population. The reason is simple: it is usually difficult and time-consuming to measure anything in a whole population. Say, for example, you wanted to find out the average height of people in your town. You could line them all up and measure them, but that would take a huge effort and a very long time, especially if your town is London or Melbourne. Much easier would be to take a random sample of a few hundred folk in your town and measure them, and hope that your sample is representative of the whole population. How confident can you be that the measurement you took actually reflects the real average height of all the townsfolk? The statisticians have a very good method to answer that question, and that is what is called the ‘confidence interval’. In a way, this is also analogous to decisions made in law. Like a judge asking a jury to be sure beyond reasonable doubt that the accused is guilty, stating the confidence interval gives us the range within which we can be certain beyond reasonable doubt that the true value of what we are interested in lies within that range. We now know that the arbitrary cut-off point for certainty in medicine is established. In medical statistics, to be beyond reasonable doubt is to be at least 95 per cent certain.

There is more than one method of working out the confidence interval, and the choice depends on the type of data one is dealing with. If you are measuring the height of people in a population, the distribution of these heights will be ‘normal’, or, in other words, it follows the well-known shape of the bell curve, with most measurements clustered around the average, and the rest becoming less and less frequent on either side of the average.

The nortmal ‘bell curve’

Certain events, such as death after heart surgery, happen rarely, say 2 per cent of the time. If we look at many patient groups, and plot all the mortalities on a graph, we do not get a normal distribution, or a bell curve. Instead, we get a skewed distribution, with most measured mortalities clustered around 0–4 per cent, then a long and diminishing ‘tail’ of higher mortalities. This sort of distribution is called a Poisson distribution, named after the 19th-century French mathematician Siméon Poisson.

A crude representation of a Poisson distribution of mortalities is shown below:

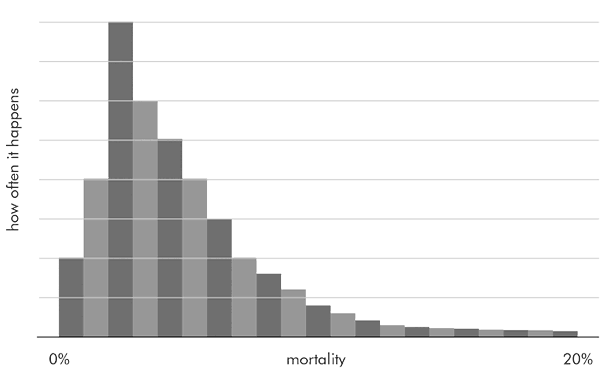
The important thing about the Poisson distribution is the longish tail, and that also applies to the confidence interval around a measurement that follows such a distribution.

So we have a measurement of mortality of 2 per cent in a decent sample of heart surgery patients. If we know the sample size, we can calculate that the 95 per cent confidence interval around this measurement is going to be, say, 1–4 per cent. This means that, based on our sample mortality of 2 per cent, we can be 95 per cent confident that the true mortality in the population will be between 1 and 4 per cent. The reason we need to know the sample size is simple. If the sample is large, we can be more confident that it will truly represent the population, and we will get a tighter confidence interval: say 1.5 to 3 per cent. If the sample is tiny (like the snake-oil salesman sample), we will have a hugely wide confidence interval, say 0.5 to 70 per cent, and our measure of 2 per cent would be meaningless.

Armed with this information, we can now use the measured sample mortality and the 95 per cent confidence interval properly and sensibly to compare outcomes. For that, take a look at these hypothetical scenarios. First, we take a surgeon whose mortality is 3 per cent, as shown by the diamond shape. EuroSCORE tells us his predicted mortality is 4 per cent, and that is shown by the vertical bar.

So, is this surgeon doing better than predicted? Maybe, but we will not know for sure until we apply the 95 per cent confidence interval, so let us do that:

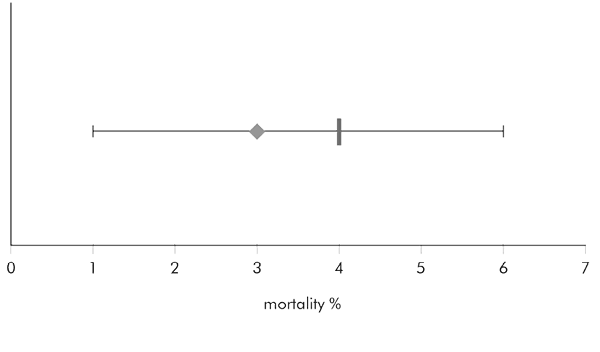
The horizontal bar around the diamond of actual mortality shows the 95 per cent confidence interval. It goes from 1 per cent to 6 per cent, which includes within its limits the predicted mortality of 4 per cent. Therefore we can be 95 per cent confident that based on our sample, the surgeon’s true mortality is 1–6 per cent, no better and no worse than predicted. This surgeon is therefore performing as expected, and there is no reason to worry (and nothing to get excited about either!).

Now look at these four hypothetical surgeons:

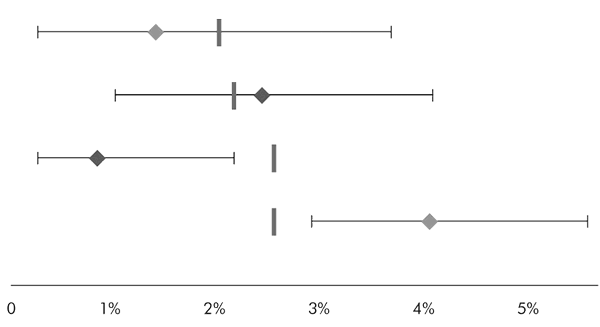
The top two are doing as well as predicted, in that there is no significant difference between their actual mortality (diamond) and their predicted mortality (vertical bar). We can say this because the predicted mortality lies within the 95 per cent confidence interval of their actual mortality (horizontal bar). The third is doing significantly better than predicted, and should perhaps be given a pay rise. The fourth is doing significantly worse, and needs some action now, before more patients suffer.

The above method is the statistically correct one for knowing if one surgeon (or unit, or service, or hospital) is performing as expected, better than expected, or less well than expected. There are other indicators, perhaps less statistically rigorous, but no less useful for that. To understand them, we shall pretend to be bankers (of the old-fashioned type that count your money and look after it, not the type that gamble with billions and cause global economic meltdown).

‘The surgeon saved my mother’s life!’

‘The surgeon killed my mother!’

Both of the above are sensationalist statements, and, in the overwhelming majority of cases, both are utterly wrong. Surgeons almost never save a whole life, and almost never kill an entire mother. They do, however, save and lose ‘bits’ of a life. Let me explain.

No operation has zero risk. In fact, no medical procedure or treatment has zero risk. A single aspirin tablet is capable of provoking a stomach bleed or an allergic reaction that can be fatal. In fact, eating just one peanut can be fatal if you have a peanut allergy, and a peanut is not even a medicine. Crossing the road, getting out of bed, and getting into bed with the wrong partner can all kill you. An average female patient having a CABG operation in the current era has a risk of dying of approximately 1 per cent. If she dies, can her son blame the surgeon? Well, yes, but not entirely. He can blame the surgeon for 99 per cent of her death, but that 1 per cent was always on the cards, no matter who the surgeon was or what the surgeon did.

Similarly, if the woman survives, can the surgeon take the credit for saving her life? Well, yes, but not entirely. In fact, there was a 99 per cent chance she would survive anyway, no matter who the surgeon was. The surgeon can, however, justifiably take the (minuscule) credit for that paltry 1 per cent of a life saved, and this brings us to the ‘bank of life’.

Imagine a bank in which we deposit not money, but lives, or parts of lives. Every surgeon has a bank account. When a patient survives an operation, the account gets a credit equal to the probability of death from the operation. Similarly, when a patient dies from an operation, the account is debited by the probability of survival.

Let us now look at what this account balance sheet would look like in graphical form.

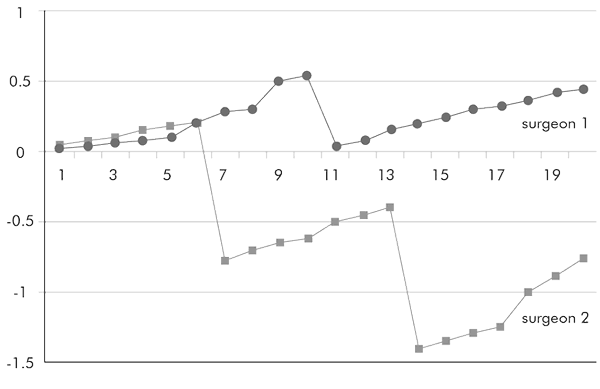
In this graph, we have two surgeons: surgeon 1 (line with circle dots) and surgeon 2 (line with square dots). On the horizontal axis, we have the total number of operations over time, and, in this graph, each surgeon has done 20 operations. On the vertical axis, we have the total number of lives ‘saved’ or, if you dip below the zero, lives ‘lost’.

To begin with, until they reach patient number 6, both surgeons are doing pretty well. All their patients are surviving, but all of their patients have a low risk of death anyway, so the account is credited with tiny ‘bits of life saved’. Note that when surgeon 1 operates on patient number 8, his line swings more sharply upwards. Patient number 8 was a high-risk patient (probability of death 25 per cent), so that surgeon 1 gets a whole ‘quarter of a life’ credited in one fell swoop. When he reaches patient number 10, another very high-risk patient, unfortunately the patient dies, but as the probability of survival for this patient was only 50 per cent anyway, the account is only debited by half a life, and surgeon 1 continues on his upwards trend afterwards.

It is a completely different story for surgeon 2. He too is doing well until patient 6, but here the patient dies. Unfortunately, however, this was a low-risk patient, with a probability of survival of 95 per cent, so that almost a whole life (0.95 of one) is debited when that patient dies. This tragedy happens again at patient 13. The two line graphs now show clearly which surgeon is doing better.

This ingenious method was described by Jocelyn Lovegrove and colleagues from University College, London (Lovegrove 1997). The beauty of it is that an enormous quantity of data (numbers of operations, survival and death, risk profile, and how they all fare over a period of time) can be seen at a glance from a simple single-line diagram. One quick look at the diagram for a particular surgeon can give a pretty good estimate of performance by looking at risk-adjusted survival over time. In simple terms, the graph says to the surgeon: ‘My friend, this is how well you’ve been doing’ (or how badly). It is one of the most useful performance measures there has ever been, and all one needs to compile the graph are numbers of operations, patients’ risk profile using EuroSCORE or some other method, and what the outcome was (dead or alive).

The method is called either the CuSum (cumulative sum) curve or sometimes VLAD (variable life-adjusted display, not Vlad the Impaler). Good institutions have data on the results achieved by their surgeons, and provide these data and graphs to them on a regular basis, and that, by taking advantage of an amazing phenomenon called the Hawthorne effect, is probably the single most important measure by which the results of medical intervention can be sustained and improved.

A real VLAD or CuSum curve for Papworth Hospital in Cambridge. Three surgeons are doing superbly well. Four are doing as expected, though, for a short time, three dipped below the zero in the ‘lives saved’ account. They were only overdrawn for a very short time, and rapidly got back to safety. Interestingly, one of them was going through an acrimonious divorce at the time, and was not concentrating on his work, and his results suffered. Another was going through an overconfident phase, was very pleased with himself, and thought he could get away with anything. He took some risks, and his results suffered. As we will see later, the psychology of surgeons (who are, after all, human beings, despite claims to the contrary) can have an impact on outcomes.

The success of EuroSCORE in becoming the world’s leading risk model went far beyond its use in medical decision-making and quality control. It actually saved lives. To understand how a mere risk model can do this, we have to go back to the early 20th century, and specifically to Cicero in Illinois, USA, home of the Hawthorne Works.

The Hawthorne Works was a factory complex built by the Western Electric Company in 1905. It had 45,000 employees at the height of its operations, making refrigerators and other electrical goods. In its heyday, it was so large that it had its own private railway to move shipments through the plant to the nearby freight depot. Sadly, in 1983, manufacturing ceased, and the plant became yet another shopping centre, but not before having secured a prominent place in history. That accolade, by the way, had absolutely nothing to do with making vacuum cleaners and refrigerators.

In the 1920s, some highly clever managers at the Hawthorne Works decided to study efficiency at the factory. They wondered whether the workers would be more productive if the ambient lighting in the factory was increased, so they turned up the lighting and measured the workers’ productivity. They found that productivity temporarily increased, and, being managers, they were very pleased with themselves.

Some time later, the very same managers postulated that productivity should go down if lighting was reduced, so they turned down the lights and measured productivity. To their surprise, productivity went up. They were baffled by this unexpected finding. They pressed on, and studied the effect of many other interventions on productivity: raising and lowering the ambient temperature, moving desks around, meaninglessly changing the order in which routine tasks were carried out, and so on. Every time they implemented a change, they measured productivity and found that it went up for a while, only to return to baseline when the experiment stopped. Eventually, in 1932, they stopped intervening (much to the relief of the workers, I imagine), and filed their results.

Twenty years later, in the 1950s, a social scientist named Henry A. Landsberger revisited the Hawthorne experiments. Having studied the data, Landsberger had a brilliant idea. He postulated that the increased productivity may have had nothing to do with lights, temperature, or position of desks, but that it was the act of measurement itself that was improving the performance (Landsberger 1958). This phenomenon became known as the Hawthorne effect: in other words, measure something, and it gets better. Though puzzling at first, it is easy, on a little reflection, to see why mere measurement is capable of improving performance.

First, workers are human. If they perceive that somebody somewhere is interested in their performance, they are naturally motivated to improve. Second, where there is no measurement, there is absolutely no incentive to improve: if a factory, or a hospital for that matter, is underperforming, but is not measuring its performance, and not comparing itself to similar organisations or institutions, it cannot be aware of the existence of an underperformance problem, and the impetus for fixing the problem simply does not exist. If the old adage says ‘If it ain’t broke, don’t fix it’, then a corollary would go ‘If you don’t even know it’s broke, why on Earth would you wanna try to fix it?’ This was, almost certainly, at least part of the problem in children’s heart surgery at the Bristol Royal Infirmary, as it probably was and unfortunately still is in many medical services around the world.

With the introduction of EuroSCORE to predict the mortality of surgery with reasonable accuracy, surgeons at last had a standard against which they could assess their own performance. They were no longer in the dark when it came to knowing how well or badly they were doing. The Hawthorne effect swung into action, and the inevitable happened. The results of cardiac surgery improved worldwide, and the greatest improvements were seen in those countries that had the most robust measurement systems. As a cause-and-effect phenomenon, this is impossible to prove. As a general rule, medicine, like everything else, gets better with time, and the improvements that followed the introduction of EuroSCORE could merely have been part and parcel of this natural progress, but the size and timing of these improvements in cardiac surgery were truly remarkable.

EuroSCORE was published in 1999 and had gained widespread acceptance in the ensuing one or two years. By 2002, a mere two to three years later, the mortality of heart surgery in many centres and in many countries had almost halved, despite the fact that older and sicker patients were being operated on. In the UK, heart surgery results are now closely monitored, scrutinised, and constantly compared with EuroSCORE prediction, and the results are published on the worldwide web for all to see (www.scts.org). The UK now boasts cardiac surgery survival rates that are among the best in the world, and if the Hawthorne effect did indeed play a part in this improvement, then EuroSCORE, a mere risk model, could be justifiably claimed to have saved up to 6,000 lives in the UK alone so far. (Nobel Prize nominating committee, please note!) Survival rates in other countries have also shown a massive improvement since the introduction of performance measurement, and the likely number of lives saved worldwide is probably several times larger.

It is difficult to prove the Hawthorne effect when other changes over time can also take credit, but it is possible and reasonable to look at what happened in heart surgery mortality as the various risk models were introduced. I did this at my own hospital, and the figure certainly and strongly suggests a Hawthorne effect in heart surgery:

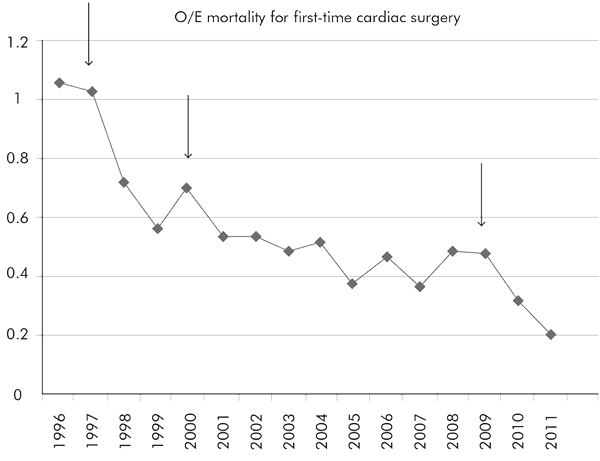
The ratio between observed (O) and expected (E) mortality at Papworth over the period during which risk models were introduced. The lower the line, the lower is the mortality (taking account of the risk profile). Each of the three arrows marks the introduction of a risk model: in 1997, Parsonnet; in 2000, EuroSCORE; and, in 2009, a tighter, modified EuroSCORE. Every single initiative was followed by a sharp drop in mortality.

Of course, for us makers of risk models, one of the downsides of the Hawthorne effect is that the risk model responsible for the improvement in outcomes falls victim to its own success. As a direct result of the better survival that follows its application for monitoring, the model becomes wildly inaccurate. By 2005, reports were trickling from some institutions that actual mortality was a lot lower than the EuroSCORE model predicted. During the following two to three years, the trickle became a flood. The model was still excellent at distinguishing between a low-risk and a high-risk patient, but its ability to measure the magnitude of that risk was inaccurate across the board. There was nothing to do but create another model, and that is exactly what we did. François Roques and I formed a new team to work on this venture, and were joined by Linda Sharples, then Medical Research Council statistician in Cambridge, now Professor of Statistics in Leeds. We collected data on more than 20,000 patients from hundreds of hospitals in over 50 countries of all continents, and recreated the model with contemporary data (Nashef 2012). This model (EuroSCORE II) is now available, and early signs indicate that the cardiac surgical community has adopted it enthusiastically.

One of the tasks of the EuroSCORE II project was to find out what exactly is a death. This is not a facetious comment: I alluded earlier to the fact that, after an operation, even death can be difficult to define. The following can all, with varying degrees of legitimacy, lay claim to the title ‘early postoperative death’. If the patient dies on the operating table, there is no argument: it is an operative death. If the patient survives the operation, but dies two days later, most people would agree that this is an ‘early’ or postoperative death. We can also define survival or death as the state that the patient is in when leaving the hospital after an operation, as this is clear and cannot be argued with, but what if the patient never leaves hospital, and goes on to die in hospital six years after an operation? Is that still a postoperative or early death? An alternative would be to say the patient is considered to have survived the operation if he or she is still alive 30 days after the operation, but even that has problems.

First, it is not much use to the patient if an operation results in complications, and the patient stays on the intensive care unit being supported by increasingly desperate measures and expensive high-tech equipment, until death occurs on day 31. Second, some patients go home and die a few days later, but by then they are no longer under the beady eye of the hospital audit department, and whoever is collecting the mortality data may never find out about the tragic events that can happen after hospital discharge. This is further complicated by the fact that many people, like Professor Paul Sergeant of Leuven in Belgium, believe, with good justification from survival data, that the true attrition rate for death after an operation does not truly level out until 90 days after an operation, not 30 days. Ninety days is an awfully long time for an audit department to track the patients, some of whom may have moved house, emigrated, or simply no longer want to stay in touch with their treating hospital because they have better things to do. Hospitals, like all organisations, are not awash with money, and many other priorities compete for their limited resources with greater clamour than the chasing of old patients around the country and beyond to see how they have fared after leaving hospital.

We therefore looked at the data that the hospitals gave us in the EuroSCORE II study, and found that all hospitals could give us 100 per cent of the data on the status of the patient on leaving hospital (dead or alive). When it came to 30 days, just over half the hospitals had data. When it came to 90 days, the proportion dropped to below half. We therefore took a drastic decision, and defined an early death as one that occurs in the same hospital during the same admission as the operation. This was arbitrary and pragmatic: these data we knew were both available and accurate, important features to consider when one chooses a benchmark. We can still learn valuable lessons from those hospitals that actually had data on patients after they left hospital. These data were very valuable in that they helped us to find out what was the attrition rate after discharge from hospital: we found that, if the mortality is 4 per cent, at 30 days it rises by another 0.6 per cent and, at 90 days, by another 0.9 per cent. As we know that the rate levels off afterwards, we can postulate that these additional risks should be proportionately taken into account when you decide to have an operation. A little risk still lingers up to 90 days, and thereafter you are probably safe. This is something to bear in mind if you ever find yourself contemplating an operation and weighing up the risks versus the benefit: most of the risk will be concentrated in the time you are an in-patient in hospital, but there is still a little bit left to go through after you go home, and this levels out when you reach 90 days.

Heart surgery today mostly has its house in order. There are at last robust and objective monitoring tools to measure the quality of surgery, even if they simply focus on the relatively crude outcome of survival. These tools are sufficient to detect underperformance, and can provide the information and impetus necessary to correct such underperformance. In the current era, a poor hospital or a rogue surgeon with terrible results will be either corrected or stopped from operating. In the United Kingdom and in many other countries, data on outcomes are routinely measured, and action is taken as soon as the data indicate substandard performance. If you seek the treatment of heart surgery for yourself or a loved one in the United Kingdom, you may not receive the best in the country, but you will certainly receive treatment that is up to a high international standard regardless of which hospital or surgeon you choose, and that is surely a comforting thought. Similar monitoring in other countries also goes a long way to ensure that heart surgery there is also likely to be of a safe standard.* In general, the more robust is the monitoring system, the safer is the surgery. Other surgical and medical specialties do not at present have anything like the level of monitoring that heart surgery has, but they are most certainly working, with varying degrees of reluctance, towards developing similar systems. My prediction is that it will not be long before all medical specialties will have robust monitoring and outcome measurements, and, when that happens, the Hawthorne effect will come into action, and the results and success of intervention in these specialties are likely to show a similar quantum leap in performance to that seen in heart surgery.

[* For instance, using AusSCORE and CuSum in Australia, or the STS score in North America.]

As well as saving tens of thousands of lives, a simple risk model such as EuroSCORE can have many direct uses. It can, for example, detect a doctor’s underperformance, and may even stop a murderer in his tracks!

Like many other countries, Britain has seen its share of serial killers over the years. Around 1890, the so-called ‘Jack the Ripper’ gruesomely killed at least five women around the Whitechapel area in East London. Perhaps a few more murders were also indeed committed by him, but that has never been confirmed because of suspicion of copycat murders by other disturbed individuals who may have admired his handiwork. In the 1960s, Ian Brady and Myra Hindley, the infamous ‘Moors Murderers’, killed five children and buried them on Saddleworth Moor in Greater Manchester. The notorious Frederick West, later assisted by his wife Rosemary, went on a rape, torture, and killing spree that lasted nearly 20 years and resulted in the deaths of at least 11 young women. Horrific as all of these murderers were, their victim toll pales into insignificance when compared with Britain’s most prolific serial killer of all time, a mild-mannered, and, by all accounts, respected and popular family doctor called Harold Shipman.

Dr Shipman was convicted for 15 proven murders over a period spanning 25 years that only ended in 1998, but he is reliably believed to have murdered more than 250 people. This is many, many more than the Ripper, the Moors Murderers, and the Wests put together. For unfathomable reasons, Shipman killed hundreds of his own patients in their own homes or in his surgery, often by injecting them with lethal doses of diamorphine (the medical term for heroin). He signed their death certificates himself, giving spurious medical causes for their demise. Despite this huge death toll, he continued to practise medicine undetected for a quarter of a century. How could this have happened in a supposedly well-regulated profession such as medicine?

At the conclusion of the final report of the inquiry into the Shipman case, the High Court Judge Dame Janet Smith specifically pointed out that there was nothing unusual in Shipman’s medical practice, such as the age and health (or otherwise) of his patients, that could possibly have explained why he had such a high death rate. Unfortunately, this observation came after the fact: until then, very little attention was paid to general practitioners in terms of measuring the mortality rates of their patients.

Following the inquiry report, an editorial comment was published in the medical journal Anaesthesia. In this editorial, the author (blessed with the somewhat unfortunate name of Dr Harmer) claimed that what happened with Shipman in general practice could not possibly happen in an NHS hospital. Dr Harmer argued that, in hospitals, doctors work in a highly regulated environment, with the slightest misdemeanour becoming common knowledge in a very short time, so that a serial killer like Dr Shipman could not possibly succeed in ‘covering his tracks’ in a modern hospital setting. My colleague Joe Arrowsmith, a consultant anaesthetist, read this editorial and was intrigued. Is it true that we would have detected a serial killer like Shipman if he was let loose in a hospital like Papworth?

Papworth Hospital already had fairly robust quality-measuring systems. One of the things we measured was risk-adjusted mortality for heart surgery. We compared our performance against EuroSCORE, and had a ‘trip-wire’: a metaphorical alarm bell would ring if any surgeon or anaesthetist had an actual mortality that was significantly greater than predicted by EuroSCORE.* This was the standard statistical test, and any surgeon or anaesthetist who ‘rang the alarm bell’ would be stopped and investigated. We also monitored all surgeons and anaesthetists using VLAD curves. These are not strictly statistical, but give a visual image of risk-adjusted performance over time. With these measures already in place, it was relatively easy to put the Shipman question to the test.

[* In this context, ‘significantly’ means that the statistics confirm that the probability of a mortality this much higher than EuroSCORE occurring due to chance and chance alone is less than 5 per cent, or, in other words, the p-value is less than 0.05.]

Joe Arrowsmith and I picked on two other colleagues as imaginary suspects (John Kneeshaw, an anaesthetist, and Stephen Large, a surgeon, who has also written an appendix to this book). Both had worked at Papworth for a long time, and had treated thousands of patients, with survival rates that were close to the average at Papworth. We turned them into virtual serial killers by developing a computer programme called Mock Unexpected Random Death Event Rate generator, an appropriate but gruesome acronym. The MURDER generator programme then randomly selected patients who were treated successfully by John and Steve, and ‘reversed’ the outcome. In other words, the computer pretended that these patients had died as a result of the treatment. We programmed it to ‘kill’ patients at random and at about the same rate that Shipman had done over his 25-year homicidal career. We then applied our standard statistics to see how long it would have taken for either of them to ring the alarm bell and be stopped in their tracks.

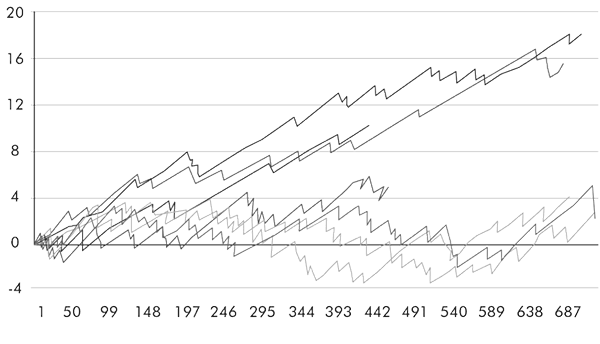
The results of the experiment were outstanding (Arrowsmith 2006). Dr Harold Shipman went undetected for 25 years, and could have conceivably gone on killing had he not become careless. In our experiment, John, the anaesthetist, was picked up after ten months, and Steve, the surgeon, was picked up even quicker, within eight months. This was purely on the basis of their patients’ death rates reaching statistical significance (in other words, a less than 5 per cent possibility of these occurring by chance). When we looked at the VLAD curves, both would have raised eyebrows and concern even earlier (see figure), probably in a matter of two to three months.

VLAD curves for serial-killer anaesthetist and surgeon. The killing starts when the curves branch out. The higher line is the true VLAD curve, the lower line is what happens to it had either of the two turned into Shipman. The arrow demonstrates when the statistical alarm bell is tripped (ten months for the anaesthetist and eight months for the surgeon), but the curves would have indicated a problem even earlier.

It is important to emphasise here that this was a fictitious scenario: both Steve and John are fine doctors with very good results. Ours was purely a computer simulation, designed to show what would happen if there was a serial killer at Papworth. There were no murders, and this simple fact was very clearly stated in the published article in Anaesthesia. Somehow, this obvious fact was not fully understood by all the tabloid newspapers, with one reporting that a serial killer went undetected at Papworth Hospital for eight months.

Of course, our quality-monitoring systems are not designed to detect serial killers, but are there to detect underperformance from any cause. What our study elegantly demonstrates is that such monitoring systems actually work. It makes a compelling argument for robust monitoring of outcomes in all hospitals, all operations, and all medical treatments in general. If we in the medical profession expect members of the public to trust us with their lives and the lives of their loved ones, then this is the least we should do.