The Four Color Map Problem – Topology turns the tables on map coloring

It had always been an unproven rule among map makers that a map drawn on a flat surface or on a sphere required only four different colors to differentiate the various countries. In 1976, the famous four color map problem was set to rest with a computer proof by K. Appel and W. Haken of the University of Illinois, but their computer proof continues to be challenged.

The problem was to prove that every map drawn on a plane can be colored with only four colors so that adjacent territories have different colors.

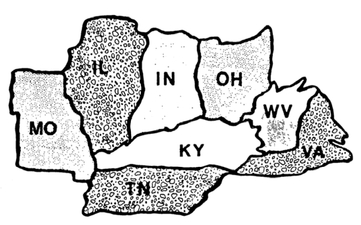
For an added twist, now consider map coloring on different topological models. Topologists study very unusually shaped surfaces—doughnuts, pretzles, Moebius shaped surfaces, and to them a sphere can be distorted into a plane by puncturing a hole in it and stretching and flattening it out. So in essence the number of colors required to color a plane and a sphere are the same. Topology is the study of properties of objects that remain unchanged when the objects are distorted—stretched or shrunk as on a rubber sheet. What type of properties remain unchanged under these conditions? Since distortion is allowed, we realize that topology cannot deal with size, shape or rigid objects. Some of the characteristics that topologists look for are the position or location of points inside or outside a curve, the number of surfaces of an object, whether an object is a simple closed curve, the number of inside and outside regions it has. So with these topological objects, map coloring is an entirely new problem since the four color map solution does not apply to them.

 

Try various map colorings on a strip of paper. Then twist it into a Moebius strip (give it a half-twist and join the ends together). Will four colors always be enough? Not likely. What is the minimum number of colors you can come up with that would work on any map. Try the same on a torus ( which has a doughnut shape). The easiest way to experiment with this object is to envision the formation of a doughnut shape from a flat sheet of paper. Color a map on one side of the paper. Roll it into a cylinder. Then imagine bending the ends of the cylinder together so as to form a doughnut. Can you determine the minimum number of colors needed for a torus?

Moebius strip.

torus