8
TIME AND CHANCE
No word came from Prince Leopoldo de’ Medici in response to Huygens’s tribute offered in Systema Saturnium, and no drawing of Galileo’s bruited pendulum clock. Had it done so, Huygens would have seen that his own invention was substantially different from, and in fact considerably superior to, anything in the possession of the Florentine court.
Although a prize for a clock that could be used to determine longitude at sea had been first announced in 1567 by King Philip II of Spain, it was the offer by the States General of the Netherlands of a reward of 10,000 florins in 1627 that had drawn Galileo’s attention to the problem. Occupied with other matters, however, it was not until 1636 that he turned to consider it properly, writing a design proposal that was duly translated and delivered in November that year. He communicated with the Dutch government through a Calvinist friend in Geneva, Elia Diodati, who had supported him in his disputes with the Vatican. Diodati in turn chose a family friend as his point of contact in Holland – Constantijn Huygens. They corresponded intermittently for the next four years, so it is entirely possible that Constantijn’s ‘little Archimedes’ became aware that a pendulum mechanism might be used to regulate the recording of time before he was even in his teens.
Galileo had devised a mechanism, but died in 1642, leaving his son Vincenzo to continue his work. Vincenzo died only seven years later, having altered his father’s design but never having built a working device. His pendulum may never have been intended to serve for a conventional clock in any case, as Galileo’s personal interest had been in timing intervals of importance in astronomy, such as transits of Jupiter’s moons, rather than daily timekeeping.
Christiaan Huygens, too, was interested in timekeeping because of his astronomy. He had in addition significant practical experience of constructing machines and a good understanding of mechanical theory. The synthesis of these skills had begun in earnest during his correspondence with Mersenne, sustained from September 1646, when Christiaan was just seventeen years old, until Mersenne’s death two years later. Their intense exchange of mathematical problems and solutions combined pure geometry with mechanical examples that gave the geometry a physical dimension. These exercises served primarily as visualizations, but also hinted at a utilitarian connection with the real world. Huygens’s analysis of the curve of the hanging chain known as the catenary, for example, proceeded by imagining weights hanging from points along the chain. Prompted by Mersenne, Huygens had moved on to investigate the ‘centre of percussion’ of different geometrical shapes, which was a problem of obvious relevance to the operation of pendulums.
A basic clock needs two things: a method of displaying the time and a means of changing the display at the correct rate. Medieval clocks used the force from a slowly descending weight or uncoiling spring to drive gears connected to hands on a clock face. A mechanism known as an escapement, often comprising a verge and foliot – a weighted spindle arrangement that repeatedly engages and releases one of the timekeeping gears – was used to regulate the speed.
Galileo had discovered that a pendulum swings back and forth with a constant period related to its overall length but notionally independent of the amplitude of its displacement from its resting position. This property of isochrony immediately suggested the pendulum’s applicability to timekeeping. The period of the swing is not completely invariable, however: an excessively high displacement oscillation takes a little longer to return to its starting point. In addition, Galileo’s law applies to a mathematically ideal pendulum based on a point mass at the end of a weightless rod or thread suspended from a frictionless pivot operating in the absence of air resistance. In reality, of course, these conditions cannot be met, and any pendulum necessarily loses energy owing to the friction in the pivot mechanism and other factors. Moreover, the rod or thread supporting the pendulum bob oscillates more slowly in summer than in winter because of the slight increase in length produced by thermal expansion.
Huygens overcame some of these difficulties by introducing a number of modifications to conventional designs. The swinging pendulum replaced the oscillating foliot. He employed a metal fork to engage with the pendulum at its centre of percussion so that the movement was as smooth as possible. It was now via this fork, rather than through gears attached to the pivot axle, that the pendulum regulated the timekeeping mechanism. Finally, Huygens affixed a pair of small, curved metal plates either side of his pendulum thread just below the pendulum pivot. These ‘wings’ (alae) or ‘cheeks’ (joues) slightly modified the path of the pendulum bob by effectively shortening the thread at the extremes of its swing, thereby correcting for the increase in period found in large-amplitude pendulum swings, and improving the overall isochrony of the mechanism.
Although his thinking about clocks appears to have begun in pure mathematics, Huygens was well aware of the important goal of solving the problem of determining longitude at sea. The Alkmaar surveyor Adriaan Metius, brother of the telescope pioneer Jacob, had proposed as long ago as 1614 that some kind of seagoing clock might provide the solution to this perennial problem of navigators, and in March 1655 Huygens himself had commended to the States General a promising invention for determining longitude, devised by a Polish fellow Cartesian, Johannes Placentinus. Now, he felt he had his own breakthrough. On 12 January 1657 he bragged to his mentor Frans van Schooten: ‘In recent days I have invented a new piece of clockwork that measures time so accurately there is no small hope that it will permit the determination of longitude with certainty if taken to sea.’
Although Huygens’s confidence with regard to marine chronometry turned out to be misplaced, and it was to be another century before the longitude problem was finally cracked, his innovations did bring a very great improvement in timekeeping accuracy, such that he can fairly be described as the inventor of the functional pendulum clock. His design was accurate to within a few seconds a day, roughly a hundredfold improvement in accuracy over previous clocks. Perhaps, though, the improvement was not much appreciated in a period when a sandglass with hourly gradations was thought adequate for household timekeeping, and the sound of a ticking clock in the next room was popularly believed to be a harbinger of death.
Huygens assigned the patent that he was awarded for his design to the Hague clock-maker Salomon Coster. Several tidy little clocks that Coster made in 1657, which are now on display in various museums, have short pendulums with spherical brass bobs and all the workings hidden inside ebony cases. In larger clocks, makers sometimes chose a pendulum of about nine and a half Rhenish inches (units of length commonly used in Holland at this time) because it gave a period of oscillation of exactly one second. A thirty-nine-inch pendulum – four times the length – has double this period, two seconds. In an indication of the importance he attached to the accurate measurement of time, Huygens even hoped to redefine distance in terms of the standard foot in relation to this fundamental unit of time, proposing that one third of this length be called the pes horarius or ‘time foot’. However, most of the clocks that Coster continued to make did not incorporate Huygens’s improvements, as great accuracy was not an important consideration for his customers, and it is likely that Huygens turned to other makers bound by agreements to secrecy in order to further his experiments with precision timekeeping.
Huygens wrote up a brief history of time along with a detailed description of his invention in a treatise titled Horologium, which he presented in 1658 to the governors of Holland, who by this time included his former mathematics classmate, Johan de Witt. In it, he made a disparaging reference to the ‘so-called science of longitude’ and promoted the merits of a clock-based solution to the problem. He knew that his innovation would be of immediate interest to astronomers, though, and he sent copies of Horologium to astronomer friends such as Hevelius in Danzig. But perhaps nothing gave him more pleasure than the praise of a senior figure such as Pascal, who wrote that, since receiving Horologium, ‘I have been among its leading admirers’.
![]()
Horologium and the clocks built according to its specification were to become almost immediately obsolete, however, and it would be thanks to a further discovery made by Huygens himself.
One of the curves that Huygens had discussed in his youthful exchange of mathematical problems with Mersenne had been the cycloid. Known as the ‘Helen of geometry’ for its beauty and its many surprising properties, as well as for its capacity to provoke disputes among mathematicians, the cycloid was a puzzle because, like the catenary, its form could not be described by algebra. The cycloid is generated by the path of a point on the circumference of a circle as it rolls along a straight line, but the sharp cusp produced in the trace each time the point meets the line makes it immediately apparent that it does not belong to the family of curves that are always smoothly changing, like the ellipse of a planetary orbit or the parabolic path of a cannonball. Yet this curve, so readily generated by the rolling of a simple wheel, surely had some fundamental relation to nature, which might be revealed by the discovery of some correspondingly simple mathematical expression.
Pure geometry had a significant allure for practical investigators as well as mathematicians. Just as a wheel rolls best when it is a perfect circle, forms pure in shape were thought to have intrinsic physical merits. Pure geometries promised conceptual clarity – and perhaps optical clarity, too. When spherical lenses – lenses with one or both surfaces comprising part of a sphere – were found to be inadequate for some purposes owing to spherical aberration, lens-grinders tried the next most perfect curves they knew, such as paraboloids and ellipsoids. Around the time, in 1635, that Huygens’s father and Descartes were struggling to make a hyperbolic lens, a Dutch astronomer, Martin van den Hove, known as Hortensius, once a student of Snel and Beeckman, even tried to make a lens in the form of a cycloid.
For his part, Huygens had long ago set aside the cycloid problem. But his interest was renewed in 1658 when Pascal pseudonymously issued a challenge to Europe’s mathematicians to characterize the cycloid by expressing attributes such as its centre of gravity and its area in algebraic terms. Christopher Wren came closest to finding a solution, when he succeeded in rectifying the curve (that is, he found a way to describe the area under the curve as a sum of squares of different sizes), but no prize was awarded. For a moment it even seemed that Pascal himself – under his real name – was claiming to have found the answer, until it became clear that he was merely communicating some additional thoughts on the problem.
Huygens was busy at the time trying to improve technical aspects of his clock design, in particular its accuracy. This was largely a matter of tedious trial and error, for example involving setting two clocks running side by side for comparison, with large and small pendulum swings respectively. Eventually, he was able to write that he had ‘so finely adjusted two clocks in this way that in three days they never had a difference between them even as much as seconds’.
Huygens found this phase of work troublesome because, although he was the inventor, he was not the maker of these clocks. While he could doubtless improvise for himself simple modifications such as adjusting the curve of the metal ‘cheeks’, he was dependent on his skilled suppliers, who included not only Coster in The Hague, but makers in a number of other Dutch cities. Keeping control of their work was not always easy. One maker called Josina in Amsterdam owed him some components but would not reply to his letters. ‘I don’t know how the sow can be so insolent when she well knows that I am still due to pay her 50 guilders,’ Huygens complained to his brother Lodewijk. There is also a possibility that Huygens instructed the leading clock-maker in Paris, Isaac Thuret, a more skilled and scientifically minded man than Coster.*
A fine draughtsman, Huygens was able to supply drawings giving enough information for such craftspeople to work from. But because he did not actually make the devices himself, he was always vulnerable to unscrupulous behaviour by his suppliers. Coster, for example, carried on his trade making unimproved clocks, but incorporated features resembling Huygens’s ‘cheeks’ as a kind of modish branding. When another supplier, Simon Douw of Rotterdam, simply copied the clock Coster had built, claiming it as his own, it enmeshed Huygens in a legal dispute between the two makers – ‘a most thankless business these thieves have caused me’.
His Parisian correspondents only added to his worries. Rumour came that Roberval had a clock of his own design, but Huygens could find out no more about it because, as Boulliau told him, Roberval had insulted his host at a recent gathering, telling Montmor in his own house that Descartes had ‘more wit than he’, and as a consequence no longer went along to the meetings. Clock-makers in Paris were just as rapacious as those in Holland, and friends warned Huygens that there too he was in danger of being ‘robbed of . . . the glory of the invention of the Pendulum’.
All this intense competition shows that Huygens was more closely involved in ‘trade’ than might be expected of a man with his social connections (and than his father may have wished him to be). He fielded frequent enquiries from his scientific friends in Paris wanting to know if he had catalogues and price lists for his clocks. Boulliau wrote under the clear impression that Huygens was selling direct: ‘I beg you to tell me the price of your clocks both ringing and without ringing, with weight and with spring.’ Huygens responded promptly with prices of five different designs: a thirty-hour spring clock would cost 80 Dutch silver pounds, for example, 120 with ringing.
In his continuing effort at improvement, Huygens had discarded the metal ‘cheeks’, having realized that they would lead to inaccuracies in any shipboard clock when it was tilted over, as it would be aboard a heeling vessel. Meanwhile, he sought other means of regulating the pendulum swing. The core problem remained: what pendulum path would produce perfectly isochronous oscillation? There had to be an answer, for modifications could be made to the path to produce swings both that were disproportionately slow and that were disproportionately fast. Somewhere in between lay the tautochrone, the curve for which the displaced pendulum would take the same time to return to the centre no matter where it started from. Huygens finally discovered the happy medium by geometrically comparing the fall of an unaltered pendulum with the acceleration of a body in vertical free fall. On 1 December 1659 he was able to pronounce that the tautochronous pendulum path was in fact nothing other than an exact cycloid. It was ‘the happiest of all the discoveries that ever fell to me’.
![]()
The distraction of Pascal’s purely theoretical challenge must have contributed to Huygens’s revelation. He was pleased to have found the key to perfectly uniform timekeeping, and still more satisfied to find that pure mathematics lay at its heart. Whereas his 1657 pendulum with its ‘cheeks’ constraining the path of the bob had been arrived at empirically, this new knowledge was the product of rigorous analysis and possessed a fundamental truth as well as great potential utility.
More was to come, however. There now arose the question of how to make a pendulum bob move along this ideal path. As Huygens went back to trials with various metal plates, he soon found that the shape that would produce a cycloidal pendulum path was itself another cycloid. For a man of Huygens’s acute sensibility to the connections between mathematical geometry and the physical world, this was a true epiphany. Huygens had his reward for his loyalty to the classical tradition of geometric analysis. It was this visually based methodology, rather than newer algebraic procedures based on numbers and functions, that kept him mindful that curves with special properties often had manifestations in the physical world, and that enabled him to find synergetic connections between theoretical forms and practical applications. It was surely most satisfying for him to find not only that a mathematical exploration prompted by a matter of practical necessity had delivered up a geometric revelation of great intrinsic elegance, but also that this revelation immediately suggested both further practical applications and new theoretical avenues to explore.
Alongside the mechanical project of drawing and fabricating precision cycloidal cheeks for his clocks, Huygens began to pursue a more general, purely mathematical, investigation of the theory of curved lines and their fundamental, but not always obvious relations to one another.* Having found that one cycloid can be used to generate another cycloid, he went on to characterize the curves that could be likewise evolved from the parabola and the ellipse. From there, he was able to establish a general formula for the relation between any curve and its evolute companion. As in his work on probability theory, Huygens moved with inexorable logic from simple cases to more complex cases, and from there to the general rule in a way that reveals him as a progenitor of modern scientific thinking. He also described the relation between the length of a pendulum and its period of oscillation – as found by Galileo – in terms of a mathematical equation for the first time, although, in typical fashion, it was to be many years before Huygens published the results of these practical and theoretical investigations.
![]()
The clocks on Dutch churches are so ubiquitous that it is easy to assume they are as old as the buildings themselves. Mostly, they are not. The church in Scheveningen now known as the Oude Kerk was constructed just behind the beach in the mid-fourteenth century. It had already stood for two centuries when it appeared in an illustration made by Adriaen Coenen for his celebrated Visboek, a fabulous bestiary of marine life. His sketch, made from a boat out at sea, shows the church spire with the hummocks of sand dunes rising up all around it. There was certainly a clock in the tower by 1500, because on the morning of the fourth of March that year the Hague magistrate went to the beach and issued a proclamation that fish were to be traded there only between the hours of six and nine in the morning and two and seven in the afternoon as rung by the clock bell.
Huygens’s work with clocks was not restricted to small devices for scientific purposes. In January 1658, he and Salomon Coster embarked upon a refurbishment of the Scheveningen church clock, making a number of alterations to the mechanism in an effort to improve its timekeeping. The two men knew each other well enough by this stage in their collaboration to use familiar forms of address, although their relationship was still clearly one of client and supplier. A short letter from Coster addressed to ‘Mijn Heer Christiaen’ reports on progress thus: ‘The mechanism at Scheveningen is now running, and ran all night, the Bob has a weight of 50 pounds, But I think to hang something less and to alter its spring and chain somewhat. It has as a guess lost a quarter in 14 hours. I am thinking of going there again tomorrow afternoon.’
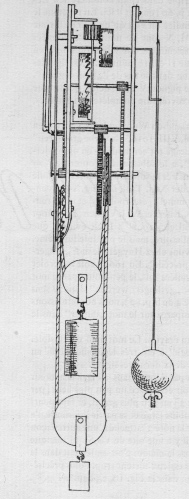
Huygens described the improvements he was making in a long letter to Jean Chapelain. A short length of silk thread supported the pendulum at the top to allow it to swing freely. The pendulum itself was a twenty-four-foot iron bar and the fifty-pound bob at the bottom was made of lead. The swinging action of the pendulum was converted to the rotary motion of the balance as frictionlessly as possible by means of a sliding brass rod between the two. A clock that Huygens and Coster went on to develop for the imposing cathedral tower at Utrecht, the tallest in the Netherlands, was on an even grander scale, although both church clocks had simpler wheel-trains than the men’s smaller brass timepieces. With the addition of several precisely drawn diagrams, Huygens’s description of the Scheveningen design was admirable in its clarity, perhaps because he knew he was writing to a poet and not to one of his more mechanically minded confreres. However, if clear communication – to Chapelain, and through him perhaps as a salutary example to the sophists among the Montmor circle – had been his intent, he was not entirely successful, for Chapelain replied to Huygens: ‘As for the construction of the clock, I admire more than I understand, either because of the obduracy of my intelligence or because of your too succinct exposition.’
![]()
To a physicist, as opposed to a clock-maker, a pendulum is simply a special case of a body in motion. To Huygens, it was a tool to develop his thinking about masses and the factors that cause them to move. From practical consideration of real pendulums and their mathematically ideal analogue, a weightless rod with a bob at the end whose mass is compressed to a single point, he developed a thorough analysis of the centre of oscillation of any object. He generalized his analysis with reference to other practical situations, such as the motion of bodies of various shapes floating in water (perhaps an especially Dutch interest).
Another priority related to pendulums and to any falling object was to establish the value of acceleration due to gravity, which was then conventionally framed by natural philosophers not as a constant of acceleration but as the distance travelled in one second by an object in free fall. Galileo, Mersenne and others had been defeated by this problem, not least because it had been difficult to agree on the precise magnitude of a second. Though hampered at first by an attempt to fit his analysis into a model of Cartesian vortices, Huygens eventually succeeded in measuring the quantity using a special conical pendulum mechanism; it came to fourteen feet (later revised to over fifteen feet, which corresponds well with the modern value of the gravitational constant g equal to 9.8 metres per second per second). The swingball-like device he used for this task also enabled Huygens to relate the outward impulse of the rotating bob, described qualitatively by Descartes, to the downward (and therefore inward) tendency owing to gravity studied by Galileo. This swiftly led him to a new description of both circular motion and fall under gravity in mathematical terms far beyond those of his distinguished predecessors. Implicit in his work was the idea that force gives rise to acceleration, which Isaac Newton would later articulate as the second law of motion. By uniting the practical work of clock construction with a readiness to conduct experiments and make measurements and a belief in the mathematical basis of mechanical phenomena, Huygens had become the first person to produce an accurate measurement of a physical constant.
Despite this breakthrough, a true understanding of the concept of force still lay some way in the future, even though Huygens did invoke the word in the title of the account of his work at this time, De vi centrifuga (‘On Centrifugal Force’). He was still worried, however, about some of the implications of his findings, and once again put off publishing. At the head of an early draft of the work he put a quotation from one of Horace’s epistles to Maecenas: ‘I was the original, who set my free footsteps upon the vacant sod; I trod not in the steps of others.’ He sensibly omitted the Roman poet’s vainglorious next sentence: ‘He who depends upon himself, as leader, commands the swarm.’
![]()
It is a characteristic of Christiaan Huygens’s intellectual life that he worked on many projects at once that might seem diverse to us now, but which to him were all facets of the same urge to learn more about the mechanics of the physical world. This was never more the case than during the first flourish of his maturity in the late 1650s, when he was working in parallel on Saturn, clocks and mathematics, constantly shifting from telescope to drawing-table and drawing-table to workshop. It is clear how much the working out of Saturn’s ring and his clock’s pendulum owe to his facility with the geometry of curves. Yet at the same time, his mind was also wrestling with a mathematical question of a very different hue: the problem of chance.
![]()
Three men are at the gaming table: a soldier and a middle-aged burgher are seated, smoking their pipes, gazing intently at the tabletop; the third braces himself against the table and prepares to throw the dice. The play has reached a pitch of expectation, and two capped peasants have come to peer over the men’s shoulders at the action, thickening the air with tension.
David Teniers II produced this painting around 1640. It is known as The Gamblers, or more exactly in Dutch as De Dobbelaars, the dice players. It was a standard artists’ subject in genre painting, and the setting, depicted in shades of brown and softly lit, suggests only the world of routine activity and simple pleasures. The painting is like many others made by the same artist after he took his own gamble and switched from grand biblical panoramas to domestic scenes. There is no movement to ruffle the calm; just the suspense of the throw about to be released.
Games of chance had a particular status in the Calvinistic republic. Whereas chess was deemed virtuous, demanding intelligence, wisdom and stamina, dice was clearly the opposite: trivial, ephemeral and governed by chance alone. Play might be willingly entered into by both sides, but it involved needless risk and was the antithesis of the prudent enterprise encouraged at all levels of Dutch society. The best that could be said for it was that it was a harmless indulgence and a way of keeping youngsters amused. University students were said to be especially fond of dice.
Yet the element of randomness made it something more, too. Gambling was routinely denounced from the pulpit, but the more imaginative clergy understood that casual demonstrations of the operation of laws of chance might serve to impress upon people a notion of divine fate, and so quash dangerous thoughts about the existence of free will. Teniers at this time was the serving kapelmeester, or director of music, at Sint-Jacobskerk in Antwerp; he would have understood these nuances.
Then, of course, there was money. Throwing dice quickly becomes dull unless there is betting on the outcome. The pecuniary aspect, and the chance that it brings of undeserved gains or considerable losses, makes play immoral, though only relatively so if the stakes are kept low. The artist is not taking us to one of those dives where more reprehensible games were played, obliging players to down drinks to the value of the number they had thrown; there is no liquor here. Teniers does not want to portray anything sinful, according to one biographer. He is fully aware that ‘thoughtful reasoning is useful for sharpening the mind’, and that the game ‘teaches one to go with fortune or adversity’.
Although these genre paintings often contain the sanctimonious or satirical implication that more is at stake than a wager on a table, there is no moralizing here, no pregnant symbol of foolishness or depravity lurking in the corners of the painting. Yes, an extinguished candle rests on the mantel and a broken pipe lies on the floor, but clay pipes break all the time, don’t they?
And the money? Similar, but unequal, wagers lie on the table, along with a piece of chalk to keep the tally. Many coins circulated in the United Provinces – ducats and national dollars of the independent republic, pieces of eight dating back to Spanish days, and numerous smaller divisions of all of these. Each of the players has some gold pieces and some silver. It is hard to be sure, but the player on the left appears to have wagered two ducats, three rijksdaalders and one schelling, the equivalent of 21.8 guilders. The other player has put down two ducats, one rijksdaalder and four schellings, a total of 17.2 guilders. (These sums would have a purchasing power of about €200 today. If you cleaned up here, you might have enough to buy a small Teniers.) At all events, we can see that the play is finely poised. It has reached a crucial stage. Why else the unbidden spectators?
![]()
Playing dice soon passed from fashion in smart Dutch society, although this was not the case in France, where church and state were more indulgent and gambling of many kinds flourished along with other modes of conspicuous consumption. On his first visit to Paris, in July 1655, Huygens may not have spent time at the gaming tables, but he was swiftly caught up in the lavish whirl, soon writing to his father to complain that his money was running out with all the clothes he was having to buy. ‘By arranging so many visits for us, I pray you not be astonished at the expense we are incurring, it being a sure thing that it’s necessary to do it in order to mingle with men of quality.’
The mathematicians Huygens met on this occasion – Roberval, Mylon, Carcavi and others – were chiefly engaged in developing methods of calculating complex geometric curves, a field in which he too was notably adept. He was readily drawn into their discussions, therefore, but these must have soon turned to other mathematical topics, for he returned to The Hague in December determined to make his own contribution to the very different matter of probability and the laws of chance.
Huygens had not sought out Pascal when he was in Paris, because he had been advised, a little misleadingly, that this greatest of the French mathematicians had lately given himself over entirely to theological study. Pascal was in effect the founder of the mathematical study of probability, which had begun naturally enough at the gaming tables of Parisian salons, but which he soon extended into matters of greater existential significance. The philosophical argument known as Pascal’s wager uses betting logic to support the existence of God: why would anybody not take the gamble of faith, Pascal suggests, a gamble where, if you win, you win everything, and there is nothing to lose? Huygens’s visit to Paris came just a year after Pascal had taken up the subject in a fruitful correspondence with Fermat over the ‘problème des points’, or how to divide the stakes fairly in games of chance. This is a clearly a matter of great practical concern to regular gamblers, but it is an appealingly tricky problem for mathematicians, too, because of the uncertain advantage that may accrue to one or another player if unequal amounts have been wagered or an unequal number of turns taken by the respective players during the progress of the game.
Teniers’s picture, painted some fifteen years before Christiaan’s visit to Paris, hangs in the Rijksmuseum in Amsterdam, and in rooms nearby there are fine engraved glass and silver dice cups from the same period: gambling was clearly not only the vice of low-lifes and addicts. Yet Huygens surely had no need, as the Lombard polymath Girolamo Cardano apparently did a century before, to use his superior awareness of the odds to augment his income. It was the quality of the problem that drew him; that and the wish to prove himself to his illustrious Parisian friends.
In his renowned exploration of play, Homo Ludens, Johan Huizinga explains that a game is an entirely voluntary transaction between the actors, more so than most trades in daily life. More important still, it is inconsequential: it has no repercussions beyond the gaming table. Nothing rides on the outcome beyond that which is staked – even if this is all one has, as in the case of the reckless gambler. It is this very inconsequentiality which makes it such a good subject for painters. And for mathematicians, too: for a game to be a true game, and not merely a fiasco or the prelude to a fight, it must have an unpredictable outcome, but an unpredictable outcome within certain bounds of expectation. It is these two factors in combination that make dice a rewarding problem for mathematical interrogation.
In that summer of 1655 when Christiaan was in Paris, Pascal and Fermat had not yet published any of their work on probability theory. However, the gossip he heard there was clearly enough to stimulate his interest in this new direction. Back in The Hague, he spent the next few months in playful correspondence with his new Parisian friends, tossing out little problems and chasing them for their answers, keen to know whether his methods were correct. By April 1656 he was able to tell Roberval, Mylon and Carcavi that he had written down his ‘foundations of the calculus of games of chance’, and that his old tutor Frans van Schooten wished to print it.
The work appeared as an addendum to van Schooten’s fifth volume of mathematical exercises, first in Latin, and a little later in Dutch, as Van Reckeningh in Spelen van Geluck (‘On Calculation in Games of Chance’). Huygens leads the reader through fourteen worked examples of gradually increasing difficulty. He begins by pointing out an important truth about the simplest chances, which is that if a number of outcomes are equally likely, then the value of any outcome is the reciprocal of the number of possibilities. Because there is a finite number of possible outcomes of a particular action in a game, such as tossing a coin or throwing a die, the sum of the values of each outcome must equal the total value, namely unity. In other words, if two outcomes are equally likely, such as heads or tails of a coin, then the value of either outcome is simply one half. When a sum of money is at stake, then the value of either outcome is half of that sum. Huygens quickly develops his analysis for any number of equally likely outcomes and for situations where the outcomes have different known chances of occurring.
This is important groundwork for the more complicated situations that he presents next. What if a game is stopped after I have played one more throw than my opponent? How is it fair then to divide the stake? For the simplest possible case, where one player has taken two turns and his opponent only one, the answer depends on who went first, and the stakes should be split either fifty-fifty or in the proportion of three-quarters to one-quarter. Again, Huygens builds up from this simplest case to look at more complex situations, such as where a player falls two turns behind, or where both players have missed turns, or where one player out of three at the table misses a turn. This leads him stepwise to a general calculus capable of handling any number of players missing any number of turns.
Combining the known probability of an event with its monetary value allows for a fair division of the spoils. This concept would be articulated in greater mathematical detail more than sixty years later, in 1718, by Abraham de Moivre as ‘expectation’. It is striking that Huygens’s imagination is clearly stimulated by scenarios that would arise in real game play – a player might easily leave the table for a turn or two. But the fact that he then moves on to generalize his method for situations far less likely to arise in reality shows the mark of a true mathematician.
Huygens next turns from the problem of fair division of the stakes to games where the exact numbers thrown up by the dice are important. We know that the odds of a given number turning up when we throw a true die are one in six. But how many throws should we expect to make before getting a six? He works it out: by the fourth throw the odds tip in your favour; by the sixth throw, you have an almost two-to-one chance of having obtained the desired result. How many throws to get a double six using two dice? Huygens works it out again in longhand arithmetic; although he could have got the answer more readily by employing logarithms, it seems that this relatively new technique was not included in van Schooten’s teaching.
After these warm-up exercises, Huygens considers a regular game played with a pair of dice. The scenario is that I win if I throw a total of seven, but my opponent wins if he throws ten, and if neither of these numbers comes up the stake is split equally between the players. For those of us who avoid casinos, the proposition appears distinctly unappetizing: the odds of a seven are one in six; the odds of a ten, one in twelve; it would seem clear who holds the advantage. But the important thing here is the order of play. I go first: if I fail to roll seven, my opponent still has some chance of recouping his stake. My combined chance of either winning on the first throw of the game and taking both stakes, or of losing that throw and relying on my opponent to lose his throw too and then recovering his stake only, leaves my opponent with the overall expectation that it is in fact he who will finish to the good (in a ratio of thirteen to eleven).
The final scenario that Huygens examines concerns the more finely balanced game that ensues when players continue by turns until either the first player throws a seven or the second player throws a six. This is a variant of the game of hazard, popular throughout Europe in the seventeenth century, from which we get the expression ‘at sixes and sevens’ as well as the word ‘hazard’ in its general sense. Here, although the first player is slightly more likely to throw a seven than the second is to throw a six, the overall expectation after repeated turns works out to be narrowly in favour of the second player by a ratio of thirty to thirty-one.
Huygens ends the Reckeningh by considering a few more problems involving dice, schijven (discs that are black and white on opposite sides), and cards, in response to challenges issued by Fermat and others. Thanks to van Schooten’s enthusiasm for his protégé, the long paper appeared in print promptly, which was not the case for all of Huygens’s work. In Dutch, it would reach a local readership; in Latin, it would be universally accessible to scholars. It won praise from the French mathematicians for whom, in a sense, it was written, and from the English mathematician John Wallis, and later also from the German mathematician and philosopher Gottfried Leibniz, and for more than fifty years it remained the only introduction to the theory of probability in existence.
![]()
In later life, Huygens returned occasionally to the mathematics of chance events, as the need to understand matters of risk gained importance in many areas of Dutch commercial life with the growth of sea trade and the introduction of marine and other forms of insurance. On one occasion, in 1669, his brother Lodewijk, then employed in the retinue of the Dutch ambassador to Spain, raised the problem of predicting mortality given a person’s present age. His enquiry was prompted by the recently published Natural and Political Observations Made upon the Bills of Mortality, a work of early epidemiological importance written in 1662 by John Graunt, who had used historical weekly death notices in London parishes as a statistical database to predict the likely progress of the plague if it were to break out in the city, as it did three years later, in 1665. Christiaan advised his brother on a better way to interpolate between infrequent data points. For example, if tables of mortality show the probability of newborns surviving to age six, sixteen, twenty-six and so on, how does one estimate the life chances of a person already aged ten or twenty? Christiaan also suggested some more entertaining variants of such problems: ‘A man of 56 years marries a woman of 16 years, how long can they live together without one or the other dying? Or if I had been promised 100 francs at the end of each year they both survived together, for how much would it be right to redeem this obligation?’ Such puzzles might seem flippant, or even distasteful, but they begin to demonstrate the applicability of mathematical methods of estimating probability to matters of social consequence, which were to lay the foundations for scientific demography and provide a rational basis for the calculation of life insurance premiums.
In the late 1670s, during his prolonged residency in Paris, Christiaan found a new game in town. Recently introduced from Venice, basset was a card game in which punters bet unlimited stakes against a taillère or banker on such ruinous terms that play had to be confined by law to the nobility, and even wealthy players were frequently bankrupted. Christiaan joined with the leading French mathematicians to try to calculate just how great the house advantage was. This concerted effort to establish the certainties underlying games of chance helped to transform a delinquent pastime into a sound commercial prospect. On this new footing, gambling could be taken over and run, professionally if not always legally, by operators who could be confident of making a steady profit.
![]()
At the same time as demonstrating that the mathematics of probability might have social consequences both trivial and profound, Huygens was at work on a practical invention that would prove to be of similarly ambivalent application. This was the magic lantern. Nothing Christiaan invented ever delighted his father more. The device appears to have been demonstrated by him at the family home one dark evening in 1659, a time when he was also experimenting with arrangements of lenses for telescopes as well as making pendulum clocks. It must have brought to his father’s mind the hazy optical projections produced by Cornelis Drebbel in London more than thirty years before.
Huygens’s apparatus displays the functional elements of a twentieth-century slide projector. A curved mirror is placed behind a source of illumination, a candle, in order to bring the maximum amount of light to pass through a condensing lens, which disperses the light onto a translucent glass plate. Two further lenses then project the luminous image on the plate for viewing on a distant screen. A rough diagram sketched by Huygens much later and labelled ‘laterna magica’ shows a similar but simplified design that makes use of only two lenses.
Drebbel’s early-century contraption appears to have been a somewhat superior version of the camera obscura, already in widespread use by artists. Many variations were attempted before Huygens addressed the subject. In 1646, for example, the Jesuit polymath Athanasius Kircher described a means of projecting an artist’s drawing using artificial light, which may have worked by capturing the light reflected from a sheet of polished metal engraved with the design. Huygens’s innovation differed crucially from these precursors in bringing together both a source of artificial light and a transparent glass plate bearing the image to be projected.
With his experience of lens-grinding and clear understanding of the optical principles involved, Huygens was able to produce images of superior quality, even using nothing more than candlepower. Primitive projections and shadow-play were popular features of fairs and markets at the time. Trompe l’oeil and theatrical image-making were facets of a broader culture in which the boundary between truth and illusion was blurred for public titillation. Such entertainments were not without a subversive and dangerous aspect, feeding popular scepticism about what was real and what was not, and even raising atheistic doubts in the minds of the faithful.
Perhaps seeing no serious use for it, Christiaan was soon bored by the possibilities of the lantern. But Constantijn’s fascination with the device developed into an obsession. In 1662, he suggested that his son make a new instrument for demonstration to Louis XIV. When Christiaan demurred, feeling the project beneath his dignity, it seems that Constantijn hinted that he might show the thing himself at the French court. Unable to refuse his father’s wish, Christiaan reluctantly set about the work with the engineer Pierre Petit. ‘You would not believe how much trouble I take over such trifles, which are already old news for me,’ he moaned to his brother Lodewijk.
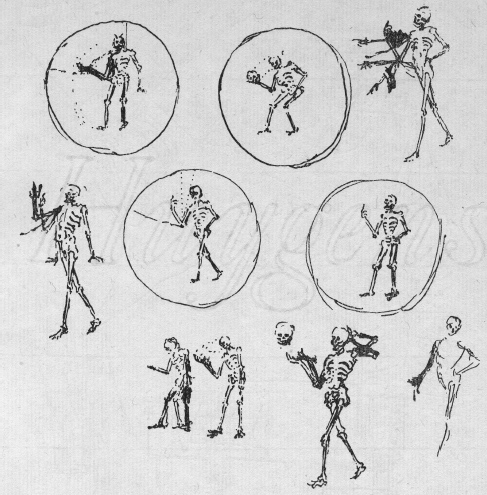
In keeping with the melodramatic expectations of the medium, Christiaan even drew a series of jaunty figures of a strolling skeleton for transfer to glass plates, loosely copied from Holbein’s famous series of woodcuts The Dance of Death. Petit started to refer to the device as the ‘lantern of fear’. Huygens’s drawings show slight shifts in the skeleton’s pose as it doffs its skull and performs other gestures, which suggests that he may have intended the plates to be switched in rapid succession in order to produce an illusion of animation. Huygens may also have produced plates depicting members of his family, as he requested a drawing of Lodewijk at this time, ‘so that I can see what you look like without a wig and greasepaint’.
A few weeks later, ‘since I cannot think of an excuse for avoiding it’, he packed off the requested magic lantern to his father in The Hague. Then he had an idea. He added a note to Lodewijk:
But when it arrives, if you see an opportunity, you could easily render it incapable of working, by removing one of the 2 lenses that are close to each other, so that 2 still remain, since there are 3 in all. I will plead ignorance that anything is missing . . . this is all for the best; because I think it does not befit my Father to make such puppet-play at the Louvre . . . As for the plates, I do not see why they make you so very afraid, for at least he will not show them to the King.
Christiaan’s exasperation with the magic lantern only grew. It did not appear to him to open up any scientific possibilities, and did little to inform his later work in optics. The basics of the design were in any case easily copied, and many did so. On this occasion, at least, Huygens was more than happy to relinquish his claim to the invention. ‘I am prepared to make [my father] Spyglass, microscope and anything he would wish, except the lantern, the creation of which ought to be counted inter artes deperditas [among the lost arts].’
![]()
After his intense period of activity during 1659 – when, besides the trivial pursuits of dice and lantern shows, he had described the concept of centrifugal force, established an accurate value for the constant of gravitational acceleration, perfected his pendulum clock and prepared detailed texts on both topics, as well as publishing his treatise on Saturn – it seems that a family wedding was not what Christiaan Huygens felt he needed in his life. He bemoaned the several days lost on the ‘solemn follies’ of his sister Susanna’s marriage to her cousin Philips Doublet in April 1660.* His mind was clearly elsewhere as he accompanied his aunt and other members of the family in following the bride up the aisle in the New Church by the Delft canal in The Hague.