© Springer Nature Switzerland AG 2021
B. G. Sidharth et al. (eds.)Fundamental Physics and Physics Education Researchhttps://doi.org/10.1007/978-3-030-52923-9_10

10. Innovation of Curriculum and Frontiers of Fundamental Physics in Secondary School: Research-Based Proposals

Marisa Michelini1  
(1)
Physics Education Research Unit, DMIF, University of Udine, Udine, Italy
 
 
Marisa Michelini
Email: marisa.michelini@uniud.it

Abstract

Conceptual knots in classical physics are often cited as motivation for the exclusion of modern physics in secondary school, but innovation in secondary school physics curriculum is a need for many aspects. The new ways of learning require new methods and active learning able to produce competences and not only knowledge; the laboratory work has to be integrated in every day school activities, as well as the contribution of ICT in the teaching/learning process; the new topics related to the physics of the last century is the main content need. Research is an urgent need in finding ways for integrating modern physics in vertical perspective in the curriculum, by means of new active methods to avoid the reductionist attitude to add not more than notions on special relativity and quantum physics as final topic in the curriculum in informative or narrative way. Modern physics in secondary school is a challenge which involves the possibility to transfer to the future generations a culture in which physics is an integrated part, not a marginal one, involving curricula innovation in a way that allows the students to manage them in moments of organized analysis, in everyday life, in social decisions. In the theoretical framework of the Model of Educational Reconstruction, we developed research-based educational proposals focused on contributions to the practice, developing coherent learning paths in vertical perspective. Design Based Research integrated with research and developments of new tools and studies on conceptual change are carried out to produce learning progression and finding ways to offer opportunities for understanding and experiencing what physics is, what it deals with, and how it works in operative way. Empirical data analysis of student reasoning in intervention modules supports proposed strategies. In this chapter, we present our research methods, we list the main path proposals prepared and implemented, and we describe in detail two of them: cross section and phenomenological approach to the superconductivity.

Keywords
Modern physicsCurriculumInnovationPhysics education research

10.1 Introduction

Innovation in Physics curricula in Secondary School is a need for many different reasons and aspects: (1) methodological aspects and strategies related to the need of student’s active learning promotion (McDermott 1993, 2008; Başer 2006; Mazur 2009; Deslauriers et al. 2011; Maloney 2011; Pizzolato et al. 2014), (2) multimedia role and relative contribution in learning process: it can be a simple support in teaching/learning in many ways integrated in school activities as learning tools (Wagner et al. 2006; Hennessy et al. 2006; Debowska et al. 2013), (3) experimental explorations or lab experiments to be integrated in an active learning process (Sokolowska and Michelini 2018), as well as (4) work activities integrated in the curriculum (Buongiorno et al. 2017) and (5) new contents to update curriculum contents (Constantinou and Papadouris 2008; Pavlin et al. 2013; Michelini et al. 2014a, b, c, d, e, f).

In the last 30 years, one of the main discussed content area is those of Modern Physics (Aubrecht 1989; Gil and Solbes 1993; Hake 2000; Ostermann and Moreira 2000; Silva 2015; Michelini et al. 2017). Modern Physics is now a chapter in the secondary school textbooks of many countries in the world, but it appears often as a final topic, added to the usual contents of a physics manual. Related contents are often organized in a traditional way, treated as information on the main ideas and research results eventually accompanied by a story telling of the main steps in the discoveries. The main topics treated are special relativity and physics of quanta story.

The different research areas aren’t clearly identified.

The frontiers of fundamental physics topics are proposed in informative way as structured notions, in a static framework, without an in-depth discussion of the new concepts and of the problematic issue. There is a lack of discussion of the crucial aspects, of the formal aspects, of the motivated theoretical choices, and of evidence-based results.

Material science physics, for example, find some role in the proposed interpretative models of electrical and thermal conduction, but updated research topics, research questions, methods, and characteristics of the research do not appear.

High energy physics, when not omitted, is treated in even more reductionist and informative way. Cosmology is sometimes introduced in narrative way.

Additional available resources for teachers are the materials prepared for outreach or the presentation of research projects for popularization goals, which do not contain proper examples for educational approaches. For not expert in the specific field is very difficult to adapt this material in formative way for secondary students, so the episodic informative style remains the prevalent employ.

Physics Education Research literature offers studies on specific topics for what concern learning difficulties and new approaches. Special thematic issues on the main global topics under discussion as quantum physics and special relativity are published by some Journal (i.e., Am J Phys 2002, Special Issues 70(3) and Phys Educ 2000, Special Issues 35(6)). Each contribution is focused on a specific approach, but the integration of modern physics in the curriculum within a vertical perspective, selecting relevant topics and adopting conceptual based approaches is up to now an open question in physics education research.

To gain the needed appropriation for an active learning approach, a particular research-oriented study is required. The analysis of conceptual referents and learning difficulties in each specific approach offered in literature and the comparison of approaches in planning the teaching proposal, together with the selection and preparation of learning materials remain a preliminary step for the educational employ. Teachers don’t have the resources and the time for that work. There is a need of research-based pilot implementation of educational proposals in the perspective of their integration in school curriculum for instructional scope and in addition support have to be guarantee to teachers.

We worked in that direction and we studied research-based proposals for new topics integration in secondary school curriculum looking in global perspective for a coherent framework and vertical paths in curriculum development and we start analyzing disciplinary, social, and educational relevance of topical areas in the different fields of updated research activities, looking to the relative educational power in gaining physics identity. We call here physics identity those conceptual competence consisting in the gained approach by students to the problems in phenomena interpretation, producing the attitude to identify the needed knowledge, instruments, and methods with the awareness of the relative power and limits for finding solutions and discuss evidence-based results by means of the treatment of formal aspects in a coherent way using basic math competences.

For this scope we selected topics and we studied vertical proposal in the research framework of the Model of Educational Reconstruction—MER (Duit et al. 2005). We carried out Design Based Research (DBR) (Anderson and Shattuck 2012) intervention modules to calibrate the proposal and to prepare educational materials useful for practice. The dimensions of such kind of research are many and include the study of relevance and of the educational reconstruction of each topic in accordance with MER, curricular studies (Constantinou and Papadouris 2008), comparative research for curricular aspects (Sokolowska et al. 2014), and empirical research on learning processes (Erickson 1998). Starting from learning difficulties and students’ reasoning we study educational paths and individual strategies in relationship with conceptual stimuli (Vosniadou 2013), the role of different representations and of personal/cooperative work on specific aspects as ideal experiments. Research and development in producing new multimedia tools and experiments accompanied our work (Michelini 2010). We developed up to now a series of proposals that we do not consider exhaustive.

After a discussion of the adopted approach for this goals, we list here the proposals developed up to now, that we don’t consider exhaustive, but examples of coherent paths in vertical perspective for modern physics in school curriculum. We leave the discussion of learning processes activated in classroom intervention modules and relative outcomes to the specific papers published during the research-based implementation of the paths development (Michelini et al. 2017, 2008; Greczyło et al. 2010; Vercellati 2010; Michelini and Stefanel 2008, 2010). Here we describe in detail two of them: cross section and phenomenologic approach to superconductivity.

10.2 The Research Approach in Building Modern Physics Proposals

Our perspective for modern physics is in the framework of content research (Meheut and Psillos 2004), oriented in building research-based proposals in a cultural perspective focusing on foundation of basic concepts as well as methods and applications in physics research, offering experience of what modern physics is in active research. Vertical paths are identified as learning corridor (diSessa 2004; Meheut and Psillos 2004; Michelini 2010) for individual learning trajectories and steps by steps concept appropriation modalities (Fedele 2005; Bradamante 2006; Vercellati and Michelini 2014).

The first step in our research approaches is to rethink the scientific contents as a problematic issue for the educational reconstruction, according to the Model of Educational Reconstruction (MER) (Duit et al. 2005). This task is integrated with empirical (Erickson 1998) research on student reasoning and research-based Teaching/Learning (T/L) intervention modules to individuate approaches able to favorite the building of scientific way of thinking on the spontaneous vision of students in phenomena description and interpretation. Cicles of Design Based Research (DBR) (Anderson and Shattuck 2012) intervention modules accompanied with action research in a collaborative dialectic between school and university produce the proposals for school activities, to contribute to classroom practice. The process includes empirical data analysis of each intervention module (Erickson 1998), which extension is growing with the path building. Data are collected in different ways. The main instruments are tutorials characterized by stimuli questions posed to promote attention in key questions; in particular students have to explain, interpret, or suggest further exploration on specific case studies or situations. Test-in and test-out on the way of interpret phenomena produce a global vision on the change in the reasoning of students as a community and for what concern individual profiles. Of course, it is often necessary to complete the data by means of semi-structured or Rogersians’ interviews. In data analysis, attention is paid to identify strategic angles and critical details (Viennot 1996) used by common knowledge to interpret phenomena (Michelini 2010) to study spontaneous reasoning paths, to find new approaches to physics knowledge (Vosniadou 2013).

The foundation of basic concepts in the context of the different physics research fields is the referent goal in selecting the contents. The cultural perspective in offering experience of what modern physics is in active research orient the selection of topics. We introduce the foundation of theoretical physics by means of Dirac approach to quantum mechanics. We privilege the new Einstein relativistic dynamic with respect to the Lorenz transformations. We focus on the foundation of new theories as quantum mechanics and on the discussion of the change in basic concepts ideas as those of state, measure, mass, energy, cross section, as well as research methods in active research and on the adopted relative basic principles applied, as energy and momentum conservation in optical and Rutherford backscattering spectroscopy (RBS).

For the advanced topics, interpreted by high formalized difficult theories, as electrical transport properties and superconductivity, we chose phenomena exploration approaches to offer methodological education by means of active learning strategies and lab work.

The basic idea is to avoid reductionism to offer opportunities of learning and not only understanding of information, to gain competences of instruments and methods, to build interpretative solutions and results to become able to manage fundamental concepts.

Modern physics is proposed along the whole curriculum, integrated in physics curriculum and not as a final appendix. Dynamic of Einstein relativity is proposed with Newtonian dynamic to discuss the work energy theorem on the light of Bertozzi experiment (Bertozzi experiment n.d., MIT). RBS and cross section concepts are proposed when collisions are treated in the curriculum. The discussion of the polarization as quantum property of light to introduce basic concepts of quantum mechanics is proposed when optical physics is treated, preferably not after electromagnetism, to avoid the automatic assumption that light is an electromagnetic wave. Optical spectroscopy becomes an extension of optics in the same context, looking on the meaning of the colors of light and the processes in light emission. A deep discussion of the concepts of mass and energy and a reflection on the meaning of state of a system as well as those of measure starts with the first steps in physics curriculum and remains a warm attention for the whole curriculum to promote a comparison of that concepts in different theories.

The main coherent vertical planned and implemented paths in school are the following: (1) Phenomena bridging theories: diffraction (Michelini et al. 2014a, b, c, d, e, f); (2) Optical spectroscopy and physics of quanta foundation (Buongiorno and Michelini 2018); (3) The physics in modern research analysis technics: RBS, TRR, R&H (Fera et al. 2014; Corni and Michelini 2018; Michelini et al. 2017); (4) Explorative approach to superconductivity (a coherent path) (Michelini et al. 2014a, b, c, d, e, f); (5) Discussion of some crucial/transversal concepts both in classical and quantum physics: state, measure, cross section (Michelini et al. 2017); (6) Foundation of theoretical thinking: quantum mechanics according to a Dirac approach (Ghirardi et al. 1996; Michelini and Stefanel 2008; Michelini et al. 2014a, b, c, d, e, f); (7) Mass-Energy discussion for a path to understand E = mc2 (Michelini et al. 2014a, b, c, d, e, f).

In the following, we describe in detail two paths very different: those on cross section and the explorative approach to superconductivity.

10.3 The Cross Section Educational Proposal

Cross section is an important concept in classical physics, it is central in the study of the interactions between elementary particles in nuclear physics at both low and high energies in atomic collisions and becomes essential in quantum mechanics where it is not possible to define the trajectory of a particle but only the probability of finding it in a certain space. We start in preparing this approach long time ago (Corni et al. 1996), starting from one-dimensional collisions and the basic elements about plane collisions for rigid bodies, using the conservation principles in classical physics to analyze the different cases and showing at the same time which associations can be derived from it.

We suggest to begin and go over a geometrical interpretation of the cross section, which is consistent only with the classical case of rigid spheres, to introduce its probabilistic meaning highlighting general aspects and showing how to relate measurements for interpretations, independently from the traditional force/equation model of motion/trajectory scheme.

In the elastic collision of two rigid spheres (1 and 2), with respect to the center of mass reference frame, in the case of infinite rigidity normal collision of identical spheres, we derive that the rebound of the two spheres is symmetrical with respect to the line through their centers. The interaction during the collision is characterized by the impulse vector I acting between the two spheres (i.e., from 2 to 1) and the comparison between the initial and final states of the system gives us all possible information about what happened during the collision. The scattering angle, θ, is connected to the distance b between the lines on which the centers of the two spheres were moving before the collision (impact parameter), as derived from the following equation: b = (R1 + R2) cos(θ/2). In more complex cases, this straightforward procedure fails. The dependence of the scattering angle θ from the impact parameter b becomes more difficult, when we replace sphere 2 with an irregular shaped object. Another cause of unpredictability is the finite precision with which the impact parameter is determined. Final states obtained with many collisions changing initial conditions can be significantly different.

To understand how the scattering angle can offer information about the collision or the geometry of the two bodies, we discuss the asymmetry of results of the experiment of Fig. 10.1, where data on the scattering angles distributed over the range (−160°, 160°) are collected for a certain number of impacts (400 events). This relation between distribution asymmetry and asymmetrical shape gives a qualitative example of how to extract the basic properties of the collision phenomenon from the scattering angle distribution. In general, a complete characterization of the collision requires the knowledge of the probability Pi for any given measurement outcome Si. For Ntot observations carried out, these probabilities Pi can be obtained from the averages Pi = 〈Ni/Ntot〉, where Ni is the number of outcomes Si.
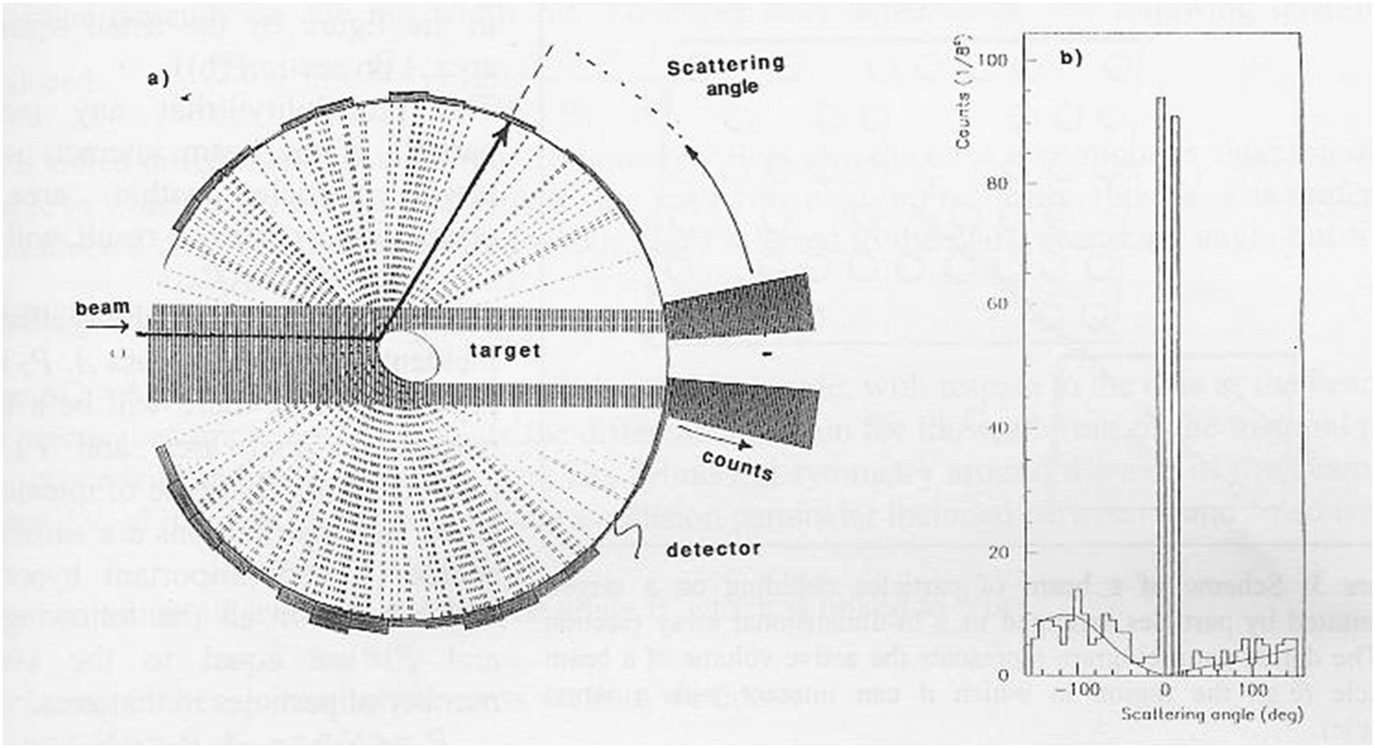
../images/467908_1_En_10_Chapter/467908_1_En_10_Fig1_HTML.png
Fig. 10.1

(a) Results of 400 scattering events of rigid spheres colliding an ellipsoidal target disk at angles distributed in the interval (−160°, 160°). (b) Number of balls scattered for each channel (channel width 8°)

In this way, it is clear that the probability, which is the element which is more related to the interaction, depends on the details of the measuring procedure. As in the considered case, the short range character of the interaction has to be considered explicitly.

To obtain a more general result, we suggest the discussion of the situation of Fig. 10.2 where an uniform beam of (identical) particles collide with a target of evenly distributed (identical) particles. The probability that an incident particle interacts with a target particle within the area A and give rise to a certain result Si, will be given by: P = P1 P2 Pint, where P1 is the probability that the incident particle impacts on the area A, P2 the probability that there is a target particle in region A, and Pint the probability that occur the specific interaction being studied.
../images/467908_1_En_10_Chapter/467908_1_En_10_Fig2_HTML.png
Fig. 10.2

An uniform beam of (identical) particles colliding with a target of evenly distributed (identical) particles

If the distributions of the particles are sufficiently sparse, P1 and P2 are proportional to the average number N′i (i = 1, 2) of particles in this area:
$$ {P}_1=\left\langle {N}_1^{\prime}\right\rangle /N1={n}_1A/N1\kern1em \left(1:\mathrm{incident}\right) $$
$$ {P}_2=\left\langle {N}_2^{\prime}\right\rangle /N2={n}_2A/N2\kern1.25em \left(2:\mathrm{target}\ \mathrm{particle}\right) $$
where n1 and n2 represent the surface densities in a projection transversal to the axis of the beam.

The two particle will certainly collide when b ≤ R1 + R2 and σtot = APint = π(R1 + R2)2. This result is valid for any reference system and can be used for a geometrical interpretation of the concept of cross section. When R1 ≪ R2, then σtot ≈ πR22, that is the projection of body 2 on a plane transversal to the direction of the collision, independently by the shape of body 2.

The histogram in Fig. 10.1b represents the angular distribution of the results of collisions in the second example we discussed; the ith bin of the histogram contains the number Ni of the outcomes for which the scattering angle is included between the extremes (θ, θ + Δθ) of the bin itself. Thus the cross section for the collisions with a scattering angle at such an interval is: σi = APi ≈ ANi/(NiA) = Ni/ni. This value depends on the bin width Δθ.

To avoid such dependency, the differential cross section is introduced:
$$ \frac{\mathrm{d}\sigma }{\mathrm{d}\theta }=\underset{\Delta \theta \to 0}{\lim}\frac{\sigma }{\Delta \theta }=\underset{\Delta \theta \to 0}{\lim}\frac{\left\langle {N}_i\right\rangle\;}{n_i}\frac{1}{\Delta \theta } $$
It is convenient to define differential cross section with respect to the solid angle:
$$ \frac{\mathrm{d}\sigma }{\mathrm{d}\varOmega }=\underset{\Delta \varOmega \to 0}{\lim}\frac{\left\langle {N}_i\right\rangle }{n_i}\frac{1}{\Delta \varOmega } $$
(3)
where ΔΩ = ΔcosθΔϕ and ϕ is the azimuthal scattering angle, with respect to the axis of the beam.
The differential section for the scattering of the material point on a sphere with radius R can be calculated considering the number dN1 of incident bodies which have a collision parameter included between b and b + db: dN1 = n1 (2πbdb), all scattered at the same angle θ, which is linked to b by: b = Rcos(θ/2). Substituting in the equation of the cross section, we derive:
$$ \frac{\mathrm{d}\sigma }{\mathrm{d}\varOmega }=\frac{R^2}{4} $$
which is independent from θ and obviously coincides with the area of the section of the sphere.

The geometric nature of cross section we find considering the collisions of point particles with other bodies derived from the model used to describe the dynamic part of the process.

The cross section calculus in the case of Coulomb interactions of point-like bodies with Z, Z′ charge is then suggested in the case in which one of the two bodies (scatterer) is much bigger than the other (incident), so that its position does not vary in the collision process and we can therefore consider it still at rest as in the case of scattering experiments to explore a solid system and in particular Rutherford Backscattering Spectroscopy (RBS) (Corni and Michelini 2018). The calculation of the differential cross section for this process is done in the same way as for the previous section: calculation of the relationship between the collision parameter and scattering angle and subsequent application of the definition. The detailed proposal is published in the path dedicated to RBS (Corni and Michelini 2018).

The discussion of the nuclear cross section and relative difficulties conclude the proposal for the last part of the curriculum. Due to the high number of nucleons involved in a nuclear reaction, we are not able to write down a simple expression for the nuclear force, then a simple expression for the cross section cannot be simply derived, but taking into account that we could have, at the same time, Coulombian and nuclear interactions for different nuclei, we can write: σNUC = AσRNNU/NR, where σR the Rutherford cross section, NNUC the number of nuclear events, NR the number of Rutherford events, and A a parameter depending on detectors’ solid angles and intrinsic efficiencies. The NNU number depends on the observed nuclear process we observe. In the case of a nuclear reaction where the two nuclei come close enough to fuse, one of these nuclei dissipate the extra energy and angular momentum removing nucleons from high energy levels to lower energy ones and emitting γ photons with energy equal to the difference of the two levels. For each nuclear fusion event, we will have a γ ray cascade from the first excited state to the ground state. The fusion cross section σFUS depend by the total number of transitions Nγ and by Rutherford scattering events as follows: σFUS = AσRNγ/NR.

Students learn how in a similar way it is possible to measure the cross section for other nuclear processes and understand why there are research fields on cross section.

10.4 A Conceptual Explorative Path to Superconductivity

Superconductivity is one of the most relevant topics of the twentieth-century physics. It is an important research field in material science for different kind of research, its application changes almost all the way in which magnetism is employed in technologies and produces new technologies as for the case of Maglev train, its theoretical interpretation founded a new theory (Bardeen et al. 1957). It can be explained at different level and in different interpretive frames (González-Jorge and Domarco 2004; Essén and Fiolhais 2012). From educational point of view, we offer to secondary school students the opportunity to experience how to perform a phenomenologic exploration, analyzing how to build explanations on observed phenomena and how to found interpretative aspects in a coherent and rigorous way. Students have to reflect on their own knowledge in electromagnetism and to put in the field the competence of using their electromagnetic knowledge in a new context. They are stimulated in the production of interpretative models and in the connections between science and in meaningful connections between classical and quantum physics technology. They analyze the history of the superconductivity discoveries and technological applications. They use kits for educational experiments and multimedia materials developed within the framework of European projects MOSEM 1–2 (Kedzierska et al. 2010; Greczylo et al. 2010; MOSEM2 Group 2011).

For the educational laboratory, we developed new systems for temperature dependence of resistivity measurements in a wide range of resistivity values (Gervasio and Michelini 2009), that we integrate in path proposal. Our educational proposal for a phenomenological exploration of superconductivity in secondary school is integrated in the electromagnetism curricula and for the feasibility study we support a group of teachers for research-oriented school implementation (Michelini and Viola 2011). From 2010 research experimentations were conducted in 20 different classes of eight different Italian schools with 393 students. Results documented the systematic interest of the students, which was not limited to the simple observation of phenomena unusual and surprising, but mostly focused on the exploration of interpretative hypotheses. Results of research-based school implementation showed that the personal involvement in the exploration of the collection of the many problematic proposed situations activates the planning of further explorations, aimed to test hypotheses able to explain the superconductor behavior. Starting from the ordinary electrical and magnetic properties of matter, students recognize the peculiar characteristics of the superconductivity behavior at liquid nitrogen (LN) temperature, comparing it to those of an ideal conductors and of diamagnetic materials (Stefanel et al. 2014).

The strategy adopted includes the following phases: presentation of a situation-problem, experimental exploration of it, student individual hypothesis for explanation and/or planning of a further exploration, discussion in little group to reach a common decision, discussion in large group at the end of each problematic issue. The following explorative steps are the core of the path proposal:

  • (S1) Interaction between a little strong magnet (M1) and an YBCO disk at room temperature (Troom) and at liquid nitrogen temperature (TNL). An YBCO disk at room temperature (Troom) does not present magnetic properties. When it reaches the temperature of TNL, the levitation of the magnet occurs. This phenomenon called Meissner effect is analyzed by students as well as the stability of the levitation.

  • (S2) Comparison of the Meissner Levitation and the cases of magnetic suspensions. Interaction between two free magnets shows the rotation of one of them to attract the opposite pole of the other and suspension occurs only when we constrain magnets to face the same pole for example putting them in a tube. Levitation occur when YBCO and the magnet are free and we have to admit a fundamental difference in the two considered situations. They conclude that a phase transition can be involved, because when T = Troom the superconductor does not evidence magnetic properties, but when T ~ TNL, suddenly, magnetic properties emerge.

  • (S3) Students design and perform free experiments to explore the phenomenology and to characterize the YBCO behavior. To individuate the kind of magnetic property acquired by YBCO at TNL, a systematic exploration of its interaction with different magnets and different materials (ferromagnetic materials in primis), in different configurations, is carried out. The superconductor is not becoming ferromagnetic, it is not a permanent magnet, it does not become like the mirror image of the levitated magnet. It always shows repulsive effects close to a magnet.

  • (S4) Study of the behavior of different materials interacting with a magnet to individuate which kind of material properties are assumed by YBCO at TNL. The levitation of pyrolytic graphite on a quadrupole of magnet is observed. Students studied the interaction of a strong neodymium magnet with paramagnetic and diamagnetic systems suspended on a wire or on a yoke in order to make evident even very small repulsive/attractive forces. Comparing the behavior of diamagnetic materials with those of the YBCO at T ~ TNL it has to be classified diamagnetic.

  • (S5) Intensity of the diamagnetic interaction. The strength of the interaction between a superconductor and a magnet is several orders of magnitude greater than those observed with ordinary diamagnetic materials, suggesting to search for a more detailed characterization of the nature of the diamagnetism of the superconductor. Starting from the evidence that the superconductor shows magnetic interaction only when a magnet is close to it and that the YBCO do not interact with a ferromagnetic object, students recognize that the interaction with a magnet does not depend on the pole put close to the surface of the magnet, the equilibrium position is always the same. Changing magnet, the equilibrium position changes, but it is always the same, for the same magnet.

  • (S6) Discussion on the magnetic field inside to the Superconductor and search for an explanation. Analysis of the situation: a sandwich composed by the magnet M1/YBCO/ferromagnetic ring at T = Troom is lifted, pulling the magnet M1. At T ~ TNL the ferromagnetic ring is no more pulled. We have to admit that when T ~ TNL the magnetic field inside the superconductor sample can be zero or very little (in this condition the magnet and the iron ring do not interact when the YBCO disk is in between). Moreover, when TNL < T < Troom the magnetic field B can exist and be different of zero inside the YBCO sample, but the magnetization of the superconductor is always adjusted to react to the external magnetic field, tending to preserve the initial situation. In particular, if B = 0 when the superconductivity state is created, the system tends to react to an external magnetic field creating a counter field that tends to maintain B = 0 inside the superconductor (Meissner effect).

  • (S7) Search for an analogy able to explain the Meissner effect. Eddy currents produced in the electromagnetic induction have a similar behavior. A magnet is evidently braked when falling down on a thick copper layer or inside a copper tube, but never it can be stopped/maintained in levitation, as in the case of the YBCO. If the magnet stops, the induced current stops due to the Joule effect. The magnet would be stopped just falling over a conductor with resistance R = 0 Ω (an ideal perfect conductor!). Supposing that an electromagnetic induction process will be at the base of the superconductivity levitation, the resistivity of the YBCO sample could be suddenly changed when T ~ TNL to have a levitation. This suggest the measurement of the resistivity of a superconductor.

  • (S8) The experimental measurement of the breakdown of the resistivity of a YBCO gives quantitative evidence to the phase transition for what concern the changes from the ordinary conductor state to the superconductor state of YBCO. The phenomenological exploration leads to the conclusion that R = 0 as well as B = 0 inside the superconductor. These two aspects characterize the Meissner effect.

  • (S9) Pinning effect in II type of superconductors is observed, when the superconductivity state is created in presence of an external field. The pinning effect, due to the penetration of the magnetic field inside the superconductor sample as vortexes created by supercurrents, emerges to explain the anchoring of the magnet to the superconductor at T ~ TNL.

  • (S10) Students build a simple MAGLEV train, where the effect is clear because never derail and look for different applications of superconductivity.

During each intervention module, these steps were systematically monitored, using tutorial worksheets, audio recording of the student dialogues, and notes by the researchers/teachers conducting the activities.

For gifted students or advanced class groups having as a prerequisite the energy level model for the electrical conduction interpretation, we often discuss how to interpret the superconductivity and not only to explain by means of an analogy. Starting from the analysis of the energy of the electron system inside of a crystal lattice, we give into account how this superconductive state can be created. Cooper pairs, or in other words the formation of pair of correlated electrons is shown to be a process energetically favored. The collapse of these Cooper pairs on the same ground state is responsible of the R = 0 property at the base of the superconductive behavior.

10.5 Concluding Remarks

The recent demanding for innovation in secondary school has an important goal in introducing modern physics topics. Our contribution for modern physics, here discussed and exemplified for the cases of cross section and superconductivity, may be divided into four kinds of researches: (a) Research and development for new systems and tools; (b) Design based research to support practice with coherent paths; (c) Empirical research to study learning trajectories, appropriation, and kind of reasoning; (d) Teacher education and professional development. Our content research theoretical framework is the Model of Educational Reconstruction and Design Based Research guides the implementation of the studied proposals by means of conceptual change analysis of student reasoning. Instruments and methods are test-in/out, tutorials, and interviews using the standard methods of qualitative research. Research is carried out in the context of IDIFO Project (Innovation in Physics Education and Guidance Project led by our research unit) of the National Plan PLS-Fisica (Plan for improving Scientific degrees—section physics), with a peer review and cooperation between 20 Italian universities for different physics education actions and characterized by a strong cooperation between school and university. It follows different learning outcomes: (1) the physics in research analysis technics; (2) explorative approach to research edge topics; (3) discussion of crucial/transversal concepts both in classical physics and in modern physics; (4) foundation of theoretical thinking; (5) contexts for personal involvement in inquiry base learning to gain critical approach and competences in experimental physics work. The perspectives in developing proposals are focused in building in young people: physics identity, physics as a cultural issue, the idea of physical epistemic nature. Avoiding the reductionism our aim is to offer opportunities to: (1) experience of quantitative exploration of crucial phenomena (diffraction and optical spectroscopy), individuating laws, fitting data, and testing basic principal ideas and results with experimental data; (2) understand the crucial role of classical physics in modern research techniques (RBS, Resistivity and Hall coefficient measurements), manipulating data and interpretation like in a research laboratory; (3) focusing on reasoning to conduct a phenomena exploration (superconductivity) understanding the role of analogies for finding explanations; (4) reflect on physics meaning of basic concepts in different theories (state, measure, cross section) revising meanings in classical physics and understanding the different perspectives of new theories; (5) approach to the new ideas of QM theory: the first step toward a coherent interpretation with a supporting formalism experiencing aspects, cardinal concepts, elements peculiar to QM; (6) privilege dynamic aspects in special relativity to revise the concepts of mass and energy and to understand the law E = mc2.

The vertical perspective with respect to the curriculum gives us the opportunity to integrate the different perspectives in different ways so each represents a specific methodological proposal. The two proposals for cross section and for superconductivity here presented offer a way to identify the different methods.

The implementations with secondary school students evidence positive learning progression concerning the crucial knots of the treated topics. It suggests to: (a) focus on the coherence of reasoning to create a reference framework, integrating hand-on and explorative work, mind-on interpretation of results, by means of real and ideal experiments and modelling; (b) use iconographic representations as conceptual tool; (c) use analogies for phenomena interpretation; (d) introduce formalism, using it to reinterpret explored situations; (e) analyze students’ ideas in the framework of different interpretative schema; (f) integrate modern physics in classical physics developing coherent paths of conceptual understanding.

Acknowledgement

I express my gratitude for the cooperation in the research work carried out to the colleagues of my physics education research group and in particular to Lorenzo Santi and Alberto Stefanel, as well as to the PhD student Daniele Buongiorno and to the teacher Alessandra Mossenta.

We thank PLS-Fisica Italian Projects and in particular IDIFO project for the support.