15.1 Introduction
Force Concept Inventory (FCI) is a multiple-choice test useful to evaluate the efficacy of teaching approaches (Hake 1998) and to validate proposed learning progressions on force and motion (Fulmer 2015). Some studies focused on students’ coherence when they answer FCI questions in different contexts (Bao and Redish 2006; Savinainen and Viiri 2008). Some authors (Bao et al. 2002; Bao and Redish 2006) used Model Analysis to analyse FCI students’ answers. A recent paper (Brewe et al. 2016) has described a new methodology for carrying out network analysis on answers to multiple-choice conceptual inventories. Moreover, studies using Factor Analysis (Scott et al. 2012; Scott and Schumayer 2017; Semak et al. 2017) analysed the possible conceptual associations made by students among FCI questions.
Commonly, instructors and researchers are interested to the correctness of the students’ answers on the FCI. Here we want to use FCI as a “tool” to find relationships among student answers to questions related to different aspects of Newtonian mechanics in order to give more complete information about their understanding.
In this study, we propose a quantitative analysis of FCI student answers and our results can help teachers and educators in designing appropriate teaching approaches. In it we apply a Cluster Analysis (ClA) method, based on the k-means algorithm (Everitt et al. 2011) to study students’ answers to FCI questions, with the aim to point out reasoning strategies based on Newtonian conceptions as well as alternative conceptions (misconceptions/nonnormative conceptions). We show that our analysis can provide new insights into the students’ conceptions of the different dimensions of the force concept, as defined by FCI’s authors (Hestenes and Halloun 1995).
15.2 Theoretical Framework
Several pieces of research studied in detail the FCI test, some of them have shown its use as a diagnostic instrument. Among these latter ones, we would like to note the following that are, in our opinion, the most significant.
The first one, based on Factor Analysis is discussed in a recent paper (Semak et al. 2017). It has shown that this method is able to gauge the changes in conceptual associations made by students when the evolution of their answer patterns is known.
It was already pointed out (Bao and Redish 2006) that a way to use the FCI test as diagnostic instruments is given by methods that allow the researchers to analyse wrong answers. Several studies have shown that different alternative knowledge frameworks can coexist in college students and that the development and use of such knowledge are context-dependent. Moreover, the reasons why a student may deploy the correct knowledge in some situations and revert to use alternative kinds of knowledge in other ones can be hidden if students’ alternative knowledge is not assessed. Such behaviour is often treated in the literature as random noise.
The second method we want to cite was introduced by Bao and Redish in 2006. It is called “Model Analysis”, and provides a quantitative representation framework. In this framework, this method is able to quantitatively assess students’ alternative knowledge and the probabilities for students to use such knowledge in a range of equivalent contexts. They take into account five FCI questions to study what kind of student’s models can be associated with the force-motion ideas. Model Analysis allowed them to analyse students’ answers in terms of predetermined mental models and graphically represented the probability that students can use each of these models.
The third method was developed by Brewe et al. (2016) to study relationships among nonnormative answers to the 30 FCI questions. By using network analysis and techniques of community detection (Grunspan et al. 2014) they were able to discover structures into patterns of answers. The result of this analysis allows the researchers to identify Modules of nonnormative answers which can highlight important underlying structures of the whole nonnormative answer network. Alternative reasoning procedures that involve student alternative conceptions are represented in Modules including high correlations among nonnormative answers to different questions, and some interesting interpretations are supplied. However, it is worth to note that the analysis provides information about patterns of nonnormative answers, but “the drawback is that we cannot investigate how these patterns relate to normative responses”, as the authors state (Brewe et al. 2016).
In the literature some studies using Cluster Analysis (ClA) methods and concerning research in education are found. ClA methods can separate a sample of students into subgroups so that students belonging to the same subgroup are more similar to each other than those are not belonging in the same ones. These subgroups can be studied to characterise students’ answers of open-ended questionnaires (Springuel et al. 2007; Fazio et al. 2013; Battaglia and Di Paola 2015; Di Paola et al. 2016; Battaglia et al. 2017a, b; Battaglia et al. 2019) or multiple-choice tests (Stewart et al. 2012). All these papers show that the use of ClA leads to individuate groups of students whose characterisation makes sense to researchers. In a recent paper, Stewart et al. (2012) analyse the student answers to seven questions by using Model Analysis. They study the state of student’s knowledge and ClA methods to characterise the distribution of students’ answers. They show that ClA is an effective method to inquiry the student understanding and to discover subgroups of a data set mathematically well-defined and meaningful for the researcher.
15.3 The Research Question
Hestenes et al. (1992) as well as successive researchers have divided the FCI test in different conceptual dimensions (Hestenes and Halloun 1995). We want to investigate the student understanding of two of such dimensions, and making diagnostic inferences about student knowledge. The research question that guided our study is:
To what extent can a ClA method reveal students’ reasoning profiles of Newtonian mechanics understanding when they answer FCI questions about the first and second laws and the concept of force?
15.4 Methodology and Sample
15.4.1 The Sample
We administered the FCI test just at the beginning of an activity that the authors proposed as an optional course about Newtonian Mechanics. The sample was composed of 148 freshman engineering students. We analysed all the students who answered to more than 80% of the questions. For this reason, we analysed a subsample composed of 116 students (73.3% male and 26.7% female).
15.4.2 FCI Questionnaire
FCI is a multiple-choice questionnaire and it was presented for the first time in a paper published in 1995 (Hestenes and Halloun 1995). It is made of 30 multiple-choice questions (each question has five possible answers). The 1995 version included a classification of the Newtonian force concept investigated in the questionnaire in different dimensions. The FC authors reported a decomposition of the force concept into six conceptual dimensions by highlighting that all six dimensions are fundamental for the Newtonian force concept. In another paper (Hestenes and Jackson 2007) another table with a taxonomy of common-sense misconceptions related to the Newtonian mechanics, and the corresponding Inventory questions is proposed.
SubA includes 15 questions. Each question requires to apply Newton’s first and/or second laws. Students have to choose among the different five answers that contains description of trajectories, kinematics quantities and/or explanations.1
SubB includes questions that allow the researcher to evaluate student ability in identifying interactions between bodies and related forces in different dynamical or static contexts.
SubC includes questions involving the Newton’s third law. They require to identify action and reaction forces acting on bodies in dynamical or static conditions.
SubD includes questions requiring student to describe motions by using the kinematics quantities and laws.
FCI questions divided into the four subtests
Subtest | Question | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
SubA | Q3 | Q6 | Q7 | Q8 | Q9 | Q10 | Q12 | Q17 | Q21 | Q22 | Q23 | Q24 | Q25 | Q26 | Q27 |
SubB | Q5 | Q11 | Q13 | Q18 | Q29 | Q30 | |||||||||
SubC | Q4 | Q15 | Q16 | Q28 | |||||||||||
SubD | Q1 | Q2 | Q14 | Q19 | Q20 | ||||||||||
15.4.3 Data Coding and k-Means Algorithm
We quantitatively analyse the answers students give to the questionnaire by using Cluster Analysis (ClA). ClA methods allow us to generate groups of students by partitioning it and producing a set of non-overlapping clusters. We decided to apply the k-means algorithm (MacQueen 1967), because of its efficiency and simplicity.
This algorithm requires a coding of the answers. We code the FCI students’ answers by using a binary code and generate a binary matrix, called “matrix of answering choices”. It is made of N rows and M columns. In this matrix, each row represents a student and has M components where only one is 1 while the other ones are zero. If in a generic row, a component is 1 in the column j means that the student associated with that row chose the j answering choice. For each question, each student can choose among five answering options (A–E), or to not answer at all. So, the total number of answering options is equal to 6. Therefore, for instance, in the case of SubA M is equal to 90 (6 × 15) and N to the number of students, is equal to 116.
In order to apply k-means algorithm we have to choose a distance index through which calculate the “similarity” between a couple of students. According to literature (Everitt et al. 2011; Mantegna 1999; Di Paola et al. 2016; Battaglia et al. 2017b) we chose a Euclidean metric (Gower 1966) to calculate this distance index and we obtain an N × N symmetric matrix that contains all the mutual similarity between our students.2
The results of k-means algorithm, several group or clusters, can be represented in a Cartesian plane by using a well-known procedure called Multidimensional Scaling (Borg and Groenen 1997).
Each cluster is made of students that are represented as points according to the mutual distances between them.
Once an appropriate partition of students has been found, each cluster has to be characterised in terms of the student behaviours. To do this we find for each cluster and each question the most frequent answers given by the students in that cluster. Those answers characterise that cluster, and according to Springuel et al. (2007) we call them “prominent” answers.
15.5 The Results
We separately analysed only the first two subsets to discover common student reasoning strategies into the different conceptual dimensions of the force concept. In the case of the 15 questions classified as SubA, the number, q, of clusters that best partitions our student sample was obtained through the maximisation of the mean value of S-function (Rouseeuw 1987), for different numbers of clusters (2 ≤ q ≤ 4). Their values and their 95% confidence intervals (C.I.) are the following: 〈S(2)〉 = 0.76 (C.I. = 0.73–0.78), 〈S(3)〉 = 0.72 (C.I. = 0.68–0.75), 〈S(4)〉 = 0.63 (C.I. = 0.58–0.68).
The values reported above show that there are two statistically equivalent best clustering solutions (into two or three clusters). In order to choose one, we apply the Variation Ratio Criterion (VRC) (Calinski and Harabasz 1974). We calculate the Calinski index for the partition into three and two clusters and obtained the following values. (VRC(3) = 219 and VRC(2) = 149). So, we chose the three-clusters solution as the best one.
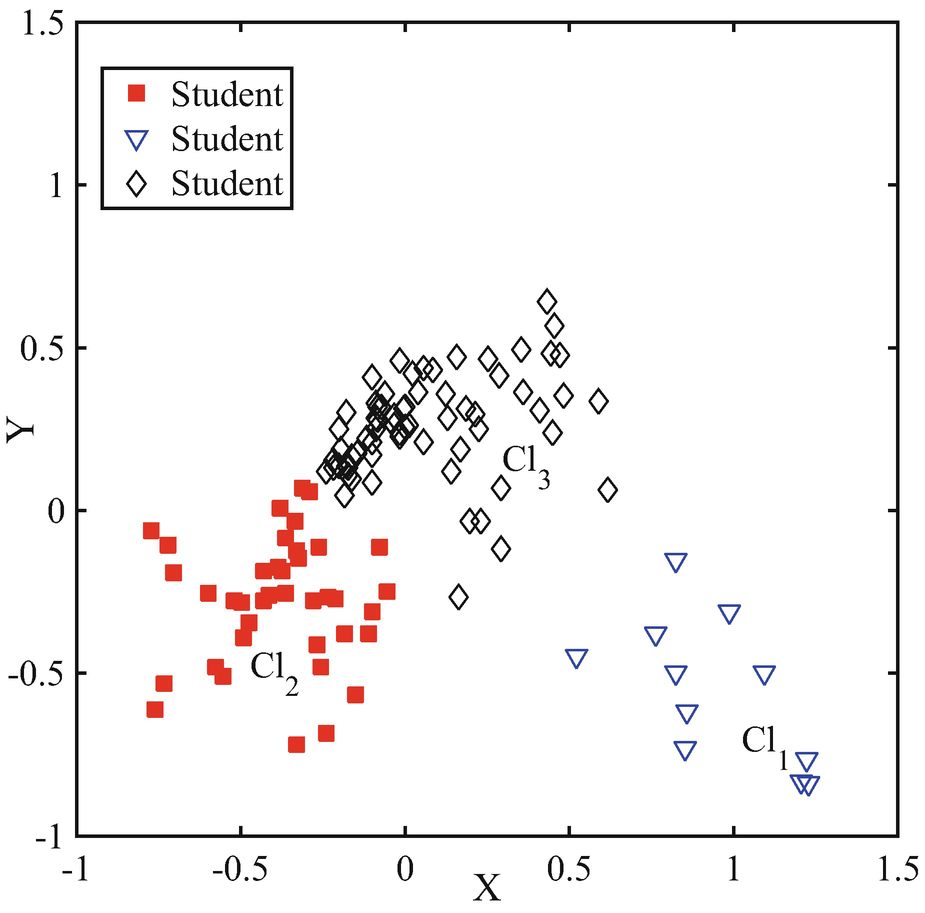
K-means solution for SubA answers where three clusters are identified. Each point in this Cartesian plane represents a student
Results for the SubA
Cluster | Cl1subA | Cl2subA | Cl3subA |
|---|---|---|---|
Number of students | 66 | 39 | 11 |
Most frequent answers | 3C, 6B, 7B, 12B, 17A, 21E, 25D, 27C | 6B, 8B, 12B, 21E, 22A, 25F, 26F, 27F | 3C, 6B, 7B, 8E, 9E, 12B, 17A, 22B, 24A, 25D, 26B, 27C |
The arrays in Table 15.2 allow us to describe the dominant behaviours of students in each given cluster.
The Students in Cl1subA supplied correct answers for questions that require the qualitative description of the motion of dynamic systems (question Q27) and the prediction of trajectories (as in questions Q6, Q7, Q12 and Q21). Only question Q3 requires also a Newtonian explanation of the phenomenon. Moreover, students in Cl1subA incorrectly answer questions Q17 and Q25 involving more forces applied to the same body, yet when the body has a constant velocity. In such cases, we think that misconceptions as “a force due to the motion” or “a force in the direction of motion” or “an impetus force which is acting on the object after the object is no longer in contact with the agent applying the impulse” may have been the cause of the students’ incorrect answers.
The Students in Cl2subA cluster supply correct answers to questions Q6, Q8, Q12, and Q21. These require the description of the motion of dynamic systems or the prediction of trajectories. However, the same students give incorrect answers in the case of questions involving explanations of the kinematic variable and the individuation of trajectories. Moreover, they fail to give a correct answer to questions that mainly require Newtonian explanations about the motions.
The students in by Cl3subA cluster supplied correct answers to questions Q6, Q7, Q12 that require the ability to describe motions and predicting trajectories. Moreover, the same students correctly solved questions Q3, Q9, Q22, Q24 requiring the ability to use the first and second Newtonian laws to find an explanation. Questions Q8, Q17, Q25, Q26 show high percentages of incorrect answers indicating in our students a persistent of naïve conceptions as that “persistence of original impetus”, “largest force determines motion”, or “motion is possible when forces overcome resistance” (Hestenes and Halloun 1995). Coherently with the previous description, the students in Cl3subA answer that for an elevator lifting up by a rope at a constant velocity the rope tension is greater than the force of gravity (17A). The idea that a constant force makes a body moving with a constant velocity is made explicit by the students in answers 25D and 26B. Differently, such students use a different model in answering question Q3 (3C). In this case, they clearly see an increase in the velocity for a falling object since the force of gravity is constant. Many nonnormative conceptions above described are strictly connected with the “Impetus Module” pointed out by Brewe et al. (2016).
As a second step, we performed the same analysis described above to obtain a partition of our student sample according to their answers to the six questions classified as SubB. The number, q, of clusters that best partitions our student sample was obtained through the maximisation of the mean value of S-function, 〈S(q)〉, calculated for q values from 2 to 4 and their 95% C.I.
We obtained 〈S(2)〉 = 0.68 (C.I. = 0.65–0.70), 〈S(3)〉 = 0.69 (C.I. = 0.64–0.73), 〈S(4)〉 = 0.62 (C.I. = 0.59–0.64).
As in the analysis of SubA, in this case, we found that the 〈S(q)〉 values for q = 2 and q = 3 are comparable. Again, we perform a further analysis by using the VRC and obtained for the results into three clusters the highest value (VRC(3) = 219 and VRC(2) = 149).
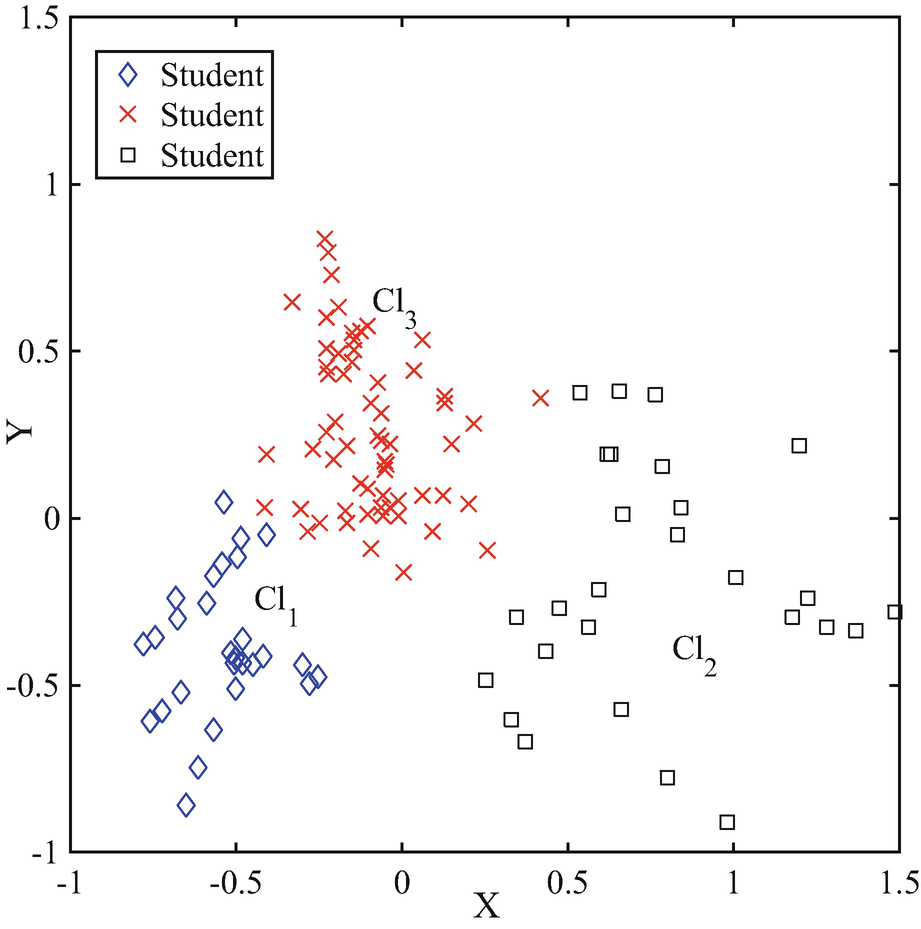
K-means graph for SubB answers where three clusters are identified. Each point in this Cartesian plane represents a student
Results for the SubB
Cluster | Cl1subB | Cl2subB | Cl3subB |
|---|---|---|---|
Number of students | 28 | 27 | 61 |
Most frequent answers | 5E, 11C, 13A, 29B, 30E | 5C, 11B, 18F, 29F, 30F | 11B, 13C, 18C, 30E |
Students in cluster Cl1sub correctly interpret the forces as quantities that describe the interaction between bodies. However, they also cite a kind of force that seems to be directly connected to the body velocity or to some hit supplied to it as a “force due to the motion” or “supplied by a hit”). We can conclude that students comprised in this cluster are characterised by a “hybrid” (Ding and Beichner 2009) or “synthetic” (Gilbert and Boulter 1998) conception of force. This idea of force unifies different features of the naïve conceptions (“obstacles exert no force” or “motion implies active force” or “velocity proportional to active force” (Hestenes and Jackson 2007) and the scientifically accepted one that considers force as a quantity to model interactions between bodies. Finally, they are able to give correct answers for question 29 in which a static situation is considered.
Cl3subB contains students that almost completely forget the interaction forces. They consider as forces acting on a moving body only the gravitational force and the one due to the motion. We think that a naive conception of force, widely discussed in the literature (see Brookes and Etkina 2009 and included references) is on the basis of the answers given by these students.
Students in Cl2subB do not answer half of the subtest questions and this is the main difference by those belonging to Cl3subB.
15.6 Discussion
The results above described allow us to answer our research question: “To what extent can a ClA method reveal students’ reasoning profiles of Newtonian mechanics understanding when they answer FCI questions about the first and second laws and the concept of force?”
The results above described show that the k-means algorithm can be a useful tool to discover latent structures within the answers on the FCI test. We highlight a cluster of students with similar answers and such clusters are characterised by correct answers as well as by non- correct answers. Moreover, these latter have allowed us to identify student’s misconceptions/nonnormative conceptions.
The method we used can identify in detail the status of knowledge of the students. We discover dominant/prevalent behaviours, and these can allow us to infer the characteristics of models used by students in different contexts.
The main results, obtained by our analysis of FCI answers supplied by our students characterised by a low level of understanding of the Newtonian dynamics, allow us to answer our research question, as reported below.
By analysing the student understanding of dynamical characteristics of motions we note that the majority of our students can’t supply a Newtonian explanation of such motions (by applying the first and/or second Newtonian laws). They show in some contexts a correct ability to describe trajectories, but not to explain them in the theoretical framework of the Newtonian Mechanics. This ability can be attributed mostly to their common life experience. Only a small number of students are able to supply correct answers to questions requiring explicative skills, but only in given contexts.
The majority of students in our sample when is required to identify forces acting on a moving body only think on the gravitational force and/or “motion force” or “impetus force”. They almost completely omit the reaction forces. Such students are characterised by a naïve idea of force, widely discussed in the literature (see Brookes and Etkina 2009 and included references) and connected with several other misconceptions (“obstacles exert no force” or “motion always implies active force” or “velocity proportional to active force”) (Hestenes and Jackson 2007). Together with this naïve idea of force, only a small group of students has a Newtonian concept of force as a quantity to describe the interaction between objects. In their minds, these two absolutely different ideas seem to coexist, as several studies also pointed out (Brookes and Etkina 2009). Finally, it is worth to highlight that, despite such a mixed idea of force, these students are able to use the first and second Newton laws and to identify correct relationships between force and motion only in some contexts.
15.7 Conclusions
We would like to outline that the results obtained here for FCI could not be generalised to all Concept Inventories (CIs). At the same time, we think that ClA applied to CIs can be useful at the level of the classroom. For instance, we see the use of CIs as diagnostic instruments that could be useful to connect instruction with student ideas on a more fine-grained level and to help them in developing pedagogical approaches that target the ideas in classes. Specifically, we found that a fundamental role in the correct analysis of mechanics problems is given by the concept of force, investigated using student ability to individuate forces acting in statics and dynamical contexts.
Educational implications from our results can be also drawn. These mostly point to the relevance for teachers and instructors to be aware that students’ difficulties with the ideas of force and motion mainly arise from their difficulty in understanding the ontological status of the force concept in physics (Jammer 1957). The contexts supplied by FCI items can provide teachers with useful examples, as well as the acknowledgement of reasoning strategies used by physicists in the historical development of force and motion concepts (Jammer 1957). Teaching approaches to Newtonian mechanics can be implemented by thinking that student alternative conceptions and mainly their reasoning strategies applied in different mechanical contexts can make the students able to speed up their mastering of such an important theoretical framework.