© Springer Nature Switzerland AG 2021
B. G. Sidharth et al. (eds.)Fundamental Physics and Physics Education Researchhttps://doi.org/10.1007/978-3-030-52923-9_1

1. Symmetries in the Standard Model

Jose Bernabeu1, 2  
(1)
Department of Theoretical Physics, University of Valencia, Valencia, Spain
(2)
IFIC, Joint Centre UV-CSIC, Burjassot, Spain
 
 
Jose Bernabeu
Email: Jose.Bernabeu@uv.es

Abstract

Symmetries in the Physical Laws of Nature lead to observable effects. Beyond the regularities and conserved magnitudes, the last decades in Particle Physics have seen the identification of symmetries, and their well-defined breaking, as the guiding principle for the elementary constituents of matter and their interactions. Flavour SU(3) symmetry of hadrons led to the Quark Model and the antisymmetry requirement under exchange of identical fermions led to the colour degree of freedom. Colour became the generating charge for flavour-independent strong interactions of quarks and gluons in the exact Colour SU(3) local gauge symmetry. Parity violation in weak interactions led to consider the chiral fields of fermions as the objects with definite transformation properties under the weak isospin SU(2) gauge group of the unifying electroweak SU(2) × U(1) symmetry, which predicted novel weak neutral current interactions. CP violation led to three families of quarks opening the field of Flavour Physics. Time-reversal violation has recently been observed with entangled neutral mesons, compatible with CPT-invariance. The cancellation of gauge anomalies, that would invalidate the gauge symmetry of the quantum field theory, leads to quark-lepton symmetry. The experimental discovery of quarks and leptons and the mediators of their interactions, with physical observables in spectacular agreement with this standard theory, is the triumph of symmetries. The gauge symmetry is exact only when the particles are massless. One needs a subtle breaking of the symmetry, providing the origin of mass, without affecting the excellent description of the interactions. This is the Brout–Englert–Higgs mechanism which produces the Higgs boson as a remnant discovered at CERN in 2012. Open present problems are addressed with the search of New Physics Beyond-the-Standard-Model.

Keywords
Flavour FamiliesColour ChargesGauge symmetriesChiralityDiscrete SymmetriesSpontaneous Breaking

1.1 Symmetry as Guiding Principle for Particles and Interactions

In ordinary life we observe symmetry of objects, like characteristic features of geometrical forms, material objects or biological bodies. The concept is related to the invariance of the object under definite transformations: One object is symmetric if, after a transformation is applied, the result remains the same, i.e. it remains “invariant”. But we also observe symmetry breaking, which is particularly of interest when it is not a random effect but follows a definite pattern. In Fig. 1.1 we show the three-span arch of the FermiLab entrance, near Chicago, which appears perfectly symmetric when viewed from below, but has a calculated asymmetry from its other views. Symmetry and symmetry breaking are very important concepts in the field of elementary particle physics, however not referring to objects but to the fundamental laws of physics.
../images/467908_1_En_1_Chapter/467908_1_En_1_Fig1_HTML.png
Fig. 1.1

Symmetry Breaking

We show here how symmetry has acted as a guiding principle for both the existence of new particles and the formulation of interactions. One can claim that “Symmetry dictates Interaction”, as stated by Yang. In Quantum Mechanics, the symmetry is implemented by a unitary transformation $$ \hat{U} $$ acting on states and observables. If the dynamics, described by the Hamiltonian $$ \hat{H} $$, is invariant under the transformation one has

$$ \left[\hat{H},\hat{U}\right]=0 $$
(1.1)

Under infinitesimal transformations generated by $$ \hat{G}={\hat{G}}^{\dagger }, $$ one obtains immediately

$$ \frac{\mathrm{d}}{\mathrm{d}t}\left\langle \hat{G}\right\rangle =i\left\langle \left[\hat{H},\hat{G}\right]\right\rangle =0 $$
(1.2)

As $$ \hat{G} $$ is Hermitian, it corresponds to an observable that satisfies a conservation law if $$ \hat{U} $$ is symmetry of $$ \hat{H} $$. Well-known examples are momentum for translations, angular momentum for rotations or charge for gauge symmetry. For local gauge symmetry, the requirement of invariance leads to a covariant derivative with a mediator field responsible of interactions. This is valid for either QED with the Abelian U(1) gauge group or non-Abelian gauge groups with the interaction field transforming as the adjoint representation.

In Sect. 2, we develop the ideas leading from hadrons to quarks and the symmetries of strong interactions. In Sect. 3, a parallel discussion is made for electroweak interactions starting from parity violation leading to the standard model with neutral currents and the need of charm plus the third family, including quark-lepton symmetry. Section 4 presents the Brout–Englert–Higgs mechanism for the origin of mass breaking the electroweak gauge symmetry. Some conclusions and outlook are given in Sect. 5.

1.2 Quarks and Strong Interactions

The proliferation of non-strange and strange Hadrons in the 60s of the twentieth century led to the Eightfold Way of Gell Mann and Ne’eman with the use of the Flavour SU(3) symmetry. The fundamental representations $$ 3,\overline{3} $$ are the elementary building blocks for arbitrary higher-dimensional representations. Mesons are $$ q-\overline{q} $$ states $$ 3\times \overline{3}=1+8 $$, Baryons are q-q-q states 3 × 3 × 3 = 1 + 8s + 8a + 10, with three quark q = u, d, s states. In Fig. 1.2, the octet and decuplet representations of Baryons are given in terms of third component of Isospin I3 and hypercharge Y axes. According to the Gell Mann–Nishijima rule, the electric charge is Q = I3 + Y/2, with Y = B + S, B the baryonic number and S strangeness.
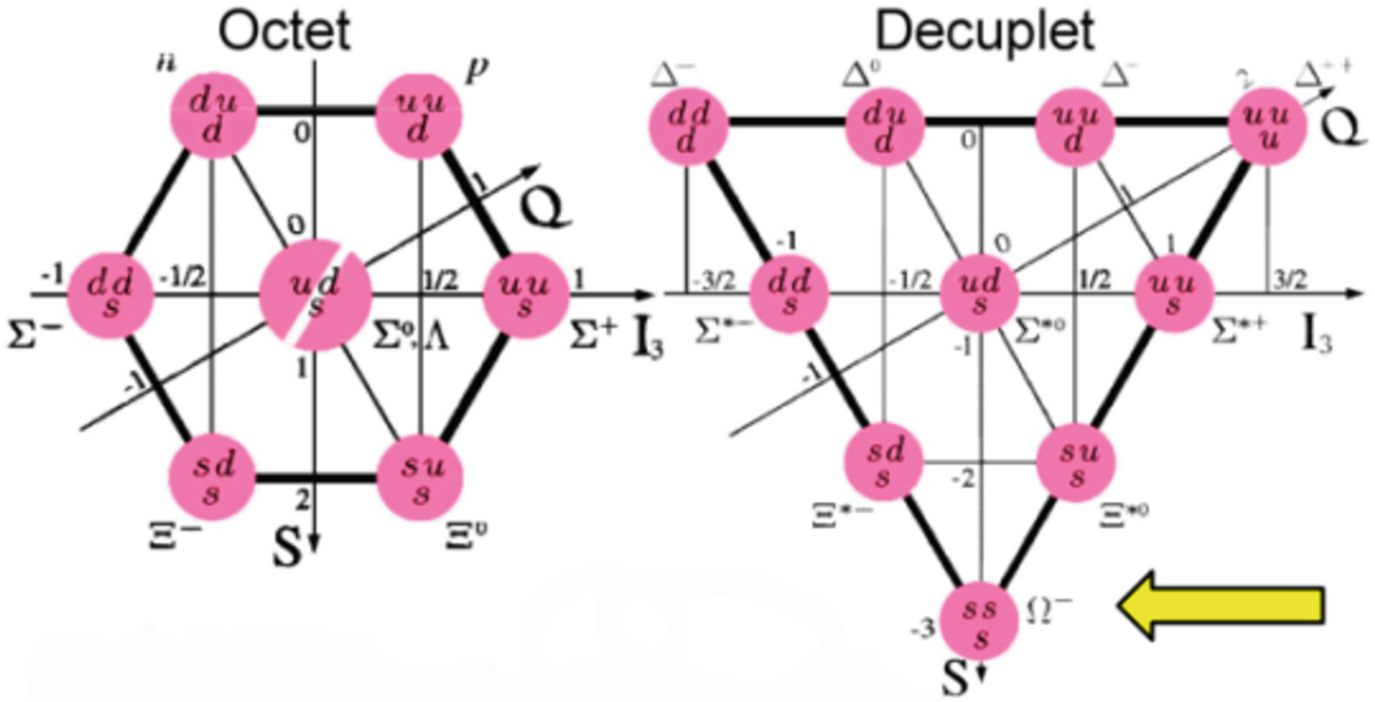
../images/467908_1_En_1_Chapter/467908_1_En_1_Fig2_HTML.png
Fig. 1.2

Octet and decuplet of baryons

At the time of this formulation, the Ω− had not been detected. Its later discovery was a great triumph of the whole scheme.

For some time, however, the quark model for hadrons (Gell Mann 1964) was considered by the scientific community as a mere theoretical construct to describe the classification of hadrons in the SU(3) symmetry. The question was “Are Quarks real?”. Since 1969, deep inelastic scattering experiments (Bloom et al. 1969) at SLAC showed that the proton contained much smaller, point-like constituents and was therefore not an elementary particle. Physicists were reluctant to firmly identify these objects with quarks at the time, instead calling them “partons”—a term coined by Feynman. The partons that were observed at SLAC would later be identified as up and down quarks. Nevertheless, “parton” remains in use as a collective term for the constituents of hadrons (quarks, antiquarks and gluons). We do know at present that leptons (electrons, muons, neutrinos) find partons in the proton with high momentum transfer events.

A “jet” is a narrow cone of hadrons produced by the hadronization of a parton. Jets were observed for the first time in the e+ e− annihilation into hadrons at the SPEAR storage ring (Hanson et al. 1975) and interpreted in terms of quarks. Quarks therefore exist, but they cannot propagate asymptotically. Quarks are then confined!

One of the reasons why the idea of real quarks was seen with scepticism was the problem of quarks with the exchange symmetry associated with the spin-statistics connection. It is easily realized with the Δ++ puzzle: The state u↑u↑u↑ with third component of spin S3 = +3/2 is evidently symmetric under exchange of flavour (u), spin (S3 = +1/2) and space (L = 0) degrees of freedom of the three quarks!.

If quarks are real and satisfy the exchange symmetry, a new degree of freedom is necessary for quarks, the “colour” (r, g, b) being antisymmetric for its exchange in baryons. Precisely the singlet colour wave function

$$ {\Psi}_{\mathrm{c}}^{qqq}=\frac{1}{\sqrt{6}}\left( rgb- rbg+ gbr- grb+ brg- bgr\right) $$
(1.3)
is antisymmetric, so that qqq states exist, but these hadrons are colourless. We conclude that colour is confined, so that colourful quarks are confined. For the requirement of antisymmetry, we need a number Nc = 3 of colours. Experimental evidence that Nc = 3 came from the interpretation of e+ e− → hadrons in terms of $$ q\ \overline{q} $$ production, with a cross-section predicted to be proportional to Nc.
The colour charge appears as generator of an exact SU(3)c local gauge symmetry, leading to colour interaction of quarks in the fundamental representation, mediated by eight massless gluons in the adjoint representation. This interaction is flavour-blind and only the quark mass terms break flavour independence. The origin of the quark mass terms should then be external to this QCD (Quantum ChromoDynamics) theory. The field tensor is covariant (A = 1, ..., 8) leading to self-interaction of the vector gluon field $$ {A}_{\mu}^A $$ in the Lagrangian term $$ -\frac{1}{4}\ {F}_{\mu \nu}^A\ {F}^{A\mu \nu} $$
$$ {F}_{\mu \nu}^A={\partial}_{\mu }{A}_{\nu}^A-{\partial}_{\nu }{A}_{\mu}^A-{g}_s{f}_{ABC}{A}_{\mu}^{\mathrm{B}}{A}_{\nu}^C $$
(1.4)

All coloured objects have strong interaction with gluons, so that quarks with gluons, gluons with themselves. Gluons have colour, so they are confined like quarks. Gluon jets were first observed in the annihilation e+e− → $$ q\ \overline{q}\ g $$ to three jets by the TASSO experiment (Brandelik et al. 1979) at the PETRA accelerator at the DESY laboratory.

The QCD coupling constant αS = gS2/(4π) is dimensionless, therefore the classical field theory in the chiral (massless) limit is scale invariant. There is a conformal symmetry. However, in the perturbative treatment of the QCD quantum theory, predictions for observables are made in terms of the renormalized coupling $$ {\alpha}_{\mathrm{S}}\left({\mu}_{\mathrm{R}}^2\right) $$, which is a function of the renormalization scale. Taking it close to the momentum transfer Q2, αS (Q2) indicates the effective strength of the interaction.

The coupling runs with the renormalization scale $$ {\mu}_{\mathrm{R}}^2 $$ and this running coupling satisfies the renormalization group equation controlled by the QCD β(αS) function. The 1 loop β function coefficient has contributions to the gluon self-energy from gluon self-couplings and fermion couplings with opposite signs. The dominance of the first term gives to QCD, distinct to QED, the property of ASYMPTOTIC FREEDOM (Gross and Wilczek 1973; Politzer 1973). The approximate analytic solution is

$$ {\alpha}_{\mathrm{s}}\left({\mu}_{\mathrm{R}}^2\right)={\left({b}_0\ln \left(\raisebox{1ex}{${\mu}_{\mathrm{R}}^2$}\!\left/ \!\raisebox{-1ex}{${\Lambda}^2$}\right.\right)\right)}^{-1},\kern1em {b}_0=\left(33-2{n}_f\right)/\left(12\ \pi \right) $$
(1.5)
with Λ a constant of integration, representing the non-perturbative scale of QCD. The running coupling has been experimentally demonstrated with Λ ~ 250 MeV. The dimensional transmutation from αS to Λ is thus originated in the quantum conformal anomaly breaking the conformal symmetry. This Λ is responsible of the nucleon mass and, as a consequence, the baryonic mass of the Universe!

1.3 Chirality and Electroweak Interaction

Parity violation by weak interactions was postulated (Lee and Yang 1956) in the 50s of the twentieth century to solve the puzzle of the different parities of the decay products of neutral kaons. It was then observed in nuclear beta decay and later in charged pion decays.

Parity (P) $$ \overline{r}\to -\overline{r} $$, charge conjugation (C) q →  − q and time reversal (T) Δt →  − Δt are discrete symmetries. In Fig. 1.3, we illustrate P and C transformations taking as reference the observed π+ → μ+ νμ decay.
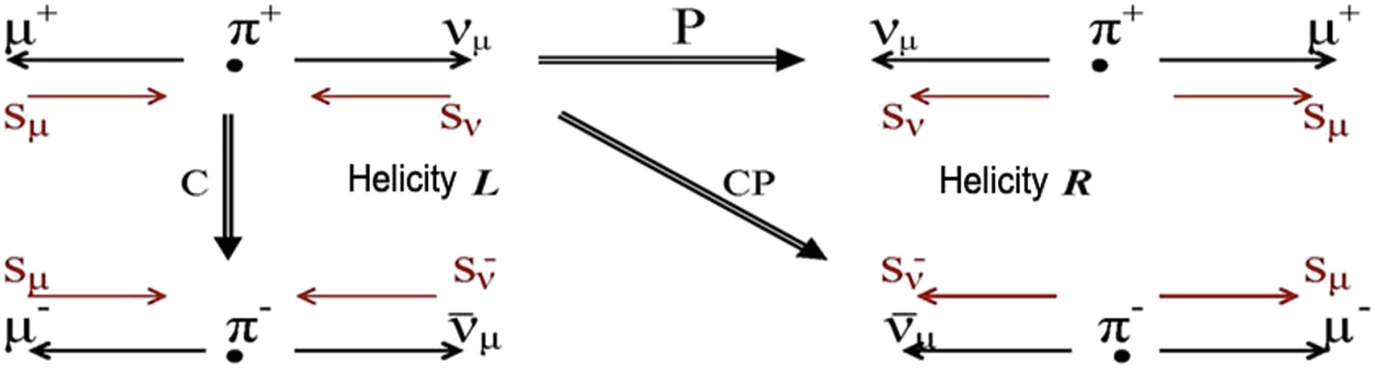
../images/467908_1_En_1_Chapter/467908_1_En_1_Fig3_HTML.png
Fig. 1.3

The P, C and CP transformations in pion decays

Whereas the P-transformed and C-transformed processes do not exist in nature, the

CP-transformed decay $$ {\pi}^{-}\to {\mu}^{-}\kern0.5em {\overline{\nu}}_{\mu } $$ is observed with the same decay rate. We conclude that parity, as well as charge conjugation, is maximally violated, whereas CP is a good symmetry for pion decays.

We call a chiral phenomenon to one which is not identical to its mirror image. The spin component of a particle along its momentum may be used to define a handedness, or helicity. For massless fermions, the helicity is invariant and this intrinsic property is the “chirality”. The invariance under parity for a Dirac fermion state ψ is called “chiral symmetry” and the transformation in Dirac space is implemented by the γ5 Dirac matrix. Using projectors, left and right chiral fermions, with definite chirality −1 and +1, are given by $$ \frac{1}{2}\left(1-{\gamma}_5\right)\psi, \kern0.75em \frac{1}{2}\left(1+{\gamma}_5\right)\psi $$. There are observables, like the vector and axial vector charges that conserve chirality of the fermions, whereas other observables, like the mass or dipole moments, connect the two chiralities.

In the unified electroweak theory (Glashow 1961; Weinberg 1967; Salam 1968) based on the SU(2)L × U(1)Y gauge group, the fermion building blocks are not the Dirac fields ψ, but the chiral fields and the gauge group transformation distinguishes them: whereas the left fields transform as doublets under SU(2)L, the right fields transform as singlets under SU(2)L. We say that this unified field theory is a CHIRAL GAUGE THEORY.

The electroweak gauge group SU(2)L × U(1)Y symmetry demands three gauge bosons W1, W2, W3 of weak isospin from SU(2)L and the B boson of weak hypercharge Y from U(1)Y. The gauge symmetry is here broken by the mass terms and the physical fields with definite mass and charge are W±, γ, Z given by

$$ \left(\begin{array}{c}\gamma \\ {}Z\end{array}\right)=\left(\begin{array}{c}\cos {\theta}_{\mathrm{w}}\\ {}-\sin {\theta}_{\mathrm{w}}\end{array}\kern1em \begin{array}{c}\sin {\theta}_{\mathrm{w}}\\ {}\cos {\theta}_{\mathrm{w}}\end{array}\right)\left(\begin{array}{c}B\\ {}{W}_3\end{array}\right),\kern1em {M}_z=\frac{M_{\mathrm{W}}}{\cos {\theta}_{\mathrm{w}}} $$
(1.6)
with θw the weak mixing angle. The theory predicts the existence of weak neutral currents mediated by the Z boson and they were discovered (Hasert et al. 1973) by the Gargamelle Bubble Chamber Collaboration at CERN in 1973 with muon neutrino interactions without muons in the final state. Ten years later, in 1983, the UA1 and UA2 experiments in the $$ S\overline{p} pS $$ Collider at CERN discovered the massive W, Z bosons as real particles reconstructed from their W+ → l+ νl, Z → l+ l− (Arnison et al. 1983; Bagnaia et al. 1983) decays. These CERN discoveries established the triumph of the standard model of electroweak interactions.

1.3.1 GIM Mechanism: Need of Charm

With u, d, s quarks only, the Cabibbo d-s mixing in the charged weak current leads, by the SU(2)L symmetry of the standard model, to strangeness-changing-neutral current at tree level implying, for example, fast KL → μ+ μ− decay, against experiment. In 1970, Glashow–Iliopoulos–Maiani (Glashow et al. 1970) solved this problem with an additional fourth quark flavour c completing two families of quark doublets

$$ \left\{\begin{array}{c}u\\ {}d\end{array}\right\}\left\{\begin{array}{c}c\\ {}s\end{array}\right\},\kern1em U=\left(\begin{array}{c}\cos \theta \kern0.75em -\sin \theta \\ {}\sin \theta \kern2em \cos \theta \end{array}\right) $$
(1.7)
and interpreting the Cabibbo mixing as a unitary mixing matrix U in d-s space, exhibiting the mismatch between weak eigenstates and mass eigenstates, with charged currents relative to both u and c quarks. SU(2)L then dictates that neutral currents are governed by U + U = I, so they are diagonal and universal. Neutral currents are flavour-conserving at tree level! At higher orders, flavour-changing-neutral currents can be induced from c-u mass difference. The KL → μ+ μ− is suppressed—not only by higher orders—by the GIM additional factor $$ \left({m}_{\mathrm{c}}^2-{m}_{\mathrm{u}}^2\right)/{M}_{\mathrm{W}}^2 $$.

The discovery (Aubert et al. 1974; Agustin et al. 1974) of the $$ c\ \overline{c} $$ J/ψ meson in 1974 at BNL and SLAC is coined as the November Revolution of particle physics. Charmed $$ c\ \overline{d},c\ \overline{s},c\ u\ d $$ ... hadrons were discovered later.

1.3.2 CP Violation

CP symmetry would imply that the Laws of Physics should be invariant in form when a particle is interchanged with its antiparticle (C) while its spatial coordinates are inverted (P). For the neutral kaon system with mixing ΔS = 2 $$ {K}^0-{\overline{K}}^0 $$ by weak interactions, the physical states of definite mass and lifetime KL, KS should be CP eigenstates leading to conservation laws: the decay KL → π π should be forbidden. Its unexpected observation (Christenson et al. 1964) in 1964 opened the entire new field of CP violation in Flavour Physics.

Can CP violation be described in the standard model? In 1973, Kobayashi and Maskawa discovered (Kobayashi and Maskawa 1973) such a possibility by breaking the CP symmetry in the standard model Lagrangian by means of enlarging the particle content of the theory. By going to, at least, three families of fermions the most general mismatch mixing matrix U between weak and mass eigenstates for d-s-b quarks contains a physical relative phase such that for antiquarks becomes its complex conjugate U*. One would need three families of fermions at least!

The $$ b\ \overline{b} $$ ϒ meson was discovered in 1977 at FermiLab and B-mesons later. Since then all known laboratory experimental results on CP violation for K, B and D physics are in agreement with the unitary mixing matrix paradigm U (CKM) with three active families of quarks. In Fig. 1.4, the three families are written and the corresponding “unitarity triangle” relation for Bd physics represented
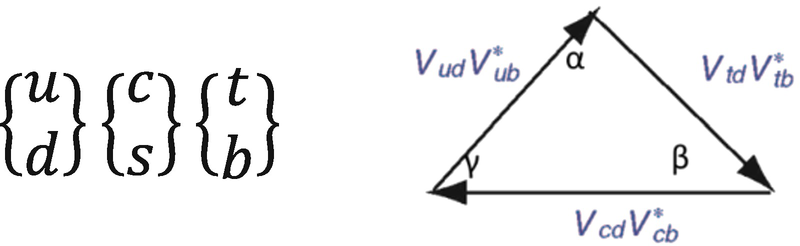
../images/467908_1_En_1_Chapter/467908_1_En_1_Fig4_HTML.png
Fig. 1.4

Three quark families and unitary triangle for Bd physics

One should notice: (a) the three upper u, c, t quarks have to be involved; (b) the three angles α, β, γ are CP violating observable phases, the first two involving the virtual $$ {B}^0-{\overline{B}}^0 $$ mixing through the heavier t quark, whereas γ is a signal of direct CP violation in the decays to i and u quarks.

However, this standard model description of CP violation is not enough to explain the matter-antimatter asymmetry in the Universe!

1.3.3 Top Quark physics

The top quark is the most massive of all observed elementary particles. With a mass of 172.44 GeV/c2, it weighs like an atom of tungsten!. It decays by weak interaction t → bW with a lifetime of 5 × 10−25 s. Such a short life is 1/20 of the timescale for quark hadronization, allowing “bare” quark studies with its entire spin density matrix in the production as well as in the decay.

The top quark was first indirectly “seen” with non-decoupling virtual quantum effects in $$ {B}^0-{\overline{B}}^0 $$ mixing (Albajar et al. 1987a, b; Albrecht et al. 1987) measured by UA1 and ARGUS in 1987, in the universal Z boson self-energy (Veltman 1980) and in the specific Z$$ \kern0.5em b\ \overline{b} $$ vertex (Bernabeu et al. 1988; Bernabeu et al. 1991), the last two observed in the LEP experiments. The direct detection of top quarks was then made in 1995 at the $$ p\ \overline{p} $$ Tevatron (Abe et al. 1995; Abachi et al. 1995). The p p collider LHC facility is at present a top quark factory by means of its strong $$ g\ g\to t\ \overline{t} $$ and weak $$ u\ \overline{d}\to t\ \overline{b} $$ production mechanisms.

1.3.4 Time Reversal

A symmetry transformation T that changes the dynamics of a physical system into another with an inverted sense of time evolution is called time reversal (reversal-in-time). It is implemented in the space of states by an antiunitary operator implying that its study has to be made with asymmetries built under the exchange of in, out states.

The decay is an irreversible process indicating that a true TRV observable, needing a definite preparation and filtering of the appropriate initial and final particle state, looks impossible for transitions in the case of decaying particles. A bypass to this NO-GO argument was found (Banuls and Bernabéu 1999, 2000) using entangled systems of unstable particles with the ingredients: (a) The decay as a filtering measurement; (b) Entanglement implying the information transfer from the decayed particle to its living partner. For the entangled $$ {B}^0-{\overline{B}}^0 $$ system produced by e+ e− collisions at the ϒ(4S) peak, one may study the time dependence in meson transitions associated to the definite flavour-CP eigenstate decay products. There are 2(Flavour) × 2(CP)—2(time ordering) = 8 transitions of this kind which can be connected by different separate genuine T, CP, CPT symmetry transformations.

In Fig. 1.5 the experimental steps to measure the time-dependent TRV asymmetry for the $$ {\overline{B}}^0\to {B}_{-} $$ and $$ {B}_{-}\to {\overline{B}}^0 $$ meson transitions between flavour and CP eigenstates are given.
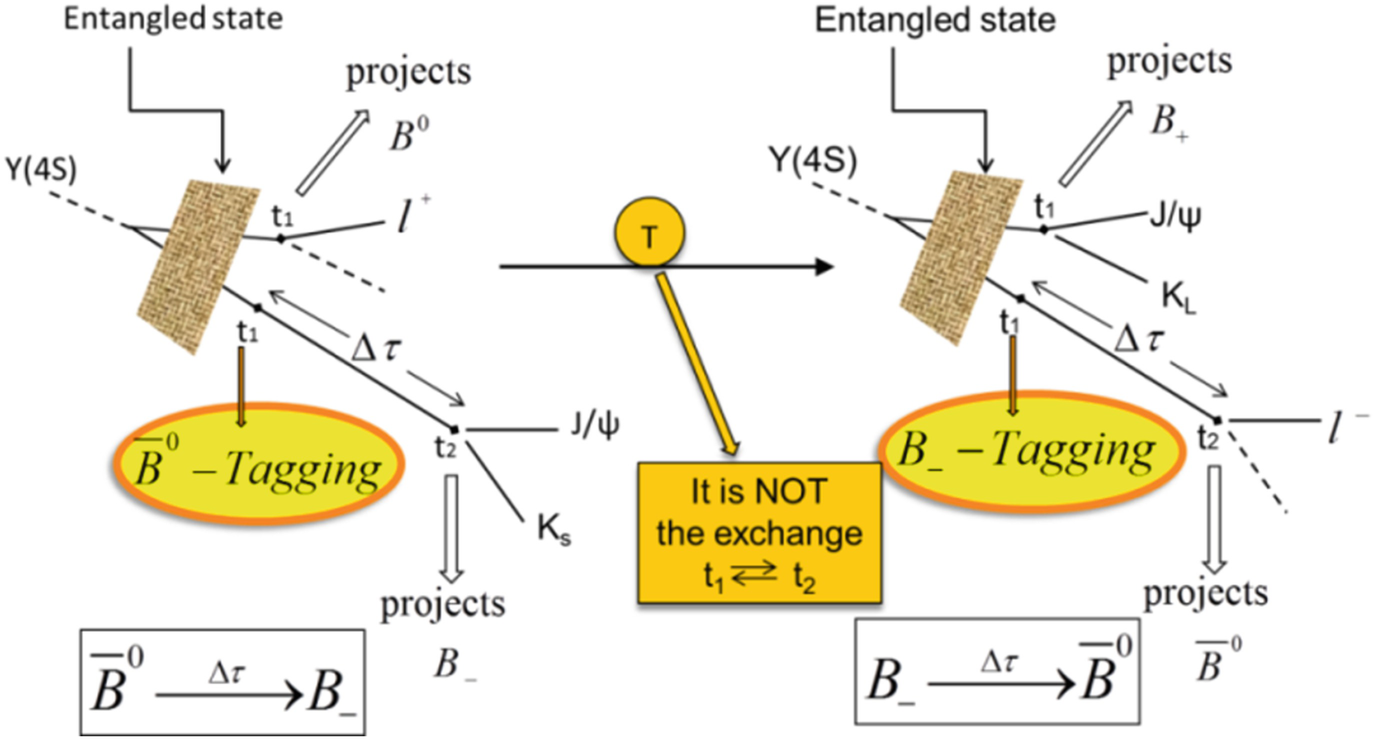
../images/467908_1_En_1_Chapter/467908_1_En_1_Fig5_HTML.png
Fig. 1.5

Experimental steps to observe TRV in the entangled Bd-system

Using these concepts, the BABAR collaboration observed (Lees et al. 2012) in 2012 a true TRV effect with 14 σ significance.

1.3.5 Gauge Anomalies: Quark-Lepton Symmetry

A gauge anomaly is a feature of quantum physics, a one-loop diagram, invalidating the gauge symmetry of a quantum field theory. All gauge anomalies must cancel out. Anomalies in gauge symmetries would destroy the required cancellation of unphysical degrees of freedom, such as a photon polarization in time direction.

Are gauge anomalies cancelled in the standard model? Anomalies appear in even D spacetime dimensions with CHIRAL fermions running in the loop with n = 1 + D/2 vertices. For D = 4, n = 3, it corresponds to vector-vector-axial couplings! The condition for cancellation involves the particle content and the relations among their couplings (Fujikawa and Suzuki 2004): the symmetrized trace over the generators of the gauge group vanishes

$$ \mathrm{tr}\left(\left\{{\tau}_i,{\tau}_j\right\}{\tau}_k\right)=0 $$
(1.8)
Such a cancellation operates within each family of quarks and leptons establishing an intriguing connection between the two sectors announcing a grand unification. For the three families required to incorporate CP violation, we then write the symmetry between quarks and leptons (Fig. 1.6).
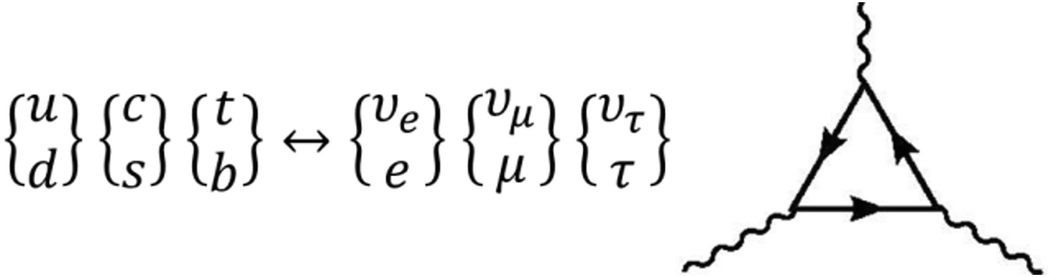
../images/467908_1_En_1_Chapter/467908_1_En_1_Fig6_HTML.png
Fig. 1.6

Quark-Lepton Symmetry requested for the cancellation of Eq. (1.8)

1.4 The Brout–Englert–Higgs Mechanism

The standard model of particle physics contains as elementary constituents the three families of fermions with the quark-lepton symmetry. Their interactions appear as a requirement of the local gauge symmetries SU(3)c × SU(2)L × U(1)Y generated by the three charges of colour, weak isospin and weak hypercharge. The last two combine to the electric charge for U(1)em. These interactions operate as exchange forces with the mediators gluon with m = 0, but confined, photon with m = 0 and the massive W±, Z bosons. The standard model not only predicted new particles and interactions, but its agreement with all precision experimental results of detailed observables in the last decades is impressive. However, these gauge symmetries are exact only in the massless limit, against the facts in nature. One should have a very subtle mechanism for the origin of mass without affecting the interactions, responsible of the SU(2)L × U(1)Y gauge symmetry breaking into U(1)em. This is the Brout–Englert–Higgs mechanism (Englert and Brout 1964; Higgs 1964).

The Spontaneous ElectroWeak Symmetry Breaking (SEWSB) is based on the possibility that a symmetric Law of Physics can lead to asymmetric solutions. One should be aware that a quantum field theory needs for its precise definition not only the Lagrangian (the physical law) but also the quantum vacuum, the lowest energy state from which particles are created and annihilated. SEWSB means that the physical law is symmetric and the vacuum is asymmetric. How?

The spacetime is filled with a “medium”, a complex scalar field with the interaction being like a “mexican hat” (Fig. 1.7).
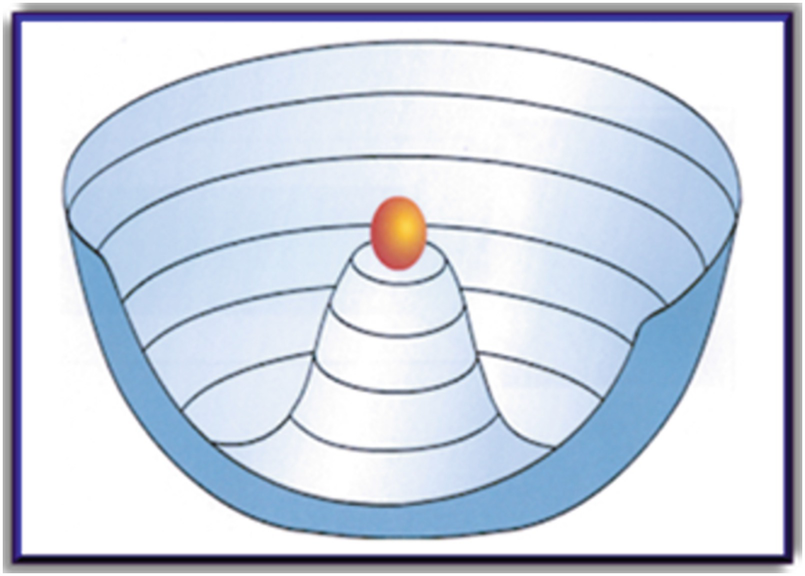
../images/467908_1_En_1_Chapter/467908_1_En_1_Fig7_HTML.png
Fig. 1.7

Interaction of the complex scalar field

This behaviour is obtained from a negative “mass square” quadratic term plus a positive quartic term. We observe that, instead of a unique symmetric lowest energy state, there are many possible vacua and one choice breaks the symmetry. This “spontaneous symmetry breaking” could be called a hidden symmetry because the results are independent of the chosen vacuum.

The physical particle created from the new vacuum is the Higgs boson, a remnant of the Brout–Englert–Higgs Mechanism, hence its importance. There is a crystal clear signature of the Higgs particle: its coupling to all particles, including to itself, is proportional to their mass, a property that breaks the gauge symmetry. The origin of mass comes from the asymmetry of the new vacuum.

On 4 July 2012, the ATLAS and CMS experiments at CERN’s Large Hadron Collider announced (Aad et al. 2012; Chatrchyan et al. 2012) they had each observed a new particle in the mass region around 125 GeV. In Fig. 1.8, we show these original data together with the comparison of the measured partial decay rates to different channels to the expected theoretical predictions in the standard model.
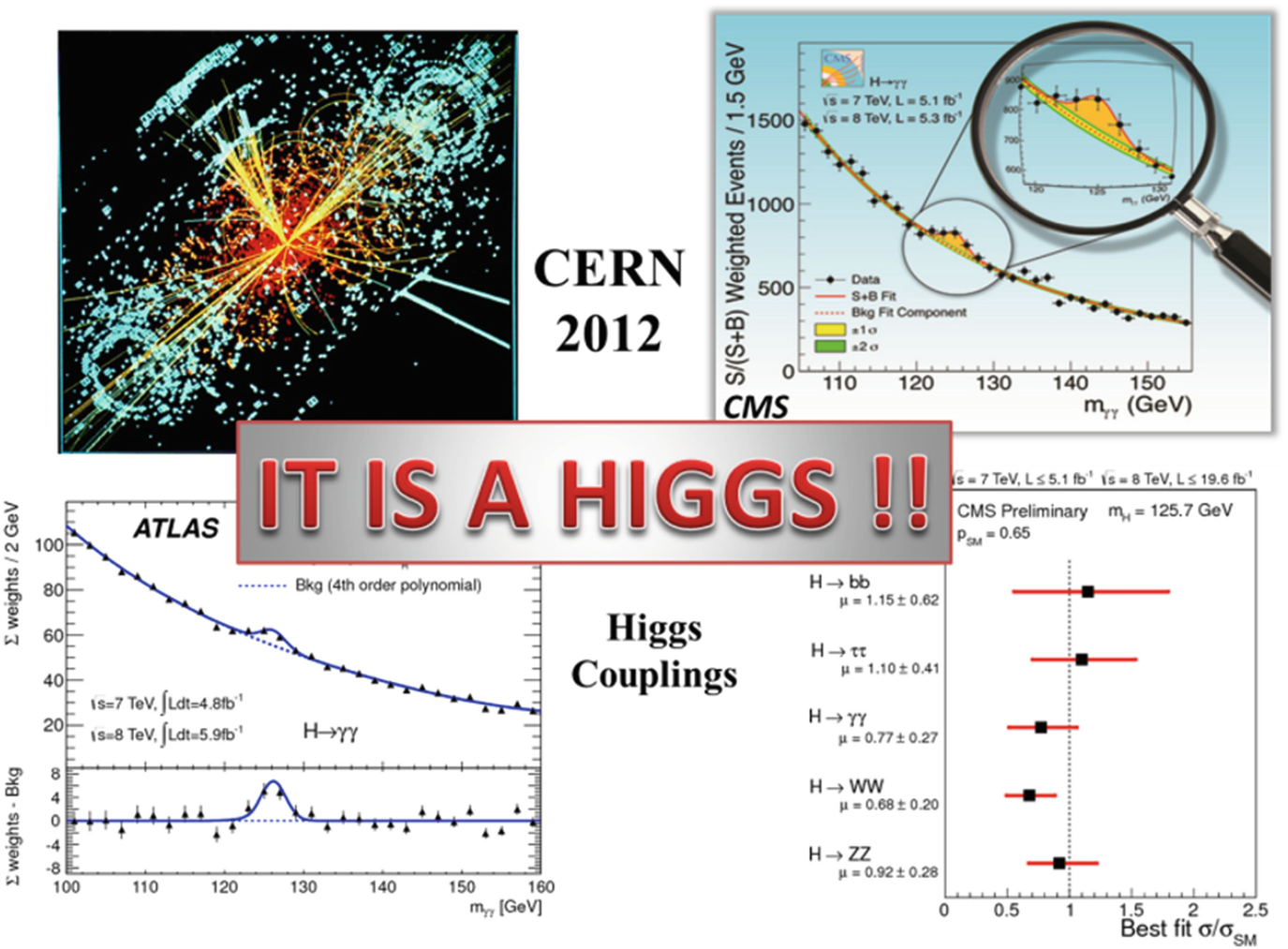
../images/467908_1_En_1_Chapter/467908_1_En_1_Fig8_HTML.png
Fig. 1.8

Production and Decay of the Higgs boson observed in the ATLAS and CMS experiments

As seen, the couplings are consistent with hose expected for a Higgs particle.

On 8 October 2013, the Nobel prize in physics was awarded jointly to François Englert and Peter Higgs “for the theoretical discovery of a mechanism that contributes to our understanding of the origin of mass of subatomic particles, and which recently was confirmed through the discovery of the predicted fundamental particle, by the ATLAS and CMS experiments at CERN’s Large Hadron Collider”.

1.5 Conclusions and Outlook

The three sectors of the standard model—strong, electroweak and Higgs—represent a tribute to the concept that symmetry, and symmetry breaking, is the guiding principle for particles and interactions.

We have emphasized the role of different definite patterns for the breaking of symmetries, like

  • Mass terms are incompatible with both gauge and chirality symmetries.

  • Quantum loop anomalies break conformal symmetry for vector theories and gauge symmetry for chiral field theories.

  • The particle content of the theory controls the breaking of discrete symmetries CP and T.

  • A gauge asymmetric vacuum leads to spontaneous symmetry breaking with hidden gauge symmetry and explaining the origin of mass for elementary particles.

What next? There are theoretical and observational reasons for searching Beyond-Standard-Model Physics at LHC experiments and in other facilities. I list some of them:

  • Why the quantization of electric charge, magnetic monopoles?

  • The principle of “Threeality” in fundamental physics.

  • The hierarchy problem for scalars, supersymmetry?

  • Grand unification, p-decay?

  • Neutrino Mass, mixing, CPV, majorana?

  • Charged lepton flavour violation?

  • Baryon asymmetry of the Universe

  • Dark matter

  • Dark energy

Most ideas tackling these points are linked to the Minkowski spacetime paradigm that symmetries will continue to be the guiding principle for fundamental physics. Among the discrete symmetries, CPT is protected by the “CPT-Theorem” in quantum field theory formulated in with interactions satisfying Lorentz invariance, locality and unitarity. But there is nothing at the level of quantum mechanics which forbids to have CPT-violation and there are sound quantum gravity arguments in favour of this ultimate symmetry breaking.

Acknowledgement

I would like to thank the organizers of Frontiers of Fundamental Physics 2017 for the opportunity of presenting these ideas and the warm atmosphere of the Conference. This research has been supported by MINECO Project FPA 2014-54459-P, Generalitat Valenciana Project GV PROMETEO/2017/033 and Severo Ochoa Excellence Centre Project SEV 2014-0398.