Chapter 8
Test-Taking Strategies for Core Math
In This Chapter
 Saving time with shortcuts
Saving time with shortcuts
 Whittling down the answer choices
Whittling down the answer choices
 Coming up with the correct answer on your own
Coming up with the correct answer on your own
Mathematical knowledge and practice are very important for taking the Praxis Core exam’s math section, but the arsenal you take into battle doesn’t have to stop there. Test-taking strategies can make your weapons even more effective. What you know is extremely important, but so is what you do with what you know. This chapter is about making the best of the knowledge you have.
Using Helpful Shortcuts
Getting answers that are correct on the Praxis Core exam is really important. However, coming up with the right answers isn’t your only concern. You must consider something else of major relevance: The exam is timed. You have two hours (120 minutes) to answer 56 problems. Any methods you can use to reduce the time you take to answer questions without sacrificing accuracy will help you. The methods we outline in the following sections are real, and they work. We encourage you to give them a trial run as you take the practice tests in Part V and online.
Solving equations versus determining what must be solved
You will almost definitely have word problems that require setting up and solving algebraic equations when you take the Praxis Core exam. Answering these problems requires more than the ability to solve equations. You also need to determine what information the problem is asking you for, that is, what needs to be solved. You can use a variable to represent the unknown quantity that must be determined.
The next step is to put the algebraic expressions into an equation and solve the equation. The solution to the equation will be the value of the first unknown. Once you know it, you can find the values of any other unknowns by putting the value of the variable for which you just solved into the expressions used to represent the variables for which you have not yet solved.
(A) 42
(B) 8
(C) 25
(D) 41
(E) 37
The correct answer is Choice (D). The question asks for John’s age, so you can make John’s age the first unknown and represent it with a variable, such as x. Because John is four years older than Adam, you can represent Adam’s age with the expression x – 4. The next step is to write an equation with the two expressions. Just translate the information in the word problem into mathematical language. John was twice Adam’s age 33 years ago. Their ages 33 years ago can be represented by subtracting 33 from their current ages:
- John: x – 33
- Adam: x – 4 – 33
“Twice Adam’s age 33 years ago” can be represented by 2 multiplied by 33 less than Adam’s current age.
- Adam: 2(x – 4 – 33)
Then set up an equation that shows their ages 33 years ago with John’s being twice as much as Adam’s:
- x – 33 = 2(x – 4 – 33)
Notice the direct translation of worded information in that equation. It says exactly the same thing in a different way. The solution to the equation is 41. (For a review of how to solve algebraic equations, turn to Chapter 5.) John’s age is therefore 41.
Using estimation and approximation
Estimation is the act of using known information to get a number that is close to the answer to a question although it may not be the actual answer. This can be helpful on the Praxis Core exam because most of the test is multiple choice. When you estimate, you have a good chance of getting the answer right by choosing the one that’s closest to your estimate. Because the test is timed, estimation may be handy for a few last answers before time’s up.
Estimation can also help you to eliminate choices that are definitely wrong, and it can help you make sure the answer you get is not something beyond the fringe of reason or the result of a miscalculation. However, don’t spend too much time estimating for just that purpose. You’ll be performing a juggling act with time and caution.
Approximation is using numbers that are very close to numbers given in a problem for the purpose of making calculating easier. This, too, can save you time when time is running short, and it can also help you eliminate wrong answers. If you have to make a wild guess, your chances of guessing the correct choice increase when you can eliminate some of the choices.
When you multiply with irrational numbers in decimal form, you often have to approximate. An irrational number is a number that can’t be represented as a ratio of two integers. An irrational number in decimal form doesn’t terminate or repeat. In other words, the digits after the decimal don’t have a pattern and continue infinitely. Because you don’t have time to calculate with an infinite number of digits, approximation can often help.
For example, the number 7.32960584965105… is an irrational number. You may come across a number like that when you use your calculator. Rounding such a number to four decimal places should be sufficient to get a correct result in almost all cases. Rounding also saves time, and time is precious on the Praxis Core exam.
Using the calculator
An on-screen calculator is provided for you on the math section of the Praxis Core exam. That makes computation easier and saves time over doing calculations on paper. The calculator’s keypad includes keys for all the digits, the four basic operations (adding, subtracting, multiplying, and dividing), square roots, making numbers negative, a decimal, parentheses, memory, clearing, transfer display (which can transfer your answers to the answer box on constructed response questions), and, of course, the highly important equal sign. The calculator is also programmed to follow the order of operations. However, you still need to know the order of operations for solving variable equations.
Identifying calculations you can make in your head
We highly encourage caution when making calculations for the Praxis Core exam. That involves writing out work on scratch paper and using the calculator, but only when you actually have time to do those things. You should write and use the calculator even for the calculations you’re sure you can do in your head when you’re keeping a good pace, though we don’t recommend using the calculator for calculations that can come from pure memory.
However, when time becomes a major issue, you need to know what more-complex calculations you can do in your head relatively safely. The first category to consider is problems for which writing and using the calculator don’t actually help you figure out the answer. For these calculations, the paper and calculator will only help you avoid careless errors. Suppose you have to calculate 2 + 2. We recommend using paper even for that when you’re good on time. Using paper allows you to write out every step of the calculations, better ensuring that you avoid careless errors. When you’re way behind time, you should speed up by making such a calculation only in your head. Timing is important, but so is caution.
While we believe in writing every step involved in answering a math question, we don’t think the calculator should be used for every single calculation. The more you have in your brain’s memory, the faster your pace will be.
The art of guessing as a last resort
If time really wears thin on the exam and you only have time to make wild guesses, go ahead and make nothing but wild guesses. A point may come where you don’t even have time to estimate, approximate, or do quick calculations in your head. That’s when you need to just start hitting answers as fast as you can.
If you make all of your choices randomly, you have some probability of getting all of them right. However, the flip side to that coin is that you have equal probability of getting all of them wrong. Still, you’ll most likely get some right if you answer enough of them that way.
A small number of questions tell you that more than one answer choice may apply. If you notice one of those during a pure guessing phase, you should mark at least two answers of the three or four answer choices presented.
A few of the questions don’t have choices presented with them. You should answer those last if you’re in a guessing phase. When you get around to guessing on them, see how much time you have left. Quickly look at the problem and give the best guess you can give. If you still have a few more seconds to actually think about the answer, do all of the thinking you have time to do and then give the best answer you can.
Working backward
When you’re in doubt about how to answer a math problem by using the conventional calculation methods, you can increase the probability of getting the correct answer by working backward. This approach can be used in various situations and in different ways. For example, if an end result is given and you’re asked about what was involved in getting the result, you can start at the end and work toward the beginning. This technique can be used for age problems, problems concerning final amounts of money, final locations, and other types of problems. The technique is sometimes the only one that will work.
(A) 24 miles
(B) 0 miles
(C) 4 miles
(D) 44 miles
(E) 6 miles
The correct answer is Choice (C). You can answer this problem by using positive and negative numbers and adding them, with north distances being positive and south distances being negative. However, you can also work backward from the final distance and trace Robert’s travel back to the beginning of the hike. If Robert was 14 miles north and had previously walked 10 miles south, he was 24 miles from his campsite before the final part of the walk. If he got to that point by walking 20 miles north, he was 20 miles back, which is 4 miles from the campsite. Choice (A) is the distance Robert was from his campsite before changing directions, but not the initial distance. Choice (D) results from adding 20 to 24 instead of subtracting it.
Narrowing Down Answer Choices
You improve your chances of choosing the right answer — and choosing it quickly — by eliminating choices that you know are wrong. This narrows the set of choices to consider and helps lead you to the right answer. We discuss this earlier in this chapter to make a case for increasing the probability of getting the right answer, but another advantage is that it helps lead you to better considerations.
How to eliminate obviously wrong answer choices
If a choice is so outrageous that it couldn’t possibly be the correct answer, you should eliminate it from consideration. For example, the length of a rectangle can never be greater than the rectangle’s perimeter. A person’s age years ago can’t be greater than his or her current age. The mean of a set of data can never be greater than the highest number. These are just some examples of impossibilities you can readily notice.
(A) 270
(B) 30
(C) 60
(D) 120
(E) 3
The correct answer is Choice (B). You can find the answer by solving the equation.
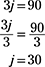
To help ensure you get the correct answer, you can eliminate Choices (A) and (D) because both of those choices are greater than 90. You have to multiply 3 by a positive number to get 90, and no positive number is greater than 3 times itself. Eliminating those choices leaves you with three choices to consider instead of five. Choices (C) and (E) are randomly incorrect.
© John Wiley & Sons, Inc.
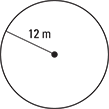
(A) 24π meters
(B) 12π meters
(C) 12 meters
(D) 144π meters
(E) 6π meters
The correct answer is Choice (A). The formula for the circumference of a circle is C = 2πr. Substituting 12 m for r, you get 2π(12 m) = 24π m. You can eliminate Choice (C) right away because neither π nor a decimal number, which would result from multiplying 12 by a decimal approximation of π, is in the answer. Another reason Choice (C) can be eliminated is because the radius of a circle can’t possibly equal the circle’s circumference. Multiplying by 2π can never be the same as multiplying by 1; 2π is not equal to 1, and it never will be, as far as we know. Choice (B) can be eliminated because multiplying by π is not the same as multiplying by 2π. You can also eliminate Choice (E) because the number that precedes π in a representation of a circumference cannot be less than its radius unless different units are used. Multiplying a positive number by 2π has to result in an increase. The three eliminations leave you with Choices (A) and (D), and that puts you closer to the right answer. Choice (D) is incorrect because it is the area of the circle, not the circumference, except with m instead of m2. If the unit were m2, you could eliminate it right away because circumference is not properly expressed in square units.
Avoiding the most common wrong answers
Other choices to watch out for and be ready to eliminate are the ones that result from the most common calculation mistakes. Memorizing the rules for all the math topics you’ll face on the Praxis is important for avoiding these common mistakes.
For geometry questions, some of the most common mistakes involve getting formulas confused, such as area and circumference. If you have a question about the area or circumference of a circle, you may have an answer choice that gives you the number involved in a measure about which you’re not being asked. Be ready to avoid such answers.
Also remember the difference between the interior angle sums of triangles and quadrilaterals. Choices may be the result of using the wrong number. Confusion between supplementary and complementary angles is common, and so is confusion between formulas for surface area and volume. Forgetting that 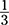 is in the formulas for the volume of pyramids and cones also happens often. (Take a spin through Chapter 6 if you need a refresher on any of these geometry topics.)
is in the formulas for the volume of pyramids and cones also happens often. (Take a spin through Chapter 6 if you need a refresher on any of these geometry topics.)
As for algebra and number and quantity questions, losing track of the fact that a number is negative is one of the most common mistakes. The distributive property is very frequently used improperly. Remember that the term right before the parentheses is supposed to be multiplied by every term in the parentheses, not just the first one. 5(x + 3) is equal to 5x + 15, not 5x + 3.
The rules for switching between decimals and percents can be easily confused. Keep in mind that moving a decimal two places to the right is multiplying by 100 and moving the decimal two places to the left is dividing by 100. Dropping a percent is multiplying by 100, and adding one is dividing by 100.
For statistics and probability questions, be careful about confusing mean, median, and mode. People often forget that the median of a set of data can be found only when the numbers are in order. When using scientific notation, be careful about the direction in which you move decimals. Numbers resulting from wrong decimal directions may be in the choices.
(A) 3,593.7
(B) 3.5937
(C) 0.35937
(D) 35,937
(E) 0.035937
The correct answer is Choice (C). To convert a percent to a decimal number, drop the percent and move the decimal two places to the left. Choice (A) results from dropping the percent and moving the decimal two places to the right. The other choices result from moving the decimal numbers other than two places to the right or left. The lesson here is that Choice (A) can be reached through a very common mistake in converting percents to decimals. You want to avoid such wrong choices. They’re lurking, so be ready.
What is the median of the preceding set of data?
(A) 28
(B) 90
(C) 17
(D) 39.4
(E) 45
The correct answer is Choice (A). When the numbers are in order, the middle number is 28. It is therefore the median. Interestingly, Choice (A) also happens to be the range of the set of data. Hopefully, you didn’t reach the correct answer because you mistook median for range. Sometimes mistakes lead to the right answers, but we don’t advise counting on that method. Choice (B) is the middle number in the set of data as it is presented, but not when the data is in order. Choice (C) is the mode and also the lowest number. Choice (D) is the mean. Choice (E) is just one of the numbers in the set of data.
Tackling the Constructed Response
Some of the questions on the Praxis Core exam’s mathematics section are not multiple choice. You’ll be asked to type the answer in a box for this type of question. These are called constructed response questions. You’ll encounter only a handful of constructed response questions, but you should be familiar with how they work and what’s expected in your answers. Because you won’t have the benefit of being able to look at any answer choices, you need to be aware of the requirements for submitting answers in the correct forms.
Tips for preparing responses and answering questions
The first thing to make sure of before you submit a constructed response is that the answer you typed is the answer you actually got. Leaving out a decimal, a digit, π, or something else essential to a correct answer will result in a wrong answer and no points for that question. Figuring out a correct answer is not the final step in a constructed response question. Submitting the correct answer is the only thing that counts.
Also, make sure you’re very clear on the instructions. A question might ask something like what measure of an angle is represented by (2x + 3)°, in which case you would have to figure out the value of a variable to determine the answer. For such a question, make sure your answer is the measure of the angle and not the value of the variable. That is one example of when paying close attention to the question is necessary.
You also need to be careful about subtle parts of instructions. A question may ask for an exact answer, an answer rounded to the nearest hundredth, or an answer in terms of π. If you’re asked to answer in terms of π, your answer should have π in it. That means you do not want to use 3.14 in your calculation. 3.14 is not π; it is a rounded approximation of it. Neglecting to follow the instructions exactly can cause an answer to be incorrect.
Some constructed response questions ask for more than one answer. If you’re given such a question, make sure you give all the required answers. People are so used to answering each question with one answer submission on a test that they can easily overlook the need for more than one answer to a constructed response question on the Praxis exam. Again, you need to follow instructions very closely.
Understanding the importance of avoiding careless errors
Careless errors are one of the major obstacles that stand between people and high levels of math success. The problem seems to apply especially to algebra students. To avoid careless errors, you must be cautious in all aspects of working through the math problem. Several methods can be used to defeat this menace:
- Work every step of a problem on scratch paper. Even if you feel like you can make a calculation correctly in your head, you should work it out completely so you have a visual account of what you are doing. This greatly helps you avoid going in a wrong direction.
- Always be on the lookout for errors. Try to catch them before they would otherwise happen. Think about how careful surgeons are when they perform surgery. One false move can be tragic. Missing a problem on the Praxis Core exam isn’t quite as tragic, but it is unfortunate. Be careful and aware of potential mistakes, just like a surgeon.
- Talk problems out in your head as you work them. This process adds one more level of attention in addition to thinking about the problems and seeing them worked out on paper.
- Go back over problems if you have time. If you finish the test before your time runs out, don’t pass up the opportunity to review your answers and possibly push up your score. Every minute you can spend reviewing your answers is valuable.
- Be especially careful when working with negative numbers. They are the number one area for careless errors. If you see a negative sign, think of it as a wet floor sign telling you to be extra cautious.
- Don’t assume that not noticing a careless error means you didn’t make one. Careless errors are sneaky. Most of them aren’t caught in the act, but the damage they cause is almost always revealed.
Some proper ways of representing answers
The instructions for constructed response questions tell you how you’re required to answer them if more than one possibility would otherwise exist. If an answer includes a unit of measurement, you need to submit it. If you’re asked to answer something in terms of some kind of unit, variable, or other representation, including it in your answer is a must.
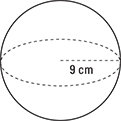
© John Wiley & Sons, Inc.

The correct answer is 972π cm3. The volume of a sphere is 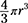 .
.
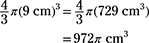
The unit used for the radius is centimeters, so the unit used for volume must be cubed centimeters (cm3). The answer to the problem has to involve a number times π and also cm3. The proper answer is therefore 972π cm3, not just 972π or the result of multiplying 972 by 3.14. You should force your constructed responses to pass a major inspection that you conduct.
 If you decide to use only one bit of advice on test-taking strategies, let it be this: Never stay on a question that looks like it will take an extreme amount of time to answer. This applies to any type of math question. You can write down the number of the question in the hope of going back to it later. Some people get so caught up in a challenge to answer a time-consuming question that they use up time they could have used to answer four or five other questions.
If you decide to use only one bit of advice on test-taking strategies, let it be this: Never stay on a question that looks like it will take an extreme amount of time to answer. This applies to any type of math question. You can write down the number of the question in the hope of going back to it later. Some people get so caught up in a challenge to answer a time-consuming question that they use up time they could have used to answer four or five other questions. All the Praxis Core exam math questions are worth the same number of points, so make sure you don’t treat any one of them as if it’s more important than the others. Whether you’re asked to solve a simple equation or find the volume of a remaining region of a cone, the question is worth as much as the other 55. Timing is part of the challenge, so use it well.
All the Praxis Core exam math questions are worth the same number of points, so make sure you don’t treat any one of them as if it’s more important than the others. Whether you’re asked to solve a simple equation or find the volume of a remaining region of a cone, the question is worth as much as the other 55. Timing is part of the challenge, so use it well. If the problem has more than one unknown, see whether you can represent the others in terms of the first. For example, if Bob’s score in bowling is in question and the problem says that Frank scored 10 points higher than Bob, you can use x to represent Bob’s score and x + 10 to represent Frank’s score.
If the problem has more than one unknown, see whether you can represent the others in terms of the first. For example, if Bob’s score in bowling is in question and the problem says that Frank scored 10 points higher than Bob, you can use x to represent Bob’s score and x + 10 to represent Frank’s score. John is four years older than Adam. John was twice Adam’s age 33 years ago. What is John’s age now?
John is four years older than Adam. John was twice Adam’s age 33 years ago. What is John’s age now?