8
SHADOWS AND REFLECTIONS
Despite their initial appearance of complexity, shadows and reflections obey the same immutable rules of perspective illustrated in the preceding sections of this book.
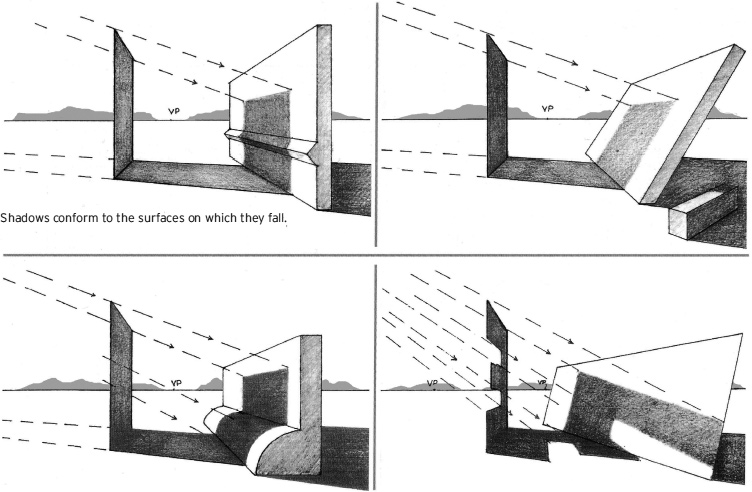
Shadows are determined by the source of light, the shape of the object, and the surface on which they are cast.
Reflections are simply an extension of the object image onto another plane or set of planes within the perspective view.
 SHADOWS
SHADOWS
The position of the light source is the critical factor in determining the final shape of the shadow cast in perspective, as summarized below and explained further in the following material.
Light source parallel to the picture plane
Light source in front of the viewer
Light source behind the viewer
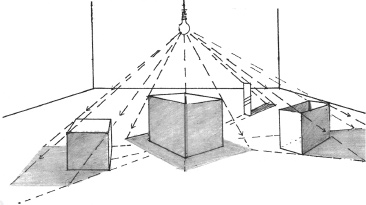
Light from a central radiating source
Light from multiple sources
Light Source Parallel to the Picture Plane
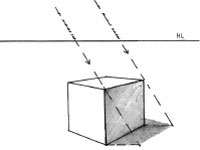
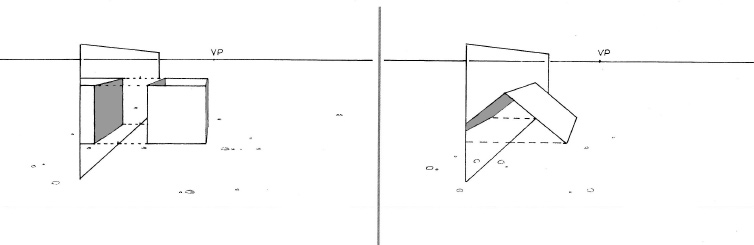
When the light source is parallel to the picture plane, parallel rays will remain parallel and define the cast shadows according to how they are blocked by the object.
The length and shape of cast shadows are determined by the intersection of the ground plane, with light rays crossing the corners and edges of the object.
Here, the ground plane lines are parallel to the picture plane.
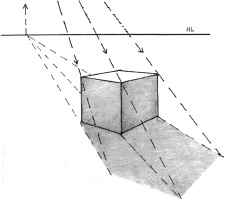
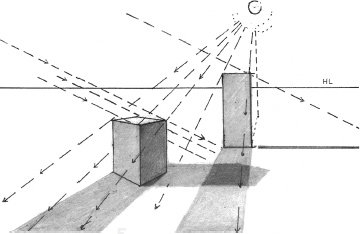
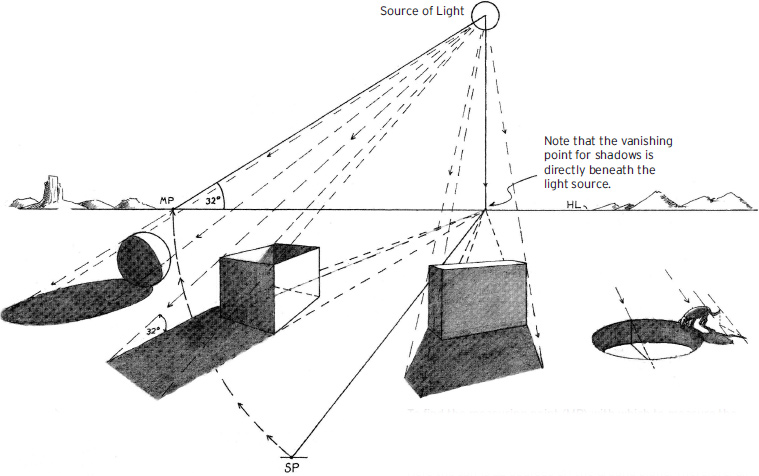
Light Source in Front of the Viewer
To find the measuring point (MP) with which to measure the angle of the light source, swing the line (vanishing point for shadows–to station point) up to the horizon as show on the left.
Here the sun is 32 degrees off the ground plane. Therefore, all the shadows must be 32 degrees off the ground plane.
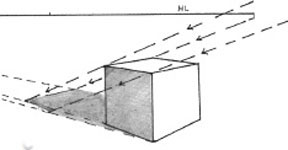
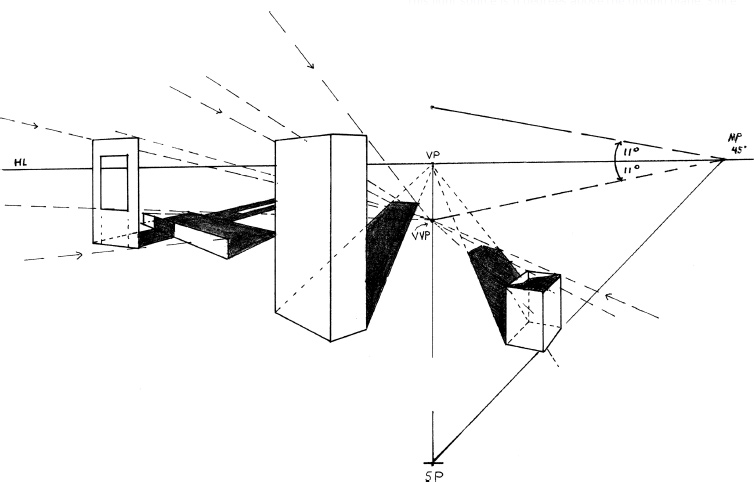
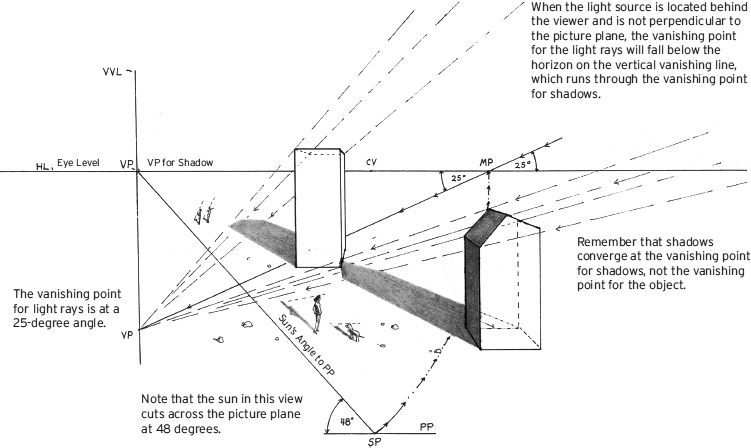
Light Source Behind the Viewer and Perpendicular to the Picture Plane
This light source is 11 degrees above the ground plane. Since the source is behind the viewer, the vanishing point for the light rays will appear 11 degrees below the horizon, on the vertical vanishing line.
The light is directly behind the viewer, so the center of vision will be the vanishing point for shadows cast on the ground plane.
If the light source were higher in the sky, the vertical vanishing point for the light rays would be further down the vertical vanishing line, and the shadows would also be cut shorter.
Light Source Behind the Viewer But Not Perpendicular to the Picture Plane
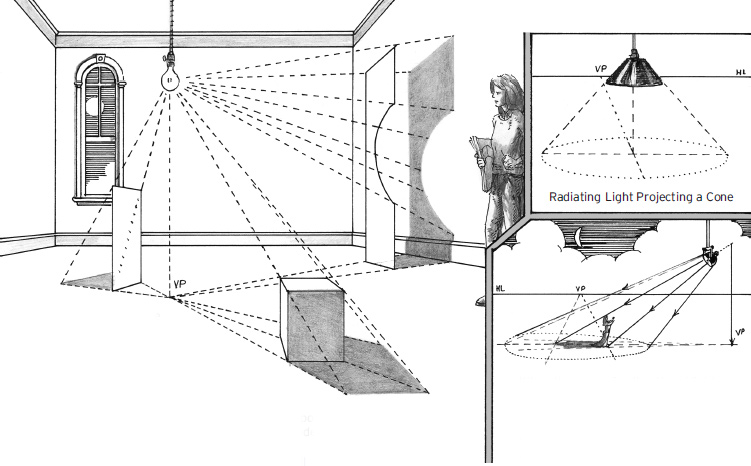
Radiating Light Sources
In the previous examples, the light source was usually assumed to be the sun. Thus, the vanishing point for shadows had fallen at a point on the horizon directly below the sun.
When the cone of a directional light strikes a flat plane at an angle, the beams spread out in an eccentric oval. Shadows within this cone of light will diminish toward a point on the ground plane beneath the light source.
Similarly, for most smaller light sources, the vanishing point for shadows will be at a point on the ground directly under the center of the light source. Since the light radiates in all directions from above this vanishing point, shadows will diminish toward this vanishing point from all sides.
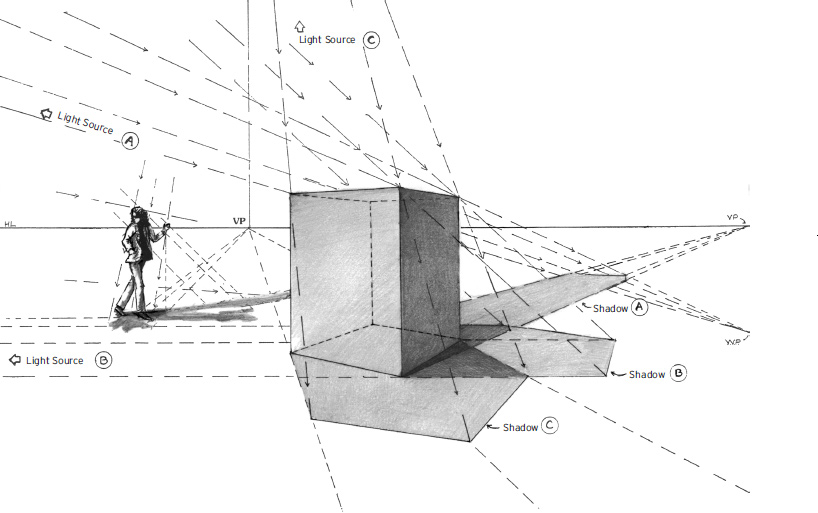
Multiple Shadows
When there is more than one light source, there will be a corresponding number of shadows.
Where the shadows overlap, the density of the shadows will increase correspondingly.
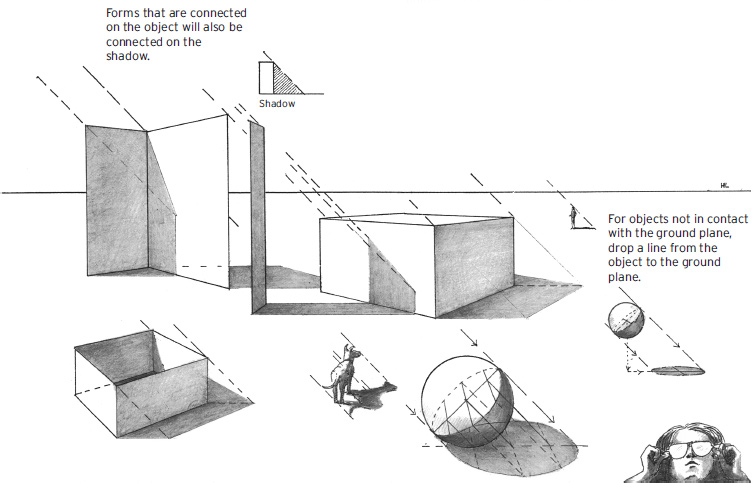
Shadows Cast on Various Surfaces
They also project the form of the object that casts them.
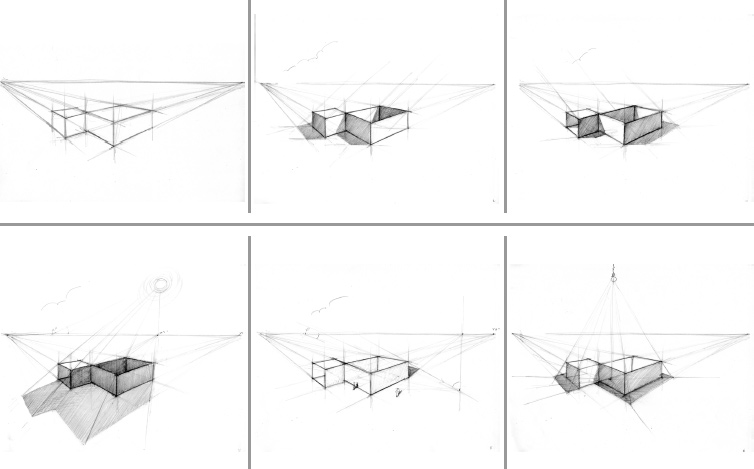
Sketching Shadows
REFLECTIONS
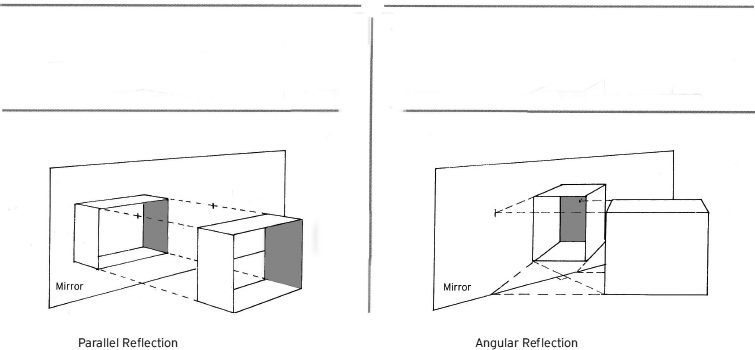
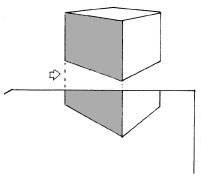
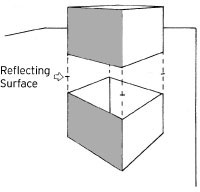
A reflection is simply the mirror image, or equal and opposite extension of, the original object and its perspective system. Drawing parallel reflections requires only a simple extension of the object through the reflecting surface, while angular reflections require more complicated calculations.
Parallel Reflections
When the object is contiguous with the reflecting surface, the image is simply doubled. The reflection uses the same vanishing point as the original.
The lines of the reflection are a continuation of the lines of the original, even when only part of the original object is reflected.
If the object does not touch the reflecting surface, lines must be extended to join the object and reflecting surface in order to determine the position of the reflection.
If an object is angled on one axis but is parallel to the picture plane on the other, the reflecting surface will still be the opposite of the original.
If both the reflecting plane and the object are perpendicular and parallel to the picture plane, the reflections will follow the same rules as those described previously in “Parallel Reflections.”
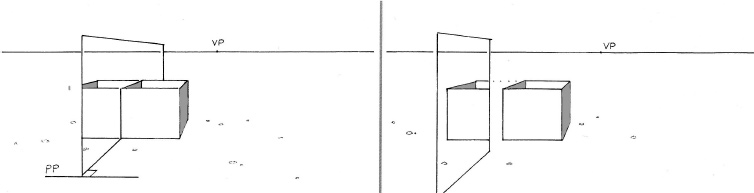
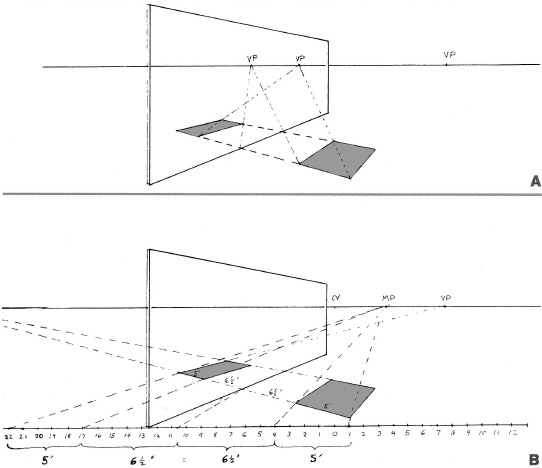
When the object and the reflecting plane are parallel to each other but not parallel to the picture plane, there are two ways to find the position of the reflection:
- Use diagonal vanishing points (top, right) to determine the perspective of the reflections. (To use diagonals, see Chapter 5.)
- Use measuring points and a scaled picture plane (bottom, right) to mark off the equivalent lengths of the reflection. (To use measuring points, see Chapter 4.)
If both the reflecting plane and the object are perpendicular and parallel to the picture plane, the reflections will follow the same rules as those described previously.
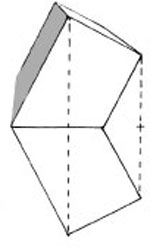
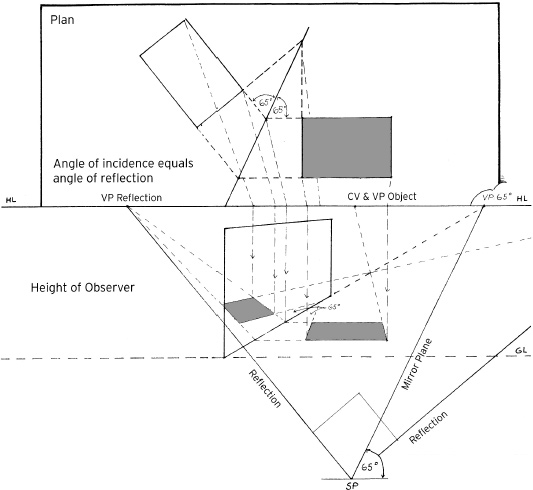
Angular Reflections
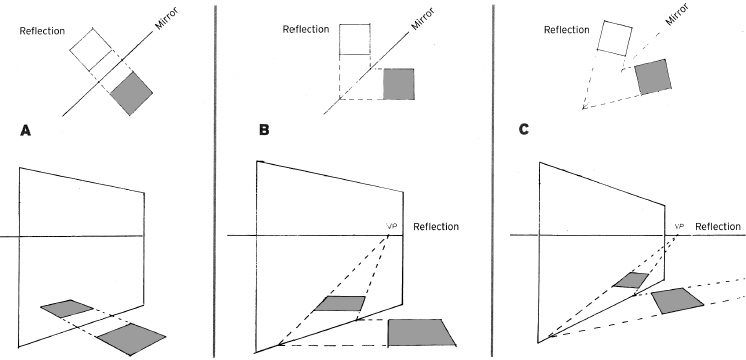
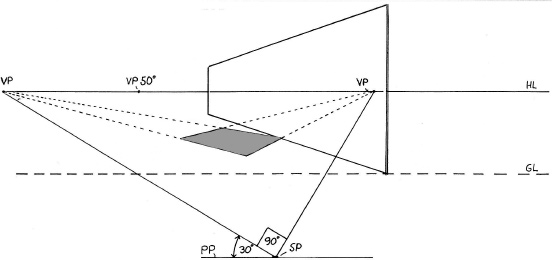
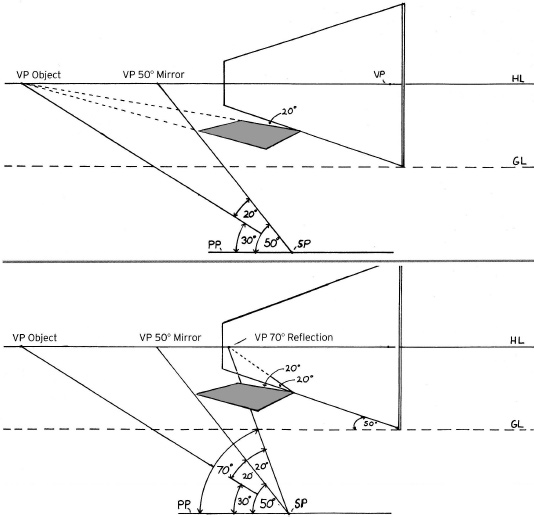
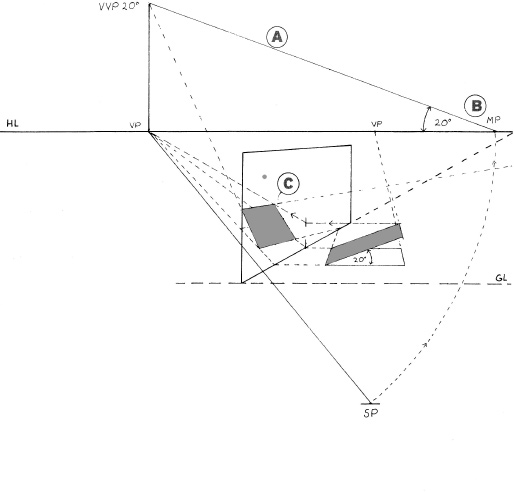
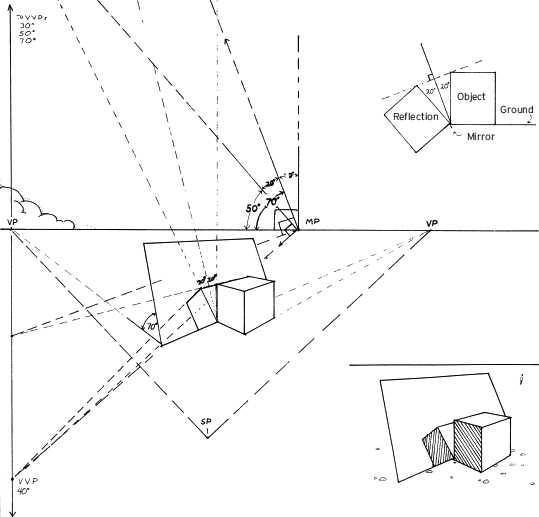
It is a relatively simple matter to find the reflection when the object and reflective surface are parallel to each other, as shown in A and B. However, when the object and reflecting surface are at anything other than 90 degrees or 45 degrees to each other, the vanishing point of the reflection will be different from that of the object or its diagonals, as in C.
To find the vanishing points of an angular reflection, follow steps 1–6.
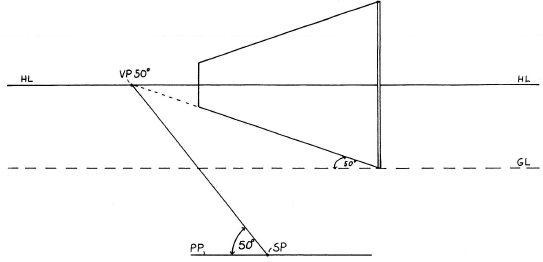
Find the vanishing point for the mirror via the station point. Here, the mirror is 50 degrees off the picture plane.
Find the two vanishing points of the object. The object is angled to the picture plane at 30 degrees and 60 degrees.
Find the angle of the object to the mirror by subtracting the 30-degree angle of the object from the 50-degree angle of the mirror; this new angle is 20 degrees.
Find the vanishing point of the reflection by doubling the 20-degree angle of the object to the mirror.
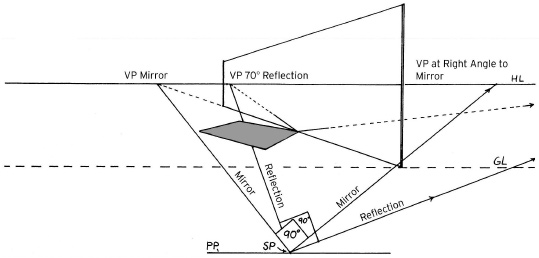
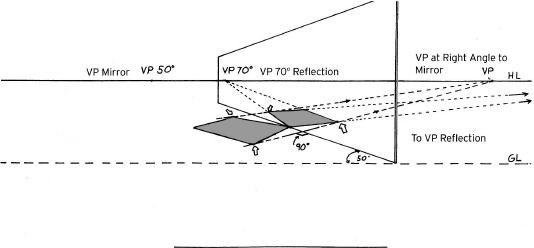
To find the right vanishing point for the reflection, draw a 90-degree angle at the intersection of the station point and the line leading to the left reflection vanishing point. (In this example, the right vanishing point for the reflection falls beyond the page.) You can also find the vanishing points for lines perpendicular to the mirror using this method.
To mark the width of the reflection, connect lines from the corners of the object to the mirror's right vanishing point. The point at which these lines cross the reflection's perspective lines marks the corners of the reflection.
Reflections Taken from a Plan
The object is parallel to the picture plane, so its single vanishing point will be the same as the center of vision.
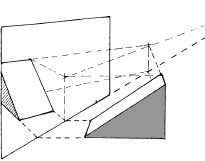
Reflections of Sloping Planes
Because the object in this example is parallel to the picture plane, the 20-degree slope (A) can be measured directly off the image.
The slope in the reflection can be found by measuring a 20-degree angle from the measuring point (B). The height of the slope in the reflection (C) will be marked by the height of the object extended to the mirror and then to the reflection's vanishing point.
In many setups, the slope can be determined by slicing off a rectangle. (See Chapter 6.)
The details of complex sloped planes can be transferred to the reflection by connecting the sloped plane axes to the mirror plane at the appropriate points.
Reflection on a Tilted Mirror
To find the vanishing points of a reflection on a tilted mirror, follow these steps:
Note that the reflection is in three-point perspective.
Sketching Reflections