shape

Mathematicians like to overthink things. It’s sort of what we do. We take some concept that everyone understands on a basic level, like symmetry or equality, and pick it apart, trying to find a deeper meaning to it.

Take shape. We all know more or less what a shape is. You look at an object and you can easily tell if it’s a circle or a rectangle or whatever else. But a mathematician would ask: What is a shape? What makes something the shape it is? When you identify an object by shape, you’re ignoring its size, its color, what it’s used for, how old it is, how heavy it is, who brought it here, and who’s responsible for taking it home when we leave. What are you not ignoring? What is it that you’re getting across when you say something is shaped like a circle?

These questions are, of course, pointless. For all practical uses, your intuitive understanding of shape is fine—no significant decision in your life will ever hinge on how exactly we define the word “shape.” It’s just an interesting thing to think about, if you have some extra time and you want to spend it thinking about shapes.

Let’s say you do. Here’s a question you might think to ask yourself:

It’s a simple enough question, but it isn’t easy to answer. A more precise and limited version of this question, called the generalized Poincaré conjecture, has been around for well over a century and we still don’t know of anyone who’s been able to solve it. Lots of people have tried, and one professional mathematician recently won a million-dollar prize for finishing up a big chunk of the problem. But there are still many categories of shapes left uncounted, so we still don’t know, as a global community, how many shapes there are.

Let’s try to answer the question. How many shapes are there? For lack of a better idea, it seems like a useful thing to do to just start drawing shapes and see where that takes us.

It looks like the answer to our question is going to depend on how exactly we divide things into different shape categories. Is a big circle the same shape as a small circle? Are we counting “squiggle” as one big category, or should we split them up based on the different ways they squiggle? We need a general rule to settle debates like this, so the question of “how many shapes” won’t come down to case-by-case judgment calls.

There are several rules we could pick here that would all do a fine job of deciding when two shapes are the same or different. If you’re a carpenter or an engineer, you’ll want a very strict and precise rule, one that calls two shapes the same only if all their lengths and angles and curves match up perfectly. That rule leads to a kind of math called geometry, where shapes are rigid and exact and you do things like draw perpendicular lines and calculate areas.

We want something a little looser. We’re trying to find every possible shape, and we don’t have time to sort through thousands of different variations of squiggles. We want a rule that’s generous about when to consider two things the same shape, that breaks up the world of shapes into a manageable number of broad categories.

New Rule

Two shapes are the same if you can turn one into the other by stretching and squeezing, without any ripping or gluing.

Now the question is well-defined and the answer is set. Is anything bigger than infinity? Yes or no—which is it? Is there anything that has leftovers when you try to match it with an infinite pile? Now’s the time to make your informed guess.

This rule is the central idea of topology, which is like a looser, trippier version of geometry. In topology, shapes are made out of a thin, endlessly stretchy material that you can twist and pull and manipulate like gum or dough. In topology, the size of a shape doesn’t matter.

Also, a square is the same as a rectangle, and a circle is the same as an oval.

Now it gets weird. If you think about it using this “stretching-and-squeezing” rule, a circle and a square are considered the same shape!

Before you go tell your loved ones that you read a book about math and learned that a square is a circle, keep in mind: Context matters. A square is a circle, in topology. A square is most certainly not a circle in art or architecture, or in everyday conversation, or even in geometry, and if you try to ride a bike with square tires you won’t get very far.

But right now we’re doing topology, and while we’re doing topology we don’t care about frivolous little details like pointy corners that can be massaged away. We look past superficial differences, things like lengths and angles, straight edges versus curved or squiggly ones. We focus only on the core, underlying shape: the basic features that make a shape the shape it is. When topologists look at a square or a circle, all they see is a closed loop. Everything else is just a feature of how you’ve happened to stretch and squeeze it at the moment.

It’s like asking, “What’s the shape of a necklace?” It’s a square if you hold it one way, and it’s a circle if you hold it another way. But no matter how you shift it around, there’s an intrinsic shape to it, something fundamental that doesn’t change, whether it’s a square, circle, octagon, heart, crescent, blob, or heptahectahexadecagon.

Since this shape comes in many different forms, it’s not quite right to call it either a circle or a square. We sometimes call it a circle anyway, but the official name for this shape in topology lore is “S-one.” S-one is the shape of a necklace or bracelet or rubber band, a racetrack or circuit, any moat or national border (assuming no Alaskas), the letters O and uppercase D, or any closed loop of any shape. Just like a square is a special type of rectangle, and a circle is a special type of oval, all these shapes are special types of S-one.

Are there any other shapes? It would be a shame if the stretching-and-squeezing rule turned out to be so loose that we accidentally collapsed all the diversity of shapes down into one broad category. Good news: We didn’t. There are still shapes that aren’t the same as a circle.

Like a line:

A line can be bent almost into a circle, but to finish the job we’d need to click the ends together—not allowed. No matter how you manipulate a line, you’ll always have those two special points on either end, where the shape just stops. You can’t get rid of end-points. You can move them around and stretch them apart, but the two end-points are an unchanging feature of the shape.

For a similar reason, a figure-eight is a different shape too. There aren’t any end-points, but there’s still a special point in the middle where the lines cross, where there are four arms reaching out instead of the usual two at any other point. Stretch and squeeze all you want, you can’t get rid of a crossing-point either.

If you think about it, this is enough information for us to answer the original “How many shapes are there?” question. The answer is infinity. Here, I’ll prove it to you.

Proof

Look at this family of shapes. You make each new shape by adding an extra hatch mark to the previous shape.

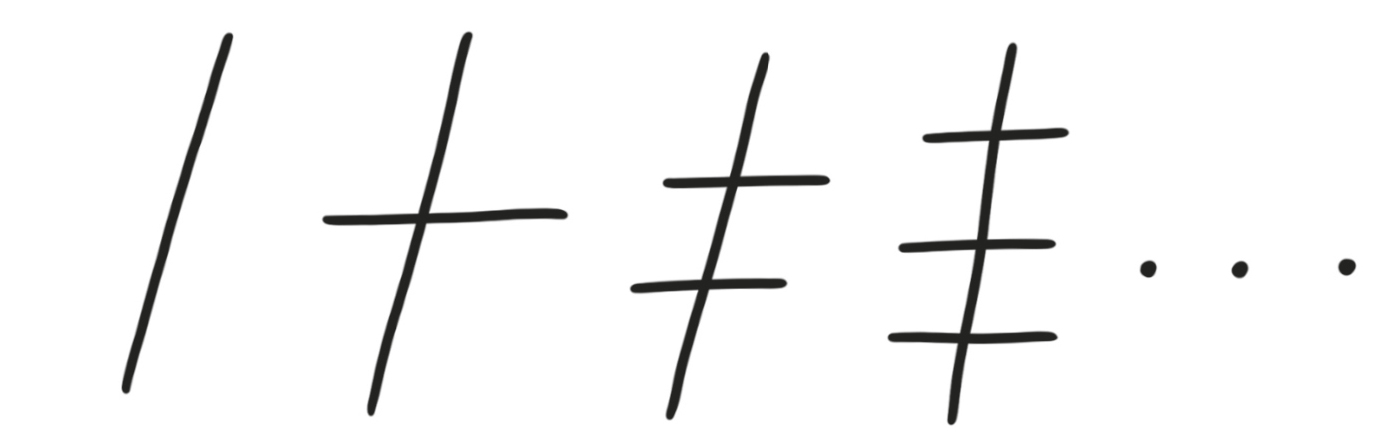
Each new shape has more crossing-points and end-points than all the ones before it. So each one must really be a different, new shape. If you keep doing this forever, you get an infinite family of different shapes, and so there are infinity shapes.

QED

Convinced? All you need to do is find any infinite family of different shapes like this, where it’s obvious how to keep making new different shapes forever.

This one would have worked just as well:

Or this one:

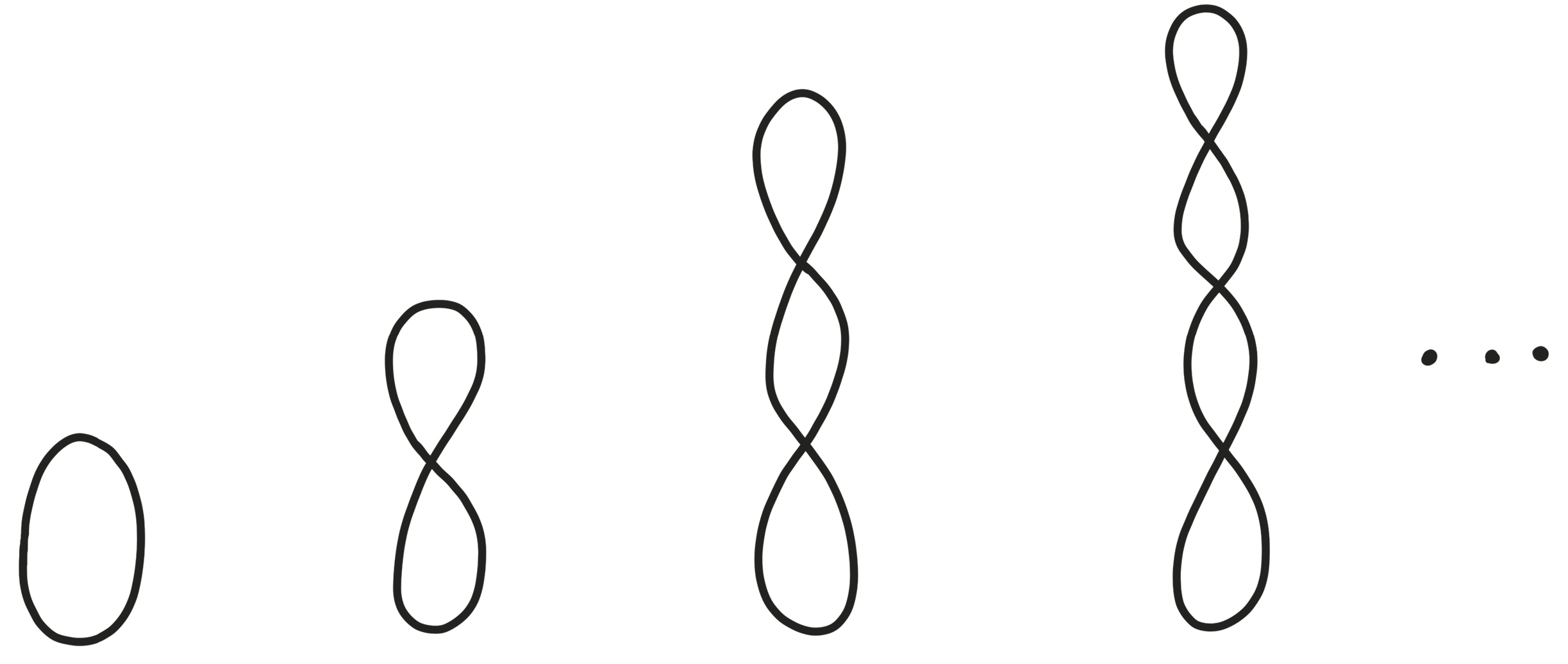
This one works too:

However you prove it, though, the basic argument is the same. You want to show there are infinitely many of something, so you describe a systematic process that keeps churning out new different examples of that thing. This is called an “infinite family” argument, and it’s a pretty common tool in math for when you want to show there’s infinity of something. I find it convincing—I don’t really see how you could argue against it. There have to be infinity of something if you can keep making more of them forever.

And it’s not just me: The math community as a whole considers “infinite family” arguments to be valid mathematical proof. There are a bunch of proof techniques like this, where the same sort of argument can be used in different contexts to prove different things. People who do a lot of math start to notice the same patterns of argument showing up over and over. We all (for the most part) agree about which ways of proving things are legit.

If you accept this proof, we’ve now answered the original “How many shapes are there?” question. The answer is infinity. It’s not a particularly interesting answer, but that’s the answer we get. Once the question is asked and the rules of engagement are set, the answer is already decided. We just have to go find it.

The first question you think to ask doesn’t always lead you to the most interesting or enlightening answer. When that happens, you can give up and find something else to think about, or you can ask a better question.