abstraction

Let’s start completely from scratch. Math is about pure abstract objects sitting in empty space, and algebra is the purest, most abstract subject of all. We’re not talking about the algebra you learn in school—hardcore mathematicians call that “school algebra” or “elementary algebra,” and they mean it dismissively. What I want to tell you about in this section is called “abstract algebra.” It’s so abstract, it’s not even about any particular type of object. It’s about the very idea of objects and relationships between objects.

“Generalized algebra” is another term for it. When you generalize something, you make it less specific. Say you have a math problem with the number four in it. Four is a specific number. If you wanted to generalize the problem, you’d replace four with x, a placeholder for any number at all. Now you can’t solve the problem the regular way and get a numerical answer, but you can sub in different values for x and see if there’s a pattern to the answers you get. There usually is. That pattern is the solution to the generalized math problem. It’s a solution that works in general.

Abstract algebra takes this idea to the next level: It tries to find a more general version of algebra itself. Instead of addition or multiplication, we use the symbol • as a placeholder for any operation at all. We sub in different operations—not just the classical four, but bizarre, never-before-used operations—and look for high-level patterns. And then it gets even worse: We abstract away the concept of number too, and now we’re working with unknown operations on unknown objects.

It’s hard to even talk about this type of algebra, because there’s no particular thing to talk about. There are processes that algebraists carry out, systematic ways of moving symbols around on paper that turn statements into other statements. But each statement doesn’t actually mean anything, or at least, it doesn’t mean any one particular thing. Every symbol is a general placeholder for an infinite cast of possible replacements. So in a sense, each statement means a million different things at once.

It’s a disorienting feeling. There’s no solid floor to stand on, no clear reference point back to reality or even to what most people normally consider math. You can stare at pages of an algebra textbook for hours, flipping back and forth to try to remember what anything is even referring to. Whenever a proof or example does finally click, there’s not usually a specific picture in your head so much as a sense of a pattern. “Something happened over here, and then a symmetrical thing happened over there, but it was flipped.” There are clear relationships and structures, but no actual objects.

In order to think about this type of algebra, you need to get in the right mindset. You have to forget about real-world things like trees and chairs, and then you have to also forget about math-world things like shapes and numbers. You have to empty your mind, like you’re preparing for a rigid and organized form of meditation.

So imagine this, if you can. Imagine you’ve never seen anything, heard anything, felt, smelt, or tasted, sensed or intuited, learned or known anything, ever. Imagine your eyes are closed forever and actually you have no eyes and you don’t know what eyes are. You’re just a disembodied consciousness floating in the void.

You have nothing to think about. Literally nothing: You don’t know of any things. It’s very boring. You have nothing to entertain you, and so you sit there completely blank for an eternity.

And then you receive a message, inserted directly into your mind. (Finally!) It says, “Something exists.” It’s a very basic message, but you’re thrilled to have something to think about. Something exists. You don’t know what it is that exists, but you know something does, and so you can give it a name, and you name it g.

Usually when you name something, the name has some kind of relevance to the thing. Not here. There’s no etymology or onomatopoeia, and knowing that the thing is called g doesn’t tell you anything at all about what the thing called g is. It’s just a name, a symbol, that you use for ease of reference. You can say things like, “g exists.” You can even draw a conceptual diagram of everything you know exists in the world.

But don’t read too far into it: The thing is not really a g, and it’s not really a point. You’re just sketching the abstract idea of the thing that you call g.

Now you’re bored again. You’ve done pretty much everything you can do with this one object that you know exists, and it turns out one generic thing existing isn’t much more interesting than nothing existing at all. So you go back to utter blankness, wishing you had thumbs to twiddle, for another few eons.

Then, thankfully, the messenger comes back with a new message. “Another thing exists.” Great news! You give this new thing the name h and you update your little schematic diagram.

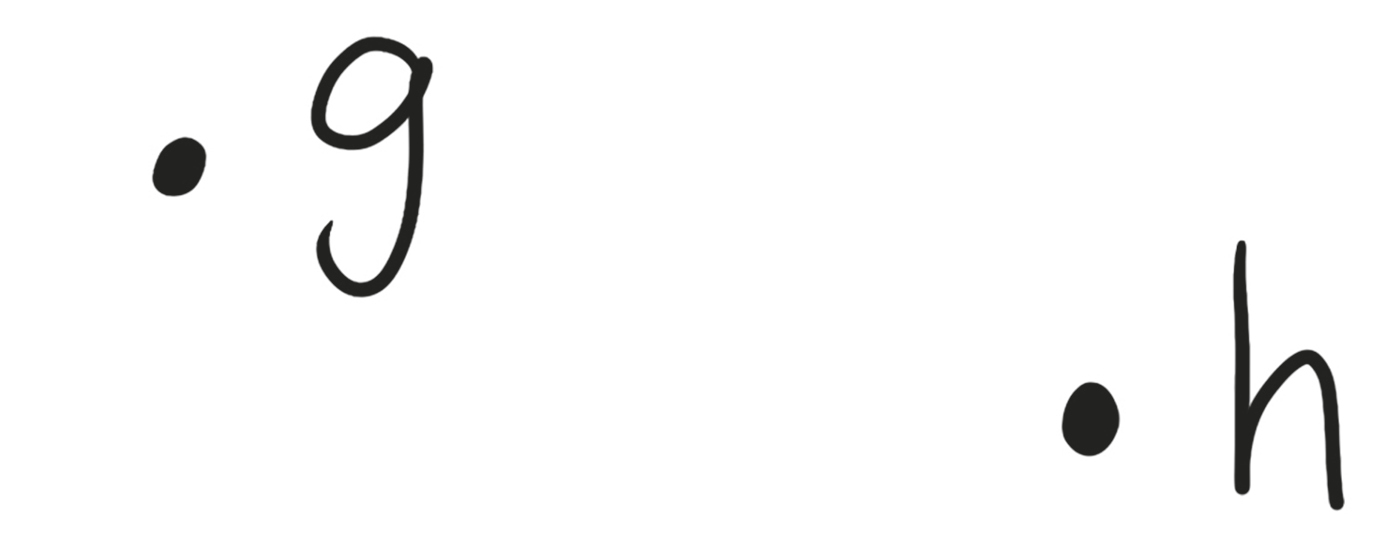
But once again, that’s about all you can do.

No matter how many new things you hear about, all you’ll be able to do is add new names to your list of names, add new dots to your dot diagram, and then go back to nothingness. If someone asked you, “Does h exist?” you could tell them that yes, it does, but you still don’t know anything beyond exactly what you’ve been told by the messenger. You can’t figure out new facts on your own. You can’t ask questions and wonder about the answers. The world consists of a list of unrelated objects, and there’s not much you can do with that. Boring!

In order for anything even remotely interesting to happen, you need to know not just whether things exist but how things relate to each other.

So consider this. The messenger comes back and gives you a message with a new twist to it. “There are five things that exist, and each of these five things has a partner-thing that also exists.” Alright, let’s think about that. What could this message be describing?

All of these scenes fit the description. They all have a similar pattern to them, even though they’re fairly different on the surface. In each case there are five pairs, or ten things split into two alternate groups. The extra information you received this time, about this “partner-thing” relationship, imposes a basic sort of structure on the world. The objects now interrelate and coexist. They have an overarching form or order. The whole is more than a collection of parts.

This is a step in the right direction, because the real world is densely structured with relationships between objects. There’s a couch and a rug, but they don’t exist in a vacuum: The couch is “above” the rug, which is “above” the floor, which is “above” your downstairs neighbors, and so on until you get to the molten core of the Earth. When you talk about a person, you probably don’t just say “Ady exists.” You say something like “Ady has long nails.” You describe a relationship of “having” between Ady and some nails, and a relationship of “being longer than” between Ady’s nails and a reference class of other nails. Even just saying “Ady is a person” implies a whole suite of relationships, between Ady and various body parts, other people, physical locations, events, habits, beliefs and desires, and so on. Our understanding of the world consists (at the very most basic, abstract, ground-floor level) of objects and relationships between objects.

In math-world too, everything we do can be understood through this basic lens. In topology, we looked at a type of object called shapes, and a relationship of “sameness” that applies to any two shapes that can be stretched and squeezed into each other. This relationship organizes a jumbled mess of shapes into an orderly classification system. In analysis, similarly, the “bigger than” relationship imposed an ordering on all sets of things, from the empty set up through infinity, the continuum, and beyond.

But I said we were leaving the real world and math-world behind. So let’s forget about all that for now and go back to your consciousness floating in the void, and those five things that exist with their five partner-things that also exist.

You want to name the objects, and you want to make a dot diagram. It doesn’t seem quite right to give ten random different names to the objects, because that doesn’t reflect what they are. You could, since the names don’t really mean anything, but to make life easier for yourself you might as well choose names that reflect the order of the world you’re describing. Same with the dot diagram. You could scatter the points randomly, but you’re better off if you indicate the partner-things.

This is one of the simplest possible worlds that has any organized structure to it. That’s good, because mathematicians like things simple. That’s the point of abstraction: It lets us investigate the nature of order and form, without getting tied up in the arbitrary specifics of any particular situation.

So what exactly do we learn about order and form? What makes this structured world, with the partner-things, qualitatively different from a collection of unrelated objects?

For one thing, this world can be talked about in a way that the previous worlds couldn’t. We can say, for instance, “g is the partner-thing of ĝ” and “h and j aren’t partner-things to each other” and “k̂ has a partner-thing but it isn’t g or the partner-thing of h.” Before, without relationships between objects, all we could say was that things exist. As in the real world, relationships are the substance of language.

This also means that we can ask questions and search for answers. Like so: “What’s the partner-thing of g?” Or, “Is there any object that is not the partner-thing of its own partner-thing?” These questions are easy to answer, because the world we’re dealing with still has hardly anything going on. But for the first time, we’re in a situation where there can be things to discover.

Backing out for a second, the big idea behind abstract algebra is that everything we deal with in math is essentially a slightly more complicated version of this basic partner-world. You have some objects, some relationships between objects, some things we know, some things we don’t know. Algebraists are convinced that any conceivable math question can be translated into abstract algebraic terms and solved with algebraic tools.

This belief extends outside of math too. Much of Western academic philosophy and science is built around the idea that everything we deal with, period, can be abstracted to simple mathematical structures. It’s an idea that sounds crazy, and quite possibly is actually crazy and wrong. At the very least, it’s a powerful idea that has helped people understand the workings of nature and build new technologies.

Because the partner-thing example is still too basic to be interesting, I want to give one more toy example of an abstract structure. Forget everything you know one last time. Ready? Here comes your message. “There are three special things, let’s call them ‘wugs,’ and each possible combination of ‘wugs’ is also a thing that exists.”

What could the messenger be describing? A simple naming system we can use would look like this:

But how should we arrange the points? What’s a visual schematic that captures this structure? There are several that would work, but here’s a good one: the vertices of a cube.

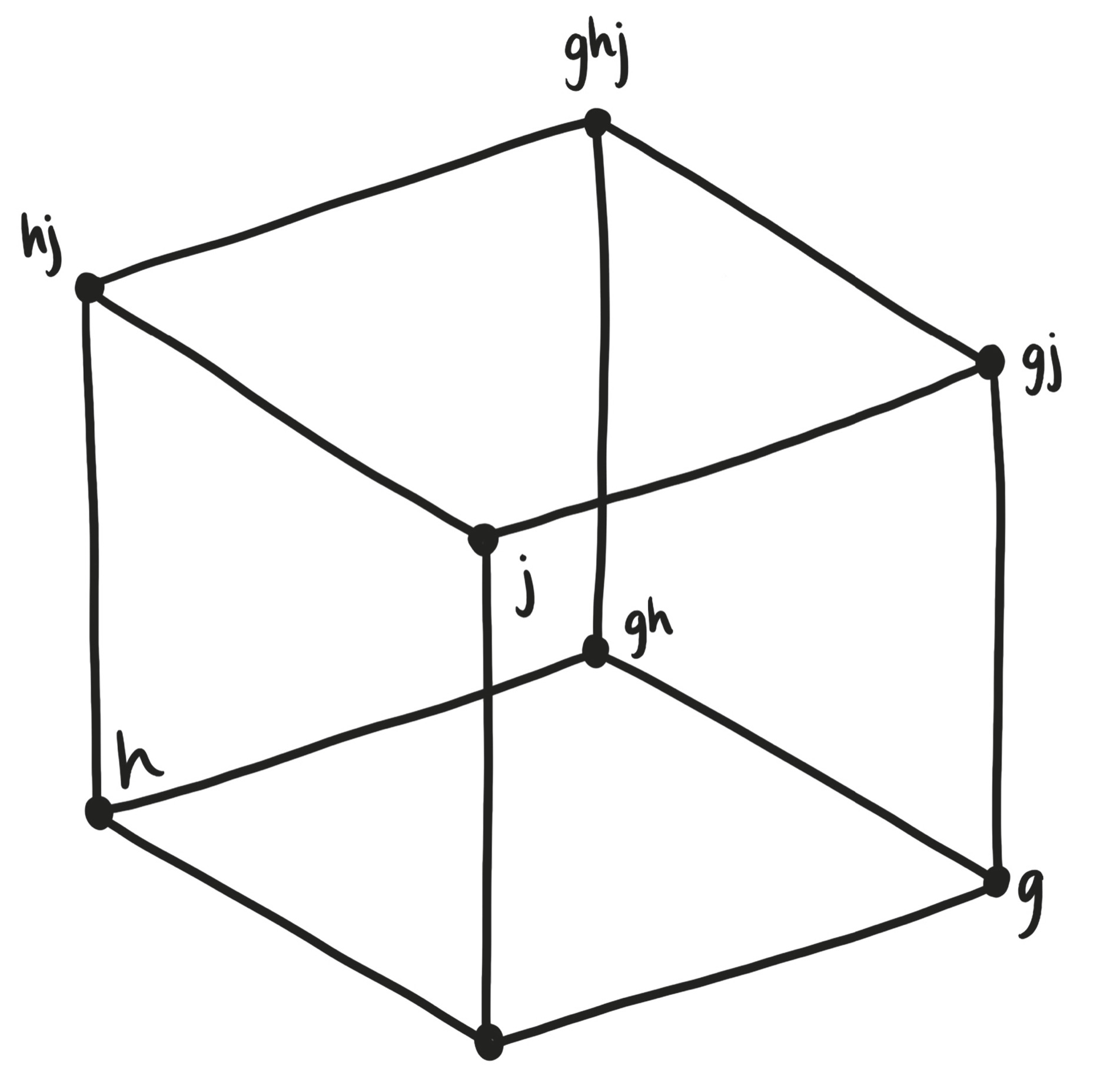
Take a minute to look at this diagram and appreciate why it works as a representation of the structure. The near corner represents the empty object—the combination of no wugs. And then, each wug corresponds to one of the three dimensions. To add the wug, travel in that direction.

Structure diagrams like this always have nice symmetries and patterns to them. See how opposite corners of the cube have opposite names? That’s a sign we’re capturing the underlying structure well.

Another world with this exact same structure to it would be the collection of all three-bit binary strings, which is to say, the possible states of three on-off switches.

Here, the wugs are the switches, and the empty object is all three off.

Another presentation of the same underlying structure: a Venn diagram with three circles.

One last system that also fits into this same pattern: colors.

Curiously, the factors of thirty also fit this exact same pattern. I’d show you what that looks like (it’s pretty neat) but I promised I wouldn’t use any numbers, so I guess you’ll have to work that one out for yourself.

Specifics aside, the general point I’m trying to make here is: The same underlying abstract structure can manifest as any number of superficially different systems. The specific objects in each case are wildly different, but the relationships between them are exactly the same.

Another way to think about this “same abstract structure” equivalence: Any sentence you can say about one set of objects is still true when translated word by word into another.

There’s a formal math term for this sort of equivalence, which doesn’t have a good translation into casual English. When two systems have the same abstract structure, we say that they’re isomorphic to each other, iso meaning “equal” and morph meaning “shape” or “form.” The colors and the bit-strings and the cube corners are all isomorphic—they have the same conceptual shape.

When you read the word “isomorphic” in a textbook, the author is probably being very precise with the definition, describing two systems that have the exact same structure, with no differences at all. But also, mathematicians sometimes call things isomorphic in real life, and then we usually mean it in a rougher, impressionistic sort of way. You might say that Uno is isomorphic to Crazy Eights or that The Lion King is isomorphic to Hamlet, even though those aren’t true in the most literal, mathematical sense.

To an algebraist, isomorphism—the state of being isomorphic—is the pinnacle of elegance and beauty. Two unrelated situations that secretly have all the same underlying dynamics? Gorgeous. The world has been simplified down one notch. What used to be two different problems or, as the case may be, a hundred or infinity different problems, has been reduced to a single problem. Our understanding is deepened. (At least, that’s my impression of an algebraist.)

We saw this kind of abstraction/reduction process in action a few chapters ago; I just didn’t call it that at the time. Think back, or flip back, to Hotel Infinity. Adding a new guest to a full hotel is a situation with the abstract structure of “infinity plus one.” Adding one new object to a bottomless bag of objects is the same thing: infinity plus one. Once you understand the dynamics of “infinity plus one” in one scenario, the exact same logic applies to any isomorphic scenario.

After all, think about it: What does “infinity” or “one” even mean? One what? These ideas are abstractions. One duck, one hair, one drop, one minute—the concept applies across a million different cases, but it doesn’t mean anything on its own. It’s a placeholder term for a recurring phenomenon. It’s an abstract object, a pure mathematical object.

What exactly is a “pure mathematical object”? Do these things really exist or are they just figments of our imagination? These are questions that philosophers of math argue about. Some people believe that mathematical objects do exist, in the most literal sense, in some far-off universe of pure abstraction. They believe we catch glimpses of this simpler world when we study math. They believe this pure math universe, the “Platonic realm,” is more fundamental and more beautiful than our world, less arbitrary, less influenced by happenstance.

I don’t know about all that, but it’s a useful way to think about abstract objects. Whatever the ghj-structure is, we can imagine it sitting in that blank, empty math-world. We can’t know what it looks like, just like we can’t know what a pure “one” looks like. We can see all these various shadows it casts onto our world—the cube, the Venn diagram, etc. But the object we’re talking about? This skeleton of an idea, this abstract algebraic shape that I’m trying to communicate from my head to yours? This is just a thing. A structure. We can give it a name, and so we name it Z-two-cubed.

Yes, of course: Mathematicians have made it a mission to find, name, and classify every possible abstract structure.