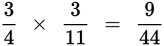Applied Arithmetic Review
While the arithmetic concepts you’ve looked at so far could appear on the Arithmetic Reasoning section of the ASVAB, it’s worth noting that, due to the very nature of word problems, most of the questions in this section will involve some form of “applied arithmetic.” On the ASVAB you will use arithmetic principles to solve practical problems. Applied arithmetic includes subjects like ratios, percent problems, rates, averages, and probability.
The Order of Operations
You must perform arithmetic operations in the proper order to get the correct answer to complex arithmetic problems. The acronym PEMDAS can help you remember that order.
P = Parentheses
E = Exponents
M D = Multiplication and Division (from left to right)
A S = Addition and Subtraction (from left to right)
For example:

One way to remember PEMDAS is to think of the phrase “Please Excuse My Dear Aunt Sally.”
Try out PEMDAS on this problem:
| Question | Analysis |
| Solve 3 × 5 + (6 × 2) − 33 | Step 1: You are given an equation. |
| Step 2: You are asked to solve that equation. | |
|
Step 3: Use PEMDAS 3 × 5 + (6 × 2) − 33 (P) 3 × 5 + 12 − 33 (E) 3 × 5 + 12 − 27 (MD) 15 + 12 − 27 (AS) 0 |
|
| Step 4: Double-check that you performed the operations in the correct order and that your math calculations were performed correctly. |
Distributive and Commutative Properties
In addition to being certain to follow the correct order of operations when solving complex arithmetic problems, you may find that you need to utilize the distributive and commutative properties of mathematics to facilitate your computations. It’s not important that you remember the specific terms “distributive” and “commutative,” but it is important that you know how to use these properties.
The distributive property says that the result of multiplying one number by the sum or difference of two numbers can be obtained by multiplying each number individually and then totaling the results.
5 × (20 + 2) = 5 × 20 + 5 × 2 = 100 + 10 = 110
5 × (20 − 2) = 5 × 20 − 5 × 2 = 100 − 10 = 90
Similarly, a fraction with multiple terms in the numerator and only one term in the denominator can be subdivided.

Do not attempt to use this property if the denominator has more than one term.
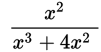 cannot be split up.
cannot be split up.
Not only is the distributive property useful in solving problems on the ASVAB, it can also help you quickly and accurately multiply in the absence of a calculator.
| Question | Analysis |
| Multiply 6 × 38 without a calculator. | You can convert that to 6 × (30 + 8) |
| Then, 6 × 30 + 6 × 8 = 180 + 48 = 228 |
Try this sample problem:
-

- 10x + 34
- 10x + 136
- 12x + 134
- 12x + 136
Explanation
Step 1: You are given an equation.
Step 2: You are asked to solve that equation.
Step 3: You can simplify multiplying 17 × 8 by treating that as (10 + 7) × 8 = 80 + 56 = 136.
The fraction is equivalent to
 .
.
Now the simplified expression is 136 + 12x − 2 = 12x + 134. Answer choice (C) is correct.
Step 4: Check your math and make sure you used the correct order of operations.
The commutative property says, in a nutshell, that order does not matter when adding or multiplying numbers. For example:
3 × 4 = 4 × 3
3 + 4 = 4 + 3
This property does not change PEMDAS; it merely gives you some flexibility when you get to the multiply or add part of the order of operations. The commutative property does not apply to subtraction or division.
4 − 3 does not equal 3 − 4
 does not equal
does not equal

This flexibility when dealing with addition and, in particular, multiplication can be a handy addition to your arithmetic toolbox as shown in the example below:
| Question | Analysis |
| Solve for 2 × 19 × 5 without a calculator. | Step 1: You are given an equation. |
| Step 2:You need to solve this equation without a calculator. | |
|
Step 3: You could answer this by first multiplying 2 × 19 = 38, then multiplying 38 × 5 = 190. However, before jumping straight into the math, use strategic logic. Note that 2 × 5 = 10. This is helpful because 10 is an easy number to multiply. If you rearrange the equation as 2 × 5 × 19 before solving, the math becomes more manageable. 2 × 5 × 19 = 10 × 19 = 190 |
|
| Step 4: Double-check your math. |
Ratios, Proportions, and Rates
Ratios represent the relationship of one quantity to another. Ratios can be presented in three different ways. They can be verbal, such as “the ratio of cats to dogs is 3 to 4.” Another way of describing a ratio is to use a colon, as in “3 : 4.” In order to use ratios in calculations, however, you will use the fractional form,
 .
Ratios do not necessarily represent the actual number of two different things. In this example, you don’t know if there are actually 3 dogs and 4 cats, or 6 cats and 8 dogs, or 600 cats and 800 dogs.
.
Ratios do not necessarily represent the actual number of two different things. In this example, you don’t know if there are actually 3 dogs and 4 cats, or 6 cats and 8 dogs, or 600 cats and 800 dogs.
Ratios are either part to part or part to whole relationships, depending upon what quantities are being compared:
A class contains 12 male students and 21 female students.
The part to part ratio of male students to female students is

The part to whole ratio of male students to all the students in the class is

Always simplify ratios to their lowest terms, as was done in the above example.
Here’s how an expert test taker would apply these basic rules for ratios to an AR question:
| Question | Analysis |
| Alicia is an avid video game player. She has a total of 21 video games. Her ratio of sports games to action games to mystery games is 4:2:1. How many action games does she have? | Step 1: The question gives the total number of video games and the ratio of different types of games in the collection. |
| Step 2: The question asks for the number of action games in the collection. | |
|
(A) 2 (B) 6 (C) 8 (D) 12 |
Step 3: The part to whole ratio of action games to total video games can be represented as
But Alicia has a total of 21 games, not 7. In order to determine how many action games Alicia has, multiply the part to whole ratio by the total number of games:
Answer choice (B) is correct. |
Step 4: You can double-check that
 does, in fact, equal the part to whole ratio of
does, in fact, equal the part to whole ratio of
 by dividing the numerator and denominator by their lowest common multiple, which is 3.
by dividing the numerator and denominator by their lowest common multiple, which is 3. |
A proportion is an equation of two ratios that shows the comparative relationship between parts, things, or elements with respect to size, amount, or degree.
When working with proportions, you can use a helpful technique called cross-multiplying to help solve the equation. To cross-multiply an equation that consists of two fractions, you multiply the numerator of the first fraction by the denominator of the second and vice versa. Here is an example of cross-multiplying:
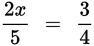
2x(4)=3(5)
Here’s an example of a proportion question in which you can use cross-multiplying:
| Question | Analysis |
|
A picture that is 4 inches wide and 6 inches long is enlarged so that it is
What is the width of the enlarged picture? |
Step 1: The question gives you the dimensions of a picture and says that the picture was then enlarged. |
| Step 2: The question asks for the new width of the picture. | |
|
Step 3: Set the given information up as a proportion. The ratio of width to length in the original picture is 4:6 and the ratio of width to length of the enlargement will be the same. The length of the enlargement will be
So, the enlarged picture is 5 inches wide. |
|
| Step 4: Double-check your math. Also, be sure you put the correct measurements in the correct places in the ratio. |
Practice working with ratios on this sample problem:
-
Micah can ride his bicycle 42 miles in 3 hours. Assuming that he travels at the same speed, how long would it take Micah to ride 70 miles? - 5.0 hours
- 5.5 hours
- 7.0 hours
- 7.5 hours
Explanation
Step 1: The problem states that Micah rides at the same speed in both instances. You are told how long it takes to ride 42 miles.
Step 2: You are asked how long it will take him to ride 70 miles.
Step 3: Micah’s distance to time relationship can be set up using a proportion.

Using the cross-multiplication technique,
 .
.
Before multiplying large numbers together and then dividing by 42, check to see if you can reduce the equation. Since 42 is a multiple of 3, you can divide both sides of the equation by 3.
70 = 14t
5 = t
Answer choice (A) is correct.
Step 4: You can double-check your math by inserting your answer into the proportion and cross-multiplying.

3(70) = 5(42)
210 = 210
A rate is simply a ratio that compares two different but related quantities, such as distance divided by time (speed), or amount divided by time, or cost per unit.
In other words:
 or
or
 or
or

Another way to look at rates is to think of them as changes in the numerator per changes in the denominator. For instance, if your rate of pay is $15/hour, you know that if you work one more hour you will earn an additional $15.
The key to solving rate problems is to set them up as proportions. Convert the units if necessary and solve for the unknown value.
Take a look at the following rate question:
| Question | Analysis |
| A waitress serves 3 diners every 5 minutes. At this rate, how many customers will she serve in one hour? |
Step 1: The question gives the rate at which a waitress can serve people. The rate is given in minutes. |
| Step 2: The question asks for the number of customers that will be served in one hour. | |
|
Step 3: Set the rate up as a proportion.
Convert units.
Cross-multiply and solve. 5x = 180 x = 36 |
|
| Step 4: Double-check your math and that the units were converted correctly. |
Pay close attention to units in ratios and proportions. Had hours not been converted to minutes in the example, the answer would have been wrong.
Try this sample problem to practice rates and units:
-
The volume of a certain substance is directly proportional to its weight. If 48 cubic inches of the substance weigh 112 ounces, what is the volume, in cubic inches, of 63 ounces of the substance? - 27
- 36
- 42
- 64
Explanation
Step 1: The problem gives the ratio of volume to weight of a certain substance.
Step 2: The problem asks for the volume of a different amount of the substance.
Step 3: Start by setting up the proportion
 .
.
You might notice that cross-multiplying this proportion looks difficult without a calculator and wonder if there is a more efficient way to answer the question. There is, by using logic.
In the given ratio, 48 is less than half of 112, so the correct answer will be less than half of 63. Looking at the answer choices, only 27 is less than half of 63.
Answer choice (A) is correct.
Step 4: You can double-check your work by reducing the proportions to their lowest form and checking that they equal each other.
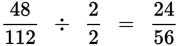




Both proportions reduce to
 , which means that the two proportions are equal and the answer choice is confirmed.
, which means that the two proportions are equal and the answer choice is confirmed.
Combined Work
You may see a problem on the ASVAB that asks you to determine how long it takes the combined effort of two people or machines to complete a task, or something similar such as how long it takes for two pipes to fill a tank.These are just a different form of rate problem.
For instance, if it takes Joe 3 hours to paint a room, then his rate of painting is
 . The tasks to be completed that are on the ASVAB are additive; the combined work of the people (or machines or pipes) can be added together to obtain a combined rate. This approach also works for more than two entities working on the same task.
. The tasks to be completed that are on the ASVAB are additive; the combined work of the people (or machines or pipes) can be added together to obtain a combined rate. This approach also works for more than two entities working on the same task.
| Question | Analysis |
| Jose can paint a room in 3 hours. Jill can paint the same room in 2 hours. How long will it take them to paint the room working together? | Step 1: The question gives the amount of time it takes two different people to paint a room. |
| Step 2: The question asks for the length of time it will take them to paint the room together. | |
|
Step 3: Express the individual times as rates.
Convert to a common denominator and add the rates.
Invert the fraction.
If it takes 6 hours to paint 5 rooms, it would take
|
|
| Step 4: Double-check your math. Also double-check that you are solving for the correct number of rooms, in this case, 1 room. |
Try this problem (which does not have answer choices) on your own:
-
There are three pipes that can be used to fill a tank. One of them can fill the tank in 2 hours, another can fill it in 3 hours, and the third can fill the tank in 6 hours. If all three pipes are used to fill the tank simultaneously, how long will it take?
Explanation
Step 1: The three times needed for each pipe to fill the tank individually are given.
Step 2: You are asked to calculate the rate at which they would be able to fill the tank together.
Step 3: The rates can be converted to
 , specifically
, specifically
 ,
,
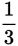 , and
, and
 . Convert their rates to a common denominator and add:
. Convert their rates to a common denominator and add:
 . Therefore to fill the one tank, the three pipes working together can accomplish the task in 1 hour.
. Therefore to fill the one tank, the three pipes working together can accomplish the task in 1 hour.
Percent Problems
Percents are ratios of an amount to 100, so the techniques used to work with ratios and proportions are valuable tools when you work with percents.
| Question | Analysis |
| A bag contains 8 marbles and 6 of them are green. What percent of the marbles in the bag are green? | Step 1: The question gives the total amount of marbles and the amount of green marbles. |
| Step 2: The question asks for the percent of total marbles that are green. | |
|
Step 3: To solve this, you can set up a proportion equating the numbers of marbles to the unknown percentage:
600 = 8g 75 = g So 75% of the marbles are green. |
|
| Step 4: Double-check to confirm your math is correct. |
To convert the English into math on a percent problem, use the following conversion table.
| English | Math Translation |
|---|---|
| % or percent | ÷ 100 (or use decimal or fractional equivalent) |
| of | × (times) |
| what | x (or n, or any variable you like) |
| is | = (equals) |
Using these translations, you can see, for instance, that 40% of 25 = 0.40 × 25 = 10.
Some ASVAB questions require you to increase or decrease a number by a given percent. To calculate such increases or decrease, take that percent of the original number and add it to or subtract it from the original number.
To increase 25 by 60%, first find 60% of 25.
25 × 0.6 = 15
Then add the result to the original number.
25 + 15 = 40
To decrease 25 by the same percent, subtract the 15.
25 − 15 = 10
Other ASVAB questions, rather than giving you the percent increase or decrease, will ask you to calculate the percentage change between an original value and a new value. In order to calculate that change, always use this formula:
Percent Change = 100% ×

If the percent change is an increase, the result will be positive. If the change is a decrease, the result will be negative. ASVAB percentage change problems ask for the change relative to the original value; using the new value in the denominator will produce an incorrect answer.
| Question | Analysis |
| A camera that originally cost $125 was sold on sale for $100. The sale price was what percent less than the original price? | Step 1: The question gives the original price and the sale price of a camera. |
| Step 2: The question asks for the percentage decrease between the sale price and the original price. | |
|
Step 3: Percent Change = 100% ×
Since the result is negative, you know that there was a price decrease. The answer is −20%. |
|
| Step 4: Briefly confirm that the answer makes sense. 20% of 125 is 25, so your answer is correct. |
Practice using the formula on this sample problem:
-
Ryan weighed 40 pounds when he finished kindergarten and 44 pounds when he started first grade. What was the percentage change in his weight between kindergarten and first grade? - 10% decrease
- 4% increase
- 10% increase
- 40% increase
Explanation
Step 1: The problem gives Ryan’s weight at various ages.
Step 2: The question asks for his percent change in weight.
Step 3:
Percent Change = 100% ×
 = 100% ×
= 100% ×
 = 100% ×
= 100% ×
 = 10%
= 10%
Since the result is positive, the answer is a 10% increase, choice (C).
Step 4: Check your calculations and check that you solved for the percent asked for.
Now practice this skill on another problem.
-
Rachel made a certain investment in the stock market but the value of her investment declined by 20%. However, the value of that investment then increased by 50%. What was the overall percentage change in the value of the investment from the original purchase price? - 30% decrease
- No change
- 20% increase
- 30% increase
Explanation
Step 1: The question gives information about the decrease and increase in the value of a stock.
Step 2: The question asks for the overall change.
Step 3: Notice that the question does not mention any specific prices. That makes this problem an excellent candidate for the Picking Numbers technique. Since the problem deals with percentages, start with an original value equal to 100.
If the investment lost 20% of its value, that would have been a loss of 20, so the value after the decrease would have been 80. Fortunately for Rachel, the value then increased 50%. Since the 50% increase was based upon a value of 80, that would be a gain of 40. This results in a final value of 80 + 40 = 120, which is a 20% increase from the original assigned value of 100, answer choice (C).
Step 4: Confirm that your math is correct and that you are solving for the correct piece of information.
Statistical Terms
Averages, like ratios, proportions, and rates, use fractions to find the answer to a problem. Here is the average formula:

What is the average of 3, 4, and 8?

Sometimes the ASVAB may not present the information in such simple terms. The formula for averages, like other three-part formulas, can be rearranged as needed.
| Question | Analysis |
| Six people went fishing and caught an average of 7 fish each. How many total fish did they catch? | Step 1: You are given the average amount of fish caught by 7 people. |
| Step 2: You are asked for the total number of fish. | |
|
Step 3: Plug the values that you are given into the formula and solve for the value needed.
Multiply both sides of the equation by 6. 6 × 7 = Total = 42 fish |
|
| Step 4: Check to be sure you used the numbers given in the problem and that you performed the calculations correctly. |
Here is a practice problem for you:
-
Lola was pleased to learn that her final grade in her history course, which was based upon her average for 4 tests, was 90. She knew that she had scored 93, 80, and 90 on her first three tests, but she could not remember her score on the last test. What was Lola’s score on the fourth test? - 87
- 90
- 93
- 97
Explanation
Step 1: You are given the score on 3 tests and the average score of 4 tests.
Step 2: The question asks for the score of the fourth test that would give the average listed.
Step 3: Use the average formula to write the equation
 with t representing the unknown score. The denominator is 4 because the final grade of 90 was based on 4 tests even though Lola only knew the results of 3 tests.
with t representing the unknown score. The denominator is 4 because the final grade of 90 was based on 4 tests even though Lola only knew the results of 3 tests.
Solving the average equation for t, add all the numbers in the numerator.

Multiply both sides of the equation by 4 to get 360 = 263 + t. Then t is 360 − 263 which equals 97, choice (D).
Step 4: Check your math. Make sure you plugged the correct values into the average formula in the beginning.
The ASVAB will not require you to make complex statistical calculations, but there are a few basic statistical terms with which you should be familiar. Mean is the same as average and is calculated the same way. The range is how “wide” the group of numbers is and can be calculated by subtracting the smallest number from the largest. The mode is the number that appears most frequently. Finally, median is the middle value of a group of numbers.
Practice by identifying these terms using the number set: 1, 2, 7, −3, 0, 5, 2.
In order to apply the statistical terms to a group of numbers, the very first thing you must do is arrange the numbers in ascending order: −3, 0, 1, 2, 2, 5, 7.
The mean of these numbers is
 .
.
The mode of the group is 2 since it is the only number that appears twice.
The range is 7 − (−3) = 10.
The median is 2, since three numbers are smaller than that and three are larger.
Should you encounter a situation whereby there are two numbers in the middle, the average of those two middle numbers is the median.
For instance, the median of −3, 0, 1, 2, 2, 5 is

Sequences
A sequence is merely a group of numbers placed in order, as in the example above. You are most likely to encounter a special type of sequence on the ASVAB called an arithmetic sequence. The property that creates an arithmetic sequence is that each number is equal to the number before it plus a constant number. The sequence 1, 3, 5, 7 is an arithmetic sequence because each number is 2 more than the previous number in the sequence. One property that makes arithmetic sequences special is that the mean equals the median.
Here’s an example of the type of sequence problem that may be on the ASVAB:
| Question | Analysis |
| What is the mean of a sequence of multiples of 3 that begins with −3 and ends with 15? | Step 1: The question gives you the rules of a sequence as well as the beginning and ending terms of that sequence. |
| Step 2: The question asks for the mean. | |
|
Step 3: Since the numbers are multiples of 3, the numbers will all be 3 apart. This is an arithmetic sequence. You can write down the sequence: −3, 0, 3, 6, 9, 12, 15. Because this is an arithmetic sequence, the median is equal to the mean, 6. |
|
| Step 4: Check that you defined the sequence properly and solved for the correct statistical term. |
Probability
Probability is the numerical likelihood that a particular outcome will occur. To find the probability that something is going to happen, use this formula:
Probability =

Probability can be expressed as a fraction, a decimal, or a percent.
| Question | Analysis |
| If there are 12 books on a shelf and 9 of them are mysteries, what is the probability of picking a mystery at random? | Step 1: The question gives the total number of books and the number of mystery books. |
| Step 2: The question asks for the probability of picking a mystery book. In other words, it asks you for the proportion of mystery books to total books. | |
|
Step 3: Probability =
This probability can also be expressed as 0.75 or 75%. |
|
| Step 4: Check that you set up and simplified the fraction appropriately. |
Probabilities are always between 0 and 1 (or between 0% and 100%). A probability of 0 means that there are no outcomes of interest and a probability of 1 means that all the possible outcomes result in the outcome of interest occurring.
To find the probability that both of two events will occur, find the probability that the first event occurs and multiply this by the probability that the second event occurs. The probability of two independent events both occurring will be less than the probability of either occurring by itself. When you see a probability question that deals with one event and another event both occurring, you will multiply the probabilities.
Study the following example.
| Question | Analysis |
| If there are 12 books on a shelf and 9 of them are mysteries, what is the probability of picking a mystery first AND a non-mystery book second if exactly two books are selected and neither of them is replaced on the shelf? | Step 1: You are given the same information about the number of mystery books compared to the number of books overall. |
| Step 2: This time, the question asks for the probability that two different events will both occur. | |
|
Step 3: The probability of picking a mystery book first:
Probability of picking a non-mystery book second (if a mystery is picked first):
(Originally there were 9 mysteries and 3 non-mysteries. After the mystery is selected first, there are 8 mysteries and 3 non-mysteries, i.e., 11 books remaining.) Probability of picking a mystery book first and then a non-mystery book second:
|
|
| Step 4: Check to be sure you set up the second proportion to incorporate the missing book that was already picked. Double-check your math and be sure you solved for the probability that was asked for. |
A question might ask you to determine the probability of one or another event occurring. In this case, you add the individual probabilities. The probability of one or another event occurring will be greater than the probability of either event occurring alone.
| Question | Analysis |
| What is the probability of rolling a 1 OR a 2 on one roll of a fair six-sided die? | Step 1: The question gives you background information that you are dealing with a die that has 6 faces and isn’t weighted. |
| Step 2: The question asks for the probability of either of two scenarios happening. | |
|
Step 3: Probability of rolling a 1 =
Probability of rolling a 2 =
Probability of rolling a 1 or a 2 =
|
|
| Step 4: Briefly check your math before moving on to the next question. |
Practice the principles of probability on the following problem:
-
If a fair coin is flipped 3 times, what is the probability that none of the occurrences will result in a head? - 0
-

-

-

Explanation
Step 1: The question sets up a scenario of flipping coins.
Step 2: The question asks for the probability of landing on tails 3 times in a row.
Step 3: In order to flip a coin 3 times with no heads, the first flip must be a tail and the second flip must also be a tail and the third flip must be a tail, too.
Therefore, the equation to determine the probability of no heads on 3 flips is
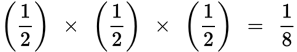 . Answer choice (B) is correct.
. Answer choice (B) is correct.
Step 4: Double-check that you solved for the correct probability and you performed the calculations correctly.
 .
.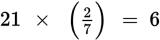 .
.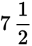 inches long.
inches long. inches, but the width is some unknown value (w). Since the width/length ratio of the two pictures must be the same, you can set the proportions equal to each other:
inches, but the width is some unknown value (w). Since the width/length ratio of the two pictures must be the same, you can set the proportions equal to each other:
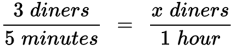
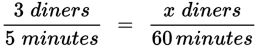
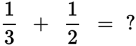
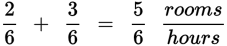

 hours to paint 1 room.
hours to paint 1 room.

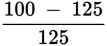 = 100% ×
= 100% ×
 = 100% ×
= 100% ×
 = −20%
= −20%