Geometry Review

Throughout the geometry problems on the ASVAB, you will be presented with shapes and diagrams. Unless otherwise noted, you cannot assume the drawings are drawn to scale. Thus, work using the information given in a diagram; don’t rely on how it looks.

Lines and Angles

Line Segments

A line segment is a piece of a line, and it has an exact measurable length. Questions may give you a segment divided into several pieces, give you the measurements of some of these pieces, and ask you for the length of another piece.

Question	Analysis
If PR = 12 and QR = 4, PQ = ?
PQ = PR − QR	Subtract QR from the whole segment to find the remaining piece, PQ.
PQ = 12 − 4 PQ = 8	Plug in the lengths given and solve.

The point exactly in the middle of a line segment, halfway between the endpoints, is called the midpoint of the line segment. To bisect means to cut in half, so the midpoint of a line segment bisects that line segment.

M is the midpoint of AB, so AM = MB.

Angles

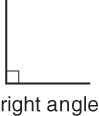
A right angle measures 90 degrees and is usually indicated in a diagram by a little box. The figure above is a right angle. Lines that intersect to form right angles are said to be perpendicular.

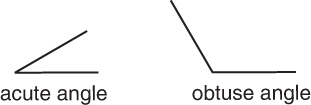
An acute angle measures less than 90 degrees. An obtuse angle measures more than 90 degrees.

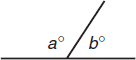
Angles that form a straight line add up to 180 degrees. In the figure above, a + b = 180.

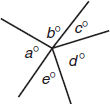
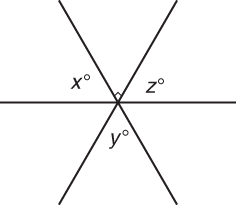
Angles around a point add up to 360 degrees. In the figure above, a + b + c + d + e = 360.

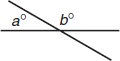
When two lines intersect, adjacent angles are supplementary, meaning they add up to 180 degrees. In the figure above, a + b = 180.

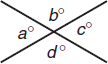
When lines intersect, angles across the vertex from each other are called vertical angles and are equal to each other. Above, a = c and b = d.

Question

Analysis

What is the value of x + y + z?

Step 1: The figure shows three intersecting lines that form six angles, which all together equal 360°. An unlabeled angle is 90°. Three labeled angles are x, y, and z.

Step 2: The question asks for the sum of the three labeled angles.

Step 3: Because the angle labeled y is a vertical angle to the right angle, y must equal 90°.

Because the angles labeled x and z form a straight line with the right angle, together they equal 180° − 90° = 90°.

y + (x + z) =

90° + 90° = 180°

(A)	90
(B)	120
(C)	180
(D)	270

Step 4: Choose option (C). Confirm that the answer includes the correct three angles and that your arithmetic is correct.

Parallel Lines

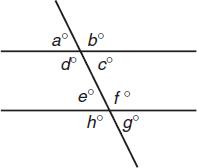
Parallel lines are lines that have the same slope as one another. The slope represents the steepness of the line and the direction it goes. Therefore, lines that are parallel never intersect each other. You can imagine them as being like railroad tracks. When parallel lines are crossed by another line, this line is called a transversal, and angles are formed. All of these angles are said to be interior angles. Angles with the same relationship to the transversal are called corresponding angles. In the gray box below, variables refer to the diagram above.

Question

Analysis

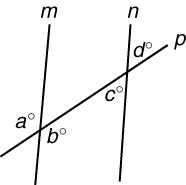
m || n

What is the value of a + b + c + d?

Step 1: The figure shows two parallel lines, m and n, crossed by transversal p.

Step 2: Find the sum of the four labeled angles.

Step 3: Two of the labeled angles are acute, and two are obtuse. Every pair of acute + obtuse angles formed by a transversal crossing parallel lines equals 180°.

Two acute + obtuse angle pairs = 2 × 180° = 360°.

(A)	120
(B)	180
(C)	200
(D)	360

Choice (D) is correct.

Step 4: Confirm that the answer includes the correct four angles and that your arithmetic is correct.

Polygons

Triangles

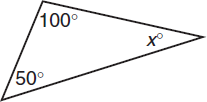
The three interior angles of any triangle add up to 180°. In the figure above, x + 50 + 100 = 180, so x = 30.

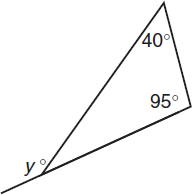
An exterior angle of a triangle is equal to the sum of the two interior angles that are not adjacent to that exterior angle. In this figure, the exterior angle labeled y is equal to the sum of the remote angles: y = 40 + 95 = 135.

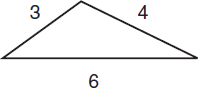
The perimeter of a polygon is the sum of the lengths of its sides. The perimeter of a triangle is the sum of the lengths of its three sides. The perimeter of the triangle in the figure above is 3 + 4 + 6 = 13.

The area of a triangle is equal to half of the base (that is, the length of one leg) multiplied by the height.

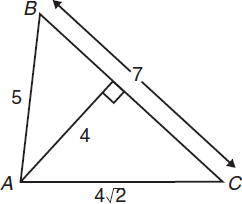
Area of triangle = (base)(height)

The height is the perpendicular distance between the side that’s chosen as the base and the opposite vertex (opposite corner). In this triangle, 4 is the height when the side with measure 7 (BC) is chosen as the base. In the triangle above:

Area = bh = (7)(4) = 14

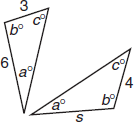
Similar triangles have the same shape, but they may be different sizes. Their corresponding angles are equal, and their corresponding sides are proportional. The triangles shown above are similar because they have the same angles.

Question	Analysis
Find the value of s in the diagram above.
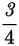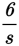
=	Because the triangles have the same angle measures, their sides are proportional. Set up a proportion.
3s = (4)(6) 3s = 24 s = 8	Cross-multiply to solve for s.

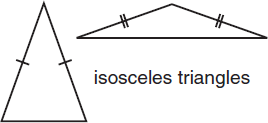
An isosceles triangle is a triangle that has two equal sides. Not only are two sides equal, but the angles opposite the equal sides, called base angles, are also equal.

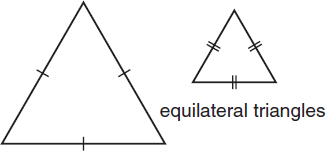
Equilateral triangles are triangles in which all three sides are equal. Since all the sides are equal, all three angles are also equal. All angles in an equilateral triangle measure 60 degrees, regardless of the length of the sides.

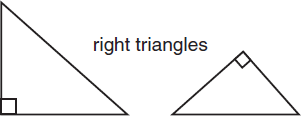
A right triangle is a triangle with a right angle. Every right triangle has exactly two acute angles. The sides opposite the acute angles are called the legs. The side opposite the right angle is called the hypotenuse. Since it’s opposite the largest angle, the hypotenuse is the longest side of a right triangle.

If you know two sides of a right triangle, you can solve for the third side using the Pythagorean theorem:

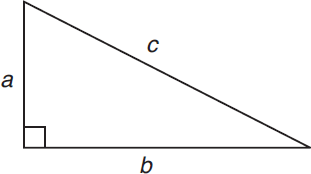
a² + b² = c²

In this equation, a and b are the perpendicular sides, or legs, of a right triangle, and c is the longest side, or hypotenuse, of the triangle.

Question	Analysis
One leg of a right triangle is 2 and the other leg is 3. What is the length of the hypotenuse?
a² + b² = c²	Use the Pythagorean theorem.
	Plug in the lengths given for the legs and solve for the hypotenuse.

Quadrilaterals

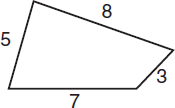
A quadrilateral is a figure with four sides.

The perimeter of a quadrilateral is the sum of the measures of all four sides. The perimeter of the quadrilateral in the figure above is 5 + 8 + 3 + 7 = 23.

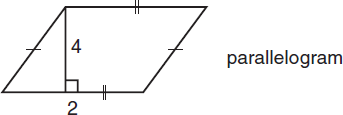
A parallelogram is a quadrilateral with two sets of parallel sides. Opposite sides are equal, as are opposite angles. The formula for the area of a parallelogram is

Area = (base)(height)

In the diagram above, the base is 2 and the height is 4, so area = 2 × 4 = 8.

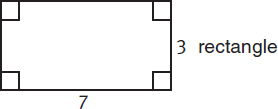
A rectangle is a parallelogram containing four right angles. Opposite sides are equal. The formula for the area of a rectangle is

Area = (length)(width)

In the diagram above, the length is 7 and the width is 3, so area = 7 × 3 = 21.

As with any other polygon, the perimeter of a rectangle is all the sides added together. Because a rectangle has two pairs of equal sides, the formula for the perimeter of a rectangle is

Perimeter = 2(ℓ+ w)

The perimeter of the above rectangle is 2(7 + 3) = 2 × 10 = 20.

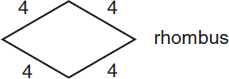
A rhombus has four equal sides, with the opposite sides parallel to one another.

The formula for the perimeter of a rhombus is

Perimeter = 4s

The perimeter of the above rhombus is 4(4) = 16.

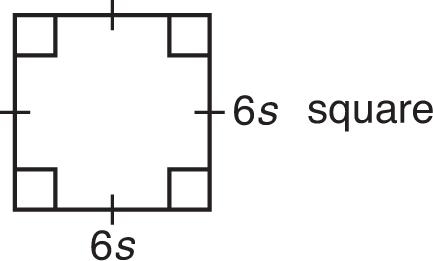
A square is a rectangle with four equal sides. Here is the formula for the area of a square:

Area = (side)²

In the diagram above, the length of each side is 6, so area = 6² = 36.

The formula for the perimeter of a square is

Perimeter = 4s

The perimeter of the above square is 4(6) = 24.

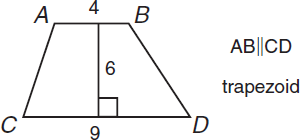
A trapezoid is a quadrilateral with one pair of parallel sides. The two parallel sides of a trapezoid are called the bases.

The formula for the area of a trapezoid is

Area = 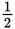(sum of the lengths of the bases)(height)

In the diagram above, the area of the trapezoid is 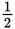(4 + 9)(6) = 39.

Study the example below.

Question Analysis

The trapezoid below has an area that is equal to greater than twice the area of the square below. Which of the following could be the value of x?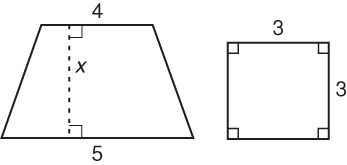

Step 1: You’re given two shapes, a square and a trapezoid.

Area of square = 9

Area of trapezoid > 2 × Area of square

Area of trapezoid > 18

Step 2: You’re asked for the value of x.

(A) 2

(B) 3

(C) 4

(D) 5

Step 3: There’s one unknown in the question and numbers in the choices, so use Backsolving.

Try choice (B): if x = 3, then

Area of trapezoid = (4 + 5)3 = 13.5

That’s too small. Eliminate (A) and (B).

Try choice (C): if x = 4, then

Area of trapezoid = (4 + 5)4 = 18

That’s also too small, since the area of the trapezoid is supposed to be greater than 18. Eliminate (C); (D) must be correct.

Step 4: Briefly check that your answer makes sense and move on to the next question.

Now try one on your own.

The value of the area of the trapezoid below is divisible by 5 with no remainder. Which of the following is a possible value of y?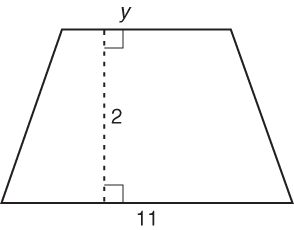

11

12

14

18

Explanation

Step 1: The area of the trapezoid is a multiple of five. So,

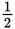(y + 11)2 = (y + 11) is a multiple of five.

Step 2: You’re asked for a possible value of y.

Step 3: Start by using Strategic Guessing Using Logic. Multiples of 5 always end in 5 or 0. To produce a number that ends in 5 or 0, y would have to end with 4 or 9. Only choice (C) fits.

Step 4: Briefly confirm: 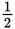(14 + 11)2 = (14 + 11) = 25, which is a multiple of 5.

Circles

Learning Objective

In this section, you will learn how to:

determine the circumference and area of a circle

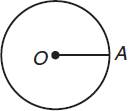
A circle is a figure in which each point is an equal distance from its center. In the diagrams in this section, O is the center of the circle.

The radius of a circle is the straight-line distance from its center to any point on the circle. All radii of a given circle have equal lengths. In the figure above, OA is a radius of circle O.

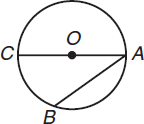
A chord is a line segment that connects any two points on a circle. Segments AB and AC are both chords. The largest chord that can be drawn in a circle is a diameter of that circle.

A diameter of a circle is a chord that passes through the circle’s center. All diameters are the same length and are equal to twice the radius. In the figure below, AC is a diameter of circle O.

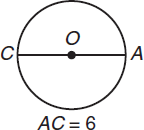
The circumference of a circle is the distance around it. It is equal to πd or 2πr. In this example,

Circumference = πd = 6π

The area of a circle equals π times the square of the radius, or πr². In this example, since AC is the diameter, r = 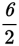= 3, and

Area = πr² = π(3²) = 9π

Study the following example.

Question Analysis

In the figure below, the radius of circle A has a length of 1 unit, and the radius of circle B has a length of 2 units. What is the ratio of the area of A to the area of B?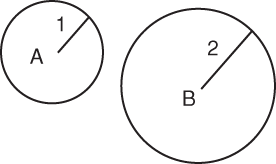

Step 1: The question gives you two circles and their radius measures.

Step 2: You need the ratio of the area of A to the area of B. The answer choices are all expressed as fractions, so it will look like this:

Step 3: Calculate the area of each.

Area of A = π1² = π

Area of B = π2² = 4π

(A)

(B)

(C)

(D)

Step 4: Choice (A) is correct. Briefly double-check your calculations and confirm.

Now, try this one on your own.

The diameter of the circle below has measure x. The area of the circle is 64π. What is the value of x?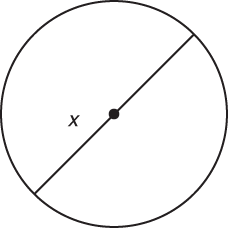

4

2π

8

16

Explanation

Step 1: The question supplies this information:

A = 64π

d = x

Step 2: You’re asked for the measure of the diameter, or x.

Step 3: Work backwards from what you know.

A = 64π = r²π

r² = 64

r = 8

x = diameter = 2r = 16

Step 4: Choice (D) is correct. Briefly double-check your math and confirm.

Solid Geometry

Learning Objective

In this section, you will learn how to:

find the volume and surface area of a rectangular solid

These formulas pertain to a rectangular solid box. Length is ℓ, width is w, and height is h.

Volume of a rectangular solid or box = ℓ × w × h

Surface area of a rectangular solid or box = 2ℓw + 2wh + 2ℓh

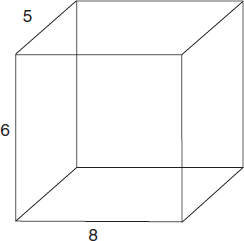
Question Analysis

Find the volume of the box in the figure above.

V = ℓ × w × h Use the formula for the volume of a rectangular solid.

V = 8 × 5 × 6 = 240 Plug in the dimensions given and solve.

Now try a problem on your own.

Find the surface area of the box above.

Explanation

Step 1: The question provides a diagram of a box.

Step 2: The question asks for the surface area of that box.

Step 3: Use the formula for surface area of a rectangular solid, plug in the values given, and solve:

SA = 2ℓw + 2wh + 2ℓh

SA = (2 × 8 × 5) + (2 × 5 × 6) + (2 × 8 × 6)

SA = 80 + 60 + 96 = 236

Step 4: Confirm that you plugged in the correct values for the correct variables.

To find the volume of a cylinder, you find the area of its base (which is a circle) and multiply it by the height.

Volume of a cylinder = πr²h

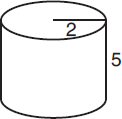
Question Analysis

Find the volume of the cylinder in the figure above.

V = πr²h Use the formula for the volume of a cylinder.

V = π × 2² × 5 = π × 4 × 5 = 20π Plug in the dimensions given and solve.

To find the surface area of any three-dimensional figure, add the areas of each side of the figure. Accordingly, finding the surface area of a cylinder involves adding the area of both of the circular ends to the area of the curved sides. Note that, if the sides of a cylinder were “unrolled,” they’d form a rectangle like this:

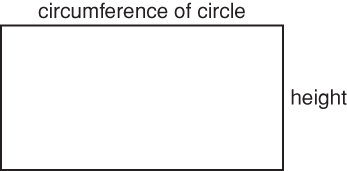
Thus, the formula for the surface area of a cylinder is:

SA = 2(πr²) + 2πrh

Combined Figures

When you are presented with a diagram that looks like two shapes put together, consider splitting the shapes to make calculations easier. For example, take a look at the next question:

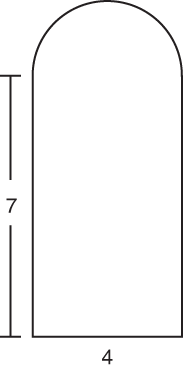
Question Analysis

Find the area of the figure above. Note that the figure is half of a circle sitting on top of a rectangle. Split the figure up and work with the two shapes independently.

Area = ℓ × w = 7 × 4 = 28 Plug the values from the diagram into the area formula for a rectangle.

Area = πr² = π(2)² = 4π Since 4 is the diameter of the circle, 2 is the radius. Use that information in the area formula for a circle.

4π ÷ 2 = 2π Since it is only half of a circle, you need to divide the area by two.

28 + 2π Add the area for the rectangle and the area of the half circle together to get your answer.

If you see a complicated figure on the test, try to break it down into more manageable components and solve for each individually.

Coordinate Geometry

Learning Objectives

In this section, you will learn how to:

choose the equation that correctly represents a given line

calculate the slope and y-intercept of a line if given two points on the line

find the distance between two given points on a coordinate plane

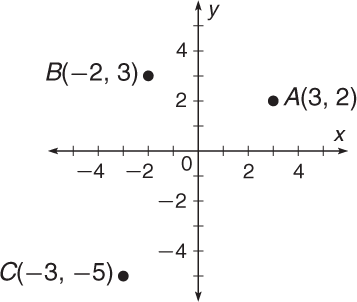
The coordinate grid is composed of a horizontal x-axis and a vertical y-axis. The place where the axes meet is called the origin. Every point on the coordinate grid has a pair of coordinates, with the first being the x-coordinate and the second being the y-coordinate. In the figure above, points A, B, and C are at (3, 2), (–2, 3), and (–3, –5), respectively.

A line on the coordinate grid can be represented by the slope-intercept form of a linear equation. In this equation, x and y are the coordinates of a point on the line, b is the y-intercept, and m is the slope. Study the examples below.

Slope-intercept form of a linear equation: y = mx + b

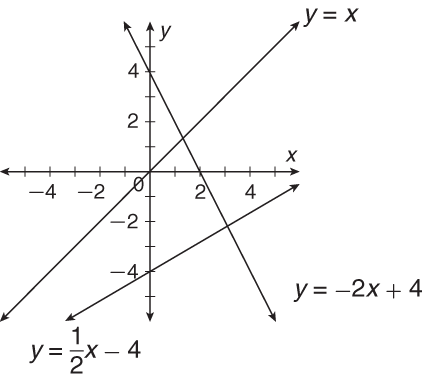
The y-intercept is the point where the line crosses the y-axis. The x-coordinate is always zero at the y-intercept.

The slope defines if a line goes down to the right or up to the right. Slope can be thought of as “rise over run” or “change in y over change in x.”

Slope =

If a line has a positive slope, then y gets larger as x gets larger. If a line has a negative slope, then y gets smaller as x gets larger. The steeper the line, the greater the absolute value of the slope. For example, lines with slopes of –3 or 3 are steeper than lines with slopes of –1 or 1, which in turn are steeper than lines with slopes of 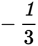or .

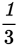Study this example about the coordinate plane.

Question Analysis

A line on the coordinate grid has a slope of 2 and a y-intercept of −8. What is the correct equation of this line?

y = mx + b Use the slope-intercept equation for a line.

y = 2x − 8 Plug in 2 for m and −8 for b.

Now try this coordinate geometry problem on your own.

The following points lie on a line on the coordinate grid: (0, 2) and (6, 5). What is the slope of this line?

Explanation

Step 1: You are given two points on a coordinate grid.

Step 2: You need to find the slope of the line that contains these two points.

Step 3: Use the formula for the slope of a line:

Slope =

Plug in the y-coordinates from the second point and the first point, respectively, and the x-coordinates in the same order.

Slope = = =

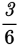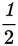
Step 4: Check your math and your fraction reduction. The line has a slope of .

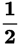If you know the slope of a line and one point on that line, you can calculate the y-intercept. Continuing the example above, plug the information into the slope-intercept formula and solve for the y-intercept.

Question Analysis

Find the y-intercept of the line that includes points (0, 2) and (6, 5).

y = mx + b Use the slope-intercept formula.

y = 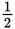x + b Plug in the slope, which was calculated above to be 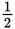, for m in the equation.

2 = 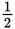x × 0 + b Plug in the x- and y-values from one pair of coordinates.

2 = 0 + b

2 = b
Solve for the variable b.

If you are given two points on a grid and asked to find the distance between them, you can do so using the Pythagorean theorem. Continuing to use the points above, find the distance between the two points on the x-axis and the difference between the two points on the y-axis. Then, using those two values as the legs of the right triangle, calculate the hypotenuse, which is the distance between the points.

Question Analysis

What is the distance between the two points (0, 2) and (6, 5)?

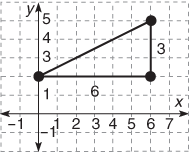
Draw the points on a coordinate plane. Then, draw a third dot that makes a right triangle when all points are connected. The third point will be drawn where the y-axis of one point crosses the x-axis of the other.

The distance along the x-axis is 6 and the distance along the y-axis is 3.

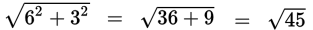
Use the Pythagorean theorem to solve for the distance between the two points.

The distance between the two points is .

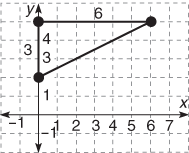
Note: The triangle also could have been drawn with the third point opposite, with the y-axis of the lower point intersecting the x-axis of the higher point. Either way, the result is the same.

If you are asked to find the distance between two points on the coordinate plane, draw a right triangle to help you use the Pythagorean theorem to solve.

Now you can try out your math knowledge—and practice the Kaplan Method for math—on the following practice sets.

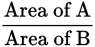
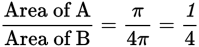
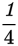
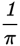
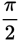
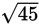Question	Analysis
Find the volume of the box in the figure above.
V = ℓ × w × h	Use the formula for the volume of a rectangular solid.
V = 8 × 5 × 6 = 240	Plug in the dimensions given and solve.

Question	Analysis
Find the volume of the cylinder in the figure above.
V = πr²h	Use the formula for the volume of a cylinder.
V = π × 2² × 5 = π × 4 × 5 = 20π	Plug in the dimensions given and solve.

Question	Analysis
Find the area of the figure above.	Note that the figure is half of a circle sitting on top of a rectangle. Split the figure up and work with the two shapes independently.
Area = ℓ × w = 7 × 4 = 28	Plug the values from the diagram into the area formula for a rectangle.
Area = πr² = π(2)² = 4π	Since 4 is the diameter of the circle, 2 is the radius. Use that information in the area formula for a circle.
4π ÷ 2 = 2π	Since it is only half of a circle, you need to divide the area by two.
28 + 2π	Add the area for the rectangle and the area of the half circle together to get your answer.

Question	Analysis
A line on the coordinate grid has a slope of 2 and a y-intercept of −8. What is the correct equation of this line?
y = mx + b	Use the slope-intercept equation for a line.
y = 2x − 8	Plug in 2 for m and −8 for b.

Question	Analysis
Find the y-intercept of the line that includes points (0, 2) and (6, 5).
y = mx + b	Use the slope-intercept formula.
y = x + b	Plug in the slope, which was calculated above to be , for m in the equation.
2 = x × 0 + b	Plug in the x- and y-values from one pair of coordinates.
2 = 0 + b 2 = b	Solve for the variable b.

Question	Analysis
What is the distance between the two points (0, 2) and (6, 5)?
	Draw the points on a coordinate plane. Then, draw a third dot that makes a right triangle when all points are connected. The third point will be drawn where the y-axis of one point crosses the x-axis of the other. The distance along the x-axis is 6 and the distance along the y-axis is 3.
	Use the Pythagorean theorem to solve for the distance between the two points. The distance between the two points is .
	Note: The triangle also could have been drawn with the third point opposite, with the y-axis of the lower point intersecting the x-axis of the higher point. Either way, the result is the same.