In this section, we'll be looking at the actual structure of a classical or dense neural network. We'll start off with a sample neural network structure, and then we'll expand that to build a visualization of the network that you would need in order to understand the MNIST digits. Then, finally, we'll learn how the tensor data is actually inserted into a network.
Let's start by looking at the structure of a dense neural network. Using the network package, we will draw a picture of a neural network. The following screenshot shows the three layers that we are setting up—an input layer, an activation layer, and then an output layer—and fully connecting them:
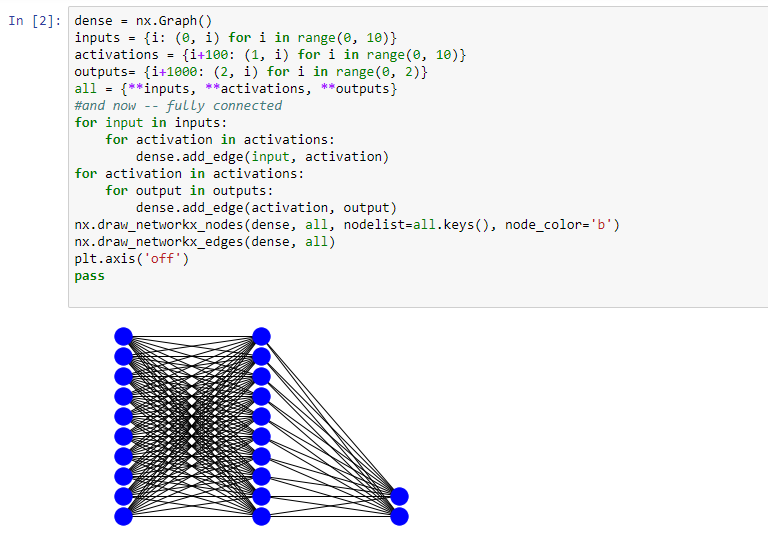
That's what these two loops in the middle are doing. They are putting an edge between every input and every activation, and then every activation and every output. That's what defines a dense neural network: the full connectivity between all inputs and all activations, and all activations and all outputs. As you can see, it generates a picture that is very densely connected, hence the name!
Now, let's expand this to two dimensions with a 28 x 28 pixel grid (that's the input network), followed by a 28 x 28 pixel activation network where the learning will take place. Ultimately, we will be landing in 10 position classification network where we'll be predicting the output digits. From the dark interconnecting lines in the following screenshot, you can see that this is a very dense structure:
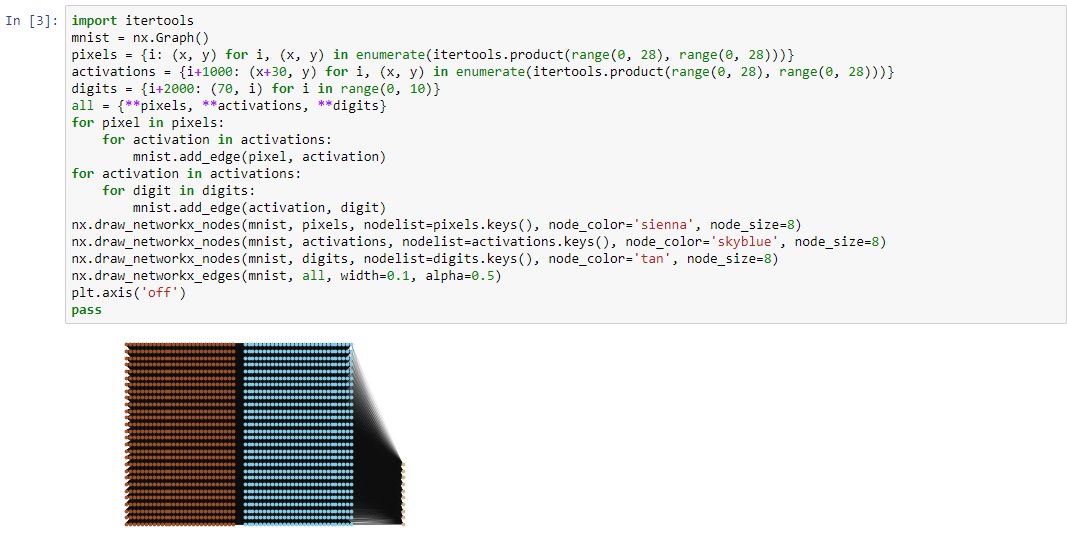
In fact, it's so dense that it's actually hard to see the edges of the individual lines. These lines are where the math will be taking place inside of the network. Activation functions, which will be covered in the next section, are the math that takes place along each one of these lines. We can see from this that the relationship between the tensors and networks is relatively straightforward: The two-dimensional grid of inputs (the pixels, in the case of this image) are where the two-dimensional encoded data that we learned about in the previous section will be placed. Inside of the network, math operations (typically a dot product followed by an activation function) are the lines connecting one layer to another.