
IN CONTEXT
Physics
1543 Nicolaus Copernicus argues that the planets orbit the Sun, not Earth.
1609 Johannes Kepler argues that the planets move freely in elliptical orbits around the Sun.
1610 Galileo’s astronomical observations support Copernicus’s views.
1846 Johann Galle discovers Neptune after French mathematician Urbain Le Verrier uses Newton’s laws to calculate where it should be.
1859 Le Verrier reports that Mercury’s orbit is not explained by Newtonian mechanics.
1915 With his general theory of relativity, Albert Einstein explains gravity in terms of the curvature of spacetime.
At the time Isaac Newton was born, the heliocentric model of the Universe, in which Earth and the other planets orbit the Sun, was the accepted explanation for the observed movements of the Sun, Moon, and planets. This model was not new, but had returned to prominence when Nicolaus Copernicus published his ideas at the end of his life in 1543. In Copernicus’s model, the Moon and each of the planets revolved in its own crystalline sphere around the Sun, with an outer sphere holding the “fixed” stars. This model was superseded when Johannes Kepler published his laws of planetary motion in 1609. Kepler dispensed with Copernicus’s crystalline spheres, and showed that the orbits of the planets were ellipses, with the Sun at one focus of each ellipse. He also described how the speed of a planet changes as it moves.
What all these models of the Universe lacked was an explanation of why the planets moved in the way they did. This is where Newton came in. He realized that the force that pulled an apple towards the centre of Earth was the same force that kept the planets in their orbits around the Sun, and demonstrated mathematically how this force changed with distance. The mathematics he used involved Newton’s three Laws of Motion and his Law of Universal Gravitation.
Changing ideas
For centuries, scientific thinking had been dominated by the ideas of Aristotle, who reached his conclusions without carrying out experiments to test them. Aristotle taught that moving objects only kept moving as long as they were being pushed, and that heavy objects fell faster than lighter ones. Aristotle explained that heavy objects fell to Earth because they were moving towards their natural place. He also said that celestial bodies, being perfect, must all move in circles at constant speeds.
Galileo Galilei came up with a different set of ideas, arrived at through experiment. He observed balls running down ramps and demonstrated that objects all fall at the same rate if air resistance is minimal. He also concluded that moving objects continue to move unless a force, such as friction, acts to slow them down. Galileo’s Principle of Inertia was to become part of Newton’s First Law of Motion. As friction and air resistance act on all moving objects that we encounter in daily life, the concept of friction is not immediately obvious. It was only by careful experiment that Galileo could show that the force keeping something moving at a steady speed was only needed to counteract friction.
Laws of motion
Newton experimented in many areas of interest, but no records of his experiments on motion survive. His three laws, however, have been verified in many experiments, holding true for speeds well below the speed of light. Newton stated his first law as: “Every body perseveres in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed thereon.” In other words, a stationary object will only start to move if a force acts on it, and a moving object continues to move with constant velocity unless a force acts on it. Here, velocity means both the direction of a moving object and its speed. So an object will only change its speed or change direction if a force acts on it. The force that is important is the net force. A moving car has many forces on it, including friction and air resistance, and also the engine driving the wheels. If the forces pushing the car forwards balance the forces trying to slow it down, there is no net force and the car will maintain a constant velocity.
Newton’s Second Law states that the acceleration (a change of velocity) of a body depends on the size of the force acting on it, and is often written down as F = ma, where F is force, m is mass, and a is acceleration. This shows that the greater the force on a body, the greater the acceleration. It also shows that the acceleration depends on the mass of a body. For a given force, a body with a small mass will accelerate faster than one with a larger mass.
The Third Law is stated as “For every action there is an equal and opposite reaction.” It means that all forces exist in pairs: if one object exerts a force on a second object, then the second object simultaneously exerts a force on the first object, and both forces are equal and opposite. In spite of the term “action”, movement is not required for this to be true. This is linked to Newton’s ideas about gravity, since one example of his Third Law is the gravitational attraction between bodies. Not only is Earth pulling on the Moon, but the Moon is pulling on Earth with the same force.
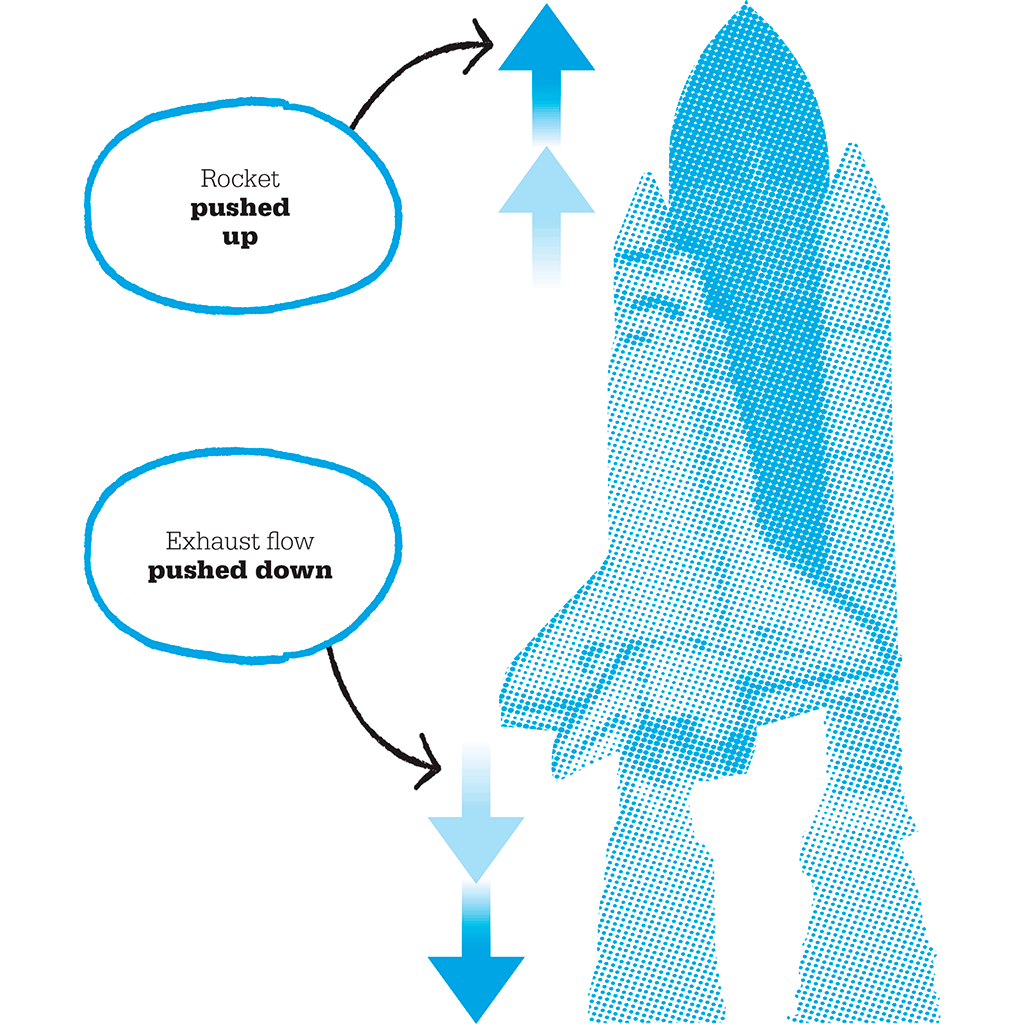
Rocket engines are an example of Newton’s Third Law in action. The rocket produces a jet that is forced downwards. The jet exerts an equal and opposite force that pushes the rocket up.
Universal attraction
Newton started thinking about gravity in the late 1660s, when he retired to the village of Woolsthorpe for a couple of years to avoid the plague that was ravaging Cambridge. At that time, several people had suggested that there was an attractive force from the Sun, and that the size of this force was inversely proportional to the square of the distance. In other words, if the distance between the Sun and another body is doubled, the force between them is only one quarter of the original force. However, it was not thought that this rule could be applied close to the surface of a large body such as Earth.
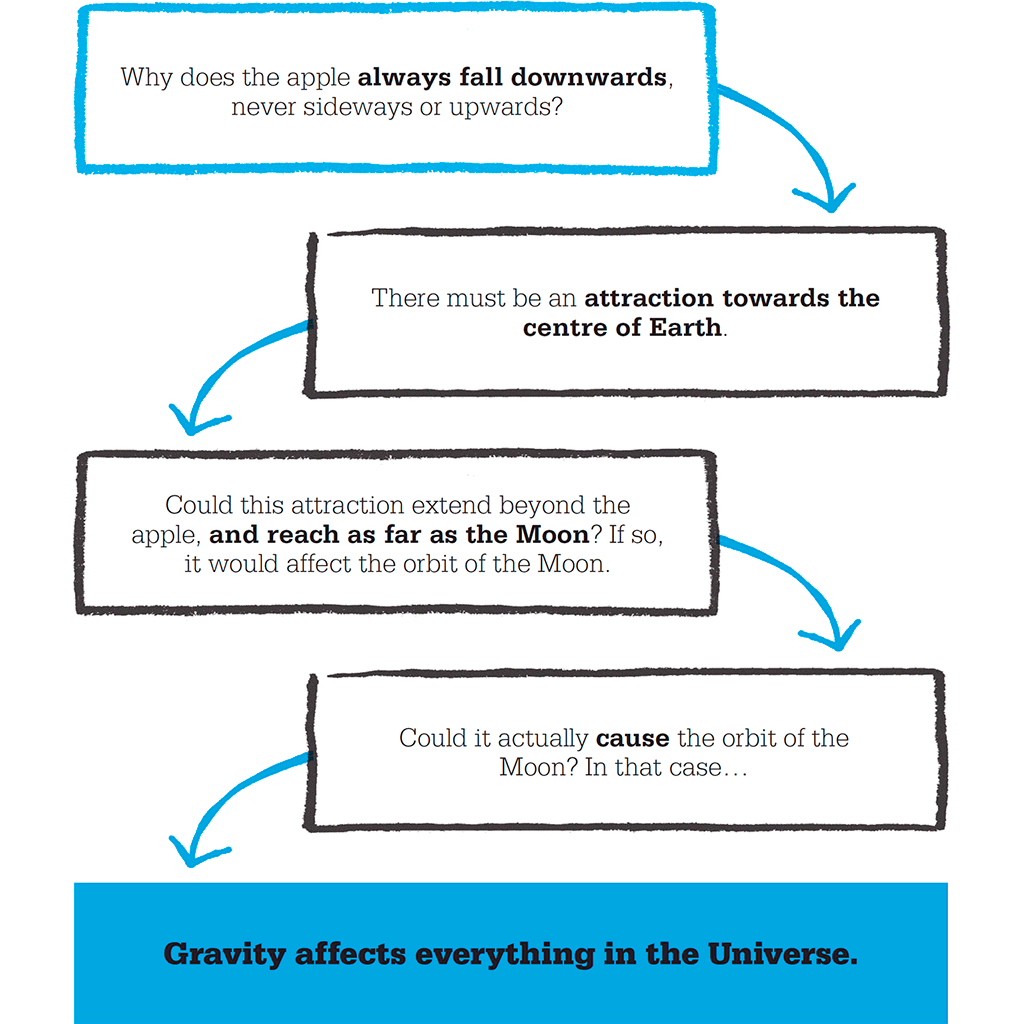
Newton, seeing an apple fall from a tree, reasoned that Earth must be attracting the apple and, as the apple always fell perpendicular to the ground, its direction of fall was directed to the centre of Earth. So the attractive force between Earth and the apple must act as if it originated in the centre of Earth. These ideas opened the way to treating the Sun and planets as small points with large masses, which made calculations much easier by measuring from their centres. Newton saw no reason to think that the force that made an apple fall was any different from the forces that kept the planets in their orbits. Gravity, then, was a universal force.
If Newton’s theory of gravity is applied to falling bodies, M1 is the mass of Earth and M2 is the mass of the falling object. So the greater the mass of an object, the greater the force pulling it downwards. However, Newton’s Second Law tells us that a larger mass does not accelerate as quickly as a smaller one if the force is the same. So the greater force is needed to accelerate the greater mass, and all objects fall at the same speed, as long as there are no other forces such as air resistance to complicate matters. With no air resistance, a hammer and a feather will fall at the same speed – a fact finally demonstrated in 1971 by astronaut Dave Scott, who carried out the experiment on the surface of the Moon during the Apollo 15 mission.
Newton described a thought experiment to explain orbits in an early draft of the Philosophiae Naturalis Principia Mathematica. He imagined a cannon on a very high mountain, firing cannon balls horizontally at higher and higher speeds. The higher the speed at which a ball is fired, the farther away it will land. If it is launched sufficiently fast, it will not land at all, but continue around Earth until it arrives back at the top of the mountain. In the same way, a satellite launched into orbit at the correct speed will continue to circle Earth. The satellite is continually being accelerated by Earth’s gravity. It moves at a constant speed, but its direction is continually changing, making it circle the planet rather than whizzing off into space in a straight line. In this case, Earth’s gravity only changes the direction of the satellite’s velocity, not its speed.
"I have not been able to discover the cause of these properties of gravity from phenomena, and I frame no hypotheses."
Isaac Newton

Newton’s Law of Gravity produces the equation below, which shows how the force produced depends on the mass of the two objects and the square of the distance between them.
Publishing the ideas
In 1684, Robert Hooke boasted to his friends Edmond Halley and Christopher Wren that he had discovered the laws of planetary motion. Halley was a friend of Newton, and asked him about this. Newton said that he had already solved the problem, but had lost his notes. Halley encouraged Newton to redo the work, and as a result, Newton produced On the Motion of Bodies in an Orbit, a short manuscript sent to the Royal Society in 1684. In this paper, Newton showed that the elliptical motion of the planets that Kepler described would result from a force pulling everything towards the Sun, where that force was inversely proportional to the distance between the bodies. Newton expanded on this work, and included other work on forces and motion, in the Principia Mathematica, which was published in three volumes and contained, among other things, the Law of Universal Gravitation and Newton’s three Laws of Motion. The volumes were written in Latin, and it was not until 1729 that the first English translation was published, based on Newton’s third edition of the Principia Mathematica.
Hooke and Newton had already fallen out over Hooke’s criticisms of Newton’s theory of light. Following Newton’s publication, however, much of Hooke’s work on planetary motion was obscured. However, Hooke had not been the only one to suggest such a law, and he had not demonstrated that it worked. Newton had shown that his Law of Universal Gravitation and laws of motion could be used mathematically to describe the orbits of planets and comets, and that these descriptions matched observations.

Newton’s thought experiment described a cannon fired horizontally from a high mountain. The greater the force firing the cannon ball, the farther it travels before falling to the ground. If it is fired hard enough, it will travel right around the planet back to the mountain.
"To myself I am only a child playing on the beach, while vast oceans of truth lie undiscovered before me."
Isaac Newton
Sceptical reception
Newton’s ideas on gravity were not welcomed everywhere. The “action at a distance” of Newton’s force of gravity, with no way of explaining how or why it happened, was seen as an “occult” idea. Newton himself refused to speculate on the nature of gravity. For him, it was enough that he had shown that the idea of an inverse-square attraction could explain planetary motions, so the mathematics was correct. However, Newton’s laws described so many phenomena that they soon came to be widely accepted, and today the internationally used unit of force is named after him.

Newton’s laws provided the tools to calculate the orbits of heavenly bodies such as Halley’s comet, shown here on the Bayeux Tapestry after its appearance in 1066.
"Why should that apple always descend perpendicularly to the ground, thought he to himself…"
William Stukeley
Using the equations
Edmond Halley used Newton’s equations to calculate the orbit of a comet seen in 1682, and showed that it was the same comet as that observed in 1531 and 1607. The comet is now called Halley’s comet. Halley successfully predicted that it would return in 1758, which was 16 years after his death. This was the first time that comets had been shown to orbit the Sun. Halley’s comet passes near to Earth every 75–76 years, and was the same comet as that seen in 1066 before the Battle of Hastings in southern England.
The equations were also used successfully to discover a new planet. Uranus is the seventh planet from the Sun, and was identified as a planet by William Herschel in 1781. Herschel found the planet by chance while making careful observations of the night sky. Further observations of Uranus allowed astronomers to calculate its orbit and to produce tables predicting where it could be observed at future dates. These predictions were not always correct, however, leading to the idea that there must be another planet beyond Uranus whose gravity was affecting the orbit of Uranus. By 1845, astronomers had calculated where this eighth planet should be in the sky, and Neptune was discovered in 1846.
Problems with the theory
For a planet with an elliptical orbit, the point of closest approach to the Sun is called the perihelion. If there were only one planet orbiting the Sun, the perihelion of its orbit would stay in the same place. However all the planets in our Solar System affect each other, so the perihelia precess (rotate) around the Sun. Like all the other planets, Mercury’s perihelion precesses, but the precession cannot be completely accounted for using Newton’s equations. This was recognized as a problem in 1859. More than 50 years later, Einstein’s Theory of General Relativity described gravity as an effect of the curvature of space-time, and calculations based on this theory do account for the observed precession of Mercury’s orbit, as well as other observations not linked to Newton’s laws.

The precession (change in the rotational axis) of the orbit of Mercury was the first phenomenon that could not be explained by Newton’s laws.
Newton’s laws today
Newton’s laws form the basis of what is referred to as “classical mechanics” – a set of equations used to calculate the effects of forces and motion. Although these laws have been superseded by equations based on Einstein’s theories of relativity, the two sets of laws agree as long as any motion involved is small compared to the speed of light. So for the calculations involved in designing aeroplanes or cars, or working out how strong the components of a skyscraper need to be, the equations of classical mechanics are both accurate enough and much simpler to use. Newtonian mechanics, while it may not strictly be correct, is still widely used.
"Nature and nature’s laws lay hid in night; God said “Let Newton be” and all was light."
Alexander Pope
ISAAC NEWTON

Born on Christmas Day in 1642, Isaac Newton attended school in Grantham, before studying at Trinity College, Cambridge, where he graduated in 1665. During his life, Newton was variously Professor of Mathematics at Cambridge, Master of the Royal Mint, Member of Parliament for Cambridge University, and President of the Royal Society. As well as his dispute with Hooke, Newton became involved in a feud with German mathematician Gottfried Leibnitz over priority in the development of calculus.
In addition to his scientific work, Newton spent much time in alchemical investigations and Biblical interpretation. A devout but unorthodox Christian, he successfully managed to avoid being ordained as a priest, which was normally a requirement for some of the offices he held.
Key works
1684 On the Motion of Bodies in an Orbit
1687 Philosophiae Naturalis Principia Mathematica
1704 Opticks
See also: Nicolaus Copernicus • Johannes Kepler • Galileo Galilei • Christiaan Huygens • William Herschel • Albert Einstein