O itinerário científico de Louis de Broglie em busca de uma interpretação causal para a mecânica ondulatória
1 Introdução
A tese de doutorado de Louis de Broglie, defendida em 1924, constitui um marco na história da Teoria Quântica. No entanto, ela costuma ser lembrada entre os físicos somente por atribuir a uma partícula material um comportamento ondulatório, com frequência v = E / h e comprimento de onda λ = h / p. Para Bacciagalupi e Valentini (2006), o trabalho desenvolvido por de Broglie durante a década de 1920 tem sido subestimado, mal representado e largamente ignorado, não somente pelos físicos, mas também por historiadores.
Em relação à vida e obra de de Broglie, Pestre (1988) afirma que, do ponto de vista historiográfico, existe muito a ser feito e aponta três grandes estudos que podem ser realizados: a) refinar as características, origens e efeitos das bases culturais e intelectuais de Louis de Broglie entre 1910 e 1930, partindo de fontes originais, dando continuidade ao trabalho de Bruce Wheaton, em seu livro The tiger and the shark, Cambridge, 1983; b) investigar os trabalhos dos membros da escola formada por de Broglie entre 1930 e 1970, suas linhas de pesquisa, métodos, e buscar compreender as razões que levaram este trabalho à marginalização; c) considerar os modos institucional e intelectual, por meio dos quais outra espécie de Física teórica entrou na França, entre os anos 1940 e 1950. Pestre não aponta o trabalho desenvolvido por de Broglie após 1952 como constituindo uma possível área de interesse para a história da ciência.
Após consulta às bases de dados Web of Science e ISIS não encontramos obra de história da ciência que discutisse as novas ideias apresentadas por de Broglie após seu retorno à busca de uma interpretação causal para a mecânica ondulatória. As fontes históricas disponíveis são os artigos originais, notas autobiográficas, livros e a biografia publicada por Georges Lochak, a quem de Broglie confiou toda a sua obra.
Neste artigo faremos uma breve apresentação da trajetória de Louis de Broglie, desde sua formação inicial até as motivações que o levaram a abandonar o programa de pesquisa em busca de uma interpretação causal para a Mecânica Ondulatória. Em seguida, apresentaremos os principais aspectos da obra de de Broglie após 1951, quando ele retomou seu programa de pesquisa em torno da Teoria da Dupla Solução e propôs a não-linearidade da equação das ondas de matéria.
Finalizaremos, citando alguns trabalhos de outros autores que também pensaram no desenvolvimento de um formalismo não-linear para a Teoria Quântica, como uma alternativa aos formalismos desenvolvidos por Schrödinger, Heisenberg e Dirac, que são essencialmente lineares.
2 O nascimento da mecânica ondulatória
Louis Victor Pierre Raymond de Broglie, príncipe francês, nasceu em 15 de outubro de 1892. Aos 18 anos obteve o título de Licenciado em História, porém, logo depois, se interessou pela Física, particularmente pela Física Quântica e a Relatividade. Louis de Broglie teve seus primeiros contatos com os fenômenos envolvendo os quanta de luz no laboratório particular de espectroscopia e difração de raios-X do seu irmão, o físico Louis Cesar Victor Maurice de Broglie (1875-1960) (ROSA, 2004).
O interesse de Louis de Broglie pela Física aumentou após ler as atas do primeiro Congresso Solvay, realizado em 1911, editadas por Paul Langevin e com a colaboração do seu irmão Maurice. Em 1913, ele obteve o título de Licenciado em Ciências e, em outubro do mesmo ano, ingressou no serviço militar, servindo durante a I Guerra Mundial na companhia de telegrafia, onde se familiarizou com os conceitos envolvendo fenômenos ondulatórios. Após a guerra, retomou os estudos que tinham despertado seu interesse pela Física, dedicando-se ao trabalho experimental com raios-X, em colaboração com seu irmão (ROSA, 2004).
Os primeiros trabalhos de de Broglie, em relação aos quanta de luz, foram publicados em 1922, porém foi somente em 1923 que ele tentou fazer uma síntese entre as teorias ondulatória e corpuscular da luz. De Broglie propôs estender para as partículas materiais a dualidade onda-partícula que Einstein havia proposto para a luz, em 1905. Para de Broglie, as condições de quantização de Bohr-Sommerfeld para as órbitas eletrônicas somente poderiam ser entendidas em termos de ondas estacionárias e foi esta observação que o levou a postular a existência das ondas de matéria (DE BROGLIE, 1929).
Os trabalhos1 publicados em 1923 constituíram a base da sua tese de doutoramento, defendida em 1924, na Sorbonne, em Paris, com o título Recherches sur la théorie des quanta2, sob orientação de Paul Langevin. A importância deste trabalho foi logo reconhecida por Einstein, que, ao fazer referência em seu segundo trabalho sobre a Teoria Quântica do gás ideal3, chamou atenção dos outros pesquisadores para a ideia que iria revolucionar a Teoria Quântica (JAMMER, 1966).
Para Bacciagalupi e Valentini (2006), pouca atenção é dada ao tema central da tese de Broglie, que consistia em desenvolver uma nova dinâmica onde a velocidade da partícula seria determinada por ondas-guia. Esta concepção se baseia na unificação dos princípios variacionais de Maupertuis e o de Fermat, produzindo uma teoria capaz de sintetizar os dois conceitos aparentemente contraditórios, onda e partícula. Para MacKinnon (1976), o fato de que o princípio de Maupertuis pudesse ser escrito em um formato que descrevesse o movimento de ondas ou partículas não constituía nenhuma novidade, isto já havia sido proposto por Hamilton no século XIX.4
A hipótese de de Broglie, ao associar cada partícula com uma onda, influenciou o alemão Erwin Schrödinger a escrever a equação de propagação das ondas de matéria. Para Schrödinger, a forma como de Broglie foi capaz de explicar as condições de quantização de Bohr-Sommerfeld sugeria a ideia que a quantização pudesse ser tratada como um problema de autovalor, muito comum no estudo das ondas (JAMMER, 1966). O formalismo desenvolvido por Schrödinger fez muito sucesso entre os físicos quânticos, pois eles estavam acostumados a resolver equações de onda ao invés de diagonalizar matrizes infinitas, tal como aparecia no formalismo de Heisenberg (DARRIGOL, 2003).
Schrödinger, ao escrever a equação de propagação das ondas de matéria proposta por de Broglie, eliminou o conceito de trajetória da partícula ao descrever seu movimento utilizando ondas contínuas. O alemão Max Born, ao utilizar o formalismo de Schrödinger para investigar o espalhamento de partículas após sofrer uma colisão, deu origem à interpretação probabilística da função de onda. Como os resultados obtidos por Schrödinger e a interpretação de Born tinham boa concordância com os dados experimentais, de Broglie acreditava que esta interpretação era correta para um feixe de partículas e, por esta razão, deveria ser mantida, porém este formalismo não seria capaz de dar conta de fenômenos individuais. Para de Broglie, a mecânica ondulatória tinha uma natureza abstrata, por considerar a função de onda Ψ propagando-se em um espaço de configuração de 3N dimensões, que é um espaço abstrato. Para explicar os fenômenos ondulatórios que ocorrem com as partículas materiais, tais como interferência e difração, seria necessário considerar uma onda se propagando no espaço tridimensional (DE BROGLIE, 1960).
Em 1926, de Broglie publicou o artigo The wave mechanics and the atomic structure of matter and of radiation5, no qual apresentou, pela primeira vez, o que chamou de “princípio da dupla solução”. Consistia em considerar que a equação de propagação das ondas de matéria deveria admitir duas soluções, uma sendo a onda Ψ, de caráter probabilístico, responsável por descrever o comportamento de um feixe de partículas, e a outra solução seria uma onda-u que, por conter uma singularidade, seria responsável por descrever cada partícula individualmente (DE BROGLIE, 1927).
Devido às dificuldades matemáticas em provar a existência das duas ondas e a relação existente entre elas, ao final do artigo de Broglie propôs uma versão simplificada, que chamou de “teoria da onda piloto”, na qual assumiu a existência da partícula material e da onda contínua, representada por Ψ, como tendo realidades distintas, e postulou que o movimento da partícula é determinado como uma função da fase da onda Ψ através da sua fórmula-guia, isto é, a onda contínua seria responsável por dirigir o movimento da partícula, seria uma onda piloto (DE BROGLIE, 1927).
O citado artigo de 1927 chamou atenção de Wolfgang Ernst Pauli, que, numa carta a Niels Bohr datada de 6 de agosto de 1927, disse: “[...] é muito rico em ideias e muito inteligente, e num nível muito mais elevado que o artigo infantil de Schrödinger”6 (PAULI, 1979 apud BACCIAGALUPI; VALENTINI, 2006, p. 73). Pauli sugeriu a Bohr que se referisse ao artigo de de Broglie na palestra que ele faria em Como, na Itália.7 No entanto, Bohr caracterizou o trabalho de de Broglie como uma tentativa de reconciliar os dois lados aparentemente contraditórios dos fenômenos quânticos, que ele já havia tinha, supostamente, resolvido com seu princípio da complementaridade. Além disso, Bohr considerava que a tentativa de resgatar a descrição determinística, ao propor que as partículas ou os quanta de luz seriam singularidades em uma onda estendida, estaria baseada em conceitos clássicos e não ajudava a resolver as dificuldades fundamentais. (VALENTINI, 2006)
Para Bacciagalupi e Valentini (2006), este artigo de de Broglie, que tem sido ignorado por físicos e historiadores, assume uma maior importância, do ponto de vista histórico, nos dias atuais do que no passado, pois dele nasceu a teoria da onda piloto, que foi aperfeiçoada pelo físico americano David Bohm (1917-1992), reiniciando a busca de uma interpretação causal para a Teoria Quântica.
De Broglie, ao ser convidado para apresentar seu trabalho no V Congresso Solvay, de 1927, optou por usar somente a teoria da onda piloto em sua comunicação intitulada: La nouvelle dynamique des quanta8. Esta comunicação não recebeu apoio da maioria dos presentes ao congresso, nem mesmo daqueles que ainda insistiam em encontrar uma interpretação causal para a mecânica ondulatória (Einstein, Langevin, Schrödinger e Lorentz). O grupo liderado por Bohr e Born defendia a interpretação puramente probabilista que eles haviam desenvolvido e se recusaram a discutir o ponto de vista adotado por de Broglie (1960). Uma notável exceção foi Pauli, que apresentou críticas à teoria apresentada por de Broglie, ao citar o exemplo do rotor de Fermi, que podia muito bem ser explicado pela interpretação puramente probabilista, mas que encontrava dificuldades na proposta causal de de Broglie. Nesta época, de Broglie não tinha claro entendimento de todos os aspectos da teoria da onda piloto, muitos dos quais só foram desenvolvidos por Bohm em 1952 (BACCIAGALUPI; VALENTINI, 2006).
Em 1928, ao ser indicado para professor da Faculté des Sciences de Paris, de Broglie resolveu abandonar a sua teoria, pois não podia ensinar um ponto de vista que não tinha condições de justificar. De Broglie afirmou que não foram as objeções de Pauli que o fizeram abandonar a teoria da onda piloto, pois ele já havia encontrado uma maneira de superá-las. As razões foram publicadas em seu primeiro livro, Introduction à l’étude de la mécanique ondulatoire, publicado em 1930 (DE BROGLIE, 1960). Dentre estas razões, duas são fundamentais9: a) a partícula, concebida como uma realidade física, não pode ser guiada pela onda Ψ − que possui um caráter subjetivo (uma mera representação de probabilidades) e é condicionada pelo conhecimento do observador; b) mesmo no caso de uma partícula simples, cujo movimento é guiado por uma onda Ψ (x, y, z, t), as coordenadas (x, y, z) não representam pontos no espaço físico, e sim as possíveis posições da partícula nesse espaço. O movimento da partícula guiada pela onda Ψ dependeria não somente da posição que a partícula tinha originalmente, como também de todas as posições que ela poderia ter ocupado, mas realmente não ocupa. Estes paradoxos convenceram de Broglie de que a teoria da onda piloto não constituía uma forma de retornar às concepções clássicas de causalidade. (DE BROGLIE, 1960)
Após 1930, Nye (1997) destaca que Michel Eberhardt sentia que Louis de Broglie “era um homem solitário, quase marginal, que se preocupava mais com fazer palestras do que fazer uma escola”. O físico nuclear francês Anatole Abragam disse que seus discípulos, com poucas exceções, “não eram aqueles com alta capacidade intelectual e nem sempre de alta honestidade intelectual”, eles assumiram uma postura de adulação reivindicando o termo “mecânica ondulatória” ao invés de “mecânica quântica”.10
3 O retorno à busca por uma interpretação causal
Em 1951, Louis de Broglie recebeu o pre-print do artigo de David Bohm11 que viria a ser publicado no The Physical Review em janeiro de 1952. Em comunicação datada de 17 de setembro de 1951, sob o título Remarques sur la théorie de l’onde pilote12, de Broglie relembrou as razões que o fizeram abandonar a tentativa de interpretação causal da mecânica ondulatória. Ele acreditava que o trabalho de Bohm encontraria dificuldades insuperáveis ao atribuir uma realidade física para a onda Ψ.
Este retorno imediato de de Broglie às suas ideias da juventude, tão logo recebeu o pre-print de Bohm, parece indicar que ele nunca aceitou completamente a interpretação puramente probabilista, tendo convivido com ela somente enquanto não encontrou uma outra alternativa de interpretação para a mecânica ondulatória. Uma análise apressada poderia atribuir esta reviravolta no pensamento de de Broglie unicamente ao trabalho de Bohm. Porém, conforme pode ser verificado em suas notas, de Broglie não concordava com Bohm em um aspecto essencial: a atribuição de uma realidade física para a onda Ψ, tal como é assumida na teoria da onda piloto.
O pensamento de de Broglie já estava se preparando para esta mudança nos anos que antecederam o artigo de Bohm. Isto pode ser comprovado através da análise do livro publicado em 1982, mas cujos manuscritos datam de 1950-1952, intitulado Les incertitudes d’Heisenberg et l’interpretation probabiliste de la mécaniqueondulatoire13. De Broglie havia confiado sua obra a Georges Lochak; dentre o material entregue havia um manuscrito com a tarja A ne pas publier14. Este manuscrito chamou a atenção de Lochak que, após analisá-lo, persuadiu de Broglie a torná-lo público, alegando que este material não pertencia a ele, mas à história da ciência. Segundo Lochak (1982), estes manuscritos seriam uma ótima oportunidade para o público em geral ver como a ciência funciona realmente. Depois de alguns meses, de Broglie autorizou a publicação, desde que fosse acompanhada de uma introdução para situar o livro dentro de sua obra geral, bem como a adição de notas suplementares ao longo do texto.
Segundo Lochak (1982), estes manuscritos foram elaborados por de Broglie com o objetivo de convencer a si mesmo sobre a interpretação usual da mecânica ondulatória e, na forma de notas, ele expressava as suas críticas. O livro publicado em 1982 divide o manuscrito em duas partes: a primeira teria sido escrita entre 1950-1951, sob o título Sur les incertitudes d’Heisenberg et l’interprétation probabiliste de la mécanique ondulatoire; e a segunda, teria sido escrita entre 1951-1952, sob o título Sur l’interprétation probabiliste de la mécanique ondulatoire et sur diverses questions qui s’y rattachent.
Esta súbita reviravolta no pensamento de de Broglie não foi bem aceita no Instituto Henri Poincaré, onde ele trabalhava como professor. Segundo Lochak (1982), as pessoas sussurravam pelos corredores do Instituto e agiam como se de Broglie tivesse contraído uma espécie de doença e do qual seria mais sábio manter distância.
4 Uma tentativa de interpretação causal e não-linear
Numa nota intitulada Sur la possibilité d’une interprétation causale et objective de la mécanique ondulatoire15, datada de 14 de janeiro de 1952, de Broglie reconheceu que a interpretação causal de Bohm tinha diversos pontos que mereciam atenção, principalmente no que se refere à análise dos procedimentos das medições que podem ser realizadas no nível quântico, e buscou uma alternativa para conciliar o seu ponto de vista com o de Bohm.
Na citada nota, de Broglie sugeriu pela primeira vez que a onda-u, responsável pela descrição objetiva da partícula material, deveria obedecer a uma equação de propagação não-linear, sendo esta a direção que sua pesquisa seguiu ao longo de toda a década de 1950. à medida que novas ideias foram surgindo, ele as registrava na forma de notas no periódico Comptes Rendus. As notas publicadas entre 1951 e 1954 constituíram a base do livro publicado em 1956, sob o título Une tentative d’interprétation causale et non linéaire de la mécanique ondulatoire – la théorie de la double solution.16
Este livro é dividido em duas partes. Na primeira, de Broglie apresenta o desenvolvimento da Mecânica Ondulatória, partindo das suas ideias iniciais, passando pela contribuição de Schrödinger e o estabelecimento da interpretação puramente probabilista que foi desenvolvida sob a liderança de Bohr e colaboradores, em Copenhague. Após apresentar as objeções a esta interpretação feita por alguns cientistas, a exemplo de Einstein, Schrödinger e ele próprio, ele chama a atenção para a única tentativa feita para evitar a interpretação puramente probabilista e desenvolver uma teoria causal e determinista, isto é, a tentativa que ele fez em 1927, a teoria da dupla solução.
Na segunda parte, de Broglie reapresenta a teoria da dupla solução, refinada em certos pontos, rediscute as objeções levantadas por Pauli em relação à teoria da onda piloto e assume que a teoria da dupla solução não parece apresentar as mesmas dificuldades. No entanto, ele introduz uma hipótese que considera fundamental: a de que a onda-u, responsável pela descrição objetiva da partícula, deveria obedecer a uma equação de propagação não-linear. Esta hipótese é levantada após J. P. Vigier chamar a atenção para o fato de que a dedução da fórmula-guia era semelhante à demonstração de Einstein e Georges Darmois para o movimento de uma partícula na Relatividade Geral, que obedecem a equações não lineares. E então, por analogia, deveria ocorrer o mesmo para as ondas de matéria.
De Broglie propôs que a equação de propagação não-linear a ser obedecida pela onda-u, na ausência de qualquer campo e numa aproximação não relativística, teria a seguinte forma:
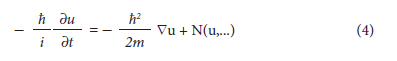
Ou seja, seria a equação de Schrödinger generalizada. Ele acreditava que a introdução de convenientes termos não-lineares N permitiria a existência de soluções sem espalhamento. De modo que a não-linearidade da equação de onda admitiria a concepção de grupos de ondas sem espalhamento, em oposição ao espalhamento natural dos trens de onda que ocorrem na teoria linear. Os termos não lineares para a equação da onda-u seriam desprezíveis na parte externa da região do trem de onda e somente se tornariam importantes na região de fronteira. De Broglie não conseguiu levar adiante a sua hipótese por desconhecer os termos não-lineares que deveriam ser introduzidos na equação de propagação das ondas de matéria.
A dificuldade encontrada por de Broglie em dar prosseguimento a sua hipótese de não-linearidade das equações de propagação das ondas de matéria é facilmente compreendida, pois, conforme ele mesmo reconhece, até aquela época ainda não havia métodos confiáveis para resolver equações diferenciais não line-ares. Porém, ele mesmo já tinha sinalizado que a hipótese dos grupos de ondas não deformadas poderia ser comparada com a teoria das “ondas solitárias” da Hidrodinâmica17.
Vale ressaltar que a hipótese da mecânica quântica vir a ser substituída por uma teoria que fosse fundamentalmente não-linear não foi descartada nem mesmo por Heisenberg, um dos maiores defensores da interpretação ortodoxa. Em 1967, ele declarou que
[...] a não linearidade é tão fundamental na natureza que seria possível que mesmo uma teoria tão fundamentalmente linear como a Teoria Quântica viesse a ser substituída por outra que fosse não linear. (HEISENBERG, 1967)
Tanto para de Broglie, quanto para Heisenberg, o sucesso em obter uma Teoria Quântica não-linear estaria completamente ligado ao desenvolvimento de métodos matemáticos para a resolução das equações dos sistemas dinâmicos não lineares.
De Broglie, ao concluir o citado livro Non-linear wave mechanics, admitiu não ter completo desenvolvimento para suas sugestões em virtude das dificuldades matemáticas colocadas desde o princípio. Ele esperava que jovens talentosos com boa percepção física e habilidade matemática se interessassem por suas sugestões para construir a verdadeira microfísica do futuro.
Rosenfeld (1958) criticou o livro publicado por de Broglie em 1956, afirmando que um argumento fraco não se torna forte por repetição. Para Rosenfeld, o livro não traz nenhuma evidência que justifique reconsiderar a impossibilidade de descrever os processos quânticos em termos clássicos e conclui:
[...] a teoria da dupla solução sofre de uma falta de originalidade na determinação dos termos não lineares da equação de onda, que a coloca em pé de igualdade com o modelo do éter do século passado. (ROSENFELD, 1958)
5 A termodinâmica da partícula isolada
De Broglie, ao tentar encontrar uma síntese entre os comportamentos ondulatório e corpuscular, comparou a expressão do quantum de energia com a expressão da energia de repouso, na Teoria da Relatividade, para obter a frequência da onda de matéria (v = m o c2 / h). Ao assumir uma equivalência entre os princípios de Fermat e Maupertuis, de Broglie propôs que o movimento da partícula seria descrito através da fase da onda equivalente.
Na década de 1960, de Broglie desenvolveu uma nova ideia, que denominou de termodinâmica da partícula isolada, na qual pretendia fazer uma comparação entre três princípios fundamentais da Física: os de Fermat, Maupertuis e Carnot. Ele comparou a expressão do quantum de energia (E = hv) com a expressão da energia na termodinâmica (E = kT) para encontrar a relação entre a frequência do movimento ondulatório e a temperatura da partícula. Esta ideia foi baseada na sugestão de Bohm e Vigier sobre a existência de um meio subquântico responsável por imprimir, nas partículas, um movimento aleatório capaz de justificar as leis de probabilidade. Para de Broglie, este meio subquântico se comportaria como uma reunião de termostatos escondidos, cuja interação com a partícula seria capaz de produzir uma espécie de movimento browniano.
De Broglie apresentou estas ideias numa nota publicada em 1961, intitulada Sur la thermodynamique du corpuscule isolé18, cujo objetivo principal era encontrar uma relação entre o princípio da mínima ação da mecânica com o segundo princípio da termodinâmica. Ele escreveu que estes dois princípios estão relacionados através da seguinte expressão,
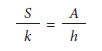
em que S é a entropia, A a grandeza ação e k a constante de Boltzmann. Em outro artigo, de Broglie interpretou estes resultados, identificando o princípio da mínima ação como um caso particular da segunda lei da termodinâmica em que os estados estacionários dos sistemas quantizados correspondem aos estados de máxima entropia (DE BROGLIE, 1967).
De Broglie considerava que seu trabalho constituía apenas sugestões para o desenvolvimento de uma nova interpretação para a mecânica ondulatória. Devido à idade avançada, ele não tinha esperança de ver até onde estas ideias poderiam levar. Ele admitiu contar com a ajuda de poucos pesquisadores que se interessaram por suas sugestões e esperava que eles pudessem dar continuidade ao seu trabalho.
6 Considerações finais
Conforme vimos, o trabalho desenvolvido por de Broglie, após seu retorno à busca por uma interpretação causal, constituiu em sugerir duas linhas de pesquisa; a) a não linearidade das equações das ondas de matéria; e b) a termodinâmica da partícula isolada. A investigação sobre como estes trabalhos influenciaram outros pesquisadores, e até onde eles foram desenvolvidos, pode constituir um importante tema de pesquisa na história dos fundamentos da Teoria Quântica. Até o presente, supomos que estas sugestões podem ter sido seguidas por estudantes de doutorado da Faculdade de Ciências de Paris que estavam sob a orientação de de Broglie. (SILVA; PEREIRA, 1970)
Em 1979, Shimony publicou um artigo no qual propôs um aparato experimental, com o objetivo de testar se a mecânica ondulatória linear seria válida ou deveria ser substituída pela sugestão dada por de Broglie, de que em dimensões inferiores a 10-12 cm seria necessária a utilização de uma teoria não-linear (SHIMONY, 1979). O aparato experimental consiste em um interferômetro de nêutrons. Este teste foi realizado por R. Gähler, A. G. Klein e A. Zeilinger, em 1981, que chegaram à conclusão de que os termos não-lineares não apareciam no limite estabelecido por Shimony e outros autores. Porém, eles afirmaram que os resultados não eram definitivos e que novos testes deveriam ser realizados. (GäHLER; KLEIN; ZEILINGER, 1981)
Segundo Pierre Lochak (1984), os desenvolvimentos matemáticos obtidos nas duas décadas anteriores, na resolução de certas classes de equações diferenciais não-lineares, permitiram reviver a ideia de uma “física quântica não linear”, cuja origem está nas ideias de de Broglie. Estes desenvolvimentos permitiram a aplicação da mecânica quântica em sistemas físicos não-lineares, a exemplo de supercondutores, superfluidos (hélio líquido), ferromagnetismo e outros (RIBEIRO FILHO; VASCONCELOS, 2006). No entanto, os chineses Pang e Feng (2005) advogam que a não-linearidade vai além dos problemas de aplicação e podem ter grande influência sobre as controvérsias que ainda permanecem em torno dos fundamentos da Teoria Quântica. Se o formalismo usual da mecânica quântica será substituído por um formalismo que seja essencialmente não linear, isto ainda é uma questão em aberto na Física.
Ainda que estas ideias não tenham progresso na Física, resgatar o extenso trabalho de Louis de Broglie durante o período que ele chamou de “o mais belo de sua vida”19 constitui uma tarefa para os historiadores da ciência e para aqueles interessados em psicologia dos cientistas. Conforme o próprio de Broglie (1962) registrou, “[...] a história da ciência pode ensinar muitos fatos importantes sobre a natureza da inteligência humana”.
Referências
BACCIAGALUPI, G.; VALENTINI, A. Quantum theory at the crossroads: reconsidering the 1927 Solvay Conference. Cambridge: Cambridge University, 2006.
BOHM, D. A suggested of the quantum theory in terms of “hidden” variables. Physical Review, v. 85, n. 2, p. 166-193, 1952. Artigos 1 e 2.
DARRIGOL, O. Quantum theory and atomic structure, 1900-1927. In: NYE, Mary Jo. The modern physical e mathematical sciences. Cambridge: Cambridge University, 2003. p. 331-349. (The Cambridge History of Science, v. 5).
DE BROGLIE, L. Les incertitudes d’heisenberg et l’interpretation probabiliste de la mécanique ondulatoire. Paris: Gauthier-Villars, 1982.
______. On the theory of quanta. Traduzido por A. F. Kracklauer. Paris: AFK, 2004. Título original: Recherches sur la theorie des quanta, 1925, Ann. de Phys., 10ª série, t. III. Disponível em: <http://www.ensmp.fr/aflb/LDB-oeuvres/De_ Broglie_Kracklauer.pdf>. Acesso em: 2 jul. 2009
______. The new dynamics of quanta. In: BACCIAGALUPI, G.; VALENTINI, A. Quantum theory at the crossroads: reconsidering the 1927 Solvay Conference. Cambridge: Cambridge University, 2006. p. 374-407.
______. A new interpretation concerning the coexistence of waves and particles. In: YOURGRAU, W.; MERWE, A. van. der (Ed.). Perspectives in Quantum Theory. New York: Dover, 1967.
______. New perspectives in physics. Traduzido por A. J. Pomerans e Oliver & Boyd. New York: Basic Books, 1963.
______. Non-linear wave mechanics: a causal interpretation. Trad. por Arthur J. Knodel e Jack C. Miller. Amsterdam: Elsevier, 1960. Original: Une tentative d’interprétation causale et non linéaire de la mécanique ondulatoire (la théorie de la double solution). 1956.
______. Une nouvelle démonstration de la formule du guidage dans la théorie de la double solution, C. R. Acad. Sci., n. 239, p. 737-739, 1954.
______. Remarques sur la théorie de l’onde pilote. C. R. Acad. Sci, n. 233, p. 641-644, 1951.
______. Sur l’interprétation causale et non linéaire de la mécanique ondulatoire. C. R. Acad. Sci., n. 237, p. 441-444, 1953.
______. Sur la possibilité d’une interprétation causale et objective de la mécanique ondulatoire. C. R. Acad. Sci., n. 234, p. 265-268, 1952.
______. Sur la thermodynamique du corpuscule isolé. C. R. Acad. Sci., n. 253,p. 1078-1081, 1961.
______. The value of the History of Science. In: OLIVER; BOYD. New Perspectives in Physics. 1962. p. 227-230.
______. The wave mechanics and the atomic structure of matter and of radiation. In: DE BROGLIE, L.; BRILLOUIN L. Selected papers on wave mechanics. London: Blackie & Son, 1928. p.113-138. Publicado originalmente no Le Journal de Physique et le Radium, n. 8, p. 255, 1927.
______. The wave nature of the electron. Nobel Lecture, 12 dec. 1929. Disponível em: <http://nobelprize.org/nobel_prizes/physics/laureates/1929/ broglie-lecture.pdf>. Acesso em: 12 jul. 2009.
EINSTEIN, A. Teoria quântica do gás ideal monoatômico - segundo tratado. RBEF, v. 27, n. 1, p.113-120, 2005. Traduzido de Quantentheorie des einatomigen idealen gases: Zweite Abhandlung, publicado nos Sitzungsberichte der Preussischen Akademie der Wissenschaften I, 3-14, 1925.
FREIRE JR., O. Science and exile: David Bohm, the cold war, and a new interpretation of quantum mechanics. Historical Studies in the Physical and Biological Sciences, v. 36, n. 1, p. 1-34, 2005.
GäHLER, A.; KLEIN, A. G.; ZEILINGER, A. Neutron optical tests of nonlinear quantum mechanics. Physical Review A, v. 23, n. 4, p. 1611-1617, 1981.
HEISENBERG, W. Nonlinear problems in physics. Physics Today, v. 20, n. 5, p. 27-32, 1967.
JAMMER, M. The conceptual development of quantum mechanics. New York: McGraw-Hill, 1966.
LOCHAK, G. The evolution of ideas of Louis de Broglie on the interpretation of wave mechanics. Foundations of Physics, v. 12, n. 10, 1982.
______. Louis de Broglie: un prince de la science. Paris: Flammarion, 1992.
LOCHAK, Pierre. Could solitons be adiabatics invariants attached to certain non linear equations. In: DE BROGLIE, Louis; DINER, Simon (Ed.). The wave-particle dualism: a tribute to Louis de Broglie on his 90th birthday. Reidel, 1984.p. 173-214.
MACKINNON, E. De Broglie’s thesis: a critical retrospective. American Journal of Physics, v. 44, n.11, 1976.
NYE, M. J. Aristocratic culture and the pursuit of science: the de Broglies in modern France. ISIS, v. 88, n. 3, p. 397-491, 1997.
PANG, X. F.; FENG, Y. P. Quantum mechanics in nonlinear systems. Singapore: World Scientific, 2005.
PESTRE, D. Louis de Broglie: un itineraire scientifique by Louis de Broglie, Georges Lochak. ISIS, v. 79, n. 4, p. 740-741, 1988.
RIBEIRO FILHO, A.; VASCONCELOS, D. S. Aspectos matemáticos em sistemas não lineares na mecânica quântica e mecânica clássica moderna. Cadernos de Ciências Humanas, v. 9, n. 16, p. 397-410, 2006.
ROSA, P. S. Louis de Broglie e as ondas de matéria. 80 p. 2004. Dissertação (Mestrado em Física) – Instituto de Física, Universidade Estadual de Campinas, Campinas. Disponível em: <http://ghtc.ifi.unicamp.br/Teses/Pedro-Sergio-Rosa. pdf>. Acesso em: 24 nov. 2008.
ROSENFELD, L. Une tentative d’interprétation causale et non linéaire de la mécanique ondulatoire (la théorie de la double solution) by Louis de Broglie. The British Journal for the Philosophy of Science, v. 9, n. 34, p. 167-168, 1958.
SHIMONY, A. Proposed neutron interferometer test of some nonlinear variants of wave mechanics. Physical Review A, v. 20, n. 2, p. 394-396, 1979.
SILVA, J. Andrade e; PEREIRA, J. Vassalo. On another formulation of the de Broglie’s hidden thermodynamics. International Journal of Theoretical Physics,v. 3, n. 1, p. 67-76, 1970.