Parte IV - Construção da Teoria Quântica – história e tendências de pesquisa

Max Planck e a física de sistemas estocásticos

Sílvio Renato Dahmen

1 Introdução

Max Planck, cujo nome associa-se ao nascimento da Mecânica Quântica, desempenhou ao longo de sua vida um destacado papel no desenvolvimento da Termodinâmica. É impossível pensar sua obra sem levar em conta um fato: seus anos formativos corresponderam justamente ao período de estabelecimento da Termodinâmica enquanto área na Física e Planck, que se tornaria uma das maiores autoridades neste assunto, se não a maior autoridade entre todas, contribuiu de maneira significativa para tal. Foi a Termodinâmica que também o levou ao seu célebre trabalho de 1900 – o problema da radiação do corpo negro – abrindo-lhe as portas para a física quântica. Uma década mais tarde, a física quântica lhe abriria as portas de outra área – a da física de sistemas estocásticos na forma da Equação de Fokker-Planck. Embora hoje saibamos que conceitualmente o caminho tomado por Planck é incorreto, sua dedução rigorosa da equação ainda é válida e se tornou um instrumento indispensável nas mãos dos praticantes da área. Neste trabalho, discuto o papel de Planck na história dos sistemas estocásticos, do ponto de vista de suas considerações a respeito da termodinâmica e da Física Quântica, em particular sua contribuição para o estabelecimento da equação que hoje leva seu nome e o nome de Fokker¹.

Com um artigo intitulado Über einen Satz der statistischen Dynamik und seine Erweiterung in der Quantentheorie publicado nos Sitzungsberichten der Preussischen Akademie der Wissenschaften (PLANCK, 1917a) e nos artigos posteriores Zur Theorie des Rotationsspektrums. Erste und Zweite Mitteilung, publicado nos Annalen der Physik (PLANCK, 1917b, 1917c), Planck fundamentou a teoria que hoje se encontra na base da física de sistemas estocásticos. Seus objetivos eram dois: por um lado, fornecer uma dedução rigorosa da equação que Adriaan Fokker (1887-1972) havia introduzido em sua tese de doutorado alguns anos antes, sem, porém, justificá-la do ponto de vista formal. (FOKKER, 1914) A equação de Fokker era uma generalização daquela equação que Albert Einstein (1879-1955) havia utilizado em sua teoria do movimento browniano. (EINSTEIN, 1906) Mas, como Planck bem enfatizou na introdução de seu primeiro artigo, Fokker apresentou “[...] apenas a forma da equação geral, sem a prova correspondente. Esta última tarefa seria deixada para uma oportunidade posterior.” (PLANCK, 1917a) Ao escrever estas linhas, três anos já haviam transcorrido sem que Fokker publicasse a prova prometida. Planck continua:

Uma vez que o teorema acima citado, em sua forma geral, é de fundamental importância para a dinâmica estatística – eu mesmo o usei em repetidas ocasiões - e dado que sua validade tem sido questionada em círculos especializados, como várias missivas a mim enviadas puderam mostrar, parece-me então justificado publicar uma prova do mesmo. Este é o primeiro objetivo deste trabalho. (PLANCK, 1917a)

O segundo objetivo que ele buscou alcançar nos trabalhos posteriores era tratar de um problema que já mantivera não apenas Fokker ocupado, mas também os mais brilhantes físicos daquela geração: o espectro rotacional de moléculas diatômicas. O problema geral de linhas espectrais tornou-se, com o tempo, um dos principais interesses de Planck (ECKERT, 2008), como podemos comprovar lendo seus artigos Die Quantenhypothese für Molekeln mit mehreren Freiheitsgraden e Bemerkungen über die Emission von Spektrallinien (PLANCK, 1915a, 1915b, 1915c). Arnold Sommerfeld (1868-1951) era a grande autoridade no assunto e para Planck, editor dos Annalen der Physik, os trabalhos do físico de Munique não passaram despercebidos. Além disso, Sommerfeld lhe enviara uma cópia de seu longo artigo sobre o tema e, com o objetivo de evitar disputas acerca de prioridades, Planck respondeu de maneira bastante polida:

O meu trabalho publicado no Sitz. Ber. locais² acerca de linhas espectrais foi apenas um breve passeio por uma área por mim ainda pouco visitada e por meio do qual eu apenas queria chamar a atenção para a relação existe entre a estrutura do espaço de fase e a fórmula de Bohr. Espero que minha publicação não suscite a impressão que há ali mais do que realmente está escrito. Vejo agora que minha preocupação era infundada, pois o problema não poderia estar em melhores mãos que as Vossas. (ECKERT, 2008)

Deste modo, foi novamente seu interesse por problemas da interação da radiação com a matéria, que há uma década haviam-no colocado no caminho da hipótese da quantização da energia, que agora o colocaria no caminho da equação de Fokker-Planck. É importante mencionar que, diferentemente do que imaginava Planck, a equação de Fokker-Planck não está de modo algum relacionada com a física quântica. No entanto, para o “revolucionário à revelia”, a questão que se colocava era a dos limites de aplicabilidade da Teoria Quântica e o “salvamento” da teoria clássica de interação radiação-matéria a la Maxwell, da qual ele não queria abrir mão:

Consideremos porém que segundo a teoria quântica os fenômenos de absorção [de radiação] seguem leis ditadas única e exclusivamente pela teoria clássica, e que apenas a emissão satisfaça algumas leis quânticas, então neste caso a lei de Einstein e Fokker se mostra ser de extrema utilidade. (PLANCK, 1917a)³

Para melhor contextualizar o trabalho de Planck e entender suas consequências até os dias atuais, dividi este texto em duas seções, nas quais tento responder às perguntas: O que é a equação de Fokker-Planck? Como foi que Planck e seus antecessores a ela chegaram? A primeira parte do trabalho, intitulada O movimento browniano e o nascimento da física de sistemas estocásticos, discute este “o quê”. O movimento irregular de pequenas partículas suspensas desempenhou para a criação da física de sistemas estocásticos o mesmo papel que a radiação do corpo negro desempenhou para a física quântica. A segunda seção, Max Planck e as linhas espectrais de moléculas em rotação, discute o caminho tomando por Planck para resolver o problema e o contexto de sua época. Como já mencionado anteriormente, o interesse de Planck era o de compreender os espectros de emissão e absorção de graus de liberdade rotacionais de moléculas diatômicas. Se por um lado moléculas na forma de halteres representam os construtos mais simples possíveis quando se trata de estudar rotações, por outro, medições a baixas temperaturas de hidrogênio molecular também contribuíram significativamente para o interesse de físicos por este problema.

Procurou-se, ao longo do texto, manter a Física e a Matemática envolvidas em um nível acessível a leitores que se interessam pela História da Física, sem necessariamente possuírem uma formação direta na área. Algumas fórmulas são imprescindíveis, mas elas são empregadas cum grano salis e apenas na medida em que são necessárias a uma melhor compreensão do texto.

2 O movimento browniano e o nascimento da Física De Sistemas Estocásticos

Do ponto de vista etimológico, a palavra estocástico vem do grego clássico στοχαστικός, que em português significa “mirar” ou “lidar segundo hipóteses” (raiz στόχος: objetivo, hipótese). O termo moderno significa aleatório. A primeira pergunta que se faz é como a aleatoriedade pode entrar numa ciência exata como a Física, que usa da mais exata de todas as linguagens para se expressar: a Matemática. A aleatoriedade entra na Física de diversas maneiras (GUTTMANN, 1999): por um lado, falamos da natureza inerentemente probabilística da física quântica, cuja formulação, enquanto teoria probabilística imanente, foi completada no final dos anos 20 do século passado. Por outro, temos a aleatoriedade da física clássica de um sistema infinito de partículas. Neste caso, a probabilidade se faz presente pelo nosso desconhecimento (e a impossibilidade do conhecimento) das condições iniciais de todas constituintes do sistema. Isto tem por consequência o fato que as equações de movimento – embora determinísticas em sua natureza – não podem ser integradas, o que faz necessário então que recorramos ao conceito de um ensemble estatístico.⁴ A dedução e o estudo deste programa metodológico levam à chamada mecânica estatística de Ludwig Boltzmann e Josiah Willard Gibbs (1839-1903) e foi de certo modo completada em 1903.⁵

A estocasticidade da equação de Fokker-Planck tem a mesma natureza mecânica da física estatística clássica e não está, de maneira alguma, relacionada à física quântica da teoria de emissão e absorção de moléculas, como Planck originalmente supusera. Mas, diferentemente da mecânica estatística de Maxwell, Boltzmann e Gibbs, no tratamento estocástico segundo Planck, abre-se mão de conceitos como espaço de fase, teorema de Liouville, bem como de toda a metodologia daquela teoria (EBELING; GUDOWSKA-NOWAK; SOKOLOV, 2008), e se imagina uma dinâmica regida por uma força irregular, ou seja, a probabilidade entra diretamente nas equações de movimento, na forma de uma força estocástica ou de um ruído (neste caso, fala-se da equação estocástica para as grandezas físicas mensuráveis) ou, o que muitas vezes é equivalente, escreve-se uma equação determinística para a distribuição de probabilidade das grandezas físicas mensuráveis. No primeiro caso, temos a chamada equação de Langevin. No segundo, a equação de Fokker-Planck.

Se nos perguntarmos qual fenômeno deu origem ao estudo de sistemas estocásticos, podemos responder sem hesitar que foi a observação do movimento irregular de pequenas partículas suspensas em um fluido. EsteS fenômenos foi pela primeira vez descrito pelo médico holandês Jan Ingenhousz (1730-1799) e discutido de maneira mais detalhada em 1827 pelo botânico escocês Robert Brown (1773-1858).⁶ A primeira equação usada para modelar o movimento browniano (KAMPEN, 1997) foi publicada em 1822 por Fourier, em seu famoso tratado Théorie analytique de la chaleur. Embora aplicada a um contexto diferente, a saber, o da transmissão de calor em uma dimensão, a equação de Fourier é, do ponto de vista matemático, a mesma que rege o movimento browniano:

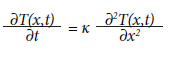
onde κ é a capacidade térmica do meio e T(x,t), a temperatura como função da posição e do tempo. Esta equação diferencial parabólica descreve a difusão de partículas, onde devemos substituir o parâmetro T(x,t) por p(x,t), a distribuição de probabilidade da coordenada x, e k por D, a constante de difusão. Neste contexto, John William Strutt (Lord Rayleigh, 1842-1919) introduziu uma equação para a distribuição de probabilidade W(v,t) da velocidade v de uma partícula difúsica em um líquido (RAYLEIGH,1891):

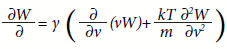
Nesta equação, γ representa o coeficiente de difusão, relacionado ao número de choques moleculares aos quais uma partícula é submetida. É interessante notar neste contexto que a distribuição de Maxwell (1860)⁷

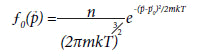
satisfaz a equação de Rayleigh, onde 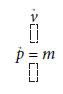representa o momento de uma partícula de massa m e κ = 1,3806503 x 10^-23J.K^-1 é a constante de Boltzmann. T representa a temperatura absoluta e p₀ o valor médio de p. Maxwell provou que esta distribuição é estacionária e descreve assim um gás em equilíbrio termodinâmico. Uma vez que não há interação entre partículas, ƒ₀ não depende da posição.

Em 1913, Adriaan Fokker, então doutorando de Hendrik Antoon Lorentz (1853-1928) e sem conhecimento prévio do trabalho de Lord Rayleigh, introduziu uma equação para a evolução temporal de uma distribuição de probabilidade W(q,t) de uma grandeza q qualquer, mas cuja dinâmica é regida por flutuações. A equação toma a forma

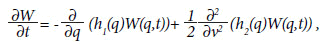
onde h₁(q) e h₂(q) são funções diretamente relacionadas às flutuações e dispersão do parâmetro q (KUBO; TODA; HASHITSUME, 1985):

Nesta equação Δt deve ser tão pequeno de tal modo a W não varie muito, mas grande o suficiente para que muitas flutuações de Δq ocorram. Esta equação, que hoje responde pelo nome de Equação de Fokker-Planck, pode ser interpretada como uma generalização da equação de difusão. Este nome foi dado por Andrei Kolmogorov que, em seu importante trabalho de 1931, deduziu uma versão ainda mais geral (KOLMOGOROV, 1931):

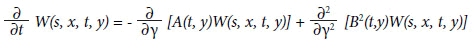
Kolmogorov chamou sua equação originalmente de segunda equação diferencial fundamental. Na matemática ela é conhecida como equação avançada de Kolmogorov. Disto é fácil concluir que existe também uma equação retardada (chamada de primeira equação fundamental por Kolmogorov). Os termos avançada refere-se ao fato que a grandeza W(s,x,t,y) apresentada acima representa a função de distribuição de uma grandeza cujo valor x no tempo s depende do valor y num tempo anterior t<s. Um ano antes de Kolmogorov esta equação foi deduzida em um contexto completamente diferente, a saber na genética, mais especificamente num trabalho de Ronald A. Fisher (1930) acerca de mutações raras:

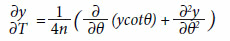
Nesta equação y é a função de distribuição para as taxas de frequência de mutações, n é o número de acasalamentos em cada geração, T o número de gerações e θ depende do quociente p/q de genes que sofreram mutação em dois loci diferentes via p / q = (1-cosθ) / (1 + cosθ).

Para Fokker, bem como para Planck, q representava o momento angular de uma molécula e W(q,t) a distribuição de probabilidade do momento angular de um gás de N moléculas, ou seja

N x W (q,t) x dq

era o número de moléculas, cujo momento angular, no tempo t, se encontrava entre q e q+dq. A equação de Fokker-Planck pode ser utilizada de maneira bastante geral quando, junto à descrição macroscópica usual de uma grandeza arbitrária, queira também se levar em conta flutuações (KAMPEN, 1997). É justamente por esta universalidade que a equação de Fokker-Planck se torna atraente enquanto descrição matemática de fenômenos estocásticos. Obviamente é necessário se determinar quem são as funções h₁(q) e h₂(q) (ou as funções A e B na notação de Kolmogorov), antes de buscar uma solução. No entanto, esta tarefa não é difícil quando se conhece a dinâmica determinística (sem flutuações) da grandeza q na forma de uma equação de movimento

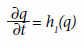
No caso determinístico, a distribuição de probabilidade é dada na forma de uma distribuição de Dirac e, ao colocar esta função na equação de Fokker-Planck, obtém-se que a função h₁(q) da equação determinística coincide com a função h₁(q) da equação de Fokker-Planck. Além disso, a mecânica estatística de equilíbrio fornece a distribuição estacionária da variável q, que coincide com a solução independente do tempo da equação de Fokker-Planck. Com isto se obtém uma relação entre h₁(q) e h₂(q), fixando assim o valor da segunda. (KAMPEN, 1997)

A equação de Fokker-Planck é um caso especial de uma equação mais geral, chamada equação de Chapman-Kolmogorov, a partir da qual aquela pode ser deduzida quando as variáveis espaciais e temporais são tomadas como sendo contínuas. Implícita nesta dedução está o fato que os processos que ela descreve possuem a propriedade markoviana. Isto significa que o sistema tem uma memória de curto alcance, ou seja, um estado no tempo t_n depende somente de um estado no passo anterior t_n-1 e não de estados mais longínquos no passado. Quão extensa é a memória depende de quão grandes são os intervalos temporais escolhidos. Quando a precisão dos aparelhos de medida é maior que o tempo de relaxação dinâmico típico do sistema, então a dinâmica é puramente estocástica (cada passo não depende do passo anterior). Processos puramente estocásticos não podem, no entanto, descrever sistemas com variáveis contínuas, uma vez que para isto são necessárias mudanças infinitesimais nas variáveis. Portanto, sistemas markovianos representam os sistemas mais simples com os quais é possível modelar sistemas estocásticos com variáveis contínuas. Um sistema com memória de longo alcance pode ser descrito por equações de Fokker-Planck mais gerais. (KUBO; TODA; HASHITSUME, 1985; RISKEN, 2003)

Nossa vantagem hoje é que podemos lançar um olhar no passado e estudar todo o desenvolvimento da física de sistemas estocásticos, uma vantagem que Planck obviamente não tinha. Para ele o interesse na equação não era tanto pelos sistemas estocásticos per se, embora isto não lhe tire o mérito da grande contribuição que deu à área. Se hoje olhamos sua atuação como físico, fica claro que sua carreira foi, em grande parte, uma tentativa de melhor entender e estender conceitos termodinâmicos – em particular a entropia – a outras áreas da Física. Um problema onde esta metodologia se fez presente foi o do calor específico de moléculas diatômicas. Mais uma vez, foi o envolvimento de Planck com problemas da interação radiação-matéria, que há alguns anos lhe havia aberto as portas da física quântica, que agora lhe abririam as portas da estocasticidade.

3 Max Planck e o espectro de moléculas em rotação

Todo estudante de física aprendeu, da mecânica estatística, que no equilíbrio termodinâmico à temperatura absoluta T, cada grau de liberdade possui, na média, uma energia no valor de

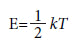
onde k é a constante de Boltzmann. Este resultado, conhecido como teorema da equipartição de energia, permite deduzir que a energia média de um gás ideal de N partículas tem um valor dado por:

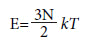
Este resultado vem do fato que cada partícula de massa m de um gás ideal (não interagente) possui apenas uma energia cinética (composta das três componentes espaciais de velocidade, uma para cada direção do espaço):

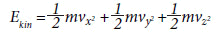
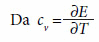segue diretamente que o valor do calor específico de tal gás é uma constante:

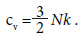
Para um sistema com n graus de liberdade por partícula, segue a chamada lei de Dulong-Petit Gesetz de 1819:

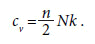
Uma vez que este resultado não depende da temperatura, dever-se-ia obter um valor constante de cv para T → 0 e, na verdade, um valor diferente de zero. Caso fosse este mesmo o caso, então de acordo com a terceira lei da termodinâmica, a entropia deveria ir a zero no zero absoluto, um resultado obviamente não físico⁸. Um caminho para a solução desta inconsistência foi mostrado por Einstein em 1906, com a introdução de frequências de vibração quantizadas para os átomos de uma rede cristalina. (EINSTEIN, 1906) Embora houvesse uma boa concordância dos resultados em altas temperaturas (Dulong-Petit), o comportamento do modelo de Einstein para baixas temperaturas desvia-se significativamente dos resultados experimentais. Foi somente com o trabalho de Peter Debye (1884-1966), alguns anos mais tarde, que esta inconsistência pode ser sanada. (DEBYE, 1911)

Porém, permanecia em aberto o problema que tanto a teoria de Einstein quanto a de Debye se aplicavam a corpos sólidos e não era claro se a mesma poderia ser estendida para gases. Porém, já era sabido que as linhas espectrais de moléculas, como hidrogênio, eram, segundo enfatizou Planck, “canalizadas” (quantizadas):

Embora os trabalhos pioneiros de N. Bohr, A. Sommerfeld, P. Epstein tenham mostrado de maneira inquestionável que a espectroscopia é regida por leis quânticas, a natureza da dos fenômenos que ocorrem durante a emissão e absorção de radiação encontra-se envolta pelo mais opaco véu. (PLANCK, 1917b, p. 491)

Antes de se determinar de maneira inequívoca o calor específico de gases, era necessário determinar se o espectro associado à rotação era também “canalizado” ou não, pois a ele estariam associados graus de liberdade e, portanto, uma contribuição não nula ao calor específico. Planck acreditava que, embora o espectro de emissão fosse quantizado – os experimentos eram claros quanto ao isso –, o espectro de absorção não o era, seguindo leis clássicas de absorção segundo Maxwell:

A primeira interpretação [ou seja, de um espectro de emissão e absorção quantizados] é atualmente a mais difundida, tendo sido utilizada recentemente por A. Einstein como ponto de partida de uma teoria, em muitos aspectos bem sucedida, sobre a radiação térmica. Porém existe nela uma dificuldade, a saber, que em cada salto que um oscilador que absorve energia realiza, de uma órbita estacionária de energia mais baixa para uma estacionária de energia mais alta, deve-se supor que ele tenha que absorver uma quantidade de energia do campo circundante, algo que se não condiz com uma velocidade finita de propagação da radiação e uma densidade espacial finita de radiação – uma dificuldade que desde já muito tempo levou a suposição que as órbitas estáticas não são as únicas possíveis, mas sim a únicas a partir das quais a emissão pode ocorrer. Essa suposição traz consigo a vantagem de ser condizente com as leis de absorção da eletrodinâmica clássica. E uma vez que estas leis são bem conhecidas, há a esperança que, ao seguirmos esta hipótese e as suas consequências, consigamos uma resposta positiva da questão, se uma pessoa que siga este caminho encontrará um resultado que contradiga os experimentos. Apenas quando esta última se provar verdadeira, aí então será inevitável deixarmos o terreno da teoria clássica da absorção. (PLANCK, 1917b)

Planck voltou-se, assim, à tarefa de entender o espectro de absorção de dipolos em rotação. Havia, apenas, um parâmetro de ajuste – o momento de inércia do dipolo – e a tarefa de calcular a função de distribuição dos momentos angulares dos dipolos, determinada a partir da equação de Fokker-Planck, e uma vez achada uma solução, utilizar a eletrodinâmica de Maxwell para estudar o movimento de um dipolo com o eixo fixo numa direção espacial (PLANCK, 1917b) e depois com um eixo que podia mudar sua orientação no espaço. (PLANCK, 1917c) Para Planck, era claro que este era o caminho a ser seguido, não obstante os resultados experimentais do espectro de emissão (Planck 1917b):

Aqui parece haver, à primeira vista, uma contradição grande entre minha hipótese a pouco introduzida e a realidade, pois o espectro de rotação é sabidamente não contínuo, mas canalizado. Ele parece ser na realidade caracterizado por máximos de absorção mais ou menos definidos em posições equidistantes dadas pelas velocidades de rotação ou frequências de oscilação ω₁, ω₂,..., ω_n,... e há todas as razões para se supor que por meio da rarefação do gas, quando então o efeito das colisões das moléculas é reduzido de maneira significativa, os máximos se apresentarão como linhas bem definidas. Esta imagem parece não poder ser interpretada do ponto de vista da toeria clássica senão que pelo fato que a absorção da radiação incidente só ocorre para aquelas moléculas que possuem uma velocidade de rotação ω_n e que de acordo com a teoria clássica de absorção certamente não estão ligadas a velocidades de rotação específicas. Disto seguiria que nenhuma outra velocidade a não ser ω_n se encontra presente no gas, que representa assim do ponto de vista da teoria quântica as “órbitas estáticas“ das moléculas em rotação.

Esta dedução tão clara é porém inapropriada. Ela não leva em conta que uma dada molécula não possui uma velocidade de rotação específica, mas que sua velocidade muda tão logo comece a absorver. Aquelas moléculas que absorvem dentro de um intervalo temporal específico uma radiação de um intervalo espectral específico, não são idênticas àquelas moléculas cujas frequências de oscilação se encontravam, no início deste período, dentro do intervalo espectra; antes disso, ocorre durante todo o processo uma troca de frequeicas entre moléculas.

Planck não parecia satisfeito com a ideia dos pacotes de luz (fótons). Para ele, era necessário salvar a teoria clássica de Maxwell onde ela ainda poderia ser salva. Assim, Planck se colocou a tarefa de melhor entender a dinâmica desta troca entre moléculas em um dado intervalo espectral. Para isto, ele necessitava do resultado de Fokker acerca da energia média de rotação de dipolos, num campo eletromagnético externo (FOKKER, 1914):

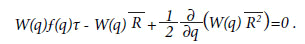
Nesta expressão, q representa o momento angular de uma molécula e W(q), a densidade de probabilidade; f(q) é a velocidade com a qual q diminui, ou seja, dq/dt. Finalmente, R é Δq, as flutuações durante o intervalo τ devido a processos térmicos aleatórios. O termo do meio, no lado esquerdo da equação, é fundamental, pois sem ele se recupera a equação da difusão já obtida por Einstein (1906).

Planck considerou, inicialmente, o caso de um sistema de dipolos, cujos eixos de rotação eram fixos (o segundo da série de três artigos. No primeiro ele apenas apresentou a dedução rigorosa da equação). Sua conclusão, após longos cálculos, era, em suas próprias palavras, um tanto quanto surpreendente (einigermassen überraschend):

Se tivemos N moléculas de um gás e o número daquelas cujas frequências de oscilação se encontram entre ω e ω+dω é dado por NxW(ω), de modo que W(ω) represente a “densidade de distribuição espectral”, então a energia absorvida por todo o gas da radiação incidente com frequência entre ω e ω+dω não é proporcional à W(ω) mas sim á . Assim, quando num dado intervalo de frequência não há qualquer absorção, como na região entre ω_n e ω_n+1, a densidade de moléculas ali é portanto diferente de zero e independe ω. E no caso onde linhas bem definidas de absorção aparecem entre nos valores de ω_n e ω_n+1, ali encontramos, em ambos os lugares, uma acentuada queda na distribuição de densidade W(ω) a medida que ω aumenta.

À mesma conclusão ele chegou no artigo seguinte, onde tratou do caso de eixos de rotação móveis. A diferença do artigo anterior é simplesmente que a energia absorvida não era mais proporcional 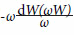à mas sim à .

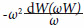Planck conclui seu último artigo, comparando os resultados por ele obtidos com dados experimentais medidos em moléculas de água. A concordância entre experimento e teoria não foi muito boa, resultado que ele atribuiu ao fato de moléculas de água não serem exatamente “dipolos simples”. O que ele não sabia é que, com a equação por ele utilizada para se determinar a continuidade ou descontinuidade dos processos de absorção, é uma equação que se aplica a sistemas clássicos e não ao mundo quântico. As variáveis na equação de Fokker-Planck são contínuas e ela tem tanta relevância na mecânica quântica quanto esta última tem no cálculo de órbitas de planetas. (KAMPEN, 1997)

4 Conclusão

Entre os anos de 1915 e 1917, na tentativa de explicar o espectro rotacional de moléculas diatômicas e assim resgatar a teoria de absorção e emissão de radiação à la Maxwell, incondizente que esta era com as observações experimentais de um espectro quantizado, Planck envolveu-se com a teoria de sistemas estocásticos, tomando-o por base para explicar a aparente contradição. O resultado de Planck pode ser assim resumido: numa série de artigos, ele foi capaz de achar uma relação funcional entre a taxa de emissão e a derivada da função distribuição f (densidade de moléculas) como função da frequência de rotação destas. Deste modo, a não observação de um espectro de emissão contínuo se dava não pela inexistência de moléculas distribuídas continuamente pele espectro, mas antes por haver regiões de frequência onde f era constante (e, portanto, a derivada nula). A função distribuição era a solução estacionária de uma equação que Planck deduziu de maneira rigorosa, uma vez que esta era a base sobre qual seu trabalho se assentava. Hoje sabemos que esta equação não se aplica ao problema original que Planck tinha em mente. Sua dedução, porém, é válida, motivo pelo qual a equação foi mais tarde batizada de Equação de Fokker-Planck, pelo matemático russo Kolmogorov, num célebre artigo onde ele a assentou sobre bases matemáticas mais sólidas.

Referências

ABBOTT, D. et al. Simple derivation of the thermal noise formula using window-limited fourier transforms and other conundrums. IEEE Transactions on Education, v. 39, n. 1, p. 1, 1996.

BOLTZMANN, L. E. Entgegnung auf die wärmtheoretischen Betrachtungen der Hrn. E. Zermelo. Annalen der Physik, v. 57, p. 773, 1896.

______. Experimentelle Bestimmung der Dielektrizitätskonstante von Isolatoren. Wiener Berichte, v. 67, p. 17-77, 1872a.

______. Experimentelle Bestimmung der Dielektrizitätskonstante einiger Gase. Wiener Berichte, v. 69, p. 795-813, 1879.

______. Über den Beweis des Maxwell’schen Geschwindigkeitsverteilungsgesetzes unter Gasmolecülen. Sitzungsber. d. k. bayer. Akad. d. Wiss. 24, 1894.

______. Über die mechanische Bedeutung des zweiten Hauptsatzes der Wärmetheorie. Wiener Berichte, v. 53, p. 195-220, 1866.

______. Über das Wärmegleichgewicht zwischen mehratomigen Gasmolekülen. Wiener Berichte, v. 63, p. 397-418, 1871.

______. Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen. Wiener Berichte, v. 66, p. 275-370, 1872b.

______. Zu Hrn. Zermelos Abhandlung, Über die mechanische Erklärung irreversibler Vorgänge. Annalen der Physik, v. 60, p. 392-398, 1897.

BRODA, E. Ludwig Boltzmann: mensch, physiker, philosoph. Viena: Franz Deuticke, 1983.

DAHMEN, S. R. Boltzmann’s works in physics. Rev. Bras. Ens. Fis., v. 28, n. 3, p. 281-295, 2006a.

______. Gödel and Einstein: what if time does not withstand a friendship?. Rev. Bras. Ens. Fis., v. 28, n. 4, p. 1-10, 2006b.

______. Max Planck on Statistical Thermodynamics and Stochastic Systems. In: [Hoffmann 2008], S. 335 ff.

EBELING, W. Max Planck on entropy and irreversibility. In: [Hoffmann 2008], S. 29 ff.

EBELING, W.; GUDOWSKA-NOWAK, E.; SOKOLOV, I.M. On stochastic dynamics in physics: remarks on history and terminology. Preprint, 2008.

ECKERT, M. Max Planck’s Later Work on Quantum Theory. In: [Hoffmann 2008], S. 643 ff.

EINSTEIN, A. Zur theorie de Brownsche Bewegung. Annalen der Physik, v. 19, p. 371, 1906.

EHRENFEST, P.; EHRENFEST, T. Begriffliche Grundlagen der statistischen Auffassung in der Mechanik. Leipzig: Enzyklopädie der Mathematischen Wissenschaften, 1911. Bd. IV. Edition in English: The Conceptual Foundations of the Statistical Approach in Mechanics. Ithaca: Cornell University, Ithaca, 1959.

FISHER, R. A. The distribution of gene ratios for rare mutations. Proc. Roy. Soc. Edinburgh, v. 50, p. 205-220, 1930.

FOKKER, A. D. Die mittlere Energie rotierender elektrischer Dipole im Strahlungsfeld. Annalen der Physik, v. 43, p. 810-820, 1914.

GÖDEL, K. An example of a new type of cosmological solutions of einstein’s field equations of gravitation. Rev. Mod. Phys., v. 21, p. 447-450, 1949.

GUTTMANN, Y. M. The Concept of Probability in Statistical Physics. Cambridge: Cambridge University, 1999.

HOFFMANN, D. (Hrsg.). Max Planck: annalen papers. Weinheim: Wiley-VCH, 2008.

HUANG, K. Statistical mechanics. 2^nd ed. New York: John Wiley and Sons, 1987.

KAMPEN, N. G. Die Fokker-Planck-Gleichung, Physikalische Blätter (Sonderdruck). Berlin: Wiley-VCH, 1997. p. 14.

KIRCHHOFF, G. Vorlesungen über die Theorie der Wärme. Ed. M. Planck. Leipzig: Teubner, 1894.

KLEIN, M. J. The development of Boltzmann’s Statistical Ideas. In: COHEN, E. G. F.; UHLENBECK, G. (Ed.). The Boltzmann Equation: theory and application. Viena: Springer, 1973.

KOLMOGOROV, A. Über die analytischen Methoden in der Wahrscheinlichkeitsrechung. Mathematische Annalen, v. 104, p. 415-570, 1931.

KUBO, R.; TODA, M.; HASHITSUME, N. Statistical Physics II, Nonequilibrium Statistical Mechanics. Berlin: Springer, 1985.

MAXWELL, J.C. Maxwell, illustrations of the dynamical theory of gases. Phil. Mag., v. 19, p. 19, 1860.

PLANCK, M. Absolute Entropie und chemische Konstante. Annalen der Physik, v. 66, p. 365-372, 1921.

______. Bemerkungen über die Emission von Spektrallinien. Sitzungsber. d. Preuss. Akad. d. Wiss., 1915c, 909-913.

______. Die Quantenhypothese für Molekeln mit mehreren Freiheitsgraden: Erste Mitteilung. Verh. der Deutsch. Phys. Ges., v. 17, p. 407-418, 1915a.

______. Die Quantenhypothese für Molekeln mit mehreren Freiheitsgraden: Zweite Mitteilung. Verh. der Deutsch. Phys. Ges., v. 17, p. 438-451, 1915b.

______. Über den Beweis des Maxwell’schen Geschwindigkeitsverteilungsgesetzes unter Gasmolecülen. Annalen der Physik, v. 55, p. 220-222, 1895. Nachd.

______. Über einen Satz der statistischen dynamik und seine Erweiterung in der Quantentheorie. Sitzungsber. d. Preuss. Akad. d. Wiss., 1917a, 324-341.

______. Planck, zur theorie des rotationsspektrums: Erste Mitteilung, Annalen der Physik, v. 52, p. 491-505, 1917b.

______. Zur theorie des rotationsspektrums: Zweite Mitteilung. Annalen der Physik, v. 53, p. 241-256, 1917c.

RAYLEIGH, Lord. Dynamical problems in illustration of the theory of gases. Phil. Mag., v. 32, p. 424, 1891.

SCHRÖDINGER, E. The statistical law in nature. Nature, v. 153, p. 704, 1944. Original de 1938.

ZERMELO 1896a] E. Über einen Satz der Dynamik und die mechanische Wärmetheorie. Annalen der Physik, v. 57, p. 485, 1896a.

______. Über mechanische Erklärungen irreversibler Vorgänge. Eine Antwort auf Hrn. Boltzmanns Entgegnung. Annalen der Physik, v. 59, p. 793, 1896b.

1 A equação de Fokker-Planck, o tema principal deste trabalho, foi deduzida de forma geral e rigorosa em 1931 pelo matemático russo A. N. Komolgorov em um trabalho seminal acerca de equações diferenciais estocásticas. (KOLMOGOROV, 1931) Um ano antes, o matemático britânicos Sir R. A. Fisher deduziu, sem o conhecimento de trabalhos prévios, a mesma equação no contexto de mutações raras na genética. (FISHER, 1930) O nome “Equação de Fokker Planck” foi sugerido por Kolmogorov. (DAHMEN, 2008)

2 Sitzungsberichte der Preussischen Akademie der Wissenschaften, os relatos das reuniões da Academia Prussiana de Ciências.

3 As linhas espectrais do espectro de emissão já eram conhecidas experimentalmente de longa data.

4 Um ensemble é um conjunto infinito de sistemas idênticos, cujos valores médios de grandezas microscopicamente definidas podem ser calculados desde que certas condições físicas e matemáticas sejam respeitadas. Estes valores médios representam as grandezas mensuráveis da termodinâmica, como, por exemplo, a pressão ou temperatura.

5 A introdução de conceitos quânticos na mecânica estatística ocorreu primordialmente, nos anos de 1920 e está associada aos nomes de Albert Einstein (1879-1955), Satyendra Nath Bose (1894-1974), Enrico Fermi (1901-1954) e Paul Adrien Maurice Dirac (1902-1984).

6 Jan Ingenhousz é mais conhecido pelo descobrimento do papel da luz na fotossíntese. Suas observações sobre pó de carvão suspenso em álcool passaram despercebidas para o público de língua não holandesa. (EBELING; GUDOWSKA-NOWAK; SOKOLOV, 2008). Robert Brown (1773-1858), um renomado botânico, que muito contribuiu para os estudos de morfologia de plantas e para a descrição da flora australiana, observou o movimento irregular de pólen suspenso em água. Para confirmar se o movimento seria causado pela força interna de “moléculas orgânicas” vivas, Brown conduziu experimentos com pólen armazenado há mais de 100 anos em seu herbário. (BRUSH, 1976, BD. 2 P. 658) Na realidade, este movimento já havia sido observado por vários estudiosos antes de Brown, mas ele foi o primeiro a fazer um estudo extensivo do fenômeno, descrevendo-o. Uma lista completa dos nomes mais importantes associados a estes estudos podem ser encontrados em Abbott e outros (1996). Hoje sabemos que o movimento irregular das partículas suspensas é provocado pelo choque com moléculas do líquido e representa uma prova da realidade atômica da matéria. (EINSTEIN, 1906)

7 Eu uso a notação moderna ao longo desse texto por uma questão de clareza, particularmente quando me refiro a Boltzmann, cuja notação difere daquela que se tornou “padrão” em livros-textos.

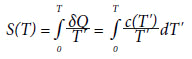8 Podemos escrever a entropia S(T) como . Para evitar que a entropi divirja no zero absoluto, temos que fazer com que o calor específico também tenda a zero neste limite.