De Louis de Broglie a Erwin Schrödinger: uma comparação
1 Introdução
O trabalho de Erwin Schrödinger sobre mecânica ondulatória começou no final de 1925, como consequência do seu estudo da tese de De Broglie de 1924. Sabe-se que a equação de onda de Schrödinger pode ser deduzida dos resultados de De Broglie, no limite clássico. Sob este ponto de vista, poderíamos pensar que a teoria de Schrödinger seria um mero desenvolvimento da teoria de De Broglie. Mas podemos realmente aceitar essa conclusão?
Este artigo compara algumas das características das teorias de De Broglie e Schrödinger. Sabe-se que, em suas primeiras tentativas de formular uma teoria quântica do átomo, Schrödinger tentou desenvolver uma teoria relativística, seguindo as ideias de De Broglie, e apenas depois começou a procurar uma equação de onda não-relativística. É muito fácil deduzir uma equação de onda para as ondas de fase de De Broglie, tanto no caso relativístico, quanto no caso nãorelativístico. Na sua tentativa relativística, Schrödinger realmente seguiu uma abordagem simples, usando a teoria de De Broglie. No entanto, ao desenvolver a formulação não-relativística, ele tentou produzir uma dedução independente da equação de onda, seguindo diversas linhas diferentes de argumentação, em vez de utilizar os resultados de De Broglie no limite clássico.
Primeiramente será feita uma breve apresentação das ideias de De Broglie e sua influência histórica sobre Schrödinger; depois, serão discutidas as primeiras deduções da equação de onda, enfatizando as diferenças e semelhanças entre as duas teorias. Será mostrado que, embora seja formalmente possível deduzir uma equação de onda a partir da teoria de De Broglie, existe uma incompatibilidade entre as duas teorias: seria impossível dar qualquer sentido às ideias de De Broglie, no caso de um corpo rígido girando, por exemplo. A abordagem de Schrödinger era, neste sentido, independente e incompatível com a teoria de De Broglie, e podia ser aplicada facilmente a muitas situações físicas diferentes.
2 A teoria de De Broglie
Louis de Broglie apresentou sua teoria primeiramente sob a forma de uma série de artigos publicados em 1923 e 1924 (DE BROGLIE, 1923a, 1923b, 1923c, 1923d, 1924a, 1924b, 1924c) e depois em sua tese de doutoramento (DE BROGLIE, 1924d, 1925).1 Ele tomou como ponto de partida a ideia de que todas as partículas (elétrons, quanta de luz etc.) sofriam algum processo periódico, obedecendo às equações de energia da relatividade e da teoria quântica, E=hν and E=mc2;, e usou a relatividade especial como principal ferramenta teórica no seu trabalho. (DE BROGLIE, 1923a)
No referencial de repouso da partícula, devemos ter E0=m0c2;=hν0 e em relação a outros referenciais, a equação correta seria:
| E=mc2;=hν | (1) |
No entanto, a massa aumenta com a velocidade, e a frequência diminui com a velocidade. Portanto, parecia que o uso de E=mc2;=hν levava a uma contradição. (DE BROGLIE, 1923a, p. 507-508) Depois de lidar com essa dificuldade por algum tempo, De Broglie reconheceu que sua teoria só poderia obedecer à teoria da relatividade especial se ele concebesse todos os quanta como sistema espacialmente extensos, em vez de partículas pontuais.
Na sua tese, ele apresentou esta ideia fundamental de um modo muito claro. De acordo com o eletromagnetismo de Maxwell, a energia de qualquer carga (incluindo um elétron) está espalhada no espaço à sua volta, embora haja uma forte concentração de energia em torno do centro. Seguindo esta ideia, De Broglie considerou o elétron como um sistema infinito. (DE BROGLIE, 1925, p. 33-34)
No referencial de repouso de um elétron, supôs que toda sua estrutura (infinita) estava pulsando em sincronia, com uma frequência dada por hν0=m0c2;. Esse fenômeno periódico pode ser descrito por uma equação como esta:

Em relação a outros referenciais, a sincronia deste fenômeno periódico seria perdida, é claro, devido a efeitos relativistas2. A transformação de Lorentz do tempo é:

onde β=v/c é a velocidade da partícula dividida pela velocidade da luz no vácuo.
Aplicando a transformação de Lorentz do tempo (3) a esta pulsação (2), De Broglie mostrou facilmente que a oscilação se transformava em uma onda, em relação a outros referenciais, e obteve a velocidade, a frequência e as outras propriedades da onda . Substituindo t0 em (2) por (3), obtemos:
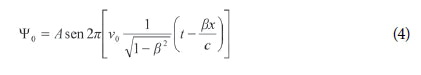
A fórmula geral de uma onda monocromática plana movendo-se na direção do eixo x é:

A comparação das equações (4) e (5) mostra que a pulsação uniforme do elétron (no referencial próprio) se transforma em uma onda plana monocromática (a “onda de fase”), em relação a outros referenciais. Identificando as quantidades correspondentes nessas duas equações, obtêm-se a frequência ν e a velocidade V da onda associada ao elétron:


O elétron deve ter alguma posição definida, portanto, a onda uniforme infinita não pode descrevê-lo completamente. O elétron livre em movimento seria equivalente a um sistema extenso, com uma forte concentração de energia em torno de um centro, viajando a uma velocidade v e, ao mesmo tempo, atravessado por uma onda monocromática de velocidade V=c2/v e frequência ν=mc2/h.
Uma onda monocromática modulada é matematicamente equivalente a um grupo de ondas, mas conceitualmente a ideia de De Broglie é muito diferente, porque no referencial próprio ela tem uma única frequência bem definida, e não deveria se espalhar à medida que se desloca.
3 Mecânica e óptica
De Broglie apresentou sua teoria sob diferentes formas. Em algumas de suas publicações ele enfatizou as semelhanças entre a mecânica e a óptica. (DE BROGLIE, 1924a, 1925, p. 46-53) Na teoria da relatividade especial, o princípio da ação mínima de Maupertuis pode ser escrito como:

onde o símbolo Ji representa as componentes do quadrivetor de momento-energia3.
Por outro lado, a versão relativística do princípio de Fermat pode ser escrita como:

onde o símbolo Oi representa as componentes do quadrivetor “onda de universo”, com componentes correspondendo às projeções do número de onda e à frequência da onda.
A analogia entre os dois princípios (Fermat e Maupertuis) e a relação E=hν que é válida para a quarta componente dos quadrivetores permitiu, então, a De Broglie estabelecer uma relação geral em quatro dimensões:

Ela contém tanto E=hν quanto p=h/λ como casos especiais da equação relativística geral. (BROWN; MARTINS, 1984)
4 Campos eletromagnéticos
Se o elétron estiver se movendo em um campo eletromagnético, sua energia total W (incluindo a energia potencial eϕ) permanece constante (DE BROGLIE, 1925, p. 60). De Broglie supôs que a frequência do elétron seria proporcional à energia total W e, portanto, também seria constante.

No entanto, a velocidade V das ondas e o seu comprimento de onda mudariam de ponto para ponto, de acordo com uma equação muito complexa (DE BROGLIE, 1925, p. 60):
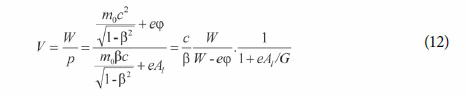
Nesta equação, o momento do elétron contém componentes proporcionais ao potencial vetor A, seguindo a teoria de Maxwell. (BORK, 1967)
De Broglie não tentou aplicar (11) e (12) a nenhuma situação específica. O único caso de partícula em um campo que ele foi capaz de tratar foi o átomo de hidrogênio. (DE BROGLIE, 1923a, p. 509-510) Ele supôs que o centro do elétron obedecia à mecânica clássica e seguia uma trajetória de Kepler. Assumiu que a onda seguiria a mesma trajetória clássica. Supondo que a onda estivesse sempre em fase com as oscilações do elétron (e não supondo que a onda fosse estacionária, como apresentado nos livros didáticos), ele provou que a regra de quantização de Bohr para o momento angular, L=pr=nh/2π, era uma consequência de sua própria teoria. (DE BROGLIE, 1925, p. 62-65)
A única previsão nova da teoria de De Broglie foi a difração de elétrons (DE BROGLIE, 1923b, p. 549, 1925, p. 104) e ela foi confirmada rapidamente. Experimentos com elétrons de alta energia provaram, depois de poucos anos, que o comprimento de onda da onda associada ao elétron obedecia à equação relativística, conforme previsto por De Broglie. (BROWN; MARTINS, 1984)
5 O papel intermediário de Einstein
Costuma-se dizer que a tese de De Broglie só foi aceita pela banca por causa da influência de Einstein sobre Paul Langevin (MEHRA; RECHENBERG, 1982-1987, v. 1-2, p. 604). Esta versão, baseada no testemunho do próprio De Broglie, não é correta.
Langevin contou a Einstein sobre o trabalho de De Broglie em julho de 1924 e no dia 27 do mesmo mês pediu a De Broglie que enviasse uma cópia de sua tese (ainda não defendida) a Einstein. (DARRIGOL, 1993, p. 355; WHEATON, 1983, p. 297) No entanto, Einstein não reagiu imediatamente. A tese de De Broglie foi apresentada e aprovada no dia 25 de novembro do mesmo ano. Somente no dia 16 de dezembro, Einstein escreveu cartas para Langevin e para Lorentz, elogiando o trabalho de Louis de Broglie: “Ele ergueu uma ponta do grande véu”. (DARRIGOL, 1993, p. 355; MEHRA; RECHENBERG, 1982-1987, v. 1-2, p. 604) No dia 13 de janeiro, Langevin escreveu uma carta para De Broglie contando-lhe sobre a opinião favorável de Einstein. (WHEATON, 1983, p. 297)
Nessa época, Einstein estava pesquisando a teoria quântica dos gases (atualmente chamada “estatística de Bose-Einstein”). Em um artigo que publicou em fevereiro de 1925, ele comentou que o trabalho de De Broglie poderia ajudar a esclarecer o significado dessa nova teoria. (JAMMER, 1966, p. 249)
Erwin Schrödinger leu esses trabalhos de Einstein e trocaram cartas sobre o assunto. (HANLE, 1977, 1979) Estimulado pela referência de Einstein ao trabalho de De Broglie, Schrödinger obteve uma cópia da tese (que havia sido publicada) e a leu em outubro de 1925.4 Em novembro do mesmo ano, Schrödinger escreveu cartas para Einstein e Landé que mostravam que ele estava muito excitado com as ideias de De Broglie. (MOORE, 1989, p. 192) Ele aplicou essa teoria aos gases em um artigo que completou, em dezembro de 1925. (REGT, 1997, p. 474) No entanto, ele considerou alguns aspectos da teoria de De Broglie difíceis de entender ou de aceitar – especialmente a teoria do átomo de hidrogênio.
No dia 23 de novembro de 1925, Schrödinger apresentou um seminário sobre as ideias de De Broglie. (MOORE, 1989, p. 192). Na ocasião, Peter Debye comentou que a abordagem de De Broglie era infantil e que era necessário usar uma equação de onda para descrever uma onda em três dimensões. (KRAGH, 1982, p. 157) Schrödinger concordou que as ondas deviam ser tratadas de um outro modo, no caso do átomo de hidrogênio. Ele também notou que ondas de De Broglie em órbitas keplerianas próximas produziriam uma frente de onda distorcida.
Em dezembro de 1925, Schrödinger começou a tentar produzir uma equação de onda a partir da teoria de De Broglie e aplicá-la ao átomo de hidrogênio. Em vez de ondas seguindo órbitas de Kepler, ele começou a pensar sobre ondas estacionárias em três dimensões, análogas a ondas sonoras em cavidades. A quantização surgiria como uma consequência do espectro discreto de frequências das ondas estacionárias no átomo.
6 A equação de onda relativística de Schrödinger
Alguns passos decisivos foram dados na época de Natal de 1925, durante uma estada de Schrödinger em Villa Herwig, nos Alpes, onde ele passou duas semanas com uma amante misteriosa. (MOORE, 1989, p. 194-195) Primeiramente, Schrödinger tentou produzir uma equação de onda relativística, seguindo a abordagem de De Broglie. (KRAGH, 1982, p. 175-178) Esta dedução não foi publicada, mas foi encontrada em um manuscrito escrito provavelmente no final de 1925. (MEHRA; RECHENBERG, 2001, v. 5.1, p. 423-430) Vamos apresentar aqui uma reconstrução dessa primeira dedução da equação de onda por Schrödinger. (KRAGH, 1982, p. 180, 1984)
A equação de onda geral, válida tanto na física clássica quanto na relativística, é:

Para qualquer onda monocromática λ=V/ν, portanto, a equação de onda geral também pode ser escrita como uma função da velocidade da onda e de sua frequência:

Na teoria de De Broglie, V = E/p onde E é a energia total do elétron:
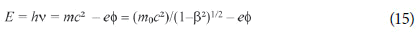
Se não for necessário levar em conta campos magnéticos, o momento p será:

Como a energia total do elétron é igual a hν (eq. 15), é possível obter v=βc como função de ν. Substituindo esse resultado nas equações de E e de p, pode-se computar a velocidade da onda V=E/p como função da frequência ν. Depois de algumas manipulações, a equação de onda geral (13) se torna:
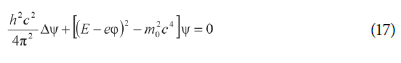
Esta é uma das formas da chamada “equação de Klein-Gordon”.
Note-se que a dedução de Schrödinger desta equação de onda relativística depende apenas de resultados que já haviam sido obtidos por De Broglie. Realmente, o próprio De Broglie chegou a este resultado, de forma independente. (KRAGH, 1984, p. 1025)
Schrödinger aplicou esta equação de onda ao átomo de hidrogênio e obteve resultados errados para os níveis de energia. (JAMMER, 1966, p. 257-258; MEHRA; RECHENBERG, 1982-1987, v. 5, p. 367-368) Depois de se debater por pouco tempo com uma teoria relativística, ele se voltou para uma abordagem não-relativística.
7 A equação de onda clássica
Obter uma equação de onda no caso da aproximação clássica é muito mais fácil do que no caso relativístico e diversos livros-texto apresentam tal tipo de dedução. Se aceitarmos a relação λ=h/p entre momento e comprimento de onda e aplicarmos a dinâmica clássica, obteremos:

Na mecânica clássica, a energia cinética K é:

Portanto, o quadrado do comprimento de onda, no limite clássico, é:
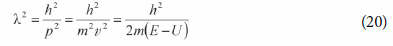
A equação de onda geral (clássica e relativística) é:

Substituindo em (21) pela expressão de (2), obtemos:

Esta é a chamada “equação de Schrödinger independente do tempo”. Portanto, usando apenas a mecânica clássica e a relação de De Broglie λ=h/p é possível deduzir a equação de onda de Schrödinger. Note que esta dedução é muito semelhante à que Schrödinger usou no caso relativístico, embora mais simples. No entanto, Schrödinger não utilizou essa dedução tão simples. Como ele apresentou a equação de onda em seus primeiros artigos?5
8 A equação de onda no primeiro artigo de Schrödinger
No primeiro artigo que publicou em 1926, Schrödinger apresentou a equação de onda como uma consequência da abordagem de Hamilton-Jacobi, de um modo bastante abstrato .(SCHRÖDINGER, 1926a, p. 361-362, 1929, p. 1-2) Ele introduziu uma função desconhecida Ψ e afirmou que a ação S poderia ser escrita como:
| S = K log Ψ | (23) |
Portanto, a função hamiltoniana H poderia ser escrita como:
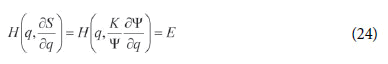
Schrödinger, então, afirmou que no caso não-relativístico essa equação “sempre pode ser transformada de modo a se tornar uma forma quadrática (de Ψ e de suas derivadas) igualada a zero” (SCHRÖDINGER, 1926a, p. 361-362; 1929, p. 1). No caso do átomo de hidrogênio (um campo coulombiano), ela se torna:
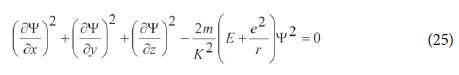
Esta é simplesmente a equação clássica da conservação da energia p2;=2m(E-V), pois os três primeiros termos correspondem ao quadrado do momento dividido por (K/Ψ), de acordo com (24).
Schrödinger (1926a, p. 362, 1929, p. 2), então. afirmou: “Agora procuramos uma função Ψ tal que para qualquer variação arbitrária dela a integral da acima referida forma quadrática, calculada sobre todo o espaço de coordenadas, é estacionária [...]”. A equação correspondente é:
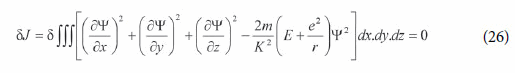
A partir deste problema variacional, Schrödinger deduziu a equação de onda para o átomo de hidrogênio:
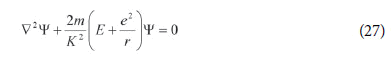
Esta dedução apresentada no primeiro artigo de Schrödinger de 1926 é completamente sem sentido, já que Ψ é uma função não definida e (26) não é um princípio variacional válido na física clássica6. Sua única “justificação” é que a equação de onda leva aos níveis de energia corretos para o átomo de hidrogênio, deduzidos cuidadosamente no restante desse mesmo artigo. (SCHRÖDINGEr, 1926a, p. 362-374, 1929, p. 2-10)
10 A dedução no segundo artigo de Schrödinger
O próprio Schrödinger não estava muito satisfeito com essa “dedução” do primeiro artigo e apresentou uma muito diferente, no seu segundo artigo de 1926 (SCHRÖDINGER, 1926b, 1929, p. 13-40), onde apresentou pela primeira vez a equação de onda genérica independente do tempo (m=1):

Apresentamos aqui uma reconstrução de sua dedução, enfatizando os seus pontos principais.
A suposição fundamental de Schrödinger foi a equação de onda geral (clássica) nesta forma (SCHRÖDINGER, 1926b, p. 510; 1929, p. 27)7:

Schrödinger já havia obtido, no mesmo artigo (1926b, p. 494-498; 1929, p. 16-20), a equação para a velocidade da onda:
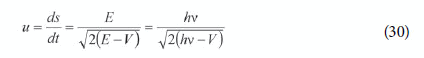
Então, supondo que a função de onda Ψ tenha a mesma forma que usualmente possui na física clássica (SCHRÖDINGER, 1926b, p. 510, 1929, p. 27):

deduzimos:
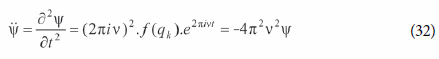
Substituindo (32) e (30) em (29), obtém-se imediatamente a equação de onda de Schrödinger:

Como E=hν, ela pode também ser escrita (SCHRÖDINGER, 1926b, p. 510; 1929, p. 27):

Portanto, na dedução que apresentou no seu segundo artigo, as únicas suposições não-clássicas são E=h e a fórmula para a velocidade u das ondas associadas ao elétron (30) que corresponde ao limite clássico da relação u=E/p de De Broglie.
No entanto, Schrödinger não tomou a fórmula de u do trabalho de De Broglie. Ele apresentou sua própria dedução original e altamente abstrata dessa relação, usando a analogia entre os princípios de Huygens e Hamilton (SCHRÖDINGER, 1926b, p. 494-498, 1929, p. 16-20). Ele se referiu ao trabalho de De Broglie neste artigo, mas enfatizou que seus próprios resultados foram obtidos de um modo mais geral e de forma independente da teoria da relatividade. Depois de apresentar sua própria dedução ele comentou:
Encontramos aqui novamente um teorema para as ‘ondas de fase’ do elétron, que o Sr. De Broglie tinha deduzido, referindo-se essencialmente à teoria da relatividade, nessas belas pesquisas às quais devo a inspiração para meu trabalho. Vemos que o teorema em questão é de uma maior generalidade, e não surge apenas da teoria da relatividade, mas é válido para qualquer sistema conservativo da mecânica comum. (SCHRÖDINGER, 1926b, p. 498, 1929, p. 20)
Portanto, Schrödinger poderia ter utilizado o trabalho de De Broglie para deduzir a equação de onda no caso não-relativístico, mas ele não o fez. Utilizou uma fórmula para a velocidade da onda associada ao elétron, que é equivalente à de De Broglie, mas apresentou uma nova dedução dessa relação – aparentemente porque queria provar que ela era válida, independentemente de considerações relativísticas.
11 As teorias de De Broglie e Schrödinger
O cuidado que Schrödinger tomou em evitar fundamentar sobre o de De Broglie poderia, talvez, ser justificado da seguinte forma: primeiramente, ele havia tentado usar a abordagem relativística e havia falhado; além disso, a equação de onda que de fato levava a resultados corretos não é o limite clássico da equação de onda relativística. Portanto, era adequado apresentar uma dedução completamente independente da teoria relativística de De Broglie, para assegurar que sua própria teoria era bem fundamentada. Provavelmente, isso era parte de sua motivação. No entanto, há outros aspectos relevantes, pois há muitas diferenças profundas entre as duas teorias.
O trabalho de De Broglie estava fundamentado na relatividade especial e suas principais equações só podiam ser deduzidas para elétrons em movimento uniforme, já que ele tomou como ponto de partida a descrição da pulsação do elétron extenso no seu referencial próprio. Sua ampliação para o caso do movimento acelerado exigia um novo modo de pensar e uma justificação diferente.
De Broglie tentou de fato proporcionar uma base para sua teoria, no caso do movimento acelerado, usando a analogia entre os princípios de Maupertuis e Fermat – que são válidos apenas para partículas isoladas e para raios. Isso o levou a uma relação geral entre as propriedades ondulatórias e mecânicas do elétron, movendo-se em um campo eletromagnético. No entanto, o elétron de De Broglie ainda descrevia uma trajetória bem definida e a onda associada podia ser descrita por raios – uma abordagem que só é satisfatória em situações correspondentes à óptica geométrica, mas inadequada nos casos de interferência e difração. Ele aplicou suas ideias com sucesso ao átomo de hidrogênio, mas foi incapaz de estudar o oscilador harmônico e outros sistemas simples. O conceito de De Broglie sobre o elétron não podia ser aplicado de forma adequada aos casos em que as dimensões do sistema eram comparáveis ao comprimento de onda. Era também difícil perceber como sua teoria poderia ser aplicada a um sistema com diversas partículas. Além disso, sua teoria não teria significado para um sólido rígido em rotação, por exemplo8.
A abordagem de Schrödinger era muito mais geral do que a de De Broglie. Suas deduções não dependiam da teoria da relatividade e, portanto, ele podia atacar diretamente os casos de sistemas acelerados e em rotação. Além disso, na dedução apresentada no seu segundo artigo de 1926, Schrödinger apresentou sua própria teoria de modo muito geral (SCHRÖDINGER, 1926b, p. 490-491, 1929, p. 14), usando coordenadas generalizadas (abrindo assim a possibilidade de aplicá-la à rotação e outros tipos de movimento) e discutindo um sistema conservativo geral (ou seja, ele não restringiu seu tratamento a uma partícula isolada). Seu modo geral e abstrato de abordar o problema lhe permitia aplicar a equação de onda a qualquer sistema físico.
No seu segundo artigo, Schrödinger usou a analogia entre os princípios de Huygens e Hamilton (não entre Fermat e Maupertuis, como De Broglie fez) e assegurou, assim, que a relação poderia ser aplicada a casos nos quais as dimensões do sistema fossem comparáveis ao comprimento de onda. Por essas razões, apenas a teoria de Schrödinger podia ser aplicada diretamente a ondas associadas a um ou mais elétrons em três dimensões (sistemas atômicos), ao oscilador harmônico e a sólidos em rotação, como ele de fato o fez. (SCHRÖDINGER, 1926b)
12 Conclusões
A equação de onda de Schrödinger pode ser deduzida dos resultados de De Broglie, no limite clássico. No entanto, a sua teoria não é uma aplicação ou desenvolvimento da teoria de De Broglie.
A teoria de Schrödinger pode ser aplicada a casos nos quais a de De Broglie não pode ser aplicada, como movimento acelerado e rotação, e para partículas em situações em que o comprimento de onda é comparável às dimensões da região que contém o elétron. Mesmo no caso de uma partícula livre, são também incompatíveis: o comprimento de onda relativístico de De Broglie foi confirmado por experimentos de difração e, portanto, o comprimento de onda clássico de Schrödinger não é válido, para velocidades altas. O valor heurístico da equação de onda de Schrödinger é outra distinção muito importante entre as duas teorias, já que a de De Broglie apenas levou a uma única predição nova: o comportamento ondulatório de elétrons em experimentos de difração. Há ainda outras diferenças entre as duas abordagens que não podem ser descritas aqui.
Embora a teoria de De Broglie tenha sido o ponto de partida do trabalho de Schrödinger e tenha tido um importante papel heurístico a esse respeito, as duas teorias são diferentes, independentes e incompatíveis.
Agradecimentos
O autor agradece o apoio recebido do Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) e da Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP), sem cujo auxílio teria sido impossível desenvolver esta pesquisa.
Referências
BORK, Alfred M. Maxwell and the vector potential. Isis, v. 58, p. 210-222, 1967.
BROWN, Harvey R.; MARTINS, Roberto de A. De Broglie’s relativistic phase waves and waves groups. American Journal of Physics, v. 52, p. 1130-1140, 1984.
DARRIGOL, Olivier. Strangeness and soundness in Louis de Broglie’s early works. Physis: Rivista Internazionale di Storia della Scienza, v. 30, p. 303-372, 1993.
DE BROGLIE, Louis. Ondes et quanta. Comptes Rendus de l’Académie des Sciences de Paris, 177, 507-510, 1923a.
______. A tentative theory of light quanta. Philosophical Magazine, v. 47, p. 446-458, 1924a.
______. Les quanta, la théorie cinétique des gaz et le principe de Fermat. Comptes Rendus de l’Académie des Sciences de Paris, 177, 630-632, 1923c.
______. Quanta de lumière, diffraction et interférences. Comptes Rendus de l’Académie des Sciences de Paris, v. 177, p. 548-550, 1923b.
______. Recherches sur la théorie des quanta. Annales de Physique, series 10, v. 3, p. 22-128, 1925.
______. Sur la définition générale de la correspondance entre onde et mouvement. Comptes Rendus de l’Académie des Sciences de Paris, v. 179, p. 39-40, 1924b.
______. Sur un théorème de M. Bohr. Comptes Rendus de l’Académie des Sciences de Paris, v. 179, p. 676-677, 1924c.
______. Thèses: recherches sur la théorie des quanta. Paris: Masson, 1924d.
______. Waves and quanta. Nature, v. 112 , p. 540, 1923d.
HANLE, Paul A. Erwin Schrödinger’s reaction to Louis de Broglie’s thesis on the quantum theory. Isis, v. 68, p. 606-609, 1977.
______. The Schrödinger-Einstein correspondence and the sources of wave mechanics. American Journal of Physics, v. 47, p. 644-648, 1979.
HEITLER, Walter. Erwin Schrödinger, 1887-1961. Biographical Memoirs of Fellows of the Royal Society, v. 7, p. 221-228, 1961.
JAMMER, Max. The conceptual development of quantum mechanics. New York: MacGraw-Hill, 1966.
KRAGH, Helge. Erwin Schrödinger and the wave equation: the crucial phase. Centaurus, v. 26, p. 154-197, 1982.
______. Equation with the many fathers. The Klein-Gordon equation in 1926. American Journal of Physics, v. 52, p. 1024-1033, 1984.
MARTINS, Roberto de A. Teoria da relatividade especial. Campinas: Grupo de História e Teoria da Ciência, 2008.
MEHRA, Jagdish; RECHENBERG, Helmut. The historical development of quantum theory. New York: Springer, 1982-1987. 5 v.
MOORE, W. J. Schrödinger: life and thought. Cambridge: Cambridge University, 1989.
RAMAN, V. V.; FORMAN, Paul. Why was it Schrödinger who developed de Broglie’s ideas? Historical Studies in the Physical Sciences, v. 1, p. 291-314, 1969.
REGT, Henk W. de. Erwin Schrödinger, Anschaulichkeit, and quantum theory. Studies in History and Philosophy of Modern Physics, v. 28, p. 461-481, 1997.
ROSA, Pedro Sérgio. Louis de Broglie e as ondas de matéria. Dissertação de Mestrado em Física. Campinas: Universidade Estadual de Campinas, 2004.
SCHRÖDINGER, Erwin. Collected papers on wave mechanics. London; Glasgow: Blackie & Son, 1929.
______. Quantisierung als Eigenwertproblem (Erste Mitteilung). Annalen der Physik, series 4, v. 79, p. 361-376, 1926a.
______. Quantisierung als Eigenwertproblem (Zweite Mitteilung). Annalen der Physik, series 4, v. 79, p. 489-527, 1926b.
WHEATON, Bruce R. The tiger and the shark: empirical roots of wave-particle dualism. London: Cambridge University, 1983.