Ontologia de Fourier, análise local por onduletas e Física Quântica
1 Breve nota sobre a complementaridade
Em linhas gerais, no plano teórico da Física clássica, imperam duas imagens dissimilares, a onda e o corpúsculo. Uma onda pode ser definida como uma flutuação num meio e associadas a ela estão noções como o comprimento de onda, frequência de vibração e interferência. Por outro lado, na Física clássica, um corpúsculo pode ser reduzido a um ponto, correspondendo ao seu centro de massa, sobre o qual se associam noções como as de posição, momento linear e trajetória. À onda, liga-se a noção do contínuo; ao corpúsculo, a do discreto. Um exemplo de objeto físico estudado a partir da concepção ondulatória seria a luz visível. No caso corpuscular, pode-se referir às bolas de uma mesa de bilhar. Enquanto os fenômenos ondulatórios são descritos eficazmente pelo Eletromagnetismo de Maxwell, os fenômenos corpusculares são descritos eficazmente pela Mecânica Newtoniana.
Assim, no contexto acima descrito, a partir do momento em que se estuda um determinado sistema físico, geralmente tem-se em mente essas distinções e identifica-se o plano teórico a ser utilizado na abordagem do problema. No caso de se estar envolvido com o estudo de corpúsculos, por exemplo, pode-se modificar o sistema das maneiras mais variadas possíveis, sem que nada ponha em dúvida o plano teórico a ser utilizado1. Isso significa que, classicamente, um objeto físico comporta-se como uma onda ou como um corpúsculo, nunca como ambos, simultaneamente. Além disso, após a identificação de uma das concepções, não se faz necessário considerar a outra ao se estudar, futuramente, os fenômenos envolvendo aquele mesmo objeto físico.
Entretanto, no nível dos fenômenos da Física Quântica2, o panorama clássico acima delineado se altera radicalmente3. É bem sabido que o edifício da Teoria Quântica ortodoxa, ou Escola de Copenhague, está fundamentado, sobretudo no pensamento de Niels Bohr, expresso pelo princípio da complementaridade. (JAMMER, 1974) No tipo de complementaridade onda/corpúsculo, a descrição de um sistema envolvendo uma mesma entidade quântica invoca as duas imagens clássicas de forma excludente, porém complementar. Ou seja, as imagens onda e corpúsculo são necessárias quando se estuda os mesmos objetos quânticos em situações distintas. Assim, diferentemente da Física Clássica, onde geralmente pode-se sugerir que um objeto físico tenha uma essência de onda ou de corpúsculo, quanto ao objeto quântico somos confrontados com um dilema: a dualidade onda/corpúsculo. Matematicamente, estas noções conceituais encontraram uma correspondência com a Análise de Fourier, cujo formalismo incorpora resultados fundamentais para a Teoria Quântica Ortodoxa, nomeadamente as conhecidas Relações de Heisenberg.
2 Análise de Fourier, Teoria Quântica ortodoxa e relações de Heisenberg
Em abril de 1928, Niels Bohr publicou um artigo em que deixou sutilmente marcada a importância que a Análise de Fourier tem para a Teoria Quântica ortodoxa. Naquele artigo, inicialmente, Bohr recorreu às fórmulas fundamentais da teoria dos quanta de luz (Relação de Planck) e das partículas materiais (Relação de Louis De Broglie):
Eτ = pλ = h |
(2.1) |
onde h denota a constante de Planck; E e p são a energia e o momento linear; τ e λ são o período de vibração e o comprimento de onda.4 Partindo desta fórmula, Bohr destacou a relação complementar entre os aspectos corpusculares e ondulatórios ao ter afirmado que:
In these formulae the two notions of light and also of matter enter in sharp contrast. While energy and momentum are associated with the concept of particles, and hence may be characterized according to the classical point of view by definite space-time co-ordinates, the period of vibration and wave-length refer to a plane harmonic wave train of unlimited extent in space and time. (BOHR, 1928, p. 581)
Após referir os tijolos básicos da Análise de Fourier, isto é, as ondas planas harmônicas monocromáticas, Bohr começa a refletir sobre o problema da extensão infinita de tais objetos no espaço. Assim, indica o princípio da superposição com o objetivo de compor um pacote de ondas ou, segundo a sua terminologia, um campo de ondas (wave fields). Um pacote de ondas, então, seria uma representação matemática de uma “entidade quântica”. A ideia que se quer deixar sublinhada aqui é a de que, para além do seu processo estritamente matemático de composição e decomposição de funções, a Análise de Fourier, na Teoria Quântica ortodoxa, foi promovida por Bohr a um estatuto ontológico com profundas implicações para a Física. Por isso, sugere-se chamar a concepção aqui envolvida por ontologia de Fourier. Este resultado importante torna-se claro no artigo mencionado, quando é considerada, como exemplo, a seguinte onda elementar:
ACos[2π(vt - xk x - yky - zk z + δ)] |
(2.2) |
onde A e δ são a amplitude e a fase inicial da onda respectivamente,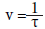 
é a frequência e kx, k y, k z são as frequências espaciais5 na direção dos eixos de coordenadas. Assim, mais adiante à fórmula (2.2) Bohr prossegue no artigo com a afirmação enfática: Rigorously speaking, a limited wave-field can only be obtained by the superposition of a manifold of elementary waves corresponding to all values of v and σx, σy, σz (BOHR, 1928, p. 581). Ou seja, dizer que, rigorosamente, as já mencionadas ondas elementares, e somente elas, são o caminho de se obter um pacote de ondas, é equivalente a afirmar que, nessa abordagem, as ondas planas harmônicas são as únicas que podem ter uma frequência pura (frequência espacial k e frequência temporal v).
Para a representação de uma certa “entidade quântica” (ver Figura 1, à direita), utiliza-se uma sobreposição de várias ondas planas, associadas a uma certa distribuição para a frequência espacial k. Formalmente, uma tal composição é descrita através de uma integral (um tipo especial de soma), envolvendo vários valores da frequência espacial k. Esta integral representa o que se costuma chamar por Transformada de Fourier e permite realizar uma correlação entre o espaço físico em questão (variável x) e o espaço de Fourier (variável k). Ou seja, a Transformada de Fourier e a Transformada Inversa de Fourier realizam uma correlação entre os pares de variáveis conjugadas x e k. O esquema a seguir pretende sintetizar esta noção, ou seja, a passagem recíproca de um espaço para o outro.
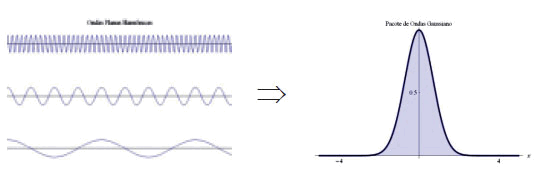
Figura 1 – Esboço gráfico explicitando a relação entre um pacote de ondas localizado e as suas ondas planas harmônicas constituintes.
Além do caráter não-local do formalismo, uma outra sutileza merece ser contrastada com o senso comum clássico. A cada uma das ondas planas harmônicas da Figura 1 à esquerda, está associada uma energia (ver as fórmulas 2.1 e 2.2). Portanto, como um pacote de ondas enfeixa uma multiplicidade de ondas elementares, ele terá uma multiplicidade de energias. Mais uma vez, ao se tentar interpretar as consequências disso através de uma concepção realista clássica, acaba-se por pensar uma “entidade quântica” como um objeto ao qual está associada, num mesmo instante, uma infinidade de energias.
Feitas essas breves notas sobre algumas das implicações a que o pensamento da Escola de Copenhague pode conduzir, um último resultado fundamental deve ser incisivamente vincado: as chamadas Relações de Heisenberg. É bem sabido que tais relações se apresentam na forma de desigualdade (fórmula 2.5) e que a sua derivação relaciona-se com a Transformada de Fourier. No caso em que se supõe uma distribuição gaussiana para as frequências espaciais k, a relação encontra o seu valor mínimo. Ou seja, a Transformada de Fourier de uma Gaussiana é também uma Gaussiana. Em consequência desse resultado, encontra-se uma relação para a largura a meia altura da distribuição nos espaços envolvidos dada a seguir:
A síntese e a análise da Transformada de Fourier explicitam uma reciprocidade entre as larguras das representações funcionais nas variáveis conjugadas x e k. Este exemplo simples refere-se ao caso particular ideal da distribuição gaussiana. Na versão geral das relações de Heisenberg tem-se:
| ΔxΔk > 1 | (2.5) |
Se a relação de Louis De Broglie (2.1) for utilizada em Δk, obtem-se uma relação com o momento linear associado à direção x. A inequação (2.5) define uma fronteira abaixo da qual não há, teoricamente, valores simultâneos permitidos (ver Figura 2). Ou seja, não se consegue ter uma previsão teórica simultaneamente de um resultado que será obtido por uma futura medição sobre a posição e a velocidade de uma partícula, com uma precisão que se situe fora do Espaço de Heisenberg.
3 A análise de onduletas
Ao contrário da ontologia de Fourier, implicitamente assumida por Bohr (1928), será considerada, a partir desta seção, a descrição da Análise de Onduletas (CROCA, 2003). Com esta consideração, pretende-se atingir dois objetivos. Em primeiro lugar, utilizar uma abordagem não linear suportada na Análise de Onduletas. Em segundo, mostrar como tal descrição causal corresponde a toda uma nova concepção sobre a natureza dos objetos quânticos, inspirando-se, em parte, na Teoria da Dupla Solução de Louis De Broglie. Para além desta conexão histórica com a Teoria da Dupla Solução, a Análise de Onduletas é um instrumento formal poderoso que permite auxiliar no tratamento de uma Teoria Quântica Causal Não Linear. Esta descrição da realidade quântica é totalmente distinta da proposta causal, não local e linear, devida ao célebre físico David Bohm (1983). No caso da proposta de Bohm, o formalismo utilizado pressupõe a conhecida equação de Schrödinger, enquanto que na teoria causal e local a ser introduzida aqui a abordagem matemática se sustenta no pressuposto da não-linearidade.
O formalismo da Análise de Onduletas ganhou impulso na década de 1980, sendo utilizado na Geofísica como ferramenta teórica no auxílio à prospecção de petróleo. Este ramo da Matemática muito se alargou, tendo sido aplicado em uma enorme variedade de áreas e dispondo de redefinições e propriedades bastante específicas para cada caso. (CHUI, 1992; HUBBARD, 1998) É importante sublinhar que serão utilizadas aqui informações que se restringem aos objetivos traçados.
Em linhas gerais, uma onduleta é uma onda localizada. Como objeto matemático, caracteriza-se por parâmetros de dilatação e de translação, devendo cumprir com algumas restrições matemáticas. Fisicamente, tal objeto presume a existência de uma onda finita com uma frequência bem definida, diferentemente da Análise de Fourier, onde as ondas de frequências bem definidas são as ondas planas harmônicas monocromáticas, infinitas nos domínios espacial e temporal.
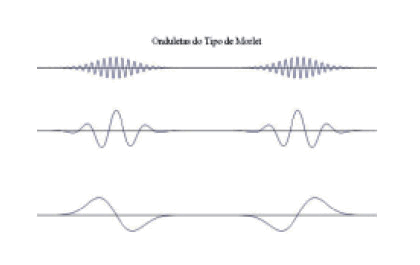
De forma a satisfazer os interesses aqui envolvidos, como exemplo de uma onduleta, será referida a Onduleta de Morlet. Entretanto, o raciocínio é extensivo para outros casos. A Onduleta de Morlet é caracterizada por uma frequência espacial k0 e por uma largura, ou parâmetro de dilatação, σ. Em contraste com a Figura 1 à esquerda, que mostra três casos de ondas planas harmônicas, as representações da Figura 3 ilustram a parte real de algumas Onduletas de Morlet (isto é, para três casos da frequência k0).
Percebe-se com a Figura 3 um forte contraste com a ontologia de Fourier. Invocando novamente uma interpretação realista, desta vez para as onduletas, estas ferramentas matemáticas, por si sós, pretendem descrever alguns aspectos, de forma objetiva, característicos dos fenômenos quânticos. Contrariamente, na Análise de Fourier, um pacote de ondas, como propôs Bohr (1928), seria representado por uma superposição de infinitas ondas planas harmônicas. Dentre os aspectos caracterizadores das onduletas, fica explícita a localidade. É certo que existe uma região σ dentro da qual a presença da onduleta é significativa. Entretanto, fora dessa região, referir uma não-localidade infinita como inerentemente a Análise de Fourier o faz, não tem, agora, qualquer sentido. Assim, a um deslocamento de tal entidade quântica, na concepção das onduletas, não há implicações no nível global do espaço (salvo o intervalo σ onde a sua presença é significativa). Um outro contraste com a ontologia de Fourier diz respeito à energia associada a uma entidade quântica. Nela, um pacote de ondas se associa a uma infinidade de energias, cada qual relacionada com uma das suas ondas elementares constituintes. Na nova abordagem causal e não-linear, rompe-se com a ontologia de Fourier e assume-se que uma onda finita, a onduleta-mãe, pode ter uma energia bem definida.
Um resultado teórico fundamental deriva da propriedade de dilatação das onduletas, permitindo um relacionamento formal com as ondas planas harmônicas. Ou seja, quando σ, o parâmetro de dilatação, tende ao infinito, a Onduleta de Morlet tende a uma onda plana harmônica. Nesse sentido, pode-se pensar, formalmente, as ondas planas harmônicas como casos particulares das Onduletas de Morlet, no limite extremo (σ → ∞).
Efetivamente, em Análise de Onduletas se sobrepõe um conjunto de funções-base, ou seja, de onduletas-mãe. No presente caso, a base utilizada é composta por Onduletas de Morlet. Assim, enquanto no caso da Teoria Quântica ortodoxa tem-se uma sobreposição de ondas planas harmônicas, a formar um pacote de ondas, na Análise de Onduletas tem-se um conjunto de entidades localizadas num dado intervalo espacial (as Onduletas de Morlet), a formar um pacote de onduletas.
Na concepção da Transformada de Onduletas, tem-se nas mãos uma ferramenta, a fim de se descrever uma estatística para um ensemble de onduletas, condicionado a uma dada distribuição. Com o objetivo de realizar um estudo comparativo com os resultados obtidos pela Teoria Quântica ortodoxa ao representar o pacote de ondas, convém assumir6 a mesma distribuição gaussiana das frequências espaciais g(k), caracterizada com uma largura a meia altura dada por Δk. Se isso for feito, em comparação com a expressão (2.4), obtém-se:
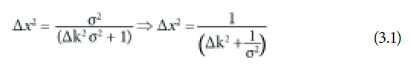
Essa expressão indica uma relação que contém, do ponto de vista formal, a Relação de Heisenberg como um caso particular. Contudo, do ponto de vista interpretativo, ambas as relações, (2.4) e (3.1), diferem bastante, como vem sendo exposto. Nota-se que quando o parâmetro de dilatação σ da Onduleta de Morlet tende ao infinito, a relação entre Δx e Δk tende, formalmente, à Relação de Heisenberg. Um esboço claro desse resultado é mostrado nos gráficos a seguir (Figura 4):
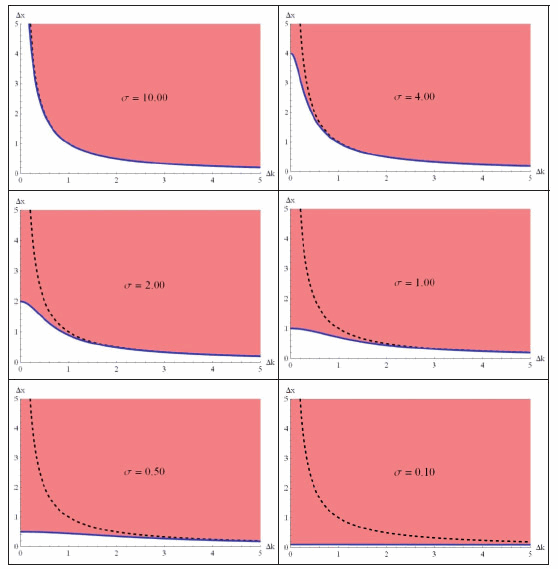
Figura 4 – Gráficos comparativos entre as Relações de Heisenberg (curva em pontilhado) e as relações mais gerais de incerteza (curva contínua).
Essa generalização permite obter uma nova previsão teórica para a distribuição das medidas sobre um conjunto de onduletas e que depende do tamanho σ da respectiva Onduleta de Morlet utilizada (a onduleta-mãe). A nova previsão teórica preenche toda a região anteriormente proibida pelas Relações de Heinsenberg. Quanto menor for o tamanho σ da onduleta-mãe, menor é a incerteza Δx para qualquer valor de Δk. Na ontologia de Fourier, o limite na precisão de grandezas conjugadas não pode ser alterado, visto que se assume o formalismo da Análise de Fourier e das ondas planas harmônicas, que são independentes do parâmetro de dilatação σ. Esses resultados reforçam ainda mais o quão necessária é a Análise de Fourier dentro de todo o pensamento da Teoria Quântica Ortodoxa.7
4 Uma alternativa não-linear
Como foi visto na seção anterior, a descrição por ondas finitas, onduletas, conduz a uma mudança conceitual distinta daquela relacionada com a ontologia de Fourier proposta por Niels Bohr. Tal consideração implica na adoção de um novo compromisso ontológico e requer uma nova formulação, descontinuada do plano teórico da Teoria Quântica Ortodoxa. Serão apresentados aqui alguns aspectos gerais de um plano teórico alternativo àquele e que encontra um traço inicial comum com algumas ideias relacionadas à Teoria da Dupla Solução de Louis De Broglie (1964).
Como se sabe, o modelo causal para uma partícula quântica proposto por De Broglie é caracterizado por uma parte estendida, representando os aspectos ondulatórios, e por uma espécie de singularidade, representando os aspectos corpusculares. Neste ponto há uma distinção fundamental com relação à noção da complementaridade do tipo onda/corpúsculo desenvolvida por Bohr. Se naquela concepção, em última análise, um fenômeno seria corpuscular ou ondulatório, na concepção da Dupla Solução, em essência, um fenômeno apresenta um comportamento, simultâneo, ou seja, corpuscular e ondulatório. Assim, pode-se sugerir que à perspectiva complementar de Bohr corresponderia uma perspectiva integrada de Louis De Broglie. Não faz parte deste artigo, porém, descrever em detalhes a Teoria da Dupla Solução. A sua citação aqui tem uma importância histórica, ao indicar em quais noções gerais a nova abordagem, causal e não-linear, encontra inspiração. (CROCA, 2003)
Nesta nova concepção da Física Quântica, uma partícula ϕ tem propriedades, essencialmente, de onda e de corpúsculo. Os aspectos ondulatórios de tal “entidade quântica” são representados por uma onduleta θ, theta, associada a uma energia praticamente desprezível. O corpúsculo ξ, denominado acron, possui uma dada energia localizada numa pequena região. Assim, a entidade quântica integral, ϕ, poderia ser representada matematicamente pela expressão:
A onda física finita, representada por uma onduleta θ, constitui uma espécie de onda-guia sobre a qual o acron se desloca. Um caminho heurístico (CROCA, 2003), para propor uma Equação Mestra Não-Linear que descreva os processos envolvidos com as onduletas, baseia-se na consideração de duas equações clássicas: a Equação de Hamilton-Jacobi e a Equação da Continuidade. Com essas equações garante-se a presença formal simultânea dos dois aspectos fundamentais: o corpuscular e o ondulatório. Se a equação de Hamilton-Jacobi relaciona-se com as propriedades de localização das partículas clássicas, a equação da Continuidade, por sua vez, refere-se às propriedades extensas dos fluidos. A partir desse sistema de equações, consegue-se obter uma Equação Mestra Não Linear em contraste com a célebre Equação de Schrödinger.
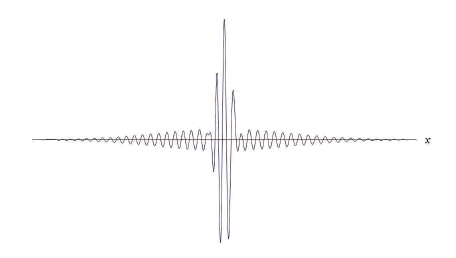
Um resultado importante que pode ser derivado da Equação Mestra Não Linear diz respeito ao caso da partícula livre (tomando o potencial nulo). Como se sabe, a equação de Schrödinger não produz soluções de estados coerentes. No caso da dinâmica descrita pela Equação Mestra Não Linear, este fato não apresenta dificuldades. Mostra-se (CROCA, 2003) que uma solução para o caso em questão, unidimensional, é dada pela Onduleta de Morlet. Uma visualização gráfica da parte real de tal solução pode ser encontrada na Figura 5.
Com vista nesse tipo de soluções, pode-se sugerir um modelo para partícula quântica, ϕ, levando-se em conta a fórmula (4.1). Tal modelo é constituído por uma parte ondulatória (a onduleta guia θ, ou onda theta) e por uma parte corpuscular ξ (o acron). Pressupõe-se, porém, que o corpúsculo possui uma amplitude muito grande relativamente à amplitude da onduleta. Além disso, o corpúsculo estaria concentrado numa região muito mais localizada do que θ.
Uma solução desse tipo incorpora as duas imagens clássicas essenciais: a onda e o corpúsculo. De maneira simultânea, os aspectos de localização e de extensão são traduzidos neste modelo. A Figura 6 dá uma ideia visual de ambos os aspectos, incorporados num único objeto matemático.
Uma extensão desse modelo para uma entidade quântica pode ser realizada para duas dimensões. A Figura 7 fornece um gráfico 3D para este caso.
A experiência da fenda dupla revisitada
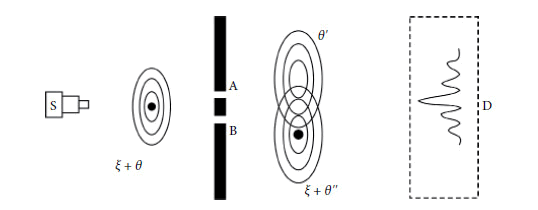
Após esta proposta expositiva sobre uma possível descrição matemática de uma entidade quântica, pode-se também realizar uma explicação intuitiva de experimentos tradicionais da Física Quântica, levando-se em consideração a natureza complexa das partículas quânticas. Partindo-se do pressuposto do modelo dado por (4.1), considera-se a célebre experiência da Fenda Dupla (Figura 8). Neste experimento, antes de encontrar as duas fendas, a entidade, emitida por uma fonte S, é representada por um corpúsculo (o acron ξ, simbolizado na figura por um pequeno círculo preenchido) e por sua onduleta- guia (a onda theta, θ, simbolizada pelas linhas de níveis em torno do acron). No instante em que a entidade encontra as duas fendas, a onda θ, estendida espacialmente, é dividida em duas parcelas (θ' e θ''), atravessando, simultaneamente, as duas fendas A e B. Entretanto, ao acron, como entidade localizada, há duas opções: ou prosseguir pela fenda A ou pela fenda B (na Figura 8 escolheu-se o caminho B como ilustração). Em qualquer uma dessas opções, o acron propaga-se com uma onda-guia associada (por exemplo, a onda θ''). Em contrapartida, a onda θ', resultante da fenda A, é uma onda theta vazia, no sentido de ser uma entidade desprovida de acron. As duas parcelas θ' e θ'' se sobrepõem no espaço. Tal sobreposição, construtiva numas regiões e destrutiva em outras, cria as condições de propagação sobre o acron, através de processos não-lineares. O acron atinge pontualmente o detector D e, após esse processo ser realizado um número suficiente de vezes, verifica-se, progressivamente, a formação do padrão de interferência.
Uma observação sobre um detalhe sutil nesse experimento acaba por sugerir uma forma para se distinguir entre a perspectiva causal e local e a perspectiva ortodoxa. Na Teoria Quântica Ortodoxa, como se sabe, esse experimento é explicado considerando-se, após as duas fendas, uma função de onda total composta pelas funções de onda ΨA e ΨB, associadas a cada uma das fendas A e B. Se dois detectores forem postos na saída de cada fenda, após uma detecção (por exemplo, no detector associado à fenda B), há um colapso da função de onda total. Neste caso, a probabilidade de se encontrar ΨA é nula. Em contraste com essa interpretação, na perspectiva causal e local, a ideia gira em torno do fato de que as ondas θ são entidades físicas com uma existência independente do acron. Logo, mesmo que uma detecção na fenda B seja realizada, o modelo supõe a existência de alguma entidade física (uma onda θ') com energia praticamente desprezível a se propagar através da fenda A.
Essa conclusão sugere a construção de aparatos experimentais que são denominados geradores de ondas theta. Na literatura, alguns trabalhos já foram publicados contendo discussões teóricas e realizações experimentais sobre essa temática. Para maiores detalhes sobre outros tipos de experimentos de geração ou de detecção de ondas theta, sugere-se ver principalmente Croca (2003); também Croca (1988), Croca e outros (1990, 1997) e Araújo e outros (2009a, 2009b).
Referências
ARAÚJO, J. et al. A causal and local interpretation of experimental realization of Wheeler’s delayed-choice Gedanken experiment. Apeiron, v. 16, n. 2, p. 179-190, 2009a.
______. Some experiments that question the completeness of orthodox quantum mechanics. Advanced Science Letter, v. 2, n. 4, p. 481-487, 2009b.
BOHM, D. Quantum theory. New York: Prentice-Hall, 1955.
______. Wholeness and the implicate order. London: Routledge, 1983.
BOHR, N. The quantum postulate and the recent development of atomic theory, Atomic Theory and the Description of Nature. Nature, v. 121, p. 580-590, 1928.
CHUI, C. K. An Introduction to wavelets. San Diego: Academic Press, CA, 1992.
Croca, J. R. Can the existence of de Broglie’s empty wave be proven experimentally? In: MERWE, A. et al. (Ed.). Microphysical Reality and Quantum Formalism. Dordrecht: Kluwer Academic, 1988.
______. Counter examples to the general validity of heisenberg uncertainty relations. Hadronic Journal, v. 22, p. 29-39, 1999a.
______. Towards a nonlinear quantum physics. London: World Scientific, 2003.
______. The uncertainty relations. Apeiron, v. 6, n. 3-4, p. 151-165, 1999b.
CROCA, J. R. et al. Quantum-optical predictions for an experiment on de Broglie waves detection. Found. Phys. Lett., v. 3, p. 557-564, 1990.
______. An experiment to test the reality of de Broglie waves. Found. Phys. Letters, v. 10, p. 441-447, 1997.
DE BROGLIE, L. The current interpretation of wave mechanics: a critical study. Amsterdam: Elsevier, 1964.
FALKENBURG, B. Particle Metaphysics: a critical account of subatomic reality. Heidelberg: Springer, 2007.
GUERET, P.; VIGIER, J. P. Lett. Nuovo Cimento, v. 38, p. 125-128, 1983.
HUBBARD, B. B. The world according to wavelets: the story of a mathematical technique in the making. 2nd. Massachusetts: AK Peters Wellesley, 1998.
JAMMER, M. The philosophy of quantum mechanics: the interpretations of quantum mechanics in historical perspective. New York: John Wiley & Sons, 1974.
MOREIRA, R. N. Instrumentalismo versus realismo - A crise na física do século XX. In: POMBO, O.; NEPOMUCENO, A. (Ed.). Lógica e filosofia da ciência. Lisboa: Centro de Filosofia das Ciências da Universidade de Lisboa, 2008. p. 121-170.
PESSOA JR., O. Conceitos de física quântica. São Paulo: Livraria da Física, 2005. v. 1
SILVA, A. Rica da et al. Nonlinear Schrödinger equation, Burger’s equation and superposition of solutions. In: JEFFERS, S. et al. (Ed.). Causality and locality in modern physics andaAstronomy. Dordrecht: Kluwer Academic, 1998. p. 421-430.
SILVA, J. Andrade e. Introdução à física moderna. Lisboa: Associação dos Estudantes da Faculdade de Ciências de Lisboa, 1995.