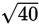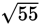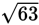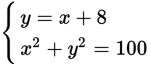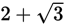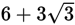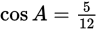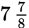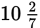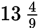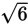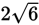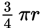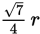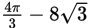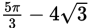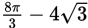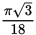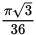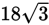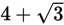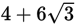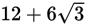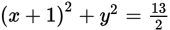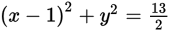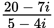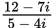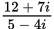Practice Questions
The following test-like questions provide an opportunity to practice Additional Topics in Math questions. The calculator icon means you are permitted to use a calculator to solve a question. It does not mean that you should use it, however.
-
A cannon is fired at a target that is placed at the edge of a cliff, as shown below. The angle of elevation from the cannon to the target is 52°. If the distance between the base of the cliff and the cannon is 200 feet, which expression could be used to approximate the distance between the cannon and the target?

- 200 sin 52°
-

-

-
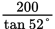
-
The longer leg of a right triangle is three times the length of the shorter leg. Given that the length of each leg is a whole number, which of the following could be the length of the hypotenuse?
-
-
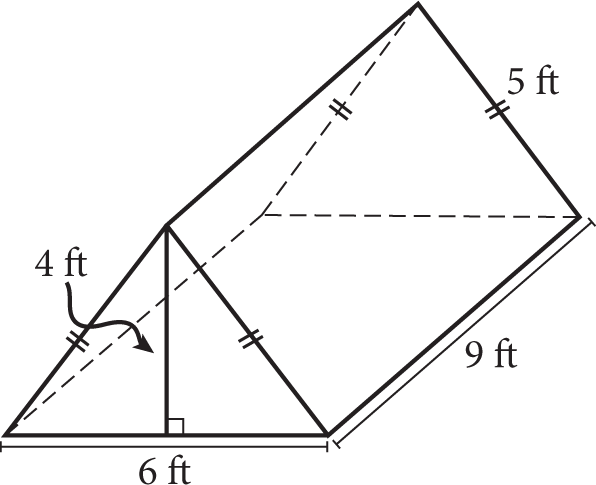
The figure above represents a camping tent that will be sprayed using a waterproofing agent. If it takes 1 ounce of the agent to cover 3 square feet, how many ounces will it take to spray the entire tent, inside and outside, including the tent bottom and its front door flaps?
- 56
- 112
- 168
- 336
-
Which of the following is NOT equal to i 25 ? (Note:
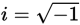 .)
.)- i 9
- i 17
- i 35
- i 49
-
Which angle has the smallest measure in the figure above?
- Angle A
- Angle B
- Angle C
- All three angles have equal measures.
-
Crude oil is being transferred from a full rectangular storage container with dimensions 4 meters by 9 meters by 10 meters into a cylindrical transportation container that has a diameter of 6 meters. What is the minimum possible length for a transportation container that will hold all of the oil?
- 40π
-

- 60π
-
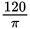
-
Rupert has a collection of Blu-ray discs he wants to store in a cubical box with edges of length 10 inches. If each Blu-ray has dimensions of 5 inches by 5 inches by
 inch, what is the maximum number of discs that can fit into the box?
inch, what is the maximum number of discs that can fit into the box?- 60
- 80
- 120
- 160
-
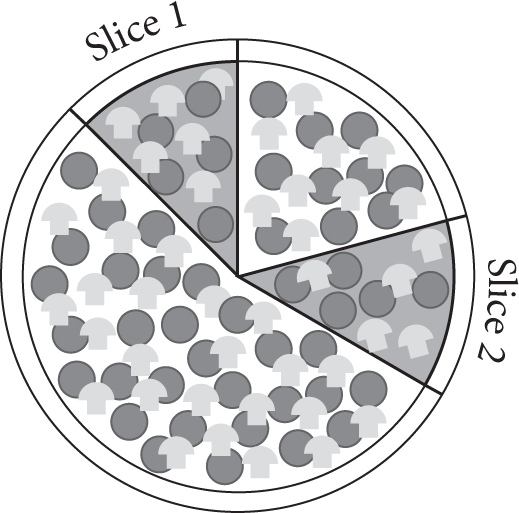
Four cuts are made from the center of a perfectly circular pizza to form Slice 1 and Slice 2. The arc lengths of the crusts of both slices are congruent. Which of the following statements regarding the two slices is true?
- The two slices may or may not be congruent, depending on the length of each side of each slice.
- The two slices may or may not be congruent, depending on the angle created by the cuts that were made.
- The two slices cannot be congruent because the side lengths of each slice cannot be the same length.
- The two slices must be congruent because the arc lengths are congruent and the side lengths of each slice are congruent.
-
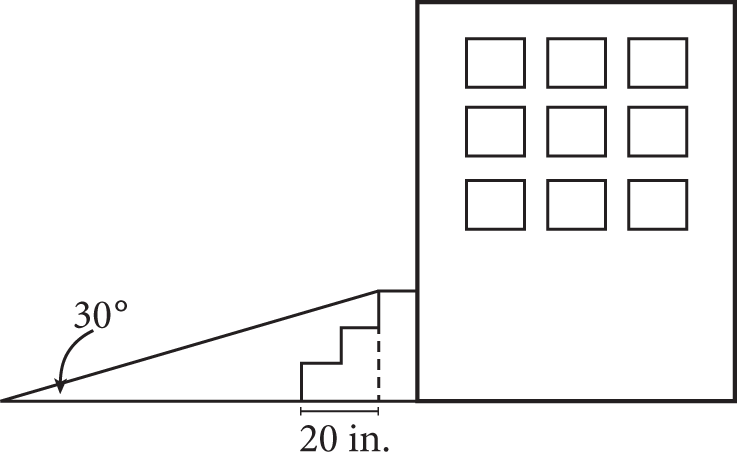
Note: Figure not drawn to scale.
A company designs removable handicapped-access ramps as temporary measures for buildings to become compliant with the Americans with Disabilities Act (ADA). The particular ramp shown in the figure must be placed at a 30° angle, eight feet from the bottom step. About how long, in inches, is the ramp? (There are 12 inches in 1 foot.)
- 67
- 116
- 128
- 134
-
One of the three most expensive cheeses in the world is a Swedish cheese made from moose milk, which sells for about $500 a pound. Suppose a moose cheesemaker produces his cheese in rectangular blocks, each with a volume of 576 cubic inches. Customers or restaurants can buy this cheese in increments of
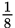 blocks. One day, a customer buys
blocks. One day, a customer buys
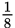 of a block and a restaurant buys
of a block and a restaurant buys
 of a block. If the height of a cheese block is always 8 inches and the width is always 6 inches, what is the difference, in inches, in the lengths of the two purchases?
of a block. If the height of a cheese block is always 8 inches and the width is always 6 inches, what is the difference, in inches, in the lengths of the two purchases?- 4.5
- 6
- 7.6
- 12
-
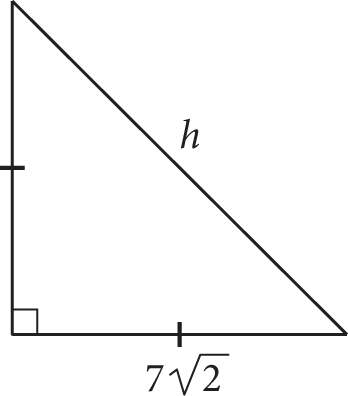
What is the value of h in the figure above?
- 3.5
- 7
- 12.5
- 14
-
If a + bi represents the complex number that results from multiplying 3 + 2i times 5 − i, what is the value of a ?
- 2
- 13
- 15
- 17
-
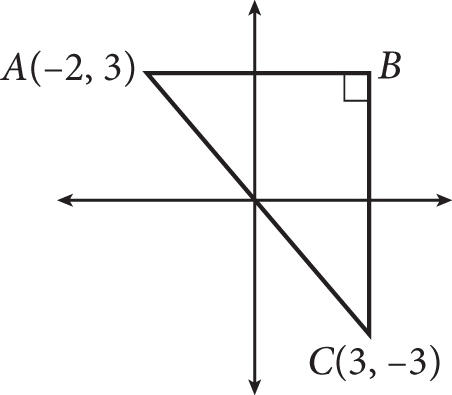
If the vertices of a right triangle have coordinates (−6, 4), (1, 4), and (1, −2), what is the length of the hypotenuse of the triangle?
- 7
- 8
-
-

-
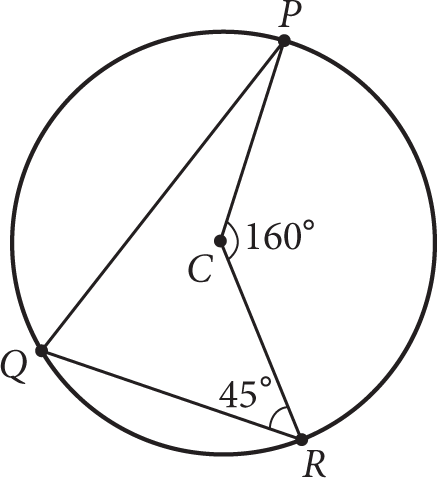
What is the measure of
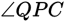 in the figure above?
in the figure above?- 25°
- 30°
- 35°
- 40°
-
A solid wood cube is cut perfectly in half diagonally from corner to corner, as shown above, to be used as chocks, which are wedges placed behind wheels of vehicles to prevent them from rolling. What is the volume in cubic inches of one of these chocks?
- 10
- 100
- 500
- 1,000
-
Which system of equations has no solution?
-
-
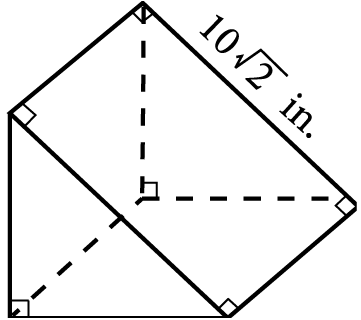
Triangle BED is similar to triangle COT. Triangle COT has side lengths of 8, 15, and 17. Which of the following could be the side lengths of triangle BED ?
- 3, 4, 5
- 5, 12, 13
- 10, 17, 19
- 24, 45, 51
-
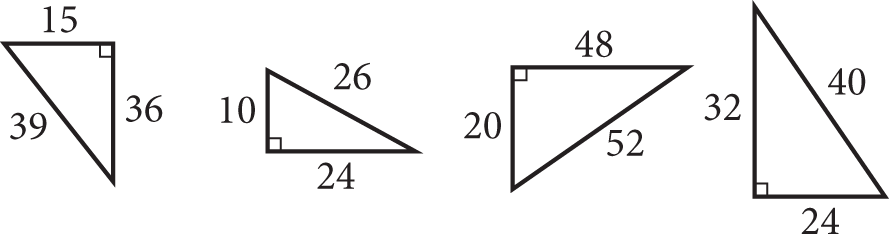
Note: Figures not drawn to scale. What is the area, in square units, of the triangle that is not similar to the other three?
- 120
- 270
- 288
- 384
-
The Washington Monument in Washington, D.C., is the world’s tallest obelisk-shaped building. The tall part of the monument is a rectangular prism-like shape that is wider at the bottom than it is at the top. At the very top of the monument, there is a regular pyramid with a square base that is 34.5 feet wide. If the volume of the pyramid top is 21,821.25 cubic feet, what is its height in feet?
- 6.1
- 18.3
- 55.0
- 210
-
The value of cos 40° is the same as which of the following?
- sin 50°
- sin(–40°)
- cos(–50°)
- cos 140°
-
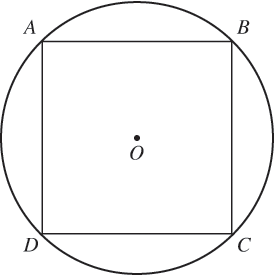
Square ABCD is inscribed in the circle with center O. If the area of the square is 64, what is the area of the circle?
- 8π
- 16π
- 24π
- 32π
-
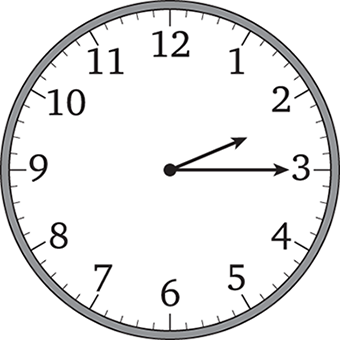
At 2:15, the short hand of an analog clock lines up exactly with the 11-minute tick mark, and the long hand lines up with the 15-minute tick mark. What central angle do the hands form at 2:15 ?
- 18°
- 20°
- 24°
- 28°
-
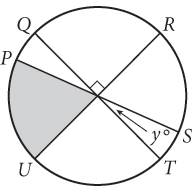
In the circle above,
 ,
,
 , and
, and
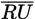 are diameters. If the shaded area is equal to
are diameters. If the shaded area is equal to
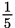 the area of the circle, what is the value of y ?
the area of the circle, what is the value of y ?- 12°
- 18°
- 30°
- 72°
-
Which of the following expressions is equivalent to (6 + 5i)3 ? (Note:
 .)
.)- 11 + 60i
- 216 – 125i
- –234 + 415i
- –3,479 + 1,320i
-
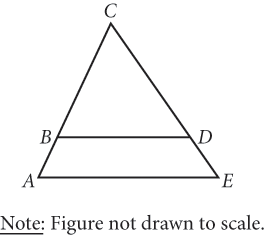
In the figure above,
 ∥
∥
 and
and
 = 6. If
= 6. If
 is twice
is twice
 , and
, and
 is 4 less than
is 4 less than
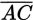 , then what is the length of
, then what is the length of
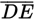 ?
?- 6
- 6.6
- 7
- 7.5
-
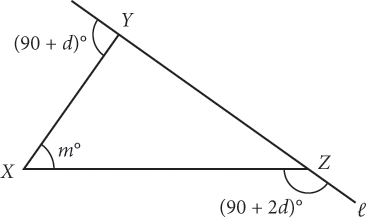
In the figure above, side
 of
of
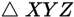 is on line l. What is m in terms of d ?
is on line l. What is m in terms of d ?-
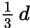
- d
- 3d
- 180 – d
-
-
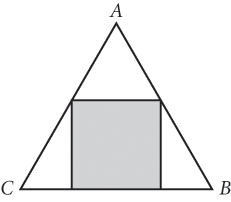
In the figure above, the shaded region is a square of area 3, and ΔABC is equilateral. What is the perimeter of ΔABC ?
-
-
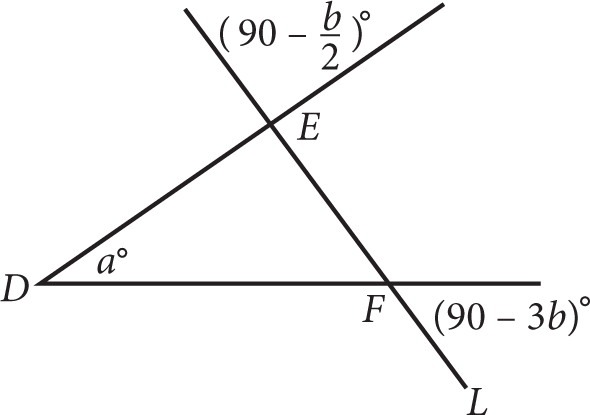
In the figure above,
 of ΔDEF is on line L. What is a in terms of b ?
of ΔDEF is on line L. What is a in terms of b ?- 3b
-

-

- 180 − b
-

Note: Figure not drawn to scale.
In the figure above, if lines j and k are parallel, which of the following statements must be true?
- a = e
- b = c
- d = 180 − c
- b + d − c = e
-

The equation of line L shown above is
 . Given that angle A
is the acute angle formed by the intersection of line L and the y-axis (marked
on the triangle), which expression could be used to find the measure of angle A ?
. Given that angle A
is the acute angle formed by the intersection of line L and the y-axis (marked
on the triangle), which expression could be used to find the measure of angle A ? -
-
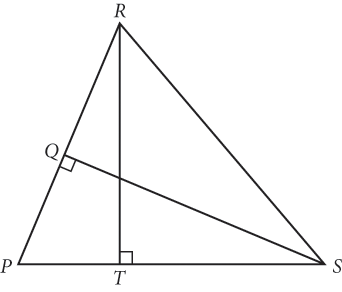
In ΔPRS above,
 is the altitude to side
is the altitude to side
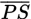 , and
, and
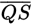 is the altitude to side
is the altitude to side
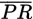 . If
. If
 = 7,
= 7,
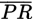 = 8, and
= 8, and
 = 9, what is the length of
= 9, what is the length of
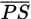 ?
? -
-
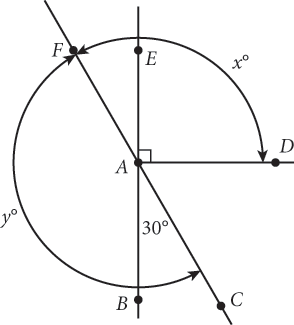
In the figure above,
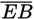 ,
,
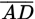 , and
, and
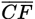 intersect at point A; and
intersect at point A; and
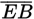 is perpendicular to
is perpendicular to
 . What is the value of
. What is the value of
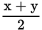 ?
?- 75
- 120
- 135
- 150
-
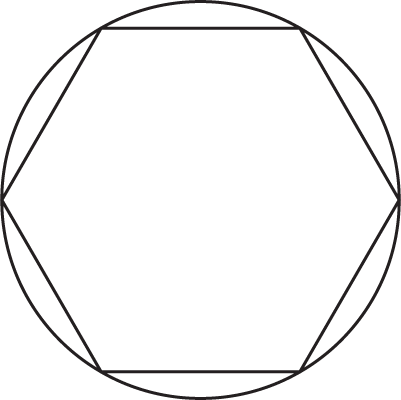
Holly is designing a kaleidoscope for a friend’s birthday gift. To the body of the kaleidoscope, she plans to arrange six identical rectangular mirrors in the shape of a hexagon inside a right cylindrical casing that is open on both ends. A cross section of the interior is shown above. If the casing is 30.5 centimeters in length and has a surface area of 61π centimeters2, what is the distance, in centimeters, between the centers of two parallel mirrors?
-
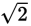
-
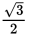
-

- 2
-
-
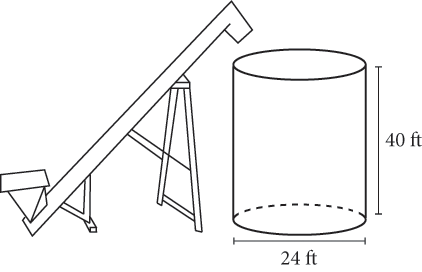
Note: Figure not drawn to scale.
A soybean distributor is filling the cylindrical grain bin shown above with dry soybeans using an auger conveyor. The conveyor can move 5,500 dry bushels of soybeans per hour. About how long will it take to fill 75% of the grain bin given that 1 dry bushel is equal to 1.24 cubic feet?
- 2 hours
- 2 hours, 40 minutes
- 3 hours, 15 minutes
- 4 hours
-
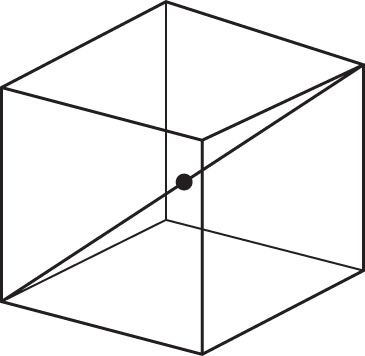
Each edge of the cube shown above measures
 centimeters. What is the distance, in centimeters, from a vertex of this cube to its center?
centimeters. What is the distance, in centimeters, from a vertex of this cube to its center? -
-
A basic megaphone is a truncated cone; that is, a cone with its apex (pointed end) removed. Suppose the openings (ends) of a megaphone have diameters of 2 inches and 10 inches. If the original cone from which the megaphone was created had a height of 20 inches, what is the volume, in cubed inches, inside the megaphone?
- 150π
-
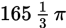
- 496π
-

-
It is given that sin A = k, where A is an angle measured in radians and
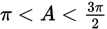 . If sin B = k, which of the following could be the value of B ?
. If sin B = k, which of the following could be the value of B ?- A − π
- π + A
- 2π − A
- 3π − A
-

As shown in the figure above, a lifeguard sees a struggling swimmer who is 40 feet from the beach. The lifeguard runs 60 feet along the edge of the water at a speed of 12 feet per second. He pauses for 1 second to locate the swimmer again, and then dives into the water and swims along a diagonal path to the swimmer at a speed of 5 feet per second. How many seconds go by between the time the lifeguard sees the struggling swimmer and the time he reaches the swimmer?
- 16
- 22
- 50
- 56
-
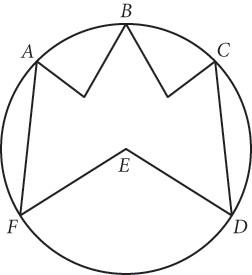
Shunyo is designing a pin for her college’s academic honor society; her basic template is shown above. If the sector whose central angle is ∠FED is one-third of the entire circle, what is the sum of the measures of ∠A, ∠B, and ∠C ?
- 60°
- 120°
- 180°
- It cannot be determined from the given information.
-
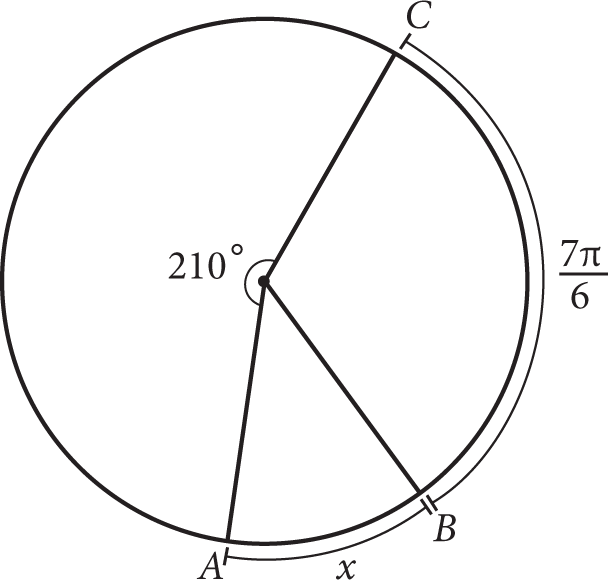
If the length of the radius of the circle shown above is 2, what is the value of x ?
-
-
The roof of a certain bell tower is in the shape of a square pyramid with a length and width of 20 feet and a slant height of 18 feet. The roof needs new shingles, which are 72 square inches in size. The shingles must overlap so that water doesn’t leak between the seams. What is the minimum number of shingles needed to cover the roof, assuming 20% extra to account for the overlap?
- 432
- 518
- 1,440
- 1,728
-
 Note: Figure not drawn to scale.
Note: Figure not drawn to scale.
The semicircle above has a radius of r inches, and chord
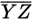 is parallel to diameter
is parallel to diameter
 . If the length of
. If the length of
 is 25% shorter than the length of
is 25% shorter than the length of
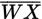 , what is the greatest distance between
, what is the greatest distance between
 and
and
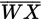 in terms of r ?
in terms of r ? -
-
When New York City built its 34th Street subway station, which has multiple underground levels, it built an elevator that runs along a diagonal track approximately 170 feet long to connect the upper and lower levels. The angle formed between the elevator track and the bottom level is just under 30 degrees. What is the approximate vertical distance in feet between the upper and lower levels of the subway station?
- 85
- 98
- 120
- 147
-
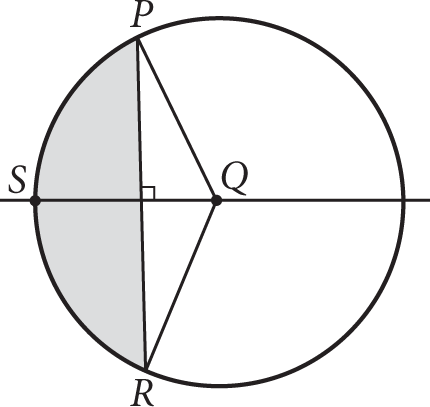
If the measure of
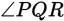 in the figure above is 120°, and the radius of the circle is 4 units, what is the area in square units of the shaded portion of the circle?
in the figure above is 120°, and the radius of the circle is 4 units, what is the area in square units of the shaded portion of the circle? -
-
A hexagonal wooden #2 pencil measures 190 millimeters in length (pencil only, no eraser or metal eraser connector; unsharpened). Normally a pencil is drilled through from one hexagonal face to the other, and this cavity is filled with graphite. A recent equipment malfunction led to pencils being drilled only halfway through, resulting in 50% less graphite than usual. If the graphite component has a diameter of 2 millimeters and the pencil’s hexagonal faces have diagonals of 8 millimeters, what fraction of one of the defective pencils is graphite?
-
-
A medical test tube is made up of a cylinder with a half-sphere on the bottom. The volume in square inches of the tube is
 . The diameter of the cylinder (and the half-sphere) is 1 inch. How tall in inches is the test tube?
. The diameter of the cylinder (and the half-sphere) is 1 inch. How tall in inches is the test tube?- 4.75
- 5
- 6
- 6.5
-
If MN in the triangle above is equal to 1,000, and
 what is the approximate length of side LN ?
what is the approximate length of side LN ? - 86
- 318
- 731
- 917
-
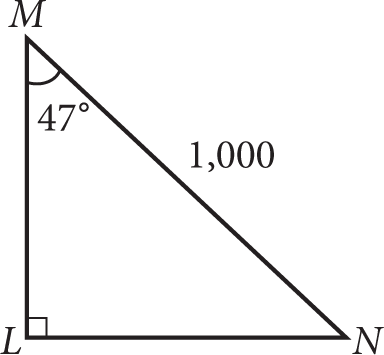
In the figure above, the shaded region is a square with an area of 12 square units, inscribed inside equilateral triangle ABC. What is the perimeter of triangle ABC ?
-
-
x2 + y2 − 4x − 8y = 16
The equation of circle O in the xy-coordinate plane is given above. What is the length of the radius of circle O ?
- 4
- 6
- 16
- 36
-
If a right cone is three times as wide at its base as it is tall, and the volume of the cone is 384π cubic inches, what is the diameter in inches of the base of the cone?
- 8
- 12
- 16
- 24
-
Which of the following shows
 written in the
form a + bi ? (Note:
written in the
form a + bi ? (Note:  .)
.)- –29 – 27i
- –29 – 3i
- 11 – 27i
- 11 – 3i
- –29 – 27i
-
Which of the following is an equation of a circle in the xy-coordinate plane with center (1, 0) and a radius with endpoint
 ?
? -
-

If the area of the smaller circle shown above is 144π square units, then what is the equation of the larger circle?
- (x + 2)2 + y 2 = 36
- (x + 2)2 + (y − 3)2 = 9
- (x + 8)2 + (y − 12)2 = 144
- (x + 8)2 + y 2 = 576
-
A rectangular block with a volume of 250 cubic inches was sliced into two cubes of equal volume. How much greater, in square inches, is the combined surface area of the two cubes than the original surface area of the rectangular block?
- 2
- 25
- 50
- 125
-
Which of the following is equivalent to the complex number
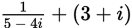 ? (Note:
? (Note:  .)
.) -
-
The absolute value of a complex number a + bi is defined as
 . What is
. What is
 ? (Note:
? (Note:
 .)
.)
-
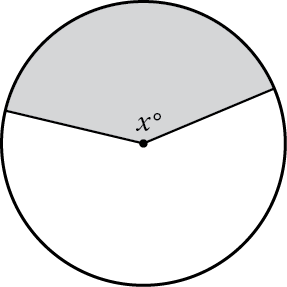
In the figure above, the ratio of the shaded area to the unshaded area is 5 to 7. What is the value of x ?

-
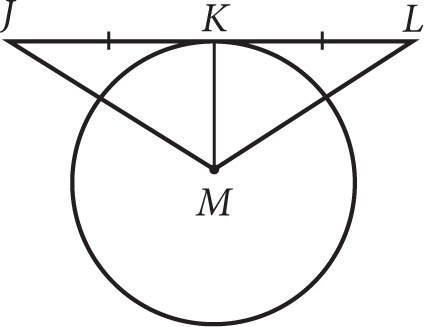
In the figure above,
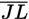 is tangent to circle M at point K. If the area of the circle is 36π, and JL = 16, what is the length of
is tangent to circle M at point K. If the area of the circle is 36π, and JL = 16, what is the length of
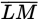 ?
?
-
If the expression
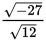 is simplified and written in the form bi, what is the value of b ? (Note:
is simplified and written in the form bi, what is the value of b ? (Note:
 .)
.)
-
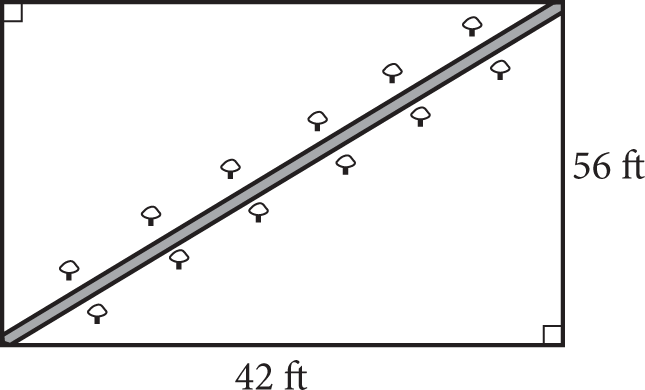
Note: Figure not drawn to scale.
A college has a sidewalk that cuts through a block of greenspace on the campus. To ensure student safety, the college decides to put lights along both sides of the sidewalk. If the lights should be placed 5 feet apart, as shown in the figure, how many lights does the college need?

-
The length, width, and height of a rectangular prism are in the ratio 4:2:1 (in that order). If the volume of the prism is 216 cubic inches, how many inches wide is the prism?
-
Steve and Autumn are skiing at a local mountain resort. Steve wants to maneuver through a mogul field at the start of a certain trail; Autumn opts to take an easier trail and meet Steve on his trail just after the mogul field ends and ski to the bottom with him. If Steve drops 375 feet in elevation after skiing through the 1,000-foot mogul field, and the two skiers will drop another 1,125 feet in elevation by the time they reach the bottom of the trail, how many feet long is the full trail Steve took?

-
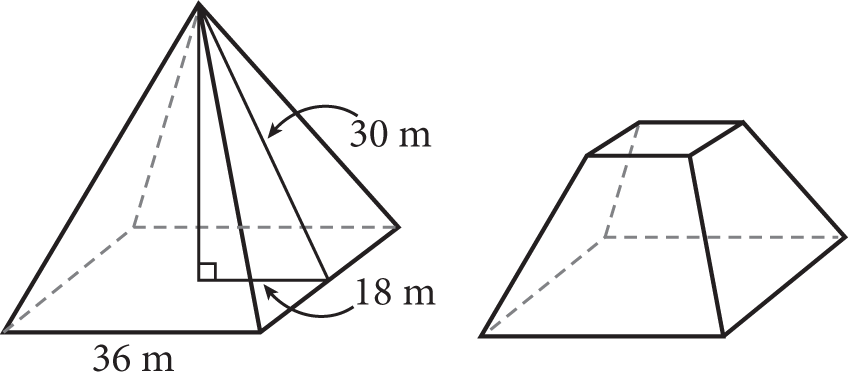
When the top of a pyramid (or a cone) is cut off, the remaining bottom part is called a frustum. Suppose the top third (based on the height) of the square pyramid shown above is cut off and discarded. What will be the volume, in cubic meters, of the remaining frustum?

-
What is the measure in degrees of the smallest angle of a triangle that has sides of length 1.5,
 , and 3 ?
, and 3 ?
-
The opening of a perfectly circular sewer tunnel has a circumference of 8π. The tunnel has a volume of 2,048π cubic feet. How many feet long is the tunnel?

-
What is the diameter of the circle given by the equation x 2 + y 2 + 10x − 4y = 20 ?

-
If the product of
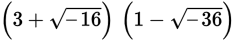 is written as a complex number in the form a + bi, what is the value of a ? (Note:
is written as a complex number in the form a + bi, what is the value of a ? (Note:
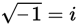 .)
.)
-

Note: Figure not drawn to scale.
In the figure above, the area of the shaded region is 52 square units. What is the height of the larger triangle?

-
In a right triangle, one angle measures x°, where
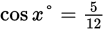 . What is the value of sin(90° – x°) for this triangle?
. What is the value of sin(90° – x°) for this triangle?
-

If the equation of the circle shown above is written in the form x2 + y2 + ax + by = c, what is the value of a + b + c ?

-
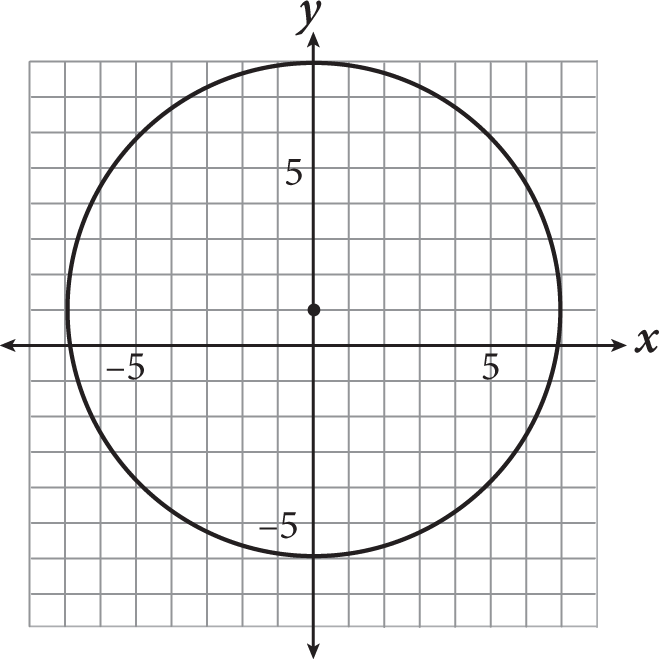
If the equation of the circle shown above is written in the form x 2 + y 2 + ax + by = c, what is the value of a + b + c ?

-
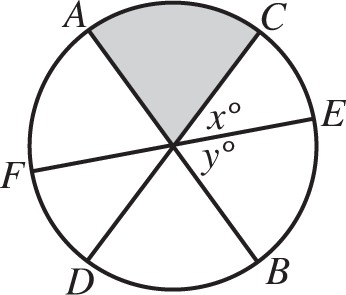
In the figure above,
 ,
,
 , and
, and
 are diameters of the circle. If y = 2x − 12, and the shaded area is
are diameters of the circle. If y = 2x − 12, and the shaded area is
 of the circle, what is the value of x ?
of the circle, what is the value of x ?
-
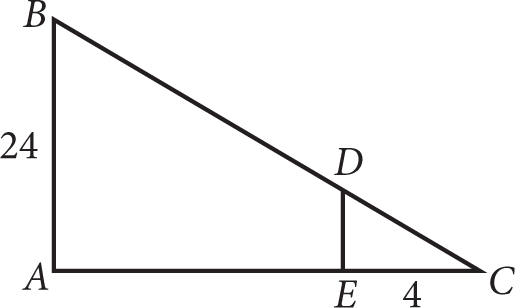
In the figure above,
 and
and
 . If AE = 28, what is the length of BD ?
. If AE = 28, what is the length of BD ?
-
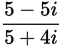
If the expression above is rewritten in the form a + bi, where a and b are real numbers, what is the value of a ? (Note:
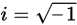 .)
.)
-
In triangle PQR, the measure of angle Q is 90°, QR = 6, and PR = 10. Triangle TUV is similar to triangle PQR, where vertices T, U, and V correspond to vertices P, Q, and R, respectively, and each side of triangle TUV is
 the length of the
corresponding side of triangle PQR.
What is the value of sin V ?
the length of the
corresponding side of triangle PQR.
What is the value of sin V ?