All this assumes that you could guide your spacecraft in carefully at the "equator" of the black hole, well away from the poles, where material is being

squirted into space from the region just above the Schwarzschild surface. The structure produced by this beaming of energy and plasma out from the central powerhouse of a quasar stretches, in some cases, across 10 million light-years. Since the material in the jet cannot move faster than light, that means that the central quasar must have been active for 10 million years. On the other hand, it is very difficult to see where the energy could come from to keep a quasar "running" for much longer than this, and at the same time the distribution of quasars and radio sources across the Universe suggests that most of the active galactic nuclei that existed in the past have now died out. The age of a galaxy today is comparable with the age of the Universe, around 10 billion years. The lifetime of a quasar, on the other hand, may be no more than 100 million years, just 1 percent of the age of the galaxy it inhabits. We conclude that dead quasars today outnumber the living ones, and that many earlier generations of quasars may now be defunct. A dead quasar would presumably be a massive black hole now almost quiescent because it is starved of fuel—starved either because it is in a galaxy that has been swept clean of gas or because it has gobbled up all the stars near it. So, on this picture, there ought to be evidence of the presence of supermassive black holes in the nuclei of quiet galaxies, like our neighbours in the Local Group and the Milky Way itself. That evidence is now coming in.

Weighing the Evidence

Over the past ten years or so, several astronomers have tried to find evidence that massive black holes do indeed lurk in the hearts of nearby galaxies. Some have claimed success, but there have always been questions

about the interpretation of the data. By the end of the 1980s, however, the weight of evidence began to tilt the balance in favour of the idea that most, perhaps all, galaxies have big black holes at their centres.

Some of the most impressive statistical evidence comes from Wallace Sargent and Alex Filippenko, of Cal Tech. At the time we are writing, in 1988, they are in the midst of a survey of five hundred galaxies, obtaining spectra of the light from the central nucleus of each of these objects. More than 10 percent of the galaxies in this sample show the characteristic features (technically, broad emission lines at the wavelength of hydrogen alpha) that are usually taken as indicating the presence of a massive black hole. By this criterion, each of those galaxies would usually be identified as a Sey-fert, the class of galaxies previously regarded as intermediate between "ordinary" galaxies and quasars. In the past, Seyfert galaxies have been identified and labelled as such because the broad emission lines are obvious features of their bright spectra; such emission lines are much more common among faint galaxies than was previously suspected. Because it is very difficult to obtain the necessary detailed spectra of faint objects, these positive identifications still probably represent only the tip of the iceberg; more detailed studies (for example, with NASA's Hubble Space Telescope) are now expected to show this low-level " quasar" activity in virtually every galaxy.

Coming closer to home, some of the latest, and best, evidence comes from studies of two near neighbours tq the Milky Way. New observational tests reveal the presence of a hole with mass around 50 million Suns in the biggest galaxy in the Local Group, the Andromeda Nebula (M 31), and one of 8 million Suns in a smaller galaxy known as M 32. Two American researchers, Alan Dressier and Douglas Richstone, carried out a spectroscopic study of the motions of stars in the inner regions of both

these galaxies. Because they are relatively nearby (only 2 million light-years away), the study showed details of orbital velocities on a fine scale, in close to the hearts of the two galaxies. These observations, and corroborative ones by John Kormendy (of M 31) and John Tonry (of M 32), are very hard to explain except by the presence of supermassive black holes. And since these two galaxies are otherwise completely ordinary and undistinguished, showing no signs of unusual activity in their nuclei, the implication may be that all galaxies harbour supermassive black holes. In which case, we surely ought to be able to find evidence of one in our own Galaxy.

At the Heart of the Milky Way

Conditions at the nucleus of our Galaxy are certainly very different from those in the neighbourhood of the Solar System. Unfortunately, because there is a lot of gas and dust in the disc of the Galaxy, and our Sun is also orbiting in the disc's plane, the central region itself is obscured from view to optical telescopes. Infrared radiation and radio waves can, however, penetrate this obscuring dust to some extent, so it is from radio and infrared observations that we glean an image of the heart of the Milky Way.

There is a very small, variable source of radio noise right at the galactic centre. This source is too small to be resolved by radio interferometers; at the distance of the galactic centre this implies a size measured not in light-years but actually less than one light-Zzowr (that is, the distance light could travel in 60 minutes) across. For comparison, it takes light from the Sun 160 minutes to reach Uranus, the farthest giant planet in our Solar System. As well as other interesting activity from

this region, there is strong gamma radiation characteristic of the kind produced when electrons and positrons pairs annihilate one another. That in turn means that electron-positron pairs are being created by some form of energetic activity, and accretion of material onto a black hole with a mass of up to a million Suns would fit the bill.

There certainly cannot be a monster black hole in our galactic centre. The way gas is moving within a few light-years of the centre shows that a million solar masses is just about the upper limit, so the evidence actually fits well together. Our Galaxy has never been a fully fledged quasar; but the balance of opinion has now shifted so far in favour of the idea that all galaxies harbour large black holes that it has become natural to ask what sort of detectable effects on a lesser scale than quasar activity such a hole might produce in our own Galaxy, and others. A little thought soon throws up some intriguing possibilities.

Jack Hills, an expert on stellar dynamics from the Los Alamos National Laboratory, in New Mexico, suggests that a million-solar-mass black hole at the centre of our Galaxy may be spitting out stars moving at 4,000 kilometres a second once every 10,000 years. If so, some two hundred such fast-moving objects ought to lie within the radius of the Sun's orbit about the galactic centre, and some of them ought to be detectable, moving at far greater than the escape velocity from the Galaxy. The discovery of one or more such objects on the way out into the depths of intergalactic space would be proof that a massive black hole lies at the centre of the Milky Way.

Hills has investigated the way pairs of stars in tight orbit around each other ("hard binaries") can be disrupted as they pass by such a black hole. Many stars occur in binary systems, and where stars are packed closely together, as they are in the core of the Galaxy,

encounters between stars can transfer orbital kinetic energy from a binary system to a passing star, "winding up" the binary and binding its two stars more closely together.

When such a binary passes near a massive black hole, however, something quite different can happen. Depending on the size of the binary system, its orbital speed, and the speed and angle at which it passes the hole, one star in the binary may be captured by the hole while its companion is ejected at very high speed (the process is reminiscent of, but actually quite different from, the way one member of a virtual pair produced near a minihole can escape while the other is captured).

The stellar density in the heart of the Milky Way is poorly known, but estimates suggest that a star should pass as close to the hole as the Earth is to the Sun once every 100 years. If just 1 percent of the stars involved in these close flybys are hard binaries, one escapee with a velocity of 4,000 kilometres per second should be produced every 10,000 years. Because it is 35,000 light-years from the galactic centre to the distance of the Sun's orbit, it will take each runaway 2 million years to get as far out from the core as we are. In that time, two hundred runaways are spat out, which is why there should be two hundred such superfast stars en route outwards but still within the radius of the Sun's orbit at any time.

Such stars ought to be easy to spot. Even at a distance of 35,000 light-years, the maximum motion of such a star across the sky would be 0.1 second of arc per year. Other hypervelocity stars will be closer, brighter, and more obvious. So why have none been reported in standard sky surveys? It may be that observers have indeed noted such objects but have assumed that they are in fact much closer stars, moving correspondingly more slowly. Since such stars will shoot

out from the central black hole randomly in all directions, there is only a very slim chance of one passing so close to us that its nature would be obvious even if you were not looking for something of this kind. If they are now identified in their true colours, they will provide the strongest evidence that our Galaxy harbours a supermassive black hole. On the other hand, the absence of evidence for such objects can never be taken as proof that they do not exist—we may simply be looking for them in the wrong place. Happily, though, there are other effects related to the production of these fast stars that would produce an unambiguous signature in a unique place, at the centres of nearby galaxies themselves.

A Flare for Black Holes

Hills has considered the fates only of binary systems moving dangerously close to large black holes. Even single stars, however, may be disrupted in interesting ways, not just swallowed whole, if they venture too close to such an engine of destruction. The dynamics of stars in the inner regions of nearby galaxies such as M 31 and M 32 indicate the presence of central black holes, and since these are nearby, well-studied galaxies we also know a great deal about the number of surrounding stars in each case and the way they move, so we can calculate how often they will be captured by the hole. The best way to test the idea that this is indeed happening is to find an effect that must be produced if the holes are there but cannot be produced by anything else. The best bet may be the distinctive features of the way energy is released when a star is partially gobbled up by the black hole.

A hard pair binary stars in which one star is swallowed and the other escapes is in many ways a simpli-

fied picture of what happens to a single star in the embrace of a supermassive black hole. As the star gets close to the hole, it experiences large tidal forces and may be disrupted, losing matter or being broken up completely. Part of the debris is expelled, at speeds up to 10,000 kilometres per second, by a gravitational slingshot effect; the remaining debris would be left gravita-tionally bound to the hole, and in orbit around it, destined to dribble down the Schwarzschild throat. How long might this take?

For black holes with a mass of only a few million Suns, it turns out that each stellar "meal" is digested long before the next close encounter occurs. The result would be a short-lived flare of activity from the nucleus of the galaxy, an outburst lasting for only a few months or years. Meanwhile, the fraction of the original star that had escaped from the hole would not remain intact, but would fan out in a stream of debris mingling with the other material of the surrounding galaxy, and producing no discernible sudden burst of energy.

As far as our own Galaxy is concerned, the fact that we do not see a flare of activity from the centre of the Milky Way today poses no problem, since we would expect such a flare only once every 10,000 years or so; we are much more likely, however, to see such flares in other galaxies. Because of the rarity of such events (in round terms, if each galaxy flares every 10,000 years, we need to study 10,000 galaxies in order to see one flare a year), it is still no surprise that no such flare has yet been seen; but with ever-improving telescopes and knowing now what they are looking for, there is every chance that observers might spot such a flare from a galaxy no farther away than the Virgo Cluster within the next few years.

In our own Galaxy, the outgoing debris, even if it is not in the form of the whole, hypervelocity stars envisaged by Hills, may be more conspicuous. Material

spraying out from the central black hole, like water from a garden sprinkler, would provide a barrier that slowed infalling gas. This would have two effects. It might reduce the activity of the hole itself, by reducing its supply of "food," and it would surely produce a hot bubble around the centre of the Galaxy, where the incoming material and the outgoing debris meet head-on. Again, now that the theoretical calculations show what form this bubble might take, observers can begin to look for predicted effects. They may not have to look far. X-ray observations show that there is indeed hot gas in the central 1,000 light-years or so of elliptical galaxies, and if this really is helping to stem the flow of material inwards, then even the quietest of nearby galaxies could be harbouring a semistarved black hole with a mass as big as a hundred million Suns.

These are all exciting prospects, far removed from the everyday world in which gravity is simply the force that causes apples to fall downwards or breaks a skier's bones in a fall. It is, perhaps, worth pointing out that all of the ideas described in this chapter represent mainstream thinking among astrophysicists today. Over the past twenty years, theorists working on this subject have sometimes had the illusion of rapid progress. What we've really had is a rather slow advance, with "sawtooth" fluctuations as fashions have come and gone (what seems like two steps forward being followed by one pace backwards). But the idea that quasars are powered by supermassive black holes at cosmological redshifts, and even the idea that a million-solar-mass black hole lies at the centre of the Milky Way, spitting out stars at speeds of thousands of kilometres per second, are now routine. If quasars had been discovered in, say, 1973, after the discovery of pulsars and compact X-ray sources in our Galaxy, and after the resulting theoretical developments, then surely a consensus around models involving massive black holes would very quickly

have emerged. It took so long to establish this as the "best buy" simply because, in the early to middle 1960s, no detailed work had been done on black holes for a quarter of a century, and nobody had expected to find big black holes at large in the Universe. By the time the black-hole models were being refined, various speculations had had time to take root and grow, and it took correspondingly long for the black-hole model to catch up and surpass them.

But there is no need to feel disappointed by the news that big black holes are routine physics, far from the cutting edge where speculation can still have free rein. If your taste is for wild-eyed conjecture, look no farther than the next chapter.

CHAPTER SEVEN

•

Cosmic String

IT MAY BE A BACKLASH against the days when exotic names were the vogue both in cosmology (quasar, blazar, supermassive black hole .. .) and particle physics (charmed quark, colour theory, grand unification ...), but two of the most important ideas in contemporary physics each go under the most prosaic of names— string. In terms of scale, the two kinds of string could hardly be more different. To a particle physicist, "strings" are the entities that replace the old concept of particles. Instead of thinking of particles in terms of mathematical points of mass-energy, tiny billiard balls, theorists are learning to describe them in terms of tiny lines or loops of one-dimensional string, far smaller than protons or neutrons. To a cosmologist, on the other hand, "string" may stretch, literally, across the Universe, although even that kind of string is far thinner than a single atom.

The two concepts are related, in that both emerge from the arena of very-high-energy physics and the search for a unified theory of all the particles and forces of nature. But they should not be confused with each other, so it helps that physicists usually refer to each type of string with an adjective attached—"cosmic

string/' for the kind that stretches across the Universe, and "superstring," for the kind particles may be made of. It's cosmic string that matters when you are worrying about how galaxies form in the first place, and why they lie in sheets and filaments* around the edges of empty bubbles in the Universe. But the approach to unified theory that gives us superstrings also has something to say about the nature of dark matter that may influence the visible Universe by its gravity alone.

A Theory of Everything?

The new theory of superstrings grew out of the search by mathematical physicists for a single theory, one set of equations, to describe all the forces and particles. Their concepts are still tentative, but theorists no longer believe that the quest is hopelessly premature—it is no longer just cranks who try to "solve" all of fundamental physics in one go. Such a "theory of everything," or TOE, must go beyond both quantum physics (which, in the form of quantum chromodynamics, QCD, successfully explains much of the particle world) and general relativity, which deals with the Universe at large and with gravity, the force most difficult to squeeze into a unified theory. But since both those theories work superbly within wide limits, a good TOE must include each of them within itself.

So far, so good. What are the problems that need to be solved? One interesting feature—not really a problem— is a kind of chicken-and-egg puzzle about general rela-

*Such filaments have also sometimes been referred to as strings of galaxies. This third application of such a prosaic term is too much of a good thing, and we shall stick to filaments, or chains, to describe the appearance on the sky of long lines of galaxies.

tivity. Starting out, as Einstein did, from a description of curved spacetime, the theory requires the existence of gravity waves, ripples in the fabric of spacetime, and the associated graviton, a particle with zero mass and spin 2. If you prefer, however, you can start out from a theory based on a zero mass, spin 2 graviton; it yields the usual form of general relativity, with curved space-time. Until recently, there was no reason to regard either view as providing a better insight into the nature of the Universe. But that may be changing.

The big problem with all particle theories prior to string theory is that they lead to infinities when gravity is included. Now, some infinities are embarrassing but can be lived with. QCD, for example, is riddled with infinities, which are swept under the carpet by a trick called renormalisation, and ignored. Renormalisation is essentially just a mathematical ploy. But it leaves a set of equations that can be used, in the right circumstances, to describe how particles behave. When gravity is included, the infinities cannot be renormalised, and cannot be ignored. They loom up in the equations and make them impossible to work with.

All this happens when particles are regarded as mathematical points, the simplest entities imaginable. So, more or less in frustration, some theorists decided to see what happened if they considered particles not as points but as the next simplest entities imaginable, little one-dimensional lines, or strings. It turns out that not only does the problem with infinities not arise, but that rather than having to add gravity into the theory, they found it there already—gravity, and specifically a mass zero, spin 2 graviton, is already a necessary part of any workable string theory of the particle world.

Why superstrings? The adjective creeps in from another particle theory, called supersymmetry . This is the theory that says that every type of particle that is

THE STUFF OF THE UNIVERSE

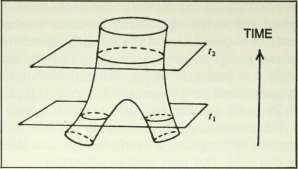
Figure 7.1 The "trouser" spacetime diagram of two super-strings that are separate at t\ but have merged by time t 2 .

associated with a force (like the graviton) must have a partner (the gravitino, in this case) that belongs to the material world, while every particle that we are used to thinking of as, well, a particle (an electron, say) has a partner belonging to the force family (the selectron). Supersymmetry plus string theory gives you super-strings, the best candidate yet for a theory of everything, and one that gives one particularly delightful image.

In string theory, particles are represented by little loops (we do mean little—typically about 10" 33 centimetres across), which sweep out tunnels through space. When two string loops meet and merge, their behaviour can be represented diagrammatically by a structure with a striking resemblance to a pair of trousers. Space-time trousers, it seems, may provide the ultimate description of the particle world.

But the most important feature of the search for a TOE remains what John Schwarz, of Cal Tech (one of the founders of superstring theory), has described as a "Deep Truth"—that every consistent variation on the string theme has one, and only one, graviton, a mass-less, spin 2 particle that leads inevitably to the spacetime-

curvature description of general relativity, and thereby, by implication, on to Newtonian gravity when the gravitational fields are weak. This is a coincidence that simply Cannot be ignored. Progress towards the ultimate physical theory can, it seems, be made only by going further along the path trodden by Einstein and by Newton himself.

There is, however, still a long way to go. Although superstring theories agree on the overall nature of strings—a typical length of about 10" 35 metres and a typical tension in the string that stores energy equivalent to 10 38 proton masses, numbers related to the Planck mass and Planck length mentioned in figure 3.1—there are many different versions of superstring theory to work with. Some of the most successful work only in ten dimensions, which introduces the problem of explaining why our Universe seems to have only four dimensions, three of space and one of time. The problem is not insurmountable—mathematicians have a ploy called compactification, which allows the extra dimensions (six, in this case) to be rolled up so small that they are unobservable. The effect is rather like the way in which a two-dimensional hosepipe, a sheet of material wrapped around a line, looks like a one-dimensional line if viewed from far enough away. Each point of our ordinary space, at each moment of time, is really a tiny but complex curled-up six-dimensional world. The interconnected structures and resonances in these extra dimensions control how the superstrings behave, and thereby determine what particles exist at each point in ordinary space, and how they interact.

There are different versions of ten-dimensional super-string theory, different versions of compactification, and even versions of string theory that start out in four dimensions. Superstring theories are not mathematically elegant (they don't hang together naturally in the

way that, say, general relativity does), which is taken as a sign that the "right" mathematical description has not yet been found; nor are they based on some deep truth, such as the geometrical principles that Einstein used as the foundation of general relativity. Schwarz himself says that it is unrealistic to expect too much too soon, and that although the way superstring theory does away with infinities and brings gravity into the fold of unified theory is striking and encouraging, it is likely to take a few decades of hard work before there is a really satisfactory understanding of what superstring theory is all about. (Unlike most physical theories, which have made use of a "mathematical language" that was already developed, superstring theory presents new challenges to pure mathematicians.)

What physicists would like to find is a unique version of superstring theory that inevitably produces families of particles that can be identified with the known quarks and leptons. That may be decades away, if it ever comes, but the fact that the search may not be completely hopeless is borne out by several modest successes to date. For example, using one particular class of super-string models, Dimitri Nanopoulos, of the University of Wisconsin, and Keith Olive, of the University of Minnesota, found that some of the simplest versions of the theory lead naturally to a prediction that the electron neutrino should have a mass of about three one-millionths of an electron Volt, the mu neutrino should have a mass of 0.01 eV, and the tau neutrino should weigh in at 30 eV. Such a combination of masses would perfectly account for the dark matter in the Universe.

We don't want to get entangled in the details of superstrings here. But we cannot leave the topic without mentioning one interpretation of the equations that made headlines in the mid-1980s—the idea of "shadow matter."

Breaking Up Is Not So Hard to Do

Symmetry is the key to the modern understanding of particles and forces. At very high energies, there is no distinction between, for example, electromagnetism and the weak force, and they are described as one force, the "electroweak." The simplest way to understand this is in terms of the masses of the particles that carry the forces. Electromagnetism is carried by photons, which have zero mass. The range of a photon is, in principle, infinite—the farthest quasar, at a redshift beyond 4.5, can exert an electromagnetic influence on the Earth itself (which is, indeed, what happens when a photon from a quasar strikes a photographic plate inside a terrestrial telescope). In practice, because positive and negative electrical charges are in balance, electromagnetic forces are not important across such very large distances.

The particles that carry the weak force, by comparison, have masses only a little less than one hundred times the mass of a proton. In order for one particle to influence another through the weak force, these force-carriers (known as bosons) have to be created. A particle with mass less than a proton cannot, obviously, "make" such a massive boson out of its own substance; the boson has to appear out of the vacuum, as allowed by quantum uncertainty, travel across to the neighbouring particle, and be absorbed back into the vacuum after making its presence felt. Because they are so massive, these virtual particles exist only for a very short time, and their range is limited to the distance they can travel in that time—roughly speaking, across the nucleus of an atom.

The electromagnetic force and the weak force become indistinguishable when there is so much energy

around that these bosons can exist in profusion, in the same way that massless photons can be produced in profusion by stars today (or even by a modest electrical current flowing through the bulb of a flashlight). If the whole Universe was at a high enough temperature, weak bosons would become real, instead of virtual, particles. Such conditions existed in the Big Bang; when the temperature fell to the point where weak bosons could no longer exist as real particles, the symmetry between weak and electromagnetic forces broke.

Symmetry breaking is important not only because it explains how the complexity of the cold Universe we live in developed from the simplicity of the hot Big Bang, but because the changes associated with some forms of symmetry breaking could have provided the energy to push the Universe through a short-lived period of exponential expansion, the inflationary era, which smoothed out the wrinkles in spacetime and made it so flat. There is a lot more to symmetry breaking, however, than the distinction between electromagnetic and weak forces, or even the power of inflation.

The deepest symmetry we have mentioned so far is supersymmetry, the supposed symmetry between particles and forces that was broken very soon after the moment of creation. But some of the most promising versions of superstring theory contain exactly twice as much symmetry as this. There is "room" in superstring theory for just one more layer of symmetry, in which the combined world of particles and forces we know about is itself balanced by another, equally complex world of particles and forces that we do not know about. According to these theories, this would be the ultimate layer of symmetry, a splitting that occurred at the same time as gravity became distinct from the other forces of nature, just 10^ 3 seconds after the moment of creation.

Out of the Shadows?

When the Universe was very young and very hot, on this picture, there was a perfect symmetry in which all forces and particles were indistinguishable. Then, as gravity broke off from the other forces, the symmetry split into two smaller, initially identical symmetries. One of those smaller symmetries then went through successive further splittings, leading to the variety of forces and particles we know. What happened to the other?

Almost anything could have happened to it. As it split further in its own right, it could have produced a variety of particles and forces, possibly identical to the ones in "our" world, probably different. But the most important thing about that other symmetry—the other world—is that because it split from us at the time gravity became distinct, gravity is the only force—the only thing—that the two worlds have in common. We might be able to detect the other world by its gravitational influence on the matter of our world, but we could never interact with it in any other way.

What else could this other universe be called except the "shadow" world; and what else could its contents be called except shadow matter? You could be living at the bottom of an ocean of shadow matter, or walking through the base of a shadow mountain, and never know it. Science fact, it seems, has run headlong into the world of science fiction.

Shadow matter is an obvious candidate for the dark stuff of the Universe—a whole second universe, interpenetrating ours and expanding with it, sharing through the effect of gravity but otherwise undetected and undetectable. If the shadow world exactly mirrored our own, with the same amount of matter forming shadow quarks and shadow leptons (and, indeed, its own shadow

dark matter, perhaps, in the form of shadow axions) then there could be shadow stars and planets within our own Galaxy. You may be reassured (or disappointed, depending on your taste for science fiction) to learn, however, that you are not living inside a shadow mountain. Although the two forms of matter could indeed interpenetrate to form a planet (or a double planet), calculations of the mass of the Earth and comparisons with the orbital motions of satellites show that there is less than 10 percent shadow matter inside our planet, and probably none at all. The prospect of shadow matter inside the Sun is even more slender—because this sort of dark stuff would sink to the core and exert a gravitational influence in the inner regions of the star without affecting it otherwise, it would make the Sun hotter in the middle, and that would show up in studies of neutrinos from the Sun (which, remember, actually suggest that the central part of the Sun is 10 percent cooler than standard theory predicts). The limit on the amount of shadow material inside the Sun is 0.1 percent, and the best guess is that there is none at all there. The clinching evidence against this kind of shadow matter comes from calculations of the way helium was manufactured in the Big Bang—the shadow matter would make the Universe expand too fast during the era of helium production, with more helium left over from the Big Bang than we actually see in old stars.

Very likely, the idea of a shadow world that exactly mirrors our own remains in the realm of science fiction. But there is no need to despair if you enjoy such speculations. Why, after all, should the shadow world have experienced exactly the same kind of symmetry breaking as our own world? Perhaps it contains different kinds of particles and forces, so that different rules of physics apply. A suitable choice of rules gets around the problem of helium production in the Big Bang and leaves the way open for speculators. All the material of

the shadow world, for example, may decay into particles with zero mass. Or there might be a perfect balance between shadow matter and shadow antimatter, so that all matter in the shadow world annihilates into radiation. Or there might be one or more types of shadow particles that together contain just the right amount of mass to make the Universe (or universes) flat, and that stay spread out uniformly through space, never clumping together into stars and galaxies. And if that is too dull for you, imagine a shadow world in which the rules of physics are such that the stars are no bigger than a house here on Earth, so that a shadow star might fall on Stockton and the inhabitants would be none the wiser.

We are not, as you may have guessed, enthusiastic about shadow matter. There is too much room for speculation, and too little prospect of experimental or observational tests—and apart from anything else, there is no need for it. Particles that are known to exist (neutrinos) or that are required by our best theories (axions; miniholes) can perfectly well contribute all the dark matter, and even provide the critical density for a flat Universe, without leaving any room for shadow matter. Shadow matter is simply too much of a good thing, in gravitational terms. But we can never, by its very nature, prove that it does not exist. Cold dark matter particles might be detected in the lab or by their influence on the Sun and stars, and their properties studied; but you can never get a handle on shadow matter.* Cosmic strings, by comparison, cry out to be noticed. They almost certainly cannot, on their own,

*Unless you are lucky enough to find a minihole. Then, as Andrei Sakharov, of the P. N. Lebedev Institute, in Moscow, has pointed out, the Hawking evaporation of the hole will produce both matter and shadow matter. As a result, the hole will radiate energy more rapidly, and its temperature will rise faster, than Hawking's theory predicts. But first, catch your black hole.

provide all of the dark stuff that we require. But they can perhaps explain how the bright stuff got to be distributed in the way we see it today.

Strings and Things

The two main puzzles about galaxies are how individual galaxies form in the first place, and how and why they group together in chains, filaments, and sheets. Cosmic-string theory offers a possibility of answering both questions in one package. Our present theories of galaxy formation assume that the Universe used to be much smoother than we see it today, and that the lumpiness that galaxies represent grew out of some small initial irregularities, or seeds. By and large, cos-mologists ignore the irregularities (except to use galaxies as convenient test particles to measure the expansion of the Universe) and deal only with equations that describe a smoothly expanding universe. But those very equations now provide a way to produce the required seeds naturally, out of the vacuum of spacetime. Symmetry breaking, so important to theories such as inflation and to modern understanding of the particle world, also provides three different, but related, kinds of flaw in the vacuum itself.

To a physicist today, the vacuum is very far from being the "nothing" that the term implies to the layperson. The vacuum out of which our Universe was born, perhaps through a vacuum fluctuation, contained a huge amount of energy, and possessed a high degree of symmetry, in the sense that there was no distinction between the fundamental particles and forces. The symmetry breaking that separated out those particles and forces was associated with a series of changes called phase transitions, in which the vacuum gave up its energy (helping to drive the expansion of the Universe).

This is rather like the way liquid water turns into ice. Compared with ice, liquid water contains a lot of energy. When water freezes, this energy is released, as latent heat; and the frozen water (ice) is less symmetric, because a crystalline lattice of ice (water) molecules does not look the same in all directions. The molecules in the lattice are aligned to make patterns, which we see in the beauty of a snowflake. A snowflake is definitely not the same in all directions.

The ice contains features that you never see in liquid water—boundaries between different crystalline regions that divide the ice up into smaller domains (for example, the boundary between one branch of a snow-flake and the central body of ice from which it "grows"). Within each domain the ice may be relatively smooth, with the water molecules all pointing in the same direction; but the orientation of molecules in the crystal in one domain (one branch of the snowflake) will be different from the orientation of molecules in the domain next door.

Boundaries between different domains in a crystal (it need not be ice; any crystalline solid is as good an example) are usually like walls around the domains. But it is possible for other defects, as they are called, to form when a liquid crystallises. Some are point defects, where the molecules are aligned so that they seem to radiate outwards from a single point; others are one-dimensional lines. And all three types of defect can, in principle, occur in the vacuum of spacetime as a result of phase transitions and symmetry breaking when the Universe was young.

The kind of two-dimensional walls, or sheets, that are the most obvious example of this symmetry breaking in ice crystals are not observed in the Universe. A single domain wall that stretched across the visible Universe would contain much more mass (stored vacuum energy from the time before the phase transition)

than all the matter we know about, including the dark stuff, and its gravitational influence would be obvious in the movement of galaxies. There may be domain walls farther away than we can see; but if so, they are being carried ever farther away by the expansion of the Universe.

At the other extreme, the kind of one-dimensional defects that form points in space turn out to be magnetic monopoles. Physicists were at first excited to discover that symmetry breaking in the early Universe could provide a means to manufacture monopoles, but were then embarrassed to find that those theories require the Universe to be swarming with monopoles that are not, in fact, detected. As we have mentioned, inflation provides a natural way to resolve this conflict; whatever its resolution, however, monopoles, like domain walls, have never been observed.

That leaves us with the intermediate type of defect, one-dimensional lines, or cosmic string, stretching across the Universe. Nobody has directly observed a cosmic string, either—but the existence of chains of galaxies in the Universe may be circumstantial evidence that cosmic strings exist.

Trapping the Vacuum

What, exactly, are cosmic strings? The concept stems from work by Tom Kibble, of the University of London, in the 1970s. It was taken up a few years later by Yakov Zel'dovich, in Moscow, and Alex Vilenkin, at Tufts University in America, each of whom realised its potential cosmic importance. They showed that during the symmetry breaking that occurred just 10" 35 seconds after the moment of creation, some of the original vacuum state of the Universe could have been trapped inside linear imperfections in space. The best way to think of a piece

of cosmic string is as a piece of the vacuum from that time, "frozen" and trapped inside a tube that has a diameter 10" 14 that of an atomic nucleus. Because the string contains energetic vacuum from the birth of the Universe, it contains a great deal of mass (energy and mass are, after all, the same thing in this context). The actual mass depends on the exact time (and energy) when symmetry breaking occurred, but a favoured estimate would imply that each centimetre of cosmic string would contain 10 trillion tonnes of mass-energy; a piece of string a metre long could weigh as much as the Earth. You can see at once why the idea of cosmic string appealed to theorists who were trying to explain where the seeds that galaxies grow on came from. A loop of cosmic string with a diameter of a few hundred light-years could indeed help to hold a clump of gas together long enough, in the expanding Universe, for a galaxy to form. But there are complications.

Strings cannot have ends, for a start (this makes sense intuitively, since if there was an end, the energetic vacuum inside could leak out; it is also an inevitable consequence of the mathematics that describes strings). This means that either a string must stretch across the entire Universe (not just the bit we can see), or it must form a closed loop, like a rubber band. Cosmic string is like a (stretched) rubber band in another way—it has tension. The tension, like the mass of the string, is on a grand scale, and this sets any loop of string vibrating ("twanging") at high speed. These oscillations will occur as fast as they possibly can, almost at the speed of light, so that a loop of string one light-year in circumference will vibrate about once a year. Large amounts of mass-energy vibrating so rapidly must, according to general relativity, radiate away energy in the form of gravitational waves (more of this in chapter 8). Like a black hole evaporating away its mass through the Hawking process, but much, much more rapidly, a

loop of vibrating cosmic string will lose energy and shrink away, eventually to nothing at all. This provides a very severe limit on the amount of mass that can still be in the form of cosmic string today. Such loops of string might have been important when the Universe was young and galaxies were forming, but they can form only a small part of the dark stuff needed to make the Universe flat today. If galaxies did indeed form around loops of string, then the galaxies we see today may be no more than the smile on the face of a vanishing Cheshire cat, showing where the body (the string) used to be.

This is particularly important because long pieces of string that stretch across the Universe will not be in straight lines. Instead, they will form a tangled mess, in which one string may cross over and tangle with other strings, or double back on itself and cross over another part of its own length. Ripples run up and down these strings at nearly the speed of light. Wherever strings cross, they will break and reconnect so that loops of string are split off and the original strings straighten out. Because the loops then radiate energy away, this ensures that string is never the dominant feature of the Universe. But it also leads to another very interesting phenomenon.

The way the Universe expands can be described in terms of the "Hubble length," a measure of the size of the Universe that is roughly the distance that light has had time to travel since the Big Bang. Since nothing can travel faster than light, objects that are more than this distance apart cannot interact with each other. That applies if the objects are separate galaxies, or if they are separate portions of an infinite length of cosmic string. The "wiggles" on a piece of infinite string are about as big as the Hubble length, so the loops that split off from the string are always about a Hubble length in diameter. This is true when the Universe is

Cosmic String

191

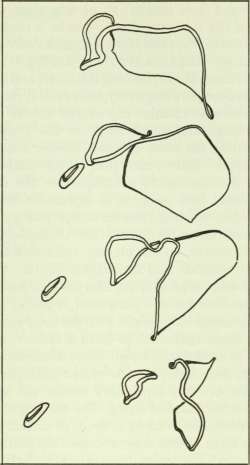
Figure 7.2 Four "snapshots" showing the computed behaviour of a loop of string that, during its oscillation, crosses itself and throws off smaller loops. (Courtesy of W. Press and R. Scherrer.)

small or when it is large; at any time, new loops of string are being broken off that can each be roughly as big as the observable Universe itself (smaller loops, of course, have already broken off, when the Universe was smaller). Each loop promptly begins to radiate gravita-

tionally and lose energy, so at any time during the history of the Universe there must be a range of loops, graded in size from the Hubble length down to nothing at all. As new loops are always appearing at the biggest size possible in the expanding Universe, and small loops are always evaporating away, the result is that although the details may change, the overall nature of the pattern of large and small loops in the Universe stays more or less the same as the Universe expands—it is "self similar/' This means that all the mathematicians have to do in order to calculate how the strings and loops should look today is to determine how the first loops looked when the Universe was young.

In round terms, for the first ten thousand years of its life the Universe, on this picture, contained only strings and hot radiation and spread-out matter. As the temperature fell, loops of string started to attract and hold on to clouds of gas and dark stuff. A galaxy could form around a small loop, while a larger loop would attract smaller loops (galaxies) to form a cluster; still longer strands of string could pull those clusters together in filaments and chains, and form new galaxies in a sheetlike wake. At every level, dark matter too would come under the influence of string. The statistical properties of the clusters and chains of loops of cosmic string that ought to form in this way resemble the statistics of the distribution of galaxies in clusters and chains in the Universe today. Once more, we are faced with a striking cosmic coincidence. We cannot prove that strings exist, but the similarity between the way string ought to be distributed and the pattern of galaxies on the sky is intriguing—the smile on the face of the Cheshire cat may, indeed, have been observed. So theorists have been encouraged to try to find out exactly how galaxies would grow around loops of string, and also to find ways of making more direct observations of the effects of string on the observable Universe today.

Making Galaxies

Cosmic string loops are a godsend to astrophysicists who try to account for the dark stuff primarily in terms of neutrinos. The problem about neutrinos is that they are "hot" particles that move very fast. In the early stages of the evolution of the Universe after the Big Bang, such hot dark matter homogenises by streaming through the baryonic gas and inhibits the growth of baryonic fluctuations. Galaxies can form in such a universe, but only after the hot dark matter has spread thin and begun to cool down—and that makes it very difficult to explain how galaxies as old as the ones we see around us can have formed in the time available since the Big Bang.

But loops of cosmic string cannot be blasted apart by fast-moving particles. They remain intact to act as gravitational seeds after the universe has expanded enough for the hot dark matter to be diluted and its influence weakened. At that point, baryonic matter can quickly begin to accumulate around the strings, producing structures that look very much like galaxies. Similar calculations can be carried through with a combination of strings and cold dark matter. Then, the opposite problem has to be tackled. Without strings, galaxies in a universe dominated by hot dark matter form too late; with strings, galaxies in a universe dominated by cold dark matter may form too soon.

The idea that massive string loops gather matter around themselves by gravity is the most obvious explanation of how they could act as seeds for the formation of galaxies. But there are other ways in which string loops can encourage the formation of galaxies, ideas that echo some earlier speculations about the foamy nature of the distribution of bright stuff across the Universe.

Ed Witten, of Princeton University, has suggested

that cosmic strings may act as superconductors. Any particles that happen to be trapped on the string will behave as if they have no mass, because the energy of the vacuum around them will be as great as the energy stored in their own mass—this is exactly equivalent to the way virtual bosons become real particles at high energies, unifying the electromagnetic and weak forces. Massless particles travel along the string without encountering any resistance, at the speed of light. If those particles happen to carry electrical charge, then enormous currents will flow unimpeded around the loops of cosmic string. When such a superconducting string oscillates, it radiates not only gravitational waves but electromagnetic waves as well, in copious quantities. A blast of electromagnetic radiation streaming out from a loop of cosmic string would push baryonic gas out of its way, forming an expanding bubble of material around the loop. Because the dark stuff does not carry electrical charge, however, it would be unaffected by the radiation and left behind. Galaxies would form where bubbles collide around the edges of voids full of dark stuff. We are left with a literally explosive scenario of galaxy formation.

Calculations made by Witten and his Princeton colleagues Jeremiah Ostriker and Christopher Thompson suggest that the resulting bubbles would produce a foamlike structure with filaments and sheets of galaxies surrounding voids up to 50 million light-years across, exactly as we see in the actual Universe. In that case, however, the string loops need not lie at the centres of galaxies, and the subtleties that distinguish galaxies formed against a background of hot dark matter from those formed against a background of cold dark matter would be lost.

This brings up another kind of cosmic coincidence. Some coincidences—mentioned in part 1 of this book, and discussed in detail in part 3—hint at the existence

of Deep Truths, as John Schwarz puts it. They give us insight into special features of the laws of physics, which have to be the way they are if we are to be here at all to puzzle over them. Other coincidences are less deep. The way galaxies are distributed across the sky resembles the way cosmic strings, if they exist, must be distributed. But we can imagine other ways to make the pattern of galaxies. It doesn't prove strings exist, but it does encourage theorists to speculate further along these lines. Long strings should be moving through the Universe like cracking whips as wiggles move along infinite strings. These moving strings would leave "wakes" behind them, regions in which density had been increased, and in which galaxies might form. That, too, could explain why galaxies form in sheets separated by large amounts of seemingly empty space. There are many different ways in which cosmic string could explain the existence of galaxies in the Universe. So how might we expect to find strings, if they really do exist in our Universe?

Seeking Strings

Like all massive objects, strings affect nearby space-time through gravity. From far away—a distance much greater than the radius of the loop—a loop of cosmic string has a gravitational influence similar to that of any concentration of mass, such as a black hole. But close up, or when the radius of the loop is much bigger than the distance to the nearest part of the loop, another distortion of spacetime dominates.

Strings are not simply supermassive objects. They are cracks in the fabric of spacetime, defects in the structure of the vacuum. Space near a string has different properties from ordinary flat space, and this can be pictured by imagining an ideal, infinitely long, straight

r a G

fill

I 8^

1=1 a

sSbs * Bis

II fi

*T3 .> 3 C

3

8 2

u COX

&, 5 °

Bill

Q ^

Sign

" 5 * »

iZ S £ 8 08

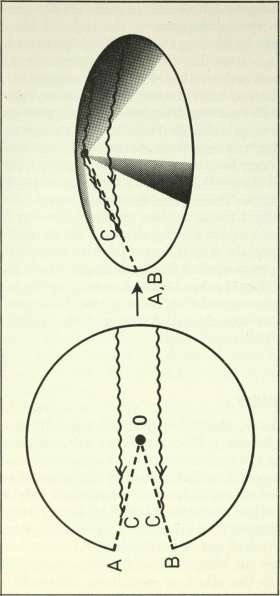
string, lying still in flat space. The string distorts space around itself to make the space (not the string) conical. The way to get a handle on this is by considering a circle drawn around the line of the string. In flat space, the Euclidean geometry that we learned in school applies, and the ratio of the circumference of a circle to its diameter is pi, 3.14159. But if you draw a circle around a length of cosmic string and measure the ratio of the circumference to the diameter, you will find that it is a little less than pi. Or imagine travelling around a loop of cosmic string in a circle. In ordinary flat space, you would get back to your starting point after you had turned through 360 degrees. But if you were travelling around a piece of cosmic string, you would get back where you started before you had travelled around 360 degrees. It is as if a small angle had been cut out of space, and the edges pasted together to close up the

gap.

The effect of this on matter is easy to visualise. Imagine two particles (or stars) moving through space parallel to each other. Because they are moving along parallel lines, like the lines of a railway track, they stay the same distance apart. But if the particles pass either side of a length of cosmic string, the distortion of conical spacetime makes their paths converge, so that eventually they will collide (this is the effect that compresses matter behind a moving string, and may encourage galaxies to form in the wake). The string distorts space as if the two particles were being pulled together by gravity—although this is not gravity in the usual sense of the term. It is a distortion of spacetime caused by the presence of a defect.

The speed with which the two particles begin to move together depends on how fast they go past the string—or, to put it another way, if we imagine the two particles at rest with a line of string passing between them, it depends on how fast the string is moving.

This makes it easy to answer the question that always arises when strings are mentioned. What would happen if one passed through the room in which you are sitting? The first point is that you would not be aware of the string through its mass in the usual gravitational sense. It is only when you view a closed loop of string from a long way away that it seems to have the gravitational field of a large mass. With a width less than that of a hydrogen atom, a string could cut at waist height right through your room, and your body, without your feeling a thing. But if the string were moving fast enough (perhaps at about the speed of light), the conical distortion of space behind it would quickly become apparent, as your head and feet (not to mention the ceiling and floor of the room) moved towards each other at a speed of several kilometres per second. It would be messy, and spectacular, proof that cosmic strings exist.

If the same thing happened to a star, the material making up the star would be squeezed, perhaps triggering a violent burst of nuclear reactions and making the star explode outwards. It is possible (we wouldn't go so far as to say likely) that an occasional stellar explosion could result from this string compression effect.

Conical space around a cosmic string would also affect the photons of the cosmic background radiation. Wherever a string moves transversely across the sky, as viewed from Earth, the radiation we see would be slightly cooler on the leading side and slightly hotter on the trailing side. If we ever find patches of the sky where the 3 K background radiation seems to differ from the average temperature, and especially if those patches have sharp edges, that might be taken as evidence in favour of cosmic string. A related effect of a length of string would be to bend light passing near it. If a piece of string happened to be passing between us and a distant galaxy, we might see two images of the galaxy,

produced by light rays that had travelled along either side of the string and been bent towards the Earth. Massive objects, such as galaxies, also bend light rays that pass near them, producing multiple images in a similar way, and such a system is usually known as a gravitational lens. We will discuss the more familiar sort of gravitational lens in the next chapter; a key distinction between such lenses and the string effect is that gravitational lenses ought to produce odd numbers of images (three, five, and so on) whereas the string effect generally produces only two, which appear equally bright. So another test for the presence of strings is to search for regions of the sky where pairs of seemingly identical galaxies (or quasars) lie above and below a more or less straight line. There have, indeed, been claims that such pairs of images have been identified, but as yet none of those claims has stood up to closer scrutiny.

The more theorists investigate the possibilities afforded by string, the more fun it seems. The scenarios cannot all be right, but some of them might be. We have already mentioned the possibility of forming galaxies in flat sheets in the wake of a moving straight string; a small, fast-moving loop of string can do a similar job simply through its conventional gravitational influence on surrounding matter, pulling in mass behind itself to produce a tubelike wake. Both processes could have been operating back at a redshift of 200 or more, sowing the seeds for galaxy formation when the Universe was young. Loops of electrically conducting string could have started "blowing bubbles" at that epoch. High-energy radiation from these strings, in the X-ray or gamma-ray bands, emitted at a time long before the first galaxy formed, might be identifiable today. Different forms of string can produce both sheets and filaments of galaxies, even if the strings that did the job have long since moved far away from where

we see the galaxies today, or have even evaporated completely.

Fast-moving loops that radiate energy asymmetrically will generally get faster, accelerating towards the speed of light, while their mass diminishes. On the other hand, if this rocket effect (due to either gravitational radiation or photons) acts to slow them down, loops that are born travelling at high speed could even slow to a halt, and then pick up speed in the opposite direction. While it is moving slowly, such a loop can gather mass around itself by gravity, and when it begins to speed up again it has to drag this mass along with it. If it accumulates enough mass, it cannot succeed in shifting it. Instead, trapped in the gravitational grip of the matter that was originally attracted by its own gravity, the loop may circle around in an orbit inside the accumulation of matter. If that matter forms a cluster of galaxies, we might look for traces of cosmic string in the form of an unusual, energetic galaxy displaced from the centre of such a system.

The observable consequences of strings depend on how heavy they are—on their mass per unit length. String theories relate this directly to one of the basic constants of unified theories, which is not yet pinned down by experiment. Were astronomers ever to find unambiguous evidence for gravitational lensing by a string, they could determine the fundamental mass quite straightforwardly. If strings indeed constitute the initial fluctuations from which galaxies formed, then we can already infer this mass to within a factor of 2. If theoretical physicists, using a different line of reasoning, were to come up with a similar mass as a requirement of their theories, this would suggest that strings did indeed trigger galaxy formation—otherwise, the agreement of the two estimates would be a simple coincidence. Moreover, there is a real prospect of de-

tecting the background of gravitational waves generated by strings, as we shall see in the next chapter.

Strings much lighter than those we have discussed might also exist. If there are equally few of them as the more massive strings, then they play no important role in the evolution of the Universe. If, however, they do not "reconnect" when they cross one another, splitting off ever-smaller loops, then it is possible that this lighter form of string could form a tangled network that has a total length so great that it contributes significantly to the dark matter. And that, perhaps, is a suitably awesome note on which to leave the subject of cosmic string—except that it must, inevitably, crop up once again as we turn our attention to ways in which to probe the dark matter content of the Universe using gravity's telescopes.

CHAPTER EIGHT

•

Gravity's Telescopes

TWANGING COSMIC STRINGS are not the only things that make gravitational waves. General relativity describes gravity in terms of variations in the fabric of spacetime. It is a geometrical theory, all to do with curvature; the only odd thing about it, from an everyday perspective, is that what is being curved can be just empty space. But this is, perhaps, easier to accept today, when physicists talk about a vacuum seething with energy, and virtual particles popping in and out of existence, than it was when Einstein first introduced the concept. The way to remember how matter and space interact is through a simple couplet:

Matter tells space how to curve Space tells matter how to move

A large mass like the Sun, as the couplet tells us, curves space in its vicinity. A smaller mass, like the Earth, follows the line of least resistance in that curved space.*

*The smaller mass also curves space, of course, and the line of least resistance is really determined by the combined curvature from both masses.

We see the effect as a force, gravity, pulling us towards the Sun, and holding our planet in orbit around the Sun. That orbit is the path of least resistance in curved space. But where do gravity waves come in?

Think of matter as solid lumps embedded in a stretched rubber sheet, spacetime; when one of those lumps vibrates, it sends ripples out through the sheet, and those ripples will set the other lumps of matter vibrating in sympathy. That is the principle behind gravitational radiation, and also behind the detectors with which physicists hope to measure gravity waves. The complications, such as they are, arise partly because space is actually three-dimensional, not a two-dimensional sheet, and, more importantly, because gravity waves are so very feeble that it pushes modern technology to the limit to hope to measure them. As far as the comparison is meaningful, since we are not really comparing like with like, gravitational radiation is only about 10" 40 times as strong as electromagnetic radiation.

Gravitational waves are produced by moving masses, in a similar way to the production of electromagnetic waves by moving electrical charges. An isolated, perfect sphere of mass, however, does not radiate gravitational waves. The amount of radiation a mass can emit, according to Einstein's theory, depends on what is known as its quadrupole moment, a property related to its shape. An American football has a large quadrupole moment, but a soccer ball has none. Gravitational waves are in a form known as quadrupole radiation, and they have a distinctive effect on spacetime as they pass through it.

The best way to visualise what is going on is by thinking of a flexible circular ring. When a gravity wave passes it, the ring is stretched in one direction and squeezed in another, at right angles, simultaneously. It becomes an ellipse. Then, the pattern reverses, and what was the long axis is squeezed while what was the

THE STUFF OF THE UNIVERSE

Figure 8.1 A circular ring is distorted into an ellipse when gravitational waves propagate through it. Waves could be detected by monitoring the position of the four masses, one in each quadrant (or, indeed, of any three of these, forming an L).

short axis is stretched. This pattern of alternate squeezing and stretching, in two directions at right angles to each other and out of step, is the characteristic "signature" of quadrupole gravitational radiation. It is not just the ring that is actually being stretched and squeezed, but the fabric of space itself. Four masses, placed one in each quadrant of the circle, will move rhythmically in and out, as though they are feeling a periodically varying gravitational (tidal) force. In fact, just three "test masses," marking an L shape, are enough to monitor the passage of gravity waves— if you have a

sensitive enough means to measure the tiny movements that the passage of gravitational radiation causes. The effort will certainly be worthwhile if and when we can measure directly gravity waves from cosmic strings, supernova explosions, and other cosmic sources—perhaps shedding some light on dark matter in the process.

In a hypothetical universe where no electrical charges existed, the only kind of radiation would be gravitational. Electromagnetic radiation dominates in our Universe as a consequence of the 40-odd powers of 10 by which electrical forces overwhelm gravity on the short scale. But this doesn't mean that we can ignore gravitational waves entirely.

Making Waves

A long straight bar of material, spinning around like a two-bladed propellor, would be a good source of gravitational quadrupole radiation. Viewing the spinning bar sideways (in the same plane as it spins), you would see it first full length, across the line of sight, then pointing to you end on, and very narrow, then full length again, and so on. This is rather like the repeated squeezing and stretching of space by gravity waves, and the motion of the bar does indeed produce that kind of radiation. A spinning dumbbell, or two stars in orbit around each other, do similar jobs of producing radiation. A binary system in which the two stars were very close together, and orbiting very rapidly, would be the best source, and in one such system the effects of gravitational radiation have been discovered.

This is a system known as the "binary pulsar," although in fact it contains only one pulsar (a rapidly spinning neutron star that radiates at radio frequencies) orbiting closely around another neutron star that is not a radio source. Pulsars are a delight to astrono-

mers because their pulses of radio noise (produced by a lighthouse effect as the pulsar spins) follow each other with exquisite precision; they are the most perfect clocks known, other than the vibrations within atoms that form the basis of modern scientific timekeeping on Earth, the atomic clocks (and some pulsars may even beat atomic clocks at timekeeping). Variations in the radio pulse rate from the binary pulsar, timed with microsecond accuracy, reveal its orbital motion around its companion. The apparent pulse rate speeds up when the pulsar moves towards us, and slows when it recedes— essentially a version of the Doppler effect. The period of the pulsar's orbit is very slowly decreasing. This means that the two neutron stars are moving slightly closer to each other as time goes by, which in turn means that the binary system is losing energy. General relativity tells us exactly how much gravitational radiation this system should be producing; it turns out that the predicted rate of gravitational radiation exactly matches the measured rate of loss of energy from the system. This is one of the greatest triumphs of Einstein's theory, and one that makes researchers confident that gravitational radiation will be measured directly, here on Earth, in the 1990s.

It was very nearly detected in 1987, when the supernova in the Large Magellanic Cloud exploded. When such a star dies, its core collapses suddenly inwards, and this collapse ought, relativity theory tells us, to produce a burst of gravity waves. The strength of the burst depends on how irregular and asymmetric the collapse is. A strictly spherical collapse radiates nothing. But even if the infall had been as chaotic as it could conceivably have been, the burst from supernova 1987A would still have been just one-tenth of the power needed to trigger existing detectors, by the time it arrived at Earth. As more sensitive detectors become operational, not just supernovae but vibrating or colliding

black holes could also be detected (assuming they exist). We have already mentioned the potential of cosmic strings as gravity wave generators. The grandest speculation of this kind, however, is that the Universe might be filled with a background of gravitational radiation, left over from the violent events that occurred during the Big Bang and in the era of galaxy formation, comparable to the background of electromagnetic radiation. It might seem a daunting prospect to measure any of these effects, since they are calculated to produce a distortion of space on Earth amounting to only about one-millionth of the diameter of a proton for every metre of space being measured; but experimenters really do believe that they will have instruments that sensitive running very soon.

Measuring Waves

The experimental challenge was taken up by Joseph Weber, at the University of Maryland, in the 1960s. He built detectors based around large cylinders of aluminium, designed to vibrate as gravity waves passed by. Twenty years of research have failed to discover any such waves, almost certainly because they are too feeble to have a noticeable influence on these detectors.* But now a second generation of detectors, based on the same principles but a hundred thousand times more sensitive, are beginning to come into operation.

A typical "resonant bar" gravity wave detector is a cylinder of aluminium weighing 4,800 kilograms, cooled

*General relativity, in fact, predicts that any gravity waves likely to be around will be too feeble to be picked up by Weber's detectors. If Weber's detectors had found gravity waves, general relativity could not have explained such strong gravitational radiation in the Universe today— unless, by coincidence, their source were very close to the Earth, or (for instance) the galactic centre was unusually active at present.

by liquid helium to a temperature of 4 K (-269 degrees C). It has to be so cold in order to minimise the thermal vibrations of the atoms in the bar, and it has to be kept in a vacuum chamber to avoid being buffeted by molecules of air. A transducer attached to the bar converts any oscillation, such as the stretch and squeeze of a passing gravity wave, into an electrical signal, which is then amplified using superconducting technology. These amplifiers are so sensitive that they can indeed record vibrations in the bar corresponding to movements a thousand times smaller than the diameter of an atomic nucleus.

The main problem with this sensitivity is that any vibration, not just a gravity wave, will trigger the detectors. But advanced detectors of this kind are now becoming operational at Stanford and at the University of Maryland in the United States, in Rome, in Australia, and at other sites around the world. Researchers should be able to pick out genuine astronomical sources by their effect on each of these detectors in turn, and the time delay between the different detectors being triggered will give an indication of where the waves are coming from.

In another, quite separate approach to the search for gravity waves, other experimenters are working with beams of laser light. These experiments are very much like the idealised example of measuring changes in a circular ring. Large masses, with mirrors attached to them, are placed at two opposite corners of a square (it needn't actually be a square, but let's keep it simple) and laser beams are shone onto the mirrors from a third corner, the angle of the "L." The light from a single laser beam is split into two beams, and one sent out to each mirror and reflected back. When the two beams return, they are combined to produce an interference pattern of light. If the lengths of the two sides of the square change as a gravity wave passes, each

laser beam will be affected, with one having farther to travel and the other less far to travel. The interference pattern will change as a result, revealing the passage of the gravity wave.

All of this involves running the laser beams through pipes evacuated to a very pure vacuum, about a metre in diameter and several kilometres long. Two such detectors are planned in the United States, to run in Southern California and in Maine; others may be built in Scotland and West Germany. Each will cost about the same as a large optical telescope, and if they work as planned, astronomers may one day be observing traces of gravitational radiation from supernovae in other galaxies and from other catastrophic events, such as collisions between two neutron stars in a binary system, or stars orbiting a black hole at the heart of the Milky Way.

Supernovae should yield gravitational wave pulses, but how strong these are depends crucially on details of the explosions and, in particular, on how symmetrical they are. Binary systems, on the other hand, are guaranteed to have big quadrupole moments, so even a pessimist could count on radiation from those. The only question is, can we detect it? About a hundred million years from now, gravitational radiation will have ground down the binary pulsar's orbit so small that the two neutron stars will revolve around each other hundreds of times per second, instead of once every eight hours (as they do today). The gravitational radiation emitted will then be enormously powerful, and during the final plunge, when the stars collide, coalesce, and form a black hole, up to 10 percent of their total mass-energy will be transformed into a burst of gravitational waves lasting only a few milliseconds. We do not know how many binary neutron stars of this type there are in the Galaxy. A reasonable guess would be a hundred or so. If each had a lifetime of a hundred

million years, then one would "die" in this way every million years—such events are ten thousand times rarer than supernova explosions. A laser interferometer capable of detecting such a burst of gravitational radiation coming from several hundred million light-years away would, however, have more than a million galaxies like our own within range. The expected rate of detections would then be one a year—sufficient motivation for experimenters, who would be unhappy if a lifetime's labours yielded only null results (only a few experimenters derive sufficient satisfaction solely from meeting the technical challenge of devising sensitive equipment, regardless of whether it actually detects anything).

More powerful bursts still could come from the massive black holes that lurk in galactic centres. Mergers between pairs of galaxies are not uncommon. If there were a black hole in the heart of each such galaxy, the two holes would settle towards the centre of the merged system, forming a binary, The binary would emit gravitational waves, and eventually coalesce, releasing perhaps a hundred million times more energy than two coalescing neutron stars. The wavelength of this radiation, however, would be a hundred million times longer, because bigger objects are involved—the burst would last for hours, not milliseconds. Unfortunately, bars and laser interferometers on Earth are not sensitive to such slow waves, because of background vibrations caused by seismic activity, changes in the weather, and other terrestrial events.

Loops of cosmic string would emit powerful gravitational radiation of longer wavelength still—one cycle per year, or even slower. For these ultraslow waves, nature has provided a detector for us, in the form of single pulsars spinning rapidly with a precision far better than terrestrial clocks. Fast-spinning pulsars pro-

vide both the best evidence for gravity waves, from the binary pulsar, and the only constraint on how much background gravitational radiation there may be in the Universe. The fastest pulsars spin once every few milliseconds, producing precisely timed ticks of radio noise a few milliseconds apart. They are known, with a slight exaggeration, as millisecond pulsars. Atomic clocks have an accuracy of about one part in ten thousand billion (one in 10" 13 ). A pulsar can be even more accurate, "losing" less than a microsecond per century.* When the first millisecond pulsar was found, there was no way to test this, because there was nothing accurate enough to compare it with; but now several millisecond pulsars are known, and by comparing them with one another astronomers hope to be able to establish a timekeeping system, a cosmic clock, even more accurate than the atomic clocks. Any background of gravitational radiation that fills the Universe will distort space between us and the pulsar as the waves pass; the resulting jitter could affect the apparent regularity of the cosmic clock. This effect provides a sensitive probe for very-low-frequency gravitational waves—ripples in spacetime with wavelengths of a few light-years. Since no such effect has yet been seen, we can say with confidence that the amount of mass-energy stored in gravitational radiation of this kind is no more than one-millionth of the amount needed to make the Universe flat by this means alone. This upper limit is already very interesting to string theorists, since it is close to the level of the expected gravitational wave background from string loops (see chapter 7). When the

*They actually slow down more rapidly than this, but in a steady and predictable manner. What matters, if we are using such a system as a clock, is the amount by which the clock might deviate from this steady change, and that could be a fraction of a microsecond per century.

pulsar timing data have been gathered for a few more years, the results will be still more restrictive. If a wave background is still not detected, we shall have to conclude that strings do not exist (or, if they do, that their mass is too low to have triggered galaxy formation).

Gravitational radiation by no means dominates the Universe, but its eagerly anticipated discovery will provide astronomers with a new kind of telescope with which to probe energetic objects. Those gravitational telescopes are sure to reveal previously unsuspected features of the Universe, as well as help us to get a handle on dark matter and, perhaps, strings. Meanwhile, dark matter itself may be bending spacetime in its vicinity sufficiently to produce gravitational lenses that give us a view of objects so distant that they could never be seen without this other form of gravitational telescope. It may, indeed, be making a spectacle of itself, even while it remains unseen; gravitational lens-ing provides the nearest we can ever come to actually seeing the dark stuff that dominates the Universe.

Gravitational Lenses

Light bending is just about the most familiar and well-tried feature of general relativity. The theory first appeared in print in 1916, complete with Einstein's prediction that light would follow curved paths through space distorted by the presence of matter. In 1919, this light-bending effect was measured during an eclipse of the Sun, showing up as a displacement in the positions of the images of stars that lay near the Sun on the sky (but far beyond in space) at the time of the eclipse. Light from those stars, coming from behind the Sun, had indeed been deflected, by exactly the amount Einstein had predicted, as it passed the edge of the Sun. The gravitational bending of light was first seen, and

photographed, more than seventy years ago. This is the basis of gravitational lensing.

A sufficiently massive object lying between us and a distant star would bend light so much that it might produce two images of the distant star, as viewed from Earth. In 1936, Einstein himself investigated this possibility, and proved that if a compact, massive object can indeed, under the right circumstances, create two separate images, one (and sometimes both) being magnified. If the alignment were perfect, the stars would appear as a complete ring of light encircling the "lens.' 1

Things become a little more complicated, and even more interesting, if either the lens itself or the object that is being lensed is an extended object, such as a galaxy. If a black hole with a hundred times the mass of our entire Galaxy lay halfway between us and a distant galaxy (not, we must admit, a very likely possibility), the image of that galaxy on the sky would be in the form of a bright ring of light, from the part of the galaxy exactly behind the black hole, with two images like the ones Einstein described, one bright and one dim, on opposite sides of the ring. With a much less massive (and correspondingly more plausible) black hole doing the imaging, the ring would be too faint to see, and the two images of the distant galaxy (or quasar) would appear on their own. In 1979, astronomers found two quasars whose images are just six seconds of arc apart on the sky—this is about the angle covered by a tennis ball at a distance of five kilometres. These two quasars are so alike, in terms of their colour and redshift, in particular, that they were soon regarded as the first identification of a pair of images from a gravitational lens; we now know that there is a large cluster of galaxies, which includes a giant elliptical, in just the right place to be acting as the lens that is producing the two images of one quasar.

More than half a dozen gravitationally lensed sys-

.<£

s

214 THE STUFF OF THE UNIVERSE

terns are now known. The exact number you choose depends on the date (observers seem to find about one more system of this kind each year) and your gullibility (sometimes, enthusiasts claim that pairs of quasars are gravitational images, but later investigation shows that they really are two distinct quasars). But there is another very interesting system, apart from the initial discovery, where the object that causes the lensing has also been identified—in this case, as a large disc galaxy relatively near to our own Galaxy. This system is particularly interesting because it shows what happens when the object that makes the lens is large and definitely not spherical. The first observations suggest that the light from a distant quasar has been split and bent to form three images, a tiny triangle on the sky with sides a few seconds of arc long. More sensitive measurements later revealed a fourth image, completing a square surrounding the galaxy's central regions; and there may even be a fifth almost exactly underlying the centre.

The number of images is crucial for any attempt to determine the nature of dark matter in the Universe using gravitational lenses. If the lens is a black hole, it should produce two, and only two, images. If the lens is a spread-out object such as a galaxy, it should produce at least three images, perhaps more, but definitely an odd number.* And if the "lens" is actually caused by the distortion of spacetime behind a cosmic string, there should be two equally bright images. Over the past couple of years, however, astronomers have been even more excited about the discovery of another kind of arc across the sky.

*It is at least slightly embarrassing that observers have yet to find a third image in the first gravitationally lensed system identified, because the lens there does seem to be an extended object. There are ways around this; perhaps the third image is too faint to be seen, perhaps the lens is actually a black hole in the intervening cluster of galaxies, and so on. The study of gravitational lenses in the real Universe (as opposed to in the mathematical dreams of theorists) dates only from 1979 and still has loose ends to be tied up.

Luminous Arcs

These features of the Universe are big. They stretch around almost perfectly circular arcs, bits of circles, for a length of more than 300,000 light-years; the width of each arc is about 30,000 light-years. Two of these huge, almost perfect arcs were discovered in the mid-1980s; each seems to lie in a cluster of galaxies. They each stretch across a distance three times bigger than the size of our Milky Way Galaxy, and are the largest known continuous bright objects in the Universe; although they look very small, it is because they are so far away. A third, more wispy arc was discovered at about the same time.

The discoveries were reported almost simultaneously by French astronomer Bernard Fort and colleagues at the Toulouse Observatory, and by Roger Lynds and Vahe Petrosian in the United States. The French team almost immediately guessed that the features might be produced by the gravitational lens effect—that they might, indeed, be "Einstein rings." At first this suggestion met with little response. Lynds and his colleagues initially suggested that the arcs might be expanding shells of material, blasting outwards from some cosmic explosion, perhaps caused by a collision between galaxies, and perhaps a common feature of clusters of galaxies. The theorists had a field day for a while, coming up with all kinds of exotic ideas to explain how such perfectly circular arrangements of stars could form. But a splash of observational cold water soon came from the French team, which showed that different segments of a single arc all had exactly the same spectrum and must therefore all be part of the same structure. Proof of the nature of the arcs came when the redshift of those spectral features was measured.

In the best example of this newly discovered astronomical phenomenon, the arc looks as if it is part of a

cluster of galaxies known as Abell 370. But this cluster is at a redshift of 0.374, while the light from the arc has a redshift of 0.724. The light from the arc actually originates almost twice as far away in the expanding Universe as the distance to the cluster. It is a magnified and distorted image of another galaxy. Intriguingly, though, calculations show that the clusters cannot produce powerful enough lensing unless they contain at least ten times as much mass as we can see in the form of bright stars in the constituent galaxies. This exactly matches the broad picture in which 90 percent, or more, of the gravitating stuff is dark.

There are many intriguing implications. First, the spectrum of light from the arcs seems to match the spectra of disc galaxies (the averaged-out light of billions of stars), magnified and brightened up to twenty-five times. This means that they may tell us what ordinary galaxies, as opposed to quasars or radio galaxies, were like when the Universe was less than half of its present age. A lot more analysis needs to be done, but it is already clear that the light from these galaxies contains a lot of ultraviolet radiation, typical of hot young stars—exactly what you would expect if we are viewing galaxies in the early stages of star formation. In addition, although these two large arcs were noticed simply because they are so large, the alignment needed to produce them must be a very rare occurrence. There should be many more systems in which there is a less perfect alignment, and only fragments of the Einstein ring are produced—and some of the peculiar objects that astronomers photograph in clusters of galaxies may well also be fragmentary images of very, very distant galaxies. Gravity really does provide a telescope with which we can view things as they were long ago and far away; but you don't necessarily need a whole cluster of galaxies to make an effective lens to use in gravity's telescope.

Shedding Light on Dark Matter

Light from the most distant objects in the Universe, the quasars, may indeed be revealing the nature of the matter that holds our Galaxy together. The double images on the sky formed by light from some quasars may be produced by galaxies, 90 percent of whose mass is in a darkjialq. Fine structure, details within those images, may, furthermore, tell us whether these haloes are made of very massive objects (VMOs) or brown dwarfs (Jupiters), and thereby decide between these two rival baryonic candidates for the halo dark matter.

If VMOs provide a substantial fraction of the halo dark matter, there could be a million black holes, each with the mass of a million Suns, together providing ten times more mass than all the bright stars of the Milky Way system put together. The probability of seeing the lensing effect due to an object in the halo of our own Galaxy is only about one in a million. But it is much more likely that light from a very distant quasar will be lensed, on its way to us, by an object in the halo of another galaxy roughly halfway along the line of sight. If the light passes through the haloes of several galaxies, as it must for very distant quasars, then clearly there is a still bigger chance of it being lensed. We are not talking now about the lensing effect of a whole galaxy, or of a cluster of galaxies (what you might call "macro" lensing); instead, we are considering light from a distant quasar being bent by a single star- or planet-sized object in the halo of a galaxy between us and the quasar (microlensing).

Such an event may be fairly likely, but would it be observable? Surprisingly, the answer is yes. If the microlensing is caused by a VMO of about a million solar masses, and this object is about halfway out across the visible Universe (at half the Hubble distance), then

THE STUFF OF THE UNIVERSE

-w

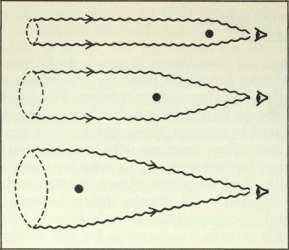
\C

Figure 8.2 The focussing of light from a very distant source by a compact mass. The lens has, in effect, a short focal length for light passing close to the compact object, and a longer focal length for more distant passages. A given object is therefore more efficient (i.e., has a larger cross-section for forming images) when it acts as a lens with very long focal length. For this reason, a black hole in a remote galaxy is more likely to cause detectable lensing than a similar hole close at hand in our own galactic halo.

the two images it produces will be separated by an angle of one-thousandth of a second of arc, as viewed from our Galaxy. This is several thousand times less than the separation of the widest known pairs of images in the gravitationally lensed systems we have discussed so far, and no optical images could be sharp enough to reveal such fine structure. But by linking together electronically radio telescopes on opposite sides of the world, astronomers can create the effect of a single instrument with the same resolving power as a radio dish the size of the Earth. This technique, known as interferometry, could measure such a small separation between the components of a double source. Many candidate objects have been observed, with no clear

Gravity's Telescopes 219

case of double images. The statistics suggest that micro-lensing is so rare that no more than one-tenth of the matter needed to make the Universe flat can be in the form of VMOs, which each have a mass of a million Suns (which, of course, gives at least a gentle push to close the door on the possibility that most of the halo mass in our own Galaxy is in the form of VMOs).

What about brown dwarfs or Jupiters? In that case, the same effect would produce images with a separation, viewed from Earth, of less than a millionth of a second of arc. This is far too small to be measured. But, equally, it is such a small angle that an object half the Hubble distance away from us and travelling at the modest speed (by astronomical standards) of a hundred kilometres a second will cross an angle of a millionth of a second of arc in a few years. This could provide a way to make images of distant quasars twinkle quickly enough to be noticed in a human lifetime. The situation is complicated if the quasar light passes through several galactic haloes and has the chance to be lensed several times on its way to us, and also because other effects, intrinsic to quasars, cause them to vary. Once again, however, such limited observational evidence as we have so far seems to rule out the possibility that more than one-tenth of the matter needed to flatten the Universe could be in this form.

There are at least some hints from these microlensing studies that haloes are neither predominantly VMOs nor Jupiters, although some such objects may be present. That suggests that the halo stuff itself is nonbaryonic, spread out, dark matter. Which raises another question: If a typical galaxy is 90 percent, or perhaps 99 percent, spread-out dark matter, with the visible stars merely a kind of icing on the cake, is it possible that some of the cakes have been left uniced? Are there, in fact, dark "haloes" that do not contain bright galaxies

\1]\\

220 THE STUFF OF THE UNIVERSE

at all? Gravitational lensing may provide the means to answer that question, as soon as the Hubble Space Telescope gets into orbit.

Dark Galaxies

Recent work on galaxy formation, such as the computer models involving cold dark matter, suggests that there may well be dark haloes in which galaxies have failed to form. Because light gets bent by matter regardless of whether that matter can shine (as the example of a black hole makes clear), these "invisible" haloes should reveal their presence by distorting light from distant bright objects. One of the most puzzling features of the known handful of cases of gravitational lensing in the Universe is the large separation between the two images in some examples. This is much bigger than you would expect if the object doing the lensing was a single ordinary galaxy or a black hole. Another puzzle is, as we have mentioned, the fact that in some of these systems there is no trace of a bright galaxy (or galaxies) in the right place to produce the lensing effect. Both these puzzles arise with full force in the case of the system with the widest separation of images, a full 7.3 seconds of arc. Could this, and other such systems, be a result of lensing by dark haloes along the line of sight?

When the appropriate calculations are carried through, it turns out that a single extended halo is unlikely to form multiple images of a bright object that lies behind it, as viewed from Earth. The light is distorted, but not strongly focussed enough to yield multiple images. On the other hand, if two dark halo-type objects lie along the line of sight to a distant source (rather like the two lenses in a simple telescope) then multiple imaging can occur. The situation is quite complicated, involving

lensing by two haloes at different redshifts, which may not be perfectly aligned with each other or with the distant quasar. In CDM models there may be more of these "failed" galaxies than there are visible, starry galaxies. In a flat universe the effect is most likely for dark haloes that lie at redshifts between 0.3 and 0.6, and then double lensing by such haloes ought to produce images separated by between 5 and 7.5 seconds of arc as viewed from our Galaxy. This is exactly in the range where the puzzlingly widely separated images are seen. With no intervening lens galaxy detected in careful searches of the sky, we feel that there is a strong case that one or two of the known gravitationally lensed systems involve lensing by two dark haloes.

Failed galaxies may be dark because the baryons in the halo have all condensed into dim objects, such as brown-dwarf stars. Alternatively, they might be haloes that contain only nonbaryonic matter, from which all the baryons have, for some reason, been pushed out. But perhaps the best bet is that they are a mixture of baryonic and nonbaryonic material, in which the baryons are spread out through the halo in the form of clouds of hydrogen gas (themselves laced with 25 percent helium produced in the Big Bang). In this section of our book, we have concentrated so far on the dark stuff that dominates the Universe, the nonbaryonic matter. But we should not forget that there may be a great deal of dark baryonic material as well. The galaxies we see, even if each contains ten times as much mass in dark stuff (possibly nonbaryonic stuff) as in the bright stars, still contribute an average density of only 10 to 20 percent of the amount required if the Universe is indeed flat. So most of the dark stuff, and most of the hydrogen atoms as well, may lie between the galaxies and clusters. There are a lot of unseen hydrogen atoms out there somewhere.

Some of the theories of galaxy formation that we have discussed suggest that the voids between bright galaxies are not really empty but contain large numbers of failed galaxies. And now, as we shall see in the next chapter, there is a way to investigate those failed galaxies by looking not at the way they bend light from distant objects but at the way they leave their imprint in the form of dark lines in the spectra of quasars.

CHAPTER NINE

*

The Lyman Forest:

Emergence and

Evolution of Galaxies

ASTRONOMERS measure distances to galaxies and quasars in terms of redshift, the displacement of lines in the spectra of these objects compared with the wavelengths at which these lines occur in the laboratory here on Earth. These spectral lines are produced when electrons in atoms move from one energy level to another. The best way to think of these energy levels are as steps on a staircase. An electron can "sit" on any step, but there is no stable position for it to rest between steps. If the atom absorbs precisely the right amount of energy, an electron can jump up one, or two, or some other whole number of steps. But it can only jump a whole number of steps, because there is nowhere else to jump to. Then, a little later, it may fall back down, again by one, or two, or some other whole number of steps. The amount of energy involved depends on the size of each step, and the number of steps the electron jumps in one hop. Electromagnetic radiation, such as light, carries energy; the shorter the wavelength of the light, the more energy it carries. If the atom absorbs energy from

background light, this leaves a sharply defined dark line in the spectrum, where the light has been taken away. If the electron falls down the steps, it radiates energy, again at a very sharply defined wavelength, producing a bright line in the spectrum.

These lines can be measured in the laboratory. Their wavelengths can also be predicted, using quantum theory. Indeed, the success of quantum theory in explaining the spectrum of hydrogen was one of the great triumphs of physics in the early twentieth century.

Because hydrogen is the simplest element, involving just one electron in orbit around a single proton, it has the simplest spectrum and the easiest to calculate. The energy levels in hydrogen are very precisely known. This is particularly useful for astronomers, because hydrogen is also by far the most ubiquitous element in the Universe, making up 75 percent of all the baryonic matter, both in bright stars and dark clouds. A thorough knowledge of the spectrum of hydrogen, together with the redshift effect, is all you need to measure cosmological distances.

Even the spectrum of hydrogen contains many lines. Think of our staircase as having just six steps from top to bottom, with the lowest step representing the lowest energy level, closest to the proton that forms the nucleus of the atom. An electron jumping from step six to step one will produce a characteristic line in the spectrum. Any other electron, making the equivalent jump in another atom, will produce the same wavelength of radiation, adding to the strength of that line in the spectrum of a cloud of hot hydrogen gas. But this is only the beginning. An electron jumping from step five to step one will produce another, different line, as will a jump from step four to step one, and so on. The result is that the spectrum of a cloud of hydrogen contains many lines, one associated with every possible jump. All the lines in this set involve jumps that end on step

one, and they will have a family resemblance. Then there will be another series of lines involving jumps that end on step two, a series involving jumps that end on step three, and all the rest (and we chose to consider only six steps; in reality there are more!). Just one of these sets of lines, however, is important to our present story.

The jumps that end on step one, for a hydrogen atom, were studied by Theodore Lyman, an American physicist, in the first two decades of this century. These lines are all in the ultraviolet part of the spectrum and involve higher energies than lines that appear in the visible part of the spectrum, at longer wavelengths than the UV. In Lyman's honour, this set of lines is called the "Lyman series," and the brightest line in the series is known as Lyman-alpha. Lyrnan-alpha occurs at 122 nanometres (nm) wavelength; this wavelength is both measured in the lab and predicted by quantum theory. Because the ozone layer of the Earth's atmosphere shields us from ultraviolet radiation, the Lyman-alpha line cannot be seen from Earth in the spectrum of the Sun or the spectra of other stars in our Galaxy. But Lyman predicted that the line ought to be present in the Sun's light, and when rockets lifted ultraviolet detectors above the stratosphere in 1959 (five years after Lyman died) his prediction was confirmed. Even in 1959, however, astronomers had no inkling of how important the Lyman-alpha line was to be in their work.

Quasars and Lyman-alpha

Quasars were first identified in the early 1960s, not long after the first direct observations of Lyman-alpha in sunlight. There are many spectral lines that can be used to measure the redshift of a quasar, but hydrogen

THE STUFF OF THE UNIVERSE

QUASAR REDSHIFTS

1101-325

1011114959.5007

n

^J\^^

AX

0.356

0.829

1.333

1.937

2.70A

MM

Wavelength (£)

Figure 9.1 The spectra of several quasars with different redshifts z, showing how the optical spectra of high-z objects reveal emission lines that are normally in the far ultraviolet.

lines are best because hydrogen is so common. Because of the redshift, the light by which we actually see (or rather, photograph) a quasar is not at the wavelength at which it was emitted. The energy that reaches Earth in the visible part of the spectrum originates from shorter wavelengths—in the ultraviolet. It happens that very hot, energetic objects such as quasars radiate a lot of energy in the ultraviolet, and because of the redshift

this energy may show up, to us, as a bright contribution to the blue end of the spectrum. It sounds paradoxical, but despite the redshift a quasar can actually look very blue, to human eyes, because the blue light we see used to be even "bluer"—that is, ultraviolet (a bigger redshift still, will of course shift the light all the way to the red end of the spectrum, so that the quasar actually looks red). With a lot of energy being radiated in the ultraviolet, the Lyman-alpha line of a quasar ought to be very strong. And with a big enough redshift, that line ought to be moved into the visible part of the spectrum, where radiation passes unaffected through the ozone layer of the stratosphere. In other words, it is actually possible to detect Lyman-alpha radiation from a high redshift quasar on the ground, without sending instruments into space. Lyman-alpha lines redshifted by as little as 1.7 (but no less) can just be detected, at a wavelength of 330 nm, using instruments on the ground. The Lyman-alpha emission line is generally so strong and clear that studies of its shape and energy can be used to infer details of the energetic processes that make the quasar shine so brightly. These are among the studies that suggest that quasars are powered by supermassive black holes. But this is far from being the end of the story. In a typical quasar spectrum, the Lyman-alpha line stands out as a high peak, like a very tall mountain. At wavelengths on the blue side of this line, however (at slightly smaller redshifts), there are very many weaker, dark lines, like a series of very narrow but steep valleys dipping down below the plain from which the Lyman-alpha mountain rises. These lines cannot be formed in the quasar itself—they are spread over a range of redshifts corresponding to distances of hundreds or thousands of millions of light-years in the expanding Universe. They must be caused

x

THE STUFF OF THE UNIVERSE

360 370 380 390 400 410 420 430 440 450 Observed wavelength (nanometres)

Figure 9.2 A spectrum of the quasar Q2206-199, with redshift 2.56, showing the many narrow lines that make up the Lyman forest. The broad Lyman-alpha emission line is on the right. (Taken by A. Boksenberg and W. Sargent, using the 5-metre telescope at Mount Palomar.)

when light from the quasar is absorbed by clouds of cold gas that lie between us and the quasar.

This forest of dark absorption lines was first noticed in 1971, but in the early 1970s spectroscopic techniques were not good enough to reveal many details of the forest. As spectroscopy has developed, however, astronomers have realised that they are looking at a whole series of Lyman-alpha lines, each one redshifted by a different amount. Like a distant searchlight silhouetting a nearby tree, the quasar light highlights hydrogen in clouds between us and the quasar. By the early 1980s, techniques had advanced sufficiently for an analysis of the Lyman forest to begin to yield information about those clouds.

Into the Forest

The study of the Lyman forest in the 1980s has been particularly exciting because it provides information only about regions of the Universe beyond a redshift of 1.7. Ordinary galaxies can be studied in detail out to a redshift of only about 0.3. This covers only a few billion

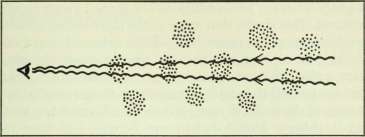
Figure 9.3 If the Lyman forests along two lines of sight—whether to neighbouring quasars or separate gravitationally lensed images of a single object—show some (but not all) lines in common, then the cloud sizes must be comparable with the transverse separation, as depicted here.

years of history, and a few billion light-years of space. All of the descriptions of bubbles, voids, sheets, and filaments of galaxies in the Universe are based on this relatively small portion of spacetime. The Lyman forest tells us about the early days, when the Universe was young—from about a billion years after the Big Bang to 4 billion years after the moment of creation. And what it tells us confirms the broad picture of a Universe dominated by dark matter, while eliminating some of the detailed models from contention and strengthening the credibility of the cold dark matter cosmology.

The light from a single quasar may contain dozens of Lyman-alpha absorption lines at different redshifts. By studying the details of a single line, astronomers deduce something about the conditions inside the cloud of gas that absorbed that particular wavelength of light.

Studies of the Lyman forest also show how big these clouds are. In some cases, very similar patterns of Lyman-alpha lines are seen in the forest from each of two nearby quasars. These may be different quasars that happen to lie nearly along the same line of sight, or they may be two images of a lensed quasar. What matters is that the light coming to us from two very

slightly different paths contains the same Lyman forest features. This shows that some of the intervening clouds are big enough to cover both of the quasar images on the sky. In other cases, pairs of nearby quasar images have quite different Lyman forest features—their light has not passed through the same clouds en route to us. A typical dark cloud turns out to be about as big as a small galaxy, 35,000 light-years across. And that in turn, adding in the estimates of the number of hydrogen atoms and protons in each cubic metre of space, tells us that the mass of a typical dark cloud is between 10 million and 100 million times the mass of our Sun, very much in the range of dwarf galaxies like the Magellanic Clouds, but a lot less than the mass of our own Galaxy. Using quasar light, we can actually weigh and measure dark clouds in space perhaps 10 billion light-years away from the Milky Way.

Another important feature of the improved spectroscopic studies is that they show no traces of lines corresponding to anything except hydrogen. The clouds ought to contain 25 percent helium, if our calculations of the Big Bang are correct, but the appropriate helium lines are too far in the ultraviolet to be seen from the ground even at these high redshifts. When the space telescope flies, it should detect these lines, as the helium forest, and tell us whether there is indeed 25 percent helium present in the clouds. The fact that no lines of heavier elements are seen is confirmation that only hydrogen and helium emerged from the Big Bang— heavier elements are made in stars, and stars have not yet formed in these clouds.

Modern techniques tell us how big individual dark clouds are and what they are made of. We can also use them to give us another handle on the nature of the nonbaryonic stuff of the Universe, by looking at what holds an individual dark cloud together, and at how the clouds are distributed across the Universe.

Large-scale Lessons

If clouds like this existed in isolation in space, they would disperse fairly quickly, as astronomical timescales go. They would, in a sense, evaporate. So what does hold them together? One school of thought holds that they are embedded in still bigger clouds of much hotter material. In those larger clouds, there would be no neutral hydrogen, only free protons and electrons, and so no Lyman lines to be seen. The pressure of the hotter gas outside would, however, stop the smaller, cooler clouds that we see from expanding and evaporating away. If this picture were correct, then as the Universe expanded this confining cloud of hot material would have cooled, so that the confinement of individual dark clouds was eased and they could disperse, leaving onl> wispy traces of gas behind. Since there do seem to be more lines in the Lyman forest at higher redshifts, suggesting that the dark clouds have gone somewhere as the Universe aged, this possibility has to be taken seriously. But we prefer an alternative scenario, which relates the presence of these dark clouds very neatly to the cold dark matter cosmology.

In the cold dark matter scenario, galaxies form from the bottom up, as small clumps of matter group together to make bigger clumps, and so on. Early in the history of the Universe, there should have been many irregularities in the distribution of the CDM on a scale smaller than the galaxies we see today. These irregularities, the gravitational potholes, would trap baryonic matter, but there is no reason to expect that in all cases all of this baryonic matter would condense into stars. A deep pothole with steep sides would pull baryons into its centre, where stars would form; a very shallow pothole might not be able to trap baryonic gas at all; but in an intermediate range of possibilities, moderately deep potholes with moderately sloping sides would trap

gas that stayed free to move about within the pothole instead of being concentrated into stars. The measured properties of the gas in the clouds that produce the Lyman forest exactly matches the calculations of the properties of this kind of pothole. The gas causing quasar absorption lines may indeed be confined in potential wells where something else, other than baryons, provides the main gravitational influence. The situation is very reminiscent of the measurements of the rotation of disc galaxies, which show that the galaxies would fly apart if they were not held in the gravitational grip of dark matter. The dark clouds of the Lyman forest will also fly apart if they are not being held together by something we cannot see. The simplest and most natural assumption is that the same kind of something—cold dark matter—is doing the holding together in each case.

But the Lyman clouds are different from the bright galaxies we observe in one important way. They are not distributed in a foamy structure surrounding empty voids. The redshifts of the Lyman-alpha lines in the forest seem to be distributed at random, apart from the tendency for there to be more of them at higher redshifts. If there are any voids that contain no Lyman clouds, then they must represent less than 5 percent of the volume of the Universe at the times corresponding to redshifts between 1.7 and 4.

This is a major discovery, which tells us that not only are bright galaxies poor indicators of where most of the mass of the Universe is, they are not even a good guide to where all the baryons are. And it fits beautifully with the idea of biased galaxy formation. Computer models tell us that in a Universe dominated by cold dark matter, bright galaxies should be clustered. But those studies also tell us that the voids should contain a density of dark matter nearly as great as the density in the surrounding sheets or filaments, and that there

should be the usual mixture of a few percent baryonic matter mixed in with the CDM in the voids, some of it confined in "minihaloes." The Lyman-alpha forest could have been predicted on the basis of the CDM theory— had it not been discovered more than ten years "too early." However, this order of events reflects on the tardiness of theorists, not on the credibility of the theory itself. The Lyman-alpha forest is strong corroboration of the simplest version of CDM cosmology, in which the Universe is indeed flat. It tells us clearly that all parts of the Universe are pervaded by Dark matter and by baryons; the huge apparent voids are not empty, but just deficient in bright galaxies. And this is still not the end of the evidence about the nature of the Universe that can be gleaned from quasar light.

Heavy Signs of a Galaxy Wall

A typical quasar spectrum contains over a hundred Lyman-alpha lines, each at a different redshift. The Lyman clouds themselves do not contain heavy elements. But the quasar spectra do show a handful of lines belonging to heavy elements. These lines must be produced when light from the quasar passes through a galaxy like the ones we see in our neighbourhood. As stars have evolved in those galaxies, some have become supernovae and spread heavy elements, built up in their interiors, into interstellar space. So hydrogen clouds in a galaxy like our own are laced with heavy elements, and light from a quasar passing through a cloud of hydrogen in a galaxy like our own will be stamped with the imprint of those heavy atoms. Bright galaxies, however, are much less common than the Lyman clouds. The chance that the line of sight to a quasar will pass right through a bright galaxy is correspondingly modest. In fact, al-

most every quasar spectrum shows a few lines due to heavy elements. This can only mean that all galaxies are embedded in large, dark haloes, about ten times bigger than the bright galaxies (which, once again, ties in very nicely with other recent studies of galaxies).

Some of the redshifts corresponding to these lines of heavy elements are between about 0.5 and 0.8, much smaller than those of the lines in the Lyman forest, and putting the galaxies responsible for the lines at the edge of the limit of observation with ground-based telescopes. With the evidence of the lines showing them where to look, astronomers have been able to identify very faint, distant galaxies with the right redshifts in many of these cases. Enough of these galaxies have now been identified to establish beyond doubt that the heavy-element lines are indeed produced in galaxies. So, without going through the tedious process of identifying every such galaxy, we can confidently assume that each redshift in this range determined from a heavy-element line in a quasar spectrum tells us the location of a distant galaxy. And, pushing our luck only a little, we can reasonably assume that the heavy-element lines corresponding to still higher redshifts, where we have no hope of identifying the galaxies involved directly, also tell us where galaxies were located when the Universe was young. The obvious question is, how are those galaxies distributed through space?

These studies are still in their infancy, but the most striking feature of this new view of the distant Universe is a huge concentration of galaxies forming a wall 30 million light-years thick and 300 million light-years across at a redshift of about 2, corresponding to a time when the Universe was just 3 billion years old. This super-supercluster, identified only in 1986, is now coming under scrutiny, and studies of features like this at such large redshifts will help to provide a picture of the way the Universe has evolved.

Into the Past

Our overall understanding of galaxy formation and evolution is now at a primitive stage—rather like our understanding of stars fifty years ago. We don't fully understand the most basic structural features—why some galaxies are discs and some are elliptical—though this basic classification was established by Edwin Hubble in the 1940s. The galaxies that Hubble observed were all within a few hundred million light-years of us; relatively close compared to the distance we can now probe. But because the Universe is much the same everywhere, Hubble got a view of a fair sample of it. His classification of galaxies has survived and stood the test of time. Hubble himself, however, was acutely aware of observational limitations, and his great book, The Realm of the Nebulae, concludes with these words:

With increasing distance our knowledge fades, and fades rapidly. Eventually we reach the dim boundary, the utmost limits of our telescope. There we measure shadows, and we search among ghostly errors of measurement for landmarks that are scarcely more substantial. The search will continue. Not until the empirical resources are exhausted need we pass on to the dreamy realm of speculation.

This search has continued, as more powerful telescopes and more sensitive detectors have been employed. Observers have invaded the speculators' territory. Because light travels at a finite speed, we see distant parts of the Universe as they were long ago. We can sample the past, even if we cannot repeat it, and we are struck by the realisation that the simple laws of physics derived from experiments here on Earth can be applied across vast reaches of cosmic space and time. To see any cosmic evolutionary trend, however, one must look back in time by a good fraction of the 10

billion-plus years for which the Universe has been expanding. The first person to do this was Sir Martin Ryle, in Cambridge, in the late 1950s. He found clear evidence that conditions were different when galaxies were young. His radio telescopes picked up electromagnetic waves from some active galaxies (the kind that we now think harbour supermassive black holes) even when these were too far away to be observed by the optical techniques of the time. He couldn't determine the distances to such galaxies by radio measurements alone, but he assumed that, at least on average, the ones that seemed fainter were really more distant than those that produced a more intense signal in his instruments. He counted the numbers of radio sources with various apparent intensities and found that there were too many faint galaxies (in other words, more-distant ones) compared to brighter, closer ones. This was discomfiting for those who supported the idea of an unchanging, steady state universe—cosmologists with whom Ryle was, at the time, involved in a running battle. But the observations were compatible with an evolving universe, if galaxies were more prone to violent outbursts in the remote past.

Optical astronomers joined this enterprise after the discovery of quasars in 1963. Because quasars are the hyperluminous nuclei of galaxies, optical astronomers have now seen some so far away that the light set out when the Universe was less than one-fifth of its present age. It is clear from quasars, as it was from Ryle's radio data, that the cosmic scene was much more violent when galaxies were young. Most of the runaway catastrophes, the formation of great black holes, happened early in galactic history, when less gas was locked up in stars and more was still available to fuel the central monsters.*

*It is an antianthropic irony that the most interesting time to have been an astronomer was at that epoch, before the Earth formed.

Galaxies at very high redshifts can be studied indirectly by using quasars as probes, as we have explained, and looking for absorption lines, or even gravitational lensing, due to galaxies along the line of sight. These ordinary galaxies, those without hyperluminous quasar nuclei, would be almost invisibly faint at such great distances. But recently the prospects of directly detecting them have brightened; the latest sensitive detectors, such as charge coupled devices (CCDs), reveal huge numbers of objects, closely packed over the sky, which are probably young galaxies at the stage when a cloud of gas is still contracting to form a disc. We must await the launch of the space telescope, and the next generation of ground-based telescopes, to image these objects. The first instrument that we expect to be up to the task will be the ten-metre Keck Telescope in Hawaii; it should produce bright images of these objects that will reveal their shape. We shall then be able to obtain "snapshots" of groups of galaxies at different distances (and therefore different evolutionary stages) and trace directly how galaxies emerged from amorphous beginnings—an initially smooth and almost featureless universal soup.

Almost, but not quite, featureless; there were (although we do not know why) small fluctuations from place to place in the expansion rate. We think we know what happened then. Embryonic galaxies were slightly over-dense regions whose expansion lagged behind the average expansion. These embryos eventually evolved into distinct clouds, whose internal expansion halted and went into reverse. The bigger ones collapsed to make the first individual galaxies when the Universe was perhaps 10 percent of its present age. Less-massive systems would have survived as stable gas clouds—these are responsible for the Lyman-alpha forest. Subsequently, the galaxies would have grouped into clusters. This, at least, is the scenario our theories suggest—

only further observations will tell whether theorists' confidence in the story is well based.

The fact that the Universe is simple enough for us to understand it is a Deep Truth. How exactly, though, do we come to be here puzzling over the nature of the Universe? Our existence depends on the production of elements heavier than hydrogen and helium. Lines corresponding to heavy-element absorption are seen at redshifts as high as 3.3 in quasar light, and this alone shows that some stars had already gone through their life cycles and spread their products through young galaxies at that early time. But, as we hinted in the first chapter of this book, those stars were able to process hydrogen and helium into heavier elements only because of an astonishing coincidence involving the energetics of carbon nuclei. Armed now with an understanding of at least the broad picture of the Universe we live in, the time has come to take a closer look at this cosmic coincidence, and others. Is the Universe really tailor-made for humankind?

PART THREE

•

The Bespoke Universe

CHAPTER TEN

•

Tailor-made for Man?

JUST AS THE electrons in an atom can occupy different energy levels, like steps on a staircase, so can the particles that make up the nucleus of an atom. The nucleons may change from a low-energy state to a high-energy state, provided they are given the right push (the right amount of energy) from outside; once they are in a high-energy state, they may fall back to a lower level, most probably the bottom step on the energy ladder, and radiate the appropriate amount of energy in the process. For the Universe at large, the greatest cosmic coincidence is that the Universe is so precisely flat, and that the amount of baryonic matter in the Universe is so close, compared with what it might have been, to the amount of dark stuff. Within that flat Universe, however, there is another coincidence almost as remarkable, which allows for the existence of carbon and heavier elements, and which depends on fine-tuning in the energy levels of a handful of atomic nuclei.

One of the reasons why the standard model of the Big Bang is regarded as a scientific triumph is that it explains the abundances of the lightest elements, revealed

by spectroscopic studies of gas clouds and of old stars. These are hydrogen, the lightest element of all, helium, which makes up some 25 percent of the baryonic matter, and small traces of deuterium (heavy hydrogen) and lithium. The standard model explains how these elements were made out of primordial baryons during a period from about one-tenth of a second after the moment of creation up to about four minutes later, It doesn't matter how the Universe got to be in the state of heat and density that existed at an "age" of 0.1 second; it would then have a temperature and density high enough to establish a state of "thermal equilibrium" that washed out all trace of its past history, so none of the debate in recent years about the very early Universe and the moment of creation itself affects these calculations. No baryonic material was processed by the Big Bang into elements heavier than lithium, which has three protons and four neutrons locked away in each nucleus. So where did everything else come from? In fact, this was a well-recognised problem by the 1950s, long before the complete and detailed standard model of the Big Bang had been worked out. The fact that we exist shows that carbon and other elements have been manufactured somewhere and dispersed through space. Even the earliest detailed studies of Big Bang physics, carried out by George Gamow and his colleagues in the United States, showed the difficulty of making anything except hydrogen and helium (a difficulty that the ebullient Gamow used to dismiss by pointing out that since his theory could explain the nature of 99 percent of the known matter in the Universe, the hydrogen and the helium, it must be counted a success!). The only place that heavier elements could have been manufactured, and could still be manufactured today, is inside stars. But how do stars do the trick?

The Beryllium Bottleneck

Astrophysicists knew that the trick, nucleosynthesis, must have something to do with sticking helium nuclei together. The most stable form of helium, helium-4, contains just two protons and two neutrons in its nucleus. This is such a stable configuration that a helium nucleus behaves like a particle in its own right, and was known, as the alpha particle, before neutrons themselves were discovered. Because the helium-4 nucleus is so stable, atoms that are made up, in effect, of whole numbers of helium-4 nuclei are themselves stable, and therefore common, compared with other nuclei. Carbon, which contains twelve nucleons, and oxygen, with sixteen, are the two most obvious examples, with great importance for life forms like us. Once carbon and oxygen exist in the Universe in the right quantities, it is relatively easy, according to the laws of physics derived from studies of, for example, the way alpha particles interact with nuclei in particle accelerators, to build up the heavier elements.

This happens, in essence, by adding alpha particles (helium nuclei) to existing nuclei, which then, sometimes, spit out the odd proton or neutron to produce a nucleus of a slightly lighter element. But there seemed to be a bottleneck at the very first step in this process.

Two alpha particles that collide with each other with the right energy (enough to overcome the electrical repulsion produced by the positively charged protons they each carry) will stick together to form a nucleus of beryllium-8. Unfortunately, however, beryllium-8 is the exception to the rule that nuclei containing whole numbers of alpha particles are stable. It is spectacularly instable, and breaks apart into lighter particles within a lifetime of only 10" 17 seconds. So how can carbon, which requires the addition of another alpha particle to a beryllium-8 nucleus, ever be built up?

Maybe, some theorists speculated, carbon-12 could be made directly inside stars, when three helium-4 nuclei just happened to collide with one another simultaneously. But a simple calculation soon showed that this is indeed about as unlikely a prospect as it sounds. It might happen occasionally, but not often enough to produce all the carbon we see around us, the key element in the chemistry of living things.

In 1952, Ed Salpeter, an American astrophysicist, suggested (more or less in desperation) that carbon-12 might be produced in a very rapid two-step process, with two alpha particles colliding to form a nucleus of beryllium-8, which was then in turn hit by a third alpha particle in the 10" 17 seconds before it had time to disintegrate. Since this did at least give 10" 17 seconds for the third particle to arrive, instead of requiring three to meet simultaneously, it was an improvement on the triple-collision idea. But since the arrival of a third particle might very effectively smash the unstable beryllium-8 nucleus to bits, it wasn't much of an improvement. Then, Fred Hoyle, who had, back in 1946, written a classic paper expounding the idea that the chemical elements were made in stars, entered the story.

Hoyle's Anthropic Insight

Hoyle (now Sir Fred) was based in Cambridge, England, but in the 1950s spent time in California, working with his friend, nuclear physicist Willy Fowler. Hoyle puzzled over the problem of how heavy nuclei might be built up in stars (stellar nucleosynthesis), and became intrigued by the possibility that the energy levels of beryllium, helium, and carbon might be just right to encourage the two-step reaction Salpeter had proposed. It all hinged on a property known as resonance. Resonance works like this. When two nuclei collide

and stick together, the new nucleus that is formed carries the combined mass-energy of the two nuclei, plus the combined energy of their motion, their kinetic energy (and minus a small amount of energy from the strong force, the binding energy that holds the new nucleus together). The new nucleus "wants" to occupy one of the steps on its own energy ladder, and if this combined energy from the incoming particles is not just right then the excess has to be eliminated, in the form of leftover kinetic energy, or as a particle ejected from the nucleus. This reduces the likelihood that the two colliding nuclei will stick together; in many cases, they simply bounce off each other and continue to lead their separate lives. If everything meshes perfectly, however, the new nucleus will be created with exactly the energy that corresponds to one of its natural levels (it can then, of course, emit packets of energy and hop down the steps to the lowest level). In that case, the interaction will proceed very effectively, and the conversion of lighter nuclei into a heavier form will be complete. This matching of energies to one of the levels appropriate for the new nucleus is the effect known as resonance, and it depends crucially on the structure of the nuclei involved in the collisions.

In 1954, Hoyle realised that the only way to make enough carbon inside stars is if there is a resonance involving helium-4, beryllium-8, and carbon-12. The mass-energy of each nucleus is fixed and cannot change; the kinetic energy that each nucleus has depends on the temperature inside a star, which Hoyle could calculate. Using that temperature calculation, Hoyle predicted that there must be a previously undetected energy level in the carbon-12 nucleus, at an energy that would resonate with the combined energies, including kinetic energy, of its constituent parts, under the conditions prevailing inside stars. He made a precise calculation of what that energy level must be, and he cajoled Willy

Fowler's somewhat sceptical nuclear physics colleagues until they carried out experiments to test his prediction. To the astonishment of everyone except Hoyle, the measurements showed that carbon-12 has an energy level just 4 percent above the calculated energy. This is so close that the kinetic energies of the colliding nuclei can readily supply the excess. This resonance greatly increases the chances of a helium-4 and a beryllium-8 nucleus sticking together, and ensures that enough alpha particles can be fused into carbon nuclei inside stars to account for our existence.

The remarkable nature of Hoyle's successful prediction cannot be overemphasised. Suppose, for example, that the energy level in carbon had turned out to be just 4 percent lower than the combined energy of helium-4 and beryllium-8. There is no way that kinetic energy could subtract rather than add the difference, so the trick simply would not have worked. This is made clear when we look at the next putative step in stellar nucleosynthesis, the production of oxygen-16 from a combination of carbon-12 and helium-4. When a carbon-12 nucleus and a helium-4 nucleus meet, they would fuse into oxygen if there were an appropriate resonance. But the nearest oxygen-16 resonance has one percent less energy than helium-4 plus carbon-12. But that 1 percent is all it takes to ensure that this time resonance does not occur. Sure, oxygen-16 is manufactured in stars, but only in small quantities (at least, at this early stage of a star's life) compared with carbon. If that oxygen energy level were 1 percent lower, then virtually all the carbon made inside stars would be processed into oxygen, and then (much of it) into heavier elements still. Carbon-based life forms like ourselves would not exist.

Most anthropic arguments are made with the benefit of hindsight. We look at the Universe, notice that it is close to flat, and say, "Oh yes, of course, it must be that way, or we wouldn't be here to notice it." But Hoyle's

prediction is different, in a class of its own. It is a genuine scientific prediction, tested and confirmed by subsequent experiments. Hoyle said, in effect, "since we exist, then carbon must have an energy level at 7.6 MeV." Then the experiments were carried out and the energy level was measured. As far as we know, this is the only genuine anthropic principle prediction; all the rest are "predictions" that might have been made in advance of the observations, if anyone had had the genius to make them, but that were never in fact made in that way.

Hoyle's remarkable insight led directly to a detailed understanding of the way in which all of the other elements are built up from hydrogen and helium inside stars. He worked closely with Willy Fowler on this, and with the husband-and-wife team Geoffrey and Margaret Burbidge. Fowler (without Hoyle) later received a Nobel Prize for his part in the study of stellar nucleosynthesis.

This combination of coincidences, just right for resonance in carbon-12, just wrong in oxygen-16, is indeed remarkable. There is no better evidence to support the argument that the Universe has been designed for our benefit—tailor-made for man. But there are alternative ways of viewing this coincidence, and others. So before we present the alternative view we should perhaps mention at least two other striking coincidences that help to make the Universe a fit place for life.

The Stellar Pressure Cooker

Making carbon, and heavier elements, inside stars solves only half the problem of how carbon-based life forms come to be here on Earth, puzzling over their origins. How do the heavy elements get out of the stars and spread across the Galaxy to become part of the clouds

of material from which new stars and planets form? The simple answer is that the heavy elements are spread when a minority of stars explode as supernovae. But what makes a supernova blow its top? It turns out that this spreading of the stuff of life across the cosmos also hinges upon a close cosmic coincidence.

Because of the failed resonance at oxygen-16, life for a very massive star is both complicated and, ultimately, disastrous. All stars start their lives by "burning" hydrogen nuclei, converting them into helium and releasing heat in the process. When hydrogen is exhausted, helium in its turn can be burned to produce carbon—at this stage of its life, a star like our Sun swells up to become a red giant. As long as helium is being converted into carbon, with a net release of energy for each carbon nucleus formed, the star can stay hot enough in the centre to support the weight of its outer layers. But eventually, after many millions of years, the helium is exhausted. What happens next depends on the mass of the star. By far the majority of stars run through some further nuclear reactions, in a last-ditch attempt to maintain their former glory, then collapse and cool down, huddling in upon themselves to form a ball of dead star material, a white-dwarf star that may have the mass of our Sun but that occupies a volume no bigger than the Earth.

In the later stages of its life, such a star may puff away large amounts of material into space. But this material comes only from the outer layers of the star and is almost entirely hydrogen and helium. These stars are of no interest to our story, because the heavy elements they have manufactured stay locked up in the dead star. But the first stages in the story of a supernova follow the same path as these more mundane objects, which goes something like this. When helium burning ends, the compression of the inner core by the weight of the outer layers of the star forces tempera-

tures up beyond 600 million K, to the point where carbon burning begins. These central temperatures are reached only in stars more than four times as massive as our Sun; lesser stars almost immediately, once their helium is burnt, settle down quietly into a respectable old age. Because of the lack of a suitable oxygen resonance, carbon burning in more massive stars is not simply a matter of adding an alpha particle to a carbon-12 nucleus to make oxygen-16. Carbon burning actually involves collisions between pairs of carbon-12 nuclei. Two carbon-12 nuclei may collide, with one alpha particle being ejected (carrying off excess kinetic energy) to produce a nucleus of neon-20. Sometimes, the two carbon nuclei stay stuck together, as magnesium-24, with excess energy removed by a burst of gamma rays; and sometimes two helium-4 nuclei are ejected from the merging pair of carbon-12 nuclei, leaving oxygen-16 behind.

This set of processes can continue only as long as there is carbon available. When it is exhausted, the gravitational collapse of the star sets in again. Once more, many stars end their lives at this stage and settle down into cooling lumps of matter. But if the mass of the star exceeds nine solar masses, the temperature rises above a billion degrees, and neon burning begins. This process rearranges the leftover material from carbon burning. One neon-20 nucleus may absorb a helium-4 nucleus to become magnesium-24, while ejecting a gamma ray; another neon-20 nucleus will absorb a gamma ray and spit out helium-4, leaving oxygen behind.

As the temperature rises above 1.5 billion K, oxygen burning begins. This is an even more complicated process, since when two oxygen-16 nuclei collide they can produce a variety of elements, including two isotopes of silicon, two forms of sulphur, phosphorus, and more magnesium. The key ingredient here is silicon,

because at the next stage of nuclear burning, at a central temperature of 3 billion degrees kelvin in a star with a mass twenty or more times that of our Sun, silicon becomes involved in a series of hundreds of nuclear reactions, which yield as their end product the ultimate stellar ash, in the form of nuclei of iron-56.