Matemáticas
|
Fotógrafo Richard Hartt. Cortesía del Instituto de Tecnología de California. |
Desearía que ustedes, señoras y señores que se hallan ahí afuera, conocieran algo de estas matemáticas. No es solo su lógica y su precisión lo que se pierden: también es la poesía.
– Entrevista en la BBC, «Una nueva fuerza en la naturaleza»
Tomemos esta ecuación pequeña y clara de aquí. Me dice todas las maneras en que un electrón puede sentirse cómodo en o alrededor de un átomo. Esta es su lógica. Su poesía es que me dice lo brillante que es el oro, por qué las rocas son duras, qué hace que la hierba sea verde, y por qué no podemos ver el viento. Y un millón de otras cosas, acerca de la manera en que funciona la naturaleza.
– Entrevista en la BBC sobre las teorías gauge, «Una nueva fuerza en la naturaleza»
No es un número grande accidental, como el número grande que es la proporción del volumen de la Tierra al volumen de una pulga.
– Registro sonoro de las Feynman Lectures on Physics, lección 7, 17 de octubre de 1961
Un vector es como un impulso que tiene una determinada dirección, o una velocidad que tiene una determinada dirección, o un movimiento que tiene una determinada dirección... y se representa en un pedazo de papel mediante una flecha en la dirección de la cosa.
– Feynman’s Tips on Physics, p. 23
¿Sabe usted?, no es cierto que lo que se denomina matemáticas «abstrusas» sea tan difícil. Tomemos algo como la programación informática, y la lógica minuciosa que se necesita para ello: el tipo de pensamiento que mamá y papá hubieran dicho que era solo para profesores. Bueno, en la actualidad forma parte de muchas actividades cotidianas, es una manera de ganarse la vida; ¡sus hijos se interesan por ella, se agencian un ordenador y hacen las cosas más alocadas y maravillosas!
– Entrevista en Omni, febrero de 1979
Pero, ¿ve usted?, desde el principio yo estaba desconectado. Intentaba encontrar una fórmula para sumar números enteros porque deseaba la fórmula. No me importaba, no significaba nada para mí que esto lo hubieran solucionado los griegos o incluso los babilonios en el 2000 a. C. Esto no me interesaba en absoluto. Era mi problema y me divertía, ¿ve usted? Siempre fue así. Yo siempre estaba jugando a mi propio juego independiente.
– Entrevista con Charles Weiner, 4 de marzo de 1966, Biblioteca y Archivos de Niels Bohr en el Centro para la Historia de la Física
A los que no conocen las matemáticas es difícil hacerles entender una sensación real de la belleza, la más profunda belleza, de la naturaleza. C. P. Snow habló de las dos culturas. Pienso realmente que estas dos culturas separan a las personas que han tenido de las que no han tenido esta experiencia de entender las matemáticas lo bastante bien para apreciar alguna vez la naturaleza.
– The Character of Physical Law, p. 58
Los errores en álgebra, diferenciación e integración son solo tonterías; son cosas que simplemente molestan a los físicos, y molestan tu mente mientras intentas analizar algo. Tendrías que poder hacer cálculos tan rápidamente como fuera posible, y con un mínimo de errores. Esto no requiere más que práctica y memoria; es la única manera de hacerlo.
– Feynman’s Tips on Physics, p. 19
Es notable, pero en este momento es posible decir que no hay discrepancia experimental en absoluto entre las teorías de la física en cualquier parte y los resultados del experimento. Esto no quiere decir que podamos computarlo todo. Las reglas del juego mediante las cuales hacemos el cómputo son la base de todo. Así es como funciona la naturaleza. Es simple.
– «Electrodinámica cuántica: fotones, corpúsculos de luz», conferencias sir Douglas Robb, Universidad de Auckland, 1979
Ahora bien, la idea es esta: queremos ver la distribución del momento de los partones del interior. Imaginad que un enjambre de abejas se dirige hacia vosotros. Supongamos que dispersáis radar procedente del enjambre. Las diferentes abejas tendrán diferentes velocidades, y cuando disperséis radar de ellas, veréis una distribución de frecuencias dispersada desde una onda de radio monocromática por un grupo de abejas en movimiento, obtendréis la distribución del momento de las abejas dentro del enjambre.
– Conferencia sobre partículas en Caltech, 1973
Las matemáticas son un lenguaje más el razonamiento; son como un lenguaje más la lógica. Las matemáticas son un instrumento para el razonamiento.
– The Character of Physical Law, p. 40
Euclides dijo: «No hay camino fácil a la geometría». Y no hay camino fácil. Los físicos no pueden mantener una conversación en ningún otro lenguaje. Si queremos aprender de la naturaleza, apreciar la naturaleza, es necesario entender el idioma en el que esta habla. La naturaleza ofrece su información de una forma solamente; no somos tan poco humildes como para pedirle que cambie antes de que le prestemos atención.
– The Character of Physical Law, p. 58
De modo que cada vez me interesé más por el asunto matemático asociado a la física. Además, las matemáticas por sí mismas me resultaban muy atractivas. Me gustaron a lo largo de toda mi vida.
– Entrevista en Future for Science
Para emplear las matemáticas con éxito, se ha de tener una determinada actitud mental: saber que hay muchas maneras de considerar cualquier problema y cualquier tema.
– «Nuevas matemáticas», preparado para el Departamento de Educación del Estado de California, 1965
Se necesita una respuesta para un determinado problema; la cuestión es cómo obtenerla. El usuario competente de matemáticas es prácticamente un inventor de nuevas maneras de obtener respuestas en situaciones dadas.
– «Nuevas matemáticas», preparado para el Departamento de Educación del Estado de California, 1965
¿Cuál es el mejor método para obtener la solución a un problema? La respuesta es: cualquier forma que funcione.
– «Nuevas matemáticas», preparado para el Departamento de Educación del Estado de California, 1965
Las matemáticas no son una ciencia desde mi punto de vista, en el sentido de que no son una ciencia natural. Quizá sean una ciencia antinatural.
– Registro sonoro de las Feynman Lectures on Physics, lección 3, 3 de octubre de 1961
El resultado final de calcular los límites se escribe todavía de otra manera, como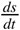 
. Ahora la cosa se torna incluso más abstracta. Estas ds no tienen que volverse a dividir. Y si les digo que lo llamaremos un pequeñísimo pedacito de tiempo y distancia, los matemáticos se enfadarán mucho conmigo. Pero funciona bien. Pueden usarlo. Si imaginan que estos dos son más pequeños que cualquier cosa, han captado la idea correcta.
– Registro sonoro de las Feynman Lectures on Physics, lección 8, 20 de octubre de 1961
Ahora están realizando cálculo. Este es un cálculo de alto nivel. Diferenciando cosas. Nada como esto.
– Registro sonoro de las Feynman Lectures on Physics, lección 8, 20 de octubre de 1961
Pueden construir su propia tabla de integrales mediante diferenciales hasta que se les pongan verdes las agallas, y encontrarán que por cada fórmula con un diferencial, tendrán una fórmula integral si le dan la vuelta.
– Registro sonoro de las Feynman Lectures on Physics, lección 8, 20 de octubre de 1961
A diferencia del caso de las matemáticas, en las que puede definirse todo y después uno no sabe de qué habla (en realidad, la gloria de las matemáticas es que uno no sabe de lo que habla). La gloria es que las leyes, los argumentos y la lógica son independientes de lo que es.
– Registro sonoro de las Feynman Lectures on Physics, lección 12, 7 de noviembre de 1961
Nunca pongo bien los signos; quizá ustedes tampoco, pero al final pueden descubrirlo.
– Registro sonoro de las Feynman Lectures on Physics, lección 13, 10 de noviembre de 1961
Siempre estoy comprobando las cosas cuando calculo, porque cometo muchas equivocaciones. Una manera de comprobar es hacer las matemáticas de manera muy minuciosa; la otra manera de comprobar es ver si los números que salen son razonables, si describen lo que realmente sucede.
– Feynman’s Tips on Physics, p. 63
La aparente facilidad con la que hago esto es falsa: ¡juro que lo hice más de una vez hasta que di con el resultado correcto!
– Feynman’s Tips on Physics, p. 62
Recuerden: si se quedan atascados en un análisis matemático, ¡siempre pueden hacerlo mediante aritmética!
– Feynman’s Tips on Physics, p. 82
Yo sabía que uno de los grandes problemas de la geometría era trisecar un ángulo. De modo que, ¡al diablo con todas estas cosas, seguiríamos adelante y resolveríamos el gran problema!, ¿ve usted? Esta es una manera de aprender, sin embargo; así se lo digo.
– Entrevista con Charles Weiner, 4 de marzo de 1966, Biblioteca y Archivos de Niels Bohr en el Centro para la Historia de la Física
No fue nada brillante, es solo que yo tenía facilidad para las matemáticas, para la manipulación matemática, como un chico que es bueno haciendo cálculos aritméticos mentales rápidamente. Este tipo de cosas. Es muy útil poder hacerlo.
– Entrevista con Charles Weiner, 5 de marzo de 1966, Biblioteca y Archivos de Niels Bohr en el Centro para la Historia de la Física
La única cosa en que podía pensar era: esto era bueno para enseñar a alguien, pero no era bueno por sí mismo. Todavía tengo esta sensación acerca de las matemáticas.
– Entrevista con Charles Weiner, 5 de marzo de 1966, Biblioteca y Archivos de Niels Bohr en el Centro para la Historia de la Física
No puedo apostar. Entiendo las matemáticas de las probabilidades. Creo firmemente que los juegos son presumiblemente imparciales. Son honestos. Si son honestos, no hay manera de apostar, porque solo es una cuestión de cómo salen los dados, y esto no me resulta interesante. Es solo un accidente.
– Entrevista con Charles Weiner, 27 de junio de 1966, Biblioteca y Archivos de Niels Bohr en el Centro para la Historia de la Física
No sé por qué la teoría de números no encuentra aplicación en física. En cambio, parece que necesitemos las matemáticas de funciones de variables continuas, números complejos y álgebra abstracta.
– Carta a Robert Boeninger, mayo de 1969
No puedo entender muy bien las matemáticas, como les he dicho, y he de tener ejemplos físicos, pero esta es solamente la manera en que mi mente trabaja.
– Carta a Bert y Mulaika Corben, 1948
Pensando que yo entiendo la geometría y necesitando cortar una pieza de madera que encaje en la diagonal de un cuadrado de 1,5 metros, intento calcular qué longitud ha de tener. Al no ser muy experto, obtengo infinito: inútil, y tampoco ayuda decir que puede ser cero, porque ambos son círculos. No es la filosofía lo que buscamos, sino el comportamiento de las cosas reales. De modo que, desesperado, lo mido directamente; ¡vaya, es de algo más de dos metros (ni infinito ni cero)! De modo que hemos medido estas cosas para las que nuestra teoría nos da números cercanos a lo que medimos. Estamos buscando la fórmula que nos dé la raíz cuadrada de cincuenta.
– Carta a Barbara Kyle, octubre de 1965 (Perfectly Reasonable Deviations from the Beaten Track, p. 152)
No estoy interesado en lo que los matemáticos de hoy en día encuentran interesante.
– Carta al Dr. John A. Wheeler, mayo de 1966
La teoría de conjuntos se utiliza algunas veces, pero no muy a menudo, en aspectos prácticos. Sus mayores usos y su belleza aparecen en el estudio de los cimientos lógicos de las matemáticas.
– Carta a Alexander Calandra, septiembre de 1965
Un matemático puro es muy impráctico: no está interesado (de hecho, a propósito no está interesado) en el significado de los símbolos, las letras y las ideas matemáticos, sino que únicamente está interesado en las interconexiones lógicas de los axiomas, mientras que el usuario de las matemáticas ha de entender la conexión de las matemáticas con el mundo real.
– «Nuevas matemáticas», preparado para el Departamento de Educación del Estado de California, 1965
El usuario de las matemáticas que tiene éxito es prácticamente un inventor de nuevas maneras de obtener respuestas a situaciones concretas.
– «Nuevas matemáticas», preparado para el Departamento de Educación del Estado de California, 1965
Hay muchas maneras de resolver un problema pero, lamentablemente, también hay maneras fijas conocidas y definidas de resolver los problemas. Lo que hemos estado haciendo en el pasado es enseñar solo una manera fijada de resolver problemas aritméticos en lugar de enseñar la flexibilidad de la mente: es decir, las diversas maneras posibles de plantear un problema, las maneras posibles de pensar en él, y las posibles maneras de resolver el problema.
– «Nuevas matemáticas», preparado para el Departamento de Educación del Estado de California, 1965
Con el fin de usar las matemáticas hay que tener una comprensión más profunda de la relación entre los objetos matemáticos y las cosas reales, y esta comprensión más profunda se opone a una tendencia a intentar hacer que todos los diferentes tipos de aplicaciones matemáticas representen la misma cosa.
– «Nuevas matemáticas», preparado para el Departamento de Educación del Estado de California, 1965
Desde un punto de vista estricto y técnico, si se supiera, la teoría de los fundamentos de las matemáticas no se halla en un estado completamente satisfactorio e implica algunas complicaciones muy grandes.
– «Nuevas matemáticas», preparado para el Departamento de Educación del Estado de California, 1965
Podría mencionar, quizá, por qué se dedica una cierta atención a diferentes sistemas de bases además de la base 10. El objetivo es únicamente aumentar de nuevo la experiencia matemática. Para dejar claro a los niños que la base 10 es un accidente de la historia humana y que no hay nada de especial acerca del número 10.
– «Nuevas matemáticas», preparado para el Departamento de Educación del Estado de California, 1965
Si estuviera dando una charla sobre matemáticas, ya le habría contestado. Las matemáticas buscan patrones.
– Conferencia en el 14.º Congreso Nacional de la Asociación de Profesores de Ciencias, «¿Qué es la ciencia?», abril de 1966
De manera que él conocía toda su aritmética, y era muy bueno en esto, y ello supuso un reto para mí. Yo no dejaba de practicar. Solíamos tener un pequeño concurso. Cada vez que teníamos que calcular algo, nos apresurábamos a encontrar la respuesta, él y yo, y yo perdía. Pasados algunos años empecé a ganar yo de vez en cuando, quizá una vez de cada cuatro. Uno tiene que darse cuenta de los números, ¿sabe?, y cada uno de nosotros lo hacía de manera diferente. Nos divertíamos mucho.
– Sobre su experiencia con el Proyecto Manhattan, «Los Álamos desde abajo», 1975
Desde luego, tienes que darte cuenta de algo divertido en relación con un número, como si tienes que multiplicar 174 por 140, por ejemplo. Adviertes que 173 por 141 es como la raíz cuadrada de 3, multiplicado por la raíz cuadrada de 2, que es la raíz cuadrada de 6, que es 245. Pero tienes que darte cuenta de los números, ¿sabe?, y cada tipo lo hacía de manera diferente; nos divertíamos mucho.
– Charla en la Universidad de California en Santa Bárbara, «Los Álamos desde abajo», febrero de 1975
Estaban estos sumos sacerdotes que podían predecir Venus, y los hombres normales, que ustedes imaginarán que decían: «¡Dios!, ¿cómo lo hacen? Esto es maravilloso, me asusta, no puedo aprender aritmética, esto es imposible», y cosas por el estilo. Ahora bien, si en aquella época hubiera habido un intento de pedagogía, en otras palabras, que los sacerdotes intentaran explicar a los profanos lo que hacían, podrían haber explicado que solo contaban, o hacían el equivalente de contar.
– Lección Esalen, «Visión de la realidad desde la mecánica cuántica» (2.ª parte), octubre de 1984
¡Les mostraré cómo hacer estos cálculos, como si sacaran habichuelas de sus botes!
– Lección Esalen, «Visión de la realidad desde la mecánica cuántica» (2.ª parte), octubre de 1984
Pienso que hemos entendido todo lo que podemos desde este punto de vista; lo que hemos encontrado en este siglo es lo bastante diferente y lo bastante oscuro para que el avance futuro requiera muchas matemáticas.
– Entrevista en Omni, febrero de 1979
No creo en la idea de que hay unas pocas personas peculiares capaces de comprender las matemáticas, y que el resto del mundo es normal. Las matemáticas son un descubrimiento humano, y no es más complicado que lo que los humanos pueden comprender.
– Entrevista en Omni, febrero de 1979
Las matemáticas solo son un lenguaje.
– Notas personales
Las matemáticas pueden permitir puntos de partida aparentes absolutamente diferentes.
– Notas personales
Las reglas del álgebra son cosas que estudian los matemáticos, ¡y los matemáticos han intentado hallar todos los objetos que puedan encontrarse que obedezcan dichas reglas! Originalmente, las reglas se hicieron para contar manzanas: se mejoraron con el uso de números negativos; se mejoraron todavía más al inventar las fracciones.
– «Electrodinámica cuántica: ajustes de reflexión y transmisión», conferencias sir Douglas Robb, Universidad de Auckland, 1979
[Sobre los números complejos]: Es interesante que los matemáticos inventaran todas estas matemáticas para estos números extraños sin tener nada a las que aplicarlas directamente en física, y que después resultara ser tan fundamental para las leyes básicas de la física usar estos números raros.
– «Electrodinámica cuántica: ajustes de reflexión y transmisión», conferencias sir Douglas Robb, Universidad de Auckland, 1979
En la actualidad, nos hemos vuelto muy refinados. En los días iniciales, cuando las matemáticas se desarrollaban por primera vez y se decía que un número es algo relacionado con cuando se cuenta el número de manzanas o de personas, o algo parecido, entonces la idea de media persona era más bien un problema. Pero hoy en día no hay ninguna dificultad, y nadie tiene ninguna sensación moral, incómoda o sangrienta cuando oye que en determinada región hay 3,2 personas por kilómetro cuadrado.
– «Electrodinámica cuántica: ajustes de reflexión y transmisión», conferencias sir Douglas Robb, Universidad de Auckland, 1979
Les sorprendería cuántos números se pueden obtener jugando con pi, y con 2 y 5, etcétera, y si no tienen nada para guiarlos excepto la respuesta, incluso pueden hacer que esta alcance varios lugares decimales jugando con ellos de forma adecuada. Es sorprendente lo mucho que puede acercarse uno a un número arbitrario jugando con números bonitos como pi.
– «Electrodinámica cuántica: nuevos interrogantes», conferencias sir Douglas Robb, Universidad de Auckland, 1979
Ahora bien, ustedes preguntan: ¿es esta la manera correcta de hacerlo? ¡No existe tal cosa! No hay maneras «correctas» de hacer nada. Una manera concreta de hacerlo puede ser correcta, pero no es la manera correcta.
– Feynman’s Tips on Physics, p. 58
Al considerar retrospectivamente el trabajo, solo puedo sentir una especie de arrepentimiento por la enorme cantidad de razonamiento físico y de reexpresión matemática que termina simplemente volviendo a expresar lo que ya se conocía previamente, aunque de una forma que es mucho más eficiente para el cálculo de problemas específicos. ¿No habría sido mucho más fácil simplemente trabajar por entero en el marco matemático para elaborar una expresión más eficiente? Ciertamente, parecería que este fuera el caso, pero debe señalarse que aunque el problema que realmente se resolvió fue solo el de dicha reformulación, el problema con el que nos enfrentamos originalmente fue el problema (que quizá esté todavía por resolver) de evitar los infinitos de la teoría usual. Por lo tanto, se buscaba una nueva teoría, no solo una modificación de la antigua. Aunque la búsqueda fue infructuosa, hemos de considerar la cuestión del valor de las ideas físicas para el desarrollo de una nueva teoría.
– Nobel Lectures, Physics 1963-1970, Elsevier, Ámsterdam, 1972
Cuando yo estaba en el instituto teníamos un equipo de álgebra, y yo estaba en el equipo de álgebra. Era algo de locos: nos encontrábamos con otro instituto, y se abría un sobre con problemas que alguien había inventado en algún lugar, y se anunciaba: «Este problema es de 45 segundos», o quizá «dos minutos y medio», y lo escribían en la pizarra. Tenías 15 segundos para pensar y después tenías que trabajar como un demonio, y trazar un círculo alrededor de tu respuesta. No importaba de qué manera conseguías la respuesta. Esto es lo que me gustaba. Yo solía practicar, para hacer esto, y logré ser muy, muy rápido. La capacidad de hacer cálculos algebraicos rápidamente, que después se convirtió en la capacidad de hacer cálculos rápidamente, siempre me sirvió mucho.
– Entrevista con Charles Weiner, 5 de marzo de 1966, Biblioteca y Archivos de Niels Bohr en el Centro para la Historia de la Física
Me parece que si usted me dice 2x = 32, sé lo que significa. x siempre representa algún número, de modo que si resulta que el número se halla ahí arriba, como un exponente, ¿supone esto alguna diferencia? Quiero decir, sabemos lo que son los exponentes. ¿Supone esto alguna diferencia para el problema?
– Entrevista con Charles Weiner, 4 de marzo de 1966, Biblioteca y Archivos de Niels Bohr en el Centro para la Historia de la Física
Cuando estuve en el MIT, leía libros sobre campos que no conocía, como la relatividad general y cosas por el estilo, o incluso en la enciclopedia, cuando extraía materiales del artículo. Yo parecía tener un sentido para extraer, en electrostática, una gran cantidad de material, pero cuando se trataba del cálculo de la capacitancia de un condensador elíptico, que era relativamente complicado, no me preocupaba el hecho de que no lo entendiera. Yo sabía que no era tan interesante como los teoremas generales sobre las leyes del cuadrado inverso, y, ¿sabe usted?, yo tenía alguna manera de saber qué era importante y qué no.
– Entrevista con Charles Weiner, 4 de marzo de 1966, Biblioteca y Archivos de Niels Bohr en el Centro para la Historia de la Física
Mi padre me explicó el número pi antes de que hubiera aprendido en la escuela los decimales para las fracciones, y me explicó los decimales. Ve usted, yo estaba realmente adelantado en aritmética. Lo recuerdo cuando me explicaba que pi era un misterio grande y maravilloso. Todo era siempre espectacular: que todos los círculos tienen la misma relación entre la distancia a su alrededor y la distancia a su través, y que este número, este número extraño, es de una gran importancia, y es un número maravilloso. De modo que es como si pi estuviera escrito en letras de oro, ¿sabe?
– Entrevista con Charles Weiner, 4 de marzo de 1966, Biblioteca y Archivos de Niels Bohr en el Centro para la Historia de la Física
Las matemáticas puras son simplemente una abstracción del mundo real, y las matemáticas puras tienen un lenguaje preciso especial para tratar de sus temas especiales y técnicos. Pero este lenguaje preciso no es preciso de ninguna manera si uno trata con objetos reales del mundo, y solo es pedante y bastante confuso usarlo a menos que haya algunas sutilezas especiales que han de distinguirse detenidamente.
– «Nuevas matemáticas», preparado para el Departamento de Educación del Estado de California, 1965