

I first learned about the number pi in my math class at school. Pi—the ratio of a circle’s circumference to its diameter—is mathematics’ most celebrated number; the name comes from the sixteenth letter of the Greek alphabet (π), the symbol being adopted by the mathematician Euler in 1737. I was immediately fascinated by it and learned as many of its decimal digits as I could find from various library books, hundreds of them in total. Then, in late 2003, I received a phone call from my father, who reminded me at the end of the conversation that it had been twenty years since my early childhood seizures. He said that I should be proud of the progress I had made in the time since. I thought about what he said for a long time afterwards and decided that I wanted to do something to show that my childhood experience of epilepsy had not held me back. Later that week I contacted the fund-raising department of the National Society for Epilepsy, the largest epilepsy charity organization in the U.K. My plan was to learn as many digits of the number pi as I could in correct sequence, before a public recitation in three months’ time on March 14—International Pi Day (March 14 is 3/14 in U.S. notation)—which is also Einstein’s birthday, to help raise funds for the NSE. The charity was excited by the idea and suggested that I attempt to break the European record, so a target of 22,500 digits was set. While I began learning the number, the charity’s fund-raising manager Simon Ekless organized the setting for the recitation selecting the Ashmolean Building at the Museum of the History of Science in Oxford, where among the various exhibits is one of Albert Einstein’s blackboards.
Pi is an irrational number, which means that it cannot be written as a simple fraction of two whole numbers. It is also infinite: the digits to the right of the decimal point go on forever in a never-ending numerical stream, so that it isn’t possible for someone to write down the number pi exactly, even if he or she had a piece of paper as big as the universe to write it on. For this reason, calculations must always use approximations of pi such as 22 ÷ 7 or 355 ÷ 113. The number appears in all sorts of unexpected places in mathematics besides circles and spheres. For example, it occurs in the distribution of primes and in the probability that a pin dropped on a set of parallel lines intersects a line. Pi also appears as the average ratio of the actual length and the direct distance between source and mouth of a meandering river.
The earliest values of pi were almost certainly found by measurement. There is good evidence that the ancient Egyptians had 4 (8/9)2 = 3.16 as a value for pi, while the Babylonians used the approximation 3 + 1/8 = 3.125. The Greek mathematician Archimedes of Syracuse gave the first theoretical calculation for the value of pi in around 250 BC. He determined the upper and lower range of pi by finding the perimeters of a polygon inscribed within a circle, which is less than the circumference of a circle (Figure 1) and of a polygon circumscribed outside a circle, which is greater than the circumference (Figure 2).
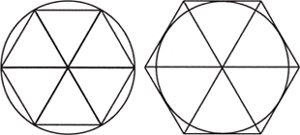
By doubling the number of sides of the hexagon to a dodecagon (twelve sides), then a twenty-four- and forty-eight-sided polygon, and finally up to a ninety-six-sided polygon, Archimedes brought the two perimeters closer and closer in length to the circle’s circumference, thereby arriving at his approximation. He calculated that pi was less than 31/7 but greater than 310/71. This translates in decimal notation to between 3.1408 and 3.1429 (rounded up to four decimal places), which is very close to the actual value of 3.1416.
During the Middle Ages, the German mathematician Ludolph van Ceulen spent a large part of his life calculating the numerical value of pi, using essentially the same methods as the ones employed by Archimedes some 1,800 years before. In 1596, he gave a value of pi to 20 decimal places in his book Van den Circkel (On the Circle), which he later expanded to 35 decimals. After his death, the digits were engraved on his tombstone.
Later mathematicians, including Isaac Newton and James Gregory, developed new arithmetical formulas to improve their calculations of the value of pi. In 1873, the Englishman William Shanks published his calculation of pi to 707 decimal places. It had taken him more than fifteen years, averaging about one decimal a week. Unfortunately, in the 1940s, when checked using mechanical calculators, it was discovered that he had made an error in the 528th place, after which all his subsequent digits were wrong.
With the advent of modern computers, it became possible to calculate pi to much greater values than ever before. The first computer calculation of pi was performed in 1949 on ENIAC (Electronic Numerical Integrator and Computer)—a huge machine that weighed 30 tons and was the size of a small house—calculating to 2,037 decimal places in seventy hours. Since then, rapid improvements in computer technology have helped researchers compute pi to an ever-increasing number of digits. In 2002, computer scientist Yasumasa Kanada and his coworkers at the University of Tokyo Information Technology Center computed pi to more than one trillion decimal places.
Over the years, many pi enthusiasts have attempted to memorize some of the number’s infinite string of digits. The most common method uses sentences and even whole poems composed of carefully chosen words, with the number of letters in each representing successive digits of pi. Perhaps the most famous example is the following, attributed to the British mathematician Sir James Jeans:
How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics!
Where the word How = 3 (having three letters) and I 1 and want 4, the complete sentence translating to 3.14159265358979, which is pi to 14 decimal places.
Another (first published in 1905) gives pi to 30 decimal places:
Sir, I send a rhyme excelling
In sacred truth and rigid spelling
Numerical sprites elucidate
For me the lexicon’s dull weight
If Nature gain
Not you complain,
Tho’ Dr. Johnson fulminate.
A challenge such writers face is how to deal with the digit 0, which first occurs in the 32nd place after the decimal point. One solution is to use punctuation, a period, for example. Another is to use a ten-letter word. Some writers use longer words for two successive digits. For example, the eleven-letter word calculating would stand for a 1 followed by another 1.
When I look at a sequence of numbers, my head begins to fill with colors, shapes and textures that knit together spontaneously to form a visual landscape. These are always very beautiful to me; as a child I often spent hours at a time exploring numerical landscapes in my mind. To recall each digit, I simply retrace the different shapes and textures in my head and read the numbers out of them.
For very long numbers, such as pi, I break the digits down into smaller segments. The size of each segment varies, depending on what the digits are. For example, if a number is very bright in my head and the next one is very dark, I would visualize them separately, whereas a smooth number followed by another smooth number would be remembered together. As the sequence of digits grows, my numerical landscapes become more complex and layered, until—as with pi—they become like an entire country in my mind, composed of numbers.
This is how I “see” the first twenty digits of pi:
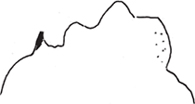
The number slopes upwards, then darkens and becomes bumpy in the middle before curving and meandering down.
And here are the first 100 digits of pi as I see them:

At the end of each segment of numbers, the landscape changes and new shapes, colors and textures appear. This process continues on and on, for as long as the sequence of digits that I am recalling.
The most famous sequence of numbers in pi is the Feynman point, which comprises the 762nd through 767th decimal places of pi: . . . 999999 . . . It is named after the physicist Richard Feynman for his remark that he would like to memorize the digits of pi as far as that point so that when reciting them, he would be able to finish with: “ . . . nine, nine, nine, nine, nine, nine, and so on.” The Feynman point is visually very beautiful to me; I see it as a deep, thick rim of dark blue light.
There is a similarly beautiful sequence of digits comprising the 19,437th through 19,453rd decimal places of pi: “ . . . 99992128599999399 . . . ,” where the digit 9 repeats first four times in a row, then very shortly afterwards five times over and then twice more again; eleven times altogether in the space of 17 decimal places. It is my favorite sequence of pi’s digits in all the more than 22,500 that I learned.
• • •
I began studying pi in December 2003, having three months to learn all the digits (22,500+) needed to attempt the record. The first problem was where to find so many digits of pi: most books only gave the number to some tens or hundreds of places. The internet proved to be the answer, though even then it took a lot of searching as most websites only listed pi to a thousand or several thousand places. Finally, Neil found the website of a Tokyo-based supercomputer which had files that stored millions of pi’s digits. This, then, became our source for the record attempt.
Neil printed the numbers onto sheets of letter-sized paper, 1,000 digits per page, to make it convenient for me to pick up a sheet at a time and study it. The digits were further broken up into “sentences” of 100 digits each, to make them as easily readable as possible and to minimize the risk that I might misread the numbers and learn some of them incorrectly.
I didn’t study the sheets of numbers every day. Some days I would be too tired or restless to sit and learn anything. Other days I would gorge on the numbers, absorbing many hundreds at a single sitting. Neil noticed that when I was learning the numbers, my body became tense and agitated—I would rock backwards and forwards in my chair or pull at my lips continuously with my fingers. In those moments, he found it nearly impossible to talk or interact with me, it was as though I were in another world.
The periods of study were often short (most were an hour or less) because my concentration fluctuates a lot. I chose the quietest rooms at the back of the house in which to learn the numbers, as even the smallest sound can make it impossible for me to concentrate on what I am doing. Sometimes I put my fingers in my ears to help keep any noise out. While learning, I often walked in circles around the room with my head down and my eyes half-open, so that I wouldn’t bump into things. At other times, I sat in a chair and closed my eyes completely and visualized my numerical landscapes and the many patterns and colors and textures within them.
As the public recitation was to be spoken and not written, it was important for me to practice reciting the numbers out loud to another person. Once a week, Neil would hold one or more of the sheets of numbers in front of him to check, while I stood or walked up and down and recited the growing sequence of memorized digits to him. It was an odd experience and difficult for me at first to say the numbers out loud, as they were entirely visual to me, and in the first practice recitation in front of Neil I was hesitant and made several errors. It was very frustrating and I worried about how I would cope when I would be expected to recite the entire sequence in front of a crowd of people. As always, Neil was patient and reassuring—he knew why I was finding it difficult to say the numbers out loud and encouraged me to relax and just to keep trying.
With practice, it gradually did become easier for me to recite the number continuously and my confidence began to rise as the date of the event approached. As the number of digits became larger and larger, it was not possible to recite all of them at one time in front of Neil, so we decided that I would practice reciting different parts of the number with him each week. At other times, I recited the number out loud to myself while sitting or walking around the house, until the flow of numbers became smooth and consistent.
To help with the fund-raising, the charity put a donation page on the internet that received donations and messages of support from people from all over the world. For example, one of the donations came from a class at a school in Warsaw, Poland. The charity also sent out a press release, while Neil and I collected donations from friends and family. A neighbor who heard about the event spoke to me about his own daughter’s epilepsy and expressed his admiration for what I was doing. Receiving such words of support, as well as cards and emails wishing me good luck, was extremely inspiring.
At the start of the weekend of the event, Saturday, March 13, Neil drove us up to Oxford for the recitation the following day. Although I had finished learning the digits several weeks before, I was still very nervous about the prospect of reciting them in public. We stayed overnight at a guesthouse close to the museum and I tried to sleep as best I could, which wasn’t easy because I kept thinking and worrying about what might happen the next day. Eventually, I fell asleep and dreamed that I was walking among my pi number landscapes—there at least I felt calm and confident.
The following morning, we both woke early. I wasn’t the only nervous one, as Neil complained of stomach cramps, which he knew was because he was feeling so tense about the day ahead. We ate breakfast together, then made our way to the museum. It was my first time in Oxford and I was excited to see it, a city famous for its university (the oldest in the English-speaking world) and known as the “city of dreaming spires” in reference to the architecture of the university buildings. We drove down a series of long, narrow cobbled roads until we arrived at our destination.
The Museum of the History of Science, located in Broad Street, is the world’s oldest surviving purpose-built museum building. Built in 1683, it was the first museum in the world to open to the public. Among its collection of around 15,000 objects, dating from antiquity to the early twentieth century, is a wide range of early mathematical instruments used for calculating, astronomy, navigation, surveying and drawing.
As we drove into the parking lot opposite the museum, we could see members of staff from the museum, journalists, cameramen and the charity’s event organizers all waiting together outside for us to arrive. Simon, the charity’s fund-raising manager, walked over as I got out from the car and shook my hand vigorously and asked how I was feeling. I replied that I was feeling fine. I was introduced to the other people waiting for me and then asked to sit on the steps of the building and have some photos taken of me. The step felt cold and damp and I tried not to fidget too much.
Inside, the room for the recitation was long and dusty and filled from end to end with glass cases containing various exhibits. Against the wall on one side was a small table and chair for me to sit at. From it, I had a direct view of Einstein’s blackboard on the wall opposite me. A little way from my table was a longer one, with sheets of paper filled with numbers and a digital clock. Seated around it were members of the department of mathematical sciences from nearby Oxford Brookes University, who had volunteered to be checkers during the recitation. Their task was to monitor my recall and ensure total accuracy, checking the numbers on the pages in front of them as I recalled the digits out loud. The clock was to be started at the beginning of the recitation, so that members of the public who came in and watched could see how long I had been reciting for. The event had been promoted in the local press and there were posters outside the building to encourage passersby inside, where charity workers were ready with information booklets and buckets for any donations.
Neil was still very tense, to the point of feeling quite sick, but was determined to stay in the hall to give me his support, and his presence was definitely reassuring. After posing for more photos inside the hall, I sat down at my chair and put the few things I had brought with me onto my table. There were bottles of water to drink whenever my throat felt dry and chocolate and bananas to provide me with energy throughout the recitation. As Simon called for silence, I was ready to start and he began the clock at five minutes past eleven.
And so I recited the by now very familiar opening digits of pi, the numerical landscapes in my head growing and changing as I went along. As I recited, the checkers crossed off each number as it was correctly recalled. There was a state of almost complete silence throughout the hall, except for the very occasional muffled cough or the sound of footsteps as someone moved from one side of the hall to the other. The noises did not bother me, because as I recited I could feel myself becoming absorbed within the visual flow of colors and shapes, textures and motion, until I was surrounded by my numerical landscapes. The reciting became almost melodic as each breath was filled with number upon number upon number and then I suddenly realized that I was totally calm, as I had been in my dream the night before. It took a little over ten minutes to complete the first thousand digits. I opened one of the bottles and drank some water, then continued the recitation.
Gradually, the hall began to fill with members of the public who stood several yards back from me and watched in silence as I recited. Though I had worried most of all about reciting pi in front of so many people, in the end I almost did not notice them as all of my thoughts were absorbed in the rhythmic and continuous flow of numbers. There was only one significant interruption that I can remember, when someone’s mobile phone started to ring. At that point I stopped reciting and waited for the noise to stop before continuing.
The rules of the event meant that I could not talk or interact with anyone during the course of the recitation. Short, prearranged breaks were allowed, during which I ate some of my chocolate or a banana. To help keep my concentration during the breaks, I walked from one side of the room to the other, backwards and forwards behind my chair, with my head down looking at the floor, avoiding the gazes of the spectators. Sitting continuously in my seat while reciting was something that I found even more difficult than I had expected, as I tend to fidget a lot. While recalling the digits, I would roll my head or cover it with my hands or gently rock myself with my eyes closed.
I reached 10,000 digits at quarter past one in the afternoon, just over two hours from the start of the recitation. As the hours passed, I could feel myself becoming more and more tired and I could see that the visual landscapes in my mind were becoming increasingly blurred, as the fatigue started to set in. I hadn’t recited all the digits together in a continuous sequence before the event and I now hoped that I would not get so tired that I would be unable to finish.
There was, in the end, only one point at which I momentarily thought I might not be able to continue. It was after reaching 16,600 digits that for just a few moments my mind went completely blank: no shapes, no colors, no textures, nothing. I hadn’t ever experienced anything like it before, as though I were looking into a black hole. I closed my eyes tight and took several deep breaths, then I felt a tingling in my head and from the darkness the colors started to flow again and I continued to recite as before.
By mid-afternoon, I was finally nearing the close of my numerical journey. I felt exhausted after five hours and was glad to have the end in sight. It felt as though I had run a marathon in my head. At exactly quarter past four, my voice shaking with relief, I recited the last digits: “67657486953587” and signaled that I had finished. I had recited 22,514 digits of pi without error in a time of five hours and nine minutes to set a new British and European record. The audience of spectators burst into loud applause and Simon ran over and surprised me with a hug. After giving my thanks to the checkers for monitoring the recitation throughout, I was asked to come outside for more photos and to receive my first-ever glass of champagne.
The subsequent response from the media to the event was phenomenal and much greater than anything the charity or I had expected. In the weeks that followed, I gave interviews for various newspapers and radio stations, including the BBC World Service and stations in places as far away as Canada and Australia.
One of the most common questions I was asked in these interviews was: Why learn a number like pi to so many decimal places? The answer I gave then as I do now is that pi is for me an extremely beautiful and utterly unique thing. Like the Mona Lisa or a Mozart symphony, pi is its own reason for loving it.