The motion of bodies that are resisted in proportion to their velocity
Proposition 1, Theorem 1
If a body is resisted in proportion to its velocity, the motion lost as a result of the resistance is as the space described in moving.
For since the motion lost in each of the equal particles of time is as the velocity, that is, as a particle of the path described, then, by composition [or componendo], the motion lost in the whole time will be as the whole path. Q.E.D.
COROLLARY. Therefore, if a body, devoid of all gravity, moves in free spaces by its inherent force alone and if there are given both the whole motion at the beginning and also the remaining motion after some space has been described, the whole space that the body can describe in an infinite time will be given. For that space will be to the space already described as the whole motion at the beginning is to the lost part of that motion.
Lemma 1
Quantities proportional to their differences are continually proportional.
Let A be to A − B as B to B − C and C to C − D, . . . ; then, by conversion [or convertendo], A will be to B as B to C and C to D, . . . . Q.E.D.
Proposition 2, Theorem 2
If a body is resisted in proportion to its velocity and moves through a homogeneous medium by its inherent force alone and if the times are taken as equal, the velocities at the beginnings of the individual times are in a geometric progression, and the spaces described in the individual times are as the velocities.
CASE 1. Divide the time into equal particles; and if, at the very beginnings of the particles, a force of resistance which is as the velocity acts with a single impulse, the decrease of the velocity in the individual particles of time will be as that velocity. The velocities are therefore proportional to their differences and thus (by book 2, lem. 1) are continually proportional. Accordingly, if any equal times are compounded of an equal number of particles, the velocities at the very beginnings of the times will be as the terms in a continual progression in which some have been skipped, omitting an equal number of intermediate terms in each interval. The ratios of these terms are indeed compounded of equally repeated equal ratios of the intermediate terms, and therefore these compound ratios are also equal to one another. Therefore, since the velocities are proportional to these terms, they are in a geometric progression. Now let those equal particles of times be diminished, and their number increased indefinitely, so that the impulse of the resistance becomes continual; then the velocities at the beginnings of equal times, which are always continually proportional, will also be continually proportional in this case. Q.E.D.
CASE 2. And by separation [or dividendo] the differences of the velocities (that is, the parts of them which are lost in the individual times) are as the wholes, while the spaces described in the individual times are as the lost parts of the velocities (by book 2, prop. 1) and are therefore also as the wholes. Q.E.D.
COROLLARY. Hence, if a hyperbola BG is described with respect to the rectangular asymptotes AC and CH and if AB and DG are perpendicular to asymptote AC and if both the velocity of the body and the resistance of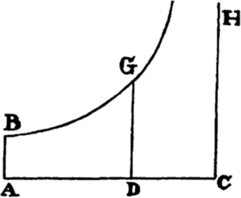 
the medium are represented, at the very beginning of the motion, by any given line AC, but after some time has elapsed, by the indefinite line DC, then the time can be represented by area ABGD, and the space described in that time can be represented by line AD. For if the area is increased uniformly by the motion of point D, in the same manner as the time, the straight line DC will decrease in a geometric ratio in the same way as the velocity, and the parts of the straight line AC described in equal times will decrease in the same ratio.
Proposition 3, Problem 1
To determine the motion of a body which, while moving straight up or down in a homogeneous medium, is resisted in proportion to the velocity, and which is acted on by uniform gravity.
When the body is moving up,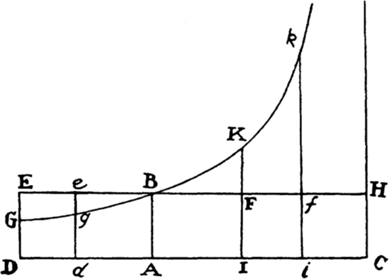 
represent the gravity by any given rectangle BACH, and the resistance of the medium at the beginning of the ascent by the rectangle BADE taken on the other side of the straight line AB. With respect to the rectangular asymptotes AC and CH, describe a hyperbola through point B, cutting perpendiculars DE and de in G and g; then the body, by ascending in the time DGgd, will describe the space EGge; and in the time DGBA will describe the space of the total ascent EGB; and in the time ABKI will describe the space of descent BFK; and in the time IKki will describe the space of descent KFfk; and the body’s velocities (proportional to the resistance of the medium) in these periods of time will be ABED, ABed, null, ABFI, and ABfi respectively; and the greatest velocity that the body can attain in descending will be BACH.
For resolve the rectangle BACH into innumerable rectangles Ak, Kl, Lm, Mn, . . . , which are as the increases of the velocities, occurring in the same number of equal times; then nil, Ak, Al, Am, An, . . . will be as the total velocities, and thus (by hypothesis) as the resistances of the medium at the beginning of each of the equal times. Make AC to AK, or ABHC to ABkK, as the force of gravity to the resistance at the beginning of the second time, and subtract the resistances from the force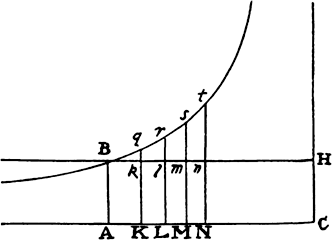 
of gravity; then the remainders ABHC, KkHC, LlHC, MmHC, . . . will be as the absolute forces by which the body is urged at the beginning of each of the times, and thus (by the second law of motion) as the increments of the velocities, that is, as the rectangles Ak, Kl, Lm, Mn, . . . , and therefore (by book 2, lem. 1) in a geometric progression. Therefore, if the straight lines Kk, Ll, Mm, Nn, . . . , produced, meet the hyperbola in q, r, s, t, . . . , areas ABqK, KqrL, LrsM, MstN, . . . will be equal, and thus proportional both to the times and to the forces of gravity, which are always equal. But area ABqK (by book 1, lem. 7, corol. 3, and lem. 8) is to area Bkq as Kq to ½kq or AC to ½AK, that is, as the force of gravity to the resistance in the middle of the first time. And by a similar argument, areas qKLr, rLMs, sMNt, . . . are to areas qklr, rlms, smnt, . . . as the force of gravity to the resistance in the middle of the second time, of the third, of the fourth, . . . . Accordingly, since the equal areas BAKq, qKLr, rLMs, sMNt, . . . are proportional to the forces of gravity, areas Bkq, qklr, rlms, smnt, . . . will be proportional to the resistance in the middle of each of the times, that is (by hypothesis), to the velocities, and thus to the spaces described. Take the sums of the proportional quantities; then areas Bkq, Blr, Bms, Bnt, . . . will be proportional to the total spaces described, and areas ABqK, ABrL, ABsM, ABtN, . . . will be proportional to the times. Therefore the body, while descending in any time ABrL, describes the space Blr, and in the time LrtN describes the space rlnt. Q.E.D. And the proof is similar for an ascending motion. Q.E.D.
COROLLARY 1. Therefore the greatest velocity that a body can acquire in falling is to the velocity acquired in any given time as the given force of gravity by which the body is continually urged to athe force of the resistance by which it is impeded at the end of that time.a
COROLLARY 2. If the time is increased in an arithmetic progression, the sum of that greatest velocity and of the velocity in the ascent, and also their difference in the descent, decreases in a geometric progression.
COROLLARY 3. The differences of the spaces which are described in equal differences of the times decrease in the same geometric progression.
COROLLARY 4. The space described by a body is the difference of two spaces, of which one is as the time reckoned from the beginning of the descent, and the other is as the velocity; and these spaces are equal to each other at the very beginning of the descent.
Proposition 4, Problem 2
Supposing that the force of gravity in some homogeneous medium is uniform and tends perpendicularly toward the plane of the horizon, it is required to determine the motion of a projectile in that medium, while it is resisted in proportion to the velocity.
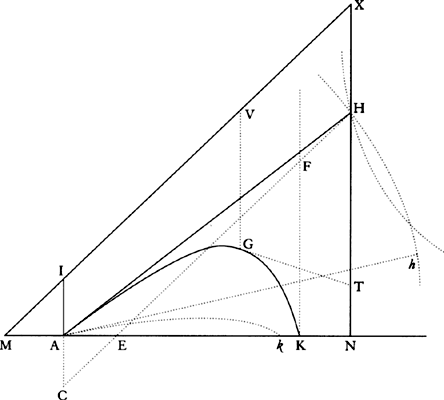
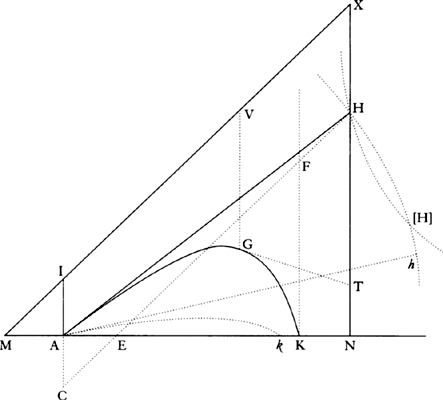
From any place D let a projectile go forth along any straight line DP, and represent its velocity at the beginning of the motion by the length DP. Drop the perpendicular PC from point P to the horizontal line DC, and cut DC in A so that DA is to AC as the resistance of the medium arising from the upward motion at the beginning is to the force of gravity; or (which comes to the same thing) so that the rectangle of DA and DP is to the rectangle of AC and CP as the whole resistance at the beginning of the motion is to the force of gravity. Describe any hyperbola GTBS with asymptotes DC and CP which cuts the perpendiculars DG and AB in G and B; and complete the parallelogram DGKC, whose side GK cuts AB in Q. Take the line N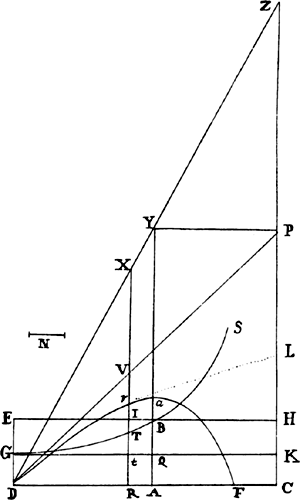 
in the same ratio to QB as DC to CP, and at any point R of the straight line DC erect the perpendicular RT which meets the hyperbola in T and the straight lines EH, GK, and DP in I, t, and V, and then on RT take Vr equal to 
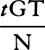, or (which comes to the same thing) take Rr equal to 
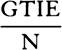. Then in the time DRTG the projectile will arrive at point r, describing the curved line DraF which point r traces out, reaching its greatest height a in the perpendicular AB, and afterward always approaching the asymptote PC. And its velocity at any point r is as the tangent rL of the curve. Q.E.I.
For N is to QB as DC to CP or DR to RV, and thus RV is equal to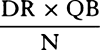 
, and Rr 
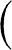that is, RV − Vr, or 
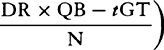is equal to 
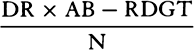. Now represent the time by area RDGT, and (by corol. 2 of the laws) divide the motion of the body into two parts, one upward and the other lateral. Since the resistance is as the motion, it also will be divided into two parts proportional to and opposite to the parts of the motion; and thus the distance described by the lateral motion will be (by book 2, prop. 2) as line DR, and the distance described by the upward motion will be (by book 2, prop. 3) as the area DR × AB − RDGT, that is, as line Rr. But at the very beginning of the motion the area RDGT is equal to the rectangle DR × AQ, and thus that line Rr 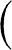or 
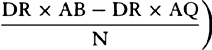is then to DR as AB − AQ or QB to N, that is, as CP to DC, and hence as the upward motion to the lateral motion at the beginning. Since, therefore, Rr is always as the distance upward, and DR is always as the distance sideward, and Rr is to DR at the beginning as the distance upward to the distance sideward, Rr must always be to DR as the distance upward to the distance sideward, and therefore the body must move in the line DraF, which the point r traces out. Q.E.D.
COROLLARY 1. Rr is therefore equal to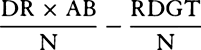 
; and thus, if RT is produced to X so that RX is equal to 
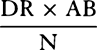, that is, if the parallelogram ACPY is completed, and DY is joined cutting CP in Z, and RT is produced until it meets DY in X, then Xr will be equal to 
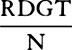, and therefore will be proportional to the time.
COROLLARY 2. Hence, if innumerable lines CR are taken (or, which comes to the same thing, innumerable lines ZX) in a geometric progression, then as many lines Xr will be in an arithmetic progression. And hence it is easy to draw curve DraF with the help of a table of logarithms.
COROLLARY 3. If a parabola is constructed with vertex D and diameter DG (produced downward) and a latus rectum that is to 2DP as the whole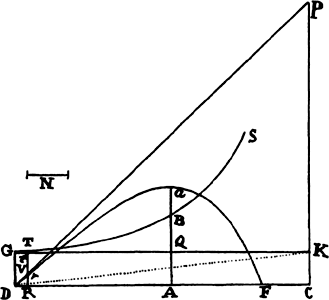 
resistance at the very beginning of the motion is to the force of gravity, then the velocity with which a body must go forth from place D along the straight line DP in order to describe curve DraF in a uniform resisting medium will be the very one with which it must go forth from the same place D along the same straight line DP in order to describe the parabola in a nonresisting space. For the latus rectum of this parabola, at the very beginning of the motion, is 
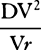; and Vr is 
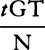or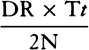 
. But the straight line that, if it were drawn, would touch the hyperbola GTS in G is parallel to DK, and thus Tt is 
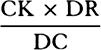, and N has been taken as 
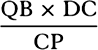. Therefore Vr is 
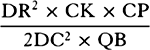, that is (because DR is to DC as DV is to DP), 
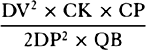; and the latus rectum 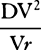comes out 
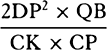, that is (because QB is to CK as DA is to AC), 
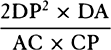, and thus is to 2DP as DP × DA to CP × AC—that is, as the resistance to the gravity. Q.E.D.
COROLLARY 4. Hence, if a body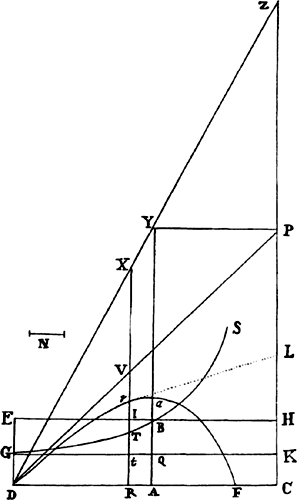 
is projected from any place D with a given velocity along any straight line DP given in position, and the resistance of the medium at the very beginning of the motion is given, the curve DraF which the body will describe can be found. For from the given velocity the latus rectum of the parabola is given, as is well known. And if 2DP is taken to that latus rectum as the force of gravity to the force of resistance, DP is given. Then, if DC is cut in A so that CP × AC is to DP × DA in that same ratio of gravity to resistance, point A will be given. And hence curve DraF is given.
COROLLARY 5. And conversely, if curve DraF is given, both the velocity of the body and the resistance of the medium in each of the places r will be given. For since the ratio of CP × AC to DP × DA is given, both the resistance of the medium at the beginning of the motion and the latus rectum of the parabola are also given; and hence the velocity at the beginning of the motion is also given. Then from the length of the tangent rL, both the velocity (which is proportional to it) and the resistance (which is proportional to the velocity) are given in any place r.
COROLLARY 6. The length 2DP is to the latus rectum of the parabola as the gravity to the resistance at D; and when the velocity is increased the resistance is increased in the same ratio, but the latus rectum of the parabola is increased in the square of that ratio; hence it is evident that the length 2DP is increased in the simple ratio and thus is always proportional to the velocity and is not increased or decreased when the angle CDP is changed unless the velocity is also changed.
COROLLARY 7. Hence the method is apparent for determining the curve DraF from phenomena approximately and for obtaining thereby the resistance and the velocity with which the body is projected. Project two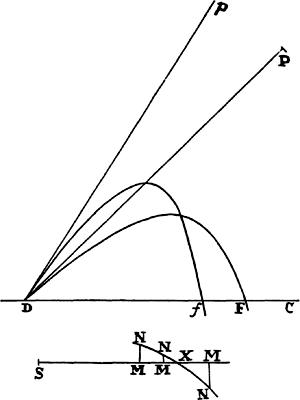 
similar and equal bodies with the same velocity from place D along the different angles CDP and CDp, and let the places F and f where they fall upon the horizontal plane DC be known. Then, taking any length for DP or Dp, suppose that the resistance at D is to the gravity in any ratio, and represent that ratio by any length SM. Then, by computation, find the lengths DF and Df from that assumed length DP, and from the ratio 
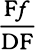(found by computation) take away the same ratio (found by experiment), and represent the difference by the perpendicular MN. Do the same thing a second and a third time, always taking a new ratio SM of resistance to gravity, and obtain a new difference MN. But draw the positive differences on one side of the straight line SM and the negative differences on the other, and through points N, N, N draw the regular curve NNN cutting the straight line SMMM in X, and then SX will be the true ratio of the resistance to the gravity, which it was required to find. From this ratio the length DF is to be obtained by calculation; then the length that is to the assumed length DP as the length DF (found out by experiment) to the length DF (just found by computation) will be the true length DP. When this is found, there will be known both the curved line DraF that the body describes and the body’s velocity and resistance in every place.
Scholium
However, the hypothesis that the resistance encountered by bodies is in the ratio of the velocity belongs more to mathematics than to nature.a In mediums wholly lacking in rigidity, the resistances encountered by bodies are as the squares of the velocities. For by the action of a swifter body, a motion that is greater in proportion to that greater velocity is communicated to a given quantity of the medium in a smaller time; and thus in an equal time, because a greater quantity of the medium is disturbed, a greater motion is communicated in proportion to the square of the velocity, and (by the second and third laws of motion) the resistance is as the motion communicated. Let us see, therefore, what kinds of motions arise from this law of resistance.
The motion of bodies that are resisted as the squares of the velocities
Proposition 5, Theorem 3
If the resistance of a body is proportional to the square of the velocity and if the body moves through a homogeneous medium by its inherent force alone and if the times are taken in a geometric progression going from the smaller to the greater terms, I say that the velocities at the beginning of each of the times are inversely in that same geometric progression and that the spaces described in each of the times are equal.
For since the resistance of the medium is proportional to the square of the velocity, and the decrement of the velocity is proportional to the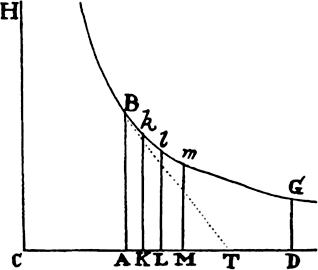 
resistance, if the time is divided into innumerable equal particles, the squares of the velocities at each of the beginnings of the times will be proportional to the differences of those same velocities. Let the particles of time be AK, KL, LM, . . . , taken in the straight line CD, and erect perpendiculars AB, Kk, Ll, Mm, . . . , meeting the hyperbola BklmG (described with center C and rectangular asymptotes CD and CH) in B, k, l, m, . . . ; then AB will be to Kk as CK to CA, and by separation [or dividendo] AB − Kk to Kk as AK to CA, and by alternation [or alternando] AB − Kk to AK as Kk to CA, and thus as AB × Kk to AB × CA. Hence, since AK and AB × CA are given, AB − Kk will be as AB × Kk; and ultimately, when AB and Kk come together, as AB2. And by a similar argument Kk − Ll, Ll − Mm, . . . will be as Kk2, Ll2, . . . . The squares of lines AB, Kk, Ll, Mm, therefore, are as their differences; and on that account, since the squares of the velocities were also as their differences, the progression of both will be similar. It follows from what has been proved that the areas described by these lines are also in a progression entirely similar to that of the spaces described by the velocities. Therefore, if the velocity at the beginning of the first time AK is represented by line AB, and the velocity at the beginning of the second time KL by line Kk, and the length described in the first time is represented by area AKkB, then all the subsequent velocities will be represented by the subsequent lines Ll, Mm, . . . , and the lengths described will be represented by areas Kl, Lm, . . . . And by composition [or componendo], if the whole time is represented by the sum of its parts AM, the whole length described will be represented by the sum of its parts AMmB. Now imagine time AM to be divided into parts AK, KL, LM, . . . in such a way that CA, CK, CL, CM, . . . are in a geometric progression; then those parts will be in the same progression, and the velocities AB, Kk, Ll, Mm, . . . will be in the same progression inverted, and the spaces described Ak, Kl, Lm, . . . will be equal. Q.E.D.
COROLLARY 1. Therefore it is evident that if the time is represented by any part AD of the asymptote, and the velocity at the beginning of the time by ordinate AB, then the velocity at the end of the time will be represented by ordinate DG, and the whole space described will be represented by the adjacent hyperbolic area ABGD; and furthermore, the space that a body in a nonresisting medium could describe in the same time AD, with the first velocity AB, will be represented by the rectangle AB × AD.
COROLLARY 2. Hence the space described in a resisting medium is given by taking that space to be in the same proportion to the space which could be described simultaneously with a uniform velocity AB in a nonresisting medium as the hyperbolic area ABGD is to the rectangle AB × AD.
COROLLARY 3. The resistance of the medium is also given by setting it to be, at the very beginning of the motion, equal to the uniform centripetal force that in a nonresisting medium could generate the velocity AB in a falling body in the time AC. For if BT is drawn, touching the hyperbola in B and meeting the asymptote in T, the straight line AT will be equal to AC and will represent the time in which the first resistance uniformly continued could annul the whole velocity AB.
COROLLARY 4. And hence the proportion of this resistance to the force of gravity or to any other given centripetal force is also given.
COROLLARY 5. And conversely, if the proportion of the resistance to any given centripetal force is given, the time AC is given in which a centripetal force equal to the resistance could generate any velocity AB; and hence point B is given, through which the hyperbola with asymptotes CH and CD must be described, as is also the space ABGD which the body, beginning its motion with that velocity AB, can describe in any time AD in a homogeneous resisting medium.
Proposition 6, Theorem 4
Equal homogeneous spherical bodies that are resisted in proportion to the square of the velocity, and are carried forward by their inherent forces alone, will, in times that are inversely as the initial velocities, always describe equal spaces, and lose parts of their velocities proportional to the wholes.
Describe any hyperbola BbEe, with rectangular asymptotes CD and CH, which cuts perpendiculars AB, ab, DE, and de in B, b, E, and e; and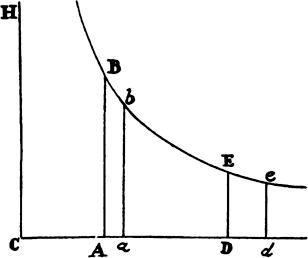 
represent the initial velocities by perpendiculars AB and DE and the times by lines Aa and Dd. Therefore Aa is to Dd as (by hypothesis) DE is to AB, and as (from the nature of the hyperbola) CA is to CD, and by composition [or componendo] as Ca is to Cd. Hence areas ABba and DEed, that is, the spaces described, are equal to each other, and the first velocities AB and DE are proportional to the ultimate velocities ab and de, and therefore, by separation [or dividendo], also to the lost parts of those velocities AB − ab and DE − de. Q.E.D.
Proposition 7, Theorem 5
Spherical bodies that are resisted in proportion to the squares of the velocities will, in times that are as the first motions directly and the first resistances inversely, lose parts of the motions proportional to the wholes and will describe spaces proportional to those times and the first velocities jointly.
For the lost parts of the motions are as the resistances and the times jointly. Therefore, for those parts to be proportional to the wholes, the resistance and time jointly must be as the motion. Accordingly, the time will be as the motion directly and the resistance inversely. Therefore, if the particles of times are taken in this ratio, the bodies will always lose particles of their motions proportional to the wholes and thus will retain velocities always proportional to their first velocities. And because the ratio of the velocities is given, they will always describe spaces that are as the first velocities and the times jointly. Q.E.D.
COROLLARY 1. Therefore, if equally swift bodies are resisted in proportion to the squares of their diameters, then homogeneous globes moving with any velocities will, in describing spaces proportional to their diameters, lose parts of their motions proportional to the wholes. For the motion of each globe will be as its velocity and mass jointly, that is, as its velocity and the cube of its diameter; the resistance (by hypothesis) will be as the square of the diameter and the square of the velocity jointly; and the time (by this proposition) is in the former ratio directly and the latter ratio inversely, that is, as the diameter directly and the velocity inversely; and thus the space, being proportional to the time and the velocity, is as the diameter.
COROLLARY 2. If equally swift bodies are resisted in proportion to the 3/2 powers of the diameters, then homogeneous globes moving with any velocities will, in describing spaces that are as the 3/2 powers of the diameters, lose parts of motions proportional to the wholes.
COROLLARY 3. And universally, if equally swift bodies are resisted in the ratio of any power of the diameters, the spaces in which homogeneous globes moving with any velocities will lose parts of their motions proportional to the wholes will be as the cubes of the diameters divided by that power. Let the diameters be D and E; and if the resistances, when the velocities are supposed equal, are as Dn and En, then the spaces in which the globes, moving with any velocities, will lose parts of their motions proportional to the wholes will be as D3−n and E3−n. And therefore homogeneous globes, in describing spaces proportional to D3−n and E3−n, will retain velocities in the same ratio to each other that they had at the beginning.
COROLLARY 4. But if the globes are not homogeneous, the space described by the denser globe must be augmented in proportion to the density. For the motion, with an equal velocity, is greater in proportion to the density, and the time (by this proposition) is increased in proportion to the motion directly, and the space described is increased in proportion to the time.
COROLLARY 5. And if the globes move in different mediums, the space in the medium that, other things being equal, resists more will have to be decreased in proportion to the greater resistance. For the time (by this proposition) will be decreased in proportion to the increase of the resistance, and the space will be decreased in proportion to the time.
Lemma 2a
The moment of a generated quantity is equal to the moments of each of the generating roots multiplied continually by the exponents of the powers of those roots and by their coefficients.
I call “generated” every quantity that is, without addition or subtraction, generated from any roots or terms: in arithmetic by multiplication, division, or extraction of roots; in geometry by the finding either of products and roots or of extreme and mean proportionals. Quantities of this sort are products, quotients, roots, rectangles, squares, cubes, square roots, cube roots, and the like.b I here consider these quantities as indeterminate and variable, and increasing or decreasing as if by a continual motion or flux; and it is their instantaneous increments or decrements that I mean by the word “moments,” in such a way that increments are considered as added or positive moments, and decrements as subtracted or negative moments. But take care: do not understand them to be finite particles! cFinite particles are not moments, but the very quantities generated from the moments.c They must be understood to be the just-now nascent beginnings of finite magnitudes. For in this lemma the magnitude of moments is not regarded, but only their first proportion when nascent. It comes to the same thing if in place of moments there are used either the velocities of increments and decrements (which it is also possible to call motions, mutations, and fluxions of quantities) or any finite quantities proportional to these velocities. And the coefficient of each generating root is the quantity that results from dividing the generated quantity by this root.
Therefore, the meaning of this lemma is that if the moments of any quantities A, B, C, . . . increasing or decreasing by a continual motion, or the velocities of mutation which are proportional to these moments are called a, b, c, . . . , then the moment or mutation of the generated rectangle AB would be aB + bA, and the moment of the generated solid ABC would be aBC + bAC + cAB, and the moments of the generated powers A2, A3, A4, A½, A3/2, A⅓, A⅔, A−1, A−2, A−½, would be 2aA, 3aA2, 4aA3, ½aA−½, 3/2aA½, ⅓aA−⅔, ⅔aA−⅓, −aA−2, −2aA−3, and −½aA−3/2 respectively. And generally, the moment of any power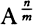 
would be 
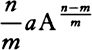. Likewise, the moment of the generated quantity A2B would be 2aAB + bA2, and the moment of the generated quantity A3B4C2 would be 3aA2B4C2 + 4bA3B3C2 + 2cA3B4C, and the moment of the generated quantity 
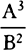or A3B−2 would be 3aA2B−2 − 2bA3B−3, and so on. The lemma is proved as follows.
CASE 1. Any rectangle AB increased by continual motion, when the halves of the moments, ½a and ½b, were lacking from the sides A and B, was A − ½a multiplied by B − ½b, or AB − ½aB − ½bA + ¼ab and as soon as the sides A and B have been increased by the other halves of the moments, it comes out A + ½a multiplied by B + ½b, or AB + ½aB + ½bA + ¼ab. Subtract the former rectangle from this rectangle, and there will remain the excess aB + bA. Therefore by the total increments a and b of the sides there is generated the increment aB + bA of the rectangle. Q.E.D.
CASE 2. Suppose that AB is always equal to G; then the moment of the solid ABC or GC (by case 1) will be gC + cG, that is (if AB and aB + bA are written for G and g), aBC + bAC + cAB. And the same is true of the solid contained under any number of sides [or the product of any number of terms]. Q.E.D.
CASE 3. Suppose that the sides A, B, and C are always equal to one another; then the moment aB + bA of A2, that is, of the rectangle AB, will be 2aA, while the moment aBC + bAC + cAB of A3, that is, of the solid ABC, will be 3aA2. And by the same argument, the moment of any power An is naAn−1. Q.E.D.
CASE 4. Hence, since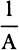 
multiplied by A is 1, the moment of 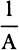multiplied by A together with 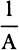multiplied by a will be the moment of 1, that is, nil. Accordingly, the moment of 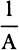or of A−1 is 
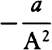. And in general, since 
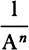multiplied by An is 1, the moment of 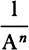multiplied by An together with 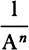multiplied by naAn−1 will be nil. And therefore the moment of 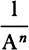or A−n will be 
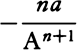. Q.E.D.
CASE 5. And since A½ multiplied by A½ is A, the moment of A½ multiplied by 2A½ will be a, by case 3; and thus the moment of A½ will be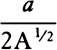 
or ½aA−½. And in general, if 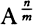is supposed equal to B, Am will be equal to Bn, and hence maAm−1 will be equal to nbBn−1 and maA−1 will be equal to nbB−1 or 
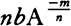, and thus 
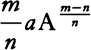equal to b, that is, equal to the moment of 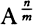. Q.E.D.
CASE 6. Therefore the moment of any generated quantity AmBn is the moment of Am multiplied by Bn, together with the moment of Bn multiplied by Am, that is, maAm−1 Bn + nbBn−1 Am; and this is so whether the exponents m and n of the powers are whole numbers or fractions, whether positive or negative. And it is the same for a solid contained by more than two terms raised to powers. Q.E.D.
COROLLARY 1. Hence in continually proportional quantities, if one term is given, the moments of the remaining terms will be as those terms multiplied by the number of intervals between them and the given term. Let A, B, C, D, E, and F be continually proportional; then, if the term C is given, the moments of the remaining terms will be to one another as −2A, −B, D, 2E, and 3F.
COROLLARY 2. And if in four proportionals the two means are given, the moments of the extremes will be as those same extremes. The same is to be understood of the sides of any given rectangle.
COROLLARY 3. And if the sum or difference of two squares is given, the moments of the sides will be inversely as the sides.
Proposition 8, Theorem 6
If a body, acted on by gravity uniformly, goes straight up or down in a uniform medium, and the total space described is divided into equal parts, and the absolute forces at the beginnings of each of the parts are found (adding the resistance of the medium to the force of gravity when the body is ascending, or subtracting it when the body is descending), I say that those absolute forces are in a geometric progression.
Represent the force of gravity by the given line AC; the resistance, by the indefinite line AK; the absolute force in the descent of the body,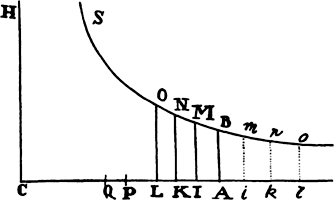 
by the difference KC; the velocity of the body, by the line AP, which is the mean proportional between AK and AC, and thus is as the square root of the resistance; the increment of the resistance occurring in a given particle of time, by the line-element KL; and the simultaneous increment of the velocity, by the line-element PQ; then with center C and rectangular asymptotes CA and CH, describe any hyperbola BNS, meeting the erected perpendiculars AB, KN, and LO in B, N, and O. Since AK is as AP2, the moment KL of AK will be as the moment 2AP × PQ of AP2, that is, as AP multiplied by KC, since the increment PQ of the velocity (by the second law of motion) is proportional to the generating force KC. Compound the ratio of KL with the ratio of KN, and the rectangle KL × KN will become as AP × KC × KN—that is, because the rectangle KC × KN is given, as AP. But the ultimate ratio of the hyperbolic area KNOL to the rectangle KL × KN, when points K and L come together, is the ratio of equality. Therefore that evanescent hyperbolic area is as AP. Hence the total hyperbolic area ABOL is composed of the particles KNOL, which are always proportional to the velocity AP, and therefore this area is proportional to the space described with this velocity. Now divide that area into equal parts ABMI, IMNK, KNOL, . . . , and the absolute forces AC, IC, KC, LC, . . . will be in a geometric progression. Q.E.D.
And by a similar argument, if—in the ascent of the body—equal areas ABmi, imnk, knol, . . . are taken on the opposite side of point A, it will be manifest that the absolute forces AC, iC, kC, lC, . . . are continually proportional. And thus, if all the spaces in the ascent and descent are taken equal, all the absolute forces lC, kC, iC, AC, IC, KC, LC, . . . will be continually proportional. Q.E.D.
COROLLARY 1. Hence, if the space described is represented by the hyperbolic area ABNK, the force of gravity, the velocity of the body, and the resistance of the medium can be represented by lines AC, AP, and AK respectively, and vice versa.
COROLLARY 2. And line AC represents the greatest velocity that the body can ever acquire by descending infinitely.
COROLLARY 3. Therefore, if for a given velocity the resistance of the medium is known, the greatest velocity will be found by taking its ratio to the given velocity as the square root of the ratio of the force of gravity to that known resistance of the medium.a
Proposition 9, Theorem 7
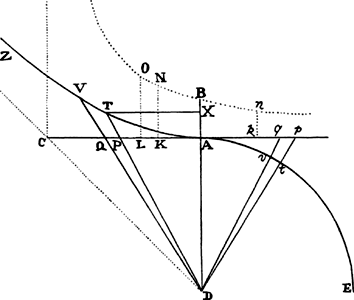
Given what has already been proved, I say that if the tangents of the angles of a sector of a circle and of a hyperbola are taken proportional to the velocities, the radius being of the proper magnitude, the whole time aof ascending to the highest placea will be as the sector of the circle, and the whole time bof descending from the highest placeb will be as the sector of the hyperbola.
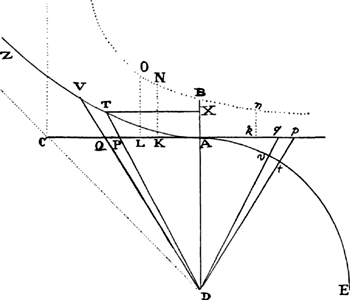
Draw AD perpendicular and equal to the straight line AC, which represents the force of gravity. With center D and semidiameter AD describe the quadrant AtE of a circle and the rectangular hyperbola AVZ having axis AX, principal vertex A, and asymptote DC. Draw Dp and DP, and the sector AtD of the circle will be as cthe whole time of ascending to the highest place,c and the sector ATD of the hyperbola will be as dthe whole time of descending from the highest place,d provided that the tangents Ap and AP of the sectors are as the velocities.
CASE 1. Draw Dvq cutting off the moments or the minimally small particles tDv and qDp, described simultaneously, of the sector ADt and of the triangle ADp. Since those particles, because of the common angle D, are as the squares of the sides, particle tDv will be as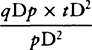 
, that is, because tD is given, as 
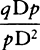. But pD2 is AD2 + Ap2, that is, AD2 + AD × Ak, or AD × Ck; and qDp is ½AD × pq. Therefore particle tDv of the sector is as 
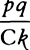, that is, directly as the minimally small decrement pq of the velocity and inversely as the force Ck that decreases the velocity, and thus as the particle of time corresponding to the decrement of the velocity. And by composition [or componendo] the sum of all the particles tDv in the sector ADt will be as the sum of the particles of time corresponding to each of the lost particles pq of the decreasing velocity Ap, until that velocity, decreased to nil, has vanished; that is, the whole sector ADt is as ethe whole time of ascending to the highest place.e Q.E.D.
CASE 2. Draw DQV cutting off the minimally small particles TDV and PDQ of the sector DAV and of the triangle DAQ; and these particles will be to each other as DT2 to DP2, that is (if TX and AP are parallel), as DX2 to DA2 or TX2 to AP2, and by separation [or dividendo] as DX2 − TX2 to DA2 − AP2. But from the nature of the hyperbola, DX2 − TX2 is AD2, and by hypothesis AP2 is AD × AK. Therefore the particles are to each other as AD2 to AD2 − AD × AK, that is, as AD to AD − AK or AC to CK; and thus the particle TDV of the sector is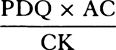 
, and hence, because AC and AD are given, as 
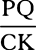, that is, directly as the increment of the velocity and inversely as the force generating the increment, and thus as the particle of time corresponding to the increment. And by composition [or componendo] the sum of the particles of time in which all the particles PQ of the velocity AP are generated will be as the sum of the particles of the sector ATD, that is, the whole time will be as the whole sector. Q.E.D.
COROLLARY 1. Hence, if AB is equal to a fourth of AC, the space that a body describes by falling in any time will be in the same ratio to the space that the body can describe by progressing uniformly in that same time with its greatest velocity AC as the ratio of area ABNK (which represents the space described in falling) to area ATD (which represents the time). For, since AC is to AP as AP to AK, it follows (by book 2, lem. 2, corol. 1) that LK will be to PQ as 2AK to AP, that is, as 2AP to AC, and hence LK will be to ½PQ as AP to ¼AC or AB; KN is also to AC or AD as AB to CK; and thus, from the equality of the ratios [or ex aequo], LKNO will be to DPQ as AP to CK. But DPQ was to DTV as CK to AC. Therefore, once again by the equality of the ratios [or ex aequo], LKNO is to DTV as AP to AC, that is, as the velocity of the falling body to the greatest velocity that the body can acquire in falling. Since, therefore, the moments LKNO and DTV of areas ABNK and ATD are as the velocities, all the parts of those areas generated simultaneously will be as the spaces described simultaneously, and thus the whole areas ABNK and ATD generated from the beginning will be as the whole spaces described from the beginning of the descent. Q.E.D.
COROLLARY 2. The same result follows for the space described in ascent: namely, the whole space is to the space described in the same time with a uniform velocity AC as area ABnk is to sector ADt.
COROLLARY 3. The velocity of a body falling in time ATD is to the velocity that it would acquire in the same time in a nonresisting space as the triangle APD to the hyperbolic sector ATD. For the velocity in a nonresisting medium would be as time ATD, and in a resisting medium is as AP, that is, as triangle APD. And the velocities at the beginning of the descent are equal to each other, as are those areas ATD and APD.
COROLLARY 4. By the same argument, the velocity in the ascent is to the velocity with which the body in the same time in a nonresisting space could lose its whole ascending motion as the triangle ApD is to the sector AtD of the circle, or as the straight line Ap is to the arc At.
COROLLARY 5. Therefore the time in which a body, by falling in a resisting medium, acquires the velocity AP is to the time in which it could acquire its greatest velocity AC, by falling in a nonresisting space, as sector ADT to triangle ADC; and the time in which it could lose the velocity Ap by ascending in a resisting medium is to the time in which it could lose the same velocity by ascending in a nonresisting space as arc At is to its tangent Ap.
COROLLARY 6. Hence, from the given time, the space described by ascent or descent is given. For the greatest velocity of a body descending infinitely is given (by book 2, prop. 8, corols. 2 and 3), and hence the time is given in which a body could acquire that velocity by falling in a nonresisting space. And if sector ADT or ADt is taken to be to triangle ADC in the ratio of the given time to the time just found, there will be given both the velocity AP or Ap and the area ABNK or ABnk, which is to the sector ADT or ADt as the required space is to the space that can be described uniformly in the given time with that greatest velocity which has already been found.
COROLLARY 7. And working backward, the time ADt or ADT will be given from the given space ABnk or ABNK of ascent or descent.
Proposition 10, Problem 3
Let a uniform force of gravity tend straight toward the plane of the horizon, and let the resistance be as the density of the medium and the square of the velocity jointly; it is required to find, in each individual place, the density of the medium that makes the body move in any given curved line and also the velocity of the body and resistance of the medium.
EXAMPLE 1. Let line PFHQ be a semicircle described on the diameter PQ, and let it be required to find the density of the medium that would make a projectile move in this semicircle.
Bisect diameter PQ in A; call AQ, n; AC, a; CH, e; and CD, o. Then DI2 or AQ2 − AD2 will be = n2 − a2 − 2ao − o2, or e2 − 2ao − o2, and when the root has been extracted by our method, DI will become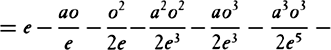 
· · · . Here write n2 for e2 + a2, and DI will come out 
· · · .
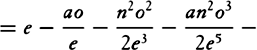I divide series of this sort into successive terms in the following manner. What I call the first term is the term in which the infinitely small quantity o does not exist; the second, the term in which that quantity is of one dimension; the third, the term in which it is of two dimensions; the fourth, the term in which it is of three dimensions; and so on indefinitely. And the first term, which here is e, will always denote the length of the ordinate CH, standing at the beginning of the indefinite quantity o. The second term, which here is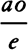 
, will denote the difference between CH and DN, that is, the line-element MN, which is cut off by completing the parallelogram HCDM and thus always determines the position of the tangent HN; as, for example, in this case by taking MN to HM as 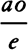is to o, or a to e. The third term, 
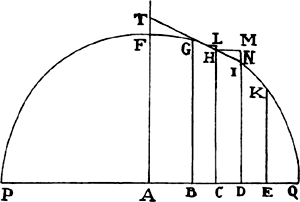which here is 
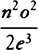, will designate the line-element IN, which lies between the tangent and the curve and thus determines the angle of contact IHN or the curvature that the curved line has in H. If that line-element IN is of a finite magnitude, it will be designated by the third term along with the terms following without limit. But if that line-element is diminished infinitely, the subsequent terms will come out infinitely smaller than the third and thus can be ignored. The fourth term determines the variation of the curvature, the fifth the variation of the variation, and so on. Hence, by the way, one can see clearly the not inconsiderable usefulness of these series in the solution of problems that depend on tangents and the curvature of curves.
cNow compare the series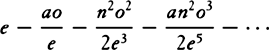 
with the series P − Qo − Ro2 − So3 − · · · , and in the same manner for P, Q, R, and S write e, 
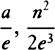, and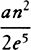 
, and for √(1 +Q2) write 
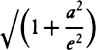or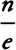 
; then the density of the medium will come outc as 
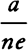, that is (because n is given), as 
, or 
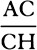, that is, as the tangent’s length HT terminated at the semidiameter AF, which stands perpendicularly upon PQ; and the resistance will be to the gravity as 3a to 2n, that is, as 3AC to the diameter PQ of the circle, while the velocity will be as √CH. Therefore, if the body goes forth from place F with the proper velocity along a line parallel to PQ, and the density of the medium in each place H is as the length of the tangent HT, and the resistance, also in some place H, is to the force of gravity as 3AC to PQ, then that body will describe the quadrant FHQ of a circle. Q.E.I.
But if the same body were to go forth from place P along a line perpendicular to PQ and were to begin to move in an arc of the semicircle PFQ, AC or a would have to be taken on the opposite side of center A, and therefore its sign would have to be changed, and −a would have to be written for +a. Thus the density of the medium would come out as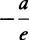 
. But nature does not admit of a negative density, that is, a density that accelerates the motions of bodies; and therefore it cannot naturally happen that a body by ascending from P should describe the quadrant PF of a circle. For this effect the body would have to be accelerated by an impelling medium, not impeded by a resisting medium.
EXAMPLE 2. Let the line PFQ be a parabola having its axis AF perpendicular to the horizon PQ, and let it be required to find the density of the medium that would make a projectile move in that parabola.
From the nature of the parabola, the rectangle PD × DQ is equal to the rectangle of the ordinate DI and some given straight line. Let that straight line be called b; PC, a; PQ, c; CH, e; and CD, o.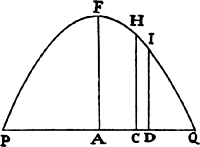 
Then the rectangle (a+o)×(c−a−o), or ac − a2 − 2ao+co ∔ o2, is equal to the rectangle b × DI, and thus DI is equal to 
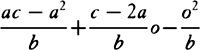. Now the second term 
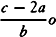of this series should be written for Qo, the third term 
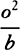likewise for Ro2. But since there are not more terms, the coefficient S of the fourth will have to vanish, and therefore the quantity 
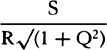, to which the density of the medium is proportional, will be nil. Therefore, if the density of the medium is null, a projectile will move in a parabola, as Galileo once proved. Q.E.I.
EXAMPLE 3. Let line AGK be a hyperbola having an asymptote NX perpendicular to the horizontal plane AK; and let it be required to find the density of the medium that would make a projectile move in this hyperbola.
Let MX be the other asymptote, meeting in V the ordinate DG produced; and from the nature of the hyperbola, the rectangle XV × VG will be given. Moreover, the ratio of DN to VX is given, and therefore the rectangle DN × VG is given also. Let this rectangle be b2. And after completing the parallelogram DNXZ, call BN a; BD, o; NX, c; and suppose the given ratio of VZ to ZX or DN to be 
. Then DN will be equal to a − o,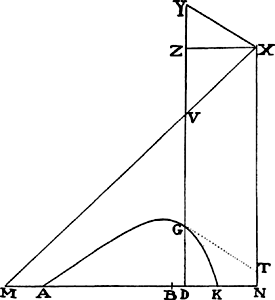 
VG will be equal to 
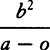, VZ will be equal to (a − o), and GD or NX − VZ − VG will be equal to c − a + o − 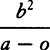. Resolve the term 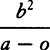into the converging series 
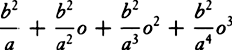. . . , and GD will become equal to c − a − 
+ o − 
o − 
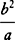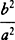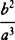o2 −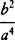 
o3 . . . . The second term o − 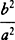oof this series is to be used for Qo, the third (with the sign changed) 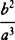o2 for Ro2, and the fourth (with the sign also changed) 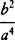o3 for So3, and their coefficients 
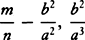, and 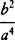are to be written in the above rule for Q, R, and S. When this is done, the density of the medium comes out as 
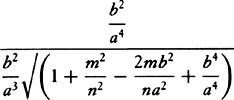or 
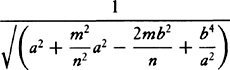, that is (if in VZ, VY is taken equal to VG), as 
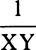. For a2 and 
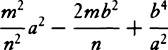are the squares of XZ and ZY. And the resistance is found to have the same ratio to gravity that 3XY has to 2YG; and the velocity is that with which the body would go in a parabola having vertex G, diameter DG, and latus rectum 
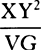. Therefore suppose that the densities of the medium in each of the individual places G are inversely as the distances XY and that the resistance in some place G is to gravity as 3XY to 2YG; then a body sent forth from place A with the proper velocity will describe that hyperbola AGK. Q.E.I.
EXAMPLE 4. Suppose generally that line AGK is a hyperbola described with center X and asymptotes MX and NX with the condition that when the rectangle XZDN is described, whose side ZD cuts the hyperbola in G and its asymptote in V, VG would be inversely as some power DNn (whose index is the number n) of ZX or DN; and let it be required to find the density of the medium in which a projectile would progress in this curve.
For BN, BD, and NX write A, O, and C respectively, and let VZ be to XZ or DN as d to e, and let VG be equal to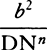 
; then DN will be equal to A − O, VG = 
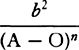,VZ = 
(A − O), and GD or NX − VZ − VG will be equal to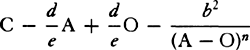 
. Resolve the term 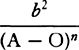into the infinite series 
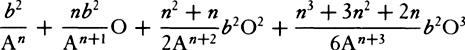. . . , and GD will become equal to 
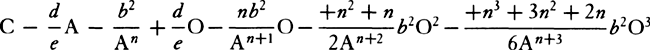. . . . The second term of this series 
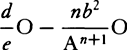is to be used for Qo, the third term 
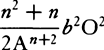for Ro2, the fourth term 
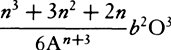for So3. And hence the density of the medium, 
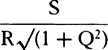, in any place G, becomes 
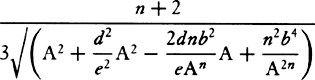, and thus if in VZ, VY is taken equal to n × VG, the density is inversely as XY. For A2 and 
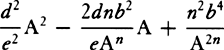are the squares of XZ and ZY. Moreover, the resistance in the same place G becomes to the gravity as 3S × 
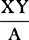is to 4R2, that is, as XY to 
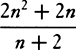VG. And the velocity in the same place is the very velocity with which a projected body would go in a parabola having vertex G, diameter GD, and latus rectum 
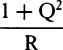or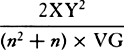 
. Q.E.I.
Since motion does not take place in a parabola except in a nonresisting medium, but does take place in the hyperbola here described if there is a continual resistance, it is obvious that the line which a projectile describes in a uniformly resisting medium approaches closer to these hyperbolas than to a parabola. At any rate, that line is of a hyperbolic kind, but about its vertex it is more distant from the asymptotes, and in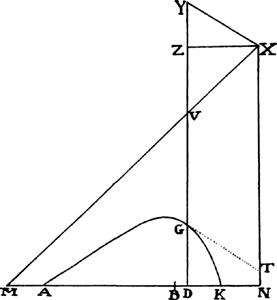 
those parts that are further from the vertex it approaches the asymptotes more closely, than the hyperbolas which I have described here. But the difference between them is not so great that one cannot be conveniently used in place of the other in practice. And the hyperbolas which I have been describing will perhaps prove to be more useful than a hyperbola that is more exact and at the same time more compounded. And they will be brought into use as follows.
Complete the parallelogram XYGT, and the straight line GT will touch the hyperbola in G, and thus the density of the medium in G is inversely as the tangent GT, and the velocity in the same place is as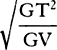 
, while the resistance is to the force of gravity as GT to 
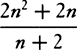× GV.
Accordingly, if a body projected from place A along the straight line AH describes the hyperbola AGK and if AH produced meets the asymptote NX in H and if AI drawn parallel to NX meets the other asymptote MX in I, then the density of the medium in A will be inversely as AH, and the velocity of the body will be as 
, and the resistance in the same place will be to the gravity as AH to 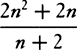× AI. Hence the following rules.
RULE 1. If both the density of the medium at A and the velocity with which the body is projected remain the same, and angle NAH is changed, lengths AH, AI, and HX will remain the same. And thus, if those lengths are found in some one case, the hyperbola can then be determined readily from any given angle NAH.
RULE 2. If both angle NAH and the density of the medium at A remain the same, and the velocity with which the body is projected is changed, the length AH will remain the same, and AI will be changed in the ratio of the inverse square of the velocity.
RULE 3. If angle NAH, the velocity of the body at A, and the accelerative gravity remain the same, and the proportion of the resistance at A to the motive gravity is increased in any ratio, the proportion of AH to AI will be increased in the same ratio, and the latus rectum of the above parabola as well as the length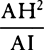 
(proportional to it) will remain the same; and therefore AH will be decreased in the same ratio, and AI will be decreased as the square of that ratio. But the proportion of the resistance to the weight is increased when the specific gravity (the volume remaining constant) becomes smaller, or the density of the medium becomes greater, or the resistance (as a result of the decreased volume) is decreased in a smaller ratio than the weight.
RULE 4. The density of the medium near the vertex of the hyperbola is greater than at place A; hence, in order to have the mean density, the ratio of the least of the tangents GT to tangent AH must be found, and the density at A must be increased in a slightly greater ratio than that of half the sum of these tangents to the least of the tangents GT.
RULE 5. If lengths AH and AI are given, and it is required to describe the figure AGK, produce HN to X so that HX is to AI as n +1 to 1, and with center X and asymptotes MX and NX, describe a hyperbola through point A in such a way that AI is to any VG as XVn to XIn.
RULE 6. The greater the number n, the more exact are these “hyperbolas” in the ascent of the body from A, and the less exact in its descent to K, and conversely. A conic hyperbola holds a mean ratio between them and is simpler than the others. Therefore, if the hyperbola is of this kind, and if it is required to find point K, where the projected body will fall upon any straight line AN passing through point A, let AN produced meet asymptotes MX and NX in M and N, and take NK equal to AM.
RULE 7. And hence a ready method of determining this kind of hyperbola from the phenomena is clear. Project two similar and equal bodies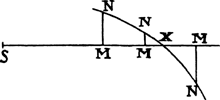 
with the same velocity in different angles HAK and hAk, and let them fall upon the plane of the horizon in K and k, and note the proportion of AK to Ak (let this be d to e). Then, having erected a perpendicular AI of any length, assume length AH or Ah in any way and from this determine graphically lengths AK and Ak by rule 6. If the ratio of AK to Ak is the same as the ratio of d to e, length AH was correctly assumed. But if not, then on the indefinite straight line SM take a length SM equal to the assumed AH, and erect perpendicular MN equal to the difference of the ratios, 
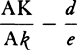, multiplied by any given straight line. From several assumed lengths AH find several points N by a similar method eand through them all draw a regular curved line NNXN cutting the straight line SMMM in X. Finally, assume AH equal to abscissa SX, and from this find length AK again; then the lengths that are to the assumed length AI and this last length AH as that length AK (found by experiment) is to the length AK (last found) will be those true lengths AI and AH which it was required to find. And these being given, the resistance of the medium in place A will also be given, inasmuch as it is to the force of gravity as AH to 2AI. The density of the medium, moreover, must be increased (by rule 4), and the resistance just found, if it is increased in the same ratio, will become more exact.e
RULE 8. If the lengths AH and HX have been found, and the position of the straight line AH is now desired along which a projectile sent forth with that given velocity falls upon any point K, erect at points A and K the straight lines AC and KF perpendicular to the horizon, of which AC tends downward and is equal to AI or ½HX. With asymptotes AK and KF describe a hyperbola whose conjugate passes through point C, and with center A and radius AH describe a circle cutting that hyperbola in point H; then a projectile sent forth along the straight line AH will fall upon point K. Q.E.I.
For point H, because length AH is given, is located somewhere in the circle described. Draw CH meeting AK and KF, the former in E, the latter in F; then, because CH and MX are parallel and AC and AI are equal, AE will be equal to AM, and therefore also equal to KN. But CE is to AE as FH to KN, and therefore CE and FH are equal. Point H therefore falls upon the hyperbola described with asymptotes AK and KF whose conjugate passes through point C, and thus H is found in the common intersection of this hyperbola and the circle described. Q.E.D.
It is to be noted, moreover, that this operation is the same whether the straight line AKN is parallel to the horizon or is inclined to the horizon at any angle, and that from the two intersections H and H two angles NAH and NAH arise, and that in a mechanical operation it is sufficient to describe a circle once, then to apply the indeterminate rule CH to point C in such a way that its part FH, placed between the circle and the straight line FK, is equal to its part CE situated between point C and the straight line AK.
What has been said about hyperbolas is easily applied to parabolas. For if XAGK designates a parabola that the straight line XV touches in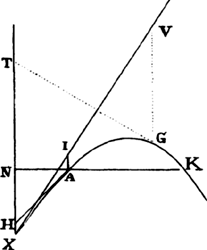 
vertex X and if ordinates IA and VG are as any powers XIn and XVn of abscissas XI and XV, draw XT, GT, and AH, of which XT is parallel to VG, and GT and AH touch the parabola in G and A; then a body projected with the proper velocity from any place A along the straight line AH (produced) will describe this parabola, provided that the density of the medium in each individual place G is inversely as tangent GT. The velocity in G, however, will be that with which a projectile would go, in a nonresisting space, in a conic parabola having vertex G, diameter VG produced downward, and latus rectum 
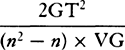. And the resistance in G will be to the force of gravity as GT to 
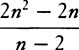VG. Hence, if NAK designates a horizontal line and if, while both the density of the medium in A and the velocity with which the body is projected remain the same, the angle NAH is changed in any way, then lengths AH, AI, and HX will remain the same; and hence vertex X of the parabola and the position of the straight line XI are given, and, by taking VG to IA as XVn to XIn, all the points G of the parabola, through which the projectile will pass, are given.
The motion of bodies that are resisted partly in the ratio of the velocity and partly in the squared ratio of the velocity
Proposition 11, Theorem 8
If a body is resisted partly in the ratio of the velocity and partly in the squared ratio of the velocity and moves in a homogeneous medium by its inherent force alone, and if the times are taken in an arithmetic progression, then quantities inversely proportional to the velocities and increased by a certain given quantity will be in a geometric progression.
With center C and rectangular asymptotes CADd and CH, describe a hyperbola BEe, and let AB, DE, and de be parallel to asymptote CH.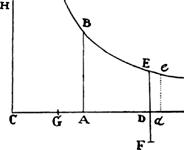 
Let points A and G be given in asymptote CD. Then if the time is represented by the hyperbolic area ABED increasing uniformly, I say that the velocity can be represented by the length DF, whose reciprocal GD together with the given quantity CG composes the length CD increasing in a geometric progression.
For let the area-element DEed be a minimally small given increment of time; then Dd will be inversely as DE and thus directly as CD. And the decrement of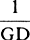 
, which (by book 2, lem. 2) is 
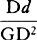, will be as 
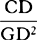or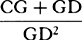 
, that is, as 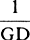+ 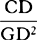. Therefore, when the time ABED increases uniformly by the addition of the given particles EDde, 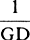decreases in the same ratio as the velocity. For the decrement of the velocity is as the resistance, that is (by hypothesis), as the sum of two quantities, of which one is as the velocity and the other is as the square of the velocity; and the decrement of 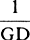is as the sum of the quantities 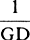and 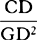, of which the former is 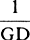itself and the latter 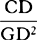is as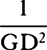 
. Accordingly, because the decrements are analogous, 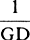is as the velocity. And if the quantity GD, which is inversely proportional to 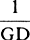, is increased by the given quantity CG, then as the time ABED increases uniformly, the sum CD will increase in a geometric progression. Q.E.D.
COROLLARY 1. Therefore if, given the points A and G, the time is represented by the hyperbolic area ABED, the velocity can be represented by 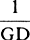, the reciprocal of GD.
COROLLARY 2. And by taking GA to GD as the reciprocal of the velocity at the beginning to the reciprocal of the velocity at the end of any time ABED, point G will be found. And when G has been found, then if any other time is given, the velocity can be found.
Proposition 12, Theorem 9
With the same suppositions, I say that if the spaces described are taken in an arithmetic progression, the velocities increased by a certain given quantity will be in a geometric progression.
Let point R be given in the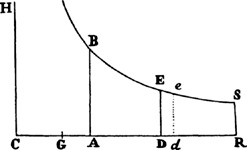 
asymptote CD, and after erecting perpendicular RS meeting the hyperbola in S, represent the described space by the hyperbolic area RSED; then the velocity will be as the length GD, which with the given quantity CG composes the length CD decreasing in a geometric progression while space RSED is increased in an arithmetic progression.
For, because the increment EDde of the space is given, the line-element Dd, which is the decrement of GD, will be inversely as ED and thus directly as CD, that is, as the sum of GD and the given length CG. But the decrement of the velocity, in the time inversely proportional to it in which the given particle DdeE of space is described, is as the resistance and the time jointly, that is, directly as the sum of two quantities (of which one is as the velocity and the other is as the square of the velocity) and inversely as the velocity; and thus is directly as the sum of two quantities, of which one is given and the other is as the velocity. Therefore the decrement of the velocity as well as of line GD is as a given quantity and a decreasing quantity jointly; and because the decrements are analogous, the decreasing quantities will always be analogous, namely, the velocity and the line GD. Q.E.D.
COROLLARY 1. If the velocity is represented by the length GD, the space described will be as the hyperbolic area DESR.
COROLLARY 2. And if point R is taken at will, point G will be found by taking GR to GD as the velocity at the beginning is to the velocity after any space RSED has been described. And when point G has been found, the space is given from the given velocity, and conversely.
COROLLARY 3. Hence, since (by prop. 11) the velocity is given from the given time, and by this prop. 12 the space is given from the given velocity, the space will be given from the given time, and conversely.
Proposition 13, Theorem 10
Supposing that a body attracted downward by uniform gravity ascends straight up or descends straight down and is resisted partly in the ratio of the velocity and partly in the squared ratio of the velocity, I say that if straight lines parallel to the diameters of a circle and a hyperbola are drawn through the ends of the conjugate diameters and if the velocities are as certain segments of the parallels, drawn from a given point, then the times will be as the sectors of areas cut off by straight lines drawn from the center to the ends of the segments, and conversely.
CASE 1. Let us suppose first that the body is ascending. With center D and any semidiameter DB describe the quadrant BETF of a circle, and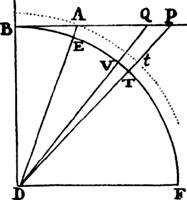 
through the end B of semidiameter DB draw the indefinite line BAP parallel to semidiameter DF. Let point A be given in that line, and take segment AP proportional to the velocity. Since one part of the resistance is as the velocity and the other part is as the square of the velocity, let the whole resistance be as AP2 + 2BA × AP. Draw DA and DP cutting the circle in E and T, and represent the gravity by DA2 in such a way that the gravity is to the resistance as DA2 to AP2 + 2BA × AP; and the time of the whole ascent will be as sector EDT of the circle.
For draw DVQ cutting off both the moment PQ of velocity AP and the moment DTV (corresponding to a given moment of time) of sector DET; then that decrement PQ of the velocity will be as the sum of the forces of the gravity DA2 and the resistance AP2 +2BA × AP, that is (by book 2, prop. 12 of the Elements), as DP2. Accordingly, the area DPQ, which is proportional to PQ, is as DP2, and the area DTV, which is to the area DPQ as DT2 to DP2, is as the given quantity DT2. The area EDT therefore decreases uniformly as the remaining time, by the subtraction of the given particles DTV, and therefore is proportional to the time of the whole ascent. Q.E.D.
CASE 2. If the velocity in the ascent of the body is represented by the length AP as in case 1, and the resistance is supposed to be as AP2 +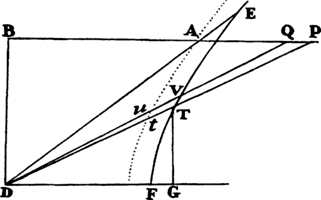 
2BA × AP, and if the force of gravity is less than what could be represented by DA2, take BD of such a length that AB2 — BD2 is proportional to the gravity, and let DF be perpendicular and equal to DB, and through the vertex F describe the hyperbola FTVE, whose conjugate semidiameters are DB and DF and which cuts DA in E and cuts DP and DQ in T and V; then the time of the whole ascent will be as the sector TDE of the hyperbola.
For the decrement PQ of the velocity occurring in a given particle of time is as the sum of the resistance AP2 + 2BA × AP and the gravity AB2 − BD2, that is, as BP2 − BD2. But area DTV is to area DPQ as DT2 to DP2 and thus, if a perpendicular GT is dropped to DF, is as GT2 or GD2 − DF2 to BD2, and as GD2 to BP2, and by separation [or dividendo] as DF2 to BP2 − BD2. Therefore, since area DPQ is as PQ, that is, as BP2 − BD2, area DTV will be as DF2, which is given. Area EDT therefore decreases uniformly in each equal particle of time, by the subtraction of the same number of given particles DTV, and therefore is proportional to the time. Q.E.D.
CASE 3. Let AP be the velocity in the descent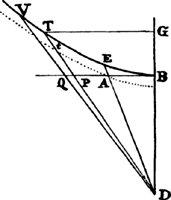 
of the body, and AP2 + 2BA × AP the resistance, and BD2 − AB2 the force of gravity, angle DBA being a right angle. And if with center D and principal vertex B the rectangular hyperbola BETV is described, cutting the produced lines DA, DP, and DQ in E, T, and V, then sector DET of this hyperbola will be as the whole time of descent.
For the increment PQ of the velocity, and the area DPQ proportional to it, is as the excess of the gravity over the resistance, that is, as BD2 − AB2 − 2BA × AP − AP2 or BD2 − BP2. And area DTV is to area DPQ as DT2 to DP2 and thus as GT2 or GD2 − BD2 to BP2, and as GD2 to BD2, and by separation [or dividendo] as BD2 to BD2 − BP2. Therefore, since area DPQ is as BD2 − BP2, area DTV will be as BD2, which is given. Therefore area EDT increases uniformly in each equal particle of time, by the addition of the same number of given particles DTV, and therefore is proportional to the time of descent. Q.E.D.
COROLLARY. If with center D and semidiameter DA, the arc At similar to arc ET and similarly subtending angle ADT is drawn through vertex A, then the velocity AP will be to the velocity that the body in time EDT in a nonresisting space could lose by ascending, or acquire by descending, as the area of triangle DAP to the area of sector DAt and thus is given from the given time. For in a nonresisting medium the velocity is proportional to the time and thus proportional to this sector; in a resisting medium the velocity is as the triangle; and in either medium, when the velocity is minimally small, it approaches the ratio of equality just as the sector and the triangle do.
Scholiuma
The case could also be proved in the ascent of the body, where the force of gravity is less than what can be represented by DA2 or AB2 + BD2 and greater than what can be represented by AB2 − BD2, and must be represented by AB2. But I hasten to other topics.
Proposition 14, Theorem 11
With the same suppositions, I say that the space described in the ascent or descent is as the difference between the area which represents the time and a certain other area that increases or decreases in an arithmetic progression, if the forces compounded of the resistance and the gravity are taken in a geometric progression.
Take AC (in the three figures) proportional to the gravity, and AK proportional to the resistance. And take them on the same side of point A if the body is descending, otherwise on opposite sides. Erect Ab, which is to DB as DB2 to 4BA × AC; and when the hyperbola bN has been described with respect to the rectangular asymptotes CK and CH, and KN has been erected perpendicular to CK, area AbNK will be increased or decreased in an arithmetic progression while the forces CK are taken in a geometric progression. I say therefore that the distance of the body from its greatest height is as the excess of area AbNK over area DET.
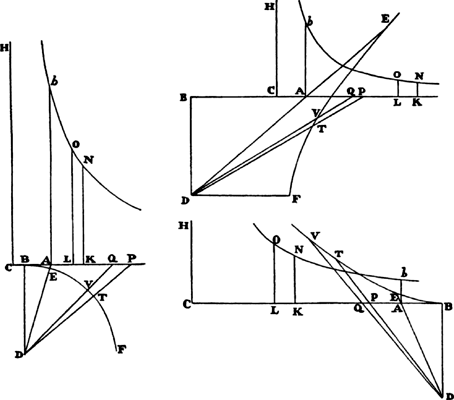
For since AK is as the resistance, that is, as AP2 + 2BA × AP, assume any given quantity Z, and suppose AK equal to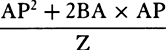 
, and (by book 2, lem. 2) the moment KL of AK will be equal to 
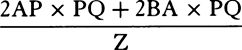or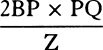 
, and the moment KLON of area AbNK will be equal to 
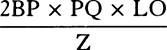or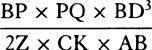 
.
CASE 1. Now, if the body is ascending and the gravity is as AB2 + BD2, BET being a circle (in the first figure), then line AC, which is proportional to the gravity, will be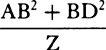 
, and DP2 or AP2 + 2BA × AP + AB2 + BD2 will be AK × Z + AC × Z or CK × Z; and thus area DTV will be to area DPQ as DT2 or DB2 or CK × Z.
CASE 2. But if the body is ascending and the gravity is as AB2 − BD2, then line AC (in the second figure) will be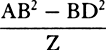 
, and DT2 will be to DP2 as DF2 or DB2 to BP2 − BD2 or AP2 + 2BA × AP + AB2 − BD2, that is, to AK × Z + AC × Z or CK × Z. And thus area DTV will be to area DPQ as DB2 to CK × Z.
CASE 3. And by the same argument, if the body is descending and therefore the gravity is as BD2 − AB2, and line AC (in the third figure) is equal to 
, then area DTV will be to area DPQ as DB2 to CK × Z, as above.
Since, therefore, those areas are always in this ratio, if for area DTV, which represents the moment of time always equal to it, any determinate rectangle is written, say BD × m, then area DPQ, that is, ½BD × PQ, will be to BD × m as CK × Z to BD2. And hence PQ × BD3 becomes equal to 2BD × m × CK × Z, and the moment KLON (found above) of area AbNK becomes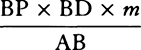 
. Take away the moment DTV or BD × m of area DET, and there will remain 
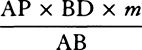. Therefore the difference of the moments, that is, the moment of the difference of the areas, is equal to 
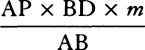, and therefore (because 
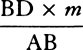is given) is as the velocity AP, that is, as the moment of the space that the body describes in ascending or descending. And thus that space and the difference of the areas, increasing or decreasing by proportional moments and beginning simultaneously or vanishing simultaneously, are proportional. Q.E.D.
COROLLARY. If the length that results from dividing area DET by the line BD is called M, and another length V is taken in the ratio to length M that line DA has to line DE, then the space that a body describes in its whole ascent or descent in a resisting medium will be to the space that the body can describe in the same time in a nonresisting medium, by falling from a state of rest, as the difference of the above areas to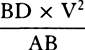 
, and thus is given from the given time. For the space in a nonresisting medium is in the squared ratio of the time, or as V2, and, because BD and AB are given, as 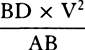. aThis area is equal to area 
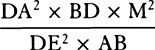, and the moment of M is m; and therefore the moment of this area is 
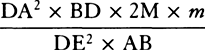. But this moment is to the moment of the difference of the above areas DET and AbNK that is, to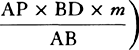 
as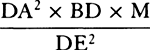 
is to ½BD × AP, or as 
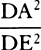× DET is to DAP; and thus, when areas DET and DAP are minimally small, in the ratio of equality. Therefore area 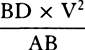and the difference of areas DET and AbNK, when all these areas are minimally small, have equal moments and thus are equal. Hence, since the velocities, and therefore also the spaces described simultaneously in both mediums at the beginning of the descent or the end of the ascent, approach equality and thus are then to one another as area 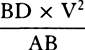and the difference of areas DET and AbNK; and furthermore since the space in a nonresisting medium is always as 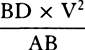, and the space in a resisting medium is always as the difference of areas DET and AbNK; it follows that the spaces described in both mediums in any equal times must be to one another as the area 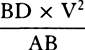and the difference of areas DET and AbNK. Q.E.D.a
Scholiumb
The resistance encountered by spherical bodies in fluids arises partly from the tenacity, partly from the friction, and partly from the density of the medium. And we have said that the part of the resistance that arises from the density of the fluid is in the squared ratio of the velocity; the other part, which arises from the tenacity of the fluid, is uniform, or as the moment of the time; and thus it would now be possible to proceed to the motion of bodies that are resisted partly by a uniform force or in the ratio of the moments of the time and partly in the squared ratio of the velocity. But it is sufficient to have opened the way to the examination of this subject in the preceding props. 8 and 9 and their corollaries. In these propositions and corollaries, in place of the uniform resistance of the ascending body, which arises from its gravity, there can be substituted the uniform resistance that arises from the tenacity of the medium, when the body is moved by its inherent force alone; and when the body is ascending straight up, it is possible to add this uniform resistance to the force of gravity, and to subtract it when the body is descending straight down. It would also be possible to proceed to the motion of bodies that are resisted partly uniformly, partly in the ratio of the velocity, and partly in the squared ratio of the velocity. And I have opened the way in the preceding props. 13 and 14, in which the uniform resistance that arises from the tenacity of the medium can also be substituted for the force of gravity, or can be compounded with it as before. But I hasten to other topics.
The revolving motion of bodies in resisting mediums
Lemma 3
Let PQR be a spiral that cuts all the radii SP, SQ, SR, . . . in equal angles. Draw the straight line PT touching the spiral in any point P and cutting the radius SQ in T; erect PO and QO perpendicular to the spiral and meeting in O, and join SO. I say that if points P and Q approach each other and coincide, angle PSO will come out a right angle, and the ultimate ratio of rectangle TQ × 2PS to PQ2 will be the ratio of equality.
For, from the right angles OPQ 
and OQR subtract the equal angles SPQ and SQR, and the equal angles OPS and OQS will remain. Therefore a circle that passes through points O, S, and P will also pass through point Q. Let points P and Q come together, and this circle will touch the spiral in the place PQ where they coincide, and thus will cut the straight line OP perpendicularly. OP will therefore become a diameter of this circle, and OSP, an angle in a semicircle, will become a right angle. Q.E.D.
Drop perpendiculars QD and SE to OP, and the ultimate ratios of the lines will be as follows: TQ will be to PD as TS (or PS) to PE, or 2PO to 2PS; likewise, PD will be to PQ as PQ to 2PO; and from the equality of the ratios in inordinate proportion [or ex aequo perturbate] TQ will be to PQ as PQ to 2PS. Hence PQ2 becomes equal to TQ × 2PS. Q.E.D.
Proposition 15, Theorem 12
If the density of a medium in every place is inversely as the distance of places from a motionless center and if the centripetal force is in the squared ratio of the density, I say that a body can revolve in a spiral that intersects in a given angle all the radii drawn from that center.
Let the same things be supposed as in lemma 3, and produce SQ to V, so that SV is equal to SP. In any time, in a resisting medium, let a body describe the minimally small arc PQ, and in twice the time, the minimally small arc PR; then the decrements of these arcs arising from the resistance, that is, 
the differences between these arcs and the arcs that would be described in the same times in a nonresisting medium, will be to each other as the squares of the times in which they are generated. The decrement of arc PQ is therefore a fourth of the decrement of arc PR. Hence also, if area QSr is taken equal to area PSQ, the decrement of arc PQ will be equal to half of the line-element Rr; and thus the force of resistance and the centripetal force are to each other as the line-elements ½Rr and TQ that they simultaneously generate. Since the centripetal force by which the body is urged in P is inversely as SP2; and since (by book 1, lem. 10) the line-element TQ, which is generated by that force, is in a ratio compounded of the ratio of this force and the squared ratio of the time in which arc PQ is described (for I ignore the resistance in this case, as being infinitely smaller than the centripetal force); then it follows that TQ × SP2, that is (by lem. 3), ½PQ2 × SP, will be in the squared ratio of the time, and thus the time is as PQ × √SP; and the body’s velocity with which arc PQ is described in that time will be as 
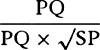or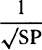 
, that is, as the square root of SP inversely. And by a similar argument, the velocity with which arc QR is described is as the square root of SQ inversely. But these arcs PQ and QR are as the velocities of description to each other, that is, as √SQ to √SP, or as SQ to √(SP × SQ); and because angles SPQ and SQr are equal and areas PSQ and QSr are equal, arc PQ is to arc Qr as SQ to SP. Take the differences of the proportional consequents, and arc PQ will become to arc Rr as SQ to SP − √(SP × SQ), or ½VQ. For, points P and Q coming together, the ultimate ratio of SP − √(SP × SQ) to ½VQ is the ratio of equality. aSince the decrement of arc PQ arising from the resistance, or its double Rr, is as the resistance and the square of the time jointly, the resistance will be as 
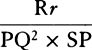.a But PQ was to Rr as SQ to ½VQ, and hence 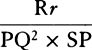becomes as 
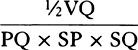, or as 
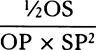. For, points P and Q coming together, SP and SQ coincide, and angle PVQ becomes a right angle; and because triangles PVQ and PSO are similar, PQ becomes to ½VQ as OP to ½OS. Therefore 
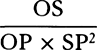is as the resistance, that is, in the ratio of the density of the medium at P and the squared ratio of the velocity jointly. Take away the squared ratio of the velocity, namely the ratio 
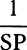, and the result will be that the density of the medium at P is as 
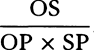. Let the spiral be given, and because the ratio of OS to OP is given, the density of the medium at P will be as 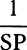. Therefore in a medium whose density is inversely as the distance SP from the center, a body can revolve in this spiral. Q.E.D.
COROLLARY 1. The velocity in any place P is always the velocity with which a body in a nonresisting medium, under the action of the same centripetal force, can revolve in a circle at the same distance SP from the center.
COROLLARY 2. The density of the medium, if the distance SP is given, is as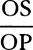 
; but if that distance is not given, it is as 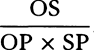. And hence a spiral can be made to conform to any density of the medium.
COROLLARY 3. The force of resistance in any place P is to the centripetal force in the same place as ½OS to OP. For those forces are to each other as ½Rr and TQ or as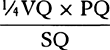 
and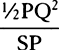 
, that is, as ½VQ and PQ, or ½OS and OP. Given the spiral, therefore, the proportion of the resistance to the centripetal force is given; and conversely, from that given proportion the spiral is given.
COROLLARY 4. The body, therefore, cannot revolve in this spiral except when the force of resistance is less than half of the centripetal force. Let the resistance become equal to half of the centripetal force; then the spiral will coincide with the straight line PS, and the body will descend to the center in this straight line with a velocity that is (as we proved in book 1, prop. 34) to the velocity with which the body descends in a nonresisting medium in the case of a parabola in the ratio of 1 to √2. bAnd the times of descent will here be inversely as the velocities, and thus are given.b
COROLLARY 5. And since at equal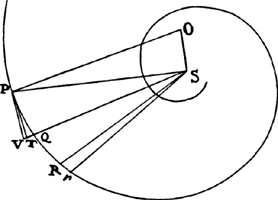 
distances from the center the velocity is the same in the spiral PQR as in the straight line SP, and since the length of the spiral is in a given ratio to the length of the straight line PS, namely the ratio of OP to OS, the time of descent in the spiral will be to the time of descent in the straight line SP in that same given ratio, and accordingly is given.
COROLLARY 6. If, with center S and any two given radii, two circles are described, and if—these circles remaining the same—the angle that the spiral contains with radius PS is changed in any way, then the number of revolutions that the body can complete between the circumferences of the circles, by revolving in the spiral from one circumference to the other, is as 
, or as the tangent of the angle that the spiral contains with radius PS. And the time of those revolutions is as 
, that is, as the secant of that angle, or inversely as the density of the medium.
COROLLARY 7. If a body, in a medium whose density is inversely as the distance of places from the center, has made a revolution about that center in any curve AEB and has cut the first radius AS in the same angle in B as it did previously in A, with a velocity that was to its prior velocity in A inversely as the square roots of distances from the center—that is, as AS to a mean proportional between AS and BS—then that body will make innumerable entirely similar revolutions BFC, CGD, . . . , and by the intersections will divide the radius AS into the continually proportional parts AS, BS, CS, DS, . . . . And the times of revolution will be as the perimeters of the orbits AEB, BFC, CGD, . . . , directly, and the velocities in the beginnings A, B, C, inversely—that is, as AS3/2, BS3/2, CS3/2. And the whole time in which the body will reach the center will be to the time of the first revolution as the sum of all the continually proportional quantities AS3/2, BS3/2, CS3/2, going on indefinitely, is to the first term AS3/2—that is, as that first term AS3/2 is to the difference of the first two terms AS3/2 − BS3/2, or very nearly as ⅔AS to AB. In this way the whole time is readily found.
COROLLARY 8. From what has been presented, it is also possible to determine approximately the motions of bodies in mediums whose density either is uniform or accords with any other assigned law. With center S and radii SA, SB, SC, . . . which are continually proportional, describe any number of circles. And suppose that the time of the revolutions between the perimeters of any two of these circles in the medium treated in corol. 7 is to the time of revolutions between those perimeters in the proposed medium very nearly as the mean density of the proposed medium between those circles is to the mean density of the medium in corol. 7 between those same circles; and suppose additionally that the secant of the angle by which the spiral in corol. 7, in the medium treated in that corollary, cuts the radius AS is in the same ratio to the secant of the angle by which the new spiral cuts that same radius in the proposed medium; and also that the numbers of all the revolutions between those same two circles are very nearly as the tangents of those same angles. If this is done throughout between every pair of circles, the motion will be continued through all the circles. And thus we can imagine without difficulty in what ways and in what times bodies would have to revolve in any regular medium.
COROLLARY 9. And even if the motions are eccentric, being performed in spirals approaching an oval shape, nevertheless by conceiving that the single revolutions of those spirals are the same distance apart from one another and approach the center by the same degrees as the spiral described above, we shall also understand how the motions of bodies are performed in spirals of this sort.
Proposition 16, Theorem 13
If the density of the medium in every place is inversely as the distance of places from a motionless center and if the centripetal force is inversely as any power of that distance, I say that a body can revolve in a spiral that intersects in a given angle all the radii drawn from that center.
This is proved by the same method as prop. 15. For if the centripetal force in P is inversely as any power SPn+1 (whose index is n + 1) of the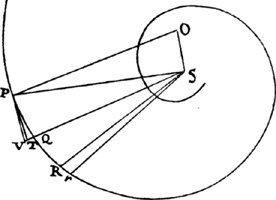 
distance SP, then it will be gathered, as above, that the time in which the body describes any arc PQ will be as PQ × PS½n, and the resistance in P will be as 
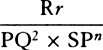, or as 
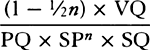, and thus as 
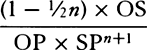, that is, because 
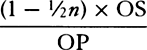is given, inversely as SPn+1. And therefore, since the velocity is inversely as SP½n, the density in P will be inversely as SP.
COROLLARY 1. The resistance is to the centripetal force as (1 − ½n) × OS to OP.
COROLLARY 2. If the centripetal force is inversely as SP3, 1 − ½n will be = 0, and thus the resistance and density of the medium will be null, as in book 1, prop. 9.
COROLLARY 3. If the centripetal force is inversely as some power of the radius SP whose index is greater than the number 3, positive resistance will be changed to negative.
Scholium
But this proposition and the previous ones, which relate to unequally dense mediums, are to be understood of the motion of bodies so small that no consideration need be taken of a greater density of the medium on one side of the body than on the other. I also suppose the resistance, other things being equal, to be proportional to the density. Hence, in mediums whose force of resisting is not as the density, the density ought to be increased or decreased to such an extent that either the excess of the resistance may be taken away or its defect supplied.
Proposition 17, Problem 4
To find both the centripetal force and the resistance of the medium by means of which a body can revolve in a given spiral, if the law of the velocity is given.
Let the spiral be PQR. The time 
will be given from the velocity with which the body traverses the minimally small arc PQ, and the force will be given from the height TQ, which is as the centripetal force and the square of the time. Then the retardation of the body will be given from the difference RSr of the areas PSQ and QSR traversed in equal particles of time, and the resistance and density of the medium will be found from the retardation.
Proposition 18, Problem 5
Given the law of the centripetal force, it is required to find in every place the density of the medium with which a body will describe a given spiral.
The velocity in every place is to be found from the centripetal force; then the density of the medium is to be sought from the retardation of the velocity, as in prop. 17.
I have presented the method of dealing with these problems in book 2, prop. 10 and lem. 2, and I do not wish to detain the reader any longer in complex inquiries of this sort. Some things must now be added on the forces of bodies in their forward motion, and on the density and resistance of the mediums in which the motions hitherto explained and motions related to these are performed.
The density and compression of fluids, and hydrostatics
Definition of a Fluid
A fluid is any body whose parts yield to any force applied to it and yielding are moved easily with respect to one another.
Proposition 19, Theorem 14
All the parts of a homogeneous and motionless fluid that is enclosed in any motionless vessel and is compressed on all sides {apart from considerations of condensation, gravity, and all centripetal forces) are equally pressed on all sides and remain in their places without any motion arising from that pressure.
CASE 1. Let a fluid be enclosed in the spherical vessel ABC and be uniformly compressed on all sides; I say that no part of this fluid will move 
as a result of that pressure. For if some one part D moves, all the parts of this sort, standing on all sides at the same distance from the center, must move simultaneously with a similar motion; and this is so because the pressure on them all is similar and equal, and every motion is supposed excluded except that which arises from the pressure. But they cannot all approach closer to the center unless the fluid is condensed at the center, contrary to the hypothesis. They cannot recede farther from it unless the fluid is condensed at the circumference, also contrary to the hypothesis. They cannot move in any direction and keep their distance from the center, since by a like reasoning they will move in the opposite direction, and the same part cannot move in opposite directions at the same time. Therefore no part of the fluid will move from its place. Q.E.D.
CASE 2. I say additionally that all the spherical parts of this fluid are equally pressed on all sides. For let EF be a spherical part of the fluid; if this part is not pressed equally on all sides, let the lesser pressure be increased until this part is pressed equally on all sides; then its parts, by case 1, will remain in their places. But before the increase of the pressure they will remain in their places, also by case 1, and by the addition of new pressure they will be moved out of their places, by the definition of a fluid. These two results are contradictory. Therefore it was false to say that the sphere EF was not pressed equally on all sides. Q.E.D.
CASE 3. I say furthermore that there is equal pressure on different spherical parts. For contiguous spherical parts press one another equally in the point of contact, by the third law of motion. But by case 2, they are also pressed on all sides by the same force. Therefore any two noncontiguous spherical parts will be pressed by the same force, since an intermediate spherical part can touch both. Q.E.D.
CASE 4. I say also that all the parts of the fluid are equally pressed on every side. For any two parts can be touched by spherical parts in any points, and there they press those spherical parts equally, by case 3, and in turn are equally pressed by them, by the third law of motion. Q.E.D.
CASE 5. Since, therefore, any part GHI of the fluid is enclosed in the remaining fluid as if in a vessel and is pressed equally on all sides, while its parts press one another equally and are at rest with respect to one another, it is manifest that all the parts of any fluid GHI which is pressed equally on all sides press one another equally and are at rest with respect to one another. Q.E.D.
CASE 6. Therefore, if that fluid is enclosed in a vessel that is not rigid and is not pressed equally on all sides, it will yield to a greater pressure, by the definition of a fluid.
CASE 7. And thus in a rigid vessel a fluid will not sustain a pressure that is greater on one side than on another, but will yield to it, and will do so in an instant of time, since the rigid side of the vessel does not follow the yielding liquid. And by yielding, it will press the opposite side, and thus the pressure will tend on all sides to equality. And since, as soon as the fluid endeavors to recede from the part that is pressed more, it is hindered by the resistance of the vessel on the opposite side, the pressure will be reduced on all sides to equality in an instant of time without local motion; and thereupon the parts of the fluid, by case 5, will press one another equally and will be at rest with respect to one another. Q.E.D.
COROLLARY. Hence the motions of the parts of the fluid with respect to one another cannot be changed by pressure applied to the fluid anywhere on the external surface, except insofar as either the shape of the surface is changed somewhere or all the parts of the fluid, by pressing one another more intensely or more remissly [i.e., by pressing one another more strongly or less strongly], flow among themselves with more or less difficulty.
Proposition 20, Theorem 15
If every part of a fluid that is spherical and homogeneous at equal distances from the center and rests upon a concentric spherical bottom gravitates toward the center of the whole, then the bottom will sustain the weight of a cylinder whose base is equal to the surface of the bottom and whose height is the same as that of the fluid resting upon it.
Let DHM be the surface of the bottom, and AEI the upper surface of the fluid. Divide the fluid into equally thick concentric spherical shellsa by 
innumerable spherical surfaces BFK, CGL; and suppose the force of gravity to act only upon the upper surface of each spherical shell, and the actions upon equal parts of all the surfaces to be equal. The highest surface AE is pressed, therefore, by the simple force of its own gravity, by which also all the parts of the highest spherical shell, and the second surface BFK (by prop. 19), are equally pressed in accordance with their measure. The second surface BFK is pressed additionally by the force of its own gravity, which, added to the previous force, makes the pressure double. The third surface CGL is acted on by this pressure, in accordance with its measure, and additionally by the force of its gravity, that is, by a triple pressure. And similarly the fourth surface is urged by a quadruple pressure, the fifth by a quintuple, and so on. The pressure by which any one surface is urged is therefore not as the solid quantity of the fluid lying upon it, but as the number of spherical shells up to the top of the fluid, and is equal to the gravity of the lowest spherical shell multiplied by the number of shells; that is, it is equal to the gravity of a solid whose ultimate ratio to the cylinder specified above will become that of equality—provided that the number of shells is increased and their thickness decreased indefinitely, in such a way that the action of gravity is made continuous from the lowest surface to the highest. The lowest surface therefore sustains the weight of the cylinder specified above. Q.E.D. And by a similar argument this proposition is evident when the gravity decreases in any assigned ratio of the distance from the center, and also when the fluid is rarer upward and denser downward. Q.E.D.
COROLLARY 1. Therefore the bottom is not pressed by the whole weight of the incumbent fluid, but sustains only that part of the weight which is described in this proposition, the rest of the weight being sustained by the vaulted shape of the fluid.
COROLLARY 2. At equal distances from the center, moreover, the quantity of pressure is always the same, whether the pressed surface is parallel to the horizon or perpendicular or oblique, or whether the fluid—continued upward from the pressed surface—rises perpendicularly along a straight line or snakes obliquely through twisted cavities and channels, regular or extremely irregular, wide or very narrow. That the pressure is not at all changed by these circumstances is gathered by applying the proof of this theorem to the various cases of fluids.
COROLLARY 3. By the same proof it is also gathered (by prop. 19) that the parts of a heavy fluid acquire no motion with respect to one another as a result of the pressure of the incumbent weight, provided that the motion arising from condensation is excluded.
COROLLARY 4. And therefore, if another body, in which there is no condensation, of the same specific gravity is submerged in this fluid, it will acquire no motion as a result of the pressure of the incumbent weight; it will not descend, it will not ascend, and it will not be compelled to change its shape. If it is spherical, it will remain spherical despite the pressure; if it is square, it will remain square; and it will do so whether it is soft or very fluid, whether it floats freely in the fluid or lies on the bottom. For any internal part of a fluid is in the same situation as a submerged body, and the case is the same for all submerged bodies of the same size, shape, and specific gravity. If a submerged body, while keeping its weight, were to liquefy and assume the form of a fluid, then, if it were formerly ascending or descending or assuming a new shape as a result of pressure, it would also now ascend or descend or be compelled to assume a new shape, and would do so because its gravity and the other causes of motions remain fixed. But (by prop. 19, case 5) this body would now be at rest and would maintain its shape. Hence, this would also be the case under the earlier conditions.
COROLLARY 5. Accordingly, a body that is of a greater specific gravity than a fluid contiguous to it will sink, and a body that is of a lesser specific gravity will ascend, and will acquire as much motion and change of shape as that excess or deficiency of gravity can bring about. For that excess or deficiency acts like an impulse by which the body, otherwise in equilibrium with the parts of the fluid, is urged; and it can be compared with the excess or deficiency of weight in either of the scales of a balance.
COROLLARY 6. The gravity of bodies in fluids is therefore twofold: the one, true and absolute; the other, apparent, common, and relative. Absolute gravity is the whole force with which a body tends downward; relative or common gravity is the excess of gravity with which the body tends downward more than the surrounding fluid. By absolute gravity the parts of all fluids and bodies gravitate in their places, and thus the sum of the individual weights is the weight of the whole. For every whole is heavy, as can be tested in vessels full of liquids, and the weight of the whole is equal to the sum of the weights of all the parts, and thus is composed of them. By relative gravity bodies do not gravitate in their places; that is, compared with one another, one is not heavier than another, but each one opposes the endeavors of the others to descend, and they remain in their places just as if they had no gravity. Whatever is in the air and does not gravitate more than the air is not commonly considered to be heavy. Things that do gravitate more are commonly considered to be heavy, inasmuch as they are not sustained by the weight of the air. Weight as commonly conceived is nothing other than the excess of the true weight over the weight of the air. Bodies are commonly called light which are less heavy than the surrounding air and, by yielding to that air, which gravitates more, move upward. They are, however, only comparatively light and not truly so, since they descend in a vacuum. Similarly, bodies in water that descend or ascend because of their greater or smaller gravity are comparatively and apparently heavy or light, and their comparative and apparent heaviness or lightness is the excess or deficiency by which their true gravity either exceeds the gravity of the water or is exceeded by it. And bodies that neither descend by gravitating more nor ascend by yielding to water which gravitates more—even though they increase the weight of the whole by their own true weights—nevertheless, comparatively and as commonly understood, do not gravitate in water. For the demonstration of all these cases is similar.
COROLLARY 7. What has been demonstrated concerning gravity is valid for any other centripetal forces.
COROLLARY 8. Accordingly, if the medium in which some body moves is urged either by its own gravity or by any other centripetal force, and the body is urged more strongly by the same force, then the difference between the forces is that motive force which we have considered to be the centripetal force in the preceding propositions. But if the body is urged more lightly by that force, the difference between the forces should be considered a centrifugal force.
COROLLARY 9. Since fluids, moreover, do not change the external shapes of enclosed bodies that they press upon, it is evident in addition (by prop. 19, corol.) that fluids will not change the situation of the internal parts with respect to one another; and accordingly, if animals are immersed, and if all sensation arises from the motion of the parts, fluids will neither harm these immersed bodies nor excite any sensation, except insofar as these bodies can be condensed by compression. And the case is the same for any system of bodies that is surrounded by a compressing fluid. All the parts of the system will be moved with the same motions as if they were in a vacuum and retained only their relative gravity, except insofar as the fluid either resists their motions somewhat or is needed to make them cohere by compression.
Proposition 21, Theorem 16
Let the density of a certain fluid be proportional to the compression, and let its parts be drawn downward by a centripetal force inversely proportional to their distances from the center; I say that if the distances are taken continually proportional, the densities of the fluid at these distances will also be continually proportional.
Let ATV designate the spherical bottom on which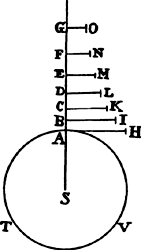 
the fluid lies, S the center, and SA, SB, SC, SD, SE, SF, . . . the continually proportional distances. Erect perpendiculars AH, BI, CK, DL, EM, FN, . . . , which are as the densities of the medium in places A, B, C, D, E, F; then the specific gravities in those places will be as 
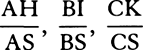, . . . , or—which is the same—as 
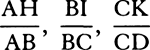, . . . . Suppose first that these gravities continue uniformly, the first from A to B, the second from B to C, the third from C to D, . . . , the decrements thus occurring by degrees at points B, C, D, . . . . Then these specific gravities multiplied by the heights AB, BC, CD, . . . will give the pressures AH, BI, CK, . . . , by which the bottom ATV (according to prop. 20) is pressed. The particle A therefore sustains all the pressures AH, BI, CK, DL, going on indefinitely; and the particle B, all the pressures except the first, AH; and the particle C, all except the first two, AH and BI; and so on. And thus the density AH of the first particle A is to the density BI of the second particle B as the sum of all the AH + BI + CK + DL indefinitely, to the sum of all the BI + CK + DL . . . . And the density BI of the second particle B is to the density CK of the third particle C as the sum of all the BI + CK + DL . . . to the sum of all the CK + DL . . . . Those sums are therefore proportional to their differences AH, BI, CK, . . . , and thus are continually proportional (by book 2, lem. 1); and accordingly the differences AH, BI, CK, . . . , proportional to those sums, are also continually proportional. Therefore, since the densities in places A, B, C, . . . are as AH, BI, CK, . . . , these also will be continually proportional. Proceed now by jumps, and from the equality of the ratios [or ex aequo], at the continually proportional distances SA, SC, SE, the densities AH, CK, EM will be continually proportional. And by the same argument, at any continually proportional distances SA, SD, SG, the densities AH, DL, GO will be continually proportional. Now let points A, B, C, D, E, . . . come together so that the progression of the specific gravities is made continual from the bottom A to the top of the fluid; and at any continually proportional distances SA, SD, SG, the densities AH, DL, GO, being always continually proportional, will still remain continually proportional now. Q.E.D.
COROLLARY. Hence, if the density of a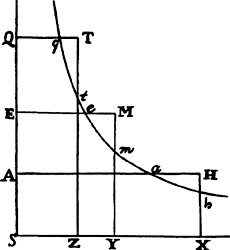 
fluid is given in two places, say A and E, its density in any other place Q can be determined. With center S and rectangular asymptotes SQ and SX describe a hyperbola cutting perpendiculars AH, EM, and QT in a, e, and q, and also perpendiculars HX, MY, and TZ, dropped to asymptote SX, in h, m, and t. Make the area YmtZ be to the given area YmhX as the given area EeqQ is to the given area EeaA; and the line Zt produced will cut off the line QT proportional to the density. For if lines SA, SE, and SQ are continually proportional, areas EeqQ and EeaA will be equal, and hence the areas proportional to these, YmtZ an XhmY, will also be equal, and lines SX, SY, and SZ—that is, AH, EM, and QT—will be continually proportional, as they ought to be. And if lines SA, SE, and SQ obtain any other order in the series of continually proportional quantities, lines AH, EM, and QT, because the hyperbolic areas are proportional, will obtain the same order in another series of continually proportional quantities.
Proposition 22, Theorem 17
Let the density of a certain fluid be proportional to the compression, and let its parts be drawn downward by a gravity inversely proportional to the squares of their distances from the center; I say that if the distances are taken in a harmonic progression, the densities of the fluid at these distances will be in a geometric progression.
Let S designate the center, and SA, SB, SC, SD, and SE the distances in a geometric progression. Erect perpendiculars AH, BI, CK, . . . , which are as the densities of the fluid in places A, B, C, D, E, . . . ; then the specific gravities in those places will be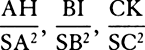 
, . . . . Imagine these specific gravities to be uniformly continued, the first from A to B, the second from B to C, the third from C to D, . . . . Then these, multiplied by the heights AB, BC, CD, DE, . . .—or, which is the same, by the distances SA, SB, SC, . . . , proportional to those heights—will yield 
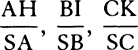, . . . , which represent the pressures. Therefore, since the densities are as the sums of these pressures, the differences (AH − BI, BI − CK, . . .) of the densities will be as the differences 
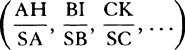of the sums. With center S and asymptotes SA and Sx describe any hyperbola that cuts the perpendiculars AH, BI, CK, . . . in a, b, c, . . . and also cuts in h, i, and k the perpendiculars Ht, Iu, and Kw, dropped to asymptote Sx; then the differences tu, uw, . . . between the densities will be as 
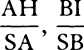, . . . . And the rectangles tu × th, uw × ui, . . . , or tp, uq, . . . , will be as 
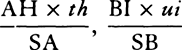, . . . , that is, as Aa, Bb, . . . . For, from the nature of the hyperbola, SA is to AH or St as th to Aa, and thus 
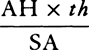is equal to Aa. And by a similar argument, 
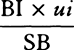is equal to Bb, . . . . Moreover, Aa, Bb, Cc, . . . are continually proportional, and therefore proportional to their differences Aa − Bb, Bb − Cc, . . . ; and thus the rectangles tp, uq, . . . are proportional to these differences, and also the sums of the rectangles tp + uq or tp + uq + wr are proportional to the sums of the differences Aa − Cc or Aa − Dd. Let there be as many terms of this sort as you wish; then the sum of all the differences, say Aa − Ff, will be proportional to the sum of all the rectangles, say zthn. Increase the number of terms and decrease the distances of points A, B, C, . . . , indefinitely; then these rectangles will come out equal to the hyperbolic area zthn, and thus the difference Aa − Ff is proportional to this area. Now take any distances, say SA, SD, SF, in a harmonic progression, and the differences Aa − Dd and Dd − Ff will be equal; and therefore the areas thlx and xlnz which are proportional to these differences will be equal to each other, and the densities St, Sx, and Sz (that is, AH, DL, and FN) will be continually proportional. Q.E.D.
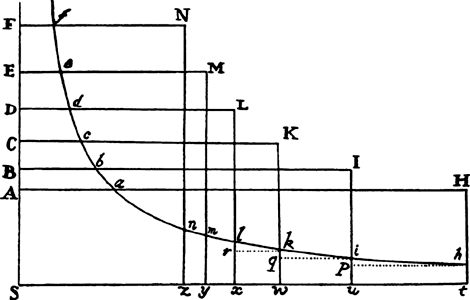
COROLLARY. Hence, if any two densities of a fluid are given, say AH and BI, the area thiu corresponding to their difference tu will be given; and accordingly the density FN at any height SF will be found by taking the area thnz to be to that given area thiu as the difference Aa − Ff is to the difference Aa − Bb.
Scholium
Similarly, it can be proved that if the gravity of the particles of a fluid is decreased as the cubes of the distances from the center, and if the reciprocals of the squares of the distances SA, SB, SC, . . . 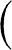namely 
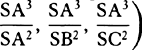are taken in an arithmetic progression, then the densities AH, BI, CK, . . . will be in a geometric progression. And if the gravity is decreased as the fourth power of the distances, and if the reciprocals of the cubes of the distances 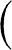say,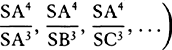 
are taken in an arithmetic progression, the densities AH, BI, CK, . . . will be in a geometric progression. And so on indefinitely. Again, if the gravity of the particles of a fluid is the same at all distances, and if the distances are in an arithmetic progression, the densities will be in a geometric progression, as the distinguished gentleman Edmond Halley has found. If the gravity is as the distance, and if the squares of the distances are in an arithmetic progression, the densities will be in a geometric progression. And so on indefinitely.
These things are so when the density of a fluid condensed by compression is as the force of the compression or, which is the same, when the space occupied by the fluid is inversely as this force. Other laws of condensation can be imagined, as, for example, that the cube of the compressing force is as the fourth power of the density, or that the force ratio cubed is the same as the density ratio to the fourth power. In this case, if the gravity is inversely as the square of the distance from the center, the density will be inversely as the cube of the distance. Imagine that the cube of the compressing force is as the fifth power of the density; then, if the gravity is inversely as the square of the distance, the density will be inversely as the 3/2 power of the distance. Imagine that the compressing force is as the square of the density, and that the gravity is inversely as the square of the distance; then the density will be inversely as the distance. It would be tedious to cover all cases. But it is established by experiments that the density of air is either exactly or at least very nearly as the compressing force; and therefore the density of the air in the earth’s atmosphere is as the weight of the whole incumbent air, that is, as the height of the mercury in a barometer.
Suppose a fluid to be enclosed in the cubic space ACE, and then by compression to be reduced into the smaller cubic space ace; then the distances 
between particles maintaining similar positions with respect to one another in the two spaces will be as the edges AB and ab of the cubes; and the densities of the mediums will be inversely as the containing spaces AB3 and ab3. On the plane side ABCD of the larger cube take the square DP equal to the plane side of the smaller cube db; then (by hypothesis) the pressure by which the square DP urges the enclosed fluid will be to the pressure by which the square db urges the enclosed fluid as the densities of the medium to each other, that is, as ab3 to AB3. But the pressure by which the square DB urges the enclosed fluid is to the pressure by which the square DP urges that same fluid as the square DB to the square DP, that is, as AB2 to ab2. Therefore, from the equality of the ratios [or ex aequo] the pressure by which the square DB urges the fluid is to the pressure by which the square db urges the fluid as ab to AB. Divide the fluid into two parts by planes FGH and fgh drawn through the middles of the cubes; then these parts will press each other with the same forces with which they are pressed by planes AC and ac, that is, in the proportion of ab to AB; and thus the centrifugal forces [or forces of repulsion] by which these pressures are sustained are in the same ratio. Because in both cubes the number of particles is the same and their situation similar, the forces that all the particles along planes FGH and fgh exert upon all the others are as the forces that each individual particle exerts upon every other particle. Therefore the forces that each particle exerts upon every other particle along the plane FGH in the larger cube are to the forces that individual particles exert on the particle next to them along the plane fgh in the smaller cube as ab to AB, that is, inversely as the distances between the particles are to one another. Q.E.D.
And conversely, if the forces of the individual particles are inversely as the distances, that is, inversely as the edges AB and ab of the cubes, the sums of the forces will be in the same ratio, and the pressures of the sides DB and db will be as the sums of the forces; and the pressure of the square DP will be to the pressure of the side DB as ab2 to AB2. And from the equality of the ratios [or ex aequo] the pressure of the square DP will be to the pressure of the side db as ab3 to AB3; that is, the one force of compression will be to the other force of compression as the one density to the other density. Q.E.D.
Scholium
By a similar argument, if the centrifugal forces [or forces of repulsion] of the particles are inversely as the squares of the distances between the centers, the cubes of the compressing forces will be as the fourth powers of the densities. If the centrifugal forces are inversely as the third or fourth powers of the distances, the cubes of the compressing forces will be as the fifth or sixth powers of the densities. And universally, if D is the distance, and E the density of the compressed fluid, and if the centrifugal forces are inversely as any power of the distance Dn, whose index is the number n, then the compressing forces will be as the cube roots of the powers En+2, whose index is the number n + 2; and conversely. In all of this, it is supposed that the centrifugal forces of particles are terminated in the particles which are next to them or do not extend far beyond them. We have an example of this in magnetic bodies. Their attractive virtue [or power] is almost terminated in bodies of their own kind which are next to them. The virtue of a magnet is lessened by an interposed plate of iron and is almost terminated in the plate. For bodies farther away are drawn not so much by the magnet as by the plate. In the same way, if particles repel other particles of their own kind that are next to them but do not exert any virtue upon more remote particles,b particles of this sort are the ones of which the fluids treated in this proposition will be composed. But if the virtue of each particle is propagated indefinitely, a greater force will be necessary for the equal condensation of a greater quantity of the fluid.c Whether elastic fluids consist of particles that repel one another is, however, a question for physics. We have mathematically demonstrated a property of fluids consisting of particles of this sort so as to provide natural philosophers with the means with which to treat that question.
Concerning the motion of asimple pendulumsa and the resistance to them
Proposition 24, Theorem 19
In simple pendulums whose centers of oscillation are equally distant from the center of suspension, the quantities of matter are in a ratio compounded of the ratio of the weights and the squared ratio of the times of oscillation in a vacuum.
For the velocity that a given force can generate in a given time in a given quantity of matter is as the force and the time directly and the matter inversely. The greater the force, or the greater the time, or the less the matter, the greater the velocity that will be generated. This is manifest from the second law of motion. Now if the pendulums are of the same length, the motive forces in places equally distant from the perpendicular are as the weights; and thus if two oscillating bodies describe equal arcs and if the arcs are divided into equal parts, then, since the times in which the bodies describe single corresponding parts of the arcs are as the times of the whole oscillations, the velocities in corresponding parts of the oscillations will be to one another as the motive forces and the whole times of the oscillations directly and the quantities of matter inversely; and thus the quantities of matter will be as the forces and the times of the oscillations directly and the velocities inversely. But the velocities are inversely as the times, and thus the times are directly, and the velocities are inversely, as the squares of the times, and therefore the quantities of matter are as the motive forces and the squares of the times, that is, as the weights and the squares of the times. Q.E.D.
COROLLARY 1. And thus if the times are equal, the quantities of matter in the bodies will be as their weights.
COROLLARY 2. If the weights are equal, the quantities of matter will be as the squares of the times.
COROLLARY 3. If the quantities of matter are equal, the weights will be inversely as the squares of the times.
COROLLARY 4. Hence, since the squares of the times, other things being equal, are as the lengths of the pendulums, the weights will be as the lengths of the pendulums if both the times and the quantities of matter are equal.
COROLLARY 5. And universally, the quantity of matter in a bob of a simple pendulum is as the weight and the square of the time directly and the length of the pendulum inversely.
COROLLARY 6. But in a nonresisting medium also, the quantity of matter in the bob of a simple pendulum is as the relative weight and the square of the time directly and the length of the pendulum inversely. For the relative weight is the motive force of a body in any heavy medium, as I have explained above, and thus fulfills the same function in such a nonresisting medium as absolute weight does in a vacuum.
COROLLARY 7. And hence a method is apparent both for comparing bodies with one another with respect to the quantity of matter in each, and for comparing the weights of one and the same body in different places in order to find out the variation in its gravity. And by making experiments of the greatest possible accuracy, I have always found that the quantity of matter in individual bodies is proportional to the weight.
Proposition 25, Theorem 20
The bobs of simple pendulums that are resisted in any medium in the ratio of the moments of time, and those that move in a nonresisting medium of the same specific gravity, perform oscillations in a cycloid in the same time and describe proportional parts of arcs in the same time.
Let AB be the arc of a cycloid, which body D describes by oscillating in a nonresisting medium in any time. Bisect the arc AB in C so that C is its lowest point; then the accelerative force by which the body is urged in any place D or d or E will be as the length of arc CD or Cd or CE. Represent that force by the appropriate arc [CD or Cd or CE], and since the resistance is as the moment of time, and thus is given, represent it by a given part CO of the arc of the cycloid, taking arc Od in the ratio to arc CD that arc OB has to arc CB; then the force by which the body at d is urged in the resisting medium (since it is the excess of the force Cd over the resistance CO) will be represented by arc Od, and thus will be to the force by which body D is urged in a nonresisting medium in place D as arc Od to arc CD, and therefore also in place B as arc OB to arc CB. Accordingly, if two bodies D and d leave place B and are urged by these forces, then, since the forces at the beginning are as arcs CB and OB, the first velocities and the arcs first described will be in the same ratio. Let those arcs be DO and Bd; then the remaining arcs CD and Od will be in the same ratio. Accordingly the forces, being proportional to CD and Od, will remain in the same ratio as at the beginning, and therefore the bodies will proceed simultaneously to describe arcs in the same ratio. Therefore the forces and the velocities and the remaining arcs CD and Od will always be as the whole arcs CB and OB, and therefore those remaining arcs will be described simultaneously. Therefore the two bodies D and d will arrive simultaneously at places C and O, the one in the nonresisting medium at place C, and the one in the resisting medium at place O. And since the velocities in C and O are as arcs CB and OB, the arcs that the bodies describe in the same time by going on further will be in the same ratio. Let those arcs be CE and Oe. The force by which body D in the nonresisting medium is retarded in E is as CE, and the force by which body d in the resisting medium is retarded in e is as the sum of the force Ce and the resistance CO, that is, as Oe; and thus the forces by which the bodies are retarded are as arcs CB and OB, which are proportional to arcs CE and Oe; and accordingly the velocities, which are retarded in that given ratio, remain in that same given ratio. The velocities, therefore, and the arcs described with those velocities are always to one another in the given ratio of arcs CB and OB; and therefore, if the whole arcs AB and aB are taken in the same ratio, bodies D and d will describe these arcs together and will simultaneously lose all motion in places A and a. The whole oscillations are therefore isochronal, and any parts of the arcs, BD and Bd or BE and Be, that are described in the same time are proportional to the whole arcs BA and Ba. Q.E.D.
COROLLARY. Therefore the swiftest motion in the resisting medium does not occur at the lowest point C, but is found in that point O by which aB, the whole arc described, is bisected. And the body, proceeding from that point to a, is retarded at the same rate by which it was previously accelerated in its descent from B to O.
Proposition 26, Theorem 21
If simple pendulums are resisted in the ratio of the velocities, their oscillations in a cycloid are isochronal.
For if two oscillating bodies equally distant from the centers of suspension describe unequal arcs and if the velocities in corresponding parts of the arcs are to one another as the whole arcs, then the resistances, being proportional to the velocities, will also be to one another as the same arcs. Accordingly, if these resistances are taken away from (or added to) the motive forces arising from gravity, which are as the same arcs, the differences (or sums) will be to one another in the same ratio of the arcs; and since the increments or decrements of the velocities are as these differences or sums, the velocities will always be as the whole arcs. Therefore, if in some one case the velocities are as the whole arcs, they will always remain in that ratio. But in the beginning of the motion, when the bodies begin to descend and to describe those arcs, the forces—since they are proportional to the arcs—will generate velocities proportional to the arcs. Therefore the velocities will always be as the whole arcs to be described, and therefore those arcs will be described in the same time. Q.E.D.
Proposition 27, Theorem 22
If simple pendulums are resisted as the squares of the velocities, the differences between the times of the oscillations in a resisting medium and the times of the oscillations in a nonresisting medium of the same specific gravity will be very nearly proportional to the arcs described during the oscillations.
For let the unequal arcs A and B be described by equal pendulums in a resisting medium; then the resistance to the body in arc A will be to the resistance to the body in the corresponding part of arc B very nearly in the squared ratio of the velocities, that is, as A2 to B2. If the resistance in arc B were to the resistance in arc A as AB to A2, the times in arcs A and B would be equal, by the previous proposition. And thus the resistance A2 in arc A, or AB in arc B, produces an excess of time in arc A over the time in a nonresisting medium; and the resistance B2 produces an excess of time in arc B over the time in a nonresisting medium. And those excesses are very nearly as the forces AB and B2 that produce them, that is, as arcs A and B. Q.E.D.
COROLLARY 1. Hence from the times of the oscillations made in a resisting medium in unequal arcs, the times of the oscillations in a nonresisting medium of the same specific gravity can be found. For the difference between these times will be to the excess of the time in the smaller arc over the time in the nonresisting medium as the difference between the arcs is to the smaller arc.
COROLLARY 2. Shorter oscillations are more isochronal, and the shortest are performed in very nearly the same times as in a nonresisting medium. In fact, the times of those that are made in greater arcs are a little greater, because the resistance in the descent of the body (by which the time is prolonged) is greater in proportion to the length described in the descent than the resistance in the subsequent ascent (by which the time is shortened). But also the time of short as well as long oscillations seems to be somewhat prolonged by the motion of the medium. For retarded bodies are resisted a little less in proportion to the velocity, and accelerated bodies a little more, than those that progress uniformly; and this is so because the medium, going in the same direction as the bodies with the motion that it has received from them, is in the first case more agitated, in the second less, and accordingly concurs to a greater or to a less degree with the moving bodies. The medium therefore resists the pendulums more in the descent, and less in the ascent, than in proportion to the velocity, and the time is prolonged as a result of both causes.
Proposition 28, Theorem 23
If a simple pendulum oscillating in a cycloid is resisted in the ratio of the moments of time, its resistance will be to the force of gravity as the excess of the arc described in the whole descent over the arc described in the subsequent ascent is to twice the length of the pendulum.
Let BC designate the arc described in the descent, Ca the arc described in the ascent, and Aa the difference between the arcs; then, with the same constructions and proofs as in prop. 25, the force by which the oscillating body is urged in any place D will be to the force of resistance as arc CD to arc CO, which is half of that difference Aa. And thus the force by which the oscillating body is urged in the beginning (or highest point) of the cycloid—that is, the force of gravity—will be to the resistance as the arc of the cycloid between that highest point and the lowest point C is to arc CO, that is (if the arcs are doubled), as the arc of the whole cycloid, or twice the length of the pendulum, is to arc Aa. Q.E.D.
Proposition 29, Problem 6
Supposing that a body oscillating in a cycloid is resisted as the square of the velocity, it is required to find the resistance in each of the individual places.
Let Ba be the arc described in an entire oscillation, and let C be the lowest point of the cycloid, and let CZ be half of the arc of the whole cycloid and be equal to the length of the pendulum; and let it be required to find the resistance to the body in any place D. Cut the indefinite straight line OQ in points O, S, P, and Q, with the conditions that—if perpendiculars OK, ST, PI, and QE are erected; and if, with center O and asymptotes OK and OQ, hyperbola TIGE is described so as to cut perpendiculars ST, PI, and QE in T, I, and E; and if, through point I, KF is drawn parallel to asymptote OQ and meeting asymptote OK in K and perpendiculars ST and QE in L and F—the hyperbolic area PIEQ is to the hyperbolic area PITS as the arc BC described during the body’s descent is to the arc Ca described during the ascent, and area IEF is to area ILT as OQ to OS. Then let perpendicular MN cut off the hyperbolic area PINM, which is to the hyperbolic area PIEQ as arc CZ is to the arc BC described in the descent. And if perpendicular RG cuts off the hyperbolic area PIGR, which is to area PIEQ as any arc CD is to the arc BC described in the whole descent, then the resistance in place D will be to the force of gravity as the area 
IEF − IGH to the area PINM.
For, since the forces which arise from gravity and by which the body is urged in places Z, B, D, and a are as arcs CZ, CB, CD, and Ca, and those arcs are as areas PINM, PIEQ, PIGR, and PITS, let the arcs and the forces be represented by these areas respectively. In addition, let Dd be the minimally small space described by the body while descending, and represent it by the minimally small area RGgr comprehended between the parallels RG and rg; and produce rg to h, so that GMhg and RGgr are decrements of areas IGH and PIGR made in the same time. And the increment GHhg − 
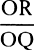IEF, or Rr × HG − IEF, of area IEF − IGH will be to the decrement RGgr, or Rr × RG, of area PIGR as HG − 
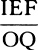, is to RG, and thus as OR × HG − 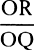IEF is to OR × GR or OP × PI, that is (because OR × HG, or OR × HR − OR × GR, ORHK − OPIK, PIHR, and PIGR + IGH are equal), as PIGR + IGH − 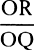IEF is to OPIK. Therefore, if area 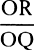IEF − IGH is called Y, and if the decrement RGgr of area PIGR is given, then the increment of area Y will be as PIGR − Y.
But if V designates the force arising from gravity, by which the body is urged in D and which is proportional to the arc CD to be described, and if R represents the resistance, then V − R will be the whole force by which the body is urged in D. The increment of the velocity is therefore jointly as V − R and that particle of time in which the increment is made. But furthermore the velocity itself is directly as the increment of the space described in the same time and inversely as that same particle of time. Hence, since the resistance, by hypothesis, is as the square of the velocity, the increment of the resistance (by lem. 2) will be as the velocity and the increment of the velocity jointly, that is, as the moment of the space and V − R jointly; and thus, if the moment of the space is given, as V − R; that is, as PIGR − Z, if for the force V there is written PIGR (which represents it), and if the resistance R is represented by some other area Z.
Therefore, as area PIGR decreases uniformly by the subtraction of the given moments, area Y increases in the ratio of PIGR − Y, and area Z increases in the ratio of PIGR − Z. And therefore, if areas Y and Z begin simultaneously and are equal at the beginning, they will continue to be equal by the addition of equal moments and, thereafter decreasing by moments that are likewise equal, will vanish simultaneously. And conversely, if they begin simultaneously and vanish simultaneously, they will have equal moments and will always be equal; and this is so because, if the resistance Z is increased, the velocity will be decreased along with that arc Ca which is described in the body’s ascent, and as the point in which there is a cessation of all motion and resistance approaches closer to point C, the resistance will vanish more quickly than area Y. And the contrary will happen when the resistance is decreased.
Now area Z begins and ends where the resistance is nil, that is, in the beginning of the motion where arc CD is equal to arc CB and the straight line RG falls upon the straight line QE, and in the end of the motion where arc CD is equal to arc Ca and RG falls upon the straight line ST. And area Y or 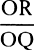IEF − IGH begins and ends where the resistance is nil, and thus where 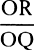IEF and IGH are equal; that is (by construction), where the straight line RG falls successively upon the straight lines QE and ST. And accordingly those areas begin simultaneously and vanish simultaneously and therefore are always equal. Therefore area 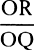IEF − IGH is equal to area Z (which represents the resistance) and therefore is to area PINM (which represents the gravity) as the resistance is to the gravity. Q.E.D.
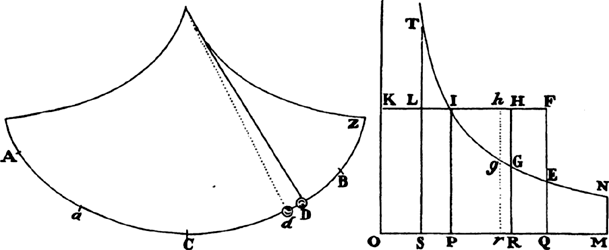
COROLLARY 1. The resistance in the lowest place C is, therefore, to the force of gravity as area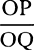 
IEF is to area PINM.
COROLLARY 2. And this resistance becomes greatest when area PIHR is to area IEF as OR is to OQ. For in that case its moment (namely, PIGR − Y) comes out nil.
COROLLARY 3. Hence also the velocity in each of the individual places can be known, inasmuch as it is as the square root of the resistance, and at the very beginning of the motion is equal to the velocity of the body oscillating without any resistance in the same cycloid.
But because the computation by which the resistance and velocity are to be found by this proposition is difficult, it seemed appropriate to add the following proposition.a
Proposition 30, Theorem 24
If the straight line aB is equal to a cycloidal arc that is described by an oscillating body, and if at each of its individual points D perpendiculars DK are erected that are to the length of the pendulum as the resistance encountered by the body in corresponding points of the arc is to the force of gravity, then I say that the difference between the arc described in the whole descent and the arc described in the whole subsequent ascent multiplied by half the sum of those same arcs will be equal to the area BKa occupied by all the perpendiculars DK.
Represent the cycloidal arc described in an entire oscillation by the straight line aB equal to it, and represent the arc that would be described in a vacuum by the length AB. Bisect AB in C, and point C will represent the lowest point of the cycloid, and CD will be as the force arising from gravity (by which the body at D is urged along the tangent of the cycloid) and will have the ratio to the length of the pendulum that the force at D has to the force of gravity. Therefore represent that force by the length CD, and the force of gravity by the length of the pendulum; then, if DK is taken in DE in the ratio to the length of the pendulum that the resistance has to the gravity, DK will represent the resistance. With center C and radius CA or CB construct semicircle BEeA. And let the body describe space Dd in a minimally small time; then, when perpendiculars DE and de have been erected, meeting the circumference in E and e, they will be as the velocities that the body in a vacuum would acquire in places D and d by descending from point B. This is evident by book 1, prop. 52. Therefore represent these velocities by perpendiculars DE and de, and let DF be the velocity that the body acquires in D by falling from B in the resisting medium. And if with center C and radius CF circle Ff M is described, meeting the straight lines de and AB in f and M, then M will be the place to which the body would then ascend if there were no further resistance, and df will be the velocity that it would acquire in d. Hence also, if Fg designates the moment of velocity that body D, in describing the minimally small space Dd, loses as a result of the resistance of the medium, and if CN is taken equal to Cg, then N will be the place to which the body would then ascend if there were no further resistance, and MN will be the decrement of the ascent arising from the loss of that velocity. Drop perpendicular Fm to df, and the decrement Fg (generated by the resistance DK) of the velocity DF will be to the increment fm (generated by the force CD) of that same velocity as the generating force DK is to the generating force CD. Furthermore, because triangles Fmf, Fhg, and FDC are similar, fm is to Fm or Dd as CD is to DF and from the equality of the ratios [or ex aequo] Fg is to Dd as DK is to DF. aLikewise Fh is to Fg as DF to CF, and from the equality of the ratios in inordinate proportion [or ex aequo perturbate] Fh or MN is to Dd as DK to CF or CM; and thus the sum of all the MN × CM will be equal to the sum of all the Dd × DK. Suppose that a rectangular ordinate is always erected at the moving point M, equal to the indeterminate CM, which in its continual motion is multiplied by the whole length Aa; then the quadrilateral described as a result of that motion—or the rectangle equal to it, Aa × ½aB—will become equal to the sum of all the MN × CM, and thus equal to the sum of all the Dd × DK, that is, equal to area BKVTa. Q.E.D.a
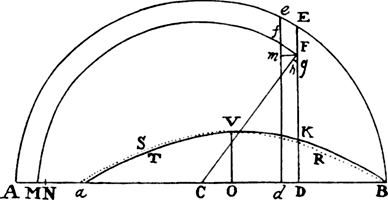
COROLLARY. Hence from the law of the resistance and the difference Aa of arcs Ca and CB, the proportion of the resistance to the gravity can be determined very nearly.
For if the resistance DK is uniform, the figure BKTa will be equal to the rectangle of Ba and DK; and hence the rectangle of ½Ba and Aa will be equal to the rectangle of Ba and DK, and DK will be equal to ½Aa. Therefore, since DK represents the resistance, and the length of the pendulum represents the gravity, the resistance will be to the gravity as ½Aa is to the length of the pendulum, exactly as was proved in prop. 28.
If the resistance is as the velocity, the figure BKTa will be very nearly an ellipse. For if a body in a nonresisting medium were to describe the length BA in a whole oscillation, the velocity in any place D would be as the ordinate DE of a circle described with diameter AB. Accordingly, since Ba in the resisting medium, and BA in a nonresisting medium, are described in roughly equal times, and the velocities in the individual points of Ba are thus very nearly to the velocities in the corresponding points of the length BA as Ba is to BA, the velocity in point D in the resisting medium will be as the ordinate of a circle or ellipse described upon diameter Ba; and thus the figure BKVTa will be very nearly an ellipse. Since the resistance is supposed proportional to the velocity, let OV represent the resistance in the midpoint O; then ellipse BRVSa, described with center O and semiaxes OB and OV, will be very nearly equal to the figure BKVTa and the rectangle equal to it, Aa × BO. Aa × BO is therefore to OV ×BO as the area of this ellipse is to OV × BO; that is, Aa is to OV as the area of the semicircle is to the square of the radius, or as 11 to 7, roughly; and therefore 7/11Aa is to the length of the pendulum as the resistance of the oscillating body in O is to its gravity.
But if the resistance DK is as the square of the velocity, the figure BKVTa will be almost a parabola having vertex V and axis OV, and thus will be very nearly equal to the rectangle contained by ⅔Ba and OV. The rectangle contained by ½Ba and Aa is therefore equal to the rectangle contained by ⅔Ba and OV, and thus OV is equal to ¾Aa; and therefore the resistance on the oscillating body in O is to its gravity as ¾Aa is to the length of the pendulum.
And I judge that these conclusions are more than accurate enough for practical purposes. For, since the ellipse or parabola BRVSa and the figure BKVTa have the same midpoint V, if it is greater than that figure on either side BRV or VSa, it will be smaller than it on the other side, and thus will be very nearly equal to it.
Proposition 31, Theorem 25
If the resistance encountered by an oscillating body in each of the proportional parts of the arcs described is increased or decreased in a given ratio, the difference between the arc described in the descent and the arc described in the subsequent ascent will be increased or decreased in the same ratio.
For that difference arises from the retardation of the pendulum by the resistance of the medium, and thus is as the whole retardation and the retarding resistance, which is proportional to it. In the previous proposition the rectangle contained under the straight line ½aB and the difference Aa of arcs CB and Ca was equal to area BKTa. And that area, if the length aB remains the same, is increased or decreased in the ratio of the ordinates DK, that is, in the ratio of the resistance, and thus is as the length aB and the resistance jointly. And accordingly the rectangle contained by Aa and ½aB is as aB and the resistance jointly, and therefore Aa is as the resistance. Q.E.D.
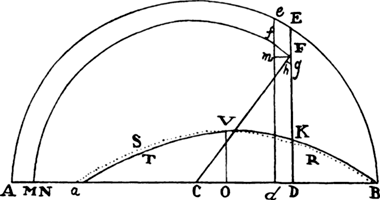
COROLLARY 1. Hence, if the resistance is as the velocity, the difference of the arcs in the same medium will be as the whole arc described; and conversely.
COROLLARY 2. If the resistance is in the squared ratio of the velocity, that difference will be in the squared ratio of the whole arc; and conversely.
COROLLARY 3. And universally, if the resistance is in the cubed or any other ratio of the velocity, the difference will be in the same ratio of the whole arc; and conversely.
COROLLARY 4. And if the resistance is partly in the simple ratio of the velocity and partly in the squared ratio of the velocity, the difference will be partly in the simple ratio of the whole arc and partly in the squared ratio of it; and conversely. The law and ratio of the resistance in relation to the velocity will be the same as the law and ratio of that difference of the arcs in relation to the length of the arc itself.
COROLLARY 5. And thus if a pendulum successively describes unequal arcs and there can be found the ratio of the increment and decrement of this difference [i.e., the difference of the arcs] in relation to the length of the arc described, then there will also be had the ratio of the increment and decrement of the resistance in relation to a greater or smaller velocity.
General Scholiuma
From these propositions it is possible to find the resistance of any mediums by means of pendulums oscillating in those mediums. In fact, I have investigated the resistance of air by the following experiments. I suspended a wooden ball by a fine thread from a sufficiently firm hook in such a way that the distance between the hook and the center of oscillation of the ball was 10½ feet; the ball weighed 577/22 ounces avoirdupois and had a diameter of 67/8 London inches. I marked a point on the thread 10 feet and 1 inch distant from the center of suspension; and at a right angle at that point I placed a ruler divided into inches, by means of which I might note the lengths of the arcs described by the pendulum. Then I counted the oscillations during which the ball would lose an eighth of its motion. When the pendulum was drawn back from the perpendicular to a distance of 2 inches and was let go from there, so as to describe an arc of 2 inches in its whole descent and to describe an arc of about 4 inches in the first whole oscillation (composed of the descent and subsequent ascent), it then lost an eighth of its motion in 164 oscillations, so as to describe an arc of 1¾ inches in its final ascent. When it described an arc of 4 inches in its first descent, it lost an eighth of its motion in 121 oscillations, so as to describe an arc of 3½ inches in its final ascent. When it described an arc of 8, 16, 32, or 64 inches in its first descent, it lost an eighth of its motion in 69, 35½, 18½, and 9⅔ oscillations respectively. Therefore the difference between the arcs described in the first descent and the final ascent, in the first, second, third, fourth, fifth, and sixth cases, was ¼, ½, 1, 2, 4, and 8 inches respectively. Divide these differences by the number of oscillations in each case, and in one mean oscillation—in which an arc of 3¾, 7½, 15, 30, 60, and 120 inches was described—the difference between the arcs described in the descent and subsequent ascent will be 1/656, 1/242, 1/69, 4/71, 8/37, and 24/29 parts of an inch respectively. In the greater oscillations, moreover, these are very nearly in the squared ratio of the arcs described, while in the smaller oscillations they are a little greater than in that ratio; and therefore (by book 2, prop. 31, corol. 2) the resistance of the ball when it moves more swiftly is very nearly in the squared ratio of the velocity; when more slowly, a little greater than in that ratio.
Now let V designate the greatest velocity in any oscillation, and let A, B, and C be given quantities, and let us imagine the difference between the arcs to be AV + BV3/2 + CV2. In a cycloid the greatest velocities are as halves of the arcs described in oscillating, but in a circle they are as the chords of halves of these arcs, and thus with equal arcs are greater in a cycloid than in a circle in the ratio of halves of the arcs to their chords, while the times in a circle are greater than in a cycloid in the inverse ratio of the velocity. Hence it is evident that the differences between the arcs (differences which are as the resistance and the square of the time jointly) would be very nearly the same in both curves. For those differences in the cycloid would have to be increased along with the resistance in roughly the squared ratio of the arc to the chord (because the velocity is increased in the simple ratio of the arc to the chord) and would have to be decreased along with the square of the time in that same squared ratio. Therefore, in order to reduce all of this to the cycloid, take the same differences between the arcs that were observed in the circle, while supposing the greatest velocities to correspond to the arcs, whether halved or entire, that is, to the numbers ½, 1, 2, 4, 8, and 16. In the second, fourth, and sixth cases, therefore, let us write the numbers 1, 4, and 16 for V; and the difference between the arcs will come out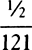 
= A + B + C in the second case; 
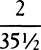= 4A + 8B + 16C in the fourth case; and 
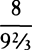= 16A + 64B + 256C in the sixth case. And by the proper analytic reduction of these equations taken together, A becomes = 0.0000916, B = 0.0010847, and C = 0.0029558. The difference between the arcs is therefore as 0.0000916V + 0.0010847V3/2 + 0.0029558V2; and therefore—since (by prop. 30, corol., applied to this case) the resistance of the ball in the middle of the arc described by oscillating, where the velocity is V, is to its weight as 7/11AV + 7/10BV3/2 + ¾CV2 is to the length of the pendulum—if the numbers found are written for A, B, and C, the resistance of the ball will become to its weight as 0.0000583V + 0.0007593V3/2 + 0.0022169V2 is to the length of the pendulum between the center of suspension and the ruler, that is, to 121 inches. Hence, since V in the second case has the value 1, in the fourth 4, and in the sixth 16, the resistance will be to the weight of the ball in the second case as 0.0030345 to 121, in the fourth as 0.041748 to 121, and in the sixth as 0.61705 to 121.
The arc which in the sixth case was described by the point marked on the thread was 120 − 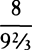or 1195/29 inches. And therefore, since the radius was 121 inches, and the length of the pendulum between the point of suspension and the center of the ball was 126 inches, the arc that the center of the ball described was 1243/31 inches. Since, because of the resistance of the air, the greatest velocity of an oscillating body does not occur at the lowest point of the arc described but is located near the midpoint of the whole arc, that velocity will be roughly the same as if the ball in its whole descent in a nonresisting medium described half that arc (623/62 inches) and did so in a cycloid, to which we have above reduced the motion of the pendulum; and therefore that velocity will be equal to the velocity which the ball could acquire by falling perpendicularly and describing in its fall a space equal to the versed sine of that arc. But that versed sine in the cycloid is to that arc (623/62) as that same arc is to twice the length of the pendulum (252) and thus is equal to 15.278 inches. Therefore the velocity is the very velocity that the body could acquire by falling and describing in its fall a space of 15.278 inches. With such a velocity, then, the ball encounters a resistance that is to its weight as 0.61705 to 121, or (if only that part of the resistance is considered which is in the squared ratio of the velocity) as 0.56752 to 121.
By a hydrostatic experiment, I found that the weight of this wooden ball was to the weight of a globe of water of the same size as 55 to 97; and therefore, since 121 is to 213.4 in the same ratio as 55 to 97, the resistance of a globe of water moving forward with the above velocity will be to its weight as 0.56752 to 213.4, that is, as 1 to 3761/50. The weight of the globe of water, in the time during which the globe describes a length of 30.556 inches with a uniformly continued velocity, could generate all that velocity in the globe if it were falling; hence it is manifest that in the same time the force of resistance uniformly continued could take away a velocity smaller in the ratio of 1 to 3761/50, that is,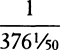 
of the whole velocity. And therefore in the same time in which the globe, with that velocity uniformly continued, could describe the length of its own semidiameter, or 37/16 inches, it would lose 1/3,342 of its motion.
I also counted the oscillations in which the pendulum lost a fourth of its motion. In the following table the top numbers denote the length of the arc described in the first descent, expressed in inches and parts of an inch; the middle numbers signify the length of the arc described in the final ascent; and at the bottom stand the numbers of oscillations. I have described this experiment because it is more accurate than when only an eighth of the motion was lost. Let anyone who wishes test the computation.
Later, using the same thread, I suspended a lead ball with a diameter of 2 inches and a weight of 26¼ ounces avoirdupois, in such a way that the distance between the center of the ball and the point of suspension was 10½ feet, and I counted the oscillations in which a given part of the motion was lost. The first of the following tables shows the number of oscillations in which an eighth of the whole motion was lost; the second shows the number of oscillations in which a fourth of it was lost.
Select the third, fifth, and seventh observations from the first table and represent the greatest velocities in these particular observations by the numbers 1, 4, and 16 respectively, and generally by the quantity V as above; then it will be the case that in the third observation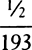 
= A + B + C, in the fifth 
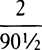= 4A + 8B + 16C, in the seventh 
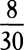= 16A + 64B + 256C. The reduction of these equations gives A = 0.001414, B = 0.000297, C = 0.000879. Hence the resistance of the ball moving with velocity V comes out to have the ratio to its own weight (26¼ ounces) that 0.0009V + 0.000208V3/2 + 0.000659V2 has to the pendulum’s length (121 inches). And if we consider only that part of the resistance which is in the squared ratio of the velocity, it will be to the weight of the ball as 0.000659V2 is to 121 inches. But in the first experiment this part of the resistance was to the weight of the wooden ball (577/22 ounces) as 0.002217V2 to 121; and hence the resistance of the wooden ball becomes to the resistance of the lead ball (their velocities being equal) as 577/22 × 0.002217 to 26¼ × 0.000659, that is, as 7⅓ to 1. The diameters of the two balls were 67/8 and 2 inches, and the squares of these are to each other as 47¼, and 4, or 1113/16 and 1, very nearly. Therefore the resistances of equally swift balls were in a smaller ratio than the squared ratio of the diameters. But we have not yet considered the resistance of the thread, which certainly was very great and ought to be subtracted from the resistance of the pendulum that has been found. I could not determine this resistance of the thread accurately, but nevertheless I found it to be greater than a third of the whole resistance of the smaller pendulum; and I learned from this that the resistances of the balls, taking away the resistance of the thread, are very nearly in the squared ratio of the diameters. For the ratio of 7⅓ − ⅓ to 1 − ⅓ or 10½ to 1, is very close to the squared ratio of the diameters 1113/16 to 1.
Since the resistance of the thread is of less significance in larger balls, I also tried the experiment in a ball whose diameter was 18¾ inches. The length of the pendulum between the point of suspension and the center of oscillation was 122½ inches; between the point of suspension and a knot in the thread, 109½ inches. The arc described by the knot in the first descent of the pendulum was 32 inches. The arc described by that same knot in the final ascent after five oscillations was 28 inches. The sum of the arcs, or the whole arc described in a mean oscillation, was 60 inches. The difference between the arcs was 4 inches. A tenth of it, or the difference between the descent and the ascent in a mean oscillation, was ⅖ inch. The ratio of the radius 109½ to the radius 122½ is the same as the ratio of the whole arc of 60 inches described by the knot in a mean oscillation to the whole arc of 67⅛ inches described by the center of the ball in a mean oscillation, and is equal to the ratio of the difference ⅖ to the new difference 0.4475. If the length of the pendulum were to be increased in the ratio of 126 to 122½ while the length of the arc described remained the same, the time of oscillation would be increased and the velocity of the pendulum would be decreased as the square root of that ratio, while the difference 0.4475 between the arcs described in a descent and subsequent ascent would remain the same. Then, if the arc described were to be increased in the ratio of 1243/31 to 67⅛, that difference 0.4475 would be increased as the square of that ratio, and thus would come out 1.5295. These things would be so on the hypothesis that the resistance of the pendulum was in the squared ratio of the velocity. Therefore, if the pendulum were to describe a whole arc of 1243/31 inches, and its length between the point of suspension and the center of oscillation were 126 inches, the difference between the arcs described in a descent and subsequent ascent would be 1.5295 inches. And this difference multiplied by the weight of the ball of the pendulum, which was 208 ounces, yields the product 318.136. Again, when the above-mentioned pendulum (made with a wooden ball) described a whole arc of 1243/31 inches by its center of oscillation (which was 126 inches distant from the point of suspension), the difference between the arcs described in the descent and ascent was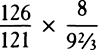 
, which multiplied by the weight of the ball (which was 577/22 ounces) yields the product 49.396. And I multiplied these differences by the weights of the balls in order to find their resistances. For the differences arise from the resistances and are as the resistances directly and the weights inversely. The resistances are therefore as the numbers 318.136 and 49.396. But the part of the resistance of the smaller ball that is in the squared ratio of the velocity was to the whole resistance as 0.56752 to 0.61675, that is, as 45.453 to 49.396; and the similar part of the resistance of the larger ball is almost equal to its whole resistance; and thus those parts are very nearly as 318.136 and 45.453, that is, as 7 and 1. But the diameters of the balls are 18¾ and 6⅞, and the squares of these diameters, 3519/16 and 4717/64, are as 7.438 and 1, that is, very nearly as the resistances 7 and 1 of the balls. The difference between the ratios is no greater than what could have arisen from the resistance of the thread. Therefore, those parts of the resistances that are (the balls being equal) as the squares of the velocities are also (the velocities being equal) as the squares of the diameters of the balls.
The largest ball that I used in these experiments, however, was not perfectly spherical, and therefore for the sake of brevity I have ignored certain minutiae in the above computation, being not at all worried about a computation being exact when the experiment itself was not sufficiently exact. Therefore, since the demonstration of a vacuum depends on such experiments, I wish that they could be tried with more, larger, and more exactly spherical balls. If the balls are taken in geometric proportion, say with diameters of 4, 8, 16, and 32 inches, it will be discovered from the progression of the experiments what ought to happen in the case of still larger balls.
To compare the resistances of different fluids with one another, I made the following experiments. I got a wooden box four feet long, one foot wide, and one foot deep. I took off its lid and filled it with fresh water, and I immersed pendulums in the water and made them oscillate. A lead ball weighing 166⅙ ounces, with a diameter of 3⅝ inches, moved as in the following table, that is, with the length of the pendulum from the point of suspension to a certain point marked on the thread being 126 inches, and to the center of oscillation being 134⅜ inches.
In the experiment recorded in the fourth column, equal motions were lost in 535 oscillations in air, and 1⅕ in water. The oscillations were indeed a little quicker in air than in water. But if the oscillations in water were accelerated in such a ratio that the motions of the pendulums in both mediums would become equally swift, the number 1⅕ oscillations in water during which the same motion would be lost as before would remain the same because the resistance is increased and the square of the time simultaneously decreased in that same ratio squared. With equal velocities of the pendulums, therefore, equal motions were lost, in air in 535 oscillations and in water in 1⅕ oscillations; and thus the resistance of the pendulum in water is to its resistance in air as 535 to 1⅕. This is the proportion of the whole resistances in the case of the fourth column.
Now let AV + CV2 designate the difference between the arcs described (in a descent and subsequent ascent) by the ball moving in air with the greatest velocity V; and since the greatest velocity in the case of the fourth column is to the greatest velocity in the case of the first column as 1 to 8, and since that difference between the arcs in the case of the fourth column is to the difference in the case of the first column as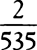 
to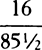 
, or as 85½ to 4,280, let us write 1 and 8 for the velocities in these cases and 85½ and 4,280 for the differences between the arcs; then A + C will become = 85½ and 8A + 64C = 4, 280 or A + 8C = 535; and hence, by reduction of the equations, 7C will become = 449½ and C = 643/14 and A = 212/7; and thus the resistance, since it is as 7/11AV + ¾CV2, will be as 136/11V + 489/56V2. Therefore, in the case of the fourth column, where the velocity was 1, the whole resistance is to its part proportional to the square of the velocity as 136/11 + 489/56 or 6112/17 to 489/56; and on that account the resistance of the pendulum in water is to that part of the resistance in air which is proportional to the square of the velocity (and which alone comes into consideration in swifter motions) as 6112/17 to 489/56 and 535 to 1⅕ jointly, that is, as 571 to 1. If the whole thread of the pendulum oscillating in water had been immersed, its resistance would have been still greater, to such an extent that the part of the resistance of the pendulum oscillating in water which is proportional to the square of the velocity (and which alone comes into consideration in swifter bodies) is to the resistance of that same whole pendulum oscillating in air, with the same velocity, as about 850 to 1, that is, very nearly as the density of water to the density of air.
In this computation also, that part of the resistance of the pendulum in water which would be as the square of the velocity ought to be taken into consideration, but (which may perhaps seem strange) the resistance in water was increased in more than the squared ratio of the velocity. In searching for the reason, I hit upon this: that the box was too narrow in proportion to the size of the ball of the pendulum, and because of its narrowness overly impeded the motion of the water as it yielded to the oscillation of the ball. For if a ball of a pendulum whose diameter was one inch was immersed, the resistance was increased in very nearly the squared ratio of the velocity. I tested this by constructing a pendulum out of two balls, so that the lower and smaller of them oscillated in the water, and the higher and larger one was fastened to the thread just above the water and, by oscillating in the air, aided the pendulum’s motion and made it last longer. And the experiments made with this pendulum came out as in the following table.
In comparing the resistances of the mediums with one another I also caused iron pendulums to oscillate in quicksilver. The length of the iron wire was about three feet, and the diameter of the ball of the pendulum was about ⅓ inch. And to the wire just above the mercury there was fastened another lead ball large enough to continue the motion of the pendulum for a longer time. Then I filled a small vessel (which held about three pounds of quicksilver) with quicksilver and common water successively, so that as the pendulum oscillated first in one and then in the other of the two fluids I might find the proportion of the resistances; and the resistance of the quicksilver came out to the resistance of the water as about 13 or 14 to 1, that is, as the density of quicksilver to the density of water. When I used ba slightly larger pendulum ball, say one whose diameter would be about ⅓ or ⅔ inch,b the resistance of the quicksilver came out in the ratio to the resistance of the water that the number 12 or 10 has to 1, roughly. But the former experiment is more trustworthy because in the latter the vessel was too narrow in proportion to the size of the immersed ball. With the ball enlarged, the vessel also would have to be enlarged. Indeed, I had determined to repeat experiments of this sort in larger vessels and in molten metals and certain other liquids, hot as well as cold; but there is not time to try them all, and from what has already been described it is clear enough that the resistance of bodies moving swiftly is very nearly proportional to the density of the fluids in which they move. I do not say exactly proportional. For the more viscous fluids, of an equal density, doubtless resist more than the more liquid fluids—as, for example, cold oil more than hot, hot oil more than rainwater, water more than spirit of wine. But in the liquids that are sufficiently fluid to the senses—as in air, in water (whether fresh or salt), in spirits of wine, of turpentine, and of salts, in oil freed of its dregs by distillation and then heated, and in oil of vitriol and in mercury, and in liquefied metals, and any others there may be which are so fluid that when agitated in vessels they conserve for some time a motion impressed upon them and when poured out are quite freely broken up into falling drops—in all these I have no doubt that the above rule holds exactly enough, especially if the experiments are made with pendulums that are larger and move more swiftly.
Finally, since csome people are of the opinionc that there exists a certain aethereal medium, by far the subtlest of all, which quite freely permeates all the pores and passages of all bodies, and that a resistance ought to arise from such a medium flowing through the pores of bodies, I devised the following experiment so that I might test whether the resistance that we experience in moving bodies is wholly on their external surface or whether the internal parts also encounter a perceptible resistance on their own surfaces. I suspended a round firwood box by a cord eleven feet long from a sufficiently strong steel hook, by means of a steel ring. The upper arc of the ring rested on the very sharp concave edge of the hook so that it might move very freely. And the cord was attached to the lower arc of the ring. I drew this pendulum away from the perpendicular to a distance of about six feet, and did so along the plane perpendicular to the edge of the hook, so that the ring, as the pendulum oscillated, would not slide to and fro on the edge of the hook. For the point of suspension, in which the ring touches the hook, ought to remain motionless. I marked the exact place to which I had drawn back the pendulum and then, letting the pendulum fall, marked another three places: those to which it returned at the end of the first, second, and third oscillations. I repeated this quite often, so that I might find those places as exactly as possible. Then I filled the box with lead and some of the other heavier metals that were at hand. But first I weighed the empty box along with the part of the cord that was wound around the box and half of the remaining part that was stretched between the hook and the suspended box. For a stretched cord always urges with half of its weight a pendulum drawn aside from the perpendicular. To this weight I added the weight of the air that the box contained. And the whole weight was about 1/78 of the box full of metals. Then, since the box full of metals increased the length of the pendulum as a result of stretching the cord by its weight, I shortened the cord so that the length of the pendulum now oscillating would be the same as before. Then, drawing the pendulum back to the first marked place and letting it fall, I counted about 77 oscillations until the box returned to the second marked place, and as many thereafter until the box returned to the third marked place, and again as many until the box on its return reached the fourth place. Hence I conclude that the whole resistance of the full box did not have a greater proportion to the resistance of the empty box than 78 to 77. For if the resistances of both were equal, the full box, because its inherent force was 78 times greater than the inherent force of the empty box, ought to conserve its oscillatory motion that much longer, and thus always return to those marked places at the completion of 78 oscillations. But it returned to them at the completion of 77 oscillations.
Let A therefore designate the resistance of the box on its external surface, and B the resistance of the empty box on its internal parts; then, if the resistances of equally swift bodies on their internal parts are as the matter, or the number of particles that are resisted, 78B will be the resistance of the full box on its internal parts; and thus the whole resistance A + B of the empty box will be to the whole resistance A + 78B of the full box as 77 to 78, and by separation [or dividendo] A + B will be to 77B as 77 to 1, and hence A + B will be to B as 77 × 77 to 1, and by separation [or dividendo] A will be to B as 5,928 to 1. The resistance encountered by the empty box on its internal parts is therefore more than 5,000 times smaller than the similar resistance on the external surface. This argument depends on the hypothesis that the greater resistance encountered by the full box does not arise from some other hidden cause but only from the action of some subtle fluid upon the enclosed metal.
I have reported this experiment from memory. For the paper on which I had once described it is lost. Hence I have been forced to omit certain fractions of numbers which have escaped my memory.
There is no time to try everything again. The first time, since I had used a weak hook, the full box was retarded more quickly. In seeking the cause, I found that the hook was so weak as to give way to the weight of the box and to be bent in this direction and that as it yielded to the oscillations of the pendulum. I got a strong hook, therefore, so that the point of suspension would remain motionless, and then everything came out as we have described it above.
to the horizon and standing upon the horizontal line PQ at points B, C, D, and E; and let BC, CD, and DE be distances between the ordinates equal to one another. From points G and H draw the straight lines GL and HN touching the curve in G and H, and meeting in L and N the ordinates CH and DI produced upward; and complete the parallelogram HCDM. Then the times in which the body describes arcs GH and HI will be as the square roots of the distances LH and NI which the body could describe in those times by falling from the tangents; and the velocities will be directly as GH and HI (the lengths described) and inversely as the times. Represent the times by T and t, and the velocities by 
and 
; and the decrement of the velocity occurring in time t will be represented by 
; but in a body describing arc HI, gravity increases the arc by only the length HI − HN or 
, and thus generates only the velocity 
. Add this velocity to the above decrement, and the result is the decrement of the velocity arising from the resistance alone, namely 
. And accordingly, since gravity generates the velocity 
to 2NI.
by adding to the resulting squares the squares of BC and CD, there will result the squares of the arcs GH and HI: o2 + Q2o2 − 2QRo3 + · · · and o2 + Q2o2 + 2QRo3 + · · · . The roots of these, o√(1 + Q2) − 
and o√(1 + Q2) + 
is 
or 
; and if the values just found of 
, the result will be 
√(1 + Q2). And since 2NI is 2Ro2, the resistance will now be to the gravity as 
or 
.
directly and 
inversely, that is, as 
. Q.E.I.
will be equal to √(1 + Q2) and thus can be written for √(1 + Q2) above. And so the resistance will be to the gravity as 3S × HT to 4R2 × AC, the velocity will be as 
, and the density of the medium will be as 
.a
in corol. 1, if the resistance is supposed to be as any power 
Vn of the velocity V, the density of the medium will turn out to be as 
. And therefore if a curve can be found under the condition that there would be given the ratio of 
to 
, or 
to (1 + Q2)n−1, body will move in this curve in a uniform medium with a resistance that is as the power Vn of the velocity. But let us return to simpler curves.d