SECTION 7a
The motion of fluids and the resistance encountered by projectiles
Proposition 32, Theorem 26
Let two similar systems of bodies consist of an equal number of particles, and let
each of the particles in one system be similar and proportional to the corresponding
particle in the other system, and let the particles be similarly situated with respect
to one another in the two systems and have a given ratio of density to one another.
And let them begin to move similarly with respect to one another in proportional
times (the particles that are in the one system with respect to the particles in that
system, and the particles in the other with respect to those in the other). Then,
if the particles that are in the same system do not touch one another except in
instants of reflection and do not attract or repel one another except by accelerative
forces that are inversely as the diameters of corresponding particles and directly as
the squares of the velocities, I say that the particles of the systems will continue to
move similarly with respect to one another in proportional times.
I say that bodies which are similar and similarly situated move similarly
with respect to one another in proportional times when their situations in
relation to one another are always similar at the end of the times—for instance,
if the particles of one system are compared with the corresponding particles
of another. Hence the times in which similar and proportional parts of similar
figures are described by corresponding particles will be proportional.
Therefore, if there are two systems of this sort, the corresponding particles, because
of the similarity of their motions at the beginning, will continue to move
similarly until they meet one another. For if they are acted upon by no forces,
they will, by the first law of motion, move forward uniformly in straight
lines. If they act upon one another by some forces and if those forces are as
the diameters of the corresponding particles inversely and the squares of the
velocities directly, then, since the situations of the particles are similar and
the forces proportional, the whole forces by which the corresponding particles
are acted upon, compounded of the separate acting forces (by corol. 2 of the
laws), will have similar directions, just as if they tended to centers similarly
placed among the particles, and those whole forces will be to one another as
the separate component forces, that is, as the diameters of the corresponding
particles inversely and the squares of the velocities directly, and therefore they
will cause corresponding particles to continue describing similar figures. This
will be so (by book 1, prop. 4, corols. 1 and 8) provided that the centers are
at rest. But if they move, since their situations with respect to the particles
of the systems remain similar (because the transferences are similar), similar
changes will be introduced in the figures which the particles describe. The
motions of corresponding similar particles will therefore be similar until they
first meet, and therefore the collisions will be similar and the reflections
similar, and then (by what has already been shown) the motions of the particles
with respect to one another will be similar until they encounter one another
again, and so on indefinitely. Q.E.D.
COROLLARY 1. Hence, if any two bodies that are similar and similarly
situated (in relation to the corresponding particles of the systems) begin to
move similarly with respect to the particles in proportional times, and if
their volumes and densities are to each other as the volumes and densities
of the corresponding particles, the bodies will continue to move similarly
in proportional times. For the case is the same for the larger parts of both
systems as for the particles.
COROLLARY 2. And if all the similar and similarly situated parts of the
systems are at rest with respect to one another, and if two of them, which are
larger than the others and correspond to each other in the two systems, begin
to move in any way with a similar motion along lines similarly situated, they
will cause similar motions in the remaining parts of the systems and will
continue to move similarly with respect to them in proportional times and
thus will continue to describe spaces proportional to their own diameters.
Proposition 33, Theorem 27
If the same suppositions are made, I say that the larger parts of the systems are
resisted in a ratio compounded of the squared ratio of their velocities and the
squared ratio of the diameters and the simple ratio of the density of the parts of
the systems.
For the resistance arises partly from the centripetal or centrifugal forces
with which the particles of the systems act upon one another and partly from
the collisions and reflections of the particles and the larger parts. Resistances
of the first kind, moreover, are to one another as the whole motive forces from
which they arise, that is, as the whole accelerative forces and the quantities
of matter in corresponding parts, that is (by hypothesis), as the squares of the
velocities directly and the distances of the corresponding particles inversely
and the quantities of matter in the corresponding parts directly. Thus, since
the distances of the particles of the one system are to the corresponding
distances of the particles of the other as the diameter of a particle or part in
the first system to the diameter of the corresponding particle or part in the
other, and since the quantities of matter are as the densities of the parts and
the cubes of the diameters, the resistances are to one another as the squares
of the velocities, the squares of the diameters, and the densities of the parts
of the systems. Q.E.D.
Resistances of the second kind are as the numbers and forces of
corresponding reflections jointly. The number of reflections in any one case,
moreover, is to the number in any other as the velocities of the
corresponding parts directly and the spaces between their reflections inversely. And the
forces of the reflections are as the velocities and volumes and densities of the
corresponding parts jointly, that is, as the velocities, the cubes of the
diameters, and the densities of the parts. And if all these ratios are compounded,
the resistances of the corresponding parts are to one another as the squares
of the velocities, the squares of the diameters, and the densities of the parts,
jointly. Q.E.D.
COROLLARY 1. Therefore, if the systems are two elastic fluids such as
air and if their parts are at rest with respect to one another, and if two
bodies which are similar and are proportional (with regard to volume and
density) to the parts of the fluids and are similarly situated with respect
to those parts are projected in any way along lines similarly situated, and
if the accelerative forces with which the particles of the fluids act upon one
another are as the diameters of the projected bodies inversely and the squares
of the velocities directly, then the bodies will cause similar motions in the
fluids in proportional times and will describe spaces that are similar and are
proportional to their diameters.
COROLLARY 2. Accordingly, in the same fluid a swift projectile
encounters a resistance that is very nearly in the squared ratio of the velocity. For if
the forces with which distant particles act upon one another were increased
in the squared ratio of the velocity, the resistance would be exactly in the
squared ratio of the velocity; and thus, in a medium whose parts act upon
one another with no forces because they are far apart, the resistance is exactly
in the squared ratio of the velocity. Let A, B, and C, therefore, be three
mediums consisting of parts that are similar and equal and regularly distributed at
equal distances. Let the parts of mediums A and B recede from one another
with forces that are to one another as T and V, and let the parts of medium
C be entirely without forces of this sort. Then, let four equal bodies D, E,
F, and G move in these mediums, the first two bodies D and E in the first
two mediums A and B respectively, and the other two bodies F and G in the
third medium C; and let the velocity of body D be to the velocity of body
E, and let the velocity of body F be to the velocity of body G, as the square
root of the ratio of the forces T to the forces V [i.e., as √T to √V]; then the
resistance of body D will be to the resistance of body E, and the resistance of
body F to the resistance of body G, in the squared ratio of the velocities; and
therefore the resistance of body D will be to the resistance of body F as the
resistance of body E to the resistance of body G. Let bodies D and F have
equal velocities, and also bodies E and G; then, if the velocities of bodies D
and F are increased in any ratio and the forces of the particles of medium B
are decreased in the same ratio squared, medium B will approach the form
and condition of medium C as closely as is desired, and on that account the
resistances of the equal and equally swift bodies E and G in these mediums
will continually approach equality, in such a way that their difference finally
comes out less than any given difference. Accordingly, since the resistances of
bodies D and F are to each other as the resistances of bodies E and G, these
also will similarly approach the ratio of equality. Therefore, the resistances
of bodies D and F, when they move very swiftly, are very nearly equal, and
therefore, since the resistance of body F is in the squared ratio of the velocity,
the resistance of body D will be very nearly in the same ratio.
COROLLARY 3. The resistance of a body moving very swiftly in any elastic
fluid is about the same as if the parts of the fluid lacked their centrifugal
forces and did not recede from one another, provided that the elastic force
of the fluid arises from the centrifugal forces of the particles and that the
velocity is so great that the forces do not have enough time to act.
COROLLARY 4. Accordingly, since the resistances of similar and equally
swift bodies, in a medium whose parts (being far apart) do not recede from
one another, are as the squares of the diameters, the resistances of equally
swift and very quickly moving bodies in an elastic fluid are also very nearly
as the squares of the diameters.
COROLLARY 5. And since similar, equal, and equally swift bodies, in
mediums which have the same density and whose particles do not recede
from one another, impinge upon an equal quantity of matter in equal times
(whether the particles are more and smaller or fewer and larger) and impress
upon it an equal quantity of motion and in turn (by the third law of motion)
undergo an equal reaction from it (that is, are equally resisted), it is manifest
also that in elastic fluids of the same density, when the bodies move very
swiftly, the resistances they encounter are very nearly equal, whether those
fluids consist of coarser particles or are made of the most subtle particles of
all. The resistance to projectiles moving very quickly is not much diminished
as a result of the subtlety of the medium.
COROLLARY 6. These statements all hold for fluids whose elastic force
originates in the centrifugal forces [i.e., forces of repulsion] of the particles.
But if that force arises from some other source, such as the expansion of the
particles in the manner of wool or the branches of trees, or from any other
cause which makes the particles move less freely with respect to one another,
then the resistance will be greater than in the preceding corollaries because
the medium is less fluid.
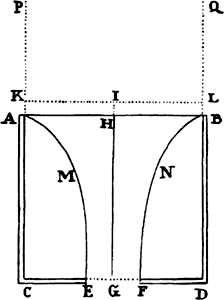
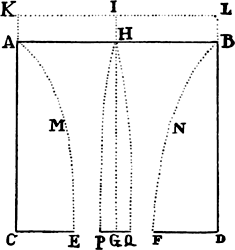
Proposition 34, Theorem 28
In a rare medium consisting of particles that are equal and arranged freely at
equal distances from one another, let a sphere and a cylinder—described with
equal diameters—move with equal velocity along the direction of the axis of the
cylinder; then the resistance of the sphere will be half the resistance of the cylinder.
For since the action of a medium on a body is (by corol. 5 of the
laws) the same whether the body moves in a medium at rest or the
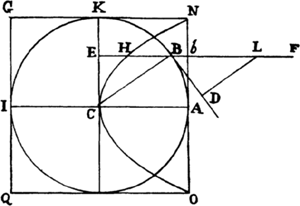 particles of the medium impinge with the
same velocity on the body at rest, let
us consider the body to be at rest and
see with what force it will be urged
by the moving medium. Let ABKI,
therefore, designate a spherical body
described with center C and
semidiameter C A, and let the particles of the
medium strike the spherical body with a given velocity along straight lines
parallel to AC; and let FB be such a straight line. On FB take LB equal
to the semidiameter CB, and draw BD touching the sphere in B. To KC
and BD drop the perpendiculars BE and LD; then the force with which a
particle of the medium, obliquely incident along the straight line FB, strikes
the sphere at B will be to the force with which the same particle would
strike the cylinder ONGQ (described with axis ACI about the sphere)
perpendicularly at b as LD to LB or BE to BC. Again, the efficacy of this force
to move the sphere along the direction FB (or AC) of its incidence is to its
efficacy to move the sphere along the direction of its determination—that
is, along the direction of the straight line BC in which it urges the sphere
directly [a direction through the center of the sphere]—as BE to BC. And,
compounding the ratios, if a particle strikes the sphere obliquely along the
straight line FB, its efficacy to move the sphere along the direction of its
incidence is to the efficacy of the same particle to move the cylinder in the
same direction, when striking the cylinder perpendicularly along the same
straight line, as BE2 to BC2. Therefore, if in bE, which is perpendicular to
the circular base NAO of the cylinder and equal to the radius AC, bH is
taken equal to
particles of the medium impinge with the
same velocity on the body at rest, let
us consider the body to be at rest and
see with what force it will be urged
by the moving medium. Let ABKI,
therefore, designate a spherical body
described with center C and
semidiameter C A, and let the particles of the
medium strike the spherical body with a given velocity along straight lines
parallel to AC; and let FB be such a straight line. On FB take LB equal
to the semidiameter CB, and draw BD touching the sphere in B. To KC
and BD drop the perpendiculars BE and LD; then the force with which a
particle of the medium, obliquely incident along the straight line FB, strikes
the sphere at B will be to the force with which the same particle would
strike the cylinder ONGQ (described with axis ACI about the sphere)
perpendicularly at b as LD to LB or BE to BC. Again, the efficacy of this force
to move the sphere along the direction FB (or AC) of its incidence is to its
efficacy to move the sphere along the direction of its determination—that
is, along the direction of the straight line BC in which it urges the sphere
directly [a direction through the center of the sphere]—as BE to BC. And,
compounding the ratios, if a particle strikes the sphere obliquely along the
straight line FB, its efficacy to move the sphere along the direction of its
incidence is to the efficacy of the same particle to move the cylinder in the
same direction, when striking the cylinder perpendicularly along the same
straight line, as BE2 to BC2. Therefore, if in bE, which is perpendicular to
the circular base NAO of the cylinder and equal to the radius AC, bH is
taken equal to 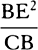 , then bH will be to bE as the effect of a particle upon
the sphere to the effect of the particle upon the cylinder. And therefore
the solid that is composed of all the straight lines bH will be to the solid
that is composed of all the straight lines bE as the effect of all the
particles upon the sphere to the effect of all the particles upon the cylinder. But
the first solid is a paraboloid described with vertex C, axis CA, and latus
rectum CA, and the second solid is a cylinder circumscribed around the
paraboloid; and it is known that a paraboloid is half of the circumscribed
cylinder. Therefore the whole force of the medium upon the sphere is half
of its whole force upon the cylinder. And therefore, if the particles of the
medium were at rest and the cylinder and the sphere were moving with
equal velocity, the resistance of the sphere would be half the resistance of the
cylinder. Q.E.D.
, then bH will be to bE as the effect of a particle upon
the sphere to the effect of the particle upon the cylinder. And therefore
the solid that is composed of all the straight lines bH will be to the solid
that is composed of all the straight lines bE as the effect of all the
particles upon the sphere to the effect of all the particles upon the cylinder. But
the first solid is a paraboloid described with vertex C, axis CA, and latus
rectum CA, and the second solid is a cylinder circumscribed around the
paraboloid; and it is known that a paraboloid is half of the circumscribed
cylinder. Therefore the whole force of the medium upon the sphere is half
of its whole force upon the cylinder. And therefore, if the particles of the
medium were at rest and the cylinder and the sphere were moving with
equal velocity, the resistance of the sphere would be half the resistance of the
cylinder. Q.E.D.
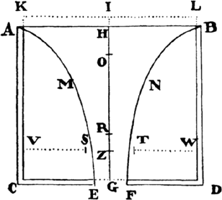
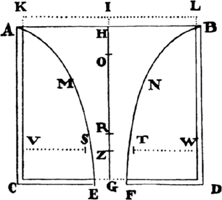
Scholium
By the same method other figures can be compared with one another with
respect to resistance, and those that are more suitable for continuing their
motions in resisting mediums can be found. For example, let it be required
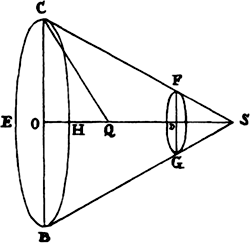 to construct a frustum CBGF of a cone with the
circular base CEBH (which is described with
center O and radius OC) and with the height
OD, which is resisted less than any other
frustum constructed with the same base and height
and moving forward along the direction of the
axis toward D; bisect the height OD in Q, and
produce OQ to S so that QS is equal to QC,
and S will be the vertex of the cone whose frustum is required.
to construct a frustum CBGF of a cone with the
circular base CEBH (which is described with
center O and radius OC) and with the height
OD, which is resisted less than any other
frustum constructed with the same base and height
and moving forward along the direction of the
axis toward D; bisect the height OD in Q, and
produce OQ to S so that QS is equal to QC,
and S will be the vertex of the cone whose frustum is required.
Note in passing that since the angle CSB is always acute, it follows
that if the solid ADBE is generated by a revolution of the elliptical or
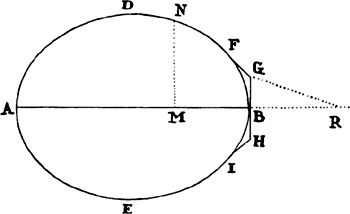 oval figure ADBE about the axis
AB, and if the generating figure
is touched by the three straight
lines FG, GH, and HI in points
F, B, and I, in such a way that
GH is perpendicular to the axis
in the point of contact B, and FG
and HI meet the said line GH at
the angles FGB and BHI of 135 degrees, then the solid that is generated by
the revolution of the figure ADFGHIE about the same axis AB is less
resisted than the former solid, provided that each of the two moves forward
along the direction of its axis AB, and the end B of each one is in front.
Indeed, I think that this proposition will be of some use for the construction
of ships.
oval figure ADBE about the axis
AB, and if the generating figure
is touched by the three straight
lines FG, GH, and HI in points
F, B, and I, in such a way that
GH is perpendicular to the axis
in the point of contact B, and FG
and HI meet the said line GH at
the angles FGB and BHI of 135 degrees, then the solid that is generated by
the revolution of the figure ADFGHIE about the same axis AB is less
resisted than the former solid, provided that each of the two moves forward
along the direction of its axis AB, and the end B of each one is in front.
Indeed, I think that this proposition will be of some use for the construction
of ships.
But suppose the figure DNFG to be a curve of such a sort that if the
perpendicular NM is dropped from any point N of that curve to the axis AB,
and if from the given point G the straight line GR is drawn, which is parallel
to a straight line touching the figure in N and cuts the axis (produced) in
R, then MN would be to GR as GR3 to 4BR × GB2. Then, in this case,
the solid that is described by a revolution of this figure about the axis AB
will, in moving in the aforesaid rare medium from A toward B, be resisted
less than any other solid of revolution described with the same length and
width.
Proposition 35a, Problem 7
If a rare medium consists of minimally small equal particles that are at rest and
arranged freely at equal distances from one another, it is required to find the
resistance encountered by a sphere moving forward uniformly in this medium.
CASE 1. Let a cylinder described with the same diameter and height as
before move forward with the same velocity along the length of its own axis
in the same medium. And let us suppose that the particles of the medium
upon which the sphere or cylinder impinges rebound with the greatest
possible force of reflection. Then the resistance of the sphere (by prop. 34) is half
the resistance of the cylinder, and the sphere is to the cylinder as 2 to 3, and
the cylinder in impinging perpendicularly upon the particles and reflecting
them as greatly as possible communicates twice its own velocity to them.
Therefore, the cylinder, in the time in which it describes half the length of
its axis by moving uniformly forward, will communicate to the particles a
motion which is to the whole motion of the cylinder as the density of the
medium is to the density of the cylinder; and the sphere, in the time in which
it describes the whole length of its diameter by moving uniformly forward,
will communicate the same motion to the particles, and in the time in which
it describes ⅔ of its diameter it will communicate to the particles a motion
which is to the whole motion of the sphere as the density of the medium to
the density of the sphere. And therefore the sphere encounters a resistance
that is to the force by which its whole motion could be either destroyed or
generated, in the time in which it describes ⅔ of its diameter by moving
uniformly forward, as the density of the medium is to the density of the
sphere.
CASE 2. Let us suppose that the particles of the medium impinging
upon the sphere or cylinder are not reflected; then the cylinder, in impinging
perpendicularly upon the particles, will communicate its whole velocity to
them and thus encounters half the resistance which it met in the former
case, and the resistance encountered by the sphere will also be half of what
it was before.
CASE 3. Let us suppose that the particles of the medium rebound from
the sphere with a force of reflection that is neither the greatest nor nil but
some intermediate force; then the resistance encountered by the sphere will
also be intermediate between the resistance in case 1 and the resistance in
case 2. Q.E.I.
COROLLARY 1. Hence, if the sphere and the particles are infinitely hard
without any elastic force and therefore also without any force of reflection,
the resistance encountered by the sphere will be to the force by which its
whole motion could be either destroyed or generated, in the time in which
the sphere describes 4/3 of its diameter, as the density of the medium is to the
density of the sphere.
COROLLARY 2. The resistance encountered by the sphere, other things
being equal, is in the squared ratio of the velocity.
COROLLARY 3. The resistance encountered by the sphere, other things
being equal, is in the squared ratio of the diameter.
COROLLARY 4. The resistance encountered by the sphere, other things
being equal, is as the density of the medium.
COROLLARY 5. The resistance encountered by the sphere is in a ratio that
is compounded of the squared ratio of the velocity and the squared ratio of
the diameter, and the simple ratio of the density of the medium.
COROLLARY 6. And the motion of the sphere with the resistance it
encounters can be represented as follows. Let AB be the time in which the
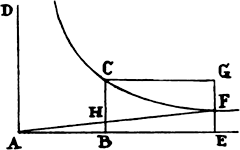 sphere can lose its whole motion when the
resistance is continued uniformly. Erect AD and BC
perpendicular to AB. And let BC be the whole
motion, and through point C with asymptotes
AD and AB describe the hyperbola CF.
Produce AB to any point E. Erect the perpendicular
EF meeting the hyperbola in F. Complete the parallelogram CBEG, and
draw AF meeting BC in H. Then, if the sphere, in any time BE, when its
first motion BC is continued uniformly, in a nonresisting medium, describes
the space CBEG represented by the area of the parallelogram, it will in a
resisting medium describe the space CBEF represented by the area of the
hyperbola, and its motion at the end of that time will be represented by the
ordinate EF of the hyperbola, with loss of part FG of its motion. And the
resistance at the end of the same time will be represented by the length BH,
with loss of part CH of the resistance. All of this is evident by book 2, prop.
5, corols. 1 and 3.
sphere can lose its whole motion when the
resistance is continued uniformly. Erect AD and BC
perpendicular to AB. And let BC be the whole
motion, and through point C with asymptotes
AD and AB describe the hyperbola CF.
Produce AB to any point E. Erect the perpendicular
EF meeting the hyperbola in F. Complete the parallelogram CBEG, and
draw AF meeting BC in H. Then, if the sphere, in any time BE, when its
first motion BC is continued uniformly, in a nonresisting medium, describes
the space CBEG represented by the area of the parallelogram, it will in a
resisting medium describe the space CBEF represented by the area of the
hyperbola, and its motion at the end of that time will be represented by the
ordinate EF of the hyperbola, with loss of part FG of its motion. And the
resistance at the end of the same time will be represented by the length BH,
with loss of part CH of the resistance. All of this is evident by book 2, prop.
5, corols. 1 and 3.
COROLLARY 7. Hence, if in time T, when the resistance R is continued
uniformly, the sphere loses its whole motion M, then in time t in a resisting
medium, when the resistance R decreases in the squared ratio of the velocity,
the sphere will lose part  of its motion M without loss of part
of its motion M without loss of part 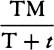 ;
and the sphere will describe a space that is to the space described by the
uniform motion M, in the same time t, as the logarithm of the number
;
and the sphere will describe a space that is to the space described by the
uniform motion M, in the same time t, as the logarithm of the number 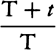 multiplied by the number 2.302585092994 is to the number
multiplied by the number 2.302585092994 is to the number 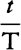 , because the
hyperbolic area BCFE is in this proportion to the rectangle BCGE.
, because the
hyperbolic area BCFE is in this proportion to the rectangle BCGE.
Scholium
In this proportion I have set forth the resistance and retardation encountered
by spherical projectiles in noncontinuous mediums, and I have shown that
this resistance is to the force by which the whole motion of a sphere could
be either destroyed or generated in the time in which the sphere describes
⅔ of its diameter, with a velocity continued uniformly, as the density of
the medium is to the density of the sphere, provided that the sphere and
the particles of the medium are highly elastic and possess the greatest force
of reflecting, and I have shown that this force is half as great when the
sphere and the particles of the medium are infinitely hard and devoid of all
force of reflecting. Moreover, in continuous mediums such as water, hot oil,
and quicksilver, in which the sphere does not impinge directly upon all the
particles of the fluid which generate resistance but presses only the nearest
particles, and these press others and these still others, the resistance is half
as great as in the second case. In extremely fluid mediums of this sort the
sphere encounters a resistance that is to the force by which its whole motion
could be either destroyed or generated, in the time in which it describes 8/3
of its diameter with the motion continued uniformly, as the density of the
medium is to the density of the sphere. We will try to show this in what
follows.
Proposition 36, Problem 8
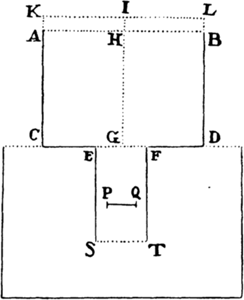
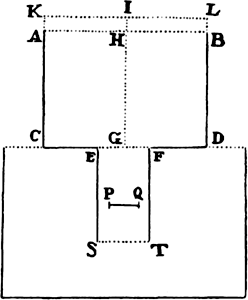
To determine the motion of water flowing out of a cylindrical vessel through a
hole in the bottom.
Let ACDB be the cylindrical vessel, AB its upper opening, CD its bottom
parallel to the horizon, EF a circular hole in the middle of the bottom, G the
center of the hole, and GH the cylinder’s axis perpendicular to the horizon.
 And imagine that a cylinder of ice APQB is
of the same width as the interior of the vessel,
has the same axis, and descends continually with
a uniform motion. Imagine also that its parts
liquefy as soon as they touch the surface AB,
that when they have turned into water they flow
down into the vessel as a result of their gravity,
and that in falling these parts form a cataract or
column of water ABNFEM and pass through
the hole EF and fill it exactly. And let the
uniform velocity of the descending ice, as well as that of the contiguous water
in the circle AB, be the velocity which the water can acquire in falling and
describing by its fall the space IH, and let IH and HG lie in a straight
line, and through point I draw the straight line KL parallel to the
horizon and meeting the sides of the ice in K and L. Then the velocity of the
water flowing out through the hole EF will be that which the water can
acquire in falling from I and describing by its fall the space IG. And thus,
by Galileo’s theorems, IG will be to IH as the square of the ratio of the
velocity of the water flowing out through the hole to the velocity of the
water in the circle AB, that is, as the square of the ratio of the circle AB
to the circle EF, for these circles are inversely as the velocities of the water
passing through them in the same time and with an equal quantity, filling
them both exactly. Here it is the velocity of the water toward the horizon that
is of concern. And the motion parallel to the horizon by which the parts of
the falling water approach one another is not considered here, since it does
not arise from gravity or change the motion perpendicular to the horizon
that does arise from gravity. Indeed, we are supposing that the parts of the
water cohere somewhat and that by their cohesion they approach one another
with motions parallel to the horizon as they fall, so that they form only one
single cataract and are not divided into several cataracts, but here we are not
considering the motion parallel to the horizon arising from that cohesion.
And imagine that a cylinder of ice APQB is
of the same width as the interior of the vessel,
has the same axis, and descends continually with
a uniform motion. Imagine also that its parts
liquefy as soon as they touch the surface AB,
that when they have turned into water they flow
down into the vessel as a result of their gravity,
and that in falling these parts form a cataract or
column of water ABNFEM and pass through
the hole EF and fill it exactly. And let the
uniform velocity of the descending ice, as well as that of the contiguous water
in the circle AB, be the velocity which the water can acquire in falling and
describing by its fall the space IH, and let IH and HG lie in a straight
line, and through point I draw the straight line KL parallel to the
horizon and meeting the sides of the ice in K and L. Then the velocity of the
water flowing out through the hole EF will be that which the water can
acquire in falling from I and describing by its fall the space IG. And thus,
by Galileo’s theorems, IG will be to IH as the square of the ratio of the
velocity of the water flowing out through the hole to the velocity of the
water in the circle AB, that is, as the square of the ratio of the circle AB
to the circle EF, for these circles are inversely as the velocities of the water
passing through them in the same time and with an equal quantity, filling
them both exactly. Here it is the velocity of the water toward the horizon that
is of concern. And the motion parallel to the horizon by which the parts of
the falling water approach one another is not considered here, since it does
not arise from gravity or change the motion perpendicular to the horizon
that does arise from gravity. Indeed, we are supposing that the parts of the
water cohere somewhat and that by their cohesion they approach one another
with motions parallel to the horizon as they fall, so that they form only one
single cataract and are not divided into several cataracts, but here we are not
considering the motion parallel to the horizon arising from that cohesion.
CASE 1. Now suppose that the interior of the vessel around the falling
water ABNFEM is filled with ice, so that the water passes through the ice as
if through a funnel. Then, if the water does not quite touch the ice, or (what
comes to the same thing) if it touches it and, because of the great smoothness
of the ice, slides through it with the greatest possible freedom and without
any resistance, the water will flow down through the hole EF with the same
velocity as before, and the whole weight of the column of water ABNFEM
will be used in generating its downflow as before, and the bottom of the
vessel will sustain the weight of the ice surrounding the column.
Now let the ice liquefy in the vessel; then the flow of the water will
remain the same as before with respect to velocity. It will not be less, since
the melted ice will endeavor to descend; and not greater, since the melted
ice cannot descend without impeding an equal descent of the original water.
The same force ought to generate the same velocity in the flowing water
[i.e., since the force is the same, the velocity that it generates will also be the
same].
But the hole in the bottom of the vessel, because of the oblique motions of
the particles of the flowing water, ought to be a little larger than before. For
now the particles of water do not all pass through the hole perpendicularly
but, flowing together from all the sides of the vessel and converging into the
hole, pass through with oblique motions and, turning their course downward,
unite into a stream of water gushing out which is narrower a little below
the hole than in the hole itself, its diameter being to the diameter of the hole
as 5 to 6, or 5½ to 6½ very nearly, provided that I measured the diameters
correctly. At any rate, I obtained a very thin flat plate perforated in the
middle, the diameter of the circular hole being ⅝ inch. And so that the
stream of water gushing out might not be accelerated in falling and made
narrower by the acceleration, I fastened this plate not to the bottom but to
the side of the vessel in such a way that the stream went out along a line
parallel to the horizon. Then, when the vessel was full of water, I opened
the hole so that the water might flow out, and the diameter of the stream,
measured as accurately as possible at a distance of about ½ inch from the
hole, came out 21/40 inch. The diameter of this circular hole, therefore, was
to the diameter of the stream very nearly as 25 to 21. Therefore the water in
passing through the hole converges from all directions, and after flowing out
of the vessel the stream is made narrower by converging and is accelerated
by narrowing until it has reached a distance of ½ inch from the hole and at
that distance becomes narrower and swifter than it is in the hole itself in the
ratio of 25 × 25 to 21 × 21 or very nearly 17 to 12, that is, roughly as the
square root of the ratio of 2 to 1. And experiments prove that the quantity
of water that flows out in a given time through a circular hole in the bottom
of a vessel is the quantity that ought to flow out in the same time, with the
velocity mentioned above, not through that hole but through a circular hole
whose diameter is to the diameter of that hole as 21 to 25. And thus the
flowing water has the downward velocity in the hole itself that a heavy body
can acquire very nearly in falling and describing by its fall a space equal to
half the height of the water standing in the vessel. But after the water has
gone out of the vessel, it is accelerated by converging until it has reached
a distance from the hole almost equal to the diameter of the hole and has
acquired a velocity that is greater approximately as the square root of the
ratio of 2 to 1, which is, as a matter of fact, very nearly the velocity that a
heavy body can acquire in falling and describing by its fall a space equal to
the whole height of the water standing in the vessel.
In what follows, therefore, let the diameter of the stream be designated by
that smaller hole which we have called EF. And suppose that another higher
 plane VW is drawn parallel to the plane of
the hole EF at a distance about equal to the
diameter of the hole and pierced by a larger
hole ST, and through this let a stream fall that
exactly fills the lower hole EF and thus has a
diameter which is to the diameter of this lower
hole as about 25 to 21. For thus the stream will
pass perpendicularly through the lower hole,
and the quantity of the water flowing out, depending on the size of this
hole, will be very nearly that which the solution of the problem demands.
Now, the space which is enclosed by the two planes and the falling stream
can be considered to be the bottom of the vessel. But so that the solution of
the problem may be simpler and more mathematical, it is preferable to use
only the lower plane for the bottom of the vessel and to imagine that the
water which flowed down through the ice as if through a funnel and came
out of the vessel through the hole EF in the lower plane keeps its motion
continually and that the ice keeps its state of rest. In what follows, therefore,
let ST be the diameter of a circular hole described with center Z, through
which a cataract flows out of the vessel when all the water in the vessel is
fluid. And let EF be the diameter of the hole which the cataract fills exactly
when falling through it, whether the water comes out of the vessel through
the upper hole ST or falls through the middle of the ice in the vessel as
if through a funnel. And let the diameter of the upper hole ST be to the
diameter of the lower hole EF as about 25 to 21, and let the perpendicular
distance between the planes of the holes be equal to the diameter of the
smaller hole EF. Then the downward velocity of the water coming out of
the vessel through the hole ST will in the hole itself be that which a body
can acquire in falling from half of the height IZ; and the velocity of both
falling cataracts will, in the hole EF, be that which a body will acquire in
falling from the whole height IG.
plane VW is drawn parallel to the plane of
the hole EF at a distance about equal to the
diameter of the hole and pierced by a larger
hole ST, and through this let a stream fall that
exactly fills the lower hole EF and thus has a
diameter which is to the diameter of this lower
hole as about 25 to 21. For thus the stream will
pass perpendicularly through the lower hole,
and the quantity of the water flowing out, depending on the size of this
hole, will be very nearly that which the solution of the problem demands.
Now, the space which is enclosed by the two planes and the falling stream
can be considered to be the bottom of the vessel. But so that the solution of
the problem may be simpler and more mathematical, it is preferable to use
only the lower plane for the bottom of the vessel and to imagine that the
water which flowed down through the ice as if through a funnel and came
out of the vessel through the hole EF in the lower plane keeps its motion
continually and that the ice keeps its state of rest. In what follows, therefore,
let ST be the diameter of a circular hole described with center Z, through
which a cataract flows out of the vessel when all the water in the vessel is
fluid. And let EF be the diameter of the hole which the cataract fills exactly
when falling through it, whether the water comes out of the vessel through
the upper hole ST or falls through the middle of the ice in the vessel as
if through a funnel. And let the diameter of the upper hole ST be to the
diameter of the lower hole EF as about 25 to 21, and let the perpendicular
distance between the planes of the holes be equal to the diameter of the
smaller hole EF. Then the downward velocity of the water coming out of
the vessel through the hole ST will in the hole itself be that which a body
can acquire in falling from half of the height IZ; and the velocity of both
falling cataracts will, in the hole EF, be that which a body will acquire in
falling from the whole height IG.
CASE 2. If the hole EF is not in the middle of the bottom of the vessel,
but the bottom is perforated elsewhere, the water will flow out with the same
velocity as before, provided that the size of the hole is the same. For a heavy
body does descend to the same depth in a greater time along an oblique
line than along a perpendicular line, but in descending it acquires the same
velocity in either case, as Galileo proved.
CASE 3. The velocity of the water flowing out through a hole in the
side of the vessel is the same. For if the hole is small, so that the distance
between the surfaces AB and KL vanishes, so far as the senses can tell, and
the stream of water gushing out horizontally forms a parabolic figure, it will
be found from the latus rectum of this parabola that the velocity of the water
flowing out is that which a body could have acquired by falling from the
height HG or IG of the water standing in the vessel. Indeed, by making an
experiment I found that when the height of the standing water above the
hole was 20 inches and the height of the hole above a plane parallel to the
horizon was also 20 inches, the stream of water gushing forth would fall
upon the plane at a distance of about 37 inches, taken from a perpendicular
that was dropped to the plane from the hole. For in the absence of resistance
the stream would have had to fall upon the plane at a distance of 40 inches,
the latus rectum of the parabolic stream being 80 inches.
CASE 4. Further, if the water flowing out has an upward motion, it
comes out with the same velocity. For a small stream of water gushing out
ascends with a perpendicular motion to the height GH or GI of the water
standing in the vessel, except insofar as its ascent is somewhat impeded by
the resistance of the air; and accordingly it flows out with the velocity that
it could have acquired in falling from that height. Any one particle of the
standing water (by book 2, prop. 19) is pressed equally from all sides and,
yielding to the pressure, goes with equal force in every direction, whether it
descends through a hole in the bottom of the vessel or flows out horizontally
through a hole in its side or comes out into a channel and ascends from
there through a small hole in the upper part of the channel. And that the
velocity with which the water flows out is that which we have designated
in this proposition is not only found by reason but is also manifest from the
well-known experiments already described.
CASE 5. The velocity of the water flowing out is the same whether the
hole is circular or square or triangular or of any other shape equal in area to
the circular one. For the velocity of the water flowing out does not depend
on the shape of the hole but on the height of the water in relation to the
plane KL.
CASE 6. If the lower part of the vessel ABDC is immersed in standing
water, and the height of the standing water above the bottom of the vessel is
 GR, the velocity with which the water in the
vessel will flow out through the hole EF into
the standing water will be that which the water
can acquire in falling and describing by its fall
the space IR. For the weight of all the water in
the vessel that is lower than the surface of the
standing water will be sustained in equilibrium
by the weight of the standing water and thus
will not at all accelerate the motion of the descending water in the vessel.
This case can also be shown by experiments, by measuring the times in which
the water flows out.
GR, the velocity with which the water in the
vessel will flow out through the hole EF into
the standing water will be that which the water
can acquire in falling and describing by its fall
the space IR. For the weight of all the water in
the vessel that is lower than the surface of the
standing water will be sustained in equilibrium
by the weight of the standing water and thus
will not at all accelerate the motion of the descending water in the vessel.
This case can also be shown by experiments, by measuring the times in which
the water flows out.
COROLLARY 1. Hence, if the height CA of the water is produced to K,
so that AK is to CK in the squared ratio of the area of a hole made in any
part of the bottom to the area of the circle AB, the velocity of the water
flowing out will be equal to the velocity that the water can acquire in falling
and describing by its fall the space KC.
COROLLARY 2. And the force by which the whole motion of the water
gushing out can be generated is equal to the weight of a cylindrical column
of water whose base is the hole EF and whose height is 2GI or 2CK. For
the gushing water, in the time in which it equals this column, can acquire
in falling (by its weight) from the height GI the very velocity with which it
gushes out.
COROLLARY 3. The weight of all the water in the vessel ABDC is to
the part of the weight that is used in making the water flow down as the
sum of the circles AB and EF to twice the circle EF. For let IO be a mean
proportional between IH and IG; then the water coming out through the
hole EF, in the time in which a drop could describe a space equal to the
height IG in falling from I, will be equal to a cylinder whose base is the circle
EF and whose height is 2IG, that is, to a cylinder whose base is the circle AB
and whose height is 2IO, for the circle EF is to the circle AB as the square
root of the ratio of the height IH to the height IG, that is, in the simple ratio
of the mean proportional IO to the height IG, and in the time in which a
drop can describe a space equal to the height IH in falling from I, the water
coming out will be equal to a cylinder whose base is the circle AB and whose
height is 2IH, and in the time in which a drop describes a space equal to
the difference HG between the heights in falling from I through H to G,
the water coming out—that is, all the water in the solid ABNFEM—will
be equal to the difference between the cylinders, that is, equal to a cylinder
whose base is AB and whose height is 2HO. And therefore all the water in
the vessel ABDC is to all the water falling in the solid ABNFEM as HG to
2HO, that is, as HO + OG to 2HO, or IH + IO to 2IH. But the weight of
all the water in the solid ABNFEM is used in making the water flow down,
and accordingly the weight of all the water in the vessel is to the part of the
weight that is used in making the water flow down as IH + IO to 2IH and
thus as the sum of the circles EF and AB to twice the circle EF.
COROLLARY 4. And hence the weight of all the water in the vessel ABDC
is to the part of the weight sustained by the bottom of the vessel as the sum
of the circles AB and EF is to the difference between these circles.
COROLLARY 5. And the part of the weight sustained by the bottom of
the vessel is to the part of the weight used in making the water flow down
as the difference between the circles AB and EF is to twice the smaller circle
EF, or as the area of the bottom to twice the hole.
COROLLARY 6. And the part of the weight which alone presses upon
the bottom is to the weight of all the water resting perpendicularly on the
bottom as the circle AB is to the sum of the circles AB and EF, or as the
circle AB is to the amount by which twice the circle AB exceeds the bottom.
For the part of the weight which alone presses upon the bottom is to the
weight of all the water in the vessel as the difference between the circles AB
and EF is to the sum of these circles, by corol. 4; and the weight of all the
water in the vessel is to the weight of all the water resting perpendicularly
on the bottom as the circle AB is to the difference between the circles AB
and EF. Therefore, from the equality of the ratios in inordinate proportion
[or ex aequo perturbate], the part of the weight which alone presses upon
the bottom is to the weight of all the water resting perpendicularly on the
bottom as the circle AB is to the sum of the circles AB and EF, or to the
amount by which twice the circle AB exceeds the bottom.
COROLLARY 7. If in the middle of the hole EF there is placed a little
circle PQ described with center G and parallel to the horizon, the weight
 of the water which that little circle sustains
is greater than the weight of ⅓ of a
cylinder of water whose base is that little circle
and whose height is GH. For let ABNFEM
be a cataract or column of falling water, with
axis GH as above, and suppose that there has
been a freezing of all the water in the vessel
(around the cataract as well as above the little
circle) whose fluidity is not required for the
very ready and very swift descent of the water. And let PHQ be the frozen
column of water above the little circle, having vertex H and height GH.
And imagine that this cataract falls with its whole weight and does not rest
or press on PHQ but slides past freely and without friction, except perhaps
at the very vertex of the ice, where at the very beginning of falling the
cataract begins to be concave. And just as the frozen water (AMEC and
BNFD) which is around the cataract is convex on the inner surface (AME
and BNF) toward the falling cataract, so also this column PHQ will be
convex toward the cataract, and therefore will be greater than a cone whose
base is the little circle PQ and whose height is GH, that is, greater than ⅓
of a cylinder described with the same base and height. And the little circle
sustains the weight of this column, that is, a weight that is greater than the
weight of the cone or of ⅓ of the cylinder.
of the water which that little circle sustains
is greater than the weight of ⅓ of a
cylinder of water whose base is that little circle
and whose height is GH. For let ABNFEM
be a cataract or column of falling water, with
axis GH as above, and suppose that there has
been a freezing of all the water in the vessel
(around the cataract as well as above the little
circle) whose fluidity is not required for the
very ready and very swift descent of the water. And let PHQ be the frozen
column of water above the little circle, having vertex H and height GH.
And imagine that this cataract falls with its whole weight and does not rest
or press on PHQ but slides past freely and without friction, except perhaps
at the very vertex of the ice, where at the very beginning of falling the
cataract begins to be concave. And just as the frozen water (AMEC and
BNFD) which is around the cataract is convex on the inner surface (AME
and BNF) toward the falling cataract, so also this column PHQ will be
convex toward the cataract, and therefore will be greater than a cone whose
base is the little circle PQ and whose height is GH, that is, greater than ⅓
of a cylinder described with the same base and height. And the little circle
sustains the weight of this column, that is, a weight that is greater than the
weight of the cone or of ⅓ of the cylinder.
COROLLARY 8. The weight of the water sustained by the little circle PQ,
when it is extremely small, appears to be less than the weight of ⅔ of a
cylinder of water whose base is that little circle and whose height is HG.
Keeping the same suppositions, imagine that half a spheroid is described,
whose base is the little circle and whose semiaxis or height is HG. Then
this figure will be equal to ⅔ of that cylinder and will comprehend the
column of frozen water PHQ whose weight that little circle sustains. In
order that the motion of the water may be straight down, the outer surface
of this column must meet the base PQ in a somewhat acute angle, because
the water in falling is continually accelerated and the acceleration makes the
column become narrower; and since that angle is less than a right angle, the
lower parts of this column will lie within the half-spheroid. But higher up,
the column will be acute or pointed, for otherwise the horizontal motion
of the water at the vertex of the spheroid would be infinitely swifter than
its motion toward the horizon. And the smaller the little circle PQ, the
more acute the vertex of the column; and if the little circle is diminished
indefinitely, the angle PHQ will be diminished indefinitely, and therefore
the column will lie within the half-spheroid. That column is therefore less
than the half-spheroid, or less than ⅔ of a cylinder whose base is that little
circle and whose height is GH. Moreover, the little circle sustains the water’s
force equal to the weight of this column, since the weight of the surrounding
water is used in making it flow down.
COROLLARY 9. The weight of the water sustained by the little circle PQ,
when it is extremely small, is very nearly equal to the weight of a cylinder
of water whose base is that little circle and whose height is ½GH. For this
weight is an arithmetical mean between the weights of the cone and the
said half-spheroid. If, however, the little circle is not extremely small but is
increased until it equals the hole EF, it will sustain the weight of all the
water resting perpendicularly on it, that is, the weight of a cylinder of water
whose base is that little circle and whose height is GH.
COROLLARY 10. And (as far as I can tell) the weight that the little circle
sustains always has the proportion to the weight of a cylinder of water whose
base is that little circle and whose height is ½GH that EF2 has to EF2 −
½PQ2, or that the circle EF has to the excess of this circle over half of the
little circle PQ, very nearly.
Lemma 4
The resistance of a cylinder moving uniformly forward in the direction of its length
is not changed by an increase or decrease in length and thus is the same as the
resistance of a circle described with the same diameter and moving forward with
the same velocity along a straight line perpendicular to its plane.
For the sides of a cylinder offer no opposition to its motion, and a cylinder
is turned into a circle if its length is decreased indefinitely.
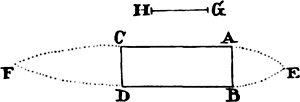
Proposition 37, Theorem 29
If a cylinder moves uniformly forward in a compressed, infinite, and nonelastic
fluid in the direction of its own length, its resistance arising from the magnitude
of its transverse section is to the force by which its whole motion can be either
destroyed or generated, while it is describing four times its length, very nearly as
the density of the medium is to the density of the cylinder.
For if the bottom CD of the vessel ABDC touches the surface of stagnant
water, and if water flows out of this vessel into the stagnant water through
 the cylindrical channel EFTS perpendicular to
the horizon, and if the little circle PQ is placed
parallel to the horizon anywhere in the middle
of the channel, and if CA is produced to K so
that CK is to AK in the squared ratio of the
circle AB to the amount by which the opening
of the channel EF exceeds the little circle PQ,
then it is obvious (by prop. 36, case 5, case 6,
and corol. 1) that the velocity of the water
passing through the annular space between the little
circle and the sides of the vessel will be that which the water can acquire in
falling and describing by its fall a space equal to the height KC or IG.
the cylindrical channel EFTS perpendicular to
the horizon, and if the little circle PQ is placed
parallel to the horizon anywhere in the middle
of the channel, and if CA is produced to K so
that CK is to AK in the squared ratio of the
circle AB to the amount by which the opening
of the channel EF exceeds the little circle PQ,
then it is obvious (by prop. 36, case 5, case 6,
and corol. 1) that the velocity of the water
passing through the annular space between the little
circle and the sides of the vessel will be that which the water can acquire in
falling and describing by its fall a space equal to the height KC or IG.
And (by prop. 36, corol. 10) if the width of the vessel is infinite, so that
the line-element HI vanishes and the heights IG and HG are equal, then the
force of the water flowing down into the little circle will be to the weight
of a cylinder whose base is that little circle, and whose height is ½IG, very
nearly as EF2 to EF2 − ½PQ2. For the force of the water flowing down
through the whole channel with uniform motion will be the same upon the
little circle PQ in whatever part of the channel it is placed.
Now let the openings EF and ST of the channel be closed, and let the
little circle ascend in the fluid compressed on all sides, and by its ascent let it
make the upper water descend through the annular space between the little
circle and the sides of the channel; then the velocity of the ascending little
circle will be to the velocity of the descending water as the difference between
the circles EF and PQ is to the circle PQ, and the velocity of the ascending
little circle will be to the sum of the velocities (that is, to the relative velocity
of the descending water, with which it flows past the ascending little circle)
as the difference between the circles EF and PQ is to the circle EF, or as
EF2 − PQ2 to EF2. Let that relative velocity be equal to the velocity with
which (as shown above) the water passes through the same annular space
while the little circle remains unmoved, that is, to the velocity that the water
can acquire in falling and describing by its fall a space equal to the height
IG; then the force of the water upon the ascending little circle will be the
same as before (by corol. 5 of the laws), that is, the resistance of the ascending
little circle will be to the weight of a cylinder of water whose base is that
little circle, and whose height is ½IG, very nearly as EF2 to EF2 − ½PQ2.
And the velocity of the little circle will be to the velocity that the water
acquires in falling, and describing by its fall a space equal to the height IG,
as EF2 − PQ2 to EF2.
Let the breadth of the channel be increased indefinitely; then those ratios
between EF2 − PQ2 and EF2 and between EF2 and EF2 − ½PQ2 will
ultimately approach ratios of equality. And therefore the velocity of the little
circle will now be that which the water can acquire in falling and describing
by its fall a space equal to the height IG, and its resistance will come out
equal to the weight of a cylinder whose base is that little circle and whose
height is half of the height IG from which the cylinder must fall in order
to acquire the velocity of the ascending little circle, and with this velocity
the cylinder will, in the time of falling, describe four times its own length.
And the resistance of the cylinder, moving forward with this velocity in the
direction of its length, is the same as the resistance of the little circle (by
lem. 4) and thus is very nearly equal to the force by which its motion can be
generated while it is describing four times its length.
If the length of the cylinder is increased or decreased, its motion, and
also the time in which it describes four times its length, will be increased or
decreased in the same ratio; and thus that force by which the increased or
decreased motion, in a time equally increased or decreased, could be generated
or destroyed will not be changed and accordingly is under these circumstances
still equal to the resistance of the cylinder; for this also remains unchanged,
by lem. 4.
If the density of the cylinder is increased or decreased, its motion, and also
the force by which the motion can be generated or destroyed in the same time,
will be increased or decreased in the same ratio. The resistance, therefore, of
any cylinder to the force by which its whole motion could be either generated
or destroyed, while it is describing four times its length, will be very nearly
as the density of the medium to the density of the cylinder. Q.E.D.
A fluid must be compressed in order to be continuous, and it must be
continuous and nonelastic in order that every pressure arising from its
compression may be propagated instantaneously and, by acting equally upon all
parts of a moving body, not change the resistance. The pressure arising from
the body’s motion is of course used in generating the motion of the parts of
the fluid and creates resistance. But the pressure arising from the
compression of the fluid, however strong it may be, if it is propagated instantaneously,
generates no motion in the parts of a continuous fluid, introduces no change
of motion at all, and thus neither increases nor decreases the resistance.
Certainly the action of a fluid that arises from its compression cannot be stronger
upon the back of a moving body than upon the front and thus cannot
decrease the resistance described in this proposition; and the action will not be
stronger upon the front than upon the back provided that its propagation is
infinitely swifter than the motion of the body pressed. And the action will
be infinitely swifter and will be propagated instantaneously provided that the
fluid is continuous and nonelastic.
COROLLARY 1. The resistances to cylinders that move uniformly forward
in the direction of their lengths in infinite and continuous mediums are in a
ratio compounded of the squared ratio of the velocities and the squared ratio
of the diameters and the ratio of the density of the mediums.
COROLLARY 2. If the breadth of the channel is not increased
indefinitely, but the cylinder moves forward in the direction of its own length
 in an enclosed medium at rest, and meanwhile
its axis coincides with the axis of the channel,
then the resistance to the cylinder will be to
the force by which its whole motion could be
either generated or destroyed, in the time in
which it describes four times its length, in a
ratio compounded of the simple ratio of EF2 to
EF2 − ½PQ2 and the squared ratio of EF2 to
EF2 − PQ2 and the ratio of the density of the
medium to the density of the cylinder.
in an enclosed medium at rest, and meanwhile
its axis coincides with the axis of the channel,
then the resistance to the cylinder will be to
the force by which its whole motion could be
either generated or destroyed, in the time in
which it describes four times its length, in a
ratio compounded of the simple ratio of EF2 to
EF2 − ½PQ2 and the squared ratio of EF2 to
EF2 − PQ2 and the ratio of the density of the
medium to the density of the cylinder.
COROLLARY 3. With the same suppositions, let the length L be to four
times the length of the cylinder in a ratio compounded of the simple ratio
of EF2 − ½PQ2 to EF2 and the squared ratio of EF2 − PQ2 to EF2; then
the resistance of the cylinder will be to the force by which its whole motion
could be either destroyed or generated, while it is describing the length L,
as the density of the medium to the density of the cylinder.
Scholium
In this proposition we have investigated the resistance arising solely from the
magnitude of the transverse section of a cylinder, without considering the
part of the resistance that can arise from the obliquity of the motions. In
prop. 36, case 1, the flow of the water through the hole EF was impeded
by the obliquity of the motions with which the parts of the water in the
vessel converged from all sides into the hole. Similarly, in this proposition,
the obliquity of the motions with which the parts of the water pressed by
the front end of the cylinder yield to the pressure and diverge on all sides
has these effects: it retards the passage of those motions through the places
around that front end toward the back of the cylinder, it makes the fluid
move to a greater distance, and it increases the resistance in nearly the ratio
with which it decreases the flow of the water from the vessel, that is, in the
squared ratio of 25 to 21, roughly.
In case 1 of prop. 36 we made the parts of the water pass through the
hole EF perpendicularly and in the greatest abundance by supposing that
all the water in the vessel that had been frozen around the cataract, and
whose motion was oblique and useless, remained without motion. Similarly,
in this proposition, in order that the obliquity of the motions may be
 annulled, and the parts of the water, by
yielding with the most direct and rapid
motion, may provide the easiest passage
to the cylinder, and in order that only
the resistance may remain that arises
from the magnitude of the transverse section and that cannot be decreased
except by decreasing the diameter of the cylinder, it must be understood
that the parts of the fluid whose motions are oblique and useless and
create resistance are at rest with respect to one another at both ends of the
cylinder and cohere and are joined to the cylinder. Let ABDC be a
rectangle, and let AE and BE be two parabolic arcs described with axis AB
and with a latus rectum that is to the space HG, which is to be described
by the falling cylinder while it is acquiring its velocity, as HG to ½AB.
Additionally, let CF and DF be two other parabolic arcs, described with
axis CD and a latus rectum that is four times the former latus rectum; and
by the revolution of the figure about its axis EF, let a solid be generated
whose middle ABDC is the cylinder with which we are dealing, and whose
extremities ABE and CDF contain the parts of the fluid which are at rest
with respect to one another and solidified into two rigid bodies that adhere
to the cylinder at the ends as head and tail. Then the resistance to the solid
EACFDB moving forward in the direction of its axis FE from F toward E
will be very nearly that which we have described in this proposition. That
is, the density of the fluid is to the density of the cylinder very nearly in
the ratio of this resistance to the force by which the whole motion of the
cylinder could be either destroyed or generated, while the length 4AC is
being described with that motion continued uniformly. And with this force the
resistance cannot be less than in the ratio of 2 to 3, by prop. 36, corol. 7.
annulled, and the parts of the water, by
yielding with the most direct and rapid
motion, may provide the easiest passage
to the cylinder, and in order that only
the resistance may remain that arises
from the magnitude of the transverse section and that cannot be decreased
except by decreasing the diameter of the cylinder, it must be understood
that the parts of the fluid whose motions are oblique and useless and
create resistance are at rest with respect to one another at both ends of the
cylinder and cohere and are joined to the cylinder. Let ABDC be a
rectangle, and let AE and BE be two parabolic arcs described with axis AB
and with a latus rectum that is to the space HG, which is to be described
by the falling cylinder while it is acquiring its velocity, as HG to ½AB.
Additionally, let CF and DF be two other parabolic arcs, described with
axis CD and a latus rectum that is four times the former latus rectum; and
by the revolution of the figure about its axis EF, let a solid be generated
whose middle ABDC is the cylinder with which we are dealing, and whose
extremities ABE and CDF contain the parts of the fluid which are at rest
with respect to one another and solidified into two rigid bodies that adhere
to the cylinder at the ends as head and tail. Then the resistance to the solid
EACFDB moving forward in the direction of its axis FE from F toward E
will be very nearly that which we have described in this proposition. That
is, the density of the fluid is to the density of the cylinder very nearly in
the ratio of this resistance to the force by which the whole motion of the
cylinder could be either destroyed or generated, while the length 4AC is
being described with that motion continued uniformly. And with this force the
resistance cannot be less than in the ratio of 2 to 3, by prop. 36, corol. 7.
Lemma 5
If a cylinder, a sphere, and a spheroid, whose widths are equal, are placed
successively in the middle of a cylindrical channel in such a way that their axes coincide
with the axis of the channel, these bodies will equally impede the flow of water
through the channel.
For the spaces through which the water passes between the channel and
the cylinder, sphere, and spheroid are equal; and water passes equally through
equal spaces.
This is so on the hypothesis that all the water is frozen which is above
the cylinder, sphere, or spheroid, and whose fluidity is not required for the
very swift passage of the water, as I have explained in prop. 36, corol. 7.
Lemma 6
With the same suppositions, these bodies are equally urged by the water flowing
through the channel.
This is evident by lem. 5 and the third law of motion. Of course, the
water and the bodies act equally upon one another.
Lemma 7
If the water is at rest in the channel, and these bodies go through the channel with
equal velocity in opposite directions, the resistances will be equal to one another.
This is clear from lem. 6; for the relative motions remain the same with
respect to one another.
Scholium
It is the same for all convex round bodies whose axes coincide with the axis
of the channel. Some difference can arise from a greater or lesser friction;
but in these lemmas we are supposing that the bodies are very smooth, that
the tenacity and friction of the medium are nil, and that the parts of the
fluid which by their oblique and superfluous motions can perturb, impede,
and retard the flow of the water through the channel are at rest with respect
to one another as if icebound and adhere to the front and back of the bodies,
as I have explained in the scholium to prop. 37. For what follows deals with
the least possible resistance of round bodies described with the greatest given
transverse sections.
Bodies moving straight ahead in fluids make the fluid ascend in front of
them and subside in back of them, especially if they are blunt in shape; and
hence they encounter a slightly greater resistance than if they had pointed
heads and tails. And bodies moving in elastic fluids, if they are blunt in
front and in back, condense the fluid a little more at the front and make
it a little less dense at the back; and hence they encounter a slightly greater
resistance than if they had pointed heads and tails. But in these lemmas and
propositions we are not dealing with elastic fluids but with nonelastic fluids,
not with bodies floating on the surface of the fluid but with bodies deeply
immersed. And once the resistance of bodies in nonelastic fluids is known,
this resistance will have to be increased somewhat for elastic fluids such as
air as well as for the surfaces of stagnant fluids such as seas and swamps.
Proposition 38, Theorem 30
The resistance to a sphere moving uniformly forward in an infinite and nonelastic
compressed fluid is to the force by which its whole motion could either be destroyed
or generated, in the time in which it describes 8/3 of its diameter, very nearly as
the density of the fluid to the density of the sphere.
For a sphere is to the circumscribed cylinder as 2 to 3, and therefore the
force that could take away all the motion of a cylinder, while the cylinder
is describing a length of four diameters, will take away all the motion of
the sphere while the sphere describes ⅔ of this length, that is, 8/3 of its own
diameter. And the resistance of the cylinder is to this force very nearly as
the density of the fluid to the density of the cylinder or sphere, by prop. 37,
and the resistance of the sphere is equal to the resistance of the cylinder, by
lems. 5, 6, and 7. Q.E.D.
COROLLARY 1. The resistances of spheres in infinite compressed
mediums are in a ratio compounded of the squared ratio of the velocity and the
squared ratio of the diameter and the ratio of the density of the mediums.
COROLLARY 2. The greatest velocity with which a sphere, by the force
of its own relative weight, can descend in a resisting fluid is that which the
same sphere with the same weight can acquire in falling without resistance
and describing by its fall a space that is to 4/3 of its diameter as the density
of the sphere to the density of the fluid. For the sphere in the time of its fall,
with the velocity acquired in falling, will describe a space that will be to 8/3
of its diameter as the density of the sphere to the density of the fluid; and
the force of its weight generating this motion will be to the force that could
generate the same motion, in the time in which the sphere describes 8/3 of its
diameter with the same velocity, as the density of the fluid to the density of
the sphere; and thus, by this proposition, the force of its weight will be equal
to the force of resistance and therefore cannot accelerate the sphere.
COROLLARY 3. Given both the density of the sphere and its velocity at
the beginning of the motion, and also the density of the compressed fluid at
rest in which the sphere moves, then by prop. 35, corol. 7, the velocity of the
sphere, its resistance, and the space described by it are given for any time.
COROLLARY 4. A sphere moving in a compressed fluid at rest, having
the same density as itself, will, by the same corol. 7, lose half of its motion
before it has described the length of two of its diameters.
Proposition 39, Theorem 31
The resistance to a sphere moving uniformly forward through a fluid enclosed and
compressed in a cylindrical channel is to the force by which its whole motion could
be either generated or destroyed, while it describes 8/3 of its diameter, in a ratio
compounded of three ratios, very nearly: the ratio of the opening of the channel
to the excess of this opening over half of a great circle of the sphere, the squared
ratio of the opening of the channel to the excess of this opening over a great circle
of the sphere, and the ratio of the density of the fluid to the density of the sphere.
This is evident by prop. 37, corol. 2, and the proof proceeds as in prop. 38.
Scholium
In the last two propositions (as in lem. 5) I assume that all the water which
is in front of the sphere, and whose fluidity increases the resistance to the
sphere, is frozen. If all that water liquefies, the resistance will be somewhat
increased. But in these propositions the increase will be small and can be
ignored because the convex surface of the sphere has almost the same effect
as ice.
Proposition 40, Problem 9
To find from phenomena the resistance of a sphere moving forward in a compressed,
very fluid medium.
Let A be the weight of the sphere in a vacuum, B its weight in a resisting
medium, D the diameter of the sphere, F a space that is to 4/3D as the density
of the sphere to the density of the medium (that is, as A to A − B), G the time
in which the sphere in falling by its weight B without resistance describes the
space F, and H the velocity that the sphere acquires by this fall. Then H will
be the greatest velocity with which the sphere can descend by its weight B in
the resisting medium, by prop. 38, corol. 2, and the resistance that the sphere
encounters while descending with this velocity will be equal to its weight B;
and the resistance that it encounters with any other velocity will be to the
weight B as the square of the ratio of this velocity to the greatest velocity H,
by prop. 38, corol. 1.
This is the resistance that arises from the inertia of matter of the fluid.
And that which arises from the elasticity, tenacity, and friction of its parts
can be investigated as follows.
Drop the sphere so that it descends in the fluid by its own weight B;
and let P be the time of falling, in seconds if the time G is in seconds. Find
the absolute number N that corresponds to the logarithm 0.4342944819 ,
and let L be the logarithm of the number
,
and let L be the logarithm of the number 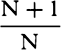 , then the velocity
acquired in falling will be
, then the velocity
acquired in falling will be 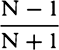 H, and the space described will be
H, and the space described will be
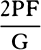 − 1.3862943611F + 4.605170186LF.
− 1.3862943611F + 4.605170186LF.
If the fluid is sufficiently deep, the term 4.605170186LF can be ignored,
and 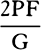 − 1.3862943611F will be the space described, very nearly. These
things are evident by book 2, prop. 9 and its corollaries, on the hypothesis
that the sphere encounters no other resistance than that which arises from
the inertia of matter. But if it encounters another resistance in addition, the
descent will be slower, and the quantity of this resistance can be found from
the retardation.
− 1.3862943611F will be the space described, very nearly. These
things are evident by book 2, prop. 9 and its corollaries, on the hypothesis
that the sphere encounters no other resistance than that which arises from
the inertia of matter. But if it encounters another resistance in addition, the
descent will be slower, and the quantity of this resistance can be found from
the retardation.
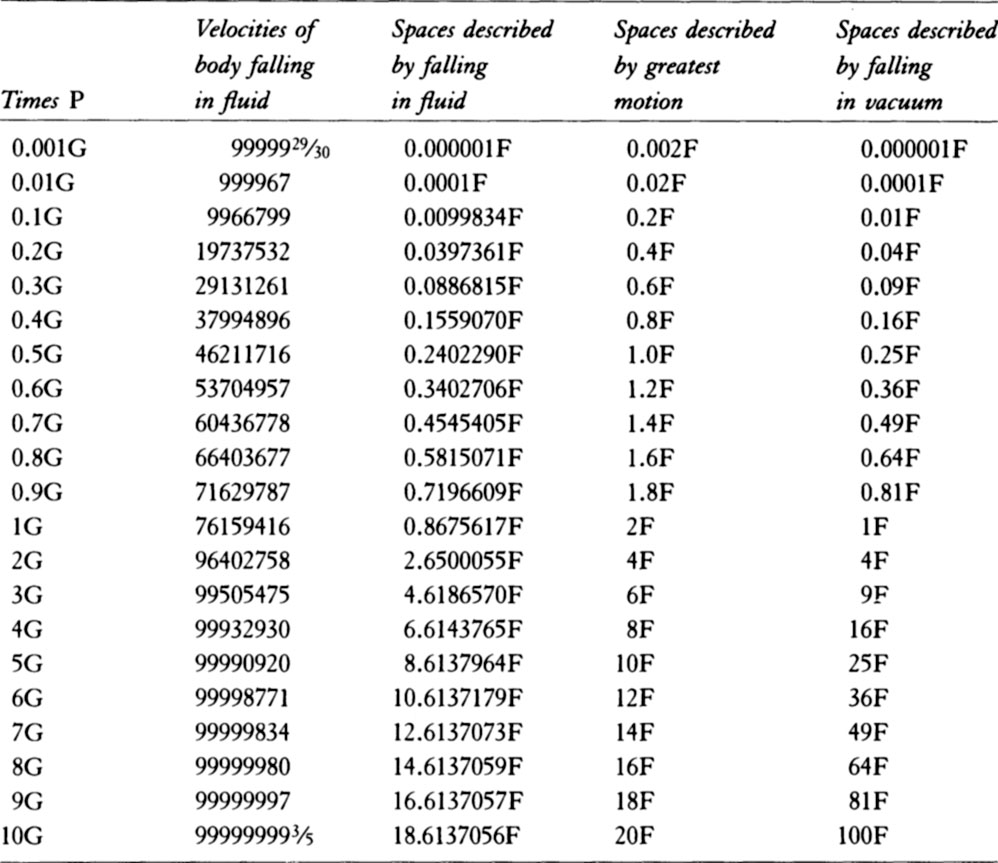
So that the velocity and descent of a body falling in a fluid may be
found more easily, I have put together the accompanying table, in which the
first column denotes the times of descent, the second shows the velocities
acquired in falling (the greatest velocity being 100,000,000), the third shows
the spaces described in falling in those times (2F being the space that the body
describes in the time G with the greatest velocity), and the fourth shows the
spaces described in the same times with the greatest velocity. The numbers
in the fourth column are  , and by subtracting the number 1.3862944 −
4.6051702L, the numbers in the third column are found, and these numbers
must be multiplied by the space F in order to get the spaces described in
falling. There has been added to these a fifth column, which contains the
spaces described in the same times by a body falling in a vacuum by the
force of its relative weight B.
, and by subtracting the number 1.3862944 −
4.6051702L, the numbers in the third column are found, and these numbers
must be multiplied by the space F in order to get the spaces described in
falling. There has been added to these a fifth column, which contains the
spaces described in the same times by a body falling in a vacuum by the
force of its relative weight B.
Scholium
In order to investigate the resistances of fluids by experiments, I got a square
wooden vessel, with an internal length and width of 9 inches (of a London
foot), and a depth of 9½ feet, and I filled it with rainwater; and making
balls of wax with lead inside, I noted the times of descent of the balls, the
space of the descent being 112 inches. A solid cubic London foot contains
76 Roman pounds [troy] of rainwater, and a solid inch of this foot contains
19/36 ounce of this pound or 253⅓ grains; and a sphere of water described
with a diameter of 1 inch contains 132.645 grains in air, or 132.8 grains in a
vacuum; and any other ball is as the excess of its weight in a vacuum over
its weight in water.
EXPERIMENT 1. A ball which weighed 156¼ grains in air and 77 grains
in water described the whole space of 112 inches [when dropped in water] in
a time of 4 seconds. And when the experiment was repeated, the ball again
fell in the same time of 4 seconds.
The weight of the ball in a vacuum is 15613/38 grains, and the excess of
this weight over the weight of the ball in water is 7913/38 grains. And hence
the diameter of the ball comes out 0.84224 inch. That excess is to the weight
of the ball in a vacuum as the density of water to the density of the ball,
and as 8/3 of the diameter of the ball (that is, 2.24597 inches) to the space 2F,
which accordingly will be 4.4256 inches. In a time of 1 second the ball will
fall in a vacuum by its whole weight of 15613/38 grains through 193⅓ inches;
and by a weight of 77 grains falling in water without resistance, it will in the
same time describe 95.219 inches; and in the time G, which is to 1 second as
the square root of the ratio of the space F or 2.2128 inches to 95.219 inches, it
will describe 2.2128 inches and will attain the greatest velocity H with which
it can descend in water. Therefore the time G is 0.15244 seconds. And in
this time G, with that greatest velocity H, the ball will describe a space 2F
of 4.4256 inches; and thus in the time of 4 seconds it will describe a space
of 116.1245 inches. Subtract the space 1.3862944F or 3.0676 inches and there
will remain a space of 113.0569 inches which the ball will describe in falling
in water in a very wide vessel in the time of 4 seconds. This space, because
of the narrowness of the wooden vessel, must be decreased in a ratio which
is compounded of the square root of the ratio of the opening of the vessel
to the excess of this opening over a great semicircle of the ball, and of the
simple ratio of that same opening to its excess over a great circle of the ball,
that is, in the ratio of 1 to 0.9914. When this has been done, the result will
be a space of 112.08 inches which the ball should, according to the theory,
have very nearly described in falling in water in this wooden vessel in the
time of 4 seconds. And it described 112 inches in the experiment.
EXPERIMENT 2. Three equal balls, each of which weighed 76⅓ grains
in air and 51/16 grains in water, were dropped successively in water, and in a
time of 15 seconds each one fell through 112 inches.
By computation the weight of a ball in a vacuum is 765/12 grains; the
excess of this weight over the weight in water is 711748 grains; the diameter
of the ball is 0.81296 inch; 8/3 of this diameter is 2.16789 inches; the space
2F is 2.3217 inches; the space that a ball describes in falling by a weight
of 51/16 grains in the time of 1 second without resistance is 12.808 inches;
and the time G is 0.301056 second. The ball, therefore, with the greatest
velocity with which it can descend in water by the force of the weight of
51/16 grains, will describe in a time of 0.301056 second a space of 2.3217
inches, and in the time of 15 seconds a space of 115.678 inches. Subtract the
space 1.3862944F or 1.609 inches, and there will remain a space of 114.069
inches which accordingly the ball ought to describe in falling in the same
time in a very wide vessel. Because of the narrowness of our vessel a space of
roughly 0.895 inch must be taken away. And thus there will remain a space
of 113.174 inches which the ball, according to the theory, should have very
nearly described in falling in this vessel in the time of 15 seconds. And it
described 112 inches in the experiment. The difference is imperceptible.
EXPERIMENT 3. Three equal balls, each of which weighed 121 grains in
air and 1 grain in water, were dropped successively in water, and in times of
46 seconds, 47 seconds, and 50 seconds, fell 112 inches.
According to the theory, these balls should have fallen in a time of
roughly 40 seconds. I am uncertain whether their falling more slowly is to
be attributed to the smaller proportion of the resistance that arises from the
force of inertia in slow motions to the resistance that arises from other causes,
or rather to some little bubbles adhering to the ball, or to the rarefaction of
the wax from the heat either of the weather or of the hand dropping the
ball, or even to imperceptible errors in weighing the balls in water. And thus
the weight of the ball in water ought to be more than 1 grain, so that the
experiment may be made certain and trustworthy.
EXPERIMENT 4. I began the experiments thus far described in order to
investigate the resistances of fluids before formulating the theory set forth in
the immediately preceding propositions. Afterward, in order to examine that
theory, I obtained a wooden vessel with an internal width of 8⅔ inches and
a depth of 15⅓ feet. Then I made four balls out of wax with lead inside,
each one weighing 139¼ grains in air and 7⅛ grains in water. And I let
them fall in water in order to measure the times of falling, using a pendulum
oscillating in half-seconds. When the balls were being weighed, and afterward
when they were falling, they were cold and had remained cold for some time,
because heat rarefies the wax and by the rarefaction diminishes the weight of
the ball in water, and the rarefied wax is not immediately brought back to its
original density by chilling. Before they fell, they were entirely immersed in
water, so that their descent might not be accelerated at the beginning by the
weight of some part projecting out of the water. And when totally immersed
and at rest, they were let fall as carefully as possible, so as not to receive
some impulse from the hand letting them fall. And they fell successively in
the times of 47½, 48½, 50, and 51 oscillations, describing a space of 15 feet
2 inches. But the weather was now a little colder than when the balls were
weighed, and so I repeated the experiment on another day, and the balls
fell in the times of 49, 49½, 50, and 53 oscillations, and on a third day in
the times of 49½, 50, 51, and 53 oscillations. The experiment was made
quite often, and the balls for the most part fell in the times of 49½ and 50
oscillations. When they fell more slowly, I suspect that they were retarded by
hitting against the sides of the vessel.
Now by computation according to the theory, the weight of a ball in a
vacuum is 139⅖ grains; the excess of this weight over the weight of the ball
in water is 13211/40 grains; the diameter of the ball is 0.99868 inch; 8/3 of the
diameter is 2.66315 inches; the space 2F is 2.8066 inches; the space that a
ball describes in falling with a weight of 7⅛ grains in the time of 1 second
without resistance is 9.88164 inches; and the time G is 0.376843 second. The
ball, therefore, with the greatest velocity with which it can descend in water
by a force of weight of 7⅛ grains, describes in the time of 0.376843 second
a space of 2.8066 inches; in the time of 1 second a space of 7.44766 inches;
and in the time of 25 seconds, or 50 oscillations, a space of 186.1915 inches.
Subtract the space 1.386294F, or 1.9454 inches, and there will remain the
space of 184.2461 inches which the ball will describe in the same time in a
very wide vessel. Because of the narrowness of our vessel, decrease this space
in a ratio that is compounded of the square root of the ratio of the opening
of the vessel to the excess of this opening over a great semicircle of the ball,
and the simple ratio of that same opening to its excess over a great circle
of the ball, and the result will be the space of 181.86 inches which the ball,
according to the theory, should very nearly have described in this vessel in
the time of 50 oscillations. And in the experiment it described a space of
182 inches in the time of 49½ or 50 oscillations.
EXPERIMENT 5. Four balls weighing 154⅜ grains in air and 21½ grains
in water were dropped often and fell in the times of 28½, 29, 29½, and 30
oscillations, and sometimes 31, 32, and 33, describing a space of 15 feet 2
inches.
By the theory they ought to have fallen in the time of very nearly 29
oscillations.
EXPERIMENT 6. Five balls weighing 212⅜ grains in air and 79½ in
water were dropped often and fell in the times of 15, 15½, 16, 17, and 18
oscillations, describing a space of 15 feet 2 inches.
By the theory they ought to have fallen in the time of very nearly 15
oscillations.
EXPERIMENT 7. Four balls weighing 293⅜ grains in air and 35⅞ grains
in water were dropped often and fell in the times of 29½, 30, 30½, 31, 32,
and 33 oscillations, describing a space of 15 feet 1½ inches.
By the theory they ought to have fallen in the time of very nearly 28
oscillations.
In investigating the reason why some of the balls which were of the
same weight and size fell more quickly and others more slowly, I hit upon
this: that when the balls were first dropped and were beginning to fall,
the side which happened to be heavier descended first and generated an
oscillatory motion, so that they oscillated around their centers. For by its
oscillations a ball communicates a greater motion to the water than if it
were descending without oscillations, and in the process loses part of its own
motion with which it should descend; and it is retarded more or retarded less
in proportion to the greatness or smallness of the oscillation. Further, the ball
always recedes from that side which is descending in the oscillation and, by
receding, approaches the sides of the vessel and sometimes strikes against the
sides. In the case of heavier balls, this oscillation is stronger, and with larger
balls, it agitates the water more. Therefore, in order to reduce the oscillation
of the balls, I constructed new balls of wax and lead, fixing the lead into one
side of the ball near its surface; and I dropped the ball in such a way that the
heavier side, as far as possible, was lowest at the beginning of the descent.
Thus the oscillations became much smaller than before, and the balls fell in
less unequal times, as in the following experiments.
EXPERIMENT 8. Four balls, weighing 139 grains in air and 6½ in water,
were dropped often and fell in the times of not more than 52 oscillations,
and not fewer than 50, and for the most part in the time of roughly 51
oscillations, describing a space of 182 inches.
By the theory they ought to have fallen in the time of roughly 52
oscillations.
EXPERIMENT 9. Four balls, weighing 273¼ grains in air and 140¾ in
water, were dropped often and fell in the times of not fewer than 12
oscillations and not more than 13, describing a space of 182 inches.
And by the theory these balls ought to have fallen in the time of very
nearly 11⅓ oscillations.
EXPERIMENT 10. Four balls, weighing 384 grains in air and 119½ in
water, were dropped often and fell in the times of 17¾, 18, 18½, and 19
oscillations, describing a space of 181½ inches. And when they fell in the
time of 19 oscillations, I sometimes heard them strike the sides of the vessel
before they reached the bottom.
And by the theory they ought to have fallen in the time of very nearly
155/9 oscillations.
EXPERIMENT 11. Three equal balls, weighing 48 grains in air and 329/32
in water, were dropped often and fell in the times of 43½, 44, 44½, 45, and
46 oscillations, and for the most part 44 and 45, describing a space of very
nearly 182½ inches.
By the theory they ought to have fallen in the time of roughly 465/9
oscillations.
EXPERIMENT 12. Three equal balls, weighing 141 grains in air and 4⅜
in water, were dropped several times and fell in the times of 61, 62, 63, 64,
and 65 oscillations, describing a space of 182 inches.
And by the theory they ought to have fallen in the time of very nearly
64½ oscillations.
From these experiments it is obvious that when the balls fell slowly
(as in the second, fourth, fifth, eighth, eleventh, and twelfth experiments),
the times of falling are shown correctly by the theory, but that when the
balls fell more quickly (as in the sixth, ninth, and tenth experiments), the
resistance was a little greater than in the squared ratio of the velocity. For
the balls oscillate somewhat while falling, and this oscillation—in balls that
are lighter and fall more slowly—ceases swiftly because the motion is weak,
while in heavier and larger balls, because the motion is strong, the oscillation
lasts longer and can be checked by the surrounding water only after more
oscillations. Additionally, the swifter the balls, the less they are pressed by the
fluid in back of them; and if the velocity is continually increased, they will
at length leave an empty space behind, unless the compression of the fluid
is simultaneously increased. The compression of the fluid, moreover, ought
(by props. 32 and 33) to be increased in the squared ratio of the velocity
in order for the resistance also to be in a squared ratio. Since this does not
happen, the swifter balls are pressed a little less from behind, and because of
this diminished pressure their resistance becomes a little greater than in the
squared ratio of the velocity.
The theory therefore agrees with the phenomena of bodies falling in
water; it remains for us to examine the phenomena of bodies falling in air.
EXPERIMENT 13. aFrom the top of St. Paul’s Cathedral in Londona in
June 1710, glass balls were dropped simultaneously in pairs, one full of
quicksilver, the other full of air; and in falling they described a space of 220 London
feet. A wooden platform was suspended at one end by iron pivots, and at the
other was supported by a wooden peg. The two balls were placed upon this
platform and were let fall simultaneously by pulling out the peg by means
of an iron wire extending to the ground, so that the platform, resting on the
iron pivots alone, might swing downward upon the pivots and at the same
moment a seconds pendulum, pulled by that iron wire, might be released
and begin to oscillate. The diameters and weights of the balls and the times
of falling are shown in the following table.
However, the observed times need to be corrected. For balls filled with
mercury will (by Galileo’s theory) describe 257 London feet in 4 seconds,
and 220 feet in only 3 seconds 42 thirds. The wooden platform, when the
peg was withdrawn, swung downward more slowly than it should have [i.e.,
more slowly than in free fall] and as a result impeded the descent of the balls
at the start. For the balls were lying upon the platform near its center, and
were in fact a little closer to the pivots than to the peg. And hence the times
of falling were prolonged by roughly 18 thirds and so need to be corrected
by taking away those thirds, especially in the larger balls, which because of
the magnitude of their diameters remained a little longer upon the platform
as it swung downward. When this has been done, the times in which the
six larger balls fell will come out 8 sec. 12 thirds, 7 sec. 42 thirds, 7 sec. 42
thirds, 7 sec. 57 thirds, 8 sec. 12 thirds, and 7 sec. 42 thirds.
Therefore the fifth of those balls filled with air, with a diameter of 5
inches and a weight of 483 grains, fell in the time of 8 sec. 12 thirds,
describing the space of 220 feet. The weight of water equal to this ball is 16,600
grains; and the weight of air equal to it is  grains, or 193/10 grains, and
thus the weight of the ball in a vacuum is 5023/10 grains, and this weight is
to the weight of air equal to the ball as 5023/10 to 193/10, as is the ratio of 2F
to 8/3 of the diameter of the ball (that is, 2F to 13⅓ inches). And hence 2F
comes out 28 feet 11 inches. The ball in falling in a vacuum, with its whole
weight of 5023/10 grains, in the time of one second describes 193⅓ inches as
above, and with a weight of 483 grains describes 185.905 inches, and with
the same weight of 483 grains also in a vacuum describes the space F, or 14
feet 5½ inches, in the time of 57 thirds 58 fourths, and attains the greatest
velocity with which it could descend in air. With this velocity the ball, in the
time of 8 sec. 12 thirds, will describe a space of 245 feet 5⅓ inches. Take
away 1.3863F, or 20 feet ½ inch, and there will remain 225 feet 5 inches. It
is this space, therefore, that the ball should, by the theory, have described in
falling in the time of 8 sec. 12 thirds. And it described a space of 220 feet in
the experiment. The difference is negligible.
grains, or 193/10 grains, and
thus the weight of the ball in a vacuum is 5023/10 grains, and this weight is
to the weight of air equal to the ball as 5023/10 to 193/10, as is the ratio of 2F
to 8/3 of the diameter of the ball (that is, 2F to 13⅓ inches). And hence 2F
comes out 28 feet 11 inches. The ball in falling in a vacuum, with its whole
weight of 5023/10 grains, in the time of one second describes 193⅓ inches as
above, and with a weight of 483 grains describes 185.905 inches, and with
the same weight of 483 grains also in a vacuum describes the space F, or 14
feet 5½ inches, in the time of 57 thirds 58 fourths, and attains the greatest
velocity with which it could descend in air. With this velocity the ball, in the
time of 8 sec. 12 thirds, will describe a space of 245 feet 5⅓ inches. Take
away 1.3863F, or 20 feet ½ inch, and there will remain 225 feet 5 inches. It
is this space, therefore, that the ball should, by the theory, have described in
falling in the time of 8 sec. 12 thirds. And it described a space of 220 feet in
the experiment. The difference is negligible.
Applying similar computations also to the remaining balls filled with air,
I constructed the following table.
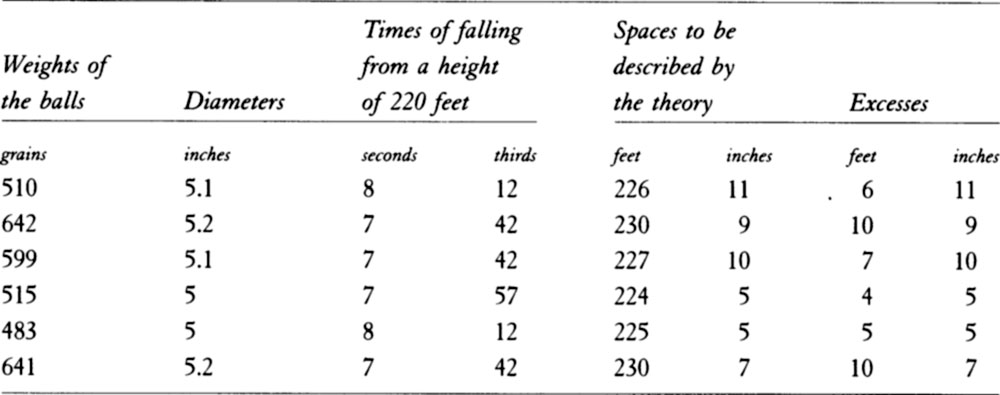
EXPERIMENT 14. In July 1719, Dr. Desaguliers made experiments of this
sort again, making hogs’ bladders into a round shape by means of a concave
wooden sphere, which the moist bladders, inflated with air, were forced to
fill; after they were dried and taken out, they were dropped bfrom the lantern
at the top of the cupola of the same cathedral, that is, from a height of 272
feet,b and at the same moment a lead ball was also dropped, whose weight
was roughly two pounds troy. And meanwhile some people standing in the
highest part of St. Paul’s where the balls were released noted the whole times
of falling, and others standing on the ground noted the difference between
the times of fall of the lead ball and of the bladder. And the times were
measured by half-second pendulums. And one of those who were standing
on the ground had a clock with an oscillating spring, vibrating four times
per second; someone else had another machine ingeniously constructed with
a pendulum also vibrating four times per second. And one of those who
were standing in the gallery of the cupola had a similar device. And these
instruments were so constructed that their motions might begin or be stopped
at will. The lead ball fell in a time of roughly 4¼ seconds. And by adding
this time to the aforesaid difference between the times, the whole time in
which the bladder fell was determined. The times in which the five bladders
continued to fall after the lead ball had completed its fall were 14¾ sec.,
12¾ sec., 14⅝ sec., 17¾ sec., and 16⅞ sec. the first time, and 14½ sec.,
14¼ sec., 14 sec., 19 sec., and 16¾ sec. the second time. Add 4¼ sec., the time
in which the lead ball fell, and the whole times in which the five bladders
fell were 19 sec., 17 sec., 18⅞ sec., 22 sec., and 21⅛ sec. the first time, and
18¾ sec., 18½ sec., 18¼ sec., 23¼ sec., and 21 sec. the second time. And the
times noted from the cupola were 19⅜ sec., 17¼ sec., 18¾ sec., 22⅛ sec.,
and 21⅝ sec. the first time, and 19 sec., 18⅝ sec., 18⅜ sec., 24 sec., and 21¼
sec. the second time. But the bladders did not always fall straight down, but
sometimes flew about and oscillated to and fro while falling. And the times
of falling were prolonged and increased by these motions, sometimes by
one-half of one second, sometimes by a whole second. The second and fourth
bladders, moreover, fell straighter down the first time, as did the first and
third the second time. The fifth bladder was wrinkled and was somewhat
retarded by its wrinkles. I calculated the diameters of the bladders from their
circumferences, measured by a very thin thread wound round them twice.
And I compared the theory with the experiments in the following table,
assuming the density of air to be to the density of rainwater as 1 to 860, and
calculating the spaces that the balls should, by the theory, have described in
falling.
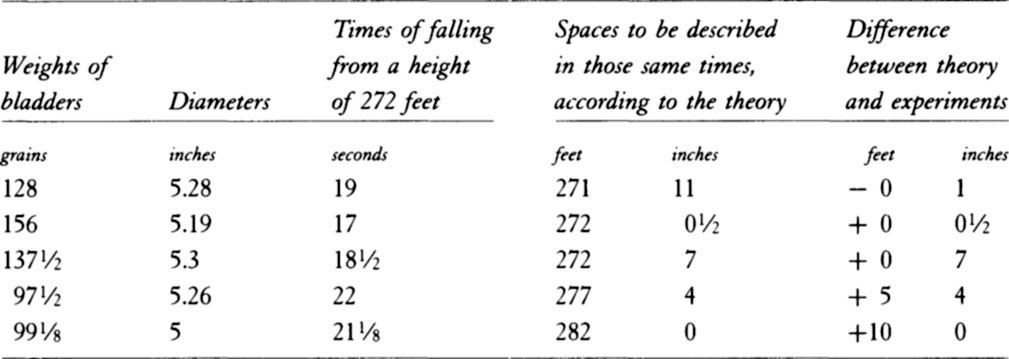
Therefore almost all the resistance encountered by balls moving in air as
well as in water is correctly shown by our theory, and is proportional to the
density of the fluids—the velocities and sizes of the balls being equal.
In the scholium at the end of sec. 6, we showed by experiments with
pendulums that the resistances encountered by equal and equally swift balls
moving in air, water, and quicksilver are as the densities of the fluids. We
have shown the same thing here more accurately by experiments with bodies
falling in air and water. For pendulums in each oscillation arouse in the fluid
a motion always opposite to the motion of the pendulum when it returns; and
the resistance arising from this motion, and also the resistance to the cord
by which the pendulum was suspended, made the whole resistance to the
pendulum greater than the resistance found by the experiments with falling
bodies. For by the experiments with pendulums set forth in that scholium, a
ball of the same density as water ought, in describing the length of its own
semidiameter in air, to lose 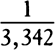 of its motion. But by the theory set forth in
this seventh section and confirmed by experiments with falling bodies, that
same ball ought, in describing that same length, to lose only
of its motion. But by the theory set forth in
this seventh section and confirmed by experiments with falling bodies, that
same ball ought, in describing that same length, to lose only 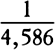 of its
motion, supposing that the density of water is to the density of air as 860
to 1. The resistances therefore were found to be greater by the experiments
with pendulums (for the reasons already described) than by the experiments
with falling balls, and in a ratio of roughly 4 to 3. But since the resistances
to pendulums oscillating in air, water, and quicksilver are increased similarly
by similar causes, the proportion of the resistances in these mediums will be
shown correctly enough by the experiments with pendulums as well as by
the experiments with falling bodies. And hence it can be concluded that the
resistances encountered by bodies moving in any fluids that are very fluid,
other things being equal, are as the densities of the fluids.
of its
motion, supposing that the density of water is to the density of air as 860
to 1. The resistances therefore were found to be greater by the experiments
with pendulums (for the reasons already described) than by the experiments
with falling balls, and in a ratio of roughly 4 to 3. But since the resistances
to pendulums oscillating in air, water, and quicksilver are increased similarly
by similar causes, the proportion of the resistances in these mediums will be
shown correctly enough by the experiments with pendulums as well as by
the experiments with falling bodies. And hence it can be concluded that the
resistances encountered by bodies moving in any fluids that are very fluid,
other things being equal, are as the densities of the fluids.
On the basis of what has been established, it is now possible to predict
very nearly what part of the motion of any ball projected in any fluid will
be lost in a given time. Let D be the diameter of the ball, and V its velocity
at the beginning of the motion, and T the time in which the ball will—with
velocity V in a vacuum—describe a space that is to the space 8/3D as the
density of the ball to the density of the fluid; then the ball projected in that
fluid will, in any other time t, lose the part 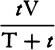 of its velocity
of its velocity 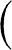 the part
the part
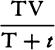 remaining
remaining  and will describe a space that is to the space described in
a vacuum in the same time with the uniform velocity V as the logarithm of
the number
and will describe a space that is to the space described in
a vacuum in the same time with the uniform velocity V as the logarithm of
the number  multiplied by the number 2.302585093 is to the number
t/T, by prop. 35, corol. 7. In slow motions the resistance can be a little
less, because the shape of a ball is a little more suitable for motion than the
shape of a cylinder described with the same diameter. In swift motions the
resistance can be a little greater, because the elasticity and the compression
of the fluid are not increased in the squared ratio of the velocity. But here I
am not considering petty details of this sort.
multiplied by the number 2.302585093 is to the number
t/T, by prop. 35, corol. 7. In slow motions the resistance can be a little
less, because the shape of a ball is a little more suitable for motion than the
shape of a cylinder described with the same diameter. In swift motions the
resistance can be a little greater, because the elasticity and the compression
of the fluid are not increased in the squared ratio of the velocity. But here I
am not considering petty details of this sort.
And even if air, water, quicksilver, and similar fluids, by some infinite
division of their parts, could be subtilized and become infinitely fluid mediums,
they would not resist projected balls any the less. For the resistance which is
the subject of the preceding propositions arises from the inertia of matter; and
the inertia of matter is essential to bodies and is always proportional to the
quantity of matter. By the division of the parts of a fluid, the resistance that
arises from the tenacity and friction of the parts can indeed be diminished,
but the quantity of matter is not diminished by the division of its parts; and
since the quantity of matter remains the same, its force of inertia—to which
the resistance discussed here is always proportional—remains the same. For
this resistance to be diminished, the quantity of matter in the spaces through
which bodies move must be diminished. And therefore the celestial spaces,
through which the globes of the planets and comets move continually in all
directions very freely and without any sensible diminution of motion, are
devoid of any corporeal fluid, except perhaps the very rarest vapors and rays
of light transmitted through those spaces.
Projectiles, of course, arouse motion in fluids by going through them,
and this motion arises from the excess of the pressure of the fluid on the
front of the projectile over the pressure on the back, and cannot be less in
infinitely fluid mediums than in air, water, and quicksilver in proportion
to the density of matter in each. And this excess of pressure, in proportion
to its quantity, not only arouses motion in the fluid but also acts upon the
projectile to retard its motion; and therefore the resistance in every fluid is
as the motion excited in the fluid by the projectile, and it cannot be less in
the most subtle aether, in proportion to the density of the aether, than in air,
water, and quicksilver, in proportion to the densities of these fluids.
SECTION 8
Motion propagated through fluids
Proposition 41, Theorem 32
Pressure is not propagated through a fluid along straight lines, unless the particles
of the fluid lie in a straight line.
If the particles a, b, c, d, and e lie in a straight line, a pressure can indeed
be propagated directly from a to e; but the particle e will urge the obliquely
 placed particles f and g obliquely, and those particles
f and g will not sustain the pressure brought upon
them unless they are supported by the further particles
h and k; but to the extent that they are supported,
they press the supporting particles, and these will not
sustain the pressure unless they are supported by the
further particles l and m and press them, and so on indefinitely. Therefore,
as soon as a pressure is propagated to particles which do not lie in a straight
line, it will begin to spread out and will be obliquely propagated indefinitely;
and after the pressure begins to be propagated obliquely, if it should impinge
upon further particles which do not lie in a straight line, it will spread out
again, and will do so as often as it impinges upon particles not lying exactly
in a straight line. Q.E.D.
placed particles f and g obliquely, and those particles
f and g will not sustain the pressure brought upon
them unless they are supported by the further particles
h and k; but to the extent that they are supported,
they press the supporting particles, and these will not
sustain the pressure unless they are supported by the
further particles l and m and press them, and so on indefinitely. Therefore,
as soon as a pressure is propagated to particles which do not lie in a straight
line, it will begin to spread out and will be obliquely propagated indefinitely;
and after the pressure begins to be propagated obliquely, if it should impinge
upon further particles which do not lie in a straight line, it will spread out
again, and will do so as often as it impinges upon particles not lying exactly
in a straight line. Q.E.D.
COROLLARY. If some part of a pressure propagated through a fluid from
a given point is intercepted by an obstacle, the remaining part (which is not
intercepted) will spread out into the spaces behind the obstacle. This can
be proved as follows. From point A let a pressure be propagated in any
direction and, if possible, along straight lines; and by the obstacle NBCK,
perforated in BC, let all the pressure be intercepted except the cone-shaped
part APQ, which passes through the circular hole BC. By transverse planes
de, fg, and hi, divide the cone APQ into frusta; then, while the cone ABC,
by propagating the pressure, is urging the further conic frustum degf on
the surface de, and this frustum is urging the next frustum fgih on the
surface fg, and that frustum is urging a third frustum, and so on indefinitely,
obviously (by the third law of motion) the first frustum defg will be as much
urged and pressed on the surface fg by the reaction of the second frustum
fghi as it urges and presses the second frustum. Therefore the frustum degf
between the cone Ade and the frustum fhig is compressed on both sides,
and therefore (by book 2, prop. 19, case 6) it cannot keep its figure unless it
is compressed by the same force on all sides. With the same force, therefore,
with which it is pressed on the surfaces de and fg, it will endeavor to yield
at the sides df and eg; and there (since it is not rigid, but altogether fluid)
it will run out and expand, unless a surrounding fluid is present to restrain
that endeavor. Accordingly, by the endeavor to run out, it will press the
surrounding fluid at the sides df and eg, as well as the frustum fghi, with
the same force; and therefore the pressure will be no less propagated from
the sides df and eg into the spaces NO on one side and KL on the other,
than it is propagated from the surface fg toward PQ. Q.E.D.
Proposition 42, Theorem 33
All motion propagated through a fluid diverges from a straight path into the
motionless spaces.
CASE 1. Let a motion be propagated from point A through a hole BC,
and let it proceed, if possible, in the conic space BCQP along straight lines
diverging from point A. And let us suppose first that this motion is that
of waves on the surface of stagnant water. And let de, fg, hi, kl, . . . be
the highest parts of the individual waves, separated from one another by the
same number of intermediate troughs. Therefore, since the water is higher
in the crests of the waves than in the motionless parts LK and NO of the
fluid, it will flow down from e, g, i, l, . . . , and d, f, h, k, . . . , the ends of
the crests, toward KL on one side and NO on the other; and since it is lower
in the troughs of the waves than in the motionless parts KL and NO of the
fluid, it will flow down from those motionless parts into the troughs of the
waves. In one case the crests of the waves, and in the other their troughs, are
expanded and propagated toward KL on one side and NO on the other. And
since the motion of the waves from A toward PQ takes place by the continual
flowing down of the crests into the nearest troughs, and thus is not quicker
than in proportion to the quickness of the descent, and since the descent of
the water toward KL on one side and NO on the other ought to occur with
the same velocity, the expansion of the waves will be propagated toward KL
on one side and NO on the other with the same velocity with which the
waves themselves progress directly from A toward PQ. And accordingly the
whole space toward KL on one side and NO on the other will be occupied
by the expanded waves rfgr, shis, tklt, vmnv, . . . . Q.E.D. Anyone can
test this in stagnant water.
CASE 2. Now let us suppose that de, fg, hi, kl, and mn designate pulses
successively propagated from point A through an elastic medium. Think of
the pulses as propagated by successive condensations and rarefactions of the
medium, in such a way that the densest part of each pulse occupies a
spherical surface described about the center A, and that the spaces which come
between successive pulses are equal. And let de, fg, hi, kl, . . . designate
the densest parts of the pulses, parts which are propagated through the hole
BC. And since the medium is denser there than in the spaces toward KL
on one side and NO on the other, it will expand toward those spaces KL
and NO situated on both sides as well as toward the rarer intervals between
the pulses; and thus, always becoming rarer next to the intervals and denser
next to the pulses, the medium will participate in their motion. And since
the progressive motion of the pulses arises from the continual slackening of
the denser parts toward the rarer intervals in front of them, and since the
pulses ought to slacken with nearly the same speed into the medium’s parts
KL on one side and NO on the other, which are at rest, those pulses will
expand on all sides into the motionless spaces KL and NO with nearly the
same speed with which they are propagated straight forward from the center
A, and thus will occupy the whole space KLON. Q.E.D. We find this by
experience in the case of sounds, which are heard when there is a mountain
in the way or which expand into all parts of a room when let in through a
window and are heard in all corners, being not so much reflected from the
opposite walls as propagated directly from the window, as far as the senses
can tell.
CASE 3. Finally, let us suppose that a motion of any kind is propagated
from A through the hole BC. That propagation does not occur except insofar
as the parts of the medium that are nearer to the center A urge and move
the further parts; and the parts that are urged are fluid and thus recede in
every direction into regions where they are less pressed, and so will recede
toward all the parts of the medium that are at rest, the parts KL and NO
on the sides as well as the parts PQ in front. And therefore all the motion,
as soon as it has passed through the hole BC, will begin to spread out and
to be propagated directly from there into all parts as if from an origin and
center. Q.E.D.
Proposition 43, Theorem 34
Every vibrating body in an elastic medium will propagate the motion of the
pulses straight ahead in every direction, but in a nonelastic medium will produce
a circular motion.
CASE 1. For the parts of a vibrating body, by going forward and
returning alternately, will in their going urge and propel the parts of the medium
that are nearest to them and by that urging will compress and condense
them; then in their return they will allow the compressed parts to recede
[i.e., to move apart from one another] and expand. Thus the parts of the
medium that are nearest to the vibrating body will go and return alternately,
like the parts of the vibrating body; and just as the parts of this body acted
upon the parts of the medium, so the latter, acted upon by similar vibrations,
will act upon the parts nearest to them, and these, similarly acted upon, will
act upon further parts, and so on indefinitely. And just as the first parts of
the medium condense in going and rarefy in returning, so the remaining
parts will condense whenever they go and will expand [i.e., rarefy] whenever
they return. And therefore they will not all go and return at the same time
(for thus, by keeping determined distances from one another, they would not
rarefy and condense alternately), but by approaching one another when they
condense and moving apart when they rarefy, some of them will go while
others return, and these conditions will alternate indefinitely. And the parts
that are going and that condense in going (because of their forward motion
with which they strike obstacles) are pulses; and therefore successive pulses
will be propagated straight ahead from every vibrating body, and they will
be so propagated at roughly equal distances from one another, because of
the equal intervals of time in which the body produces each pulse by each
of its vibrations. And even if the parts of the vibrating body go and return
in some fixed and determined direction, nevertheless the pulses propagated
from there through the medium will (by prop. 42) expand sideways and will
be propagated in all directions from the vibrating body as if from a common
center, in surfaces almost spherical and concentric. We have an example of
this in waves, which, if they are produced by a wagging finger, not only will
go to and fro according to the finger’s motion but will immediately surround
the finger like concentric circles and will be propagated in all directions. For
the gravity of the waves takes the place of the elastic force.
CASE 2. But if the medium is not elastic, then, since its parts, pressed by
the oscillating parts of the vibrating body, cannot be condensed, the motion
will be propagated instantly to the parts where the medium yields most easily,
that is, to the parts that the vibrating body would otherwise leave empty
behind it. The case is the same as the case of a body projected in any medium.
A medium, in yielding to projectiles, does not recede indefinitely, but goes
with a circular motion to the spaces that the body leaves behind it. Therefore,
whenever a vibrating body goes toward any place [or in any direction], the
medium, in yielding, will go with a circular motion to the spaces that the
body leaves; and whenever the body returns to its former place, the medium
will be forced out and will return to its former place. And even though the
vibrating body is not rigid but completely pliant, if it nevertheless remains
of a fixed size, then, since it cannot urge the medium by its vibrations in
any one place without simultaneously yielding to it in another, that body will
make the medium, by receding from the parts where it is pressed, go always
with a circular motion to the parts that yield to it. Q.E.D.
COROLLARY. Therefore it is a delusion to believe that the agitation of the
parts of flame conduces to the propagation of a pressure along straight lines
through a surrounding medium. A pressure of this sort must be derived not
only from the agitation of the parts of the flame but from the dilation of the
whole.
Proposition 44, Theorem 35
If water ascends and descends alternately in the vertical arms KL and MN of
a tube, and if a pendulum is constructed whose length between the point of
suspension and the center of oscillation is equal to half of the length of the water
in the tube, then I say that the water will ascend and descend in the same times
in which the pendulum oscillates.
I measure the length of the water along the axes of the tube and the
arms and make it equal to the sum of these axes, and I do not here consider
the resistance of the water that arises from the friction of the tube. Let AB
and CD therefore designate the mean height of the water in the two arms,
and when the water in the arm KL ascends to the height EF, the water
in the arm MN will have descended to the height GH. Moreover, let P
be a pendulum bob, VP the cord, V the point of suspension, RPQS the
cycloid described by the pendulum, P its lowest point, and PQ an arc equal
to the height AE. The force by which the motion of the water is alternately
accelerated and retarded is the amount by which the weight of the water
in one of the two arms exceeds the weight in the other. And thus, when
the water in the arm KL ascends to EF, and in the other arm descends to
GH, that force is twice the weight of the water EABF and therefore is to
the weight of all the water as AE or PQ to VP or PR. Furthermore, the
force by which the weight P in any place Q is accelerated and retarded in
the cycloid is (by book 1, prop. 51, corol.) to its whole weight as its distance
PQ from the lowest place P to the length PR of the cycloid. Therefore the
motive forces of the water and the pendulum, describing the equal spaces
AE and PQ, are as the weights that are to be moved; and thus, if the water
and the pendulum are at rest in the beginning, those forces will move them
equally in equal times and will cause them to go and return synchronously
with an alternating motion. Q.E.D.
COROLLARY 1. Therefore all the alternations of the ascending and
descending water are isochronous, whether the motion is of greater intension
or greater remission.a
COROLLARY 2. If the length of all the water in the tube is 61/9 Paris
feet, the water will descend in the time of one second and will ascend in
another second and will continue to alternate in this way indefinitely. For a
pendulum 31/18 feet long oscillates in the time of one second.
COROLLARY 3. When the length of the water is increased or decreased,
moreover, the time of alternation is increased or decreased as the square root
of the length.
Proposition 45, Theorem 36
The velocity of waves is as the square roots of the lengths.
This follows from the construction of the following proposition.
Proposition 46, Problem 10
To find the velocity of waves.
Set up a pendulum whose length between the point of suspension and
the center of oscillation is equal to the length of the waves; and in the same
time in which the pendulum performs each of its oscillations, the waves as
they move forward will traverse nearly their own lengths.

By length of a wave I mean the transverse distance either between
bottoms of troughs or between tops of crests. Let ABCDEF designate the surface
of stagnant water ascending and descending in successive waves; and let A,
C, E, . . . be the crests of the waves, and B, D, F, . . . the troughs in between.
Since the motion of the waves is caused by the successive ascent and descent
of the water, in such a way that its parts, A, C, E, . . . , which now are
highest, soon become lowest, and since the motive force by which the highest
parts descend and the lowest ascend is the weight of the elevated water, the
alternate ascent and descent will be analogous to the alternating motion of
the water in the tube and will observe the same laws with respect to times;
and therefore (by prop. 44), if the distances between the highest places A,
C, and E of the waves and the lowest, B, D, and F, are equal to twice the
length of a pendulum, the highest parts A, C, and E will in the time of one
oscillation come to be the lowest, and in the time of a second oscillation will
ascend once again. Therefore there will be a time of two oscillations between
successive waves; that is, a wave will describe its own length in the time in
which the pendulum oscillates twice; but in the same time a pendulum whose
length is four times as great, and thus equals the length of the waves, will
oscillate once. Q.E.I.
COROLLARY 1. Therefore waves with a length of 31/18 Paris feet will
move forward through their own length in the time of one second and thus
in the time of one minute will traverse 183⅓ feet, and in the space of an
hour very nearly 11,000 feet.
COROLLARY 2. And the velocity of waves of greater or smaller length
will be increased or decreased as the square root of the length.
What has been said is premised on the hypothesis that the parts of the
water go straight up or straight down; but this ascent and descent takes place
more truly in a circle, and thus I admit that in this proposition the time has
been determined only approximately.
Proposition 47, Theorem 37
If pulses are propagated through a fluid, the individual particles of the fluid, going
and returning with a very short alternating motion, are always accelerated and
retarded in accordance with the law of an oscillating pendulum.
 Let AB, BC, CD, . . . designate the
equal distances between successive pulses;
ABC the line of motion of the pulses,
propagated from A toward B; E, F, and
G three physical points in the medium
at rest, situated at equal intervals along
the straight line AC; Ee, Ff, and Gg
very short equal spaces through which
those points go and return in each
vibration with an alternating motion; ε, φ, γ
any intermediate positions of those same
points; and EF and FG physical
line-elements or linear parts of the medium,
put between those points and successively
transferred into the places εφ, φγ and
ef, fg. Draw the straight line PS equal
to the straight line Ee. Bisect PS in O,
and with center O and radius OP
describe the circle SIPi.
Let AB, BC, CD, . . . designate the
equal distances between successive pulses;
ABC the line of motion of the pulses,
propagated from A toward B; E, F, and
G three physical points in the medium
at rest, situated at equal intervals along
the straight line AC; Ee, Ff, and Gg
very short equal spaces through which
those points go and return in each
vibration with an alternating motion; ε, φ, γ
any intermediate positions of those same
points; and EF and FG physical
line-elements or linear parts of the medium,
put between those points and successively
transferred into the places εφ, φγ and
ef, fg. Draw the straight line PS equal
to the straight line Ee. Bisect PS in O,
and with center O and radius OP
describe the circle SIPi.
Let the whole circumference of this
circle with its parts represent the whole
time of one vibration with its
proportional parts, in such a way that when
any time PH or PHSh is completed, if
the perpendicular HL or hl is dropped
to PS, and if Eε is taken equal to PL
or Pl, then the physical point E is found
in ε. By this law any point E, in going
from E through ε to e and returning
from there through ε to E, will perform each vibration with the same
degrees of acceleration and retardation as the oscillating pendulum. It is to be
proved that each of the physical points of the medium must move in such a
way. Let us imagine, therefore, that there is such a motion in the medium,
arising from any cause, and see what follows.
In the circumference PHSh take the equal arcs HI and IK or hi and
ik, having the ratio to the whole circumference that the equal straight lines
EF and FG have to the whole interval BC between pulses. Drop the
perpendiculars IM and KN and also im and kn. Then the points E, F, and G
are successively agitated with similar motions and carry out their complete
vibrations (consisting of a going and returning) while a pulse is transferred
from B to C; accordingly, if PH or PHSh is the time from the beginning
of the motion of point E, PI or PHSi will be the time from the beginning
of the motion of point F, and PK or PHSk will be the time from the
beginning of the motion of point G; and therefore Eε, Fφ, and Gγ will be
equal respectively to PL, PM, and PN in the going of the points, or to Pl,
Pm, and Pn in the returning of the points. Hence εγ or EG + Gγ − Eε
will be equal to EG − LN in the going of the points, and will be equal to
EG + ln in their returning. But εγ is the width or expansion of the part of
the medium EG in the place εγ; and therefore the expansion of that part in
the going is to its mean expansion as EG − LN to EG, and in the returning
is as EG + ln or EG + LN to EG. Therefore, since LN is to KH as IM to
the radius OP, and KH is to EG as the circumference PHShP to BC, that
is (if V is put for the radius of a circle having a circumference equal to the
interval between the pulses BC), as OP to V, and since, from the equality of
the ratios [or ex aequo], LN is to EG as IM to V, the expansion of the part
EG or of the physical point F in the place εγ will be to the mean expansion
which that part has in its own first place EG as V − IM to V in the going,
and as V + im to V in the returning. Hence the elastic force of point F in
the place εγ is to its mean elastic force in the place EG as 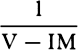 to
to 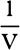 in
the going, and as
in
the going, and as 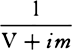 to
to 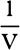 in the returning. And by the same argument
the elastic forces of the physical points E and G in the going are as
in the returning. And by the same argument
the elastic forces of the physical points E and G in the going are as 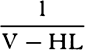 and
and 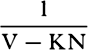 to
to 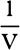 ; and the difference between the forces is to the mean
elastic force or the medium as
; and the difference between the forces is to the mean
elastic force or the medium as 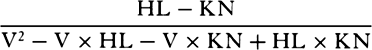 to
to
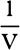 , that is, as
, that is, as 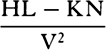 to
to 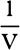 , or as HL − KN to V, provided that
(because of the narrow limits of the vibrations) we suppose HL and KN to
be indefinitely smaller than the quantity V. Therefore, since the quantity V
is given, the difference between the forces is as HL — KN, that is, as OM
(because HL − KN is proportional to HK and OM to OI or OP; and HK
and OP are given)—that is, if Ff is bisected in Ω, as Ωφ. And by the same
argument the difference between the elastic forces of the physical points ε
and γ, in the returning of the physical line-element εγ, is as Ωφ. But that
difference (that is, the amount by which the elastic force of point ε exceeds
the elastic force of point γ) is the force by which the intervening physical
line-element εγ of the medium is accelerated in the going and retarded in
the returning; and therefore the accelerative force of the physical line-element
εγ is as its distance from the midpoint Ω of the vibration. Accordingly, the
time (by book 1, prop. 38) is correctly represented by the arc PI, and the
linear part εγ of the medium moves by the law previously mentioned, that
is, by the law of an oscillating pendulum; and the same is true of all the
linear parts of which the whole medium is composed. Q.E.D.
, or as HL − KN to V, provided that
(because of the narrow limits of the vibrations) we suppose HL and KN to
be indefinitely smaller than the quantity V. Therefore, since the quantity V
is given, the difference between the forces is as HL — KN, that is, as OM
(because HL − KN is proportional to HK and OM to OI or OP; and HK
and OP are given)—that is, if Ff is bisected in Ω, as Ωφ. And by the same
argument the difference between the elastic forces of the physical points ε
and γ, in the returning of the physical line-element εγ, is as Ωφ. But that
difference (that is, the amount by which the elastic force of point ε exceeds
the elastic force of point γ) is the force by which the intervening physical
line-element εγ of the medium is accelerated in the going and retarded in
the returning; and therefore the accelerative force of the physical line-element
εγ is as its distance from the midpoint Ω of the vibration. Accordingly, the
time (by book 1, prop. 38) is correctly represented by the arc PI, and the
linear part εγ of the medium moves by the law previously mentioned, that
is, by the law of an oscillating pendulum; and the same is true of all the
linear parts of which the whole medium is composed. Q.E.D.
COROLLARY. Hence it is evident that the number of pulses propagated
is the same as the number of vibrations of the vibrating body and does not
increase as the pulses move forward. For as soon as the physical line-element
εγ has returned to its first place, it will be at rest and will not move afterward
unless it receives a new motion either by the impact of the vibrating body or
by the impact of pulses that are propagated from the vibrating body. It will
be at rest, therefore, as soon as the pulses cease to be propagated from the
vibrating body.
Proposition 48, Theorem 38
The velocities of pulses propagated in an elastic fluid are as the square root of the
elastic force directly and the square root of the density inversely, provided that the
elastic force of the fluid is proportional to its condensation.
CASE 1. If the mediums are homogeneous and the distances between
pulses in these mediums are equal to one another, but the motion in one
medium is more intense, then the contractions and expansions of
corresponding parts will be as the motions. In fact, this proportion is not exact. Even so,
unless the contractions and expansions are extremely intense, the error will
not be perceptible, and thus the proportion can be considered physically
exact. But the motive elastic forces are as the contractions and expansions; and
the velocities—generated in the same time—of equal parts are as the forces.
And thus equal and corresponding parts of corresponding pulses will go and
return together through spaces proportional to the contractions and
expansions, with velocities that are as the spaces; and therefore the pulses, which
advance through their own length in the time of one going and returning
and which always succeed into the places of the immediately preceding pulses,
will progress in both mediums with an equal velocity, because of the equality
of the distances.
CASE 2. But if the distances between pulses, or their lengths, are greater
in one medium than in the other, let us suppose that the corresponding
parts by going and returning in each alternation describe spaces
proportional to the lengths of the pulses; then their contractions and expansions
will be equal. And thus if the mediums are homogeneous, those motive
elastic forces by which they are agitated with an alternating motion will
also be equal. But the matter to be moved by these forces is as the length
of the pulses; and the space through which they must move by going and
returning in each alternation is in the same ratio. And the time of going
and returning is jointly proportional to the square root of the matter and
the square root of the space and thus is as the space. But the pulses
advance through their own lengths in the times of one going and returning,
that is, traverse spaces proportional to the times, and therefore have equal
velocities.
CASE 3. In mediums of the same density and elastic force, therefore,
all pulses have equal velocities. But if either the density or the elastic force
of the medium is intended [i.e., increased], then, since the motive force is
increased in the ratio of the elastic force, and the matter to be moved is
increased in the ratio of the density, the time in which the same motions as
before can be performed will be increased as the square root of the density
and will be decreased as the square root of the elastic force. And therefore
the velocity of the pulses will be jointly proportional to the square root of
the density of the medium inversely and the square root of the elastic force
directly. Q.E.D.
This proposition will be clearer from the construction of the following
proposition.
Proposition 49, Problem 11
Given the density and elastic force of a medium, it is required to find the velocity
of the pulses.
Let us imagine the medium to be compressed, as our air is, by an
incumbent weight and let A be the height of a homogeneous medium whose
weight is equal to the incumbent weight and whose density is the same as
the density of the compressed medium in which the pulses are propagated.
 And suppose that a pendulum is set up,
whose length between the point of
suspension and the center of oscillation is
A; then, in the same time in which that
pendulum performs an entire oscillation
composed of a going and a returning, a
pulse will advance through a space equal
to the circumference of a circle described
with radius A.
And suppose that a pendulum is set up,
whose length between the point of
suspension and the center of oscillation is
A; then, in the same time in which that
pendulum performs an entire oscillation
composed of a going and a returning, a
pulse will advance through a space equal
to the circumference of a circle described
with radius A.
For with the same constructions as
in prop. 47, if any physical line EF,
describing the space PS in each single
vibration, is urged in the extremities P
and S of each going and returning by an
elastic force that is equal to its weight,
it will perform each single vibration
in the time in which it could oscillate
in a cycloid whose whole perimeter is
equal to the length PS; and this is so
because equal forces will simultaneously
impel equal corpuscles through equal
spaces. Therefore, since the times of the
oscillations are as the square root of the
length of the pendulums, and since the
length of the pendulum is equal to half
the arc of the whole cycloid, the time of
one vibration would be to the time of
oscillation of a pendulum whose length
is A as the square root of the length
½PS or PO to the length A. But the elastic force by which the physical
line-element EG is urged in its extremities P and S was (in the proof of
prop. 47) to its whole elastic force as HL − KN to V, that is (since point K
now falls upon P), as HK to V; and that whole force, that is, the incumbent
weight by which the line-element EG is compressed, is to the weight of the
line-element as the height A of the incumbent weight to the length EG of
the line-element; and thus from the equality of the ratios [or ex aequo] the
force by which the line-element EG is urged in its places P and S is to the
weight of that line-element as HK × A to V × EG, or as PO × A to V2
(for HK was to EG as PO to V). Therefore, since the times in which equal
bodies are impelled through equal spaces are inversely as the square root of
the forces, the time of one vibration under the action of that elastic force will
be to the time of the vibration, under the action of the force of weight, as the
square root of V2 to PO × A, and thus will be to the time of oscillation of a
pendulum having a length A as 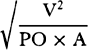 and
and 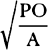 jointly, that is, as V
to A. But in the time of one vibration, composed of a going and returning,
a pulse advances through its own length BC. Therefore the time in which
the pulse traverses the space BC is to the time of one oscillation (composed
of a going and returning) as V to A, that is, as BC to the circumference of
a circle whose radius is A. But the time in which the pulse will traverse the
space BC is in the same ratio to the time in which it will traverse a length
equal to this circumference; and thus in the time of such an oscillation the
pulse will traverse a length equal to this circumference. Q.E.D.
jointly, that is, as V
to A. But in the time of one vibration, composed of a going and returning,
a pulse advances through its own length BC. Therefore the time in which
the pulse traverses the space BC is to the time of one oscillation (composed
of a going and returning) as V to A, that is, as BC to the circumference of
a circle whose radius is A. But the time in which the pulse will traverse the
space BC is in the same ratio to the time in which it will traverse a length
equal to this circumference; and thus in the time of such an oscillation the
pulse will traverse a length equal to this circumference. Q.E.D.
COROLLARY 1. The velocity of the pulses is that which heavy bodies
acquire in falling with a uniformly accelerated motion and describing by
their fall half of the height A. For in the time of this fall, with the velocity
acquired in falling, the pulse will traverse a space equal to the whole height
A; and thus in the time of one oscillation (composed of a going and returning)
it will traverse a space equal to the circumference of a circle described with
radius A; for the time of fall is to the time of oscillation as the radius of the
circle to its circumference.
COROLLARY 2. Hence, since that height A is as the elastic force of the
fluid directly and its density inversely, the velocity of the pulses will be as the
square root of the density inversely and the square root of the elastic force
directly.
Proposition 50, Problem 12
To find the distances between pulses.
In a given time, find the number of vibrations of the body by whose
vibration the pulses are excited. Divide by that number the space that a pulse
could traverse in the same time, and the part found will be the length of one
pulse. Q.E.I.
Scholium
The preceding propositions apply to the motion of light and of sounds. For
since light is propagated along straight lines, it cannot consist in action alone
(by props. 41 and 42). And because sounds arise from vibrating bodies, they
are nothing other than propagated pulses of air (by prop. 43). This is
confirmed from the vibrations that they excite in bodies exposed to them,
provided that they are loud and deep, such as the sounds of drums. For swifter
and shorter vibrations are excited with more difficulty. But it is also well
known that any sounds impinging upon strings in unison with the sonorous
bodies excite vibrations in them. It is confirmed also from the velocity of
sounds. For since the specific weights of rainwater and quicksilver are to
each other as roughly 1 to 13⅔, and since, when the mercury in a barometer
reaches a height of 30 English inches, the specific weight of the air and that
of rainwater are to each other as roughly 1 to 870, the specific weights of
air and quicksilver will be as 1 to 11,890. Accordingly, since the height of
the quicksilver is 30 inches, the height of uniform air whose weight could
compress our air lying beneath it will be 356,700 inches, or 29,725 English
feet. And this height is the very one that we called A in the construction
of prop. 49. The circumference of a circle described with a radius of 29,725
feet is 186,768 feet. And since a pendulum 39⅕ inches long completes an
oscillation composed of a going and returning in the time of 2 seconds, as is
known, a pendulum 29,725 feet or 356,700 inches long must complete an
entirely similar oscillation in the time of 190¾ seconds. In that time, therefore,
sound will advance 186,768 feet, and thus in the time of one second, 979 feet.
aBut in this computation no account is taken of the thickness of the solid
particles of air, a thickness through which sound is of course propagated
instantaneously. Since the weight of air is to the weight of water as 1 to 870,
and since salts are nearly twice as dense as water, if the particles of air are
supposed to be of roughly the same density as the particles of either water or
salts, and if the rarity of air arises from the distances between the particles,
the diameter of a particle of air will be to the distance between the centers of
the particles roughly as 1 to 9 or 10, and to the distance between the particles
as 1 to 8 or 9. Accordingly, to the 979 feet which sound will travel in the
time of 1 second according to the above calculation, 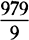 feet or roughly 109
feet may be added, because of the density of the particles of air; and thus
sound will travel roughly 1,088 feet in the time of 1 second.
feet or roughly 109
feet may be added, because of the density of the particles of air; and thus
sound will travel roughly 1,088 feet in the time of 1 second.
Additionally, the vapors lying hidden in the air, since they are of another
elasticity and another tone, participate scarcely or not at all in the motion of
the true air by which sounds are propagated. And when these vapors are at
rest, that motion will be propagated more swiftly through the true air alone
as the square root of the ratio of the total atmosphere of air and vapor to the
matter of the particles of air alone. For example, if the atmosphere consists
of 10 parts of true air and 1 part of vapors, the motion of sounds will be
swifter as the square root of the ratio of 11 to 10, or in roughly the ratio of
21 to 20, than if it were propagated through 11 parts of true air; and thus
the motion of sounds that was found above will have to be increased in this
ratio. Thus in the time of 1 second, sound will travel 1,142 feet.
These things ought to be so in the springtime and autumn, when the air
is rarefied by the temperate heat and its elastic force is somewhat intended
[i.e., increased]. But in winter, when the air is condensed by the cold, and
its elastic force is remitted [i.e., decreased], the motion of sounds should be
slower as the square root of the density; and alternately, in summer it should
be swifter.
It is established by experiments, moreover, that in the time of 1 second
sounds advance through more or less 1,142 London feet, or 1,070 Paris feet.
Once the velocity of sounds has been found, the intervals between the
pulses can also be found. Sauveur found by making experiments that an open
pipe, whose length is more or less 5 Paris feet, produces a sound with the
same pitch as the sound of a string that vibrates a hundred times in 1 second.
Accordingly, there are more or less 100 pulses in the space of 1,070 Paris feet,
the distance which sound travels in the time of 1 second, and thus 1 pulse
occupies a space of about 107/10 Paris feet, that is, roughly twice the length
of the pipe. Hence it is likely that the lengths of the pulses in the sounds of
all open pipes are equal to twice the lengths of the pipes.a
Furthermore, it is evident from book 2, prop. 47, corol., why sounds
immediately cease when the motion of the sonorous body ceases, and why
they are not heard for a longer time when we are very far distant from the
sonorous bodies than when we are very close. Why sounds are very much
increased in megaphones is also manifest from the principles set forth. For
every reciprocal motion is increased at each reflection by the generating cause.
And the motion is lost more slowly and is reflected more strongly in tubes
that impede the expansion of sounds, and therefore is more increased by the
new motion impressed at each reflection. And these are the major phenomena
of sounds.
SECTION 9
The circular motion of fluids
Hypothesis
The resistance that arises from the friction [lit. lack of lubricity or slipperiness] of
the parts of a fluid is, other things being equal, proportional to the velocity with
which the parts of the fluid are separated from one another.
Proposition 51, Theorem 39
If an infinitely long solid cylinder revolves with a uniform motion in a uniform
and infinite fluid about an axis given in position, and if the fluid is made to
revolve by only the impulse of the cylinder, and if each part of the fluid perseveres
uniformly in its motion, then I say that the periodic times of the parts of the fluid
are as their distances from the axis of the cylinder.
Let AFL be the cylinder made to revolve uniformly about the axis S,
and divide the fluid into innumerable concentric solid cylindrical orbsa of
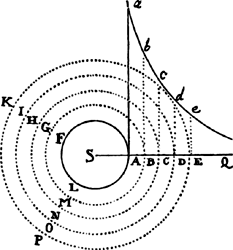 the same thickness by the concentric
circles BGM, CHN, DIO, EKP, . . . . Then,
since the fluid is homogeneous, the
impressions that contiguous orbs make upon one
another will (by hypothesis) be as their
relative displacements and the contiguous
surfaces on which the impressions are made.
If the impression upon some orb is greater
or less on its concave side than on its
convex side, the stronger impression will
prevail and will either accelerate or retard the motion of the orb, according as it
is directed the same way as its motion or the opposite way. Consequently, so
that each orb may persevere uniformly in its motion, the impressions on each
of the two sides should be equal and be made in opposite directions. Hence,
since the impressions are as the contiguous surfaces and their relative
velocities, the relative velocities will be inversely as the surfaces, that is, inversely as
the distances of the surfaces from the axis. And the differences between the
angular motions about the axis are as these relative velocities divided by the
distances, or as the relative velocities directly and the distances
inversely—that is, if the ratios are compounded, as the squares of the distances inversely.
Therefore, if the perpendiculars Aa, Bb, Cc, Dd, Ee, . . . , inversely
proportional to the squares of SA, SB, SC, SD, SE, . . . , are erected to each of
the parts of the infinite straight line SABCDEQ and if a hyperbolic curve
is understood to be drawn through the ends of the perpendiculars, then the
sums of the differences, that is, the whole angular motions, will be as the
corresponding sums of the lines Aa, Bb, Cc, Dd, Ee; that is, if, in order to
make the medium uniformly fluid, the number of orbs is increased and their
width decreased indefinitely, as the hyperbolic areas AaQ, BbQ, CcQ, DdQ,
EeQ, . . . , corresponding to these sums. And the times, which are inversely
proportional to the angular motions, will also be inversely proportional to
these areas. The periodic time of any particle D, therefore, is inversely as
the area DdQ, that is (by the known quadratures of curves), directly as the
distance SD. Q.E.D.
the same thickness by the concentric
circles BGM, CHN, DIO, EKP, . . . . Then,
since the fluid is homogeneous, the
impressions that contiguous orbs make upon one
another will (by hypothesis) be as their
relative displacements and the contiguous
surfaces on which the impressions are made.
If the impression upon some orb is greater
or less on its concave side than on its
convex side, the stronger impression will
prevail and will either accelerate or retard the motion of the orb, according as it
is directed the same way as its motion or the opposite way. Consequently, so
that each orb may persevere uniformly in its motion, the impressions on each
of the two sides should be equal and be made in opposite directions. Hence,
since the impressions are as the contiguous surfaces and their relative
velocities, the relative velocities will be inversely as the surfaces, that is, inversely as
the distances of the surfaces from the axis. And the differences between the
angular motions about the axis are as these relative velocities divided by the
distances, or as the relative velocities directly and the distances
inversely—that is, if the ratios are compounded, as the squares of the distances inversely.
Therefore, if the perpendiculars Aa, Bb, Cc, Dd, Ee, . . . , inversely
proportional to the squares of SA, SB, SC, SD, SE, . . . , are erected to each of
the parts of the infinite straight line SABCDEQ and if a hyperbolic curve
is understood to be drawn through the ends of the perpendiculars, then the
sums of the differences, that is, the whole angular motions, will be as the
corresponding sums of the lines Aa, Bb, Cc, Dd, Ee; that is, if, in order to
make the medium uniformly fluid, the number of orbs is increased and their
width decreased indefinitely, as the hyperbolic areas AaQ, BbQ, CcQ, DdQ,
EeQ, . . . , corresponding to these sums. And the times, which are inversely
proportional to the angular motions, will also be inversely proportional to
these areas. The periodic time of any particle D, therefore, is inversely as
the area DdQ, that is (by the known quadratures of curves), directly as the
distance SD. Q.E.D.
COROLLARY 1. Hence the angular motions of the particles of the fluid
are inversely as the distances of the particles from the axis of the cylinder,
and the absolute velocities are equal.
COROLLARY 2. If the fluid is contained in a cylindrical vessel of an
infinite length and contains another inner cylinder, and if both cylinders revolve
about a common axis, and the times of the revolutions are as the
semidiameters of the cylinders, and each part of the fluid perseveres in its motion, then
the periodic times of the individual parts will be as their distances from the
axis of the cylinders.
COROLLARY 3. If any common angular motion is added to, or taken
away from, the cylinder and the fluid moving in this way, then, since the
mutual friction of the parts of the fluid is not changed by this new motion,
the motions of the parts with respect to one another will not be changed. For
the relative velocities of the parts depend upon the friction. Any part will
persevere in that motion which is not more accelerated than retarded by the
friction on opposite sides in opposite directions.
COROLLARY 4. Hence, if all the angular motion of the outer cylinder is
taken away from the whole system of the cylinders and fluid, the result will
be the motion of the fluid in the cylinder at rest.
COROLLARY 5. Therefore, if, while the fluid and outer cylinder are at
rest, the inner cylinder revolves uniformly, a circular motion will be
communicated to the fluid and will be propagated little by little through the whole
fluid, and it will not cease to be increased until the individual parts of the
fluid acquire the motion defined in corol. 4.
COROLLARY 6. And since the fluid endeavors to propagate its own
motion even further, its force will make the outer cylinder also revolve, unless
that cylinder is forcibly held in place, and the motion of that cylinder will
be accelerated until the periodic times of both cylinders become equal. But
if the outer cylinder is forcibly held in place, it will endeavor to retard the
motion of the fluid, and unless the inner cylinder conserves that motion by
some force impressed from outside, the outer cylinder will cause the motion
to cease little by little.
All of this can be tested in deep stagnant water.
Proposition 52, Theorem 40
If a solid sphere revolves with a uniform motion in a uniform and infinite fluid
about an axis given in position, and if the fluid is made to revolve by only the
impulse of this sphere, and if each part of the fluid perseveres uniformly in its
motion, then I say that the periodic times of the parts of the fluid will be as the
squares of the distances from the center of the sphere.
CASE 1. Let AFL be a sphere made to
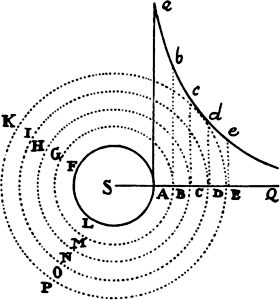 revolve uniformly about the axis S, and
divide the fluid into innumerable concentric
orbsa of the same thickness by means of
the concentric circles BGM, CHN, DIO,
EKP, . . . . And imagine the orbs to be
solid; then, since the fluid is homogeneous,
the impressions that the contiguous orbs
make upon one another will (by the
hypothesis) be as their relative velocities and
the contiguous surfaces on which the impressions are made. If the impression
upon some orb is greater or less on the concave side than on the convex side,
the stronger impression will prevail and will either accelerate or retard the
velocity of the orb, according as it is directed the same way as the motion of
the orb or the opposite way. Consequently, so that each orb may persevere
uniformly in its motion, the impressions on each of the two sides will have to
be equal and to be made in opposite directions. Hence, since the impressions
are as the contiguous surfaces and their relative velocities, the relative
velocities will be inversely as the surfaces, that is, inversely as the squares of the
distances of the surfaces from the center. But the differences in the angular
motions about the axis are as these relative velocities divided by the distances,
or as the relative velocities directly and the distances inversely—that is, if the
ratios are compounded, as the cubes of the distances inversely. Therefore, if
to each of the parts of the infinite straight line SABCDEQ there are erected
the perpendiculars Aa, Bb, Cc, Dd, Ee, . . . , inversely proportional to the
cubes of SA, SB, SC, SD, SE, . . . , then the sums of the differences, that is,
the whole angular motions, will be as the corresponding sums of the lines
Aa, Bb, Cc, Dd, Ee—that is (if, to make the medium uniformly fluid, the
number of orbs is increased and their width decreased indefinitely), as the
hyperbolic areas AaQ, BbQ, CcQ, DdQ,
EeQ, . . . , corresponding to these
sums. And the periodic times, inversely proportional to the angular motions,
will also be inversely proportional to these areas. Therefore the periodic time
of any orb DIO is inversely as the area DdQ, that is (by the known methods
of quadratures of curves), directly as the square of the distance SD. And this
is what I wanted to prove in the first place.
revolve uniformly about the axis S, and
divide the fluid into innumerable concentric
orbsa of the same thickness by means of
the concentric circles BGM, CHN, DIO,
EKP, . . . . And imagine the orbs to be
solid; then, since the fluid is homogeneous,
the impressions that the contiguous orbs
make upon one another will (by the
hypothesis) be as their relative velocities and
the contiguous surfaces on which the impressions are made. If the impression
upon some orb is greater or less on the concave side than on the convex side,
the stronger impression will prevail and will either accelerate or retard the
velocity of the orb, according as it is directed the same way as the motion of
the orb or the opposite way. Consequently, so that each orb may persevere
uniformly in its motion, the impressions on each of the two sides will have to
be equal and to be made in opposite directions. Hence, since the impressions
are as the contiguous surfaces and their relative velocities, the relative
velocities will be inversely as the surfaces, that is, inversely as the squares of the
distances of the surfaces from the center. But the differences in the angular
motions about the axis are as these relative velocities divided by the distances,
or as the relative velocities directly and the distances inversely—that is, if the
ratios are compounded, as the cubes of the distances inversely. Therefore, if
to each of the parts of the infinite straight line SABCDEQ there are erected
the perpendiculars Aa, Bb, Cc, Dd, Ee, . . . , inversely proportional to the
cubes of SA, SB, SC, SD, SE, . . . , then the sums of the differences, that is,
the whole angular motions, will be as the corresponding sums of the lines
Aa, Bb, Cc, Dd, Ee—that is (if, to make the medium uniformly fluid, the
number of orbs is increased and their width decreased indefinitely), as the
hyperbolic areas AaQ, BbQ, CcQ, DdQ,
EeQ, . . . , corresponding to these
sums. And the periodic times, inversely proportional to the angular motions,
will also be inversely proportional to these areas. Therefore the periodic time
of any orb DIO is inversely as the area DdQ, that is (by the known methods
of quadratures of curves), directly as the square of the distance SD. And this
is what I wanted to prove in the first place.
CASE 2. From the center of the sphere draw as many infinite straight
lines as possible which with the axis contain given angles exceeding one
another by equal differences, and imagine the orbs to be cut into innumerable
rings by the revolution of these straight lines about the axis; then each ring
will have four rings contiguous to it, one inside, another outside, and two at
the sides. Each ring cannot be urged equally and in opposite directions by
the friction of the inner ring and of the outer ring, except in a motion made
according to the law of case 1. This is evident from the proof of case 1. And
therefore any series of rings proceeding straight from the sphere indefinitely
will be moved in accordance with the law of case 1, except insofar as it
is impeded by the friction of the rings at the sides. But in motion made
according to this law the friction of the rings at the sides is nil, and thus it
will not impede the motion from being made according to this law. If rings
equally distant from the center revolved either more quickly or more slowly
near the poles than near the ecliptic, the slower rings would be accelerated
and the swifter would be retarded by mutual friction, and thus the periodic
times would always tend toward equality, in accordance with the law of
case 1. This friction, therefore, does not prevent the motion from being made
according to the law of case 1, and therefore that law will hold good; that
is, the periodic time of each of the rings will be as the square of its distance
from the center of the sphere. This is what I wanted to prove in the second
place.
CASE 3. Now let each ring be divided by transverse sections into
innumerable particles constituting an absolutely and uniformly fluid substance;
then, since these sections have no relation to the law of circular motion but
contribute only to the constitution of the fluid, the circular motion will
continue as before. As a result of this sectioning, all the minimally small rings
either will not change the unevenness and the force of their mutual friction
or will change them equally. Furthermore, since the proportion of the causes
remains the same, the proportion of the effects—that is, the proportion of
the motions and periodic times—will also remain the same. Q.E.D.
But since the circular motion, along with the centrifugal force arising
from it, is greater at the ecliptic than at the poles, there must be some cause
by which each of the particles is kept in its circle; otherwise the matter at
the ecliptic would always recede from the center and move on the outside of
the vortex to the poles, and return from there along the axis to the ecliptic
with a continual circulation.
COROLLARY 1. Hence the angular motions of the parts of the fluid about
the axis of the sphere are inversely as the squares of the distances from the
center of the sphere, and the absolute velocities are inversely as those same
squares divided by the distances from the axis.
COROLLARY 2. If a sphere, in a homogeneous and infinite fluid at rest,
revolves with a uniform motion about an axis given in position, it will
communicate a motion to the fluid like that of a vortex, and this motion will be
propagated little by little without limit, and this motion will not cease to be
accelerated in each part of the fluid until the periodic time of each of the
parts is as the squares of the distances from the center of the sphere.
COROLLARY 3. Since the inner parts of a vortex, because of their greater
velocity, rub and push the outer parts and continually communicate motion
to them by this action, and since those outer parts simultaneously transfer
the same quantity of motion to others still further out and by this action
conserve the quantity of their motion completely unaltered, it is evident that
the motion is continually transferred from the center to the circumference
of the vortex and is absorbed in that limitless circumference. The matter
between any two spherical surfaces concentric with the vortex will never be
accelerated, because all of the motion it receives from the inner matter is
continually transferred to the outer matter.
COROLLARY 4. Accordingly, for a vortex to conserve the same state of
motion constantly, some active principle is required from which the sphere
may always receive the same quantity of motion that it impresses on the
matter of the vortex. Without such a principle, it is necessary for the sphere
and the inner parts of the vortex, always propagating their motion to outer
parts and not receiving any new motion, to slow down little by little and
cease to be carried around.
COROLLARY 5. If a second sphere were to be immersed in this vortex
at a certain distance from the center, and meanwhile by some force were to
revolve constantly about an axis given in inclination, then the fluid would
be drawn into a vortex by the motion of this sphere; and first this new and
tiny vortex would revolve along with the sphere about the center of the first
vortex, and meanwhile its motion would spread more widely and little by
little would be propagated without limit, in the same way as the first vortex.
And for the same reason that the sphere of the new vortex was drawn into the
motion of the first vortex, the sphere of the first vortex would also be drawn
into the motion of this new vortex, in such a way that the two spheres would
revolve about some intermediate point and because of that circular motion
would recede from each other unless constrained by some force. Afterward,
if the continually impressed forces by which the spheres persevere in their
motions were to cease, and everything were left to the laws of mechanics, the
motion of the spheres would weaken little by little (for the reason assigned
in corols. 3 and 4), and the vortices would at last be completely at rest.
COROLLARY 6. If several spheres in given places revolved continually
with certain velocities around axes given in position, the same number of
vortices, going on without limit, would be made. For all of the spheres, for
the same reason that any one of them propagates its motion without limit,
will also propagate their motions without limit, in such a way that each part
of the infinite fluid is agitated by that motion which results from the actions
of all the spheres. Hence the vortices will not be limited by fixed bounds but
will little by little run into one another, and the spheres will be continually
moved from their places by the actions of the vortices upon one another, as
was explained in corol. 5; nor will they keep any fixed position with respect to
one another, unless constrained by some force. And when those forces, which
conserve the motions by being continually impressed upon the spheres, cease,
the matter—for the reason assigned in corols. 3 and 4—will little by little
come to rest and will no longer be made to move in vortices.
COROLLARY 7. If a homogeneous fluid is enclosed in a spherical vessel
and is made to revolve in a vortex by the uniform rotation of a sphere placed
in the center, and if the sphere and the vessel revolve in the same direction
about the same axis, and if their periodic times are as the squares of the
semidiameters, then the parts of the fluid will not persevere in their motions
without acceleration and retardation until their periodic times are as the
squares of the distances from the center of the vortex. No other constitution
of a vortex can be stable.
COROLLARY 8. If the vessel, the enclosed fluid, and the sphere conserve
this motion and additionally revolve with a common angular motion about
any given axis, then, since the friction of the parts of the fluid upon one
another is not changed by this new motion, the motions of the parts with
respect to one another will not be changed. For the relative velocities of
the parts with respect to one another depend upon friction. Any part will
persevere in that motion by which the friction on one side does not retard it
more than the friction on the other accelerates it.
COROLLARY 9. Hence, if the vessel is at rest, and if the motion of the
sphere is given, the motion of the fluid will be given. For imagine that a plane
passes through the axis of the sphere and revolves with an opposite motion,
and suppose that the sum of the time of the revolution of the plane and the
revolution of the sphere is to the time of the revolution of the sphere as the
square of the semidiameter of the vessel to the square of the semidiameter
of the sphere; then the periodic times of the parts of the fluid with respect
to the plane will be as the squares of their distances from the center of the
sphere.
COROLLARY 10. Accordingly, if the vessel moves with any velocity either
about the same axis as the sphere or about some different axis, the motion
of the fluid will be given. For if the angular motion of the vessel is taken
away from the whole system, all the motions with respect to one another will
remain the same as before, by corol. 8. And these motions will be given by
corol. 9.
COROLLARY 11. If the vessel and the fluid are at rest, and if the sphere
revolves with a uniform motion, then the motion will be propagated little
by little through the whole fluid to the vessel, and the vessel will be driven
around unless forcibly constrained, and the fluid and vessel will not cease to
be accelerated until their periodic times are equal to the periodic times of the
sphere. But if the vessel is constrained by some force or revolves with any
continual and uniform motion, the medium will little by little come to the
state of the motion defined in corols. 8, 9, and 10, nor will it ever persevere
in any other state. But then if, when those forces cease by which the vessel
and the sphere were revolving with fixed motions, the whole system is left to
the laws of mechanics, the vessel and the sphere will act upon each other by
means of the intervening fluid and will not cease to propagate their motions
to each other through the fluid until their periodic times are equal and the
whole system revolves together like one solid body.
Scholium
In the preceding propositions, I have been supposing the fluid to consist of
matter which is uniform in density and fluidity. The fluid is such that a given
sphere, set anywhere in it, would with a given motion in a given interval of
time be able to propagate similar and equal motions, at distances always
equal from itself. Indeed, matter endeavors by its circular motion to recede
from the axis of a vortex and therefore presses all the further matter. From
this pressure the friction of the parts becomes stronger and their separation
from one another more difficult, and consequently the fluidity of the matter is
decreased. Again, if there is any place where the parts of the fluid are thicker
or larger, the fluidity will be less there, because the surfaces separating the
parts from one another are fewer. In cases of this sort, I suppose the deficiency
in fluidity to be supplied either by the slipperiness of the parts or by their
pliancy or by some other condition. If this does not happen, the matter will
cohere more and will be more sluggish where it is less fluid, and thus will
receive motion more slowly and will propagate it further than according
to the ratio assigned above. If the shape of the vessel is not spherical, the
particles will move in paths which are not circular but correspond to the
shape of the vessel, and the periodic times will be very nearly as the squares
of the mean distances from the center. In the parts between the center and
the circumference where the spaces are wider, the motions will be slower,
and where the spaces are narrower the motions will be swifter, and yet the
swifter particles will not seek the circumference. For they will describe
less-curved arcs, and the endeavor to recede from the center will not be less
decreased by the decrement of this curvature than it will be increased by the
increment of the velocity. In going from the narrower spaces into the wider,
they will recede a little further from the center, but they will be retarded
by this receding, and afterward in approaching the narrower spaces from the
wider ones they will be accelerated, and thus each of the particles will forever
alternately be retarded and accelerated. All of this will be so in a rigid vessel.
For the constitution of vortices in an infinite fluid can be found by corol. 6
of this proposition.
Moreover, in this proposition I have tried to investigate the properties of
vortices in order to test whether the celestial phenomena could be explained
in any way by vortices. For it is a phenomenon that the periodic times of
the secondary planets that revolve about Jupiter are as the 3/2 powers of the
distances from the center of Jupiter; and the same rule applies to the planets
that revolve about the sun. Moreover, these rules apply to both the primary
and the secondary planets very exactly, as far as astronomical observations
have shown up to now. And thus if those planets are carried along by vortices
revolving about Jupiter and the sun, the vortices will also have to revolve
according to the same law. But the periodic times of the parts of a vortex
turned out to be in the squared ratio of the distances from the center of
motion, and that ratio cannot be decreased and reduced to the 3/2 power,
unless either the matter of the vortex is the more fluid the further it is from
the center, or the resistance arising from a deficiency in the slipperiness of
the parts of the fluid (as a result of the increased velocity by which the parts
of the fluid are separated from one another) is increased in a greater ratio
than the ratio in which the velocity is increased. Yet neither of these seems
reasonable. The thicker and less-fluid parts, if they are not heavy toward
the center, will seek the circumference; and although—for the sake of the
proofs—I proposed at the beginning of this section a hypothesis in which the
resistance would be proportional to the velocity, it is nevertheless likely that
the resistance is in a lesser ratio than that of the velocity. If this is conceded,
then the periodic times of the parts of a vortex will be in a ratio greater than
the squared ratio of the distances from its center. But if vortices (as is the
opinion of some) move more quickly near the center, then more slowly up
to a certain limit, then again more quickly near the circumference, certainly
neither the 3/2 power nor any other fixed and determinate ratio can hold. It
is therefore up to philosophers to see how that phenomenon of the 3/2 power
can be explained by vortices.
Proposition 53, Theorem 41
Bodies that are carried along in a vortex and return in the same orbit have the
same density as the vortex and move according to the same law as the parts of the
vortex with respect to velocity and direction.
For if some tiny part of the vortex is composed of particles or physical
points which preserve a given situation with respect to one another and is
supposed to be frozen, then this part will move according to the same law
as before, since it is not changed with respect to its density, or its inherent
force or figure. And conversely, if a frozen and solid part of the vortex has
the same density as the rest of the vortex and is resolved into a fluid, this
part will move according to the same law as before, except insofar as its
particles, which have now become fluid, move with respect to one another.
Therefore, the motion of the particles with respect to one another may be
ignored as having no relevance to the progressive motion of the whole, and
the motion of the whole will be the same as before. But this motion will be
the same as the motion of other parts of the vortex that are equally distant
from the center, because the solid resolved into a fluid becomes a part of the
vortex similar in every way to the other parts. Therefore, if a solid is of the
same density as the matter of the vortex, it will move with the same motion
as the parts of the vortex and will be relatively at rest in the immediately
surrounding matter. But if the solid is denser, it will now endeavor to recede
from the center of the vortex more than before; and thus, overcoming that
force of the vortex by which it was formerly kept in its orbit as if set in
equilibrium, it will recede from the center and in revolving will describe
a spiral and will no longer return into the same orbit. And by the same
argument, if the solid is rarer, it will approach the center. Therefore, the
solid will not return into the same orbit unless it is of the same density as
the fluid. And it has been shown that in this case the solid would revolve
according to the same law as the parts of the fluid that are equally distant
from the center of the vortex. Q.E.D.
COROLLARY 1. Therefore a solid that revolves in a vortex and always
returns into the same orbit is relatively at rest in the fluid in which it is immersed.
COROLLARY 2. And if the vortex is of a uniform density, the same body
can revolve at any distance from the center of the vortex.
Scholium
Hence it is clear that the planets are not carried along by corporeal
vortices. For the planets, which—according to the Copernican hypothesis—move
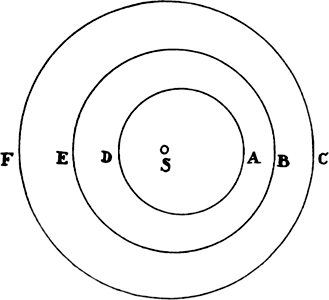 about the sun, revolve in ellipses having a focus in the sun, and by radii
drawn to the sun describe areas
proportional to the times. But the parts
of a vortex cannot revolve with such
a motion. Let AD, BE, and CF
designate three orbits described about the
sun S, of which let the outermost CF
be a circle concentric with the sun, and
let A and B be the aphelia of the two inner ones, and D and E their perihelia. Therefore, a body that revolves in
the orbit CF, describing areas proportional to the times by a radius drawn
to the sun, will move with a uniform motion. And a body that revolves in
the orbit BE will, according to the laws of astronomy, move more slowly
in the aphelion B and more swiftly in the perihelion E, although according
to the laws of mechanics the matter of the vortex ought to move more swiftly
in the narrower space between A and C than in the wider space between
D and F, that is, more swiftly in the aphelion than in the perihelion. These
two statements are contradictory. Thus in the beginning of the sign of Virgo,
where the aphelion of Mars now is, the distance between the orbits of Mars
and Venus is to the distance between these orbits in the beginning of the sign
of Pisces as roughly 3 to 2, and therefore the matter of the vortex between
these orbits in the beginning of Pisces must move more swiftly than in the
beginning of Virgo in the ratio of 3 to 2. For the narrower the space through
which a given quantity of matter passes in the given time of one revolution,
the greater the velocity with which it must pass. Therefore, if the earth,
relatively at rest in this celestial matter, were carried by it and revolved along
with it about the sun, its velocity in the beginning of Pisces would be to its
velocity in the beginning of Virgo as 3 to 2. Hence the apparent daily motion
of the sun in the beginning of Virgo would be greater than 70 minutes, and
in the beginning of Pisces less than 48 minutes, although (as experience bears
witness) the apparent motion of the sun is greater in the beginning of Pisces
than in the beginning of Virgo, and thus the earth is swifter in the beginning
of Virgo than in the beginning of Pisces. Therefore the hypothesis of vortices
can in no way be reconciled with astronomical phenomena and serves less
to clarify the celestial motions than to obscure them. But how those motions
are performed in free spaces without vortices can be understood from book
1 and will now be shown more fully in book 3 on the system of the world.
about the sun, revolve in ellipses having a focus in the sun, and by radii
drawn to the sun describe areas
proportional to the times. But the parts
of a vortex cannot revolve with such
a motion. Let AD, BE, and CF
designate three orbits described about the
sun S, of which let the outermost CF
be a circle concentric with the sun, and
let A and B be the aphelia of the two inner ones, and D and E their perihelia. Therefore, a body that revolves in
the orbit CF, describing areas proportional to the times by a radius drawn
to the sun, will move with a uniform motion. And a body that revolves in
the orbit BE will, according to the laws of astronomy, move more slowly
in the aphelion B and more swiftly in the perihelion E, although according
to the laws of mechanics the matter of the vortex ought to move more swiftly
in the narrower space between A and C than in the wider space between
D and F, that is, more swiftly in the aphelion than in the perihelion. These
two statements are contradictory. Thus in the beginning of the sign of Virgo,
where the aphelion of Mars now is, the distance between the orbits of Mars
and Venus is to the distance between these orbits in the beginning of the sign
of Pisces as roughly 3 to 2, and therefore the matter of the vortex between
these orbits in the beginning of Pisces must move more swiftly than in the
beginning of Virgo in the ratio of 3 to 2. For the narrower the space through
which a given quantity of matter passes in the given time of one revolution,
the greater the velocity with which it must pass. Therefore, if the earth,
relatively at rest in this celestial matter, were carried by it and revolved along
with it about the sun, its velocity in the beginning of Pisces would be to its
velocity in the beginning of Virgo as 3 to 2. Hence the apparent daily motion
of the sun in the beginning of Virgo would be greater than 70 minutes, and
in the beginning of Pisces less than 48 minutes, although (as experience bears
witness) the apparent motion of the sun is greater in the beginning of Pisces
than in the beginning of Virgo, and thus the earth is swifter in the beginning
of Virgo than in the beginning of Pisces. Therefore the hypothesis of vortices
can in no way be reconciled with astronomical phenomena and serves less
to clarify the celestial motions than to obscure them. But how those motions
are performed in free spaces without vortices can be understood from book
1 and will now be shown more fully in book 3 on the system of the world.
 particles of the medium impinge with the
same velocity on the body at rest, let
us consider the body to be at rest and
see with what force it will be urged
by the moving medium. Let ABKI,
therefore, designate a spherical body
described with center C and
semidiameter C A, and let the particles of the
medium strike the spherical body with a given velocity along straight lines
parallel to AC; and let FB be such a straight line. On FB take LB equal
to the semidiameter CB, and draw BD touching the sphere in B. To KC
and BD drop the perpendiculars BE and LD; then the force with which a
particle of the medium, obliquely incident along the straight line FB, strikes
the sphere at B will be to the force with which the same particle would
strike the cylinder ONGQ (described with axis ACI about the sphere)
perpendicularly at b as LD to LB or BE to BC. Again, the efficacy of this force
to move the sphere along the direction FB (or AC) of its incidence is to its
efficacy to move the sphere along the direction of its determination—that
is, along the direction of the straight line BC in which it urges the sphere
directly [a direction through the center of the sphere]—as BE to BC. And,
compounding the ratios, if a particle strikes the sphere obliquely along the
straight line FB, its efficacy to move the sphere along the direction of its
incidence is to the efficacy of the same particle to move the cylinder in the
same direction, when striking the cylinder perpendicularly along the same
straight line, as BE2 to BC2. Therefore, if in bE, which is perpendicular to
the circular base NAO of the cylinder and equal to the radius AC, bH is
taken equal to
particles of the medium impinge with the
same velocity on the body at rest, let
us consider the body to be at rest and
see with what force it will be urged
by the moving medium. Let ABKI,
therefore, designate a spherical body
described with center C and
semidiameter C A, and let the particles of the
medium strike the spherical body with a given velocity along straight lines
parallel to AC; and let FB be such a straight line. On FB take LB equal
to the semidiameter CB, and draw BD touching the sphere in B. To KC
and BD drop the perpendiculars BE and LD; then the force with which a
particle of the medium, obliquely incident along the straight line FB, strikes
the sphere at B will be to the force with which the same particle would
strike the cylinder ONGQ (described with axis ACI about the sphere)
perpendicularly at b as LD to LB or BE to BC. Again, the efficacy of this force
to move the sphere along the direction FB (or AC) of its incidence is to its
efficacy to move the sphere along the direction of its determination—that
is, along the direction of the straight line BC in which it urges the sphere
directly [a direction through the center of the sphere]—as BE to BC. And,
compounding the ratios, if a particle strikes the sphere obliquely along the
straight line FB, its efficacy to move the sphere along the direction of its
incidence is to the efficacy of the same particle to move the cylinder in the
same direction, when striking the cylinder perpendicularly along the same
straight line, as BE2 to BC2. Therefore, if in bE, which is perpendicular to
the circular base NAO of the cylinder and equal to the radius AC, bH is
taken equal to 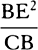 , then bH will be to bE as the effect of a particle upon
the sphere to the effect of the particle upon the cylinder. And therefore
the solid that is composed of all the straight lines bH will be to the solid
that is composed of all the straight lines bE as the effect of all the
particles upon the sphere to the effect of all the particles upon the cylinder. But
the first solid is a paraboloid described with vertex C, axis CA, and latus
rectum CA, and the second solid is a cylinder circumscribed around the
paraboloid; and it is known that a paraboloid is half of the circumscribed
cylinder. Therefore the whole force of the medium upon the sphere is half
of its whole force upon the cylinder. And therefore, if the particles of the
medium were at rest and the cylinder and the sphere were moving with
equal velocity, the resistance of the sphere would be half the resistance of the
cylinder. Q.E.D.
, then bH will be to bE as the effect of a particle upon
the sphere to the effect of the particle upon the cylinder. And therefore
the solid that is composed of all the straight lines bH will be to the solid
that is composed of all the straight lines bE as the effect of all the
particles upon the sphere to the effect of all the particles upon the cylinder. But
the first solid is a paraboloid described with vertex C, axis CA, and latus
rectum CA, and the second solid is a cylinder circumscribed around the
paraboloid; and it is known that a paraboloid is half of the circumscribed
cylinder. Therefore the whole force of the medium upon the sphere is half
of its whole force upon the cylinder. And therefore, if the particles of the
medium were at rest and the cylinder and the sphere were moving with
equal velocity, the resistance of the sphere would be half the resistance of the
cylinder. Q.E.D. to construct a frustum CBGF of a cone with the
circular base CEBH (which is described with
center O and radius OC) and with the height
OD, which is resisted less than any other
frustum constructed with the same base and height
and moving forward along the direction of the
axis toward D; bisect the height OD in Q, and
produce OQ to S so that QS is equal to QC,
and S will be the vertex of the cone whose frustum is required.
to construct a frustum CBGF of a cone with the
circular base CEBH (which is described with
center O and radius OC) and with the height
OD, which is resisted less than any other
frustum constructed with the same base and height
and moving forward along the direction of the
axis toward D; bisect the height OD in Q, and
produce OQ to S so that QS is equal to QC,
and S will be the vertex of the cone whose frustum is required. oval figure ADBE about the axis
AB, and if the generating figure
is touched by the three straight
lines FG, GH, and HI in points
F, B, and I, in such a way that
GH is perpendicular to the axis
in the point of contact B, and FG
and HI meet the said line GH at
the angles FGB and BHI of 135 degrees, then the solid that is generated by
the revolution of the figure ADFGHIE about the same axis AB is less
oval figure ADBE about the axis
AB, and if the generating figure
is touched by the three straight
lines FG, GH, and HI in points
F, B, and I, in such a way that
GH is perpendicular to the axis
in the point of contact B, and FG
and HI meet the said line GH at
the angles FGB and BHI of 135 degrees, then the solid that is generated by
the revolution of the figure ADFGHIE about the same axis AB is less
 sphere can lose its whole motion when the
resistance is continued uniformly. Erect AD and BC
perpendicular to AB. And let BC be the whole
motion, and through point C with asymptotes
AD and AB describe the hyperbola CF.
Produce AB to any point E. Erect the perpendicular
EF meeting the hyperbola in F. Complete the parallelogram CBEG, and
draw AF meeting BC in H. Then, if the sphere, in any time BE, when its
first motion BC is continued uniformly, in a nonresisting medium, describes
the space CBEG represented by the area of the parallelogram, it will in a
resisting medium describe the space CBEF represented by the area of the
hyperbola, and its motion at the end of that time will be represented by the
ordinate EF of the hyperbola, with loss of part FG of its motion. And the
resistance at the end of the same time will be represented by the length BH,
with loss of part CH of the resistance. All of this is evident by book 2, prop.
5, corols. 1 and 3.
sphere can lose its whole motion when the
resistance is continued uniformly. Erect AD and BC
perpendicular to AB. And let BC be the whole
motion, and through point C with asymptotes
AD and AB describe the hyperbola CF.
Produce AB to any point E. Erect the perpendicular
EF meeting the hyperbola in F. Complete the parallelogram CBEG, and
draw AF meeting BC in H. Then, if the sphere, in any time BE, when its
first motion BC is continued uniformly, in a nonresisting medium, describes
the space CBEG represented by the area of the parallelogram, it will in a
resisting medium describe the space CBEF represented by the area of the
hyperbola, and its motion at the end of that time will be represented by the
ordinate EF of the hyperbola, with loss of part FG of its motion. And the
resistance at the end of the same time will be represented by the length BH,
with loss of part CH of the resistance. All of this is evident by book 2, prop.
5, corols. 1 and 3. of its motion M without loss of part
of its motion M without loss of part 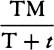 ;
and the sphere will describe a space that is to the space described by the
uniform motion M, in the same time t, as the logarithm of the number
;
and the sphere will describe a space that is to the space described by the
uniform motion M, in the same time t, as the logarithm of the number 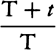 multiplied by the number 2.302585092994 is to the number
multiplied by the number 2.302585092994 is to the number 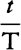 , because the
hyperbolic area BCFE is in this proportion to the rectangle BCGE.
, because the
hyperbolic area BCFE is in this proportion to the rectangle BCGE. And imagine that a cylinder of ice APQB is
of the same width as the interior of the vessel,
has the same axis, and descends continually with
a uniform motion. Imagine also that its parts
And imagine that a cylinder of ice APQB is
of the same width as the interior of the vessel,
has the same axis, and descends continually with
a uniform motion. Imagine also that its parts
 plane VW is drawn parallel to the plane of
the hole EF at a distance about equal to the
diameter of the hole and pierced by a larger
hole ST, and through this let a stream fall that
exactly fills the lower hole EF and thus has a
diameter which is to the diameter of this lower
hole as about 25 to 21. For thus the stream will
pass perpendicularly through the lower hole,
and the quantity of the water flowing out, depending on the size of this
hole, will be very nearly that which the solution of the problem demands.
Now, the space which is enclosed by the two planes and the falling stream
can be considered to be the bottom of the vessel. But so that the solution of
the problem may be simpler and more mathematical, it is preferable to use
only the lower plane for the bottom of the vessel and to imagine that the
water which flowed down through the ice as if through a funnel and came
out of the vessel through the hole EF in the lower plane keeps its motion
continually and that the ice keeps its state of rest. In what follows, therefore,
let ST be the diameter of a circular hole described with center Z, through
which a cataract flows out of the vessel when all the water in the vessel is
fluid. And let EF be the diameter of the hole which the cataract fills exactly
when falling through it, whether the water comes out of the vessel through
the upper hole ST or falls through the middle of the ice in the vessel as
if through a funnel. And let the diameter of the upper hole ST be to the
diameter of the lower hole EF as about 25 to 21, and let the perpendicular
distance between the planes of the holes be equal to the diameter of the
smaller hole EF. Then the downward velocity of the water coming out of
the vessel through the hole ST will in the hole itself be that which a body
can acquire in falling from half of the height IZ; and the velocity of both
falling cataracts will, in the hole EF, be that which a body will acquire in
falling from the whole height IG.
plane VW is drawn parallel to the plane of
the hole EF at a distance about equal to the
diameter of the hole and pierced by a larger
hole ST, and through this let a stream fall that
exactly fills the lower hole EF and thus has a
diameter which is to the diameter of this lower
hole as about 25 to 21. For thus the stream will
pass perpendicularly through the lower hole,
and the quantity of the water flowing out, depending on the size of this
hole, will be very nearly that which the solution of the problem demands.
Now, the space which is enclosed by the two planes and the falling stream
can be considered to be the bottom of the vessel. But so that the solution of
the problem may be simpler and more mathematical, it is preferable to use
only the lower plane for the bottom of the vessel and to imagine that the
water which flowed down through the ice as if through a funnel and came
out of the vessel through the hole EF in the lower plane keeps its motion
continually and that the ice keeps its state of rest. In what follows, therefore,
let ST be the diameter of a circular hole described with center Z, through
which a cataract flows out of the vessel when all the water in the vessel is
fluid. And let EF be the diameter of the hole which the cataract fills exactly
when falling through it, whether the water comes out of the vessel through
the upper hole ST or falls through the middle of the ice in the vessel as
if through a funnel. And let the diameter of the upper hole ST be to the
diameter of the lower hole EF as about 25 to 21, and let the perpendicular
distance between the planes of the holes be equal to the diameter of the
smaller hole EF. Then the downward velocity of the water coming out of
the vessel through the hole ST will in the hole itself be that which a body
can acquire in falling from half of the height IZ; and the velocity of both
falling cataracts will, in the hole EF, be that which a body will acquire in
falling from the whole height IG. GR, the velocity with which the water in the
vessel will flow out through the hole EF into
the standing water will be that which the water
can acquire in falling and describing by its fall
the space IR. For the
GR, the velocity with which the water in the
vessel will flow out through the hole EF into
the standing water will be that which the water
can acquire in falling and describing by its fall
the space IR. For the  of the water which that little circle sustains
is greater than the weight of ⅓ of a
cylinder of water whose base is that little circle
and whose height is GH. For let ABNFEM
be a cataract or column of falling water, with
axis GH as above, and suppose that there has
been a freezing of all the water in the vessel
(around the cataract as well as above the little
circle) whose fluidity is not required for the
very ready and very swift descent of the water. And let PHQ be the frozen
column of water above the little circle, having vertex H and height GH.
And imagine that this cataract falls with its whole weight and does not rest
or press on PHQ but slides past freely and without friction, except perhaps
at the very vertex of the ice, where at the very beginning of falling the
cataract begins to be concave. And just as the frozen water (AMEC and
BNFD) which is around the cataract is convex on the inner surface (AME
and BNF) toward the falling cataract, so also this column PHQ will be
convex toward the cataract, and therefore will be greater than a cone whose
base is the little circle PQ and whose height is GH, that is, greater than ⅓
of a cylinder described with the same base and height. And the little circle
sustains the weight of this column, that is, a weight that is greater than the
weight of the cone or of ⅓ of the cylinder.
of the water which that little circle sustains
is greater than the weight of ⅓ of a
cylinder of water whose base is that little circle
and whose height is GH. For let ABNFEM
be a cataract or column of falling water, with
axis GH as above, and suppose that there has
been a freezing of all the water in the vessel
(around the cataract as well as above the little
circle) whose fluidity is not required for the
very ready and very swift descent of the water. And let PHQ be the frozen
column of water above the little circle, having vertex H and height GH.
And imagine that this cataract falls with its whole weight and does not rest
or press on PHQ but slides past freely and without friction, except perhaps
at the very vertex of the ice, where at the very beginning of falling the
cataract begins to be concave. And just as the frozen water (AMEC and
BNFD) which is around the cataract is convex on the inner surface (AME
and BNF) toward the falling cataract, so also this column PHQ will be
convex toward the cataract, and therefore will be greater than a cone whose
base is the little circle PQ and whose height is GH, that is, greater than ⅓
of a cylinder described with the same base and height. And the little circle
sustains the weight of this column, that is, a weight that is greater than the
weight of the cone or of ⅓ of the cylinder. the cylindrical channel EFTS perpendicular to
the horizon, and if the little circle PQ is placed
parallel to the horizon anywhere in the middle
of the channel, and if CA is produced to K so
that CK is to AK in the squared ratio of the
circle AB to the amount by which the opening
of the channel EF exceeds the little circle PQ,
then it is obvious (by prop. 36, case 5, case 6,
and corol. 1) that the velocity of the water
passing through the annular space between the little
circle and the sides of the vessel will be that which the water can acquire in
falling and describing by its fall a space equal to the height KC or IG.
the cylindrical channel EFTS perpendicular to
the horizon, and if the little circle PQ is placed
parallel to the horizon anywhere in the middle
of the channel, and if CA is produced to K so
that CK is to AK in the squared ratio of the
circle AB to the amount by which the opening
of the channel EF exceeds the little circle PQ,
then it is obvious (by prop. 36, case 5, case 6,
and corol. 1) that the velocity of the water
passing through the annular space between the little
circle and the sides of the vessel will be that which the water can acquire in
falling and describing by its fall a space equal to the height KC or IG. in an enclosed medium at rest, and meanwhile
its axis coincides with the axis of the channel,
then the resistance to the cylinder will be to
the force by which its whole motion could be
either generated or destroyed, in the time in
which it describes four times its length, in a
ratio compounded of the simple ratio of EF2 to
EF2 − ½PQ2 and the squared ratio of EF2 to
EF2 − PQ2 and the ratio of the density of the
medium to the density of the cylinder.
in an enclosed medium at rest, and meanwhile
its axis coincides with the axis of the channel,
then the resistance to the cylinder will be to
the force by which its whole motion could be
either generated or destroyed, in the time in
which it describes four times its length, in a
ratio compounded of the simple ratio of EF2 to
EF2 − ½PQ2 and the squared ratio of EF2 to
EF2 − PQ2 and the ratio of the density of the
medium to the density of the cylinder. annulled, and the parts of the water, by
yielding with the most direct and rapid
motion, may provide the easiest passage
to the cylinder, and in order that only
the resistance may remain that arises
from the magnitude of the transverse section and that cannot be decreased
except by decreasing the diameter of the cylinder, it must be understood
that the parts of the fluid whose motions are oblique and useless and
create resistance are at rest with respect to one another at both ends of the
cylinder and cohere and are joined to the cylinder. Let ABDC be a
rectangle, and let AE and BE be two parabolic arcs described with axis AB
and with a latus rectum that is to the space HG, which is to be described
by the falling cylinder while it is acquiring its velocity, as HG to ½AB.
Additionally, let CF and DF be two other parabolic arcs, described with
axis CD and a latus rectum that is four times the former latus rectum; and
by the revolution of the figure about its axis EF, let a solid be generated
whose middle ABDC is the cylinder with which we are dealing, and whose
extremities ABE and CDF contain the parts of the fluid which are at rest
with respect to one another and solidified into two rigid bodies that adhere
to the cylinder at the ends as head and tail. Then the resistance to the solid
EACFDB moving forward in the direction of its axis FE from F toward E
will be very nearly that which we have described in this proposition. That
is, the density of the fluid is to the density of the cylinder very nearly in
the ratio of this resistance to the force by which the whole motion of the
cylinder could be either destroyed or generated, while the length 4AC is
being described with that motion continued uniformly. And with this force the
resistance cannot be less than in the ratio of 2 to 3, by prop. 36, corol. 7.
annulled, and the parts of the water, by
yielding with the most direct and rapid
motion, may provide the easiest passage
to the cylinder, and in order that only
the resistance may remain that arises
from the magnitude of the transverse section and that cannot be decreased
except by decreasing the diameter of the cylinder, it must be understood
that the parts of the fluid whose motions are oblique and useless and
create resistance are at rest with respect to one another at both ends of the
cylinder and cohere and are joined to the cylinder. Let ABDC be a
rectangle, and let AE and BE be two parabolic arcs described with axis AB
and with a latus rectum that is to the space HG, which is to be described
by the falling cylinder while it is acquiring its velocity, as HG to ½AB.
Additionally, let CF and DF be two other parabolic arcs, described with
axis CD and a latus rectum that is four times the former latus rectum; and
by the revolution of the figure about its axis EF, let a solid be generated
whose middle ABDC is the cylinder with which we are dealing, and whose
extremities ABE and CDF contain the parts of the fluid which are at rest
with respect to one another and solidified into two rigid bodies that adhere
to the cylinder at the ends as head and tail. Then the resistance to the solid
EACFDB moving forward in the direction of its axis FE from F toward E
will be very nearly that which we have described in this proposition. That
is, the density of the fluid is to the density of the cylinder very nearly in
the ratio of this resistance to the force by which the whole motion of the
cylinder could be either destroyed or generated, while the length 4AC is
being described with that motion continued uniformly. And with this force the
resistance cannot be less than in the ratio of 2 to 3, by prop. 36, corol. 7.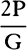 ,
and let L be the logarithm of the number
,
and let L be the logarithm of the number 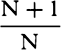 , then the velocity
acquired in falling will be
, then the velocity
acquired in falling will be 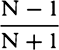 H, and the space described will be
H, and the space described will be
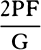 − 1.3862943611F + 4.605170186LF.
− 1.3862943611F + 4.605170186LF.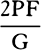 − 1.3862943611F will be the space described, very nearly. These
things are evident by book 2, prop. 9 and its corollaries, on the hypothesis
that the sphere encounters no other
− 1.3862943611F will be the space described, very nearly. These
things are evident by book 2, prop. 9 and its corollaries, on the hypothesis
that the sphere encounters no other 
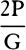 , and by subtracting the number 1.3862944 −
4.6051702L, the numbers in the third column are found, and these numbers
must be multiplied by the space F in order to get the spaces described in
falling. There has been added to these a fifth column, which contains the
spaces described in the same times by a
, and by subtracting the number 1.3862944 −
4.6051702L, the numbers in the third column are found, and these numbers
must be multiplied by the space F in order to get the spaces described in
falling. There has been added to these a fifth column, which contains the
spaces described in the same times by a 
 grains, or 193/10 grains, and
thus the weight of the ball in a
grains, or 193/10 grains, and
thus the weight of the ball in a 

 of its motion. But by the theory set forth in
this seventh section and confirmed by experiments with falling bodies, that
same ball ought, in describing that same length, to lose only
of its motion. But by the theory set forth in
this seventh section and confirmed by experiments with falling bodies, that
same ball ought, in describing that same length, to lose only  of its
motion, supposing that the density of water is to the density of air as 860
to 1. The resistances therefore were found to be greater by the experiments
with pendulums (for the reasons already described) than by the experiments
with falling balls, and in a ratio of roughly 4 to 3. But since the resistances
to pendulums oscillating in air, water, and quicksilver are increased similarly
by similar causes, the proportion of the resistances in these mediums will be
shown correctly enough by the experiments with pendulums as well as by
the experiments with falling bodies. And hence it can be concluded that the
resistances encountered by bodies moving in any fluids that are very fluid,
other things being equal, are as the densities of the fluids.
of its
motion, supposing that the density of water is to the density of air as 860
to 1. The resistances therefore were found to be greater by the experiments
with pendulums (for the reasons already described) than by the experiments
with falling balls, and in a ratio of roughly 4 to 3. But since the resistances
to pendulums oscillating in air, water, and quicksilver are increased similarly
by similar causes, the proportion of the resistances in these mediums will be
shown correctly enough by the experiments with pendulums as well as by
the experiments with falling bodies. And hence it can be concluded that the
resistances encountered by bodies moving in any fluids that are very fluid,
other things being equal, are as the densities of the fluids.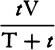 of its velocity
of its velocity 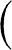 the part
the part
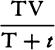 remaining
remaining  and will describe a space that is to the space described in
a vacuum in the same time with the uniform velocity V as the logarithm of
the number
and will describe a space that is to the space described in
a vacuum in the same time with the uniform velocity V as the logarithm of
the number  multiplied by the number 2.302585093 is to the number
t/T, by prop. 35, corol. 7. In slow motions the resistance can be a little
less, because the shape of a ball is a little more suitable for motion than the
shape of a
multiplied by the number 2.302585093 is to the number
t/T, by prop. 35, corol. 7. In slow motions the resistance can be a little
less, because the shape of a ball is a little more suitable for motion than the
shape of a  placed particles f and g obliquely, and those particles
f and g will not sustain the pressure brought upon
them unless they are supported by the further particles
h and k; but to the extent that they are supported,
they press the supporting particles, and these will not
sustain the pressure unless they are supported by the
further particles l and m and press them, and so on indefinitely. Therefore,
as soon as a pressure is propagated to particles which do not lie in a straight
line, it will begin to spread out and will be obliquely propagated indefinitely;
and after the pressure begins to be propagated obliquely, if it should impinge
upon further particles which do not lie in a straight line, it will spread out
again, and will do so as often as it impinges upon particles not lying exactly
in a straight line. Q.E.D.
placed particles f and g obliquely, and those particles
f and g will not sustain the pressure brought upon
them unless they are supported by the further particles
h and k; but to the extent that they are supported,
they press the supporting particles, and these will not
sustain the pressure unless they are supported by the
further particles l and m and press them, and so on indefinitely. Therefore,
as soon as a pressure is propagated to particles which do not lie in a straight
line, it will begin to spread out and will be obliquely propagated indefinitely;
and after the pressure begins to be propagated obliquely, if it should impinge
upon further particles which do not lie in a straight line, it will spread out
again, and will do so as often as it impinges upon particles not lying exactly
in a straight line. Q.E.D.



 Let AB, BC, CD, . . . designate the
equal distances between successive pulses;
ABC the line of motion of the pulses,
propagated from A toward B; E, F, and
G three physical points in the medium
at rest, situated at equal intervals along
the straight line AC; Ee, Ff, and Gg
very short equal spaces through which
those points go and return in each
Let AB, BC, CD, . . . designate the
equal distances between successive pulses;
ABC the line of motion of the pulses,
propagated from A toward B; E, F, and
G three physical points in the medium
at rest, situated at equal intervals along
the straight line AC; Ee, Ff, and Gg
very short equal spaces through which
those points go and return in each
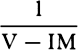 to
to 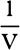 in
the going, and as
in
the going, and as 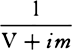 to
to 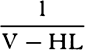 and
and 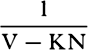 to
to 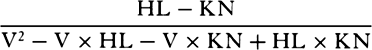 to
to
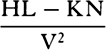 to
to  And suppose that a pendulum is set up,
whose length between the point of
suspension and the center of oscillation is
A; then, in the same time in which that
pendulum performs an entire oscillation
composed of a going and a returning, a
pulse will advance through a space equal
to the circumference of a circle described
with radius A.
And suppose that a pendulum is set up,
whose length between the point of
suspension and the center of oscillation is
A; then, in the same time in which that
pendulum performs an entire oscillation
composed of a going and a returning, a
pulse will advance through a space equal
to the circumference of a circle described
with radius A.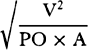 and
and 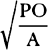 jointly, that is, as V
to A. But in the time of one vibration, composed of a going and returning,
a pulse advances through its own length BC. Therefore the time in which
the pulse traverses the space BC is to the time of one oscillation (composed
of a going and returning) as V to A, that is, as BC to the circumference of
a circle whose radius is A. But the time in which the pulse will traverse the
space BC is in the same ratio to the time in which it will traverse a length
equal to this circumference; and thus in the time of such an oscillation the
pulse will traverse a length equal to this circumference. Q.E.D.
jointly, that is, as V
to A. But in the time of one vibration, composed of a going and returning,
a pulse advances through its own length BC. Therefore the time in which
the pulse traverses the space BC is to the time of one oscillation (composed
of a going and returning) as V to A, that is, as BC to the circumference of
a circle whose radius is A. But the time in which the pulse will traverse the
space BC is in the same ratio to the time in which it will traverse a length
equal to this circumference; and thus in the time of such an oscillation the
pulse will traverse a length equal to this circumference. Q.E.D. feet or roughly 109
feet may be added, because of the density of the particles of air; and thus
sound will travel roughly 1,088 feet in the time of 1 second.
feet or roughly 109
feet may be added, because of the density of the particles of air; and thus
sound will travel roughly 1,088 feet in the time of 1 second. the same thickness by the concentric
the same thickness by the concentric
 revolve uniformly about the axis S, and
divide the fluid into innumerable concentric
orbs
revolve uniformly about the axis S, and
divide the fluid into innumerable concentric
orbs about the
about the