In the preceding books I have presented principles of philosophya that are not, however, philosophical but strictly mathematical—that is, those on which the study of philosophy can be based. These principles are the laws and conditions of motions and of forces, which especially relate to philosophy. But in order to prevent these principles from seeming sterile, I have illustrated them with some philosophical scholiums [i.e., scholiums dealing with natural philosophy], treating topics that are general and that seem to be the most fundamental for philosophy, such as the density and resistance of bodies, spaces void of bodies, and the motion of light and sounds. It still remains for us to exhibit the system of the world from these same principles. On this subject I composed an earlier version of book 3 in popular form, so that it might be more widely read. But those who have not sufficiently grasped the principles set down here will certainly not perceive the force of the conclusions, nor will they lay aside the preconceptions to which they have become accustomed over many years; and therefore, to avoid lengthy disputations, I have translated the substance of the earlier version into propositions in a mathematical style, so that they may be read only by those who have first mastered the principles. But since in books 1 and 2 a great number of propositions occur which might be too time-consuming even for readers who are proficient in mathematics, I am unwilling to advise anyone to study every one of these propositions. It will be sufficient to read with care the Definitions, the Laws of Motion, and the first three sections of book 1, and then turn to this book 3 on the system of the world, consulting at will the other propositions of books 1 and 2 which are referred to here.
Proposition 1, Theorem 1
The forces by which the circumjovial planets [or satellites of Jupiter] are continually drawn away from rectilinear motions and are maintained in their respective orbits are directed to the center of Jupiter and are inversely as the squares of the distances of their places from that center.
The first part of the proposition is evident from phen. 1 and from prop. 2 or prop. 3 of book 1, and the second part from phen. 1 and from corol. 6 to prop. 4 of book 1.
The same is to be understood for the planets that are Saturn’s companions [or satellites] by phen. 2.
Proposition 2, Theorem 2
The forces by which the primary planets are continually drawn away from rectilinear motions and are maintained in their respective orbits are directed to the sun and are inversely as the squares of their distances from its center.
The first part of the proposition is evident from phen. 5 and from prop. 2 of book 1, and the latter part from phen. 4 and from prop. 4 of the same book. But this second part of the proposition is proved with the greatest exactness from the fact that the aphelia are at rest. For the slightest departure from the ratio of the square would (by book 1, prop. 45, corol. 1) necessarily result in a noticeable motion of the apsides in a single revolution and an immense such motion in many revolutions.
Proposition 3, Theorem 3
The force by which the moon is maintained in its orbit is directed toward the earth and is inversely as the square of the distance of its places from the center of the earth.
The first part of this statement is evident from phen. 6 and from prop. 2 or prop. 3 of book 1, and the second part from the very slow motion of the moon’s apogee. For that motion, which in each revolution is only three degrees and three minutes forward [or in consequentia, i.e., in an easterly direction] can be ignored. For it is evident (by book 1, prop. 45, corol. 1) that if the distance of the moon from the center of the earth is to the semidiameter of the earth as D to 1, then the force from which such a motion may arise is inversely as D24/243, that is, inversely as that power of D of which the index is 24/243; that is, the proportion of the force to the distance is inversely as a little greater than the second power of the distance, but is 59¾ times closer to the square than to the cube. Now this motion of the apogee arises from the action of the sun (as will be pointed out below) and accordingly is to be ignored here. The action of the sun, insofar as it draws the moon away from the earth, is very nearly as the distance of the moon from the earth, and so (from what is said in book 1, prop. 45, corol. 2) is to the centripetal force of the moon as roughly 2 to 357.45, or 1 to 17829/40. And if so small a force of the sun is ignored, the remaining force by which the moon is maintained in its orbit will be inversely as D2. And this will be even more fully established by comparing this force with the force of gravity as is done in prop. 4 below.
COROLLARY. If the mean centripetal force by which the moon is maintained in its orbit is increased first in the ratio of 17729/40 to 17829/40, then also in the squared ratio of the semidiameter of the earth to the mean distance of the center of the moon from the center of the earth, the result will be the lunar centripetal force at the surface of the earth, supposing that that force, in descending to the surface of the earth, is continually increased in the ratio of the inverse square of the height.
Proposition 4, Theorem 4
The moon gravitates toward the earth and by the force of gravity is always drawn back from rectilinear motion and kept in its orbit.
The mean distance of the moon from the earth in the syzygies is, according to Ptolemy and most astronomers, 59 terrestrial semidiameters, 60 according to Vendelin and Huygens, 60⅓ according to Copernicus, 60⅖ according to Street, and 56½ according to Tycho. But Tycho and all those who follow his tables of refractions, by making the refractions of the sun and moon (entirely contrary to the nature of light) be greater than those of the fixed stars—in fact greater by about four or five minutes—have increased the parallax of the moon by that many minutes, that is, by about a twelfth or fifteenth of the whole parallax. Let that error be corrected, and the distance will come to be roughly 60½ terrestrial semidiameters, close to the value that has been assigned by others. Let us assume a mean distance of 60 semidiameters in the syzygies; and also let us assume that a revolution of the moon with respect to the fixed stars is completed in 27 days, 7 hours, 43 minutes, as has been established by astronomers; and that the circumference of the earth is 123,249,600 Paris feet, according to the measurements made by the French. If now the moon is imagined to be deprived of all its motion and to be let fall so that it will descend to the earth with all that force urging it by which (by prop. 3, corol.) it is [normally] kept in its orbit, then in the space of one minute, it will by falling describe 151/12 Paris feet. This is determined by a calculation carried out either by using prop. 36 of book 1 or (which comes to the same thing) by using corol. 9 to prop. 4 of book 1. For the versed sine of the arc which the moon would describe in one minute of time by its mean motion at a distance of 60 semidiameters of the earth is roughly 151/12 Paris feet, or more exactly 15 feet, 1 inch, and 14/9 lines [or twelfths of an inch]. Accordingly, since in approaching the earth that force is increased as the inverse square of the distance, and so at the surface of the earth is 60 × 60 times greater than at the moon, it follows that a body falling with that force, in our regions, ought in the space of one minute to describe 60 × 60 × 151/12 Paris feet, and in the space of one second 151/12 feet, or more exactly 15 feet, 1 inch, and 14/9 lines. And heavy bodies do actually descend to the earth with this very force. For a pendulum beating seconds in the latitude of Paris is 3 Paris feet and 8½ lines in length, as Huygens observed. And the height that a heavy body describes by falling in the time of one second is to half the length of this pendulum as the square of the ratio of the circumference of a circle to its diameter (as Huygens also showed), and so is 15 Paris feet, 1 inch, 17/9 lines. And therefore that force by which the moon is kept in its orbit, in descending from the moon’s orbit to the surface of the earth, comes out equal to the force of gravity here on earth, and so (by rules 1 and 2) is that very force which we generally call gravity. For if gravity were different from this force, then bodies making for the earth by both forces acting together would descend twice as fast, and in the space of one second would by falling describe 30⅙ Paris feet, entirely contrary to experience.
This calculation is founded on the hypothesis that the earth is at rest. For if the earth and the moon move around the sun and in the meanwhile also revolve around their common center of gravity, then, the law of gravity remaining the same, the distance of the centers of the moon and earth from each other will be roughly 60½ terrestrial semidiameters, as will be evident to anyone who computes it. And the computation can be undertaken by book 1, prop. 60.
Scholium
The proof of the proposition can be treated more fully as follows. If several moons were to revolve around the earth, as happens in the system of Saturn or of Jupiter, their periodic times (by the argument of induction) would observe the law which Kepler discovered for the planets, and therefore their centripetal forces would be inversely as the squares of the distances from the center of the earth, by prop. 1 of this book 3. And if the lowest of them were small and nearly touched the tops of the highest mountains, its centripetal force, by which it would be kept in its orbit, would (by the preceding computation) be very nearly equal to the gravities of bodies on the tops of those mountains. And this centripetal force would cause this little moon, if it were deprived of all the motion with which it proceeds in its orbit, to descend to the earth—as a result of the absence of the centrifugal force with which it had remained in its orbit—and to do so with the same velocity with which heavy bodies fall on the tops of those mountains, because the forces with which they descend are equal. And if the force by which the lowest little moon descends were different from gravity and that little moon also were heavy toward the earth in the manner of bodies on the tops of mountains, this little moon would descend twice as fast by both forces acting together. Therefore, since both forces—namely, those of heavy bodies and those of the moons—are directed toward the center of the earth and are similar to each other and equal, they will (by rules 1 and 2) have the same cause. And therefore that force by which the moon is kept in its orbit is the very one that we generally call gravity. For if this were not so, the little moon at the top of a mountain must either be lacking in gravity or else fall twice as fast as heavy bodies generally do.
Proposition 5, Theorem 5
The circumjovial planets [or satellites of Jupiter] gravitate toward Jupiter, the circumsaturnian planets [or satellites of Saturn] gravitate toward Saturn, and the circumsolar [or primary] planets gravitate toward the sun, and by the force of their gravity they are always drawn back from rectilinear motions and kept in curvilinear orbits.
For the revolutions of the circumjovial planets about Jupiter, of the circumsaturnian planets about Saturn, and of Mercury and Venus and the other circumsolar planets about the sun are phenomena of the same kind as the revolution of the moon about the earth, and therefore (by rule 2) depend on causes of the same kind, especially since it has been proved that the forces on which those revolutions depend are directed toward the centers of Jupiter, Saturn, and the sun, and decrease according to the same ratio and law (in receding from Jupiter, Saturn, and the sun) as the force of gravity (in receding from the earth).
COROLLARY 1. Therefore, there is gravity toward all planets universally. For no one doubts that Venus, Mercury, and the rest [of the planets, primary and secondary,] are bodies of the same kind as Jupiter and Saturn. And since, by the third law of motion, every attraction is mutual, Jupiter will gravitate toward all its satellites, Saturn toward its satellites, and the earth will gravitate toward the moon, and the sun toward all the primary planets.
COROLLARY 2. The gravity that is directed toward every planet is inversely as the square of the distance of places from the center of the planet.
COROLLARY 3. All the planets are heavy toward one another by corols. 1 and 2. And hence Jupiter and Saturn near conjunction, by attracting each other, sensibly perturb each other’s motions, the sun perturbs the lunar motions, and the sun and moon perturb our sea, as will be explained in what follows.
Scholium
Hitherto we have called “centripetal” that force by which celestial bodies are kept in their orbits. It is now established that this force is gravity, and therefore we shall call it gravity from now on. For the cause of the centripetal force by which the moon is kept in its orbit ought to be extended to all the planets, by rules 1, 2, and 4.
Proposition 6, Theorem 6
All bodies gravitate toward each of the planets, and at any given distance from the center of any one planet the weight of any body whatever toward that planet is proportional to the quantity of matter which the body contains.
Others have long since observed that the falling of all heavy bodies toward the earth (at least on making an adjustment for the inequality of the retardation that arises from the very slight resistance of the air) takes place in equal times, and it is possible to discern that equality of the times, to a very high degree of accuracy, by using pendulums. I have tested this with gold, silver, lead, glass, sand, common salt, wood, water, and wheat. I got two wooden boxes, round and equal. I filled one of them with wood, and I suspended the same weight of gold (as exactly as I could) in the center of oscillation of the other. The boxes, hanging by equal eleven-foot cords, made pendulums exactly like each other with respect to their weight, shape, and air resistance. Then, when placed close to each other [and set into vibration], they kept swinging back and forth together with equal oscillations for a very long time. Accordingly, the amount of matter in the gold (by book 2, prop. 24, corols. 1 and 6) was to the amount of matter in the wood as the action of the motive force upon all the gold to the action of the motive force upon all the [added] wood—that is, as the weight of one to the weight of the other. And it was so for the rest of the materials. In these experiments, in bodies of the same weight, a difference of matter that would be even less than a thousandth part of the whole could have been clearly noticed. Now, there is no doubt that the nature of gravity toward the planets is the same as toward the earth. For imagine our terrestrial bodies to be raised as far as the orbit of the moon and, together with the moon, deprived of all motion, to be released so as to fall to the earth simultaneously; and by what has already been shown, it is certain that in equal times these falling terrestrial bodies will describe the same spaces as the moon, and therefore that they are to the quantity of matter in the moon as their own weights are to its weight. Further, since the satellites of Jupiter revolve in times that are as the 3/2 power of their distances from the center of Jupiter, their accelerative gravities toward Jupiter will be inversely as the squares of the distances from the center of Jupiter, and, therefore, at equal distances from Jupiter their accelerative gravities would come out equal. Accordingly, in equal times in falling from equal heights [toward Jupiter] they would describe equal spaces, just as happens with heavy bodies on this earth of ours. And by the same argument the circumsolar [or primary] planets, let fall from equal distances from the sun, would describe equal spaces in equal times in their descent to the sun. Moreover, the forces by which unequal bodies are equally accelerated are as the bodies; that is, the weights [of the primary planets toward the sun] are as the quantities of matter in the planets. Further, that the weights of Jupiter and its satellites toward the sun are proportional to the quantities of their matter is evident from the extremely regular motion of the satellites, according to book 1, prop. 65, corol. 3. For if some of these were more strongly attracted toward the sun in proportion to the quantity of their matter than the rest, the motions of the satellites (by book 1, prop. 65, corol. 2) would be perturbed by that inequality of attraction. If, at equal distances from the sun, some satellite were heavier [or gravitated more] toward the sun in proportion to the quantity of its matter than Jupiter in proportion to the quantity of its own matter, in any given ratio, say d to e, then the distance between the center of the sun and the center of the orbit of the satellite would always be greater than the distance between the center of the sun and the center of Jupiter and these distances would be to each other very nearly as the square root of d to the square root of e, as I found by making a certain calculation. And if the satellite were less heavy [or gravitated less] toward the sun in that ratio of d to e, the distance of the center of the orbit of the satellite from the sun would be less than the distance of the center of Jupiter from the sun in that same ratio of the square root of d to the square root of e. And so if, at equal distances from the sun, the accelerative gravity of any satellite toward the sun were greater or smaller than the accelerative gravity of Jupiter toward the sun, by only a thousandth of the whole gravity, the distance of the center of the orbit of the satellite from the sun would be greater or smaller than the distance of Jupiter from the sun by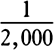 
of the total distance, that is, by a fifth of the distance of the outermost satellite from the center of Jupiter; and this eccentricity of the orbit would be very sensible indeed. But the orbits of the satellites are concentric with Jupiter, and therefore the accelerative gravities of Jupiter and of the satellites toward the sun are equal to one another. And by the same argument the weights [or gravities] of Saturn and its companions toward the sun, at equal distances from the sun, are as the quantities of matter in them; and the weights of the moon and earth toward the sun are either nil or exactly proportional to their masses. But they do have some weight, according to prop. 5, corols. 1 and 3.
But further, the weights [or gravities] of the individual parts of each planet toward any other planet are to one another as the matter in the individual parts. For if some parts gravitated more, and others less, than in proportion to their quantity of matter, the whole planet, according to the kind of parts in which it most abounded, would gravitate more or gravitate less than in proportion to the quantity of matter of the whole. But it does not matter whether those parts are external or internal. For if, for example, it is imagined that bodies on our earth are raised to the orbit of the moon and compared with the body of the moon, then, if their weights were to the weights of the external parts of the moon as the quantities of matter in them, but were to the weights of the internal parts in a greater or lesser ratio, they would be to the weight of the whole moon in a greater or lesser ratio, contrary to what has been shown above.
COROLLARY 1. Hence, the weights of bodies do not depend on their forms and textures. For if the weights could be altered with the forms, they would be, in equal matter, greater or less according to the variety of forms, entirely contrary to experience.
COROLLARY 5. The force of gravity is of a different kind from the magnetic force. For magnetic attraction is not proportional to the [quantity of] matter attracted. Some bodies are attracted [by a magnet] more [than in proportion to their quantity of matter], and others less, while most bodies are not attracted [by a magnet at all]. And the magnetic force in one and the same body can be intended and remitted [i.e., increased and decreased] and is sometimes far greater in proportion to the quantity of matter than the force of gravity; and this force, in receding from the magnet, decreases not as the square but almost as the cube of the distance, as far as I have been able to tell from certain rough observations.
Proposition 7, Theorem 7
Gravity exists in all bodies universally and is proportional to the quantity of matter in each.
We have already proved that all planets are heavy [or gravitate] toward one another and also that the gravity toward any one planet, taken by itself, is inversely as the square of the distance of places from the center of the planet. And it follows (by book 1, prop. 69 and its corollaries) that the gravity toward all the planets is proportional to the matter in them.
Further, since all the parts of any planet A are heavy [or gravitate] toward any planet B, and since the gravity of each part is to the gravity of the whole as the matter of that part to the matter of the whole, and since to every action (by the third law of motion) there is an equal reaction, it follows that planet B will gravitate in turn toward all the parts of planet A, and its gravity toward any one part will be to its gravity toward the whole of the planet as the matter of that part to the matter of the whole. Q.E.D.
COROLLARY 1. Therefore the gravity toward the whole planet arises from and is compounded of the gravity toward the individual parts. We have examples of this in magnetic and electric attractions. For every attraction toward a whole arises from the attractions toward the individual parts. This will be understood in the case of gravity by thinking of several smaller planets coming together into one globe and composing a larger planet. For the force of the whole will have to arise from the forces of the component parts. If anyone objects that by this law all bodies on our earth would have to gravitate toward one another, even though gravity of this kind is by no means detected by our senses, my answer is that gravity toward these bodies is far smaller than what our senses could detect, since such gravity is to the gravity toward the whole earth as [the quantity of matter in each of] these bodies to the [quantity of matter in the] whole earth.
COROLLARY 2. The gravitation toward each of the individual equal particles of a body is inversely as the square of the distance of places from those particles. This is evident by book 1, prop. 74, corol. 3.
Proposition 8, Theorem 8
If two globes gravitate toward each other, and their matter is homogeneous on all sides in regions that are equally distant from their centers, then the weight of either globe toward the other will be inversely as the square of the distance between the centers.
After I had found that the gravity toward a whole planet arises from and is compounded of the gravities toward the parts and that toward each of the individual parts it is inversely proportional to the squares of the distances from the parts, I was still not certain whether that proportion of the inverse square obtained exactly in a total force compounded of a number of forces, or only nearly so. For it could happen that a proportion which holds exactly enough at very great distances might be markedly in error near the surface of the planet, because there the distances of the particles may be unequal and their situations dissimilar. But at length, by means of book 1, props. 75 and 76 and their corollaries, I discerned the truth of the proposition dealt with here.
COROLLARY 3. The densities of the planets can also be found. For the weights of equal and homogeneous bodies toward homogeneous spheres are, on the surfaces of the spheres, as the diameters of the spheres, by book 1, prop. 72; and therefore the densities of heterogeneous spheres are as those weights divided by the diameters of the spheres. Now, the true diameters of the sun, Jupiter, Saturn, and the earth were found to be to one another as 10,000, 997, 791, and 109, and the weights toward them are as 10,000, 943, 529, and 435 respectively, and therefore the densities are as 100, 94½, 67, and 400. The density of the earth that results from this computation does not depend on the parallax of the sun but is determined by the parallax of the moon and therefore is determined correctly here. Therefore the sun is a little denser than Jupiter, and Jupiter denser than Saturn, and the earth four times denser than the sun. For the sun is rarefied by its great heat. And the moon is denser than the earth, as will be evident from what follows [i.e., prop. 37, corol. 3].
cCOROLLARY 4. Therefore, other things being equal, the planets that are smaller are denser. For thus the force of gravity on their surfaces approaches closer to equality. But, other things being equal, the planets that are nearer to the sun are also denser; for example, Jupiter is denser than Saturn, and the earth is denser than Jupiter. The planets, of course, had to be set at different distances from the sun so that each one might, according to the degree of its density, enjoy a greater or smaller amount of heat from the sun.c If the earth were located in the orbit of Saturn, our water would freeze; in the orbit of Mercury, it would immediately go off in a vapor. For the light of the sun, to which its heat is proportional, is seven times denser in the orbit of Mercury than on earth, and I have found with a thermometer that water boils at seven times the heat of the summer sun. And there is no doubt that the matter of the planet Mercury is adapted to its heat and therefore is denser than this matter of our earth, since all denser matter requires a greater heat for the performance of the operations of nature.
Proposition 9, Theorem 9
In going inward from the surfaces of the planets, gravity decreases very nearly in the ratio of the distances from the center.
If the matter of the planets were of uniform density, this proposition would hold true exactly, by book 1, prop. 73. Therefore the error is as great as can arise from the nonuniformity of the density.
Proposition 10, Theorem 10
The motions of the planets can continue in the heavens for a very long time.
In the scholium to prop. 40, book 2, it was shown that a globe of frozen water moving freely in our air would, as a result of the resistance of the air, lose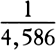 
of its motion in describing the length of its own semidiameter. And the same proportion obtains very nearly in any globes, however large they may be and however swift their motions. Now, I gather in the following way that the globe of our earth is denser than if it consisted totally of water. If this globe were wholly made of water, whatever things were rarer than water would, because of their smaller specific gravity, emerge from the water and float on the surface. And for this reason a globe made of earth that was covered completely by water would emerge somewhere, if it were rarer than water; and all the water flowing away from there would be gathered on the opposite side. And this is the case for our earth, which is in great part surrounded by seas. If the earth were not denser than the seas, it would emerge from those seas and, according to the degree of its lightness, a part of the earth would stand out from the water, while all those seas flowed to the opposite side. By the same argument the spots on the sun are lighter than the solar shining matter on top of which they float. And in whatever way the planets were formed, at the time when the mass was fluid, all heavier matter made for the center, away from the water. Accordingly, since the ordinary matter of our earth at its surface is about twice as heavy as water, and a little lower down, in mines, is found to be about three or four or even five times heavier than water, it is likely that the total amount of matter in the earth is about five or six times greater than it would be if the whole earth consisted of water, especially since it has already been shown above that the earth is about four times denser than Jupiter. Therefore, if Jupiter is a little denser than water, then in the space of thirty days (during which this planet describes a length of 459 of its semidiameters) it would, in a medium of the same density as our air, lose almost a tenth of its motion. But since the resistance of mediums decreases in the ratio of their weight and density (so that water, which is 13⅗ times lighter than quicksilver, resists 13⅗ times less; and air, which is 860 times lighter than water, resists 860 times less), it follows that up in the heavens, where the weight of the medium in which the planets move is diminished beyond measure, the resistance will nearly cease. We showed in the scholium to prop. 22, book 2, that at a height of two hundred miles above the earth, the air would be rarer than on the surface of the earth in a ratio of 30 to 0.0000000000003998, or 75,000,000,000,000 to 1, roughly. And hence the planet Jupiter, revolving in a medium with the same density as that upper air, would not, in the time of a million years, lose a millionth of its motion as a result of the resistance of the medium. In the spaces nearest to the earth, of course, nothing is found that creates resistance except air, exhalations, and vapors. If these are exhausted with very great care from a hollow cylindrical glass vessel, heavy bodies fall within the glass vessel very freely and without any sensible resistance; gold itself and the lightest feather, dropped simultaneously, fall with equal velocity and, in falling through a distance of four or six or eight feet, reach the bottom at the same time, as has been found by experiment. And therefore in the heavens, which are void of air and exhalations, the planets and comets, encountering no sensible resistance, will move through those spaces for a very long time.
Hypothesis 1
The center of the system of the world is at rest.
No one doubts this, although some argue that the earth, others that the sun, is at rest in the center of the system. Let us see what follows from this hypothesis.
Proposition 11, Theorem 11
The common center of gravity of the earth, the sun, and all the planets is at rest.
For that center (by corol. 4 of the Laws) either will be at rest or will move uniformly straight forward. But if that center always moves forward, the center of the universe will also move, contrary to the hypothesis.
Proposition 12, Theorem 12
The sun is engaged in continual motion but never recedes far from the common center of gravity of all the planets.
For since (by prop. 8, corol. 2) the matter in the sun is to the matter in Jupiter as 1,067 to 1, and the distance of Jupiter from the sun is to the semidiameter of the sun in a slightly greater ratio, the common center of gravity of Jupiter and the sun will fall upon a point a little outside the surface of the sun. By the same argument, since the matter in the sun is to the matter in Saturn as 3,021 to 1, and the distance of Saturn from the sun is to the semidiameter of the sun in a slightly smaller ratio, the common center of gravity of Saturn and the sun will fall upon a point a little within the surface of the sun. And continuing the same kind of calculation, if the earth and all the planets were to lie on one side of the sun, the distance of the common center of gravity of them all from the center of the sun would scarcely be a whole diameter of the sun. In other cases the distance between those two centers is always less. And therefore, since that center of gravity is continually at rest, the sun will move in one direction or another, according to the various configurations of the planets, but will never recede far from that center.
COROLLARY. Hence the common center of gravity of the earth, the sun, and all the planets is to be considered the center of the universe. For since the earth, sun, and all the planets gravitate toward one another and therefore, in proportion to the force of the gravity of each of them, are constantly put in motion according to the laws of motion, it is clear that their mobile centers cannot be considered the center of the universe, which is at rest. If that body toward which all bodies gravitate most had to be placed in the center (as is the commonly held opinion), that privilege would have to be conceded to the sun. But since the sun itself moves, an immobile point will have to be chosen for that center from which the center of the sun moves away as little as possible and from which it would move away still less, supposing that the sun were denser and larger, in which case it would move less.
Proposition 13, Theorem 13
The planets move in ellipses that have a focus in the center of the sun, and by radii drawn to that center they describe areas proportional to the times.
We have already discussed these motions from the phenomena. Now that the principles of motions have been found, we deduce the celestial motions from these principles a priori. Since the weights of the planets toward the sun are inversely as the squares of the distances from the center of the sun, it follows (from book 1, props. 1 and 11, and prop. 13, corol. 1) that if the sun were at rest and the remaining planets did not act upon one another, their orbits would be elliptical, having the sun in their common focus, and they would describe areas proportional to the times. The actions of the planets upon one another, however, are so very small that they can be ignored, and they perturb the motions of the planets in ellipses about the mobile sun less (by book 1, prop. 66) than if those motions were being performed about the sun at rest.
Yet the action of Jupiter upon Saturn is not to be ignored entirely. For the gravity toward Jupiter is to the gravity toward the sun (at equal distances) as 1 to 1,067; and so in the conjunction of Jupiter and Saturn, since the distance of Saturn from Jupiter is to the distance of Saturn from the sun almost as 4 to 9, the gravity of Saturn toward Jupiter will be to the gravity of Saturn toward the sun as 81 to 16 × 1,067, or roughly as 1 to 211. And hence arises a perturbation of the orbit of Saturn in every conjunction of this planet with Jupiter so sensible that astronomers have been at a loss concerning it. According to the different situations of the planet Saturn in these conjunctions, its eccentricity is sometimes increased and at other times diminished, the aphelion sometimes is moved forward and at other times perchance drawn back, and the mean motion is alternately accelerated and retarded. Nevertheless, all the error in its motion around the sun, an error arising from so great a force, can almost be avoided (except in the mean motion) by putting the lower focus of its orbit in the common center of gravity of Jupiter and the sun (by book 1, prop. 67); in which case, when that error is greatest, it hardly exceeds two minutes. And the greatest error in the mean motion hardly exceeds two minutes per year. But in the conjunction of Jupiter and Saturn the accelerative gravities of the sun toward Saturn, of Jupiter toward Saturn, and of Jupiter toward the sun are almost as 16, 81, and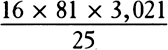 
, or 156,609, and so the difference of the gravities of the sun toward Saturn and of Jupiter toward Saturn is to the gravity of Jupiter toward the sun as 65 to 156,609, or 1 to 2,409. But the greatest power of Saturn to perturb the motion of Jupiter is proportional to this difference, and therefore the perturbation of the orbit of Jupiter is far less than that of Saturn’s. The perturbations of the remaining orbits are still less by far, except that the orbit of the earth is sensibly perturbed by the moon. The common center of gravity of the earth and the moon traverses an ellipse about the sun, an ellipse in which the sun is located at a focus, and this center of gravity, by a radius drawn to the sun, describes areas (in that ellipse) proportional to the times; the earth, during this time, revolves around this common center with a monthly motion.
Proposition 14, Theorem 14
The aphelia and nodes of the [planetary] orbits are at rest.
The aphelia are at rest, by book 1, prop. 11, as are also the planes of the orbits, by prop. 1 of the same book; and if these planes are at rest, the nodes are also at rest. But yet from the actions of the revolving planets and comets upon one another some inequalities will arise, which, however, are so small that they can be ignored here.
COROLLARY 1. The fixed stars also are at rest, because they maintain given positions with respect to the aphelia and nodes.
COROLLARY 2. And so, since the fixed stars have no sensible parallax arising from the annual motion of the earth, their forces will produce no sensible effects in the region of our system, because of the immense distance of these bodies from us. Indeed, the fixed stars, being equally dispersed in all parts of the heavens, by their contrary attractions annul their mutual forces, by book 1, prop. 70.
Scholium
Since the planets nearer to the sun (namely, Mercury, Venus, the earth, and Mars) act but slightly upon one another because of the smallness of their bodies [i.e., because their masses are small], their aphelia and nodes will be at rest, except insofar as they are disturbed by the forces of Jupiter, Saturn, and any bodies further away. And by the theory of gravity it follows that their aphelia move slightly forward [or in consequentia] with respect to the fixed stars, and do this as the 3/2 powers of the distances of these planets from the sun. For example, if in a hundred years the aphelion of Mars is carried forward [or in consequentia] 33′20″ with respect to the fixed stars, then in a hundred years the aphelia of the earth, Venus, and Mercury will be carried forward 17′40″, 10′53″, and 4′16″ respectively. And these motions are ignored in this proposition because they are so small.
Proposition 15, Problem 1
To find the principal diameters of the [planetary] orbits.
These diameters are to be taken as the ⅔ powers of the periodic times by book 1, prop. 15; and then each one is to be increased in the ratio of the sum of the masses of the sun and each revolving planet to the first of two mean proportionals between that sum and the sun, by book 1, prop. 60.
Proposition 16, Problem 2
To find the eccentricities and aphelia of the [planetary] orbits.
The problem is solved by book 1, prop. 18.
Proposition 17, Theorem 15
The daily motions of the planets are uniform, and the libration of the moon arises from its daily motion.
This is clear from the first law of motion and book 1, prop. 66, corol. 22. With respect to the fixed stars Jupiter revolves in 9h56m, Mars in 24h39m, Venus in about 23 hours, the earth in 23h56m, the sun in 25½ days, and the moon in 27d7h43m. That these things are so is clear from phenomena. With respect to the earth, the spots on the body of the sun return to the same place on the sun’s disc in about 27½ days; and therefore with respect to the fixed stars the sun revolves in about 25½ days. Now, since a lunar day (the moon revolving uniformly about its own axis) is a month long [i.e., is equal to a lunar month, the periodic time of the moon’s revolution in its orbit], the same face of the moon will always very nearly look in the direction of the further focus of its orbit, and therefore will deviate from the earth on one side or the other according to the situation of that focus. This is the moon’s libration in longitude; for the libration in latitude arises from the latitude of the moon and the inclination of its axis to the plane of the ecliptic. Mr. N. Mercator, in his book on astronomy, published in the beginning of the year 1676, set forth this theory of the moon’s libration more fully on the basis of a letter from me.
The outermost satellite of Saturn seems to revolve about its own axis with a motion similar to our moon’s, constantly presenting the same aspect toward Saturn. For in revolving about Saturn, whenever it approaches the eastern part of its own orbit, it is just barely seen and for the most part disappears from sight; and possibly this occurs because of certain spots in that part of its body which is then turned toward the earth, as Cassini noted. The outermost satellite of Jupiter also seems to revolve about its own axis with a similar motion, because in the part of its body turned away from Jupiter it has a spot which, whenever the satellite passes between Jupiter and our eyes, appears as if it were on the body of Jupiter.
Proposition 18, Theorem 16
The axes of the planets are smaller than the diameters that are drawn perpendicularly to those axes.
If it were not for the daily circular motion of the planets, then, because the gravity of their parts is equal on all sides, they would have to assume a spherical figure. Because of that circular motion it comes about that those parts, by receding from the axis, endeavor to ascend in the region of the equator. And therefore if the matter is fluid, it will increase the diameters at the equator by ascending, and will decrease the axis at the poles by descending. Thus the diameter of Jupiter is found by astronomical observations to be shorter between the poles than from east to west. By the same argument, if our earth were not a little higher around the equator than at the poles, the seas would subside at the poles and, by ascending in the region of the equator, would flood everything there.
Proposition 19a, Problem 3
To find the proportion of a planet’s axis to the diameters perpendicular to that axis.
b cOur fellow countryman Norwood, in about the year 1635, measured a distance of 905,751 London feet between London and York and observed the difference of latitudes between those places to be 2°28′ and thereby found the measure of one degree to be 367,196 London feet, that is, 57,300 Paris toises. Picard measured an arc of 1°22′55″ along the meridian between Amiens and Malvoisine and found an arc of one degree to be 57,060 Paris toises. The elder Cassini [Gian Domenico or Jean-Dominique] measured the distance along the meridian from the town of Collioure in Roussillon to the Paris observatory; and his son [Jacques] added the distance from the observatory to the tower of the city of Dunkerque. The total distance was 486,156½ toises, and the difference in latitudes between the town of Collioure and the city of Dunkerque was 8°31′11⅚″. Thus an arc of one degree comes out to be 57,061 Paris toises. And from these measures the circumference of the earth is found to be 123,249,600 Paris feet, and its semidiameter 19,615,800 feet, on the hypothesis that the earth is spherical.
A body revolving uniformly in a circle at a distance of 19,615,800 feet from the center, making a revolution in a single sidereal day of 23h56m4s, will describe an arc of 1,433.46 feet in the time of one second, an arc whose versed sine is 0.0523656 feet, or 7.54064 lines. And therefore the force by which heavy bodies descend at the latitude of Paris is to the dcentrifugald force of bodies on the equator (which arises from the daily motion of the earth) as 2,174 to 7.54064.
The centrifugal force of bodies on the earth’s equator is to the centrifugal force by which bodies recede rectilinearly from the earth at the latitude of Paris (48°50′10″) as the square of the radius to the square of the cosine of that latitude, that is, as 7.54064 to 3.267. Let this force be added to the force by which heavy bodies descend at the latitude of Paris; then a body falling at that latitude with the total force of gravity will, in the time of one second, describe 2,177.267 lines, or 15 Paris feet 1 inch and 5.267 lines. And the total force of gravity at that latitude will be to the ecentrifugale force of bodies on the earth’s equator as 2,177.267 to 7.54064 or 289 to 1.b
Therefore, if APBQ represents the figure of the earth, which is now no longer spherical but generated by the rotation of an ellipse about its minor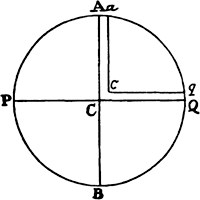 
axis PQ; and if ACQqca is a channel full of water, going from the pole Qq to the center Cc and from that center out to the equator Aa; then the weight of the water in the leg ACca will have to be to the weight of the water in the other leg QCcq as 289 to 288, because the centrifugal force arising from the circular motion will sustain and take away one of the 289 parts of weight of the water in the leg ACca, and consequently the 288 parts of weight of the water in the leg QCcq will sustain the 288 parts remaining in the leg ACca. Further, on making the computation (according to book 1, prop. 91, corol. 2), I find that if the earth were composed of uniform matter and were deprived of all its motion, and its axis PQ were to its diameter AB as 100 to 101, then the gravity in place Q toward the earth would be to the gravity in the same place Q toward a sphere described about the center C with a radius PC or QC as 126 to 125. And by the same argument, the gravity in place A toward a spheroid generated by the rotation of the ellipse APBQ about the axis AB is to the gravity in the same place A toward a sphere described about a center C with a radius AC as 125 to 126. Moreover, the gravity in place A toward the earth is a mean proportional between the gravity toward the spheroid and the gravity toward the sphere, because the sphere, when its diameter PQ is diminished in the ratio of 101 to 100, is transformed into the figure of the earth; and this figure, when a third diameter (perpendicular to the two given diameters AB and PQ) is diminished in the same ratio, is transformed into the said spheroid; and the gravity in A, in either case, is diminished in very nearly the same ratio. Therefore the gravity in A toward a sphere described about the center C with a radius AC is to the gravity in A toward the earth as 126 to 125½; and the gravity in place Q, toward a sphere described about the center C with a radius QC, is to the gravity in place A, toward a sphere described about the center C with a radius AC, in the ratio of the diameters (by book 1, prop. 72), that is, as 100 to 101. Now let these three ratios (126 to 125, 126 to 125½, and 100 to 101) be combined, and the gravity in place Q toward the earth will become to the gravity in place A toward the earth as 126 × 126 × 100 to 125 × 125½ × 101, or as 501 to 500.
Now, since (by book 1, prop. 91, corol. 3) the gravity in either leg ACca or QCcq of the channel is as the distance of places from the earth’s center, if those legs are separated by transverse, equidistant surfaces into parts proportional to the wholes, the weights of any number of these individual parts in the leg ACca will be to the weights of the same number of individual parts in the other leg as their magnitudes and accelerative gravities jointly, that is, as 101 to 100 and 500 to 501, which is as 505 to 501. And accordingly, if the centrifugal force of each part of the leg ACca (which force arises from the daily motion) had been to the weight of the same part as 4 to 505, so that it would take away four parts from the weight of each part (supposing it to be divided into 505 parts), the weights would remain equal in each leg, and therefore the fluid would stay at rest in equilibrium. But the centrifugal force of each part is to the weight of the same part as 1 to 289; that is, the fcentrifugalf force, which ought to have been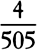 
of the weight, is only 
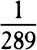of it. And therefore I say, according to the golden rule [or rule of three], that if a centrifugal force of 
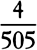of the weight makes the height of the water in the leg ACca exceed the height of the water in the leg QCcq by a hundredth of its total height, the centrifugal force of 
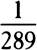of the weight will make the excess of the height in the leg ACca be only 
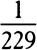of the height of the water in the other leg QCcq. Therefore the diameter of the earth at the equator is to its diameter through the poles as 230 to 229. And thus, since the mean semidiameter of the earth, according to Picard’s measurement, is 19,615,800 Paris feet, or 3,923.16 miles (supposing a mile to be 5,000 feet), the earth will be 85,472 feet or 171/10 miles higher at the equator than at the poles. And its height at the equator will be about 19,658,600 feet, and at the poles will be about 19,573,000 feet.
If a planet is larger or smaller than the earth, while its density and periodic time of daily revolution remain the same, the ratio of centrifugal force to gravity will remain the same, and therefore the ratio of the diameter between the poles to the diameter at the equator will also remain the same. But if the daily motion is accelerated or retarded in any ratio, the centrifugal force will be increased or decreased in that same ratio squared, and therefore the difference between the diameters will be increased or decreased very nearly in the same squared ratio. And if the density of a planet is increased or decreased in any ratio, the gravity tending toward the planet will also be increased or decreased in the same ratio, and the difference between the diameters in turn will be decreased in the ratio of the increase in the gravity or will be increased in the ratio of the decrease in the gravity. Accordingly, since the earth revolves [i.e., rotates] with respect to the fixed stars in 23h56m, and Jupiter in 9h56m, and the squares of their periodic times are as 29 to 5, and the densities of these revolving bodies are as 400 to 94½, the difference between the diameters of Jupiter will be to its smaller diameter as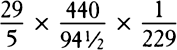 
to 1, or very nearly as 1 to 9⅓. Therefore Jupiter’s diameter taken from east to west is to its diameter between the poles very nearly as 10⅓ to 9⅓. gThus, since its larger diameter is 37″, its smaller diameter (which lies between the poles) will be 33″25‴. Because of the erratic light let about 3″ be added, and the apparent diameters of this planet will come out to be 40″ and 36″25‴, which are to each other nearly as 11⅙ to 10⅙. This argument has been based on the hypothesis that the body of Jupiter is uniformly dense. But if its body is denser toward the plane of the equator than toward the poles, its diameters can be to each other as 12 to 11, or 13 to 12, or even 14 to 13. As a matter of fact, Cassini observed in the year 1691 that the diameter of Jupiter extending from east to west would exceed its other diameter by about a fifteenth part of itself. Moreover, our fellow countryman Pound, with a 123-foot-long telescope and the best micrometer, measured the diameters of Jupiter in the year 1719 with the following results.
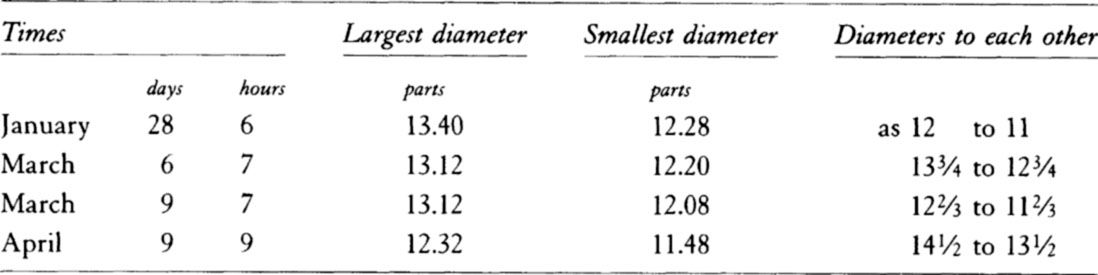
Therefore the theory agrees with the phenomena. Further, the planets are more exposed to the heat of sunlight toward their equators and as a result hare somewhat more thoroughly heated thereh than toward the poles.
Proposition 20, Problem 4
To find and compare with one another the weights of bodies in different regions of our earth.
Since the weights of the unequal legs of the water-channel ACQqca are equal, and the weights of any parts that are proportional to the whole legs and similarly situated in those legs are to one another as the weights of the wholes, and thus are also equal to one another, the weights of parts that are equal and similarly situated in the legs will be inversely as the legs, that is, inversely as 230 to 229. This is likewise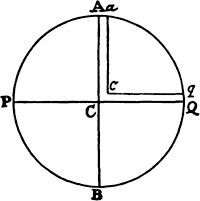 
the case for any homogeneous equal bodies that are similarly situated in the legs of the channel. The weights of these bodies are inversely as the legs, that is, inversely as the distances of the bodies from the earth’s center. Accordingly, if the bodies are in the topmost parts of the channels, or on the surface of the earth, their weights will be to one another inversely as their distances from the center. And by the same argument, weights that are in any other regions whatever, anywhere on the whole surface of the earth, are inversely as the distances of those places from the center; and therefore, on the hypothesis that the earth is a spheroid, the proportion of those weights is given.
From this the following theorem is deduced:a The increase of weight in going from the equator to the poles is very nearly as the versed sine of twice the latitude, or (which is the same) as the square of the sine of the latitude. bAnd the arcs of degrees of latitude on a meridian are increased in about the same ratio. Now, the latitude of Paris is 48°50′, the latitude of places on the equator 00°00′, and that of places at the poles 90°; the versed sines of twice those arcs of latitude are 11,334 and 00,000 and 20,000 (the radius being taken to be 10,000); the gravity at the pole is to the gravity at the equator as 230 to 229; and the excess of the gravity at the pole to the gravity at the equator is as 1 to 229. Hence the excess of the gravity at the latitude of Paris will be to the gravity at the equator as 1 ×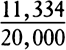 
to 229, or 5,667 to 2,290,000. And therefore the total gravities in these places will be to each other as 2,295,667 to 2,290,000. And thus, since the lengths of pendulums oscillating with equal periods are as the gravities, and at the latitude of Paris the length of a seconds pendulum is 3 Paris feet and 8½ lines (or rather, because of the weight of the air, 85/9 lines), the length of a pendulum at the equator will be shorter than the length of a pendulum with the same period at Paris in the amount of 1.087 lines. And a similar computation yields the following table.
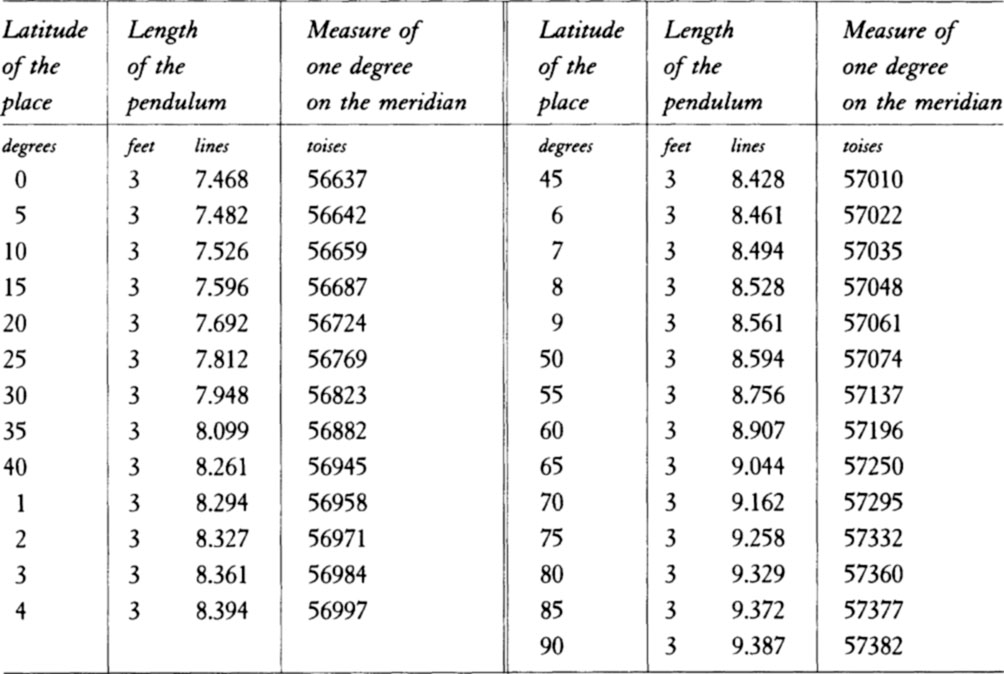
Now some astronomers, sent to distant regions to make astronomical observations, have observed that their pendulum clocks went more slowly near the equator than in our regions. And indeed M. Richer first observed this in the year 1672 on the island of Cayenne. For while he was observing the transit of the fixed stars across the meridian in the month of August, he found that his clock was going more slowly than in its proper proportion to the mean motion of the sun, the difference being 2m28s every day. Then by constructing a simple pendulum that would oscillate in seconds as measured by the best clock, he noted the length of the simple pendulum, and he did this frequently, every week for ten months. Then, when he had returned to France, he compared the length of this pendulum with the length of a seconds pendulum at Paris (which was 3 Paris feet and 8⅗ lines long) and found that it was shorter than the Paris pendulum, the difference being 1¼ lines.d
M. Picard, at any rate, observed that an iron rod, which in wintertime when the weather was freezing was 1 foot long, came to be 1 foot and ¼ of a line long when heated by a fire. Later M. La Hire observed that an iron rod, which in an exactly similar winter was 6 feet long, came to be 6 feet and ⅔ of a line long when it was exposed to the summer sun. The heat [i.e., temperature] was greater in the first example than in the second, and in the second it was greater than that of the external parts of the human body. For metals grow extremely hot in the summer sun. But the pendulum rod in a pendulum clock is ordinarily never exposed to the heat of the summer sun, and never acquires a heat equal to that of the external surface of the human body. And, therefore, although a 3-foot-long pendulum rod in a clock will indeed be a little longer in summertime than in wintertime, this increase will scarcely surpass ¼ of 1 line. Accordingly, all of the difference in the length of pendulums with the same period in different regions cannot be attributed to differences in heat. Nor can this difference be attributed to errors made by the astronomers sent from France. For although their observations do not agree perfectly with one another, the errors are so small that they can be ignored. And in this they all agree: that at the equator, pendulums are shorter than pendulums with the same period at the Royal Observatory in Paris, ethe difference being neither less than 1¼ lines nor more than 2⅔ lines. By the observations of M. Richer made in Cayenne the difference was 1¼ lines. By those of M. Des Hayes that difference when corrected became 1½ or 1¾ lines. By the less accurate observations made by others, this difference came out as more or less 2 lines. And this discrepancy could have arisen partly from errors in observations, partly from the dissimilitude of the internal parts of the earth and from the height of mountains, and partly from the differences in heat [i.e., temperatures] of the air.
Proposition 21, Theorem 17
The equinoctial points regress, and the earth’s axis, by a nutation in every annual revolution, inclines twice toward the ecliptic and twice returns to its former position.
This is clear by book 1, prop. 66, corol. 20. This motion of nutation, however, must be very small—either scarcely or not at all perceptible.
Proposition 22, Theorem 18
All the motions of the moon and all the inequalities in its motions follow from the principles that have been set forth.
That the major planets, while they are being carried about the sun, can carry other or minor planets [or satellites], revolving around them, and that those minor planets must revolve in ellipses having their foci in the centers of the major planets, is evident from book 1, prop. 65. Moreover, their motions will be perturbed in many ways by the sun’s action, and they will be influenced by those inequalities that are observed in our moon. Our moon, in any case (by book 1, prop. 66, corols. 2, 3, 4, and 5), moves more swiftly, and by a radius drawn to the earth describes an area greater for the time, and has a less curved orbit, and therefore approaches closer to the earth, in the syzygies than in the quadratures, except insofar as these effects are hindered by the motion of eccentricity. For the eccentricity is greatest (by book 1, prop. 66, corol. 9) when the moon’s apogee is in the syzygies, and least when it stands in the quadratures; and thus the moon in its perigee is swifter and closer to us, while in its apogee it is slower and more remote, in the syzygies than in the quadratures. Additionally, the apogee advances and the nodes regress, but with a nonuniform motion. And indeed the apogee (by prop. 66, corols. 7 and 8) advances more swiftly in its syzygies, regresses more slowly in the quadratures, and by the excess of the advance over the regression is annually carried forward [or in consequentia, i.e., from east to west in the direction of the signs]. But the nodes (by prop. 66, corol. 2) are at rest in their syzygies and regress most swiftly in the quadratures. The moon’s greatest latitude is also greater in its quadratures (by prop. 66, corol. 10) than in its syzygies, and (by prop. 66, corol. 6) the mean motion of the moon is slower in the earth’s perihelion than in its aphelion. And these are the more significant inequalities [of the moon’s motion] taken note of by astronomers.
There are also certain other inequalities not observed by previous astronomers, by which the lunar motions are so perturbed that until now these motions have not been reducible, by any law, to any definite rule. For the velocities or hourly motions of the moon’s apogee and nodes, and their equations, and also the difference between the greatest eccentricity in the syzygies and the least in the quadratures, and that inequality which is called the variation, are increased and decreased annually (by prop. 66, corol. 14) as the cube of the sun’s apparent diameter. And, additionally, the variation is increased or decreased very nearly as the square of the time between the quadratures (by book 1, lem. 10, corols. 1 and 2, and prop. 66, corol. 16), but in astronomical calculations this inequality is generally included under the moon’s prosthaphaeresis [or equation of the center] and confounded with it.
Proposition 23, Problem 5
To derive the unequal motions [i.e., the inequalities in the motions] of the satellites of Jupiter and of Saturn from the motions of our moon.
From the motions of our moon the analogous motions of the moons or satellites of Jupiter are derived as follows. The mean motion of the nodes of Jupiter’s outermost satellite is (by book 1, prop. 66, corol. 16) to the mean motion of the nodes of our moon in a ratio compounded of the square of the ratio of the earth’s periodic time about the sun to Jupiter’s periodic time about the sun, and of the simple ratio of the satellite’s periodic time about Jupiter to the moon’s periodic time about the earth, and so in one hundred years that node completes 8°24′ backward [or in antecedentia, i.e., counter to the order of the signs]. The mean motions of the nodes of the inner satellites are (by the same corollary) to the motion of this outermost satellite as the periodic times of those inner satellites are to the periodic time of the outermost satellite and hence are given. Moreover (by the same corollary), the forward [or direct] motion of the upper apsis of each satellite [or its motion in consequentia] is to the backward [or retrograde] motion of its nodes [or the motion in antecedentia] as the motion of the apogee of our moon to the motion of its nodes, and hence is also given. However, the motion of the upper apsis found in this way must be decreased in the ratio of 5 to 9, or about 1 to 2, for a reason which would take too much time to explain here. The greatest equations of the nodes and upper apsis of each satellite are approximately to the greatest equations of the nodes and upper apsis of our moon respectively as the motions of the nodes and upper apsis of the satellites in the time of one revolution of the former equations are to the motions of the nodes and apogee of our moon in the time of one revolution of the latter equations. By the same corollary, the variation of a satellite as it would be observed from Jupiter is to the variation of our moon in the same proportion as the total motions of their nodes during the times in which respectively the satellite and our moon revolve as reckoned in relation to the sun; and therefore in the outermost satellite the variation does not exceed 5″12‴.
Proposition 24, Theorem 19
The ebb and flow of the sea arise from the actions of the sun and moon.
It is clear from book 1, prop. 66, corols. 19 and 20, that the sea should twice rise and twice fall in every day, lunar as well as solar, and also that the greatest height of the water, in deep and open seas, should occur less than six hours after the appulse of the luminaries to the meridian of a place, as happens in the whole eastern section of the Atlantic Ocean and the Ethiopic [or South Atlantic] Sea between France and the Cape of Good Hope, and also on the Chilean and Peruvian shore of the Pacific Ocean; on all these shores the tide comes in at about the second, third, or fourth hour, except in cases when the motion has been propagated from the deep ocean through shallow places and is delayed until the fifth, sixth, or seventh hour, or later. I number the hours from the appulse of either luminary to the meridian of a place, below the horizon as well as above, and by hours of a lunar day I mean twenty-fourths of that time in which the moon, by its apparent daily motion, returns to the meridian of the place. The force of the sun or moon to raise the sea is greatest in the very appulse of the luminary to the meridian of the place. But the force impressed upon the sea at that time remains for a while and is increased by a new force subsequently impressed, until the sea has ascended to its greatest height, which will happen in one or two hours, but more frequently at the shores in about three hours or even more if the sea is shallow.
Moreover, the two motions which the two luminaries excite will not be discerned separately but will cause what might be called a mixed motion. In the conjunction or the opposition of the luminaries their effects will be combined, and the result will be the greatest ebb and flow. In the quadratures the sun will raise the water while the moon depresses it and will depress the water while the moon raises it; and the lowest tide of all will arise from the difference between these two effects. And since, as experience shows, the effect of the moon is greater than that of the sun, the greatest height of the water will occur at about the third lunar hour. Outside of the syzygies and quadratures, the highest tide, which by the lunar force alone would always have to occur at the third lunar hour, and by the solar force alone at the third solar hour, will occur, as a result of the combining of the lunar and solar forces, at some intermediate time which is closer to the third lunar hour [than to the third solar hour]; and thus in the transit of the moon from the syzygies to the quadratures, when the third solar hour precedes the third lunar hour, the greatest height of the water will also precede the third lunar hour, and will do so by the greatest interval a little after the octants of the moon; and the highest tide will follow the third lunar hour with the same intervals in the transit of the moon from the quadratures to the syzygies. This is what happens in the open sea. For in the mouths of rivers the higher tides, other things being equal, will come to their peaks later.
Additionally, the effects of the luminaries depend on their distances from the earth. For at smaller distances their effects are greater, and at greater distances smaller, and this varies as the cubes of their apparent diameters. Therefore the sun in wintertime, when it is in its perigee, produces greater effects and makes the tides a little higher in the syzygies and a little lower (other things being equal) in the quadratures than in summertime; and the moon in its perigee every month produces higher tides than fifteen days before or after, when it is in its apogee. Accordingly, it happens that the two very highest tides do not follow each other in successive syzygies.
The effect of each luminary depends also on its declination, or distance from the equator. For if the luminary should be at one of the poles, it would constantly draw the individual parts of water, without intension and remission of action, and thus would produce no reciprocation of motion. Therefore the luminaries, in receding from the equator toward a pole, will lose their effects by degrees, and for this reason will produce lower tides in the solstitial syzygies than in the equinoctial syzygies. In the solstitial quadratures, however, they will produce higher tides than in the equinoctial quadratures, because the effect of the moon, which is now at the equator, most exceeds the effect of the sun. Therefore the highest tides occur at the syzygies of the luminaries, and the lowest at their quadratures, at about the times of either of the two equinoxes. And the highest tide in the syzygies is always acompanied by the lowest tide in the quadratures, as has been learned by experience. Moreover, as a result of the smaller distance of the sun from the earth in winter than in summer, it comes about that the highest and lowest tides more often precede the vernal equinox than follow it, and more often follow the autumnal equinox than precede it.
The effects of the luminaries depend also on the latitude of places. Let ApEP represent the earth covered everywhere with deep waters, C its center, P and p the poles, AE the equator, F any place not on the equator, Ff the parallel of that place, Dd the parallel corresponding to it on the other side of the equator, L the place that the 
moon was occupying three hours earlier, H the place on the earth situated perpendicularly beneath L, h the place opposite H, K and k places 90 degrees distant from H and h, CH and Ch the greatest heights of the sea (measured from the center of the earth), and CK and Ck the least heights. If an ellipse is described with axes Hh, Kk, and then if by the revolution of this ellipse about the major axis Hh a spheroid HPKhpk is described, this spheroid will represent the figure of the sea very nearly, and CF, Cf, CD, Cd will be the heights of the sea at places F, f, D, d. Further, if in the aforesaid revolution of the ellipse any point N describes a circle NM which cuts parallels Ff, Dd in any places R, T, and cuts the equator AE in S, CN will be the height of the sea in all places R, S, T located on this circle. Hence, in the daily revolution of any place F, the greatest flood tide will be in F at the third hour after the appulse of the moon to the meridian above the horizon; afterward, the greatest ebb tide will be in Q at the third hour after the setting of the moon; then the greatest flood tide will be in f at the third hour after the appulse of the moon to the meridian below the horizon; finally, the greatest ebb tide will be in Q at the third hour after the rising of the moon; and the latter flood tide in f will be smaller than the former flood tide in F.
For the whole sea is divided into just two hemispherical flows [or flowing bodies of water], one in the hemisphere KHk verging to the north, the other in the opposite hemisphere Khk; and these may therefore be called the northern flow and the southern flow. These flowing bodies of waters, which are always opposite to each other, come by turns to the meridian of every single place, with an interval of twelve lunar hours between them. And since the northern regions partake more of the northern flow, and the southern regions more of the southern flow, higher and lower tides arise from them alternately, in every single place not on the equator in which the luminaries rise and set. Moreover, the higher tide, when the moon declines toward the vertex of the place, will occur at about the third hour after the appulse of the moon to the meridian above the horizon, and when the moon changes its declinationa, this higher tide will be turned into a lower one. And the greatest difference between these tides will occur at the times of the solstices, especially if the ascending node of the moon is in the first of Aries. Thus it has been found by experience that in winter, morning tides exceed evening tides and that in summer, evening tides exceed morning tides, at Plymouth by a height of about one foot, and at Bristol by a height of fifteen inches, according to the observations of Colepress and Sturmy.
Moreover, the motions hitherto described are changed somewhat by the force of reciprocation of the waters, by which a tide of the sea, even if the actions of the luminaries were to cease, would be able to persevere for a while. This conservation of impressed motion lessens the difference between alternate tides; and it makes the tides immediately after the syzygies higher and makes those immediately after the quadratures lower. Hence it happens that alternate tides at Plymouth and Bristol do not differ from each other by much more than a height of one foot or fifteen inches, and that the very highest tides in those same harbors are not the first tides after the syzygies but the third. All the motions are made slower also in their passing through shallows, to such an extent that the very highest tides, in certain straits and the mouths of rivers, are the fourth or even the fifth after the syzygies.
Further, it can happen that a tide is propagated from the ocean through different channels to the same harbor and passes more quickly through some channels than through others; in this case the same tide, divided into two or more tides arriving successively, can compose new motions of different kinds. Let us suppose that two equal tides come from different places to the same harbor and that the first precedes the second by a space of six hours and occurs at the third hour after the appulse of the moon to the meridian of the harbor. If the moon is on the equator at the time of this appulse to the meridian, then every six hours there will be equal flood tides coming upon corresponding equal ebb tides and causing those ebb tides to be balanced by the flood tides, and thus during the course of that day they will cause the water to stay quiet and still. If at that time the moon is declining from the equator, there will be alternately higher and lower tides in the ocean, as has been said; and from the ocean, two higher and two lower tides will each be alternately propagated toward this harbor. Moreover, the two greater flood tides will produce the highest water in the middle time between them; the greater and lesser flood tides will make the water ascend to its mean height in the middle time between them; and between the two lesser flood tides the water will ascend to its least height. Thus in the space of twenty-four hours, the water will only once reach its greatest height, not twice as usually happens, and will only once reach its least height; and the greatest height, if the moon is declining toward the pole above the horizon of the place, will occur at either the sixth or the thirtieth hour after the appulse of the moon to the meridian; and when the moon changes its declination, this flood tide will be changed into an ebb tide. An example of all these things has been given by Halley, on the basis of sailors’ observations, in Batsha harbor in the kingdom of Tonkin at a latitude of 20°50′ N. There the water stays still on the day following the transit of the moon over the equator; then, when the moon declines toward the north, the water begins to ebb and flow—not twice, as in other harbors, but only once every day; and the flood tide occurs at the setting of the moon, and the greatest ebb tide at its rising. This flood tide increases with the declination of the moon until the seventh or eighth day; then during the next seven days it decreases at the same rate at which it had previously increased. And when the moon changes its declination, the flood ceases and is then turned into an ebb. For thereafter the ebb tide occurs at the setting of the moon and the flood tide at its rising, until the moon again changes its declination. There are two different approaches from the ocean into this harbor and the neighboring channels, the one from the China Sea between the continent and the island of Leuconia, the other from the Indian Ocean between the continent and the island of Borneo. But whether there are tides coming through these channels in twelve hours from the Indian Ocean and in six hours from the China Sea, which thus occurring at the third and ninth lunar hours compound motions of this sort, or whether there is any other condition of those seas, I leave to be determined by observations of the neighboring shores.
Hitherto I have given the causes of the motions of the moon and seas. It is now proper to subjoin some things about the quantity of those motions.
Proposition 25, Problem 6
To find the forces of the sun that perturb the motions of the moon.
Let S designate the sun, T the earth, P the moon, CADB the orbit of the moon. On SP take SK equal to ST; and let SL be to SK as SK2 to SP2, and draw LM parallel to PT; and if the accelerative gravity of the earth toward the sun is represented by the distance ST or SK, SL will be the accelerative gravity of the moon toward the sun. This is compounded of the parts SM and LM, of which LM and the part TM of SM perturb the motion of the moon, as has been set forth in book 1, prop. 66 and its corollaries. Insofar as the earth and moon revolve around their common center of gravity, the motion of the earth about that center will also be perturbed by entirely similar forces; but it is possible to refer the sums of the forces and the sums of the motions to the moon, and to represent the sums of the forces by the lines TM and ML that correspond to them. The force ML, in its mean quantity, is to the centripetal force by which the moon could revolve in its orbit, about an earth at rest at a distance PT, as the square of the ratio of the periodic time of the moon about the earth to that of the earth about the sun (by book 1, prop. 66, corol. 17), that is, as the square of the ratio of 27d7h43m to 365d6h9m, that is, as 1,000 to 178,725, or 1 to 17829/40. But we found in prop. 4 of this book 3 that if the earth and moon revolve about their common center of gravity, their mean distance from each other will be very nearly 60½ mean semidiameters of the earth. And the force by which the moon could revolve in orbit about the earth at rest at a distance PT of 60½ terrestrial semidiameters is to the force by which it could revolve in the same time at a distance of 60 semidiameters as 60½ to 60; and this force is to the force of gravity on the earth as 1 to 60 × 60 very nearly. And so the mean force ML is to the force of gravity on the surface of the earth as 1 × 60½ to 60 × 60 × 60 × 17829/40, or as 1 to 638,092.6. From this and from the proportion of the lines TM and ML, the force TM is also given; and these are the forces of the sun by which the motions of the moon are perturbed. Q.E.I.
Proposition 26, Problem 7
To find the hourly increase of the area that the moon, by a radius drawn to the earth, describes in a circular orbit.
We have said that the area which the moon describes by a radius drawn to the earth is proportional to the time, except insofar as the motion of the moon is disturbed by the action of the sun. We propose to investigate here the inequality of the moment, or of the hourly increase [under the foregoing condition of disturbance]. To make the computation easier, let us imagine that the orbit of the moon is circular, and let us ignore all inequalities with the sole exception of the one under discussion here. Because of the enormous distance of the sun, let us suppose also that the lines SP and ST are parallel to each other. By this means the force LM will always be reduced to its mean quantity TP, and so will the force TM be reduced to its mean quantity 3PK. These forces (by corol. 2 of the laws of motion) compose the force TL; and if a perpendicular LE is dropped to the radius TP, this force is resolved into the forces TE and EL, of which TE, always acting along the radius TP, neither accelerates nor retards the description of the area TPC made by that radius TP; and EL, acting along the perpendicular to the radius, accelerates or retards the description of the area, as much as it accelerates or retards the moon. That acceleration of the moon, made in each individual moment of time, in the transit of the moon from the quadrature C to the conjunction A, is as the accelerating force itself EL, that is, as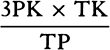 
. Let the time be represented by the mean motion of the moon or (which comes to about the same thing) by the angle CTP or by the arc CP. On CT erect a normal CG (equal to CT). And when the quadrantal arc AC has been divided into innumerable equal particles Pp, . . . , by which the same innumerable quantity of equal particles of time can be represented, and when a perpendicular pk has been drawn to CT, draw TG meeting KP and kp (produced) in F and f; and FK will be equal to TK, and Kk will be to PK as Pp to Tp, that is, in a given ratio; and therefore FK × Kk, or the area FKkf, will be as 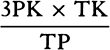, that is, as EL; and, by compounding, the total area GCKF will be as the sum of all the forces EL impressed on the moon in the total time CP, and so also as the velocity generated by this sum, that is, as the acceleration of the description of the area CTP, or the increase of its moment. The force by which the moon could revolve in its periodic time CADB of 27d7h43m about the earth at rest, at the distance TP, would make a body, by falling in the time CT, describe the space ½CT, and at the same time acquire a velocity equal to the velocity with which the moon moves in its orbit. This is evident from book 1, prop. 4, corol. 9. However, since the perpendicular Kd dropped to TP is a third of EL, and is equal to a half of TP or ML in the octants, the force EL in the octants (where it is greatest) will exceed the force ML in the ratio of 3 to 2, and so will be to that force by which the moon could revolve in its periodic time about the earth at rest as 100 to ⅔ × 17,872½, or 11,915, and should in the time CT generate a velocity which would be 
of the moon’s velocity; but in the time CPA this force would generate a greater velocity in the ratio of CA to CT or TP. Let the greatest force EL in the octants be represented by the area FK × Kk equal to the rectangle ½TP × Pp. And the velocity which that greatest force could generate in any time CP will be to the velocity which any other lesser force EL generates, in the same time, as the rectangle ½TP × CP to the area KCGF; but the velocities generated in the whole time CPA will be to each other as the rectangle ½TP × CA to the triangle TCG, or as the quadrantal arc CA to the radius TP. And so (by book 5, prop. 9 of the Elements) the latter velocity generated in the whole time will be of the velocity of the moon. Change this velocity of the moon, which corresponds to the mean moment of the area, by adding and subtracting half of the other velocity; and if the mean moment is represented by the number 11,915, the sum 11,915 + 50 (or 11,965) will represent the greatest moment of the area in the syzygy A, and the difference 11,915 − 50 (or 11,865) the least moment of the same area in the quadratures. Therefore the areas which are described in equal times in the syzygies and quadratures are to each other as 11,965 to 11,865. To the least moment 11,865 add the moment that is to the difference (100) of the two above-mentioned moments as the quadrilateral FKCG is to the triangle TCG or, which comes to the same thing, as the square of the sine PK to the square of the radius TP (that is, as Pd to TP); then the sum will represent the moment of the area when the moon is in any intermediate place P.
All these things are so on the hypothesis that the sun and earth are at rest, and that the moon has a synodic period of revolution of 27d7h43m. But since the moon’s synodic period is actually 29d12h44m, the increments of the moments should be increased in the ratio of the time, that is, in the ratio of 1,080,853 to 1,000,000. In this way the total increment, which was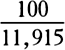 
of the mean moment, will now become 
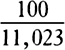of it. And so the moment of the area in the quadrature of the moon will be to its moment in the syzygy as 11,023 − 50 to 11,023 + 50, or as 10,973 to 11,073; and to its moment, when the moon is in any other intermediate place P, as 10,973 to 10,973 + Pd, taking TP to be equal to 100.
Therefore the area that the moon, by a radius drawn to the earth, describes in every equal particle of time is very nearly as the sum of the number 219.46 and of the versed sine of twice the distance of the moon from the nearest quadrature, with respect to a circle whose radius is unity. These things are so when the variation in the octants is at its mean magnitude. But if the variation there is greater or less, that versed sine should be increased or decreased in the same ratio.
Proposition 27, Problem 8
From the hourly motion of the moon, to find its distance from the earth.
The area that the moon, by a radius drawn to the earth, describes in every moment of time is as the hourly motion of the moon and the square of the distance of the moon from the earth jointly. And therefore the distance of the moon from the earth is directly proportional to the square root of the area and inversely proportional to the square root of the hourly motion. Q.E.I.
COROLLARY 1. Hence the apparent diameter of the moon is given, since it is inversely as the distance of the moon from the earth. Let astronomers test how accurately this rule agrees with the phenomena.
COROLLARY 2. Hence also the lunar orbit can be defined more exactly from the phenomena than could have been done before now.
Proposition 28, Problem 9
To find the diameters of the orbit in which the moon would have to move, if there were no eccentricity.
The curvature of the trajectory that a moving body describes, if it is attracted in a direction which is everywhere perpendicular to that trajectory, is as the attraction directly and the square of the velocity inversely. I reckon the curvatures of lines as being among themselves in the ultimate ratio of the sines or of the tangents of the angles of contact, with respect to equal radii, when those radii are diminished indefinitely. Now, the attraction of the moon toward the earth in the syzygies is the excess of its gravity toward the earth over the solar force 2PK (as in the figure to prop. 25), by which force the accelerative gravity of the moon toward the sun exceeds the accelerative gravity of the earth toward the sun or is exceeded by it. In the quadratures that attraction is the sum of the gravity of the moon toward the earth and the solar force KT (which draws the moon toward the earth). And these attractions, if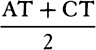 
is called N, are very nearly as 
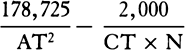and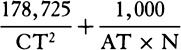 
, or as 178,725N × CT2 − 2000AT2 × CT and 178,725N × AT2 + 1,000CT2 × AT. For if the accelerative gravity of the moon toward the earth is represented by the number 178,725, then the mean force ML, which in the quadratures is PT or TK and draws the moon toward the earth, will be 1,000, and the mean force TM in the syzygies will be 3,000; if the mean force ML is subtracted from that, there will remain the force 2,000 by which the moon in the syzygies is drawn apart from the earth and which I have called 2PK above. Now, the velocity of the moon in the syzygies (A and B) is to its velocity in the quadratures (C and D) jointly as CT is to AT and as the moment of the area that the moon (by a radius drawn to the earth) describes in the syzygies is to the moment of that same area as described in the quadratures, that is, as 11,073CT to 10,973AT. Take this ratio squared inversely and the above ratio directly, and the curvature of the moon’s orbit in the syzygies will become to its curvature in the quadratures as 120,406,729 × 178,725AT2 × CT2 × N − 120,406,729 × 2,000AT4 × CT to 122,611,329 × 178,725AT2 × CT2 × + 122,611,329 × 1,000CT4 × AT, that is, as 2,151,969AT × CT × N − 24,081AT3 to 2,191,371AT × CT × N + 12,261CT3.
Since the figure of the lunar orbit is unknown, in its place let us assume an ellipse DBCA, in whose center T the earth is placed, and let its major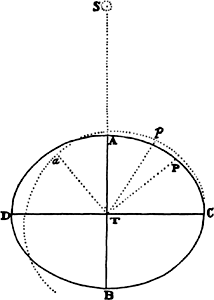 
axis DC lie between the quadratures and its minor axis AB between the syzygies. And since the plane of this ellipse revolves about the earth with an angular motion, and since the trajectory whose curvature we are considering ought to be described in a plane that is entirely devoid of any angular motion, we must consider the figure that the moon, while revolving in that ellipse, describes in this place, that is, the figure Cpa, whose individual points p are found by taking any point P on the ellipse to represent the place of the moon, and by drawing Tp equal to TP in such a way that the angle PTp is equal to the apparent motion of the sun since the time of quadrature C, or (which comes to almost the same thing) in such a way that the angle CTp is to the angle CTP as the time of a synodic revolution of the moon is to the time of a periodic revolution, or as 29d12h44m to 27d7h43m. Therefore, take the angle CTa in this same ratio to the right angle CTA, and let the length Ta be equal to the length TA, then a will be the lower apsis and c the upper apsis of this orbit Cpa. And by making calculations I find that the difference between the curvature of the orbit Cpa at the vertex a and the curvature of the circle described with center T and radius TA has a ratio to the difference between the curvature of the ellipse at the vertex A and the curvature of that circle which is equal to the ratio of the square of the angle CTP to the square of the angle CTp and that the curvature of the ellipse at A is to the curvature of that circle in the ratio of TA2 to TC2; and the curvature of that circle is to the curvature of a circle described with center T and radius TC as TC to TA; but this curvature is to the curvature of the ellipse at C in the ratio of TA2 to TC2; and the difference between the curvature of the ellipse at the vertex C and the curvature of this last circle is to the difference between the curvature of the figure Tpa at the vertex C and the curvature of the same circle in the ratio of the square of the angle CTp to the square of the angle CTP. And these ratios are easily gathered from the sines of the angles of contact and of the differences of the angles. Moreover, by comparing these, the curvature of the figure Cpa at a comes out to its curvature at C as AT3 + 
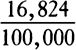CT2 × AT to CT3 + 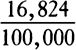AT2 × CT; where the factor 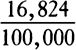represents the difference of the squares of the angles CTP and CTp divided by the square of the smaller angle CTP, or (which is the same) the difference of the squares of the times 27d7h43m and 29d12h44m divided by the square of the time 27d7h43m.
Therefore, since a designates the syzygy of the moon and C its quadrature, the proportion just found must be the same as the proportion of the curvature of the orbit of the moon in the syzygies to its curvature in the quadratures, which we found above. Accordingly, to find the proportion of CT to AT, I multiply the extremes by the means. And the resulting terms divided by AT × CT become 2,062.79CT4 − 2,151,969N × CT3 + 368,676N × AT × CT2 + 36,342AT2 × CT2 − 362,047N × AT2 × CT + 2,191,371N × AT3 + 4,051.4AT4 = 0. When I take the half-sum N of the terms AT and CT to be 1, and their half-difference to be x, there results CT = 1 + x and AT = 1 − x; and when these values are put into the equation and the resulting equation is resolved, x is found equal to 0.00719, and hence the semidiameter CT comes out 1.00719 and the semidiameter AT 0.99281. These numbers are very nearly as 701/24 and 691/24. Therefore the distance of the moon from the earth in the syzygies is to its distance in the quadratures (setting aside, that is, any consideration of eccentricity) as 691/24 to 701/24, or in round numbers as 69 to 70.
Proposition 29, Problem 10
To find the variation of the moon.
This inequality arises partly from the elliptical form of the orbit of the moon and partly from the inequality of the moments of the area that the moon describes by a radius drawn to the earth. If the moon P moved in the ellipse DBCA about the earth at rest in the center of the ellipse and, by a radius TP drawn to the earth, described the area CTP proportional to the time, and if furthermore the greatest semidiameter CT of the ellipse were to the least semidiameter TA as 70 to 69, then the tangent of the angle CTP would be to the tangent of the angle of the mean motion (reckoned from the quadrature C) as the semidiameter TA of the ellipse to its semidiameter TC, or as 69 to 70. Moreover, the description of the area CTP ought, in the progress of the moon from quadrature to syzygy, to be accelerated in such a way that the moment of this area in the syzygy of the moon will be to its moment in its quadrature as 11,073 to 10,973, and in such a way that the excess of the moment in any intermediate place P over the moment in the quadrature will be as the square of the sine of the angle CTP. And this will occur exactly enough if the tangent of angle CTP is diminished in the ratio of √10,973 to √11,073, or in the ratio of 68.6877 to 69. In this way the tangent of angle CTP will now be to the tangent of the mean motion as 68.6877 to 70; and the angle CTP in the octants, where the mean motion is 45°, will be found to be 44°27′28″, which, when subtracted from the angle of the mean motion of 45°, leaves the greatest variation 32′32″. These things would be so if the moon, in going from quadrature to syzygy, described an angle CTA of only 90°. But because of the motion of the earth, by which the sun is transferred forward [or in consequentia] in its apparent motion, the moon, before it reaches the sun, describes an angle CTa greater than a right angle, in the ratio of the time of a synodic revolution of the moon to the time of its periodic revolution, that is, in the ratio of 29d12h44m to 27d7h43m. And in this way all the angles about the center T are enlarged in the same ratio; and the greatest variation, which would otherwise be 32′32″, now increased in the same ratio, becomes 35′10″.
This is the magnitude of the greatest variation at the mean distance of the sun from the earth, ignoring the differences that can arise from the curvature of the earth’s orbit and the greater action of the sun upon the sickle-shaped and the new moon than upon the gibbous and the full moon. At other distances of the sun from the earth, the greatest variation is directly as the square of the time of synodic revolution and inversely as the cube of the distance of the sun from the earth. And therefore in the apogee of the sun the greatest variation is 33′14″, and in its perigee 37′11″ provided that the eccentricity of the sun is to the transverse semidiameter of the great orbit [i.e., the earth’s orbit] as 1615/16 to 1,000.
Hitherto we have investigated the variation in a noneccentric orbit, in which the moon in its octants is always at its mean distance from the earth. If the moon, because of its eccentricity, is more distant or less distant from the earth than if it were placed in this orbit, the variation can be a little greater or a little less than according to the rule asserted here; but I leave the excess or deficiency for astronomers to determine from phenomena.
Proposition 30, Problem 11
To find the hourly motion of the nodes of the moon in a circular orbit.
Let S designate the sun, T the earth, P the moon, NPn the orbit of the moon, Npn the projection of the orbit in the plane of the ecliptic; N and n the nodes, nTNm the line of the nodes, indefinitely produced; PI and PK perpendiculars dropped to the lines ST and Qq; Pp a perpendicular dropped to the plane of the ecliptic; A and B the syzygies of the moon in the plane of the ecliptic; AZ a perpendicular to the line of the nodes Nn; Q and q the quadratures of the moon in the plane of the ecliptic; and pK a perpendicular to the line Qq, which lies between the quadratures. The force of the sun to perturb the motion of the moon has (by prop. 25) two components, one proportional to the line LM in the figure of that proposition, the other proportional to the line MT in that same figure. And the moon is attracted toward the earth by the first of these forces, and by the second it is attracted toward the sun along a line parallel to the straight line ST drawn from the earth to the sun. The first force LM acts in the plane of the moon’s orbit and therefore can make no change in the position of that plane. Therefore this force is to be ignored. The second force MT, by which the plane of the lunar orbit is perturbed, is the same as the force 3PK or 3IT. And this force (by prop. 25) is to the force by which the moon could revolve uniformly in a circle in its periodic time about the earth at rest as 3IT to the radius of the circle multiplied by the number 178.725, or as IT to the radius multiplied by 59.575. But in this calculation and in what follows, I consider all lines drawn from the moon to the sun to be parallel to the line drawn from the earth to the sun, because the inclination diminishes all effects in some cases nearly as much as it increases them in others; and we are here seeking the mean motions of the nodes, ignoring those niceties of detail which would make the calculation too cumbersome.
Now let PM represent the arc that the moon describes in a minimally small given time, and ML the line-element one-half of which the moon could describe in the same time by the impulse of the above-mentioned force 3IT. Draw PL and MP, and produce them to m and l, and let them cut the plane of the ecliptic there, and upon Tm drop the perpendicular PH. Since the straight line ML is parallel to the plane of the ecliptic and so cannot meet with the straight line ml (which lies in that plane) and yet these straight lines lie in a common plane LMPml, these straight lines will be parallel, and therefore the triangles LMP and lmP will be similar. Now, since MPm is in the plane of the orbit in which the moon was moving while in place P, the point m will fall upon the line Nn drawn through the nodes N and n of that orbit. The force by which half of the line-element LM is generated—if all of it were impressed all at once in place P—would generate that whole line and would cause the moon to move in an arc whose chord would be LP, and so would transfer the moon from the plane MPmT into the plane LPlT; therefore the angular motion of the nodes that is generated by that force will be equal to the angle mTl. Moreover, ml is to mP as ML is to MP, and so, since MP is given (because the time is given), ml is as the rectangle ML × mP, that is, as the rectangle IT × mP. And, provided that the angle Tml is a right angle, the angle mTl is as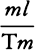 
, and therefore as 
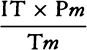, that is (because Tm is to mP as TP is to PH), as 
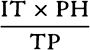; and so, because TP is given, as IT × PH. But if the angle Tml or STN is oblique, the angle mTl will be still smaller, in the ratio of the sine of the angle STN to the radius, or of AZ to AT. Therefore the velocity of the nodes is as IT × PH × AZ, or as the solid contained by [or the product of] the sines of the three angles TPI, PTN, and STN.
If those angles are right angles, as happens when the nodes are in the quadratures and the moon is in the syzygy, the line-element ml will go off indefinitely and the angle mTl will become equal to the angle mPl. But in this case the angle mPl is to the angle PTM, which the moon describes about the earth in the same time by its apparent motion, as 1 to 59.575. For the angle mPl is equal to the angle LPM, that is, to the angle of the deflection of the moon from the straight-line path that the aforesaid solar force 3IT could generate by itself in that given time, if the gravity of the moon were then to cease; and the angle PTM is equal to the angle of the deflection of the moon from the straight-line path that the force by which the moon is kept in its orbit would generate in the same time, if the solar force 3IT were then to cease. And these forces, as we have said above, are to each other as 1 to 59.575. Therefore, since the mean hourly motion of the moon with respect to the fixed stars is 32′56″27‴12iv½, the hourly motion of the node in this case will be 33″10‴33iv12v. But in other cases this hourly motion will be to 33″10‴33iv12v as the solid contained by [or the product of] the sines of the three angles TPI, PTN, and STN (or the distance of the moon from the quadrature, of the moon from the node, and of the node from the sun) to the cube of the radius. And whenever the sign of any of the angles is changed from positive to negative and from negative to positive, retrograde motion will have to be changed into progressive motion, and progressive into retrograde. Hence it happens that the nodes advance whenever the moon is between either of the quadratures and the node nearest to that quadrature. In other cases, the nodes are retrograde, and they are carried backward [or in antecedentia] each month by the excess of the retrograde motion over the progressive.
COROLLARY 1. Hence, if from the ends P and M of the minimally small given arc PM, the perpendiculars PK and Mk are dropped to the line Qq that joins the quadratures, and these perpendiculars are produced until they cut the line of the nodes Nn in D and d, then the hourly motion of the nodes will be as the area MPDd and the square of the line AZ jointly. For let PK, PH, and AZ be the above-mentioned three sines—namely, PK the sine of the distance of the moon from the quadrature, PH the sine of the distance of the moon from the node, and AZ the sine of the distance of the node from the sun—then the velocity of the node will be as the solid [or product] PK × PH × AZ. But PT is to PK as PM to Kk, and so, because PT and PM are given, Kk is proportional to PK. Also, AT is to PD as AZ to PH, and therefore PH is proportional to the rectangle PD × AZ; and, combining these ratios, PK × PH is as the solid Kk × PD × AZ, and PK × PH × AZ is as Kk × PD × AZ2, that is, as the area PDdM and AZ2 jointly. Q.E.D.
COROLLARY 2. In any given position of the nodes, the mean hourly motion is half of their hourly motion in the moon’s syzygies, and thus is to 16″55‴16iv36v as the square of the sine of the distance of the nodes from the syzygies is to the square of the radius, or as AZ2 to AT2. For if the moon traverses the semicircle QAq with uniform motion, the sum of all the areas PDdM during the time in which the moon goes from Q to M will be the area QMdE, which is terminated at the tangent QE of the circle; and in the time in which the moon reaches point n, that sum will be the total area EQAn, which the line PD describes; then as the moon goes from n to q, the line PD will fall outside the circle and will describe the area nqe (which is terminated at the tangent qe of the circle)—which, since the nodes were previously retrograde but now are progressive, must be subtracted from the former area, and (since it is equal to the area QEN) will leave the semicircle NQAn. Therefore, during the time in which the moon describes a semicircle, the sum of all the areas PDdM is the area of that semicircle; and in the time in which the moon describes a circle, the sum of all those areas is the area of the whole circle. But the area PDdM, when the moon is in the syzygies, is the rectangle of the arc PM and the radius PT; and in the time in which the moon describes a circle, the sum of all the areas that are equal to this one is the rectangle of the whole circumference and the radius of the circle; and this rectangle, since it is equal to two circles, is twice as large as the former rectangle. Accordingly, if the nodes moved with the same velocity uniformly continued that they have in the lunar syzygies, they would describe a space twice as large as the space which they really describe; and therefore the mean motion—with which, if it were continued uniformly, they would describe the space that they really cover with their nonuniform motion—is one-half of the motion which they have in the moon’s syzygies. Hence, since the greatest hourly motion of the nodes, if the nodes are in the quadratures, is 33″10‴33iv12v, their mean hourly motion in this case will be 16″35‴16iv36v. And since the hourly motion of the nodes is always as AZ2 and the area PDdM jointly, and therefore the hourly motion of the nodes in the moon’s syzygies is as AZ2 and the area PDdM jointly, that is (because the area PDdM described in the syzygies is given), as AZ2, the mean motion will also be as AZ2; and hence this motion, when the nodes are outside the quadratures, will be to 16″35‴16iv36v as AZ2 to AT2. Q.E.D.
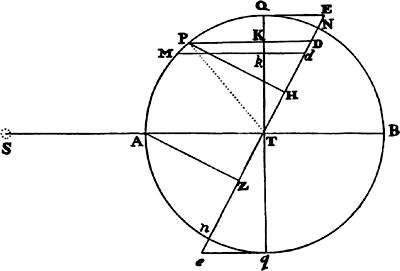
Proposition 31, Problem 12
To find the hourly motion of the nodes of the moon in an elliptical orbit.
Let Qpmaq represent an ellipse described with a major axis Qq and a minor axis ab, QAqB a circle circumscribed about this ellipse, T the earth in the common center of both, S the sun, p the moon moving in the ellipse, and pm the arc that the moon describes in a minimally small given particle of time, N and n the nodes joined by the line Nm, pK and mk perpendiculars dropped to the axis Qq and produced on both sides until they meet the circle at P and M and the line of the nodes at D and d. And if the moon, by a radius drawn to the earth, describes an area proportional to the time, the hourly motion of the node in the ellipse will be as the area pDdm and AZ2 jointly.
To demonstrate this, let PF touch the circle at P and, produced, meet TN at F; let pf touch the ellipse at p and, produced, meet the same TN at f; and let these tangents come together on the axis TQ at Y. And let ML designate the space that the moon, revolving in a circle, would describe by a transverse motion under the action and impulse of the aforesaid force 3IT or 3PK, while it describes the arc PM; and let ml designate the space that the moon, revolving in an ellipse, could describe in the same time, also under the action of the force 3IT or 3PK. Further, let Lp and lp be produced until they meet the plane of the ecliptic at G and g; and let FG and fg be drawn, of which let FG produced cut pf, pg, and TQ at c, e, and R respectively; and let fg produced cut TQ at r. Then, since the force 3IT or 3PK in the circle is to the force 3IT or 3pK in the ellipse as PK is to pK, or as AT to aT, the space ML generated by the first force will be to the space ml generated by the second force as PK to pK, that is (because the figures PYKp and FYRc are similar), as FR to cR. Moreover, ML is to FG (because the triangles PLM and PGF are similar) as PL to PG, that is (because Lk, PK, and GR are parallel), as pl to pe, that is (because the triangles plm and cpe are similar), as lm to ce; and thus LM is to lm, or FR is to cR, as FG is to ce. And therefore if fg were to ce as fY to cY, that is, as fr to cR (that is, as fr to FR and FR to cR jointly, that is, as fT to FT and FG to ce jointly), then, since the ratio FG to ce taken away from both sides leaves the ratios fg to FG and fT to FT, the ratio fg to FG would be as fT to FT, and so the angles that FG and fg would subtend at the earth T would be equal to each other. But these angles (by what we have set forth in the preceding prop. 30) are the motions of the nodes in the time in which the moon traverses the arc PM in the circle, and the arc pm in the ellipse; and therefore the motions of the nodes in the circle and in the ellipse would be equal to each other. These things would be so, if only fg were to ce as fY to cY, that is, if fg were equal to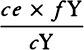 
. But because the triangles fgp and cep are similar, fg is to ce as fp to cp, and so fg is equal to 
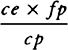; and therefore the angle that fg really subtends is to the former angle that FC subtends (that is, the motion of the nodes in the ellipse is to the motion of the nodes in the circle) as this fg or 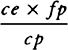to the former fg or 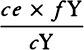, that is, as fp × cY to fY × cp, or as fp to fY and cY to cp; that is (if ph, parallel to TN, meets FP at h), as Fh to FY and FY to FP; that is, as Fh to FP or Dp to DP, and so as the area Dpmd to the area DPMd. And therefore, since (by prop. 30, corol. 1) the latter area and AZ2 jointly are proportional to the hourly motion of the nodes in the circle, the former area and AZ2 jointly will be proportional to the hourly motion of the nodes in the ellipse. Q.E.D.
COROLLARY. Therefore, since in any given position of the nodes, the sum of all the areas pDdm, in the time in which the moon goes from the quadrature to any place m, is the area mpQEd, which is terminated at the tangent QE of the ellipse, and the sum of all those areas in a complete revolution is the area of the whole ellipse, the mean motion of the nodes in the ellipse will be to the mean motion of the nodes in the circle as the ellipse to the circle, that is, as Ta to TA, or as 69 to 70. And therefore, since (by prop. 30, corol. 2) the mean hourly motion of the nodes in the circle is to 16″35‴16iv36v as AZ2 to AT2 if the angle 16″21‴3iv30v is taken to the angle 16″35‴16iv36v as 69 to 70, the mean hourly motion of the nodes in the ellipse will be to 16″21‴3iv30v as AZ2 to AT2, that is, as the square of the sine of the distance of the node from the sun to the square of the radius.
But the moon, by a radius drawn to the earth, describes an area more swiftly in the syzygies than in the quadratures, and on that account the time is shortened in the syzygies and lengthened in the quadratures, and along with the time the motion of the nodes is increased and decreased. Now, the moment of an area in the quadratures of the moon was to its moment in the syzygies as 10,973 to 11,073; and therefore the mean motion in the octants is to the excess in the syzygies and to the deficiency in the quadratures as the half-sum 11,023 of the numbers is to their half-difference 50. Accordingly, since the time of the moon in each equal particle of its orbit is inversely as its velocity, the mean time in the octants will be to the excess of time in the quadratures and its deficiency in the syzygies, arising from this cause, as 11,023 to 50 very nearly. With regard to positions of the moon between the quadratures and the syzygies, I find that the excess of the moments of the area in any one of these positions over the least moment in the quadratures is very nearly as the square of the sine of the distance of the moon from the quadratures; and therefore the difference between the moment in any position and the mean moment in the octants is as the difference between the square of the sine of the distance of the moon from the quadratures and the square of the sine of 45°, or half of the square of the radius; and the increase of the time in any one of the positions between the octants and the quadratures, and its decrease between the octants and the syzygies, is in the same ratio. But the motion of the nodes, in the time in which the moon traverses each equal particle of its orbit, is accelerated or retarded as the square of the time.
For that motion, while the moon traverses PM, is (other things being equal) as ML, and ML is in the squared ratio of the time. Therefore, the motion of the nodes in the syzygies, a motion completed in the time in which the moon traverses given particles of its orbit, is diminished as the square of the ratio of the number 11,073 to the number 11,023; and the decrement is to the remaining motion as 100 to 10,973 and to the total motion as 100 to 11,073 very nearly. But the decrement in positions between the octants and syzygies and the increment in positions between the octants and quadratures are to this decrement very nearly as [i] the total motion in those positions to the total motion in the syzygies and as [ii] the difference between the square of the sine of the distance of the moon from the quadrature and half of the square of the radius to half of the square of the radius, jointly. Hence, if the nodes are in the quadratures and two positions are taken equally distant from the octant, one on one side and one on the other, and another two are taken at the same distance from the syzygy and from the quadrature, and if from the decrements of the motions in the two positions between the syzygy and octant are subtracted the increments of the motions in the remaining two positions that are between the octant and quadrature, the remaining decrement will be equal to the decrement in the syzygy, as will be easily apparent upon examination. And accordingly the mean decrement, which must be subtracted from the mean motion of the nodes, is a fourth of the decrement in the syzygy. The total hourly motion of the nodes in the syzygies (when it was supposed the moon described, by a radius drawn to the earth, an area proportional to the time) was 32″42‴7iv. And according to what we have just said, the decrement of the motion of the nodes, in the time when the moon—now moving more swiftly—describes the same space, is to this motion as 100 to 11,073; and so the decrement is 17‴43iv11v, of which a fourth (4‴25iv48v) subtracted from the mean hourly motion found above (16″21‴3iv30v) leaves 16″16‴37iv42v, the corrected mean hourly motion.
If the nodes are beyond the quadratures and two places equally distant from the syzygies are considered, one on one side and one on the other, the sum of the motions of the nodes when the moon is in these positions will be to the sum of their motions when the moon is in the same positions and the nodes are in the quadratures as AZ2 to AT2. And the decrements of the motions, arising from the causes just now set forth, will be to each other as the motions themselves, and therefore the remaining motions will be to each other as AZ2 to AT2, and the mean motions will be as the remaining motions. Therefore the corrected mean hourly motion, in any given situation of the nodes, is to 16″16‴37iv42v as AZ2 to AT2, that is, as the square of the sine of the distance of the nodes from the syzygies to the square of the radius.
Proposition 32, Problem 13
To find the mean motion of the nodes of the moon.
The mean annual motion is the sum of all the mean hourly motions in a year. Suppose that the node is in N and that as each hour is completed, it is drawn back into its former place so that, notwithstanding its own proper motion, it always maintains some given position with respect to the fixed stars. And suppose that during this same time the sun S, as a result of the motion of the earth, advances from the node and completes its apparent annual course with a uniform apparent motion. Moreover, let Aa be the minimally small given arc that the straight line TS, always drawn to the sun, describes in a minimally small given time by its intersection with the circle NAn; then (by what has already been shown) the mean hourly motion will be as AZ2, that is (because AZ and ZY are proportional), as the rectangle of AZ and ZY, that is, as the area AZYa. And the sum of all the mean hourly motions from the beginning will be as the sum of all the areas aYZA, that is, as the area NAZ. Moreover, the greatest area AZYa is equal to the rectangle of the arc Aa and the radius of the circle; and therefore the sum of all such rectangles in the whole circle will be to the sum of the same number of greatest rectangles as the area of the whole circle to the rectangle of the whole circumference and the radius, that is, as 1 to 2. Now, the hourly motion corresponding to the greatest rectangle was 16″16‴37iv42v, and this motion, in a whole sidereal year of 365d6h9m, adds up to 39°38′7″50‴. And so half of this, 19°49′3″55‴, is the mean motion of the nodes that corresponds to the whole circle. And the motion of the nodes in the time during which the sun goes from N to A is to 19°49′3″55‴ as the area NAZ is to the whole circle.
These things are so on the hypothesis that each hour the node is drawn back to its former place, in such a way that when a whole year is completed, the sun returns to the same node from which it had initially departed. But as a result of the motion of that node, it comes about that the sun returns to the node more quickly; and now this shortening of the time must be computed. Since in a total year the sun travels through 360°, and in the same time the node with its greatest motion would travel through 39°38′7″50‴, or 39.6355°, and the mean motion of the node in any place N is to its mean motion in its quadratures as AZ2 to AT2, the motion of the sun will be to the motion of the node in N as 360AT2 to 39.6355AZ2, that is, as 9.0827646AT2 to AZ2. Hence, if the circumference NAn of the whole circle is divided into equal particles Aa, then the time in which the sun traverses the particle Aa (the circle being at rest) will be to the time in which it traverses the same particle (if the circle revolves along with the nodes about the center T) inversely as 9.0827646AT2 to 9.0827646AT2 + AZ2. For the time is inversely as the velocity with which the particle [of arc] is traversed, and this velocity is the sum of the velocities of the sun and of the node. Let the sector NTA represent the time in which the sun, without the motion of the node, would traverse the arc NA, and let the particle ATa of the sector represent the particle of time in which it would traverse the minimally small arc Aa; furthermore, drop a perpendicular aY to Nn and on AZ take dZ of a length such that the rectangle of dZ and ZY is to the particle ATa of the sector as AZ2 is to 9.0827646AT2 + AZ2 (that is, such that dZ is to ½AZ as AT2 is to 9.0827646AT2 + AZ2); then the rectangle of dZ and ZY will designate the decrement of time arising from the motion of the node during the total time in which the arc Aa is traversed. And if the point d touches the curve NdGn,a the curvilinear area NdZ will be the total decrement in the time in which the whole arc NA is traversed; and therefore the excess of the sector NAT over the area NAZ will be that total time. And since the motion of the node in a smaller time is smaller in proportion to the time, the area AaYZ also will have to be diminished in the same proportion. And this will happen if on AZ the length eZ is taken, which is to the length AZ as AZ2 is to 9.0827646AT2 + AZ2. For thus the rectangle of eZ and ZY will be to the area AZYa as the decrement of the time in which the arc Aa is traversed is to the total time in which it would be traversed if the node were at rest; and therefore that rectangle will correspond to the decrement of the motion of the node. And if the point e touches the curve NeFn,b the total area NeZ, which is the sum of all the decrements of that motion, will correspond to the total decrement in the time during which the arc AN is traversed, and the remaining area NAe will correspond to the remaining motion, which is the true motion of the node in the time in which the total arc NA is traversed by the joint motions of the sun and the node. Now, the area of the semicircle is to the area of the figure NeFn, found by the method of infinite series, nearly as 793 to 60. And the motion that corresponds to the whole circle was 19°49′3″55‴, and therefore the motion that corresponds to double the figure NeFn is 1°29′58″2‴. Subtracting this from the former motion leaves 18°19′5″53‴, the total motion of the node with respect to the fixed stars between its successive conjunctions with the sun; and this motion, subtracted from the annual motion of the sun of 360°, leaves 341°40′54″7‴, the motion of the sun between the same conjunctions. And this motion is to the annual motion of 360° as the motion of the node just found (18°19′5″53‴) to its annual motion, which will therefore be 19°18′1″23‴. This is the mean motion of the nodes in a sidereal year. From the astronomical tables this is 19°21′21″50‴. The difference is less than 
of the total motion and seems to arise from the eccentricity of the moon’s orbit and its inclination to the plane of the ecliptic. By the eccentricity of the orbit, the motion of the nodes is too much accelerated; and on the other hand, by its inclination it is retarded somewhat, and reduced to its correct velocity.
Proposition 33, Problem 14
To find the true motion of the nodes of the moon.
In the time which is as the area NTA ‒ NdZ (in the preceding figure), that motion is as the area NAe, and hence is given. But because the calculation is too difficult, it is preferable to use the following construction of the problem. With center C and any interval CD as radius, describe a circle BEFD. Produce DC to A so that AB is to AC as the mean motion is to half of the true mean motion when the nodes are in the quadratures (that is, as 19°18′1″23‴ to 19°49′3″55‴); and thus BC will be to AC as the difference of the motions (0°31′2″32‴) to the latter motion (19°49′3″55‴), that is, as 1 to 383/10. Next, through point D draw the indefinite line Gg, touching the circle in D; and let the angle BCE or BCF be taken equal to twice the distance of the sun from the place of the node, as found from the mean motion, and let AE or AF be drawn cutting the perpendicular DG in G. The true motion of the nodes will be found if now an angle is taken that is to the total motion of the node between its syzygies (that is, to 9°11′3″) as the tangent DG is to the total circumference of the circle BED, and if that angle (for which the angle DAG can be used) is added to the mean motion of the nodes when the nodes are passing from quadratures to syzygies and is subtracted from the same mean motion when they are passing from syzygies to quadratures. For the true motion thus found will agree very nearly with the true motion which results from representing the time by the area NTA — NdZ and the motion of the node by the area NAe, as will be evident to anyone considering the matter and performing the computations. This is the semimonthly equation of the motion of the nodes. There is also a monthly equation, but it is not at all needed in order to find the latitude of the moon. For, since the variation of the inclination of the moon’s orbit to the plane of the ecliptic is subject to a double inequality, one semimonthly and the other monthly, the monthly inequality of the variation and the monthly equation of the nodes so moderate and correct each other that both can be ignored in determining the latitude of the moon.
COROLLARY. From this and the preceding proposition it is clear that the nodes are stationary in their syzygies; in the quadratures, however, they regress by an hourly motion of 16″19‴26iv. It is also clear that the equation of the motion of nodes in the octants is 1°30′. This all squares exactly with celestial phenomena.
Scholium
J. Machin, Gresham Professor of Astronomy, and Henry Pemberton, M.D., have independently found the motion of the nodes by yet another method. Some mention of the latter’s method has been made elsewhere. And the papers (which I have seen) of both men contained two propositions, which agreed with each other. Here I shall present Mr. Machin’s paper, since it was the first to come into my hands.
ON THE MOTION OF THE NODES OF THE MOON
Proposition 1
The mean motion of the sun from the node is defined by a mean geometrical proportional between the mean motion of the sun and that mean motion with which the sun recedes most swiftly from the node in the quadratures.
Let T be the place where the earth is, Nn the line of the nodes of the moon at any given time, KTM a line drawn at right angles to this line, and TA a straight line revolving around the center with the angular velocity with which the sun and the node recede from each other, in such a way that the angle between the straight line Nm (which is at rest) and TA (which is revolving) is always equal to the distance between the places of the sun and of the node. Now, if any straight line TK is divided into parts TS and SK, which are to each other as the hourly mean motion of the sun is to the hourly mean motion of the nodes in the quadratures, and if the straight line TH is taken so as to be a mean proportional between the part TS and the whole TK, this straight line among the rest will be proportional to the mean motion of the sun from the node.
For describe a circle NKnM with center T and radius TK, and with the same center and the semiaxes TH and TN describe an ellipse NHnL, and in the time in which the sun recedes from the node through the arc Na, if the straight line Tba is drawn, the area of the sector NTa will represent the sum of the motions of the node and sun in that same time. Therefore let Aa be the minimally small arc that the straight line Tba—revolving according to the aforesaid law—uniformly describes in a given particle of time, and the minimally small sector TAa will be as the sum of the velocities whereby the sun and the node are carried separately in that time. The velocity of the sun, however, is nearly uniform, since its small inequality introduces scarcely any variation in the mean motion of the nodes. The other part of this sum, namely the velocity of the node in its mean quantity, increases in receding from the syzygies as the square of the sine of its distance from the sun (by Principia, book 3, prop. 31, corol.) and, when it is greatest in the quadratures to the sun at K, has the same ratio to the velocity of the sun that SK has to TS; that is, it is as (the difference of the squares of TK and TH or) the rectangle KH × HM is to TH2. But the ellipse NBH divides the sector ATa, which represents the sum of these two velocities, into two parts ABba and BTb, which are proportional to the velocities. For, produce BT to the circle in β, and, from point B to the major axis, drop a perpendicular BG which, produced in both directions, meets the circle in points F and f. Then, since the space ABba is to the sector TBb as the rectangle AB × Bβ to BT2 (for that rectangle is equal to the difference of the squares of TA and TB because the straight line Aβ is cut equally at T and unequally at B), this ratio—when the space ABba is greatest at K—will be the same as the ratio of the rectangle KH × HM to HT2; but the greatest mean velocity of the node was [previously shown to be] in this ratio to the velocity of the sun. Therefore, in the quadratures, the sector ATa is divided into parts proportional to the velocities. And since the rectangle KH × HM is to HT2 as FB × Bf to BG2 and since the rectangle AB × Bβ is equal to the rectangle FB × Bf, it follows that the area-element ABba when it is greatest will be to the remaining sector TBb as the rectangle AB × Bβ to BG2. But the ratio of the area-elements was always as the rectangle AB × Bβ to BT2; and therefore the area-element ABba in the place A is smaller than the corresponding area-element in the quadratures, in the ratio of BG2 to BT2, that is, as the square of the sine of the distance of the sun from the node. And accordingly the sum of all the area-elements ABba (namely, the space ABN) will be as the motion of the node in the time in which the sun departs from the node and passes through the arc NA. And the remaining space (namely, the elliptical sector NTB) will be as the mean motion of the sun in the same time. And, therefore, since the mean annual motion of the node is the motion that it makes in the time during which the sun has completed its period, the mean motion of the node from the sun will be to the mean motion of the sun itself as the area of the circle to the area of the ellipse, that is, as the straight line TK to the straight line TH (which is the mean proportional between TK and TS); or, which comes to the same thing, as the mean proportional TH to the straight line TS.
Proposition 2
Given the mean motion of the nodes of the moon, to find the true motion.
Let the angle A be the distance of the sun from the mean place of the node, or the mean motion of the sun from the node. Then if angle B is taken so that its tangent is to the tangent of angle A as TH to TK—that is, as the square root of the ratio of the mean hourly motion of the sun to the mean hourly motion of the sun from the node when the node is in the quadratures—that same angle B will be the distance of the sun from the true place of the node. For draw FT, and (by the proof of the previous proposition) the angle FTN will be the distance of the sun from the mean place of the node, while the angle ATN will be the distance from the true place, and the tangents of these angles are to each other as TK to TH.
COROLLARY. Hence the angle FTA is the equation of the moon’s nodes, and the sine of this angle, when it is greatest in the octants, is to the radius as KH to TK + TH. And the sine of this equation in any other place A is to the greatest sine as the sine of the sum of the angles FTN + ATN is to the radius—that is, nearly as the sine of 2FTN (that is, twice the distance of the sun from the mean place of the node) is to the radius.
Scholium
If the mean hourly motion of the nodes in the quadratures is 16″16‴37iv42v (that is, 39°38′7′50‴ in a whole sidereal year), then TH will be to TK as the square root of the ratio of the number 9.0827646 to the number 10.0827646, that is, as 18.6524761 to 19.6524761. And therefore TH is to HK as 18.6524761 to 1, that is, as the motion of the sun in a sidereal year to the mean motion of the node, which is 19°18′1″23⅔‴.
But if the mean motion of the nodes of the moon in twenty Julian years is 386°50′15″, as is deduced from observations used in the theory of the moon, the mean motion of the nodes in a sidereal year will be 19°20′31″58‴. And TH will be to HK as 360° to 19°20′31′58‴, that is, as 18.61214 to 1. Hence the mean hourly motion of the nodes in the quadratures will come out 16″18‴48iv. And the greatest equation of the nodes in the octants will be l°29′57″.
Proposition 34, Problem 15
To find the hourly variation of the inclination of the lunar orbit to the plane of the ecliptic.
Let A and a represent the syzygies, Q and q the quadratures, N and n the nodes, P the place of the moon in its orbit, p the projection of that place on the plane of the ecliptic, and mTl the momentaneous motion of the nodes as above. Drop the perpendicular PG to the line Tm, join pG and produce it until it meets Tl in g, and also join Pg; then the angle PGp will be the inclination of the moon’s orbit to the plane of the ecliptic when the moon is in P, and the angle Pgp will be the inclination of the same orbit after a moment of time has been completed; and thus the angle GPg will be the momentaneous variation of the inclination. But this angle GPg is to the angle GTg as TG to PG and Pp to PG jointly. And therefore, if an hour is substituted for the moment of time, then—since the angle GTg (by prop. 30) is to the angle 33″10‴33iv as IT × PG × AZ to AT3—the angle GPg (or the hourly variation of the inclination) will be to the angle 33″10‴33iv as IT × AZ × TG × 
to AT3. Q.E.I.
These things are so on the hypothesis that the moon revolves uniformly in a circular orbit. But if that orbit is elliptical, the mean motion of the nodes will be diminished in the ratio of the minor axis to the major axis, as has been set forth above. And the variation of the inclination will also be diminished in the same ratio.
COROLLARY 1. If the perpendicular TF is erected on Nn, and pM is the hourly motion of the moon in the plane of the ecliptic, and if the perpendiculars pK and Mk are dropped to QT and produced in both directions to meet TF at H and h, then IT will be to AT as Kk to Mp, and TG to Hp as TZ to AT, and so IT × TG will be equal to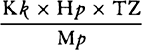 
, that is, equal to the area HpMh multiplied by the ratio 
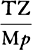; and therefore the hourly variation of the inclination will be to 33″10‴33iv as HpMh multiplied by AZ × 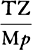× is to AT3.
COROLLARY 2. And so, if the earth and the nodes, as each hour is completed, were drawn back from their new places and were always restored instantly to their former places, so that their given position remained unchanged throughout an entire periodic month, the total variation of the inclination during the time of that month would be to 33″10‴33iv as the sum of all the areas HpMh which are generated during a revolution of the point p (these areas being summed according to their proper signs + and −) multiplied by AZ × TZ × 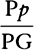is to Mp × AT3, that is, as the whole circle QAqa multiplied by AZ × TZ × 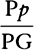is to Mp × AT3, that is, as the circumference QAqa multiplied by AZ × TZ × 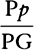is to 2Mp × AT2.
COROLLARY 3. Accordingly, in a given position of the nodes, the mean hourly variation, from which, continued uniformly for a month, that monthly variation could be generated, is to 33″10‴33iv as AZ × TZ × 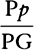to 2AT2, or as Pp × 
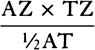to PG × 4AT, that is (since Pp is to PG as the sine of the above-mentioned inclination to the radius, and 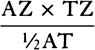is to 4AT as the sine of twice the angle ATn to four times the radius), as the sine of that same inclination multiplied by the sine of twice the distance of the nodes from the sun to four times the square of the radius.
COROLLARY 4. Since the hourly variation of the inclination, when the nodes are in the quadratures, is (by this proposition) to the angle 33310433iv as IT × AZ × TG × 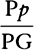to AT3, that is, as 
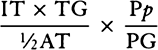to 2AT, that is, as the sine of twice the distance of the moon from the quadratures multiplied by 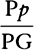is to twice the radius, it follows that the sum of all the hourly variations, in the time in which the moon in this situation of the nodes passes from quadrature to syzygy (that is, in the space of 177⅙ hours), will be to the sum of the same number of angles 33″10‴33iv, or 5,878″, as the sum of all the sines of twice the distance of the moon from the quadratures multiplied by 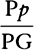is to the sum of the same number of diameters; that is, as the diameter multiplied by 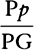is to the circumference; that is, if the inclination is 5°1′, as 7 × 
to 22, or 278 to 10,000. And accordingly the total variation, composed of the sum of all the hourly variations in the aforesaid time, is 163″, or 2′43″.
Proposition 35, Problem 16
To find the inclination of the moon’s orbit to the plane of the ecliptic at a given time.
Let AD be the sine of the greatest inclination, and AB the sine of the least inclination. Bisect BD in C, and with center C and radius BC describe a circle BGD. On AC take CE in the ratio to EB that EB has to 2BA. Now if, for the given time, the angle AEG is set equal to twice the distance of the nodes from the quadratures, and the perpendicular GH is dropped to AD, then AH will be the sine of the required inclination.
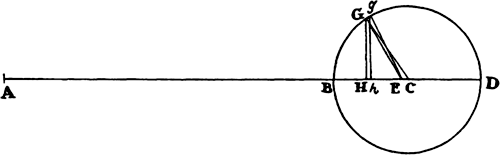
For GE2 is equal to GH2 + HE2 = BH × HD + HE2 = HB × BD + HE2 − BH2 = HB × BD + BE2 − 2BH × BE = BE2 + 2EC × BH = 2EC × AB + 2EC × BH = 2EC × AH. And thus, since 2EC is given, GE2 is as AH. Now let AEg represent twice the distance of the nodes from the quadratures after some given moment of time has been completed, and the arc Gg (because the angle GEg is given) will be as the distance GE. Moreover, Hh is to Gg as GH to GC, and therefore Hh is as the solid [or product] GH × Gg, or GH × GE; that is, as 
× GE2 or × AH, that is, as AH and the sine of the angle AEG jointly. Therefore, if AH, in any given case, is the sine of the inclination, it will be increased by the same increments as the sine of the inclination, by corol. 3 of the preceding prop. 34, and therefore will always remain equal to that sine. But when the point G falls upon either point B or D, AH is equal to this sine and therefore remains always equal to it. Q.E.D.
In this demonstration, I have supposed that the angle BEG, which is twice the distance of the nodes from the quadratures, increases uniformly. For there is no time to consider all the minute details of inequalities. Now suppose that the angle BEG is a right angle and that in this case Gg is the hourly increment of twice the distance of the nodes and sun from each other; then (by corol. 3 of prop. 34) the hourly variation of the inclination in the same case will be to 33″10‴33iv as the solid [or product] of the sine AH of the inclination and the sine of the right angle BEG (which is twice the distance of the nodes from the sun) is to four times the square of the radius; that is, as the sine AH of the mean inclination to four times the radius; that is (since that mean inclination is about 5°8½′), as its sine (896) to four times the radius (40,000), or as 224 to 10,000. And the total variation, corresponding to BD, the difference of the sines, is to that hourly variation as the diameter BD to the arc Gg; that is, as the diameter BD to the semicircumference BGD and the time of 2,0797/10 hours (during which the node goes from the quadratures to the syzygies) to 1 hour jointly; that is, as 7 to 11 and 2,0797/10 to 1. Therefore, if all the ratios are combined, the total variation BD will become to 33″10‴33iv as 224 × 7 × 2,0797/10 to 110,000, that is, as 29,645 to 1,000, and hence that variation BD will come out 16′23½″.
This is the greatest variation of the inclination insofar as the place of the moon in its orbit is not considered. For if the nodes are in the syzygies, the inclination is not at all changed by the various positions of the moon. But if the nodes are in the quadratures, the inclination is less when the moon is in the syzygies than when it is in the quadratures, by a difference of 2′43″, as we have indicated in corol. 4 of prop. 34. And the total mean variation BD, diminished when the moon is in its quadratures by 1′21½″ (half of this excess), becomes 15′2″; while in the syzygies it is increased by the same amount and becomes 17′45″. Therefore, if the moon is in the syzygies, the total variation in the passage of the nodes from quadratures to syzygies will be 17′45″; and so if the inclination, when the nodes are in the syzygies, is 5°17′20″, it will be 4°59′35″ when the nodes are in the quadratures and the moon in the syzygies. And that these things are so is confirmed by observations.
If now it is desired to find the inclination of the orbit when the moon is in the syzygies and the nodes are in any position whatever, let AB become to AD as the sine of 4°59′35″ is to the sine of 5°17′20″, and take the angle ABG equal to twice the distance of the nodes from the quadratures; then AH will be the sine of the required inclination. The inclination of the orbit is equal to this inclination when the moon is 90° distant from the nodes. In other positions of the moon, the monthly inequality that occurs in the variation of the inclination is compensated for in the calculation of the latitude of the moon (and, in a manner, canceled) by the monthly inequality in the motion of the nodes (as we have said above) and thus can be neglected in calculating that latitude.
Proposition 36, Problem 17
To find the force of the sun to move the sea.
The sun’s force ML or PT to perturb the motions of the moon, in the moon’s quadratures, was (by prop. 25 of this book 3) to the force of gravity here on earth as 1 to 638,092.6. And the force TM—LN or 2PK in the moon’s syzygies is twice as great. Now these forces, in the descent to the surface of the earth, are diminished in the ratio of the distances from the center of the earth, that is, in the ratio 60½ to 1; and so the first force on the surface of the earth is to the force of gravity as 1 to 38,604,600. By this force the sea is depressed in places that are 90 degrees distant from the sun. By the other force, which is twice as great, the sea is elevated both in the region directly under the sun and in the region opposite to the sun. The sum of these forces is to the force of gravity as 1 to 12,868,200. And since the same force arouses the same motion, whether it depresses the water in the regions that are 90 degrees distant from the sun or elevates the water in regions under the sun and opposite to the sun, this sum will be the total force of the sun to agitate the sea, and it will have the same effect as if all of it elevated the sea in regions under the sun and opposite it and had no action at all in regions that are 90 degrees distant from the sun.
This is the force of the sun to put the sea in motion in any given place when the sun is in the Zenith of the place as well as at its mean distance from the earth. In other positions of the sun, the force for raising the sea is directly as the versed sine of twice the altitude of the sun above the horizon of the place and inversely as the cube of the distance of the sun from the earth.
COROLLARY. The centrifugal force of the parts of the earth, arising from the daily motion of the earth (a force that is to the force of gravity as 1 to 289), causes the height of the water under the equator to exceed its height under the poles by a measure of 85,472 Paris feet (as was seen above in prop. 19); therefore, the solar force with which we have been dealing (since it is to the force of gravity as 1 to 12,868,200 and so to that centrifugal force as 289 to 12,868,200 or 1 to 44,527) will cause the height of the water in regions directly under the sun and directly opposite to the sun to exceed its height in places that are 90 degrees distant from the sun by a measure of only 1 Paris foot and 111/30 inches. For this measure is to the measure of 85,472 feet as 1 to 44,527.
Proposition 37, Problem 18
To find the force of the moon to move the sea.
COROLLARY 1. Since the water acted on by the force of the sun ascends to a height of 1 foot and 111/30 inches, by the force of the moon it will ascend to a height of 8 feet and 75/22 inches, and by both forces to a height of 10½ feet, and when the moon is in its perigee the water will ascend to a height of 12½ feet and beyond, especially when the tide is made greater by winds. And so great a force is more than sufficient to give rise to all the motions of the sea and corresponds exactly to the quantity of the motions. For in seas that extend widely from east to west, as in the Pacific Ocean and the parts of the Atlantic Ocean and the Ethiopic [or South Atlantic] Sea, which are outside the tropics, the water is generally raised to a height of 6, 9, 12, or 15 feet. And in the Pacific Ocean, which is deeper and wider, the tides are said to be greater than in the Atlantic Ocean and the Ethiopic Sea. For, to have the tide be full, the width of the sea from east to west should be no less than 90 degrees. In the Ethiopic Sea the ascent of the water within the tropics is less than in the temperate zones, because of the narrowness of the sea between Africa and the southern part of America. In the middle of the sea the water cannot rise unless it simultaneously falls on both shores, both the eastern and the western; nevertheless, in our narrow seas, the water ought to rise alternately on the two shores, that is, rise on one shore while it falls on the other. For this reason the ebb and flow are generally very small in islands that are farthest from the shores. In certain harbors, where the water is compelled to flow in and flow out with great impetus through shallow places, so as to fill and empty bays alternately, the ebb and flow must be greater than usual, as at Plymouth and Chepstow Bridge in England, at Mont-Saint-Michel and the city of Avranches in Normandy, at Cambay and Pegu bin the East Indies.b In these places the sea, coming in and going back out with great velocity, at times inundates the shores and at other times leaves them dry for many miles. And the impetus of flowing in or going back out cannot be broken before the water is raised or depressed to 30, 40, or 50 feet and more. And the same is true of oblong and shallow straits, such as the Straits of Magellan and that channel by which England is surrounded [presumably, the channel and seas, but not the ocean, bordering England]. The tide in harbors and straits of this sort is increased beyond measure by the impetus of running in and back. But on shores that face the deep and open sea with a steep descent, where the water can be raised and can fall without the impetus of flowing out and coming back, the magnitude of the tide corresponds to the forces of the sun and moon.
COROLLARY 3.c Since the force of the moon to move the sea is to the similar force of the sun as 4.4815 to 1, and since those forces (by book 1, prop. 66, corol. 14) are as the densities of the bodies of the moon and sun and the cubes of their apparent diameters jointly, the density of the moon will be to the density of the sun as 4.4815 to 1 directly and as the cube of the diameter of the moon to the cube of the diameter of the sun inversely, that is (since the apparent mean diameters of the moon and the sun are 31′16½″ and 32′12″), as 4,891 to 1,000. Now, the density of the sun was to the density of the earth as 1,000 to 4,000, and therefore the density of the moon is to the density of the earth as 4,891 to 4,000, or 11 to 9. Therefore the body of the moon is denser and more earthy than our earth.
COROLLARY 7. And the mean distance of the center of the moon from the center of the earth (in the octants of the moon) will be nearly 60⅖ greatest semidiameters of the earth. For the greatest semidiameter of the earth was 19,658,600 Paris feet, and the mean distance between the centers of the earth and the moon, which consists of 60⅖ such semidiameters, is equal to 1,187,379,440 feet. And this distance (by the preceding corollary) is to the distance of the center of the moon from the common center of gravity of the earth and the moon as 40.788 to 39.788; and hence the latter distance is 1,158,268,534 feet. And since the moon revolves with respect to the fixed stars in 27d7h434/9m, the versed sine of the angle that the moon describes in the time of one minute is 12,752,341, the radius being 1,000,000,000,000,000. And the radius is to this versed sine as 1,158,268,534 feet to 14.7706353 feet. The moon, therefore, falling toward the earth under the action of that force with which it is kept in its orbit, will in the time of one minute describe 14.7706353 feet. And by increasing this force in the ratio of 17829/40 to 17729/40, the total force of gravity in the orbit of the moon will be found by prop. 3, corol. [of this book 3]. And falling toward the earth under the action of this force, the moon will describe 14.8538067 feet in the time of one minute. And at 1/60 of the distance of the moon from the center of the earth, that is, at a distance of 197,896,573 feet from the center of the earth, a heavy body—falling in the time of one second—will likewise describe 14.8538067 feet. eAnd so, at a distance of 19,615,800 feet (which is the mean semidiameter of the earth), a heavy body in falling will describe—in the time of one second—15.11175 feet, or 15 feet 1 inch and 41/11 lines. This will be the descent of bodies at a latitude of 45 degrees. And by the foregoing table, presented in prop. 20, the descent will be a little greater at the latitude of Paris by about ⅔ of a line. Therefore, by this computation, heavy bodies falling in a vacuum at the latitude of Paris will—in the time of one second—describe approximately 15 Paris feet 1 inch and 425/33 lines. And if gravity is diminished by taking away the centrifugal force that arises from the daily motion of the earth at that latitude, heavy bodies falling there will—in the time of one second—describe 15 feet 1 inch and 1½ lines. And that heavy bodies do fall with this velocity at the latitude of Paris has been shown above in props. 4 and 19 [of this book 3].e
COROLLARY 8. fThe mean distance between the centers of the earth and the moon in the syzygies of the moon is 60 greatest semidiameters of the earth, taking away roughly 1/30 of a semidiameter. And in the moon’s quadratures, the mean distance between these centers is 605/6 semidiameters of the earth. For these two distances are to the mean distance of the moon in the octants as 69 and 70 to 69½, by prop. 28.f
Proposition 38, Problem 19
To find the figure of the body of the moon.
If the body of the moon were fluid like our sea, the force of the earth to elevate that fluid in both the nearest and farthest parts would be to the force of the moon by which our sea is raised in the regions both under the moon and opposite to the moon as the accelerative gravity of the moon toward the earth is to the accelerative gravity of the earth toward the moon and as the diameter of the moon is to the diameter of the earth, jointly—that is, as 39.788 to 1 and 100 to 365 jointly, or as 1,081 to 100. Hence, since our sea is raised by the force of the moon to 8⅗ feet, the lunar fluid would have to be raised by the force of the earth to 93 feet. And for this reason the figure of the moon would be a spheroid, the greatest diameter of which, produced, would pass through the center of the earth and would exceed by 186 feet the diameters perpendicular to that one. Therefore, it is just such a figure that the moon has and must have had from the beginning. Q.E.I.
COROLLARY. And hence it happens that the same face of the moon is always turned toward the earth. For in any other position, the moon cannot remain at rest, but by a motion of oscillation will always return to this position. But those oscillations would nevertheless be extremely slow because the forces producing them are small in magnitude; so that the face of the moon that should always look toward the earth can (for the reason given in prop. 17) be turned toward the other focus of the moon’s orbit and not at once be drawn back from there and turned toward the earth.
aLemma 1
Let APEp represent the earth, uniformly dense, with a center C and poles P and p and equator AE, and suppose a sphere Papeb to be described with center C and radius CP. Let QR be the plane on which a straight line drawn from the center of the sun to the center of the earth stands perpendicularly. Then, if the individual particles of the whole exterior earth PapAPepE, which is higher than the sphere just described, endeavor to recede in both directions from the plane QR, and the endeavor of each particle is as its distance from the plane, I say, first of all, that the total force and efficacy of all the particles that lie in the circle of the equator AE (disposed uniformly outside the globe, in the manner of a ring completely encircling that globe) to rotate the earth around its center will be to the total force and efficacy of the same number of particles standing at point A of the equator (which is most distant from the plane QR) to move the earth with a similar circular motion around its center as 1 is to 2. And that circular motion will be performed around an axis lying in the common section of the equator and the plane QR.
For let IK be any smaller circle parallel to the equator AE, and let L and l be any two equal particles situated in this circle outside the globe 
Pape.c And if perpendiculars LM and lm are dropped to the plane QR, which is perpendicular to a radius drawn to the sun, the total forces with which the particles recede from the plane QR will be proportional to the perpendiculars LM and lm. Now, let the straight line Ll be parallel to the plane Pape; bisect Ll at X; through the point X draw Nn parallel to the plane QR and meeting the perpendiculars LM and lm at N and n; and drop a perpendicular XY to the plane QR. Then the contrary forces of the particles L and l to rotate the earth in opposite directions are as LM × MC and lm × mC, that is, as LN × MC + NM × MC and in × mC − nm × mC, or LN × MC + NM × MC and LN × mC − NM × mC; and their difference LN × Mm − NM × (MC + mC) is the force of both particles taken together to rotate the earth. The positive part of this difference, LN × Mm or 2LN × NX, is to the force 2AH × HC of two particles of the same magnitude located at A as LX2 to AC2. And the negative part, NM × (MC + mC) or 2XY × CY is to the force 2AH × HC of the same particles located at A as CX2 to AC2. And accordingly the difference of the parts, that is, the force of the two particles L and l (taken together) to rotate the earth, is to the force of two particles equal to those and standing in the place A, likewise to rotate the earth, as LX2 − CX2 to AC2. But if the circumference IK of the circle IK is divided into innumerable equal particles L, all the LX2 will be to as many IX2 as 1 to 2 (by lem. 1), and to this same number of AC2 as IX2 to 2 AC2; and just as many CX2 will be to the same number of AC2 as 2CX2 to 2AC2. Therefore the combined forces of all the particles in the circumference of the circle IK are to the combined forces of as many particles in the place A as IX2 − 2CX2 to 2AC2, and therefore (by lem. 1) to the combined forces of as many particles in the circumference of the circle AE as IX2 − 2CX2 to AC2.
Now, if the diameter Pp of the sphered is divided into innumerable equal parts, on which the same number of circles IK stand, the matter in the perimeter of each circle IK will be as IX2; and so the force of that matter to rotate the earth will be as IX2 multiplied by IX2 − 2CX2. And the force of the same matter, if it stood in the perimeter of the circle AE, would be as IX2 multiplied by AC2. And therefore the force of all the particles of the total matter standing outside the globe in the perimeters of all the circles is to the force of as many particles standing in the perimeter of the greatest circle AE as all the IX2 multiplied by IX2 − 2CX2 to as many IX2 multiplied by AC2, that is, as all the AC2 − CX2 multiplied by AC2 − 3CX2 to as many AC2 − CX2 multiplied by AC2, that is, as all the AC4 − 4AC2 × CX2 + 3CX4 to as many AC4 − AC2 × CX2, that is, as the total fluent quantity whose fluxione is AC4 − 4AC2 × CX2 + 3CX4 to the total fluent quantity whose fluxion is AC4 − AC2 × CX2; and accordingly, by the method of fluxions, as AC4 × CX − 4/3AC2 × CX3 + ⅗CX5 to AC4 × CX − ⅓AC2 × CX3, that is, if the whole of Cp or AC is written in place of CX, as 4/15 AC5 to ⅔AC5, or as 2 to 5. Q.E.D.
, and 
. And when the distances are increased or decreased, the weights are decreased or increased as the squares of the distances. The weights of equal bodies toward the sun, Jupiter, Saturn, and the earth at distances of 10,000, 997, 791, and 109 respectively from their centers (and hence their weights on the surfaces) will be as 10,000, 943, 529, and 435. What the weights of bodies are on the surface of the moon will be shown below.a
, and 
respectively. If the parallax of the sun is taken as greater or less than 10″30‴, the quantity of matter in the earth will have to be increased or decreased in the cubed ratio.b
lines already found from the theory. Moreover, Richer repeated his observations in Cayenne every week during a ten-month period, and compared the lengths he found there for a pendulum consisting of an iron rod with its lengths similarly found in France [i.e., with its lengths adjusted in Paris so as to have the same period]. This diligence and caution seem to have been lacking in other observers. If his observations are to be trusted, the earth will be higher at the equator than at the poles by an excess of about seventeen miles, as came out above by the theory.b e
than in its aphelion, and does so inversely as the cube of the distance of the earth from the sun. Because the equation of the center of the sun is comprehended in the annual argument, the center of the moon’s orbit moves more swiftly in the epicycle BDA inversely as the square of the distance of the earth from the sun. In order for the center of the moon’s orbit to move still more swiftly, inversely in the simple ratio of the distance, draw a straight line DE from the center D of the orbit toward the apogee of the moon, or parallel to the straight line TC, and take the angle EDF equal to the excess of the above-mentioned annual argument over the distance of the apogee of the moon from the perigee of the sun in a forward direction [or in consequentia]; or, which is the same, take the angle CDF equal to the complement of the true anomaly of the sun to 360°. And let DF be to DC jointly as twice the eccentricity of the earth’s orbit is to the mean distance of the sun from the earth and as the daily mean motion of the sun from the apogee of the moon is to the daily mean motion of the sun from its own apogee, that is, as 33⅞ to 1,000 and 52′27″16‴ to 59′8″10‴ jointly, or as 3 to 100. And suppose that the center of the moon’s orbit is located in point F and revolves in an epicycle whose center is D and whose radius is DF, while the point D advances in the circumference of the circle DABD. For in this manner the velocity with which the center of the moon’s orbit will move in a certain curved line described about the center C will be very nearly inversely as the cube of the distance of the sun from the earth, as it ought to be.
20°43′40″, and of its apogee 
7°44′30″; and the mean motion of the moon 
15°21′00″, and of its apogee 
8°20′00″, and of its ascending node 
27°24′20″; and the difference between the meridians of this observatory and the Royal Paris Observatory 0h9m20s; but the mean motions of the moon and of its apogee have not as yet been determined with sufficient exactness.a