Proposition 39, Problem 20
To find the precession of the equinoxes.
The mean hourly motion of the nodes of the moon in a circular
orbit was, for the nodes in the quadratures, 16″35‴16iv36v, and half of this,
8″17‴38iv18v, is (for the reasons explained above [at the end of corol. 2 to
prop. 30]) the mean hourly motion of the nodes in such an orbit; and in a
whole sidereal year the mean motion adds up to 20°11′46″ [see beginning of
prop. 32]. Therefore, since in a year the nodes of the moon would, in such
an orbit, move backward [or in antecedentia] through 20°11′46″; and since, if
there were more moons, the motion of the nodes of each (by book 1, prop. 66,
corol. 16) would be as the periodic times; it follows that if the moon revolved
near the surface of the earth in the space of a sidereal day, the annual motion
of the nodes would be to 20°11′46″ as a sidereal day of 23h56m is to the
periodic time of the moon, 27d7h43m—that is, as 1,436 to 39,343. And the same
is true of the nodes of a ring of moons surrounding the earth, whether those
moons do not touch one another, or whether they become liquid and take
the form of a continuous ring, or finally whether that ring becomes rigid and
inflexible.
Let us imagine therefore that this ring, as to its quantity of matter, is
equal to all of the earth PapAPepE that lies outside of the globe
Papea (as in
the figure to lem. 2). This globe is to the earth that lies outside of it as aC2
to AC2 − aC2, that is (since the earth’s smaller semidiameter PC or aC is to
its greater semidiameter AC as 229 to 230), as 52,441 to 459. Hence, if this
ring girded the earth along the equator and both together revolved about the
diameter of the ring, the motion of the ring would be to the motion of the
interior globe (by lem. 3 of this third book) as 459 to 52,441 and 1,000,000
to 925,275 jointly, that is, as 4,590 to 485,223; and so the motion of the ring
would be to the sum of the motions of the ring and globe as 4,590 to 489,813.
Hence, if the ring adheres to the globe and communicates to the globe its
own motion with which its nodes or equinoctial points regress, the motion
that will remain in the ring will be to its former motion as 4,590 to 489,813,
and therefore the motion of the equinoctial points will be diminished in the
same ratio. Therefore the annual motion of the equinoctial points of a body
composed of the ring and the globe will be to the motion 20°11′46″ as 1,436
to 39,343 and 4,590 to 489,813 jointly, that is, as 100 to 292,369. But the forces
by which the nodes of the moons [i.e., a ring of moons] regress (as I have
explained above), and so by which the equinoctial points of the ring regress
(that is, the forces 3IT in the figure to prop. 30), are—in the individual
particles—as the distances of those particles from the plane QR, and it is
with these forces that the particles recede from the plane; and therefore (by
lem. 2), if the matter of the ring were scattered over the whole surface of
the globe, as in the configuration PapAPepE, so as to constitute that exterior
part of the earth, the total force and efficacy of all the particles to rotate the
earth about any diameter of the equator, and thus to move the equinoctial
points, would come out less than before in the ratio of 2 to 5. And hence
the annual regression of the equinoxes would now be to 20°11′46″ as 10 to
73,092, and accordingly would become 9″56‴50iv.
bBut because of the inclination of the plane of the equator to the plane of
the ecliptic, this motion must be diminished in the ratio of the sine 91,706
(which is the sine of the complement of 23½ degrees [or the cosine of 23½
degrees]) to the radius 100,000. And thus this motion will now become 9″7‴20iv.
This is the annual precession of the equinoxes that arises from the force of
the sun.
Now, the force of the moon to move the sea was to the force of the sun
as roughly 4.4815 to 1. And the force of the moon to move the equinoxes
is to the force of the sun in this same proportion. And so the annual
precession of the equinoxes that arises from the force of the moon comes out
40″52‴52iv, and the total annual precession arising from both forces will be
50″00‴12iv. And this motion of precession agrees with the phenomena. For,
from astronomical observations, the precession of the equinoxes is more or
less 50 seconds annually.
If the height of the earth at the equator exceeds its height at the poles
by more than 17⅙ miles, its matter will be rarer at the circumference than
at the center; and the precession of the equinoxes has to be increased because
of that excess in height, and diminished because of the greater rarity.b
We have now described the system of the sun, the earth, the moon, and
the planets; something must still be said about comets.
Lemma 4
The comets are higher than the moon and move in the planetary regions.
Just as the lack of diurnal parallax requires that comets be located
beyond the sublunar regions, so the fact that comets have an annual parallax
is convincing evidence that they descend into the regions of the planets. For
comets which move forward according to the order of the signs are all,
toward the end of their visibility, either slower than normal or retrograde if
the earth is between them and the sun, but swifter than they should be if
the earth is approaching opposition. And conversely those comets that move
contrary to the order of the signs are swifter than they should be, at the end
of their visibility when the earth is between them and the sun, and slower
than they should be or retrograde if the earth is on the opposite side of the
sun. This happens principally as a result of the motion of the earth in its
different positions [with respect to the comets], just as is the case for the
planets, which, according as the motion of the earth is either in the same
direction or in an opposite one, are sometimes retrograde, and sometimes
seem to advance more slowly and at other times more swiftly. If the earth
goes in the same direction as the comet and by its angular motion is carried
about the sun so much more swiftly that a straight line continually drawn
through the earth and the comet converges toward the regions beyond the
comet, then the comet as seen from the earth will appear to be retrograde
because of its slower motion; but if the earth is going more slowly, the
motion of the comet (taking away the motion of the earth) becomes at least
slower. But if the earth goes in a direction opposite to the comet’s motion,
the motion of the comet will as a result appear speeded up. And from the
acceleration or retardation or retrograde motion, the distance of the comet
may be ascertained in the following way.
Let  QA,
QA,  QB, and
QB, and  QC be three observed longitudes of a comet
at the beginning of its [visible] motion, and let
QC be three observed longitudes of a comet
at the beginning of its [visible] motion, and let  QF be its last observed
longitude, just as the comet ceases to be seen. Draw the straight line ABC,
whose parts AB and BC placed between the straight lines QA and QB,
and between the straight lines QB and QC, are to each other as the times
between the first three observations. Let AC be produced to G, so that AG
is to AB as the time between the first and the last observation is to the time
between the first and the second observation, and let QG be joined. Then,
if the comet moved uniformly in a straight line and the earth were either
at rest or also moved forward in a straight line with uniform motion, the
angle
QF be its last observed
longitude, just as the comet ceases to be seen. Draw the straight line ABC,
whose parts AB and BC placed between the straight lines QA and QB,
and between the straight lines QB and QC, are to each other as the times
between the first three observations. Let AC be produced to G, so that AG
is to AB as the time between the first and the last observation is to the time
between the first and the second observation, and let QG be joined. Then,
if the comet moved uniformly in a straight line and the earth were either
at rest or also moved forward in a straight line with uniform motion, the
angle  QG would be the longitude of the comet at the time of the last
observation. Therefore, the angle FQG, which is the difference between the
longitudes, arises from the inequality of the motions of the comet and of the
earth. And this angle, if the earth and comet move in opposite directions, is
added to the angle
QG would be the longitude of the comet at the time of the last
observation. Therefore, the angle FQG, which is the difference between the
longitudes, arises from the inequality of the motions of the comet and of the
earth. And this angle, if the earth and comet move in opposite directions, is
added to the angle  QG, and thus makes the apparent motion of the comet
swifter; but if the comet is going in the same direction as the earth, this angle
is subtracted from that same angle
QG, and thus makes the apparent motion of the comet
swifter; but if the comet is going in the same direction as the earth, this angle
is subtracted from that same angle  QG and makes the motion of the comet
either slower or possibly retrograde, as I have just explained. Therefore this
angle arises chiefly from the motion of the earth and on that account is rightly
regarded as the parallax of the comet, ignoring, of course, any increase or
decrease in it which could arise from the nonuniform motion of the comet
in its own orbit. And the distance of the comet may be ascertained from this
parallax in the following manner.
QG and makes the motion of the comet
either slower or possibly retrograde, as I have just explained. Therefore this
angle arises chiefly from the motion of the earth and on that account is rightly
regarded as the parallax of the comet, ignoring, of course, any increase or
decrease in it which could arise from the nonuniform motion of the comet
in its own orbit. And the distance of the comet may be ascertained from this
parallax in the following manner.

Let S represent the sun, acT the earth’s orbit, a the place of the earth
in the first observation, c the place of the earth in the third observation,
 T the place of the earth in the
last observation, and let T
T the place of the earth in the
last observation, and let T be a
straight line drawn toward the
beginning of Aries. Let angle
be a
straight line drawn toward the
beginning of Aries. Let angle  TV
be taken equal to angle
TV
be taken equal to angle  QF,
that is, equal to the longitude of
the comet when the earth is in T.
Let ac be drawn and produced
to g, so that ag is to ac as AG
to AC; then g will be the place
which the earth would reach at
the time of the last observation,
with its motion uniformly continued in the straight line ac. And so if g
QF,
that is, equal to the longitude of
the comet when the earth is in T.
Let ac be drawn and produced
to g, so that ag is to ac as AG
to AC; then g will be the place
which the earth would reach at
the time of the last observation,
with its motion uniformly continued in the straight line ac. And so if g is drawn parallel to T
is drawn parallel to T and the angle
and the angle  gV is taken equal to the angle
gV is taken equal to the angle
 QG, this angle
QG, this angle  gV will be equal to the longitude of the comet as seen
from place g, and the angle TVg will be the parallax that arises from the
transfer of the earth from place g to place T; and accordingly V will be the
place of the comet in the plane of the ecliptic. And this place V is ordinarily
lower than the orbit of Jupiter.
gV will be equal to the longitude of the comet as seen
from place g, and the angle TVg will be the parallax that arises from the
transfer of the earth from place g to place T; and accordingly V will be the
place of the comet in the plane of the ecliptic. And this place V is ordinarily
lower than the orbit of Jupiter.
The same may be ascertained from the curvature of the path of comets.
These bodies go almost in great circles as long as they move more swiftly,
but at the end of their course, when that part of their apparent motion which
arises from parallax has a greater proportion to the total apparent motion,
they tend to deviate from such circles, and whenever the earth moves in one
direction, they tend to go off in the opposite direction. Because this deviation
corresponds to the motion of the earth, it arises chiefly from parallax, and its
extraordinary quantity, according to my computation, has placed disappearing
comets quite far below Jupiter. Hence it follows that when comets are closer
to us, in their perigees and perihelions, they very often descend below the
orbits of Mars and of the inferior planets.
The nearness of comets is confirmed also from the light of their heads.
For the brightness of a heavenly body illuminated by the sun and going off
into distant regions is diminished as the fourth power of the distance; that is,
it is diminished as the square because of the increased distance of the body
from the sun and diminished as the square again because of the diminished
apparent diameter. Thus, if both the quantity of light [i.e., brightness] and
the apparent diameter of the comet are given, its distance will be found by
taking its distance to the distance of some planet directly in the ratio of
diameter to diameter and inversely as the square root of the ratio of light
to light. Thus, as observed by Flamsteed through a sixteen-foot telescope
and measured with a micrometer, the least diameter of the
comaa of the
comet of the year 1682 equaled 2′0″, while the nucleus or star in the middle
of the head occupied scarcely a tenth of this width and therefore was only
11″ or 12″ wide. But in the light and brilliance of its head it surpassed the
head of the comet of the year 1680 and rivaled stars of the first or second
magnitude. Let us suppose that Saturn with its ring was about four times
brighter; then, because the light of the ring almost equals the light of the
globe within it, and the apparent diameter of the globe is about 21″, so that
the light of the globe and the ring together would equal the light of a globe
whose diameter was 30″, it follows that the distance of the comet will be
to the distance of Saturn as 1 to √4 inversely and 12″ to 30″ directly, that
is, as 24 to 30 or as 4 to 5. Again, on the authority of Hevelius, the comet
of April 1665 surpassed in its brilliance almost all the fixed stars, and even
Saturn itself (that is, by reason of its far more vivid color). Indeed, this comet
was brighter than the one which had appeared at the end of the preceding
year and was comparable to stars of the first magnitude. The width of the
comet’s coma was about 6′, but the nucleus, when compared with the planets
by the aid of a telescope, was clearly smaller than Jupiter and was judged to
be sometimes smaller than the central body of Saturn and sometimes equal to
it. Further, since the diameter of the coma of comets rarely exceeds 8′ or 12′,
and the diameter of the nucleus or central star is about a tenth or perhaps a
fifteenth of the diameter of the coma, it is evident that such stars generally
have the same apparent magnitude as the planets. Hence, since their light
can often be compared to the light of Saturn and sometimes surpasses it, it is
manifest that all the comets in their perihelions should be placed either below
Saturn or not far above. Those who banish the comets almost to the region
of the fixed stars are, therefore, entirely wrong; certainly in such a situation,
they would not be illuminated by our sun any more than the planets in our
solar system are illuminated by the fixed stars.
In treating these matters, we have not been considering the obscuring
of comets by that very copious and thick smoke by which the head is
surrounded, always gleaming dully as if through a cloud. For the darker the
body is rendered by this smoke, the closer it must approach to the sun for
the amount of light reflected from it to rival that of the planets. This makes
it likely that the comets descend far below the sphere of Saturn, as we have
proved from their parallax.
But this same result is, to the highest degree, confirmed from their tails.
These arise either from reflection by the smoke scattered through the aether
or from the light of the head. In the first case the distance of the comets
must be diminished, since otherwise the smoke always arising from the head
would be propagated through spaces far too great, with such a velocity and
expansion as to be unbelievable. In the second case, all the light of both the
tail and the coma must be ascribed to the nucleus of the head. Therefore, if
we suppose that all this light is united and condensed within the disc of the
nucleus, then certainly that nucleus, whenever it emits a very large and very
bright tail, will far surpass in its brilliance even Jupiter itself. Therefore, if it
has a smaller apparent diameter and is sending forth more light, it will be
much more illuminated by the sun and thus will be much closer to the sun.
By the same argument, furthermore, the heads ought to be located below the
orbit of Venus, when they are hidden under the sun and emit tails both very
great and very bright like fiery beams, as they do sometimes. For if all of
that light were understood to be gathered together into a single star, it would
sometimes surpass Venus itself, not to say several Venuses combined.
Finally, the same thing may be ascertained from the light of the heads,
which increases as comets recede from the earth toward the sun and decreases
as they recede from the sun toward the earth. Thus the latter comet of 1665
(according to the observations of Hevelius), from the time when it began to be
seen, was always decreasing in its apparent motion and therefore had already
passed its perigee; but the splendor of its head nevertheless increased from
day to day until the comet, concealed by the sun’s rays, ceased to be visible.
The comet of 1683 (also according to the observations of Hevelius) at the end
of July, when it was first sighted, was moving very slowly, advancing about
40′ or 45′ in its orbit each day. From that time its daily motion kept increasing
continually until 4 September, when it came to about 5°. Therefore, in all
this time the comet was approaching the earth. This is gathered also from the
diameter of the head, as measured with a micrometer, since Hevelius found
it to be on 6 August only 6′5″ including the coma, but on 2 September 9′7″.
Therefore the head appeared far smaller at the beginning than at the end
of the motion; yet at the beginning the head showed itself far brighter in
the vicinity of the sun than toward the end of its motion, as Hevelius also
reports. Accordingly, in all this time, because of its receding from the sun, it
decreased with respect to its light, notwithstanding its approach to the earth.
The comet of 1618, about the middle of December, and that of 1680,
about the end of the same month, were moving very swiftly and therefore
were then in their perigees. Yet the greatest splendor of their heads occurred
about two weeks earlier, when they had just emerged from the sun’s rays,
and the greatest splendor of their tails occurred a little before that, when they
were even nearer to the sun. The head of the first of these comets, according
to the observations of [Johann Baptist] Cysat, seemed on 1 December to be
greater than stars of the first magnitude, and on 16 December (being now in
its perigee) it had failed little in magnitude, but very much in the splendor
or clarity of its light. On 7 January Kepler, being uncertain about its head,
brought his observing to an end. On 12 December the head of the second
of these comets was sighted, and was observed by Flamsteed at a distance of
9° from the sun, a thing which would scarcely have been possible in a star
of the third magnitude. On 15 and 17 December it appeared as a star of the
third magnitude, since it was diminished by the brightness of clouds near
the setting sun. On 26 December, moving with the greatest speed and being
almost in its perigee, it was less than the mouth of Pegasus, a star of the third
magnitude. On 3 January it appeared as a star of the fourth magnitude, on
9 January as a star of the fifth magnitude, and on 13 January it disappeared
from view, as a result of the splendor of the crescent moon. On 25 January
it scarcely equaled stars of the seventh magnitude. If equal times are taken
on both sides of the perigee (before and after), then the head, being placed
at those times in distant regions, ought to have shone with equal brilliance
because of its equal distances from the earth, but it appeared brightest in
the region [on the side of the perigee] toward the sun and disappeared on
the other side of the perigee. Therefore from the great difference of light
in these two situations, it is concluded that there is a great nearness of the
sun and the comet in the first of these situations. For the light of comets
tends to be regular and be greatest when the heads move most swiftly, and
accordingly are in their perigees, except insofar as this light becomes greater
in the vicinity of the sun.
COROLLARY 1. Therefore comets shine by the sun’s light reflected from
them.
COROLLARY 2. From what has been said it will also be understood why
comets appear so frequently in the region of the sun. If they were visible
in the regions far beyond Saturn, they would have to appear more often in
the parts of the sky opposite to the sun. For those that were in these parts
would be nearer to the earth; and the sun, being in between, would obscure
the others. Yet in running through the histories of comets, I have found
that four or five times more have been detected in the hemisphere toward
the sun than in the opposite hemisphere, besides without doubt not a few
others which the sun’s light hid from view. Certainly, in their descent to our
regions comets neither emit tails nor are so brightly illuminated by the sun
that they show themselves to the naked eye so as to be discovered before they
are closer to us than Jupiter itself. But by far the greater part of the space
described about the sun with so small a radius is situated on the side of the
earth that faces the sun, and comets are generally more brightly illuminated
in that greater part, since they are much closer to the sun.
COROLLARY 3. Hence also it is manifest that the heavens are lacking in
resistance. For the comets, following paths that are oblique and sometimes
contrary to the course of the planets, move in all directions very freely and
preserve their motions for a very long time even when these are contrary to
the course of the planets. Unless I am mistaken, comets are a kind of planet
and revolve in their orbits with a continual motion. For there seems to be
no foundation for the allegation of some writers, basing their argument on
the continual changes of the heads, that comets are meteors. The heads of
comets are encompassed with huge atmospheres, and the atmospheres must
be denser as one goes lower. Therefore, it is in these clouds, and not in the
very bodies of the comets, that those changes are seen. Thus, if the earth were
viewed from the planets, it would doubtless shine with the light of its own
clouds, and its solid body would be almost hidden beneath the clouds. Thus,
the belts of Jupiter are formed in the clouds of that planet, since they change
their situation relative to one another, and the solid body of Jupiter is seen
with greater difficulty through those clouds. And the bodies of comets must
be much more hidden beneath their atmospheres, which are both deeper and
thicker.
Proposition 40, Theorem 20
Comets move in conics having their foci in the center of the sun, and by radii
drawn to the sun, they describe areas proportional to the times.
This is evident by corol. 1 to prop. 13 of the first book compared with
props. 8, 12, and 13 of the third book.
COROLLARY 1. Hence, if comets revolve in orbits, these orbits will be
ellipses, and the periodic times will be to the periodic times of the planets
as the 3/2 powers of their principal axes. And therefore comets, for the most
part being beyond the planets and on that account describing orbits with
greater axes, will revolve more slowly. For example, if the axis of the orbit
of a comet were four times greater than the axis of the orbit of Saturn, the
time of a revolution of the comet would be to the time of a revolution of
Saturn (that is, to 30 years) as 4√4 (or 8) to 1, and accordingly would be 240
years.
COROLLARY 2. But these orbits will be so close to parabolas that
parabolas can be substituted for them without sensible errors.
COROLLARY 3. And therefore (by book 1, prop. 16, corol. 7)
the velocity
of every comet will always be to the velocity of any planet, [considered to
be] revolving in a circle about the sun, very nearly as the square root of
twice the distance of the planet from the center of the sun to the distance of
the comet from the center of the sun. Let us take the radius of the earth’s
orbit (or the greatest semidiameter of the ellipse in which the earth revolves)
to be of 100,000,000 parts; then the earth will describe by its mean daily
motion 1,720,212 of these parts, and by its hourly motion 71,675½ parts.
And therefore the comet, at the same mean distance of the earth from the
sun, and having a velocity that is to the velocity of the earth as √2 to 1, will
describe by its daily motion 2,432,747 of these parts, and by its hourly motion
101,364½ parts. But at greater or smaller distances, both the daily and the
hourly motion will be to this daily and hourly motion as the square root of
the ratio of the distances inversely, and therefore is given.
COROLLARY 4. Hence, if the latus rectum of a parabola is four times
greater than the radius of the earth’s orbit, and if the square of that radius is
taken to be 100,000,000 parts, the area that the comet describes each day by
a radius drawn to the sun will be l,216,373½ parts, and in each hour that
area will be 50,682¼ parts. But if the latus rectum is greater or smaller in
any ratio, then the daily and hourly area will be greater or smaller, as the
square root of that ratio.
Lemma 5
To find a parabolic curve that will pass through any number of given points.
Let the points be A, B, C, D, E, F, . . . , and from them to any straight
line HN, given in position, drop the perpendiculars AH, BI, CK, DL, EM,
FN, . . . .
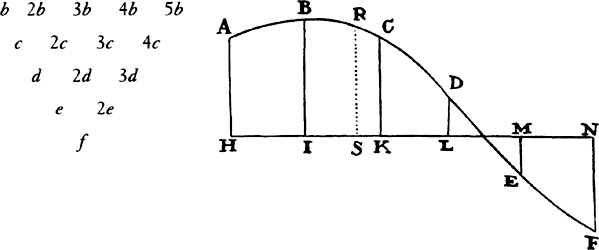
CASE 1. If the intervals HI, IK, KL, . . . between the points H, I, K,
L, M, N are equal, take the first differences b, b2, b3, b4, b5, . . . of the
perpendiculars AH, BI, CK, . . . ;
the second differences c, c2, c3, c4, . . . ; the
third differences d, d2, d3, . . . ; that is, in such a way that AH − BI = b,
BI − CK = b2, CK − DL = b3, DL + EM = b4 −EM + FN = b5, . . . ,
then b − b2 = c, . . . , and go on in this way to the last difference, which here
is f. Then, if any perpendicular RS is erected, which is to be an ordinate to
the required curve, in order to find its length, suppose each of the intervals
HI, IK, KL, LM, . . . to be unity, and let AH be equal to a, −HS = p,
½p × (−IS) = q, ⅓q × (+SK) = r, ¼r × (+SL) = s, ⅕s × (+SM) = t,
proceeding, that is, up to the penultimate perpendicular ME, and prefixing
negative signs to the terms HS, IS, . . . , which lie on the same side of the
point S as A, and positive signs to the terms SK, SL, . . . , which lie on the
other side of the point S. Then if the signs are observed exactly, RS will
be = a + bp + cq + dr + es + ft + . . . .
CASE 2. But if the intervals HI, IK, . . . between the points H, I, K,
L, . . . are unequal, take b, b2, b3, b4, b5, . . . , the first differences of the
perpendiculars AH, BI, CK, . . . divided by the intervals between the
perpendiculars; take c, c2, c3, c4, . . . , the second differences divided by each two
intervals; d, d2, d3, . . . , the third differences divided by each three intervals; e,
e2, . . . , the fourth differences divided by each four intervals, and so on—that
is, in such a way that  , . . . , and
then
, . . . , and
then  , . . . , and afterward
, . . . , and afterward
 . . . . When these differences have been found, let AH
be equal to a, −HS = p, p × (−IS) = q, q × (+SK) = r, r × (+SL) = s,
s × (+SM) = t, proceeding, that is, up to the penultimate perpendicular
ME; then the ordinate RS will be = a + bp + cq + dr + es + ft + . . . .
. . . . When these differences have been found, let AH
be equal to a, −HS = p, p × (−IS) = q, q × (+SK) = r, r × (+SL) = s,
s × (+SM) = t, proceeding, that is, up to the penultimate perpendicular
ME; then the ordinate RS will be = a + bp + cq + dr + es + ft + . . . .
COROLLARY. Hence the areas of all curves can be found very nearly.
For if several points are found of any curve which is to be squared [i.e.,
any curve whose area is desired] and a parabola is understood to be drawn
through them, the area of this parabola will be very nearly the same as the
area of that curve which is to be squared. Moreover, a parabola can always
be squared geometrically by methods which are very well known.
Lemma 6
From several observed places of a comet, to find its place at any given intermediate
time.
Let HI, IK, KL, LM represent the times between the observations (in
the figure to lem. 5), HA, IB, KC, LD, ME five observed longitudes of
the comet, and HS the given time between the first observation and the
required longitude. Then, if a regular curve ABCDE is understood to be
drawn through the points A, B, C, D, E, and if the ordinate RS is found by
the above lemma, RS will be the required longitude.
By the same method the latitude at a given time is found from five
observed latitudes.
If the differences of the observed longitudes are small, say only 4 or 5
degrees, three or four observations would suffice for finding the new
longitude and latitude. But if the differences are greater, say 10 or 20 degrees, five
observations must be used.
Lemma 7
To draw a straight line BC through a given point P, so that the parts PB and
PC of that line, cut off by two straight lines AB and AC, given in position, have
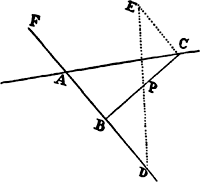 a given ratio to each other.
a given ratio to each other.
From that point P draw any straight line
PD to either of the straight lines, say AB, and
produce PD toward the other straight line AC
as far as E, so that PE is to PD in the given
ratio. Let EC be parallel to AD; and if CPB is
drawn, PC will be to PB as PE to PD. Q.E.F.
Lemma 8
Let ABC be a parabola with focus S. Let the segment ABCI be cut off by the
chord AC (which is bisected at I), let its diameter be Iμ, and let its vertex be μ.
On Iμ produced, take μO equal to half of Iμ. Join OS and produce it to ξ, so
that Sξ is equal to 2SO. Then, if a comet B moves in the arc CBA, and if ξB
is drawn cutting AC in E, I say that the point E will cut off from the chord AC
the segment AE very nearly proportional to the time.
For join EO, cutting the parabolic arc ABC in Y, and draw μX so as to
touch the same arc in the vertex μ and meet EO in X; then the curvilinear
area AEXμA will be to the curvilinear area ACYμA as AE to AC. And
thus, since triangle ASE is in the same ratio to triangle ASC as the ratio
of those curvilinear areas, the total area ASEXμA will be to the total area
ASCYμA as AE to AC. Moreover, since ξO is to SO as 3 to 1, and EO
is in the same ratio to XO, SX will be parallel to EB; and therefore, if
BX is joined, the triangle SEB will be equal to the triangle XEB. Thus, if
the triangle EXB is added to the area ASEXμA and from that sum the
triangle SEB is taken away, there will remain the area ASBXμA equal to
the area ASEXμA, and thus it will be to the area ASCYμA as AE to AC.
But the area ASBYμA is very nearly equal to the area ASBXμA, and the
area ASBYμA is to the area ASCYμA as the time in which the arc AB is
described to the time of describing the total arc AC. And thus AE is to AC
very nearly in the ratio of the times. Q.E.D.
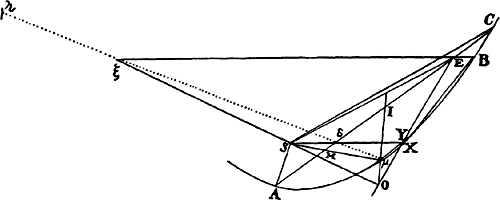
COROLLARY. When point B falls upon the vertex μ of the parabola, AE
is to AC exactly in the ratio of the times.
Scholium
If μξ is joined, cutting AC at δ, and if ξn, which is to μB as 27MI to
16Mμ, is taken in this line, then when Bn is drawn it will cut the chord
AC more nearly in the ratio of the lines than before. But the point n is to
be taken so as to lie beyond point ξ if point B is more distant than point μ
from the principal vertex of the parabola; and contrariwise if B is less distant
from that vertex.
Lemma 9
The straight lines Iμ and μM and the length
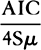 are equal to one another.
are equal to one another.
For 4Sμ is the latus rectum of a parabola, extending to the vertex μ.
Lemma 10
Let Sμ be produced to N and P, so that μN is one-third of μI, and so that
SP is to SN as SN to Sμ. Then, in the time in which a comet describes the arc
AμC, it would—if it moved forward always with the velocity that it has at a
height equal to SP—describe a length equal to the chord AC.
For if the comet were to move forward in the same time uniformly
in the straight line that touches the parabola at μ, and with the
 velocity that it has in μ, then the area that
it would describe by a radius drawn to
point S would be equal to the parabolic
area ASCμ. And hence the space
determined by the length described along the
tangent and the length Sμ would be to
the space determined by the lengths AC
and SM as the area ASCμ to the
triangle ASC, that is, as SN to SM.
Therefore, AC is to the length described along the tangent as Sμ to SN. But the
velocity of the comet at the height SP is (by book 1, prop. 16, corol. 6) to its
velocity at the height Sμ as the square root of the ratio of SP to Sμ inversely,
that is, in the ratio of Sμ to SN; hence the length described in the same time
with this velocity will be to the length described along the tangent as Sμ to
SN. Therefore, since AC and the length described with this new velocity are
in the same ratio to the length described along the tangent, they are equal to
each other. Q.E.D.
velocity that it has in μ, then the area that
it would describe by a radius drawn to
point S would be equal to the parabolic
area ASCμ. And hence the space
determined by the length described along the
tangent and the length Sμ would be to
the space determined by the lengths AC
and SM as the area ASCμ to the
triangle ASC, that is, as SN to SM.
Therefore, AC is to the length described along the tangent as Sμ to SN. But the
velocity of the comet at the height SP is (by book 1, prop. 16, corol. 6) to its
velocity at the height Sμ as the square root of the ratio of SP to Sμ inversely,
that is, in the ratio of Sμ to SN; hence the length described in the same time
with this velocity will be to the length described along the tangent as Sμ to
SN. Therefore, since AC and the length described with this new velocity are
in the same ratio to the length described along the tangent, they are equal to
each other. Q.E.D.
COROLLARY. Therefore, in that same time, the comet, with the velocity
that it has at the height Sμ + ⅔Iμ, would describe the chord AC very nearly.
Lemma 11
Suppose a comet, deprived of all motion, to be let fall from the height SN or
Sμ + ⅓Iμ, so as to fall toward the sun, and suppose this comet to be urged
toward the sun always by that force, uniformly continued, by which it is urged at
the beginning. Then in half of the time in which the comet describes the arc AC
in its orbit, it would—in this descent toward the sun—describe a space equal to
the length Iμ.
For by lem. 10, in the same time in which the comet describes the
parabolic arc AC, it will—with the velocity that it has at the height
SP—describe the chord AC; and hence (by book 1, prop. 16, corol. 7), revolving
by the force of its own gravity, it would—in that same time, in a circle whose
semidiameter was SP—describe an arc whose length would be to the chord
AC of the parabolic arc in the ratio of 1 to √2. And therefore, falling from
the height SP toward the sun with the weight that it has toward the sun at
that height, it would in half that time (by book 1, prop. 4, corol. 9) describe
a space equal to the square of half of that chord, divided by four times the
height SP, that is, the space 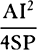 . Thus, since the weight of the comet toward
the sun at the height SN is to its weight toward the sun at the height SP
as SP to Sμ, the comet—falling toward the sun with the weight that it has
at the height SN—will in the same time describe the space
. Thus, since the weight of the comet toward
the sun at the height SN is to its weight toward the sun at the height SP
as SP to Sμ, the comet—falling toward the sun with the weight that it has
at the height SN—will in the same time describe the space
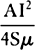 , that is, a
space equal to the length Iμ or Mμ. Q.E.D.
, that is, a
space equal to the length Iμ or Mμ. Q.E.D.
Proposition 41, Problem 21
To determine the trajectory of a comet moving in a parabola, from three given
observations.
Having tried many approaches to this exceedingly difficult problem, I
devised certain problems [i.e., propositions] in book 1 which are intended for
its solution. But later on, I conceived the following slightly simpler solution.
Let three observations be chosen, distant from one another by nearly
equal intervals of time. But let that interval of time when the comet moves
more slowly be a little greater than the other, that is, so that the difference of
the times is to the sum of the times as the sum of the times to more or less
six hundred days, or so that the point E (in the figure to lem. 8) falls very
nearly on the point M and deviates from there toward I rather than toward
A. If such observations are not at hand, a new place of the comet must be
found by the method of lem. 6.
Let S represent the sun; T, t, and τ three places of the earth in its orbit;
TA, tB, and τC three observed longitudes of the comet; V the time between
the first observation and the second; W the time between the second and the
third; X the length that the comet could describe in that total time [V + W]
with the velocity that it has in the mean distance of the earth from the sun
(which length is to be found by the method of book 3, prop. 40, corol. 3); and
let tV be a perpendicular to the chord Tτ. In the mean observed longitude
tB, let the point B be taken anywhere at all for the place of the comet in
the plane of the ecliptic, and from there toward the sun S draw line BE so
as to be to the sagitta tV as the contenta of SB and St2 to the cube of the
hypotenuse of the right-angled triangle whose sides are SB and the tangent
of the latitude of the comet in the second observation to the radius tB. And
through point E (by lem. 7 of this third book) draw the straight line AEC
so that its parts AE and EC, terminated in the straight lines TA and τC,
are to each other as the times V and W. Then A and C will be the places
of the comet in the plane of the ecliptic in the first and third observations
very nearly, provided that B is its correctly assumed place in the second
observation.

Upon AC, bisected in I, erect a perpendicular Ii. Through point B let
a line Bi be imagined,b drawn parallel to AC. Let Si be a line imagined as
cutting AC at λ, and complete the parallelogram iIλμ. Take Iσ equal to
3Iλ, and through the sun S draw the dotted line σξ equal to 3Sσ + 3iλ.
And after deleting the letters A, B, C, and I, let a new imagined line BE
be drawn from the point B toward the point ξ so that it is to the former
line BE as the square of the distance BS to the quantity Sμ + ⅓iλ. And
through point E again draw the straight line AEC according to the same
rule as before, that is, so that its parts AE and EC are to each other as the
times V and W between observations. Then A and C will be the places of
the comet more exactly.
Upon AC, bisected in I, erect the perpendiculars AM, CN, and IO, so
that, of these perpendiculars, AM and CN are the tangents of the
latitudesc
in the first and third observations (to the radii TA and τC). Join MN, cutting
IO in O. Construct the rectangle iIλμ as before. On IA produced, take ID
equal to Sμ + ⅔iλ. Then on MN, toward N, take MP so that it is to the
length X found above as the square root of the ratio of the mean distance
of the earth from the sun (or of the semidiameter of the earth’s orbit) to the
distance OD. If point P falls upon point N, then A, B, and C will be three
places of the comet, through which its orbit is to be described in the plane of
the ecliptic. But if point P does not fall upon point N, then on the straight
line AC take CG equal to NP, in such a way that points G and P lie on the
same side of the straight line NC.
Using the same method by which points E, A, C, and G were found from
the assumed point B, find from other points b and β (assumed in any way
whatever) the new points e, a, c, g, and
ε, α, κ, γ. Then if the circumference
of circle Ggγ is drawn through G, g, and γ, cutting the straight line τC in
Z, Z will be a place of the comet in the plane of the ecliptic. And if on AC,
ac, and ακ, there are taken AF, af, and αφ, equal respectively to CG, cg,
and κγ, and if the circumference of a circle Ffφ is drawn through points
F, f, and φ, cutting the straight line AT in X, then point X will be another
place of the comet in the plane of the ecliptic. At the points X and Z, erect
the tangents of the latitudes of the comet (to the radii TX and τZ), and two
places of the comet in its orbit will be found. Finally (by book 1, prop. 19), let
a parabola with focus S be described through those two places; this parabola
will be the trajectory of the comet. Q.E.I.
The demonstration of this construction follows from the lemmas, since
the straight line AC is cut in E in the ratio of the times, by lem. 7, as required
by lem. 8; and since BE, by lem. 11, is that part of the straight line BS or Bξ
which lies in the plane of the ecliptic between the arc ABC and the chord
AEC; and since MP (by lem. 10, corol.) is the length of the chord of the arc
that the comet must describe in its orbit between the first observation and
the third, and therefore would be equal to MN, provided that B is a true
place of the comet in the plane of the ecliptic.
But it is best not to choose the points B, b, and β any place whatever,
but to take them as close to true as possible. If the angle AQt, at which the
projection of the orbit described in the plane of the ecliptic cuts the straight
line tB, is known approximately, imagine the straight line AC drawn at that
angle so that it is to 4/3Tτ as the square root of the ratio of SQ to St. And
by drawing the straight line SEB, so that its part EB is equal to the length
Vt, point B will be determined, which may be used the first time around.
Then, after deleting the straight line AC and drawing AC anew according
to the preceding construction, and after additionally finding the length MP,
take point b on tB according to the rule that if TA and τC cut each other
in Y, the distance Yb is to the distance YB in a ratio compounded of the
ratio of MP to MN and the square root of the ratio of SB to Sb. And the
third point β will have to be found by the same method, if it is desired to
repeat the operation for the third time. But by this method two operations
would, for the most part, be sufficient. For if the distance Bb happens to be
very small, then after the points F, f and G, g have been found, the straight
lines Ff and Gg (when drawn) will cut TA and τC in the required points
X and Z.
EXAMPLE. Let the comet of 1680 be proposed as the example. The
following table shows its motion as observed by Flamsteed and as calculated
by him from these observations, and corrected by Halley on the basis of the
same observations.
To these add certain observations of my own.

These observations were made with a seven-foot telescope, and a
micrometer the threads of which were placed in the focus of the telescope; and
with these instruments we determined both the positions of the fixed stars
in relation to one another and the positions of the comet in relation to the
fixed stars. Let A represent the star of the fourth magnitude in the left heel
of Perseus (Bayer’s ο), B the following star of the third magnitude in the left
foot (Bayer’s ζ), C the star of the sixth magnitude in the heel of the same
foot (Bayer’s n) and D, E, F, G, H, I, K, L, M, N, O, Z, α, β, γ, and δ
other smaller stars in the same foot. And let p, P, Q, R, S, T, V, and X be
the places of the comet in the observations described above; and, the distance
AB being reckoned at 807/12 parts, AC was 52¼ parts, BC 58⅚, AD 575/12,
BD 826/11, CD 23⅔, AE 294/7, CE 57½, DE 4911/12, AI 277/12, BI 52⅙, CI
367/12, DI 535/11, AK 38⅔, BK 43, CK 315/9, FK 29, FB 23, FC 36¼, AH
186/7, DH 50⅞, BN 465/12, CN 31⅓, BL 455/12, NL 315/7. HO was to HI
as 7 to 6 and, when produced, passed between stars D and E in such a way
that the distance of star D from this straight line was ⅙CD. LM was to LN
as 2 to 9 and, when produced, passed through star H. Thus the positions of
the fixed stars in relation to one another were determined.

Finally our fellow countryman Pound again observed the positions of
these fixed stars in relation to one another and recorded their longitudes and
latitudes, as in the following table.
I observed the positions of the comet in relation to these fixed stars as
follows.
On Friday, 25 February (O.S.), at 8h30m P.M., the distance of the comet,
which was at p, from star E was less than 3/13 AE, and greater than ⅕AE, and
thus was approximately 3/14AE; and the angle ApE was somewhat obtuse,
but almost a right angle. For if a perpendicular were dropped from A to pE,
the distance of the comet from that perpendicular was ⅕pE.
On the same night at 9h30m, the distance of the comet (which was at P)
from star E was greater than  AE and less than
AE and less than 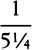 AE, and thus was
very nearly
AE, and thus was
very nearly 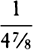 AE, or 8/39AE. And the distance of the comet from a
perpendicular dropped from star A to the straight line PE was ⅘PE.
AE, or 8/39AE. And the distance of the comet from a
perpendicular dropped from star A to the straight line PE was ⅘PE.
On Sunday, 27 February, at 8h15m P.M., the distance of the comet (which
was at Q) from star O equaled the distance between stars O and H; and
the straight line QO, produced, passed between stars K and B. Because of
intervening clouds, I could not determine the position of this straight line
more exactly.
On Tuesday, 1 March, at 11h P.M., the comet (which was at R) lay exactly
between stars K and C; and the part CR of the straight line CRK was a
little greater than ⅓CK and a little smaller than ⅓CK + ⅛CR, and thus
was equal to ⅓CK + 1/16CR, or 16/45CK.
On Wednesday, 2 March, at 8h P.M., the distance of the comet (which
was at S) from star C was very close to 4/9FC. The distance of star F from
the straight line CS, produced, was 1/24FC, and the distance of star B from
that same straight line was five times greater than the distance of star F.
Also, the straight line NS, produced, passed between stars H and I and was
five or six times nearer to star H than to star I.
On Saturday, 5 March, at 11h30m P.M. (when the comet was at T), the
straight line MT was equal to ½ML, and the straight line LT, produced,
passed between B and F four or five times closer to F than to B, cutting
off from BF a fifth or sixth part of it toward F. And MT, produced,
passed outside the space BF on the side of star B and was four times closer
to star B than to star F. M was a very small star that could scarcely be
seen through the telescope, and L was a greater star, of about the eighth
magnitude.
On Monday, 7 March, at 9h30m P.M. (when the comet was at V), the
straight line Vα, produced, passed between B and F, cutting off 1/10BF from
BF on the side of F, and was to the straight line Vβ as 5 to 4. And the
distance of the comet from the straight line αβ was ½Vβ.
On Wednesday, 9 March, at 8h30m P.M. (when the comet was at X), the
straight line γX was equal to ¼γδ, and a perpendicular dropped from star
δ to the straight line γX was ⅖γδ.
On the same night at 12h (when the comet was at Y), the straight line γY
was equal to ⅓γδ or a little smaller, say 5/16γδ, and a perpendicular dropped
from star δ to the straight line γY was equal to about ⅙ or 1/7γδ. But the
comet could scarcely be discerned because of its nearness to the horizon, nor
could its place be determined so surely as in the preceding observations.
From observations of this sort, by constructions of diagrams, and by
calculations, I found the longitudes and latitudes of the comet, and from the
corrected places of the fixed stars our fellow countryman Pound corrected
the places of the comet, and these corrected places are given above. I used
a crudely made micrometer, but nevertheless the errors of longitudes and
latitudes (insofar as they come from my observations) scarcely exceed one
minute. Moreover, the comet (according to my observations) at the end of its
motion began to decline noticeably toward the north from the parallel which
it had occupied at the end of February.
Now, in order to determine the orbit of the comet, I selected—from the
observations hitherto described—three that Flamsteed made, on 21
December, 5 January, and 25 January. From these observations I found St to be of
9,842.1 parts, and Vt to be of 455 parts (10,000 such parts being the
semidiameter of the earth’s orbit). Then for the first operation, assuming tB to be
of 5,657 parts, I found SB to be of 9,747, BE the first time 412, Sμ 9,503, iλ
413; BE the second time 421, OD 10,186, X 8,528.4, MP 8,450, MN 8,475,
NP 25. Hence for the second operation I reckoned the distance tb to be
5,640. And by this operation I found at last the distance TX to be 4,775 and
the distance τZ to be 11,322. In determining the orbit from these distances,
I found the descending node in  1°53′ and the ascending node in
1°53′ and the ascending node in 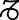 1°53′,
and the inclination of its plane to the plane of the ecliptic to be 61°20⅓′. I
found that its vertex (or the perihelion of the comet) was 8°38′ distant from
the node and was in
1°53′,
and the inclination of its plane to the plane of the ecliptic to be 61°20⅓′. I
found that its vertex (or the perihelion of the comet) was 8°38′ distant from
the node and was in  27°43′ with a latitude 7°34′ S; and that its latus
rectum was 236.8, and that the area described each day by a radius drawn to the
sun was 93,585, supposing the square of the semidiameter of the earth’s orbit
to be 100,000,000; and I found that the comet had advanced in this orbit in
the order of the signs, and was on 8 December 0h4m A.M. in the vertex of the
orbit or the perihelion. I made all these determinations graphically by a scale
of equal parts and by chords of angles, taken from the table of natural sines,
constructing a fairly large diagram, that is, one in which the semidiameter
of the earth’s orbit (of 10,000 parts) was equal to 16⅓ inches of an English
foot.
27°43′ with a latitude 7°34′ S; and that its latus
rectum was 236.8, and that the area described each day by a radius drawn to the
sun was 93,585, supposing the square of the semidiameter of the earth’s orbit
to be 100,000,000; and I found that the comet had advanced in this orbit in
the order of the signs, and was on 8 December 0h4m A.M. in the vertex of the
orbit or the perihelion. I made all these determinations graphically by a scale
of equal parts and by chords of angles, taken from the table of natural sines,
constructing a fairly large diagram, that is, one in which the semidiameter
of the earth’s orbit (of 10,000 parts) was equal to 16⅓ inches of an English
foot.
Finally, in order to establish whether the comet moved truly in the
orbit thus found, I calculated—partly by arithmetical and partly by graphical
operations—the places of the comet in this orbit at the times of certain
observations, as can be seen in the following table.

dLater, our fellow countryman Halley determined the orbit more exactly
by an arithmetical calculation than could be done graphically [lit. by the
descriptions of lines]; and while he kept the place of the nodes in  1°53′
and in
1°53′
and in 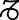 1°53′ and the inclination of the plane of the orbit to the ecliptic
61°20⅓′, and also the time of the perihelion of the comet 8 December 0h4m,
he found the distance of the perihelion from the ascending node (measured in
the orbit of the comet) to be 9°20′, and the latus rectum of the parabola to be
2,430 parts, the mean distance of the sun from the earth being 100,000 parts.
And by making the same kind of arithmetical calculation exactly (using these
data), he calculated the places of the comet at the times of the observations,
as follows.
1°53′ and the inclination of the plane of the orbit to the ecliptic
61°20⅓′, and also the time of the perihelion of the comet 8 December 0h4m,
he found the distance of the perihelion from the ascending node (measured in
the orbit of the comet) to be 9°20′, and the latus rectum of the parabola to be
2,430 parts, the mean distance of the sun from the earth being 100,000 parts.
And by making the same kind of arithmetical calculation exactly (using these
data), he calculated the places of the comet at the times of the observations,
as follows.

This comet also appeared in the preceding November and was observed by
Mr. Gottfried Kirch at Coburg in Saxony on the fourth, sixth, and eleventh
days of this month (O.S.); and from its positions with respect to the nearest
fixed stars (observed with sufficient accuracy, sometimes through a two-foot
telescope and sometimes through a ten-foot telescope), from the difference of
the longitudes of Coburg and London, eleven degrees, and from the places
of the fixed stars observed by our fellow countryman Pound, our own Halley
has determined the places of the comet as follows.
On 3 November 17h2m, apparent time at London, the comet was in
 29°51′ with latitude 1°17′45″ N.
29°51′ with latitude 1°17′45″ N.
On 5 November 15h58m, the comet was
in 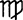 3°23′ with latitude 1°6′ N.
3°23′ with latitude 1°6′ N.
On 10 November 16h31m, the comet was equally distant from the stars
σ and τ (Bayer) of Leo; it had not yet reached the straight line joining these
stars, but was not far from it. In Flamsteed’s catalog of stars, σ then was in
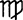 14°15′ with latitude about 1°41′ N, while τ was in
14°15′ with latitude about 1°41′ N, while τ was in
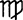 17°3½′ with latitude
0°34′ S. And the midpoint between these stars was
17°3½′ with latitude
0°34′ S. And the midpoint between these stars was 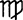 15°39¼′ with latitude
0°33½′ N. Let the distance of the comet from that straight line be about 10′
or 12′; then the difference of the longitudes of the comet and that midpoint
will be 7′ and the difference of the latitudes roughly 7½′. And thus the
comet was in
15°39¼′ with latitude
0°33½′ N. Let the distance of the comet from that straight line be about 10′
or 12′; then the difference of the longitudes of the comet and that midpoint
will be 7′ and the difference of the latitudes roughly 7½′. And thus the
comet was in 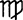 15°32′ with roughly latitude 26′ N.
15°32′ with roughly latitude 26′ N.
The first observation of the position of the comet in relation to certain
small fixed stars was more than exact enough. The second also was exact
enough. In the third observation, which was less exact, there could have been
an error of six or seven minutes, but hardly a greater one. And the longitude
of the comet in the first observation, which was more exact than the others,
being computed in the parabolic orbit mentioned above, was  29°30′22″, its
latitude 1°25′7″ N, and its distance from the sun 115,546.
29°30′22″, its
latitude 1°25′7″ N, and its distance from the sun 115,546.
Further, Halley noted that a remarkable comet had appeared four times
at intervals of 575 years—namely, in September after the murder of Julius
Caesar; in A.D. 531 in the consulship of Lampadius and Orestes; in February
A.D. 1106; and toward the end of 1680—and that this comet had a long and
remarkable tail (except that in the year of Caesar’s death the tail was less
visible because of the inconvenient position of the earth); and he set out to
find an elliptical orbit whose major axis would be 1,382,957 parts, the mean
distance of the earth from the sun being 10,000 parts, that is, an orbit in
which a comet might revolve in 575 years. Then he computed the motion of
the comet in this elliptical orbit with the following conditions: the ascending
node in  2°2′, the inclination of the plane of the orbit to the plane of the
ecliptic 61°6′48″, the perihelion of the comet in this plane in
2°2′, the inclination of the plane of the orbit to the plane of the
ecliptic 61°6′48″, the perihelion of the comet in this plane in  22°44′25″,
the equated time of the perihelion 7 December 23h9m, the distance of the
perihelion from the ascending node in the plane of the ecliptic 9°17′35″,
and the conjugate axis 18,481.2. The places of this comet, as deduced from
observations as well as calculated for this orbit, are displayed in the following
table [page 912].
22°44′25″,
the equated time of the perihelion 7 December 23h9m, the distance of the
perihelion from the ascending node in the plane of the ecliptic 9°17′35″,
and the conjugate axis 18,481.2. The places of this comet, as deduced from
observations as well as calculated for this orbit, are displayed in the following
table [page 912].
The observations of this comet from beginning to end agree no less with
the motion of a comet in the orbit just described than the motions of the
planets generally agree with planetary theories, and this agreement provides
proof that it was one and the same comet which appeared all this time and
that its orbit has been correctly determined here.d
eIn this table we have omitted the observations made on 16, 18, 20, and
23 November as being less exact. Yet the comet was observed at these times
also.e In fact, [Giuseppe Dionigi] Ponteo and his associates, on 17 November
(O.S.) at 6h A.M. in Rome, that is, at 5h10m London time, using threads
applied to the fixed stars, observed the comet in  8°30′ with latitude 0°40′ S.
Their observations may be found in the treatise which Ponteo published
about this comet. [Marco Antonio] Cellio, who was present and sent his own
observations in a letter to Mr. Cassini, saw the comet at the same hour in
8°30′ with latitude 0°40′ S.
Their observations may be found in the treatise which Ponteo published
about this comet. [Marco Antonio] Cellio, who was present and sent his own
observations in a letter to Mr. Cassini, saw the comet at the same hour in
 8°30′ with latitude 0°30′ S. At the same hour
Gallet in Avignon (that is, at
5h42m A.M. London time) saw the comet in
8°30′ with latitude 0°30′ S. At the same hour
Gallet in Avignon (that is, at
5h42m A.M. London time) saw the comet in  8° with null latitude; at which
time, according to the theory, the comet was in
8° with null latitude; at which
time, according to the theory, the comet was in  8°16′45″ with latitude
0°53′7″ S.
8°16′45″ with latitude
0°53′7″ S.

On 18 November at 6h30m A.M. in Rome (that is, at 5h40m London time)
Ponteo saw the comet in  3°30′ with latitude 1°20′ S; Cellio saw it in
3°30′ with latitude 1°20′ S; Cellio saw it in
 13°30′ with latitude 1°00′ S. Moreover, Gallet at 5h30m A.M. in Avignon
saw the comet in
13°30′ with latitude 1°00′ S. Moreover, Gallet at 5h30m A.M. in Avignon
saw the comet in  13°00′ with latitude l°00′ S. And the Reverend Father
Ango at the College of La Flèche in France, at 5h A.M. (that is, at 5h9m
London time), saw the comet midway between two small stars, of which
one is the middle star of three in a straight line in the southern hand of
Virgo, Bayer’s ψ, and the other is the outermost star of the wing, Bayer’s ϑ.
Thus the comet was then in
13°00′ with latitude l°00′ S. And the Reverend Father
Ango at the College of La Flèche in France, at 5h A.M. (that is, at 5h9m
London time), saw the comet midway between two small stars, of which
one is the middle star of three in a straight line in the southern hand of
Virgo, Bayer’s ψ, and the other is the outermost star of the wing, Bayer’s ϑ.
Thus the comet was then in  12°46′ with latitude 50′ S. On the same day
at Boston in New England, at a latitude of 42½°, at 5h A.M. (that is, 9h44m
London time), the comet was seen near
12°46′ with latitude 50′ S. On the same day
at Boston in New England, at a latitude of 42½°, at 5h A.M. (that is, 9h44m
London time), the comet was seen near  14° with latitude 1°30′ S, as I was
informed by the distinguished Halley.
14° with latitude 1°30′ S, as I was
informed by the distinguished Halley.
On 19 November at 4h30m A.M. in Cambridge, the comet (according to
the observation of a certain young man) was about 2 degrees distant from
Spica Virginis toward the northwest. And Spica was in  19°23′47″ with
latitude 2°1′59″ S. On the same day at 5h A.M. at Boston in New England,
the comet was 1 degree distant from Spica Virginis, the difference of latitudes
being 40 minutes. On the same day on the island of Jamaica, the comet was
about 1 degree distant from Spica. On the same day Mr. Arthur Storer,
at the Patuxent River, near Hunting Creek in Maryland, which borders on
Virginia, at latitude 38½°, at 5h A.M. (that is, 10h London time), saw the comet
above Spica Virginis and almost conjoined with Spica, the distance between
them being about ¾ of a degree. And comparing these observations with
one another, I gather that at 9h44m in London the comet was in
19°23′47″ with
latitude 2°1′59″ S. On the same day at 5h A.M. at Boston in New England,
the comet was 1 degree distant from Spica Virginis, the difference of latitudes
being 40 minutes. On the same day on the island of Jamaica, the comet was
about 1 degree distant from Spica. On the same day Mr. Arthur Storer,
at the Patuxent River, near Hunting Creek in Maryland, which borders on
Virginia, at latitude 38½°, at 5h A.M. (that is, 10h London time), saw the comet
above Spica Virginis and almost conjoined with Spica, the distance between
them being about ¾ of a degree. And comparing these observations with
one another, I gather that at 9h44m in London the comet was in  18°50′
with latitude roughly l°25′ S. And by the theory the comet was then in
18°50′
with latitude roughly l°25′ S. And by the theory the comet was then in
 18°52′15″ with latitude 1°26′54″
S.f
18°52′15″ with latitude 1°26′54″
S.f
On 20 November, Mr. Geminiano Montanari, professor of astronomy in
Padua, at 6h A.M. in Venice (that is, 5h10m London time), saw the comet in
 23° with latitude l°30′ S. On the same day at Boston the comet was distant
from Spica by 4 degrees of longitude eastward and so was approximately in
23° with latitude l°30′ S. On the same day at Boston the comet was distant
from Spica by 4 degrees of longitude eastward and so was approximately in
 23°24′.
23°24′.
On 21 November, Ponteo and his associates at 7h15m A.M. observed the
comet in  27°50′ with latitude 1°16′ S, Cellio in
27°50′ with latitude 1°16′ S, Cellio in
 28°, Ango at 5h A.M. in
28°, Ango at 5h A.M. in
 27°45′, Montanari in
27°45′, Montanari in  27°51′. On the same day on the island of Jamaica
the comet was seen near the beginning of Scorpio and had roughly the same
latitude as Spica Virginis, that is, 2°2′. On the same day at 5h A.M. at Balasore
in the East Indies (that is, at 11h20m the preceding night, London time) the
comet was distant 7°35′ eastward from Spica Virginis. It was in a straight line
between Spica and the scale [or pan of the Balance] and so was in
27°51′. On the same day on the island of Jamaica
the comet was seen near the beginning of Scorpio and had roughly the same
latitude as Spica Virginis, that is, 2°2′. On the same day at 5h A.M. at Balasore
in the East Indies (that is, at 11h20m the preceding night, London time) the
comet was distant 7°35′ eastward from Spica Virginis. It was in a straight line
between Spica and the scale [or pan of the Balance] and so was in  26°58′
with latitude roughly 1°11′ S, and after 5 hours and 40 minutes (that is, at 5h
A.M. London time) was in
26°58′
with latitude roughly 1°11′ S, and after 5 hours and 40 minutes (that is, at 5h
A.M. London time) was in  28°12′ with latitude 1°16′ S. And by the theory
the comet was then in
28°12′ with latitude 1°16′ S. And by the theory
the comet was then in  28°10′36″ with latitude 1°53′35″ S.
28°10′36″ with latitude 1°53′35″ S.
On 22 November, the comet was seen by Montanari in  2°33′, while at
Boston in New England it appeared in approximately
2°33′, while at
Boston in New England it appeared in approximately  3°, with about the
same latitude as before, that is, 1°30′. On the same day at 5h A.M. at Balasore
the comet was observed in
3°, with about the
same latitude as before, that is, 1°30′. On the same day at 5h A.M. at Balasore
the comet was observed in  1°50′, and so at 5h A.M. in London the comet
was approximately in
1°50′, and so at 5h A.M. in London the comet
was approximately in  3°5′. On the same day at London at 6h30m A.M.
our fellow countryman Hooke saw the comet in approximately
3°5′. On the same day at London at 6h30m A.M.
our fellow countryman Hooke saw the comet in approximately  3°30′, on
a straight line that passes between Spica Virginis and the heart of Leo, not
exactly indeed, but deviating a little from that line toward the north.
Montanari likewise noted that a line drawn from the comet through Spica passed,
on this day and the following days, through the southern side of the heart
of Leo, there being a very small interval between the heart of Leo and this
line. The straight line passing through the heart of Leo and Spica Virginis
cut the ecliptic in
3°30′, on
a straight line that passes between Spica Virginis and the heart of Leo, not
exactly indeed, but deviating a little from that line toward the north.
Montanari likewise noted that a line drawn from the comet through Spica passed,
on this day and the following days, through the southern side of the heart
of Leo, there being a very small interval between the heart of Leo and this
line. The straight line passing through the heart of Leo and Spica Virginis
cut the ecliptic in 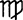 3°46′, at an angle of 2°51′. And if the comet had been
located in this line in
3°46′, at an angle of 2°51′. And if the comet had been
located in this line in  3°, its latitude would have been 2°26′. But since
the comet, by the agreement of Hooke and Montanari, was at some distance
from this line toward the north, its latitude was a little less. On the 20th,
according to the observation of Montanari, its latitude almost equaled the
latitude of Spica Virginis and was roughly 1°30′; and by the agreement of
Hooke, Montanari, and Ango, the latitude was continually increasing and
so now (on the 22d) was sensibly greater than 1°30′. And the mean latitude
between the limits now established, 2°26′ and 1°30′, will be roughly 1°58′.
The tail of the comet, by the agreement of Hooke and Montanari, was
directed toward Spica Virginis, declining somewhat from that star—southward
according to Hooke, northward according to Montanari; and so that
declination was hardly perceptible, and the tail, being almost parallel to the equator,
was deflected somewhat northward from the opposition of the sun.
3°, its latitude would have been 2°26′. But since
the comet, by the agreement of Hooke and Montanari, was at some distance
from this line toward the north, its latitude was a little less. On the 20th,
according to the observation of Montanari, its latitude almost equaled the
latitude of Spica Virginis and was roughly 1°30′; and by the agreement of
Hooke, Montanari, and Ango, the latitude was continually increasing and
so now (on the 22d) was sensibly greater than 1°30′. And the mean latitude
between the limits now established, 2°26′ and 1°30′, will be roughly 1°58′.
The tail of the comet, by the agreement of Hooke and Montanari, was
directed toward Spica Virginis, declining somewhat from that star—southward
according to Hooke, northward according to Montanari; and so that
declination was hardly perceptible, and the tail, being almost parallel to the equator,
was deflected somewhat northward from the opposition of the sun.
On 23 November (O.S.) at 5h A.M. at Nuremberg (that is, at 4h30m
London time) Mr. [Johann Jacob] Zimmermann saw the comet in  8°8′ with
latitude 2°31′ S, determining its distances from the fixed stars.
8°8′ with
latitude 2°31′ S, determining its distances from the fixed stars.
On 24 November before sunrise the comet was seen by Montanari in
 12°52′ on the northern side of a straight line drawn through the heart of
Leo and Spica Virginis, and so had a latitude a little less than 2°38′. This
latitude (as we have said), according to the observations of Montanari, Ango,
and Hooke, was continually increasing, and so it was now (on the 24th) a little
greater than 1°58′, and at its mean magnitude can be taken as 2°18′ without
perceptible error. Ponteo and Gallet would have the latitude decreased now,
and Cellio and the observer in New England would have it retained at
about the same magnitude, namely 1 or 1½ degrees. The observations of
Ponteo and Cellio are rather crude, especially those that were made by taking
azimuths and altitudes, and so are those of Gallet; better are the ones that
were made by means of the positions of the comet in relation to fixed stars by
Montanari, Hooke, Ango, and the observer in New England, and sometimes
by Ponteo and Cellio. On the same day at 5h A.M. at Balasore, the comet was
observed in
12°52′ on the northern side of a straight line drawn through the heart of
Leo and Spica Virginis, and so had a latitude a little less than 2°38′. This
latitude (as we have said), according to the observations of Montanari, Ango,
and Hooke, was continually increasing, and so it was now (on the 24th) a little
greater than 1°58′, and at its mean magnitude can be taken as 2°18′ without
perceptible error. Ponteo and Gallet would have the latitude decreased now,
and Cellio and the observer in New England would have it retained at
about the same magnitude, namely 1 or 1½ degrees. The observations of
Ponteo and Cellio are rather crude, especially those that were made by taking
azimuths and altitudes, and so are those of Gallet; better are the ones that
were made by means of the positions of the comet in relation to fixed stars by
Montanari, Hooke, Ango, and the observer in New England, and sometimes
by Ponteo and Cellio. On the same day at 5h A.M. at Balasore, the comet was
observed in  11°45′, and so at 5h A.M. at London it was nearly in
11°45′, and so at 5h A.M. at London it was nearly in  13°.
And by the theory the comet was at that time in
13°.
And by the theory the comet was at that time in  13°22′42″.
13°22′42″.
On 25 November before sunrise Montanari observed the comet
approximately in  17¾°. And Cellio observed at the same time that the comet
was in a straight line between the bright star in the right thigh of Virgo and
the southern scale of Libra, and this straight line cuts the path of the comet
in
17¾°. And Cellio observed at the same time that the comet
was in a straight line between the bright star in the right thigh of Virgo and
the southern scale of Libra, and this straight line cuts the path of the comet
in  18°36′. And by the theory the comet was at that time approximately in
18°36′. And by the theory the comet was at that time approximately in
 18⅓°.
18⅓°.
Therefore these observations agree with the theory insofar as they agree
with one another, and by such agreement they prove that it was one and the
same comet that appeared in the whole time from the 4th of November to the
9th of March. The trajectory of this comet cut the plane of the ecliptic twice
and therefore was not rectilinear. It cut the ecliptic not in opposite parts of the
heavens, but at the end of Virgo and at the beginning of Capricorn, at points
separated by an interval of about 98 degrees; and thus the course of the comet
greatly deviated from a great circle. For in November its course declined
by at least 3 degrees from the ecliptic toward the south, and afterward in
December verged from the ecliptic 29 degrees toward the north: the two
parts of its orbit, in which the comet tended toward the sun and returned
from the sun, declining from each other by an apparent angle of more than
30 degrees, as Montanari observed. This comet moved through nine signs,
namely from the last degree of Leo to the beginning of Gemini, besides [that
part of] the sign of Leo through which it moved before it began to be seen;
and there is no other theory according to which a comet may travel over so
great a part of the heaven with a motion according to some rule. Its motion
was extremely nonuniform. For about the 20th of November it described
approximately 5 degrees per day; then, with a retarded motion between 26
November and 12 December, that is, during 15½ days, it described only 40
degrees; and afterward, with its motion accelerated again, it described about
5 degrees per day until its motion began to be retarded again. And the theory
that corresponds exactly to so nonuniform a motion through the greatest part
of the heavens, and that observes the same laws as the theory of the planets,
and that agrees exactly with exact astronomical observations cannot fail to be
true.
Furthermore, it seemed appropriate to show the trajectory that the comet
described and the actual tail that it projected in different positions, as in
the accompanying figure, in the plane of the trajectory; in this figure, ABC
denotes the trajectory of the comet, D the sun, DE the axis of the trajectory,
DF the line of nodes, GH the intersection of the sphere of the earth’s orbit
with the plane of the trajectory, I the place of the comet on 4 November
1680, K its place on 11 November, L its place on 19 November, M its place
on 12 December, N its place on 21 December, O its place on 29 December,
P its place on 5 January of the following year, Q its place on 25 January, R
its place on 5 February, S its place on 25 February, T its place on 5 March,
and V its place on 9 March. I used the following observations in determining
the tail.

On 4 and 6 November the tail was not yet visible. On 11 November
the tail, which had now begun to be seen, was observed through a ten-foot
telescope to be no more than half a degree long. On 17 November the tail
was observed by Ponteo to be more than 15 degrees long. On 18 November
the tail was seen in New England to be 30 degrees long and directly opposite
to the sun, and it was extended out to the star ♂ [i.e., the planet Mars],
which was then in 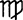 9°54′. On 19 November, in Maryland, the tail was
seen to be 15 or 20 degrees long. On 10 December the tail (according to the
observations of Flamsteed) was passing through the middle of the distance
between the tail of Serpens (the Serpent of Ophiuchus) and the star δ in the
southern wing of Aquila and terminated near the stars A, ω, b in Bayer’s
tables. Therefore the end of the comet’s tail was in
9°54′. On 19 November, in Maryland, the tail was
seen to be 15 or 20 degrees long. On 10 December the tail (according to the
observations of Flamsteed) was passing through the middle of the distance
between the tail of Serpens (the Serpent of Ophiuchus) and the star δ in the
southern wing of Aquila and terminated near the stars A, ω, b in Bayer’s
tables. Therefore the end of the comet’s tail was in 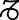 19½° with a latitude
of about 34¼° N. On 11 December the tail was rising as far as the head of
Sagitta (Bayer’s α, β), terminating in
19½° with a latitude
of about 34¼° N. On 11 December the tail was rising as far as the head of
Sagitta (Bayer’s α, β), terminating in 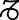 26°43′, with a latitude of 38°34′ N.
On 12 December the tail was passing through the middle of Sagitta and did
not extend very much further, terminating in
26°43′, with a latitude of 38°34′ N.
On 12 December the tail was passing through the middle of Sagitta and did
not extend very much further, terminating in  4°, with a latitude of about
42½° N.
4°, with a latitude of about
42½° N.
These things are to be understood of the length of the brighter part of
the tail. For when the light was fainter and the sky perhaps clearer, on 12
December at 5h40m in Rome, the tail was observed by Ponteo to extend to 10
degrees beyond the uropygium of Cygnus [i.e., the rump of the Swan], and its
side toward the northwest terminated 45 minutes from this star. Moreover, in
those days the tail was 3 degrees wide near its upper end, and so the middle
of it was 2°15′ distant from that star toward the south, and its upper end was
in  22° with a latitude of 61° N. And hence the tail was about 70 degrees
long.
22° with a latitude of 61° N. And hence the tail was about 70 degrees
long.
On 21 December the tail rose almost to Cassiopeia’s Chair, being equally
distant from β and Schedar [= α Cassiopeiae] and having a distance from
each of them equal to their distance from each other, and so terminating in
 24° with a latitude of 47½°. On 29 December the tail was touching Scheat,
which was situated to the left of it, and exactly filled the space between
the two stars in the northern foot of Andromeda; it was 54 degrees long;
accordingly it terminated in
24° with a latitude of 47½°. On 29 December the tail was touching Scheat,
which was situated to the left of it, and exactly filled the space between
the two stars in the northern foot of Andromeda; it was 54 degrees long;
accordingly it terminated in  19° with a latitude of 35°. On 5 January the
tail touched the star π in the breast of Andromeda on the right side and
the star μ in the girdle on the left side, and (according to our observations)
was 40 degrees long; but it was curved, and its convex side faced to the
south. Near the head of the comet, the tail made an angle of 4 degrees with
the circle passing through the sun and the head of the comet; but near the
other end, it was inclined to that circle at an angle of 10 or 11 degrees, and
the chord of the tail contained an angle of 8 degrees with that circle. On
13 January the tail was visible enough between Alamech and Algol [= β
Persei], but it ended in a very faint light toward the star κ in Perseus’s side.
The distance of the end of the tail from the circle joining the sun and the
comet was 3°50′, and the inclination of the chord of the tail to that circle
was 8½ degrees. On 25 and 26 January the tail shone with a faint light to a
length of 6 or 7 degrees; and, a night or so later, when the sky was extremely
clear, it attained a length of 12 degrees and a little more, with a light that
was very faint and scarcely to be perceived. But its axis was directed exactly
toward the bright star in the eastern shoulder of Auriga, and accordingly
declined from the opposition of the sun toward the north at an angle of 10
degrees. Finally on 10 February, my eyes armed [with a telescope], I saw
the tail to be 2 degrees long. For the fainter light mentioned above was not
visible through the glasses. But Ponteo writes that on 7 February he saw the
tail with a length of 12 degrees. On 25 February and thereafter, the comet
appeared without a tail.
19° with a latitude of 35°. On 5 January the
tail touched the star π in the breast of Andromeda on the right side and
the star μ in the girdle on the left side, and (according to our observations)
was 40 degrees long; but it was curved, and its convex side faced to the
south. Near the head of the comet, the tail made an angle of 4 degrees with
the circle passing through the sun and the head of the comet; but near the
other end, it was inclined to that circle at an angle of 10 or 11 degrees, and
the chord of the tail contained an angle of 8 degrees with that circle. On
13 January the tail was visible enough between Alamech and Algol [= β
Persei], but it ended in a very faint light toward the star κ in Perseus’s side.
The distance of the end of the tail from the circle joining the sun and the
comet was 3°50′, and the inclination of the chord of the tail to that circle
was 8½ degrees. On 25 and 26 January the tail shone with a faint light to a
length of 6 or 7 degrees; and, a night or so later, when the sky was extremely
clear, it attained a length of 12 degrees and a little more, with a light that
was very faint and scarcely to be perceived. But its axis was directed exactly
toward the bright star in the eastern shoulder of Auriga, and accordingly
declined from the opposition of the sun toward the north at an angle of 10
degrees. Finally on 10 February, my eyes armed [with a telescope], I saw
the tail to be 2 degrees long. For the fainter light mentioned above was not
visible through the glasses. But Ponteo writes that on 7 February he saw the
tail with a length of 12 degrees. On 25 February and thereafter, the comet
appeared without a tail.
Whoever considers the orbit just described and turns over in his mind the
other phenomena of this comet will without difficulty agree that the bodies
of comets are solid, compact, fixed, and durable, like the bodies of planets.
For if comets were nothing other than vapors or exhalations of the earth, the
sun, and the planets, this one ought to have been dissipated at once during
its passage through the vicinity of the sun. For the heat of the sun is as the
density of its rays, that is, inversely as the square of the distance of places
from the sun. And thus, since the distance of the comet from the center of
the sun on 8 December, when it was in its perihelion, was to the distance
of the earth from the center of the sun as approximately 6 to 1,000, the heat
of the sun on the comet at that time was to the heat of the summer sun here
on earth as 1,000,000 to 36, or as 28,000 to 1. But the heat of boiling water is
about three times greater than the heat that dry earth acquires in the summer
sun, as I have found [by experiment]; and the heat of incandescent iron (if
I conjecture correctly) is about three or four times greater than the heat of
boiling water; and hence the heat that dry earth on the comet would have
received from the sun’s rays, when it was in its perihelion, would be about
two thousand times greater than the heat of incandescent iron. But with so
great a heat, vapors and exhalations, and all volatile matter, would have to
have been consumed and dissipated at once.
Therefore the comet, in its perihelion, received an immense heat at [i.e.,
when near] the sun, and it can retain that heat for a very long time. For a
globe of incandescent iron, one inch wide, standing in the air would scarcely
lose all its heat in the space of one hour. But a larger globe would preserve
its heat for a longer time in the ratio of its diameter, because its surface
(which is the measure according to which it is cooled by contact with the
surrounding air) is smaller in that ratio with respect to the quantity of hot
matter it contains. And so a globe of incandescent iron equal to this earth of
ours—that is, more or less 40,000,000 feet wide—would scarcely cool off in
as many days, or about 50,000 years. Nevertheless, I suspect that the duration
of heat is increased in a smaller ratio than that of the diameter because of
some latent causes, and I wish that the true ratio might be investigated by
experiments.
Further, it should be noted that in December, when the comet had just
become hot at the sun, it was emitting a far larger and more splendid tail
than it had done earlier in November, when it had not yet reached its
perihelion. And, universally, the greatest and brightest tails all arise from comets
immediately after their passage through the region of the sun. Therefore the
heating up of the comet is conducive to a great size of its tail, and from this
I believe it can be concluded that the tail is nothing other than extremely
thin vapor that the head or nucleus of the comet emits by its heat.
There are indeed three opinions about the tails of comets: that the tails
are the brightness of the sun’s light propagated through the translucent heads
of comets; that the tails arise from the refraction of light in its progress from
the head of the comet to the earth; and finally that these tails are a cloud
or vapor continually rising from the head of the comet and going off in
a direction away from the sun. The first opinion is held by those who are
not yet instructed in the science of optics. For beams of sunlight are not
seen in a dark room except insofar as the light is reflected from particles of
dust and smoke always flying about through the air, and for this reason in
air darkened with thicker smoke the beams of sunlight appear brighter and
strike the eye more strongly, while in clearer air these beams are fainter and
are perceived with greater difficulty, but in the heavens, where there is no
matter to reflect these beams of sunlight, they cannot be seen at all. Light is
not seen insofar as it is in the beam, but only to the degree that it is reflected
to our eyes; for vision results only from rays that impinge upon the eyes.
Therefore some reflecting matter must exist in the region of the tail, since
otherwise the whole sky, illuminated by the light of the sun, would shine
uniformly.
The second opinion is beset with many difficulties. The tails are never
variegated in color, and yet colors are generally the inseparable concomitants
of refractions. The light of the fixed stars and the planets which is
transmitted to us is distinct [i.e., clearly defined]; this demonstrates that the celestial
medium is empowered with no refractive force. It is said that the Egyptians
sometimes saw the fixed stars surrounded by a head of hair, but this happens
very rarely, and so it must be ascribed to some chance refraction by clouds.
The radiation and scintillation of the fixed stars also should be referred to
refractions both by the eyes and by the tremulous air, since they disappear
when these stars are viewed through telescopes. By the tremor of the air and
of the ascending vapors it happens that rays are easily turned aside
alternately from the narrow space of the pupil of the eye but not at all from the
wider aperture of the objective lens of a telescope. Thus it is that scintillation
is generated in the former case while it ceases in the latter; and the
cessation of scintillation in the latter case demonstrates the regular transmission
of light through the heavens without any sensible refraction. And to counter
the argument that tails are not generally seen in comets when their light is
not strong enough, for the reason that the secondary rays do not then have
enough force to affect the eyes, and that this is why the tails of the fixed stars
are not seen, it should be pointed out that the light of the fixed stars can be
increased more than a hundred times by means of telescopes, and yet no tails
are seen. The planets also shine with more light, but they have no tails; and
often comets have the greatest tails when the light of their heads is faint and
exceedingly dull. For such was the case for the comet of 1680; in December,
at a time when the light from its head scarcely equaled stars of the second
magnitude, it was emitting a tail of notable splendor as great as 40, 50, 60, or
70 degrees in length and more. Afterward, on 27 and 28 January, the head
appeared as a star of only the seventh magnitude, but the tail extended to
6 or 7 degrees in length with a very faint light that was sensible enough;
and with a very dim light, which could scarcely be seen, it stretched out as
far as 12 degrees or a little further, as was said above. But even on 9 and
10 February, when the head had ceased to be seen by the naked eye, the
tail—when I viewed it through a telescope—was 2 degrees long. Further, if
the tail arose from refraction by celestial matter, and if it deviated from the
opposition of the sun in accordance with the form of the heavens, then, in
the same regions of the heavens, that deviation ought always to take place
in the same direction. But the comet of 1680, on 28 December at 8h30m P.M.
London time, was in  8°41′ with a latitude of 28°6′ N, the sun being in
8°41′ with a latitude of 28°6′ N, the sun being in
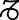 18°26′. And the comet of 1577, on 29 December, was in
18°26′. And the comet of 1577, on 29 December, was in  8°41′ with a
latitude of 28°40′ N, the sun again being in approximately
8°41′ with a
latitude of 28°40′ N, the sun again being in approximately 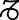 18°26′. In both
cases the earth was in the same place and the comet appeared in the same
part of the sky; yet in the former case the tail of the comet (according to
my observations and those made by others) was declining by an angle of 4½
degrees from the opposition of the sun toward the north, but in the latter
case (according to the observations of Tycho) the declination was 21 degrees
toward the south. Therefore, since refraction by the heavens has been
rejected, the remaining possibility is to derive the phenomena of comets’ tails
from some matter that reflects light.
18°26′. In both
cases the earth was in the same place and the comet appeared in the same
part of the sky; yet in the former case the tail of the comet (according to
my observations and those made by others) was declining by an angle of 4½
degrees from the opposition of the sun toward the north, but in the latter
case (according to the observations of Tycho) the declination was 21 degrees
toward the south. Therefore, since refraction by the heavens has been
rejected, the remaining possibility is to derive the phenomena of comets’ tails
from some matter that reflects light.
Moreover, the laws which the tails of comets observe prove that these
tails arise from the heads and ascend into regions turned away from the
sun. For example, if the tails lie in planes of the comets’ orbits which pass
through the sun, they always deviate from being directly opposite the sun
and point toward the region which the heads, advancing in those orbits, have
left behind. Again, to a spectator placed in those planes, the tails appear in
regions directly turned away from the sun; while for observers not in those
planes, the deviation gradually begins to be perceived and appears greater
from day to day. Furthermore, other things being equal, the deviation is less
when the tail is more oblique to the orbit of the comet, and also when the
head of the comet approaches closer to the sun, especially if the angle of
deviation is taken near the head of the comet. And besides, the tails that do
not deviate appear straight, while those that do deviate are curved. Again, this
curvature is greater when the deviation is greater, and more sensible when
the tail, other things being equal, is longer; for in shorter tails the curvature
is scarcely noticed. Then, too, the angle of deviation is smaller near the head
of the comet and larger near the other extremity of the tail; and thus the
convex side of the tail faces the direction from which the deviation is made
and which is along a straight line drawn from the sun through the head of
the comet indefinitely. Finally, the tails that are more extended and wider
and that shine with a more vigorous light are a little more resplendent on
their convex sides and are terminated by a less indistinct limit than on their
concave sides. For all these reasons, then, the phenomena of the tail depend
on the motion of the head and not on the region of the sky in which the
head is seen; and therefore these phenomena do not come about through
refraction by the heavens, but arise from the head supplying the matter. For
as in our air the smoke of any ignited body seeks to ascend and does so either
perpendicularly (if the body is at rest) or obliquely (if the body is moving
sideways), so in the heavens, where bodies gravitate toward the sun, smoke
and vapors must ascend with respect to the sun (as has already been said)
and move upward either directly, if the smoking body is at rest, or obliquely,
if the body by advancing always leaves the places from which the higher
parts of the vapor have previously ascended. And the swifter the ascent of
the vapor, the less the obliquity, namely in the vicinity of the sun and near
the smoking body. Moreover, as a result of this difference in obliquity, the
column of vapor will be curved; and since the vapor on that side of the
column in the direction of the comet’s motion is a little more recent [i.e.,
more recently exhaled], so also the column will be somewhat more dense on
that same side, and therefore will reflect light more abundantly and will be
terminated by a less indistinct limit. I add nothing here concerning sudden
and uncertain agitations of the tails, nor concerning their irregular shapes
(which are sometimes described), because either these effects may arise from
changes in our air and the motions of the clouds that may obscure those tails
in one part or the other; or, perhaps, these effects may arise because some
parts of the Milky Way may be confused with the tails as they pass by and
may be considered as if they were parts of the tails.
Moreover, the rarity of our own air makes it understandable that
vapors sufficient to fill such immense spaces can arise from the atmospheres of
comets. For the air near the surface of the earth occupies a space about 850
times greater than water of the same weight, and thus a cylindrical column of
air 850 feet high has the same weight as a foot-high column of water of the
same width. Further, a column of air rising to the top of our atmosphere is
equal in weight to a column of water about 33 feet high; and therefore if the
lower part, 850 feet high, of the whole air column is taken away, the
remaining upper part will be equal in weight to a column of water 32 feet high. And
hence (by a rule confirmed by many experiments, that the compression of air
is as the weight of the incumbent atmosphere and that gravity is inversely as
the square of the distance of places from the center of the earth), by making
a computation using the corollary of prop. 22, book 2, I found that air, at a
height above the surface of the earth of one terrestrial semidiameter, is rarer
than here on earth in a far greater ratio than that of all space below the orbit
of Saturn to a globe described with a diameter of one inch. And thus a globe
of our air one inch wide, with the rarity that it would have at the height of
one terrestrial semidiameter, would fill all the regions of the planets as far
out as the sphere of Saturn and far beyond. Accordingly, since still higher
air becomes immensely rare and since the comag or atmosphere of a comet
is (as reckoned from the center) about ten times higher than the surface of
the nucleus is, and the tail then ascends even higher, the tail will have to
be exceedingly rare. And even if, because of the much thicker atmosphere of
comets and the great gravitation of bodies toward the sun and the gravitation
of the particles of air and vapors toward one another, it can happen that the
air in the celestial spaces and in the tails of comets is not so greatly rarefied,
it is nevertheless clear from this computation that a very slight quantity of
air and vapors is abundantly sufficient to produce all those phenomena of
the tails. For the extraordinary rarity of the tails is also evident from the fact
that stars shine through them. The terrestrial atmosphere, shining with the
light of the sun, by its thickness of only a few miles obscures and utterly
extinguishes the light not only of all the stars but also of the moon itself; yet
the smallest stars are known to shine, without any loss in their brightness,
through the immense thickness of the tails, which are likewise illuminated
by the light of the sun. Nor is the brightness of most cometary tails generally
greater than that of our air reflecting the light of the sun in a beam, one or
two inches wide, let into a dark room.
The space of time in which the vapor ascends from the head to the end
of the tail can more or less be found by drawing a straight line from the
end of the tail to the sun and noting the place where this straight line cuts
the trajectory. For if the vapor has been ascending in a straight line away
from the sun, then the vapor that is now in the end of the tail must have
begun to ascend from the head at the time when the head was in that place
of intersection. But the vapor does not ascend in a straight line away from
the sun, but rather ascends obliquely, since the vapor retains the motion of
the comet which it had before its ascent and this motion is compounded
with the motion of its own ascent. And therefore the solution of the problem
will be nearer the true one if the straight line that cuts the orbit is drawn
parallel to the length of the tail, or rather (because of the curvilinear motion
of the comet) if it diverges from the line of the tail. In this way I found that
the vapor that was in the end of the tail on 25 January had begun to ascend
from the head before 11 December and thus had spent more than forty-five
days in its total ascent. But all of the tail that appeared on 10 December had
ascended in the space of those two days that had elapsed after the time of
the perihelion of the comet. The vapor, therefore, rose most swiftly at the
beginning of its ascent, in the vicinity of the sun, and afterward proceeded
to ascend with a motion always retarded by the vapor’s own gravity; and as
the vapor ascended, it increased the length of the tail. The tail, however, as
long as it was visible, consisted of almost all the vapor which had ascended
from the comet’s head since the time of the comet’s perihelion; and that
vapor which was the first to ascend, and which composed the end of the
tail, did not disappear from view until its distance both from the sun which
illuminated it and from our eyes became too great for it to be seen any
longer. Hence it happens, also, that in other comets which have short tails,
those tails do not rise up with a swift and continual motion from the heads
of the comets and soon disappear, but are permanent columns of vapors and
exhalations (propagated from the heads by a very slow motion that lasts many
days) which, by sharing in the motion that the heads had at the beginning of
the exhalations of the vapors, continue to move along through the heavens
together with the heads. And hence again it may be concluded that the
celestial spaces are lacking in any force of resisting, since in them not only
the solid bodies of the planets and comets but also the rarest vapors of the
tails move very freely and preserve their extremely swift motions for a very
long time.
The ascent of the tails of comets from the atmospheres of the heads and
the movement of the tails in directions away from the sun are ascribed by
Kepler to the action of rays of light that carry the matter of the tail along
with them. And it is not altogether unreasonable to suppose that in very free
[or empty] spaces, the extremely thin upper air should yield to the action of
the rays, despite the fact that gross substances in the very obstructed regions
here on earth cannot be sensibly propelled by the rays of the sun. Someone
else believes that there can be particles with the property of levity as well
as gravity and that the matter of the tails levitates and through its levitation
ascends away from the sun. But since the gravity of terrestrial bodies is as the
quantity of matter in the bodies and thus, if the quantity of matter remains
constant, cannot be intended and remitted [or increased and decreased], I
suspect that this ascent arises rather from the rarefaction of the matter of
the tails. Smoke ascends in a chimney by the impulse of the air in which
it floats. This air, rarefied by heat, ascends because of its diminished specific
gravity and carries along with it the entangled smoke. Why should the tail
of a comet not ascend away from the sun in the same manner? For the sun’s
rays do not act on the mediums through which they pass except in reflection
and refraction. The reflecting particles, warmed by this action, will warm the
aethereal upper air in which they are entangled. This will become rarefied
on account of the heat communicated to it; and because its specific gravity,
with which it was formerly tending toward the sun, is diminished by this
rarefaction, it will ascend and will carry with it the reflecting particles of
which the tail is composed. This ascent of the vapors is also increased by the
fact that they revolve about the sun and endeavor by this action to recede
from the sun, while the atmosphere of the sun and the matter of the heavens
are either completely at rest or revolve more slowly only by the motion that
they have received from the rotation of the sun.
These are the causes of the ascent of tails of comets in the vicinity of the
sun, where the orbits are more curved, and the comets are within the denser
(and, on that account, heavier) atmosphere of the sun and soon emit extremely
long tails. For the tails which arise at that point, by conserving their motion
and meanwhile gravitating toward the sun, will move about the sun in ellipses
as the heads of the comets do; and by that motion they will always accompany
the heads and will very freely adhere to them. For the gravity of the vapors
toward the sun will no more cause the tails to fall afterward from the heads
toward the sun than the gravity of the heads can cause them to fall from
the tails. By their common gravity they will either fall simultaneously and
together toward the sun or will be simultaneously retarded in their ascent;
and therefore this gravity does not hinder the tails and heads of comets from
very easily acquiring (whether from the causes already described or any others
whatsoever), and afterward very freely preserving, any position in relation to
one another.
The tails that are formed when comets are in their perihelia will therefore
go off into distant regions together with their heads, and either will return
to us from there together with the heads after a long series of years or rather,
having been rarefied there, will disappear by degrees. For afterward, in the
descent of the heads toward the sun, new little tails should be propagated
from the heads with a slow motion, and thereupon should be immeasurably
increased in the perihelia of those comets which descend as far as the
atmosphere of the sun. For vapor in those very free spaces becomes continually
rarefied and dilated. For this reason it happens that every tail at its upper
extremity is broader than near the head of the comet. Moreover, it seems
reasonable that by this rarefaction the vapor—continually dilated—is finally
diffused and scattered throughout the whole heavens, and then is by degrees
attracted toward the planets by its gravity and mixed with their atmospheres.
For just as the seas are absolutely necessary for the constitution of this earth,
so that vapors may be abundantly enough aroused from them by the heat of
the sun, which vapors either—being gathered into clouds—fall in rains and
irrigate and nourish the whole earth for the propagation of vegetables,
or—being condensed in the cold peaks of mountains (as some philosophize with
good reason)—run down into springs and rivers; so for the conservation of
the seas and fluids on the planets, comets seem to be required, so that from
the condensation of their exhalations and vapors, there can be a continual
supply and renewal of whatever liquid is consumed by vegetation and
putrefaction and converted into dry earth. For all vegetables grow entirely from
fluids and afterward, in great part, change into dry earth by putrefaction,
and slime is continually deposited from putrefied liquids. Hence the bulk of
dry earth is increased from day to day, and fluids—if they did not have an
outside source of increase—would have to decrease continually and finally to
fail. Further, I suspect that that spirit which is the smallest but most subtle
and most excellent part of our air, and which is required for the life of all
things, comes chiefly from comets.
In the descent of comets to the sun, their atmospheres are diminished by
running out into tails and (certainly in that part which faces toward the sun)
are made narrower; and, in turn, when comets are receding from the sun,
and when they are now running out less into tails, they become enlarged, if
Hevelius has correctly noted their phenomena. Moreover, these atmospheres
appear smallest when the heads, after having been heated by the sun, have
gone off into the largest and brightest tails, and the nuclei are surrounded in
the lowest parts of their atmospheres by smoke possibly coarser and blacker.
For all smoke produced by great heat is generally coarser and blacker. Thus,
at equal distances from the sun and the earth, the head of the comet which
we have been discussing appeared darker after its perihelion than before. For
in December it was generally compared to stars of the third magnitude, but
in November to stars of the first magnitude and the second magnitude. And
those who saw both describe the earlier appearance as a greater comet. For
a certain young man of Cambridge, who saw this comet on 19 November,
found its light, however leaden and pale, to be equal to Spica Virginis and to
shine more brightly than afterward. And on 20 November (O.S.) the comet
appeared to Montanari greater than stars of the first magnitude, its tail being
2 degrees long. And Mr. Storer, in a letter that came into our hands, wrote
that in December, at a time when the largest and brightest tail was being
emitted, the head of the comet was small and in visible magnitude was far
inferior to the comet which had appeared in November before sunrise. And
he conjectured that the reason for this was that in the beginning the matter
of the head was more copious and had been gradually consumed.
It seems to pertain to the same point that the heads of other comets
that emitted very large and very bright tails appeared rather dull and very
small. For on 5 March 1668 (N.S.) at 7h P.M., the Reverend Father Valentin
Stansel, in Brazil, saw a comet very close to the horizon toward the southwest
with a very small head that was scarcely visible, but with a tail so shining
beyond measure that those who were standing on the shore easily saw its
appearance reflected from the sea. In fact it had the appearance of a brilliantly
shining torch with a length of 23 degrees, verging from west to south and
almost parallel to the horizon. But so great a splendor lasted only three days,
decreasing noticeably immediately afterward; and meanwhile, as its splendor
was decreasing, the tail was increasing in size. Thus in Portugal the tail is
said to have occupied almost a quarter of the sky—that is, 45
degrees—stretched out from west to east with remarkable splendor, and yet not all of
the tail was visible, since in those regions the head was always hidden below
the horizon. From the increase of the size of the tail and the decrease of the
splendor, it is manifest that the head was receding from the sun and had been
nearest to the sun at the beginning of its visibility, as was the case for the
comet of 1680. And in the Anglo-Saxon Chronicle, one reads about a similar
comet of 1106, “of which the star was small and dim
h(as was that of
1680),h but the splendor that came out of it stretched out extremely bright and like
a huge torch toward the northeast” as Hevelius also has it from Simeon the
Monk of Durham. This comet appeared at the beginning of February, and
thereafter was seen at about evening toward the southwest. And from this
and from the position of the tail it is concluded that the head was near
the sun. “Its distance from the sun,” says Matthew of Paris, “was about one
cubit, as from the third hour (more correctly, the sixth) until the ninth hour
it emitted a long ray from itself.” Such also was that fiery comet described
by Aristotle (Meteor. 1.6), “whose head, on the first day, was not seen because
it had set before the sun, or at least was hidden under the sun’s rays; but on
the following day, it was seen as much as it could be. For it was distant from
the sun by the least possible distance, and soon set. Because of the excessive
burning (of the tail, that is), the scattered fire of the head did not yet appear,
but as time went on,” says Aristotle, “since (the tail) was now flaming less,
the comet’s own face came back to (the head). And it extended its splendor
as far as a third of the sky (that is, to 60 degrees). Moreover, it appeared
in the winter (in the 4th year of the 101st Olympiad) and, ascending up to
Orion’s belt, vanished there.”
The comet of 1618 which emerged out of the sun’s rays with a very large
tail seemed to equal stars of the first magnitude, or even to surpass them a
little, but a number of greater comets have appeared which had shorter tails.
Some of these are said to have equaled Jupiter, others
Venus or even the moon.
We said that comets are a kind of planet revolving about the sun in
very eccentric orbits. And just as among the primary planets (which have
no tails) those which revolve in smaller orbits closer to the sun are generally
smaller, so it seems reasonable also that the comets which approach closer
to the sun in their perihelia are for the most part smaller, since otherwise
they would act on the sun too much by their attraction. I leave the transverse
diameters of the orbits and the periodic times of revolution of the comets to
be determined by comparing comets that return in the same orbits after long
intervals of time. Meanwhile the following proposition may shed some light
on this matter.
Proposition 42, Problem 22
To correct a comet’s trajectory that has been found [by the method of prop. 41].
OPERATION 1. Assume the position of the plane of the trajectory, as
found by prop. 41, and select three places of the comet which have been
determined by very accurate observations and which are as greatly distant from
one another as possible; let A be the time between the first and second
observations, and B the time between the second and third. The comet should
be in its perigee in one of these places, or at least not far from perigee. From
these apparent places find, by trigonometric operations, three true places of
the comet in that assumed plane of the trajectory. Then through those places
thus found, describe a conic about the center of the sun as focus, by
arithmetical operations made along the lines of prop. 21, book 1; and let D and
E be areas of the conic which are bounded by radii drawn from the sun to
those places—namely, D the area between the first and second observations,
and E the area between the second and third. And let T be the total time
in which the total area D + E should be described by the comet, with the
velocity as found by prop. 16, book 1.
OPERATION 2. Let the longitude of the nodes of the plane of the
trajectory be increased by adding 20 or 30 minutes (which can be called P) to that
longitude; but keep constant the inclination of that plane to the plane of the
ecliptic. Then from the three aforesaid observed places of the comet, let three
true places of the comet be found in this new plane (as in oper. 1); and also
the orbit passing through those places, two of its areas (which can be called
d and e) described between observations, and the total time t in which the
total area d + e should be described.
OPERATION 3. Keep constant the longitude of the nodes in the first
operation, and let the inclination of the plane of the trajectory to the plane of
the ecliptic be increased by adding 20 or 30 minutes (which can be called Q)
to that inclination. Then from the aforesaid three observed apparent places
of the comet, let three true places be found in this new plane; and also the
orbit passing through those places, two of its areas (which can be called δ
and ϵ) described between observations, and the total time τ in which the
total area δ + ϵ should be described.
Now take C so as to be to 1 as A to B, and take G to 1 as D to E, and
g to 1 as d to e, and γ to 1 as δ to ϵ, and let S be the true time between the
first and third observations; and carefully observing the signs + and −, seek
the numbers m and n, by the rule that 2G − 2C = mG − mg + nG − nγ; and
2T − 2S = mT − mt + nT − nτ. And if, in the first operation, I designates
the inclination of the plane of the trajectory to the plane of the ecliptic,
and K the longitude of either node, I + nQ will be the true inclination of
the plane of the trajectory to the plane of the ecliptic, and K + mP will
be the true longitude of the node. And finally if in the first, second, and
third operations, the quantities R, r, and ρ designate the latera recta of the
trajectory, and the quantities  the transverse diameters [or latera
transversa] respectively, R + mr − mR + nρ − nR will be the true latus
rectum, and
the transverse diameters [or latera
transversa] respectively, R + mr − mR + nρ − nR will be the true latus
rectum, and  will be the true transverse diameter
of the trajectory that the comet describes. And given the transverse diameter,
the periodic time of the comet is also given. Q.E.I.
will be the true transverse diameter
of the trajectory that the comet describes. And given the transverse diameter,
the periodic time of the comet is also given. Q.E.I.
But the periodic times of revolving comets, and the transverse diameters
[latera transversa] of their orbits, will by no means be determined exactly
enough except by the comparison with one another of comets that appear at
diverse times. If several comets are found, after equal intervals of times, to
have described the same orbit, it will have to be concluded that all these are
one and the same comet revolving in the same orbit. And then finally from
the times of their revolutions the transverse diameters of the orbits will be
given, and from these diameters the elliptical orbits will be determined.
To this end, therefore, the trajectories of several comets should be
calculated on the hypothesis that they are parabolic. For such trajectories will
always agree very nearly with the phenomena. This is clear not only from
the parabolic trajectory of the comet of 1680, which I compared above with
the observations, but also from the trajectory of that remarkable comet which
appeared in 1664 and 1665 and was observed by Hevelius. He calculated the
longitudes and latitudes of this comet from his own observations, but not
very accurately. From the same observations our own Halley calculated the
places of this comet anew, and then finally he determined the trajectory of the
comet from the places thus calculated. And he found its ascending node in
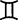 21°13′55″, the inclination of its orbit to the plane of the ecliptic 21°18′40″,
the distance of its perihelion from the node in the orbit 49°27′30″. The
perihelion in
21°13′55″, the inclination of its orbit to the plane of the ecliptic 21°18′40″,
the distance of its perihelion from the node in the orbit 49°27′30″. The
perihelion in  8°40′30″ with heliocentric latitude 16°1′45″ S. The comet in its
perihelion on 24 November, 11h52m P.M. mean time [lit. equated time] at
London, or 13h8m (O.S.) at Gdansk, and the latus rectum of the parabola 410,286,
the mean distance of the earth from the sun being 100,000. How exactly the
calculated places of the comet in this orbit agree with the observations will
be evident from the following table calculated by Halley [p. 932].
8°40′30″ with heliocentric latitude 16°1′45″ S. The comet in its
perihelion on 24 November, 11h52m P.M. mean time [lit. equated time] at
London, or 13h8m (O.S.) at Gdansk, and the latus rectum of the parabola 410,286,
the mean distance of the earth from the sun being 100,000. How exactly the
calculated places of the comet in this orbit agree with the observations will
be evident from the following table calculated by Halley [p. 932].
In February, in the beginning of 1665, the first star of Aries, which I
shall from here on call γ, was in  28°30′15″ with latitude 7°8′58″ N. The
second star of Aries was in
28°30′15″ with latitude 7°8′58″ N. The
second star of Aries was in  29°17′18″ with latitude 8°28′16″ N. And a
certain other star of the seventh magnitude, which I shall call A, was in
29°17′18″ with latitude 8°28′16″ N. And a
certain other star of the seventh magnitude, which I shall call A, was in
 28°24′45″ with latitude 8°28′33″ N. And on 7 February at 7h30m Paris
time (that is, 7 February at 8h30m Gdansk time) (O.S.), the comet made a
right triangle with those stars γ and A, with the right angle at γ. And the
distance of the comet from the star γ was equal to the distance between
the stars γ and A, that is, 1°19′46″ along a great circle, and therefore it
was 1°20′26″ in the parallel of the latitude of the star γ. Therefore, if the
longitude 1°20′26″ is taken away from the longitude of the star γ, there will
remain the longitude of the comet
28°24′45″ with latitude 8°28′33″ N. And on 7 February at 7h30m Paris
time (that is, 7 February at 8h30m Gdansk time) (O.S.), the comet made a
right triangle with those stars γ and A, with the right angle at γ. And the
distance of the comet from the star γ was equal to the distance between
the stars γ and A, that is, 1°19′46″ along a great circle, and therefore it
was 1°20′26″ in the parallel of the latitude of the star γ. Therefore, if the
longitude 1°20′26″ is taken away from the longitude of the star γ, there will
remain the longitude of the comet  27°9′49″. Auzout, who had made this
observation, put the comet in roughly
27°9′49″. Auzout, who had made this
observation, put the comet in roughly  27°0′. And from the diagram with
which Hooke delineated its motion, it was then in
27°0′. And from the diagram with
which Hooke delineated its motion, it was then in  26°59′24″. Taking the
mean, I have put it in
26°59′24″. Taking the
mean, I have put it in  27°4′46″. From the same observation, Auzout took
the latitude of the comet at that time to be 7° and 4′ or 5′ toward the north.
He would have put it more correctly at 7°3′29″, since the difference of the
latitudes of the comet and of the star γ was equal to the difference of the
longitudes of the stars γ and A.
27°4′46″. From the same observation, Auzout took
the latitude of the comet at that time to be 7° and 4′ or 5′ toward the north.
He would have put it more correctly at 7°3′29″, since the difference of the
latitudes of the comet and of the star γ was equal to the difference of the
longitudes of the stars γ and A.
On 22 February at 7h30m in London (that is, 22 February at 8h46m
Gdansk time), the distance of the comet from the star A, according to Hooke’s
observation (which he himself delineated in a diagram) and also according to
Auzout’s observations (delineated in a diagram by Petit), was a fifth of the
distance between the star A and the first star of Aries, or 15′57″. And the
distance of the comet from the line joining the star A and the first star of
Aries was a fourth of that same fifth part, that is, 4′. And hence the comet
was in  28°29′46″ with latitude 8°12′36″ N.
28°29′46″ with latitude 8°12′36″ N.
On 1 March at 7h0m at London (that is, 1 March at 8h16m Gdansk time),
the comet was observed near the second star of Aries, the distance between
them being to the distance between the first and second stars of Aries, that
is, to 1°33′, as 4 to 45 according to Hooke, or as 2 to 23 according to [Gilles
François] Gottigniez. Accordingly, the distance of the comet from the second
star of Aries was 8°16″ according to Hooke, or 8′5″ according to Gottigniez;
or, taking the mean, was 8′10″. And according to Gottigniez the comet had
now just gone beyond the second star of Aries by about a space of a fourth
or a fifth of the course completed in one day, that is, roughly 1′35″ (and
Auzout agrees well enough with this), or a little less according to Hooke,
say 1′. Therefore, if 1′ is added to the longitude of the first star of Aries, and
8′10″ to its latitude, the longitude of the comet will be found to be  29°18′,
and its latitude 8°36′26″ N.
29°18′,
and its latitude 8°36′26″ N.

On 7 March at 7h30m in Paris (that is, 7 March at 8h37m Gdansk time),
the distance of the comet from the second star of Aries, according to Auzout’s
observations, was equal to the distance of the second star of Aries from the
star A, that is, 52′29″. And the difference between the longitudes of the comet
and of the second star of Aries was 45′ or 46′ or, taking the mean, 45′30″.
And therefore the comet was in  0°2′48″. From the diagram of Auzout’s
observations that Petit constructed, Hevelius determined the latitude of the
comet to be 8°54′. But the engraver curved the path of the comet irregularly
toward the end of its motion, and Hevelius corrected the irregular curving
in a diagram of Auzout’s observations drawn by Hevelius himself, and thus
made the latitude of the comet 8°55′30″. And by correcting the irregularity
a little more, the latitude can come out to be 8°56′, or 8°57′.
0°2′48″. From the diagram of Auzout’s
observations that Petit constructed, Hevelius determined the latitude of the
comet to be 8°54′. But the engraver curved the path of the comet irregularly
toward the end of its motion, and Hevelius corrected the irregular curving
in a diagram of Auzout’s observations drawn by Hevelius himself, and thus
made the latitude of the comet 8°55′30″. And by correcting the irregularity
a little more, the latitude can come out to be 8°56′, or 8°57′.
This comet was also seen on 9 March and then must have been located
in  0°18’ with latitude roughly 9°3½′ N.
0°18’ with latitude roughly 9°3½′ N.
This comet was visible for three months in all, during which time it
passed through about six signs, completing about 20 degrees in each day.
Its path deviated considerably from a great circle, being curved northward;
and toward the end, its motion changed from retrograde to direct. And
notwithstanding so unusual a path, the theory agrees with the observations
from beginning to end no less exactly than theories of the planets tend to
agree with observations of them, as will be clear upon examination of the
table. Nevertheless, roughly 2 minutes must be subtracted when the comet
was swiftest, and this will result by taking away 12 seconds from the angle
between the ascending node and the perihelion, or by making that angle
49°27′18″. The annual parallax of each of the two comets (both this one and
the previous one) was quite pronounced, and as a result it gave proof of the
annual motion of the earth in its orbit.
The theory is confirmed also by the motion of the comet that appeared
in 1683. It had a retrograde motion in an orbit whose plane contained almost
a right angle with the plane of the ecliptic. Its ascending node (by Halley’s
calculation) was in 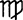 23°23′; the inclination of its orbit to the ecliptic 83°11′;
its perihelion in
23°23′; the inclination of its orbit to the ecliptic 83°11′;
its perihelion in 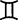 25°29′30″; its perihelial distance from the sun 56,020, the
radius of the earth’s orbit being taken at 100,000, and the time of its perihelion
2 July 3h50m. And the places of the comet in this orbit, as calculated by Halley
and compared with the places observed by Flamsteed, are displayed in the
following table.
25°29′30″; its perihelial distance from the sun 56,020, the
radius of the earth’s orbit being taken at 100,000, and the time of its perihelion
2 July 3h50m. And the places of the comet in this orbit, as calculated by Halley
and compared with the places observed by Flamsteed, are displayed in the
following table.

The theory is confirmed also by the motion of the retrograde comet
that appeared in 1682. Its ascending node (by Halley’s calculation) was in
 21°16′30″. The inclination of the orbit to the plane of the ecliptic 17°56′0″.
Its perihelion in
21°16′30″. The inclination of the orbit to the plane of the ecliptic 17°56′0″.
Its perihelion in  2°52′50″. Its perihelial distance from the sun 58,328, the
radius of the earth’s orbit being 100,000. And the perihelion 4 September
7h39m mean [lit. equated] time. And the places calculated from Flamsteed’s
observations and compared with the places calculated by the theory are shown
in the following table.
2°52′50″. Its perihelial distance from the sun 58,328, the
radius of the earth’s orbit being 100,000. And the perihelion 4 September
7h39m mean [lit. equated] time. And the places calculated from Flamsteed’s
observations and compared with the places calculated by the theory are shown
in the following table.

aThe theory is confirmed also by the retrograde motion of the comet
that appeared in 1723. Its ascending node (by the calculation of Mr. Bradley,
Savilian professor of astronomy at Oxford) was in  14°16′. The inclination
of the orbit to the plane of the ecliptic 49°59′. Its perihelion in
14°16′. The inclination
of the orbit to the plane of the ecliptic 49°59′. Its perihelion in  12°15′20″.
Its perihelial distance from the sun 998,651, the radius of the earth’s orbit
being 1,000,000, and the mean [lit. equated] time of the perihelion being 16
September 16h10m. And the places of the comet in this orbit, as calculated
by Bradley and compared with the places observed by himself and his uncle
Mr. Pound, and by Mr. Halley, are shown in the following
table.a
12°15′20″.
Its perihelial distance from the sun 998,651, the radius of the earth’s orbit
being 1,000,000, and the mean [lit. equated] time of the perihelion being 16
September 16h10m. And the places of the comet in this orbit, as calculated
by Bradley and compared with the places observed by himself and his uncle
Mr. Pound, and by Mr. Halley, are shown in the following
table.a
By these examples it is more than sufficiently evident that the motions
of comets are no less exactly represented by the theory that we have set forth
than the motions of planets are generally represented by planetary theories.
And therefore the orbits of comets can be calculated by this theory, and
the periodic time of a comet revolving in any orbit whatever can then be
determined, and finally the transverse diameters [lit. latera transversa] of
their elliptical orbits and their aphelian distances will become known.
The retrograde comet that appeared in 1607 described an orbit whose
ascending node (according to Halley’s calculation) was in  20°21′; the
inclination of the plane of its orbit to the plane of the ecliptic was 17°2′; its
perihelion was in
20°21′; the
inclination of the plane of its orbit to the plane of the ecliptic was 17°2′; its
perihelion was in  2°16′; and its perihelial distance from the sun was 58,680,
the radius of the earth’s orbit being 100,000. And the comet was in its
perihelion on 16 October at 3h50m. This orbit agrees very closely with the orbit of
the comet that was seen in 1682. If these two comets should be one and the
same, this comet will revolve in a space of seventy-five years and the major
axis of its orbit will be to the major axis of the earth’s orbit as ∛(75 × 75)
to 1, or roughly 1,778 to 100. And the aphelial distance of this comet from
the sun will be to the mean distance of the earth from the sun as roughly
35 to 1. And once these quantities are known, it will not be at all difficult
to determine the elliptical orbit of this comet. What has just been said will
be found to be true if the comet returns hereafter in this orbit in a space of
seventy-five years. The other comets seem to revolve in a greater time and
to ascend higher.
2°16′; and its perihelial distance from the sun was 58,680,
the radius of the earth’s orbit being 100,000. And the comet was in its
perihelion on 16 October at 3h50m. This orbit agrees very closely with the orbit of
the comet that was seen in 1682. If these two comets should be one and the
same, this comet will revolve in a space of seventy-five years and the major
axis of its orbit will be to the major axis of the earth’s orbit as ∛(75 × 75)
to 1, or roughly 1,778 to 100. And the aphelial distance of this comet from
the sun will be to the mean distance of the earth from the sun as roughly
35 to 1. And once these quantities are known, it will not be at all difficult
to determine the elliptical orbit of this comet. What has just been said will
be found to be true if the comet returns hereafter in this orbit in a space of
seventy-five years. The other comets seem to revolve in a greater time and
to ascend higher.

But because of the great number of comets, and the great distance of their
aphelia from the sun, and the long time that they spend in their aphelia, they
should be disturbed somewhat by their gravities toward one another, and
hence their eccentricities and times of revolutions ought sometimes to be
increased a little and sometimes decreased a little. Accordingly, it is not to
be expected that the same comet will return exactly in the same orbit, and
with the same periodic times. It is sufficient if no greater changes are found
to occur than those that arise from the above-mentioned causes.
And hence a reason appears why comets are not restricted to the zodiac
as planets are, but depart from there and are carried with various motions
into all regions of the heavens—namely, for this purpose, that in their aphelia,
when they move most slowly, they may be as far distant from one another
as possible and may attract one another as little as possible. And this is the
reason why comets that descend the lowest, and so move most slowly in their
aphelia, should also ascend to the greatest heights.
The comet that appeared in 1680 was distant from the sun in its
perihelion by less than a sixth of the sun’s diameter; and because its velocity was
greatest in that region and also because the atmosphere of the sun has some
density, the comet must have encountered some resistance and must have
been somewhat slowed down and must have approached closer to the sun;
and by approaching closer to the sun in every revolution, it will at length
fall into the body of the sun. But also, in its aphelion, when it moves most
slowly, the comet can sometimes be slowed down by the attraction of other
comets and as a result fall into the sun. So also fixed stars, which are
exhausted bit by bit in the exhalation of light and vapors, can be renewed by
comets falling into them and then, kindled by their new nourishment, can
be taken for new stars. Of this sort are those fixed stars that appear all of
a sudden, and that at first shine with maximum brilliance and subsequently
disappear little by little. Of such sort was the star that Cornelius Gemma
saw in Cassiopeia’s Chair on 9 November 1572; it was shining brighter than
all the fixed stars, scarcely inferior to Venus in its brilliance. But he did not
see it at all on 8 November, when he was surveying that part of the sky on
a clear night. Tycho Brahe saw this same star on the 11th of that month,
when it shone with the greatest splendor; and he observed it decreasing little
by little after that time, and he saw it disappearing after the space of sixteen
months. In November, when it first appeared, it equaled Venus in
brightness. In December, somewhat diminished, it equaled Jupiter. In January 1573
it was less than Jupiter and greater than Sirius, and it became equal to Sirius
at the end of February and the beginning of March. In April and May it was
equal to stars of the second magnitude; in June, July, and August, to stars
of the third magnitude; in September, October, and November, to stars of
the fourth magnitude; in December and in January 1574, to stars of the fifth
magnitude; and in February, to stars of the sixth magnitude; and in March,
it vanished from sight. Its color at the start was clear, whitish, and bright;
afterward it became yellowish, and in March of 1573 reddish like Mars or
the star Aldebaran, while in May it took on a livid whiteness such as we
see in Saturn, and it maintained this color up to the end, yet all the while
becoming fainter. Such also was the star in the right foot of Serpentarius,
the beginning of whose visibility was observed by the pupils of Kepler in
1604, on 30 September (O.S.); they saw it exceeding Jupiter in its light,
although it had not been visible at all on the preceding night. And from that
time it decreased little by little and in the space of fifteen or sixteen months
vanished from sight. It was when such a new star appeared shining beyond
measure that Hipparchus is said to have been stimulated to observe the fixed
stars and to put them into a catalog. But fixed stars that alternately appear
and disappear, and increase little by little, and are hardly ever brighter than
fixed stars of the third magnitude, seem to be of another kind and, in
revolving, seem to show alternately a bright side and a dark side. And the vapors
that arise from the sun and the fixed stars and the tails of comets can fall
by their gravity into the atmospheres of the planets and there be condensed
and converted into water and humid spirits, and then—by a slow heat—be
transformed gradually into salts, sulphurs, tinctures, slime, mud, clay, sand,
stones, corals, and other earthy substances.
 QA,
QA,  QB, and
QB, and  QC be three observed longitudes of a comet
at the beginning of its [visible] motion, and let
QC be three observed longitudes of a comet
at the beginning of its [visible] motion, and let  QF be its last observed
longitude, just as the comet ceases to be seen. Draw the straight line ABC,
whose parts AB and BC placed between the straight lines QA and QB,
and between the straight lines QB and QC, are to each other as the times
between the first three observations. Let AC be produced to G, so that AG
is to AB as the time between the first and the last observation is to the time
between the first and the second observation, and let QG be joined. Then,
if the comet moved uniformly in a straight line and the earth were either
at rest or also moved forward in a straight line with uniform motion, the
angle
QF be its last observed
longitude, just as the comet ceases to be seen. Draw the straight line ABC,
whose parts AB and BC placed between the straight lines QA and QB,
and between the straight lines QB and QC, are to each other as the times
between the first three observations. Let AC be produced to G, so that AG
is to AB as the time between the first and the last observation is to the time
between the first and the second observation, and let QG be joined. Then,
if the comet moved uniformly in a straight line and the earth were either
at rest or also moved forward in a straight line with uniform motion, the
angle  QG would be the longitude of the comet at the time of the last
observation. Therefore, the angle FQG, which is the difference between the
longitudes, arises from the inequality of the motions of the comet and of the
earth. And this angle, if the earth and comet move in opposite directions, is
added to the angle
QG would be the longitude of the comet at the time of the last
observation. Therefore, the angle FQG, which is the difference between the
longitudes, arises from the inequality of the motions of the comet and of the
earth. And this angle, if the earth and comet move in opposite directions, is
added to the angle  QG, and thus makes the apparent motion of the comet
swifter; but if the comet is going in the same direction as the earth, this angle
is subtracted from that same angle
QG, and thus makes the apparent motion of the comet
swifter; but if the comet is going in the same direction as the earth, this angle
is subtracted from that same angle  QG and makes the motion of the comet
either slower or possibly retrograde, as I have just explained. Therefore this
angle arises chiefly from the motion of the earth and on that account is rightly
regarded as the parallax of the comet, ignoring, of course, any increase or
decrease in it which could arise from the nonuniform motion of the comet
in its own orbit. And the distance of the comet may be ascertained from this
parallax in the following manner.
QG and makes the motion of the comet
either slower or possibly retrograde, as I have just explained. Therefore this
angle arises chiefly from the motion of the earth and on that account is rightly
regarded as the parallax of the comet, ignoring, of course, any increase or
decrease in it which could arise from the nonuniform motion of the comet
in its own orbit. And the distance of the comet may be ascertained from this
parallax in the following manner.
 T the place of the earth in the
last observation, and let T
T the place of the earth in the
last observation, and let T
 , . . . , and
then
, . . . , and
then  , . . . , and afterward
, . . . , and afterward
 . . . . When these differences have been found, let AH
be equal to a, −HS = p, p × (−IS) = q, q × (+SK) = r, r × (+SL) = s,
s × (+SM) = t, proceeding, that is, up to the penultimate perpendicular
ME; then the ordinate RS will be = a + bp + cq + dr + es + ft + . . . .
. . . . When these differences have been found, let AH
be equal to a, −HS = p, p × (−IS) = q, q × (+SK) = r, r × (+SL) = s,
s × (+SM) = t, proceeding, that is, up to the penultimate perpendicular
ME; then the ordinate RS will be = a + bp + cq + dr + es + ft + . . . . a given ratio to each other.
a given ratio to each other.
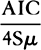 are equal to one another.
are equal to one another.
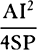 . Thus, since the weight of the comet toward
the sun at the height SN is to its weight toward the sun at the height SP
as SP to Sμ, the comet—falling toward the sun with the weight that it has
at the height SN—will in the same time describe the space
. Thus, since the weight of the comet toward
the sun at the height SN is to its weight toward the sun at the height SP
as SP to Sμ, the comet—falling toward the sun with the weight that it has
at the height SN—will in the same time describe the space
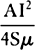 , that is, a
space equal to the length Iμ or Mμ. Q.E.D.
, that is, a
space equal to the length Iμ or Mμ. Q.E.D.




 AE and less than
AE and less than  AE, and thus was
very nearly
AE, and thus was
very nearly 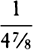 AE, or 8/39AE. And the distance of the comet from a
perpendicular dropped from star A to the straight line PE was ⅘PE.
AE, or 8/39AE. And the distance of the comet from a
perpendicular dropped from star A to the straight line PE was ⅘PE. 1°53′ and the ascending node in
1°53′ and the ascending node in 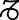 1°53′,
and the inclination of its plane to the plane of the ecliptic to be 61°20⅓′. I
found that its vertex (or the perihelion of the comet) was 8°38′ distant from
the node and was in
1°53′,
and the inclination of its plane to the plane of the ecliptic to be 61°20⅓′. I
found that its vertex (or the perihelion of the comet) was 8°38′ distant from
the node and was in  27°43′ with a latitude 7°34′ S; and that its latus
rectum was 236.8, and that the area described each day by a radius drawn to the
sun was 93,585, supposing the square of the semidiameter of the earth’s orbit
to be 100,000,000; and I found that the comet had advanced in this orbit in
the order of the signs, and was on 8 December 0h4m A.M. in the vertex of the
orbit or the perihelion. I made all these determinations
27°43′ with a latitude 7°34′ S; and that its latus
rectum was 236.8, and that the area described each day by a radius drawn to the
sun was 93,585, supposing the square of the semidiameter of the earth’s orbit
to be 100,000,000; and I found that the comet had advanced in this orbit in
the order of the signs, and was on 8 December 0h4m A.M. in the vertex of the
orbit or the perihelion. I made all these determinations 

 29°51′ with latitude 1°17′45″ N.
29°51′ with latitude 1°17′45″ N.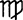 3°23′ with latitude 1°6′ N.
3°23′ with latitude 1°6′ N. 8°30′ with latitude 0°40′ S.
Their observations may be found in the treatise which Ponteo published
about this comet.
8°30′ with latitude 0°40′ S.
Their observations may be found in the treatise which Ponteo published
about this comet. 
 2°33′, while at
Boston in New England it appeared in approximately
2°33′, while at
Boston in New England it appeared in approximately 
 4°, with a latitude of about
42½° N.
4°, with a latitude of about
42½° N. 22° with a latitude of 61° N. And hence the tail was about 70 degrees
long.
22° with a latitude of 61° N. And hence the tail was about 70 degrees
long. 19° with a latitude of 35°. On 5 January the
tail touched the star π in the breast of Andromeda on the right side and
the star μ in the girdle on the left side, and (according to our observations)
was 40 degrees long; but it was curved, and its convex side faced to the
south. Near the head of the comet, the tail made an angle of 4 degrees with
the circle passing through the sun and the head of the comet; but near the
other end, it was inclined to that circle at an angle of 10 or 11 degrees, and
the chord of the tail contained an angle of 8 degrees with that circle. On
13 January the tail was visible enough between Alamech and Algol [= β
Persei], but it ended in a very faint light toward the star κ in Perseus’s side.
The distance of the end of the tail from the circle joining the sun and the
comet was 3°50′, and the inclination of the chord of the tail to that circle
was 8½ degrees. On 25 and 26 January the tail shone with a faint light to a
length of 6 or 7 degrees; and, a night or so later, when the sky was extremely
clear, it attained a length of 12 degrees and a little more, with a light that
was very faint and scarcely to be perceived. But its axis was directed exactly
toward the bright star in the eastern shoulder of Auriga, and accordingly
declined from the opposition of the sun toward the north at an angle of 10
degrees. Finally on 10 February, my eyes armed [with a telescope], I saw
the tail to be 2 degrees long. For the fainter light mentioned above was not
visible through the glasses. But
19° with a latitude of 35°. On 5 January the
tail touched the star π in the breast of Andromeda on the right side and
the star μ in the girdle on the left side, and (according to our observations)
was 40 degrees long; but it was curved, and its convex side faced to the
south. Near the head of the comet, the tail made an angle of 4 degrees with
the circle passing through the sun and the head of the comet; but near the
other end, it was inclined to that circle at an angle of 10 or 11 degrees, and
the chord of the tail contained an angle of 8 degrees with that circle. On
13 January the tail was visible enough between Alamech and Algol [= β
Persei], but it ended in a very faint light toward the star κ in Perseus’s side.
The distance of the end of the tail from the circle joining the sun and the
comet was 3°50′, and the inclination of the chord of the tail to that circle
was 8½ degrees. On 25 and 26 January the tail shone with a faint light to a
length of 6 or 7 degrees; and, a night or so later, when the sky was extremely
clear, it attained a length of 12 degrees and a little more, with a light that
was very faint and scarcely to be perceived. But its axis was directed exactly
toward the bright star in the eastern shoulder of Auriga, and accordingly
declined from the opposition of the sun toward the north at an angle of 10
degrees. Finally on 10 February, my eyes armed [with a telescope], I saw
the tail to be 2 degrees long. For the fainter light mentioned above was not
visible through the glasses. But  the transverse diameters [or latera
transversa] respectively, R + mr − mR + nρ − nR will be the true latus
rectum, and
the transverse diameters [or latera
transversa] respectively, R + mr − mR + nρ − nR will be the true latus
rectum, and  will be the true transverse diameter
of the trajectory that the
will be the true transverse diameter
of the trajectory that the 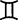 21°13′55″, the inclination of its orbit to the plane of the ecliptic 21°18′40″,
the distance of its perihelion from the node in the orbit 49°27′30″. The
perihelion in
21°13′55″, the inclination of its orbit to the plane of the ecliptic 21°18′40″,
the distance of its perihelion from the node in the orbit 49°27′30″. The
perihelion in 


