A Brief History of the Principia
The Origins of the Principia
Isaac Newton’s Principia was published in 1687. The full title is Philosophiae
Naturalis Principia Mathematica, or Mathematical Principles of Natural Philosophy.
A revised edition appeared in 1713, followed by a third edition in 1726, just one
year before the author’s death in 1727. The subject of this work, to use the name
assigned by Newton in the first preface, is “rational mechanics.” Later on, Leibniz
introduced the name “dynamics.” Although Newton objected to this name,1
“dynamics” provides an appropriate designation of the subject matter of the Principia,
since “force” is a primary concept of that work. Indeed, the Principia can quite
properly be described as a study of a variety of forces and the different kinds of
motions they produce. Newton’s eventual goal, achieved in the third of the three
“books” of which the Principia is composed, was to apply the results of the prior
study to the system of the world, to the motions of the heavenly bodies. This subject
is generally known today by the name used a century or so later by Laplace,
“celestial mechanics.”
The history of how the Principia came into being has been told and retold.2
In the summer of 1684, the astronomer Edmond Halley visited Newton in order
to find out whether he could solve a problem that had baffled Christopher Wren,
Robert Hooke, and himself: to find the planetary orbit that would be produced
by an inverse-square central force. Newton knew the answer to be an ellipse.3 He
had solved the problem of elliptical orbits earlier, apparently in the period
1679–1680 during the course of an exchange of letters with Hooke. When Halley heard
Newton’s reply, he urged him to write up his results. With Halley’s prodding and
encouragement, Newton produced a short tract which exists in several versions
and will be referred to as De Motu4 (On Motion), the common beginning of all
the titles Newton gave to the several versions. Once started, Newton could not
restrain the creative force of his genius, and the end product was the Principia.
In his progress from the early versions of De Motu to the Principia, Newton’s
conception of what could be achieved by an empirically based mathematical science
had become enlarged by several orders of magnitude.
As first conceived, the Principia consisted of two “books” and bore the simple
title De Motu Corporum (On the Motion of Bodies).5 This manuscript begins, as
does the Principia, with a series of Definitions and Laws of Motion, followed by a
book 1 whose subject matter more or less corresponds to book 1 of the Principia.6
The subject matter of book 2 of this early draft is much the same as that of book
3 of the Principia. In revising this text for the Principia, Newton limited book 1
to the subject of forces and motion in free spaces, that is, in spaces devoid of any
resistance. Book 2 of the Principia contains an expanded version of the analysis
of motion in resisting mediums, plus discussions of pendulums,7 of wave motion,
and of the physics of vortices. In the Principia, the system of the world became the
subject of what is there book 3, incorporating much that had been in the older
book 2 but generally recast in a new form. As Newton explained in the final
Principia, while introducing book 3, he had originally presented this subject in a
popular manner, but then decided to recast it in a more mathematical form so
that it would not be read by anyone who had not first mastered the principles
of rational mechanics. Even so, whole paragraphs of the new book 3 were copied
word for word from the old book 2.8
Steps Leading to the Composition and Publication of the Principia
The history of the development of Newton’s ideas concerning mechanics, more
specifically dynamics, has been explored by many scholars and is still the subject
of active research and study.9 The details of the early development of Newton’s
ideas about force and motion, however interesting in their own right, are not
directly related to the present assignment, which is to provide a reader’s guide to
the Principia. Nevertheless, some aspects of this prehistory should be of interest
to every prospective reader of the Principia. In the scholium to book 1, prop. 4,
Newton refers to his independent discovery (in the 1660s) of the 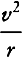 rule for the
force in uniform circular motion (at speed v along a circle of radius r), a discovery
usually attributed to Christiaan Huygens, who formally announced it to the world
in his Horologium Oscillatorium of 1673.10 It requires only the minimum skill in
algebraic manipulation to combine the
rule for the
force in uniform circular motion (at speed v along a circle of radius r), a discovery
usually attributed to Christiaan Huygens, who formally announced it to the world
in his Horologium Oscillatorium of 1673.10 It requires only the minimum skill in
algebraic manipulation to combine the 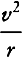 rule with Kepler’s third law in order
to determine that in a system of bodies in uniform circular motion the force is
proportional to
rule with Kepler’s third law in order
to determine that in a system of bodies in uniform circular motion the force is
proportional to  or is inversely proportional to the square of the distance. Of
course, this computation does not of itself specify anything about the nature of the
force, whether it is a centripetal or a centrifugal force or whether it is a force in
the sense of the later Newtonian dynamics or merely a Cartesian “conatus,” or
endeavor. In a manuscript note Newton later claimed that at an early date, in the
1660s, he had actually applied the
or is inversely proportional to the square of the distance. Of
course, this computation does not of itself specify anything about the nature of the
force, whether it is a centripetal or a centrifugal force or whether it is a force in
the sense of the later Newtonian dynamics or merely a Cartesian “conatus,” or
endeavor. In a manuscript note Newton later claimed that at an early date, in the
1660s, he had actually applied the 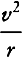 rule to the moon’s motion, much as he does
later on in book 3, prop. 4, of the Principia, in order to confirm his idea of the
force of “gravity extending to the Moon.”11 In this way he could counter Hooke’s
allegation that he had learned the concept of an inverse-square force of gravity
from Hooke.
rule to the moon’s motion, much as he does
later on in book 3, prop. 4, of the Principia, in order to confirm his idea of the
force of “gravity extending to the Moon.”11 In this way he could counter Hooke’s
allegation that he had learned the concept of an inverse-square force of gravity
from Hooke.
A careful reading of the documents in question shows that sometime in the
1660s, Newton made a series of computations, one of which was aimed at proving
that what was later known as the outward or centrifugal force arising from the
earth’s rotation is less than the earth’s gravity, as it must be for the Copernican
system to be possible. He then computed a series of forces. Cartesian vortical
endeavors are not the kind of forces that, in the Principia, are exerted by the sun
on the planets to keep them in a curved path or the similar force exerted by the
earth on the moon. At this time, and for some years to come, Newton was deeply
enmeshed in the Cartesian doctrine of vortices. He had no concept of a “force of
gravity” acting on the moon in anything like the later sense of the dynamics of the
Principia. These Cartesian “endeavors” (Newton used Descartes’s own technical
term, “conatus”) are the magnitude of the planets’ endeavors to fly out of their
orbits. Newton concludes that since the cubes of the distances of the planets from
the sun are “reciprocally as the squared numbers of their revolutions in a given
time,” their “conatus to recede from the Sun will be reciprocally as the squares of
their distances from the Sun.”12
Newton also made computations to show that the endeavor or “conatus” of
receding from the earth’s surface (caused by the earth’s daily rotation) is 12½
times greater than the orbital endeavor of the moon to recede from the earth. He
concludes that the force of receding at the earth’s surface is “4000 and more times
greater than the endeavor of the Moon to recede from the Earth.”
In other words, “Newton had discovered an interesting mathematical correlation
within the solar vortex,”13 but he plainly had not as yet invented the radically
new concept of a centripetal dynamical force, an attraction that draws the planets
toward the sun and the moon toward the earth.14 There was no “twenty years’
delay” (from the mid-1660s to the mid-1680s) in Newton’s publication of the theory
of universal gravity, as was alleged by Florian Cajori.15
In 1679/80, Hooke initiated an exchange of correspondence with Newton on
scientific topics. In the course of this epistolary interchange, Hooke suggested to
Newton a “hypothesis” of his own devising which would account for curved orbital
motion by a combination of two motions: an inertial or uniform linear component
along the tangent to the curve and a motion of falling inward toward a center.
Newton told Hooke that he had never heard of this “hypothesis.”16 In the course of
their letters, Hooke urged Newton to explore the consequences of his hypothesis,
advancing the opinion or guess that in combination with the supposition of an
inverse-square law of solar-planetary force, it would lead to the true planetary
motions.17 Hooke also wrote that the inverse-square law would lead to a rule
for orbital speed being inversely proportional to the distance of a planet from
the sun.18 Stimulated by Hooke, Newton apparently then proved that the
solar-planetary force is as the inverse square of the distance, a first step toward the
eventual Principia.
We cannot be absolutely certain of exactly how Newton proceeded to solve
the problem of motion in elliptical orbits, but most scholars agree that he more
or less followed the path set forth in the tract De Motu which he wrote after
Halley’s visit a few years later in 1684.19 Essentially, this is the path from props. 1
and 2 of book 1 to prop. 4, through prop. 6, to props. 10 and 11. Being secretive
by nature, Newton didn’t tell Hooke of his achievement. In any event, he would
hardly have announced so major a discovery to a jealous professional rival, nor in
a private letter. What may seem astonishing, in retrospect, is not that Newton did
not reveal his discovery to Hooke, but that Newton was not at once galvanized
into expanding his discovery into the eventual Principia.
Several aspects of the Hooke-Newton exchange deserve to be noted. First,
Hooke was unable to solve the problem that arose from his guess or his intuition;
he simply did not have sufficient skill in mathematics to be able to find the orbit
produced by an inverse-square force. A few years later, Wren and Halley were
equally baffled by this problem. Newton’s solution was, as Westfall has noted, to
invert the problem, to assume the path to be an ellipse and find the force rather
than “investigating the path in an inverse-square force field.”20 Second, there is no
certainty that the tract De Motu actually represents the line of Newton’s thought
after corresponding with Hooke; Westfall, for one, has argued that a better
candidate would be an essay in English which Newton sent later to John Locke, a
position he maintains in his biography of Newton.21 A third point is that Newton
was quite frank in admitting (in private memoranda) that the correspondence with
Hooke provided the occasion for his investigations of orbital motion that eventually
led to the Principia.22 Fourth, as we shall see in §3.4 below, the encounter
with Hooke was associated with a radical reorientation of Newton’s philosophy of
nature that is indissolubly linked with the Principia. Fifth, despite Newton’s success
in proving that an elliptical orbit implies an inverse-square force, he was not at
that time stimulated—as he would be some four years later—to move ahead and
to create modern rational mechanics. Sixth, Newton’s solution of the problems of
planetary force depended on both his own new concept of a dynamical measure
of force (as in book 1, prop. 6) and his recognition of the importance of Kepler’s
law of areas.23 A final point to be made is that most scholarly analyses of
Newton’s thoughts during this crucial period concentrate on conceptual formulations
and analytical solutions, whereas we know that both Hooke24 and Newton made
important use of graphical methods, a point rightly stressed by Curtis Wilson.25
Newton, in fact, in an early letter to Hooke, wrote of Hooke’s “acute Letter having
put me upon considering . . . the species of this curve,” saying he might go on to
“add something about its description quam proxime,”26 or by graphic methods.
The final proposition in the Principia (book 3, prop. 42) declared its subject (in the
first edition) to be: “To correct a comet’s trajectory found graphically.” In the
second and third editions, the text of the demonstration was not appreciably altered,
but the statement of the proposition now reads: “To correct a comet’s trajectory
that has been found.”
When Newton wrote up his results for Halley (in the tract De Motu) and
proved (in the equivalent of book 1, prop. 11) that an elliptical orbit implies an
inverse-square central force, he included in his text the joyous conclusion:
“Therefore the major planets revolve in ellipses having a focus in the center of the sun;
and the radii to the sun describe areas proportional to the times, exactly [“omnino”]
as Kepler supposed.”27 But after some reflection, Newton recognized that he had
been considering a rather artificial situation in which a body moves about a mathematical
center of force. In nature, bodies move about other bodies, not about
mathematical points. When he began to consider such a two-body system, he came
to recognize that in this case each body must act on the other. If this is true for
one such pair of bodies, as for the sun-earth system, then it must be so in all such
systems. In this way he concluded that the sun (like all the planets) is a body on
which the force acts and also a body that gives rise to the force. It follows at once
that each planet must exert a perturbing force on every other planet in the solar
system. The consequence must be, as Newton recognized almost at once, that “the
displacement of the sun from the center of gravity” may have the effect that “the
centripetal force does not always tend to” an “immobile center” and that “the
planets neither revolve exactly in ellipses nor revolve twice in the same orbit.” In other
words, “Each time a planet revolves it traces a fresh orbit, as happens also with
the motion of the moon, and each orbit is dependent upon the combined motions
of all the planets, not to mention their actions upon each other.”28 This led him
to the melancholy conclusion: “Unless I am much mistaken, it would exceed the
force of human wit to consider so many causes of motion at the same time, and to
define the motions by exact laws which would allow of any easy calculation.”
We don’t know exactly how Newton reached this conclusion, but a major
factor may have been the recognition of the need to take account of the third
law, that to every action there must be an equal and opposite reaction. Yet, in the
texts of De Motu, the third law does not appear explicitly among the “laws” or
“hypotheses.” We do have good evidence, however, that Newton was aware of the
third law long before writing De Motu.29 In any event, the recognition that there
must be interplanetary perturbations was clearly an essential step on the road to
universal gravity and the Principia.30
In reviewing this pre-Principia development of Newton’s dynamics, we should
take note that by and large, Newton has been considering exclusively the motion
of a particle, of unit mass. Indeed, a careful reading of the Principia will show
that even though mass is the subject of the first definition at the beginning of
the Principia, mass is not a primary variable in Newton’s mode of developing
his dynamics in book 1. In fact, most of book 1 deals exclusively with particles.
Physical bodies with significant dimensions or shapes do not appear until sec. 12,
“The attractive forces of spherical bodies.”
Newton’s concept of mass is one of the most original concepts of the Principia.
Newton began thinking about mass some years before Halley’s visit. Yet, in a
series of definitions which he wrote out some time after De Motu and before
composing the Principia, mass does not appear as a primary entry. We do not
have documents that allow us to trace the development of Newton’s concept of
mass with any precision. We know, however, that two events must have been
important, even though we cannot tell whether they initiated Newton’s thinking
about mass or reinforced ideas that were being developed by Newton. One of
these was the report of the Richer expedition, with evidence that indicated that
weight is a variable quantity, depending on the terrestrial latitude. Hence weight is
a “local” property and cannot be used as a universal measure of a body’s quantity
of matter. Another was Newton’s study of the comet of 1680. After he recognized
that the comet turned around the sun and after he concluded that the sun’s action
on the comet cannot be magnetic, he came to believe that Jupiter must also exert
an influence on the comet. Clearly, this influence must derive from the matter in
Jupiter, Jupiter acting on the comet just as it does on its satellites.
Once Newton had concluded that planets are centers of force because of their
matter or mass, he sought some kind of empirical confirmation of so bold a
concept. Since Jupiter is by far the most massive of all the planets, it was obvious
that evidence of a planetary force would be most manifest in relation to the
action of Jupiter on a neighboring planet. In happened that in 1684/85 the orbital
motions of Jupiter and Saturn were bringing these two planets to conjunction. If
Newton’s conclusion were correct, then the interactions of these two giant planets
should show the observable effects of an interplanetary force. Newton wrote to the
astronomer John Flamsteed at the Royal Observatory at Greenwich for
information on this point. Flamsteed reported that Saturn’s orbital speed in the vicinity of
Jupiter did not exactly follow the expected path, but he could not detect the kind
of effect or perturbation that Newton had predicted.31 As we shall see, the effect
predicted by Newton does occur, but its magnitude is so tiny that Flamsteed could
never have observed it. Newton needed other evidence to establish the validity of
his force of universal gravity.
Newton’s discovery of interplanetary forces as a special instance of universal
gravity enables us to specify two primary goals of the Principia. The first is to
show the conditions under which Kepler’s laws of planetary motion are exactly or
accurately true; the second is to explore how these laws must be modified in the
world of observed nature by perturbations, to show the effects of perturbations on
the motions of planets and their moons.32
It is well known that after the Principia was presented to the Royal Society,
Hooke claimed that he should be given credit for having suggested to Newton the
idea of universal gravity. We have seen that Hooke did suggest to Newton that
the sun exerts an inverse-square force on the planets, but Newton insisted that
he didn’t need Hooke to suggest to him that there is an inverse-square relation.
Furthermore, Newton said that this was but one of Hooke’s guesses. Newton again
and again asserted that Hooke didn’t know enough mathematics to substantiate
his guess, and he was right. As the mathematical astronomer Alexis Clairaut said
of Hooke’s claim, a generation later, it serves “to show what a distance there is
between a truth that is glimpsed and a truth that is demonstrated.”33
In explaining his position with respect to Hooke’s guess, Newton compared
his own work with that of Hooke and Kepler. Newton evidently believed that he
himself had “as great a right” to the inverse-square law “as to the ellipsis.” For,
just “as Kepler knew the orb to be not circular but oval, and guessed it to be
elliptical, so Mr. Hooke, without knowing what I have found out since his letters
to me,”34 knew only “that the proportion was duplicata quam proxime at great
distances from the centre,” and “guessed it to be so accurately, and guessed amiss
in extending that proportion down to the very centre.” But, unlike Hooke, “Kepler
guessed right at the ellipsis,” so that “Mr. Hooke found less of the proportion than
Kepler of the ellipsis.”35 Newton believed that he himself deserved credit for the
law of elliptical orbits, as well as the law of the inverse square, on the grounds that
he had proved both in their generality.36 In the Principia (e.g., in the “Phenomena”
in book 3), Newton gave Kepler credit only for the third or harmonic law. At the
time that Newton was writing his Principia, there were alternatives to the area law
that were in use in making tables of planetary motion. Newton proposed using
the eclipses of Jupiter’s satellites (and later of those of Saturn) to show that this
law holds to a high degree. But the law of elliptical orbits was of a different sort
because there was no observational evidence that would distinguish between an
ellipse and other ovals. Thus there may have been very different reasons for not
giving Kepler credit for these two laws.
At one point during the exchange of letters with Halley on Hooke’s claims
to recognition, Newton—in a fit of pique—threatened to withdraw book 3
altogether.37 We do not know how serious this threat was, but Halley was able
to explain matters and to calm Newton’s rage. Halley deserves much praise for
his services as midwife to Newton’s brainchild. Not only was he responsible for
goading Newton into writing up his preliminary results; he encouraged Newton
to produce the Principia. At an early stage of composition of the Principia, as I
discovered while preparing the Latin edition with variant readings, Halley even
helped Newton by making suggestive comments on an early draft of book 1, the
manuscript of which no longer exists.38
Although publication of the Principia was sponsored by the Royal Society, there
were no funds available for the costs of printing, and so Halley had to assume those
expenses.39 Additionally, he edited the book for the printer, saw to the making of
the woodcuts of the diagrams, and read the proofs. He wrote a flattering ode to
Newton that introduces the Principia in all three editions,40 and he also wrote a
book review that was published in the Royal Society’s Philosophical Transactions.41
Revisions and Later Editions
Within a decade of publication of the Principia, Newton was busy with a
number of radical revisions, including an extensive restructuring of the opening
sections.42 He planned to remove secs. 4 and 5, which are purely geometrical and
not necessary to the rest of the text, and to publish them separately.43 He also
developed plans to include a mathematical supplement on his methods of the calculus,
his treatise De Quadratura. Many of the proposed revisions and restructurings of the
1690s are recorded in Newton’s manuscripts; others were reported in some detail
by David Gregory.44 When Newton began to produce a second edition, however,
with the aid of Roger Cotes, the revisions were of a quite different sort. Some
of the major or most interesting alterations are given in the notes to the present
translation. The rest are to be found in the apparatus criticus of our Latin edition
of the Principia with variant readings.45
There were a number of truly major emendations that appeared in the second
edition, some of which involved a complete replacement of the original text. One
of these was the wholly new proof of book 2, prop. 10, a last-minute alteration in
response to a criticism made by Johann Bernoulli.46 Another occurred in book 2,
sec. 7, on the motion of fluids and the resistance encountered by projectiles, where
most of the propositions and their proofs are entirely different in the second edition
from those of the first edition. That is, the whole set of props. 34–40 of the first
edition were cast out and replaced.47 This complete revision of sec. 7 made it more
appropriate to remove to the end of sec. 6 the General Scholium on pendulum
experiments which originally had been at the end of sec. 7. This was a more
thorough revision of the text than occurred in any other part of the Principia.
Another significant novelty of the second edition was the introduction of a
conclusion to the great work, the celebrated General Scholium that appears at the
conclusion of book 3. The original edition ended rather abruptly with a discussion
of the orbits of comets, a topic making up about a third of book 3. Newton
had at first essayed a conclusion, but later changed his mind. His intentions were
revealed in 1962 by A. Rupert Hall and Marie Boas Hall, who published the
original drafts. In these texts, Newton shows that he intended to conclude the
Principia with a discussion of the forces between the particles of matter, but then
thought better of introducing so controversial a topic. While preparing the second
edition, Newton thought once again of an essay on “the attraction of the small
particles of bodies,” but on “second thought” he chose “rather to add but one short
Paragraph about that part of Philosophy.”48 The conclusion he finally produced
is the celebrated General Scholium, with its oft-quoted slogan “Hypotheses non
fingo.” This General Scholium ends with a paragraph about a “spirit” which has
certain physical properties, but whose laws have not as yet been determined by
experiment. Again thanks to the researches of A. Rupert Hall and Marie Boas
Hall, we now know that while composing this paragraph, Newton was thinking
about the new phenomena of electricity.49
Another change that occurs in the second edition is in the beginning of book 3.
In the first edition, book 3 opened with a preliminary set of Hypotheses.50 Perhaps
in reply to the criticism in the Journal des Sçavans,51 Newton now renamed the
“hypotheses” and divided them into several classes. Some became Regulae
Philosophandi, or “Rules for Natural Philosophy,” with a new rule (no. 3). Others became
“Phenomena,” with new numerical data. Yet another was transferred to a later
place in book 3, where it became “hypothesis 1.”
Newton also made a slight modification in the scholium following lem. 2
(book 2, sec. 2), in reference to Leibniz’s method of the calculus. He had originally
written that Leibniz’s method “hardly differed from mine except in the forms
of words and notations.” In the second edition Newton altered this statement
by adding that there was another difference between the two methods, namely, in
“the generation of quantities.” This scholium and its successive alterations attracted
attention because of the controversy over priority in the invention of the calculus.
In the third edition, Newton eliminated any direct reference to Leibniz.
Critical readers of the Principia paid close attention to the alteration in the
scholium following book 3, prop. 35. In the second edition, the original short
text was replaced by a long discussion of Newton’s attempts to apply the theory
of gravity to some inequalities of the moon’s motion.52 Much of the text of this
scholium had been published separately by David Gregory.53
Many of Newton’s plans for the actual revisions of the first edition, in order to
produce a second edition, were entered in two personal copies of the Principia. One
of these was specially bound and interleaved. Once the second edition had been
published, Newton again prepared an interleaved copy and kept track of proposed
alterations or emendations in his interleaved copy and in an annotated copy. These
four special copies of the Principia have been preserved among Newton’s books,
and their contents have been noted in our Latin edition with variant readings.54
Soon after the appearance of the second edition, Newton began planning for
yet another revision. The preface which he wrote for this planned edition of the
late 1710s is of great interest in that it tells us in Newton’s own words about some
of the features of the Principia he believed to be most significant. It is printed below
in §3.2. Newton at this time once again planned to have a treatise on the calculus
published together with the Principia. In the end he abandoned this effort. Later
on, when he was in his eighties, he finally decided to produce a new edition. He
chose as editor Dr. Henry Pemberton, a medical doctor and authority on pharmacy
and an amateur mathematician.
The revisions in the third edition were not quite as extensive as those in the
second edition.55 A new rule 4 was added on the subject of induction, and there
were other alterations, some of which may be found in the notes to the present
translation. An important change was made in the “Leibniz Scholium” in book 2,
sec. 2. The old scholium was replaced by a wholly different one. Newton now
boldly asserted his own claims to be the primary inventor of the calculus, referring
to some correspondence to prove the point.56 Even though Leibniz had been dead
for almost a decade, Newton still pursued his rival with dogged obstinacy. Another
innovation in the third edition appeared in book 3, where Newton inserted
(following prop. 33) two propositions by John Machin, astronomy professor at Gresham
College, whose academic title would later lead to the invention of a fictitious
scientist in the Motte-Cajori edition.57
By the time of the third edition, Newton seems to have abandoned his earlier
attempts to explain the action of gravity by reference to electrical phenomena and
had come rather to hope that an explanation might be found in the actions of
an “aethereal medium” of varying density.58 In his personal copy of the Principia,
in which he recorded his proposed emendations and revisions, he at first had
entered an addition to specify that the “spirit” to which he had referred in the
final paragraph of the General Scholium was “electric and elastic.”59 Later on, he
apparently decided that since he no longer believed in the supreme importance
of the electrical theory, he would cancel the whole paragraph. Accordingly, he
drew a line through the text, indicating that this paragraph should be omitted.
It is one of the oddities of history that Andrew Motte should have learned of
Newton’s planned insertion of the modifier “electricus et elasticus” but not of
Newton’s proposed elimination of the paragraph. Without comment, Motte entered
“electric and elastic” into his English version of 1729. These words were in due
course preserved in the Motte-Cajori version and have been quoted in the
English-speaking world ever since.
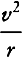 rule for the
force in uniform circular motion (at speed v along a circle of radius r), a discovery
usually attributed to Christiaan Huygens, who formally announced it to the world
in his Horologium Oscillatorium of 1673.10 It requires only the minimum skill in
algebraic manipulation to combine the
rule for the
force in uniform circular motion (at speed v along a circle of radius r), a discovery
usually attributed to Christiaan Huygens, who formally announced it to the world
in his Horologium Oscillatorium of 1673.10 It requires only the minimum skill in
algebraic manipulation to combine the 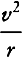 rule with Kepler’s third law in order
to determine that in a system of bodies in uniform circular motion the force is
proportional to
rule with Kepler’s third law in order
to determine that in a system of bodies in uniform circular motion the force is
proportional to  or is inversely proportional to the square of the distance. Of
course, this computation does not of itself specify anything about the nature of the
force, whether it is a centripetal or a centrifugal force or whether it is a force in
the sense of the later Newtonian dynamics or merely a Cartesian “conatus,” or
endeavor. In a manuscript note Newton later claimed that at an early date, in the
1660s, he had actually applied the
or is inversely proportional to the square of the distance. Of
course, this computation does not of itself specify anything about the nature of the
force, whether it is a centripetal or a centrifugal force or whether it is a force in
the sense of the later Newtonian dynamics or merely a Cartesian “conatus,” or
endeavor. In a manuscript note Newton later claimed that at an early date, in the
1660s, he had actually applied the 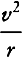 rule to the moon’s motion, much as he does
later on in book 3, prop. 4, of the Principia, in order to confirm his idea of the
force of “gravity extending to the Moon.”11 In this way he could counter Hooke’s
allegation that he had learned the concept of an inverse-square force of gravity
from Hooke.
rule to the moon’s motion, much as he does
later on in book 3, prop. 4, of the Principia, in order to confirm his idea of the
force of “gravity extending to the Moon.”11 In this way he could counter Hooke’s
allegation that he had learned the concept of an inverse-square force of gravity
from Hooke.