AXIOMS, OR THE LAWS OF MOTION

Law 1 Every body perseveres in its state of being at rest or of moving ^auniformly straight forward,^a except insofar as ^bit^b is compelled to change ^cits^c state by forces impressed.

Projectiles persevere in their motions, except insofar as they are retarded by the resistance of the air and are impelled downward by the force of gravity. A spinning hoop,^d which has parts that by their cohesion continually draw one another back from rectilinear motions, does not cease to rotate, except insofar as it is retarded by the air. And larger bodies—planets and comets—preserve for a longer time both their progressive and their circular motions, which take place in spaces having less resistance.

Law 2 A change in motion is proportional to the motive force impressed and takes place along the straight line in which that force is impressed.

If some force generates any motion, twice the force will generate twice the motion, and three times the force will generate three times the motion, whether the force is impressed all at once or successively by degrees. And if the body was previously moving, the new motion (since motion is always in the same direction as the generative force) is added to the original motion if that motion was in the same direction or is subtracted from the original motion if it was in the opposite direction or, if it was in an oblique direction, is combined obliquely and compounded with it according to the directions of both motions.

Law 3 To any action there is always an opposite and equal reaction; in other words, the actions of two bodies upon each other are always equal and always opposite in direction.

Whatever presses or draws something else is pressed or drawn just as much by it. If anyone presses a stone with a finger, the finger is also pressed by the stone. If a horse draws a stone tied to a rope, the horse will (so to speak) also be drawn back equally toward the stone, for the rope, stretched out at both ends, will urge the horse toward the stone and the stone toward the horse by one and the same endeavor to go slack and will impede the forward motion of the one as much as it promotes the forward motion of the other. If some body impinging upon another body changes the motion of that body in any way by its own force, then, by the force of the other body (because of the equality of their mutual pressure), it also will in turn undergo the same change in its own motion in the opposite direction. By means of these actions, equal changes occur in the motions, not in the velocities—that is, of course, if the bodies are not impeded by anything else.^a For the changes in velocities that likewise occur in opposite directions are inversely proportional to the bodies because the motions are changed equally. This law is valid also for attractions, as will be proved in the next scholium.

Corollary 1 A body acted on by [two] forces acting jointly describes the diagonal of a parallelogram in the same time in which it would describe the sides if the forces were acting separately.

Let a body in a given time, by force M 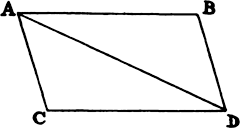alone impressed in A, be carried with uniform motion from A to B, and, by force N alone impressed in the same place, be carried from A to C; then complete the parallelogram ABDC, and by both forces the body will be carried in the same time along the diagonal from A to D. For, since force N acts along the line AC parallel to BD, this force, by law 2, will make no change at all in the velocity toward the line BD which is generated by the other force. Therefore, the body will reach the line BD in the same time whether force N is impressed or not, and so at the end of that time will be found somewhere on the line BD. By the same argument, at the end of the same time it will be found somewhere on the line CD, and accordingly it is necessarily found at the intersection D of both lines. And, by law 1, it will go with [uniform] rectilinear motion from A to D.

Corollary 2 And hence the composition of a direct force AD out of any oblique forces AB and BD is evident, and conversely the resolution of any direct force AD into any oblique forces AB and BD. And this kind of composition and resolution is indeed abundantly confirmed from mechanics.

For example, let OM and ON be unequal spokes going out from the 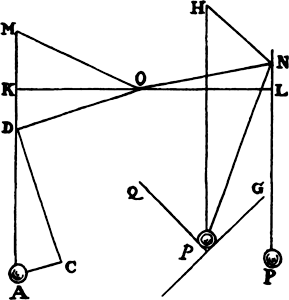center O of any wheel, and let the spokes support the weights A and P by means of the cords MA and NP; it is required to find the forces of the weights to move the wheel. Draw the straight line KOL through the center O, so as to meet the cords perpendicularly at K and L; and with center O and radius OL, which is the greater of OK and OL, describe a circle meeting the cord MA at D; and draw the straight line OD, and let AC be drawn parallel to it and DC perpendicular to it. Since it makes no difference whether points K, L, and D of the cords are attached or not attached to the plane of the wheel, the weights will have the same effect whether they are suspended from the points K and L or from D and L. And if now the total force of the weight A is represented by line AD, it will be resolved into forces [i.e., components] AC and CD, of which AC, drawing spoke OD directly from the center, has no effect in moving the wheel, while the other force DC, drawing spoke DO perpendicularly, has the same effect as if it were drawing spoke OL (equal to OD) perpendicularly; that is, it has the same effect as the weight P, provided that the weight P is to the weight A as the force DC is to the force DA; that is (because triangles ADC and DOK are similar), as OK to OD or OL. Therefore, the weights A and P, which are inversely as the spokes OK and OL (which are in a straight line), will be equipollent and thus will stand in equilibrium, which is a very well known property of the balance, the lever, and the wheel and axle. But if either weight is greater than in this ratio, its force to move the wheel will be so much the greater.

But if the weight p, equal to the weight P, is partly suspended by the cord Np and partly lies on the oblique plane pG, draw pH perpendicular to the plane of the horizon and NH perpendicular to the plane pG; then if the force of the weight p tending downward is represented by the line pH, it can be resolved into the forces [i.e., components] pN and HN. If there were some plane pQ perpendicular to the cord pN and cutting the other plane pG in a line parallel to the horizon, and the weight p were only lying on these planes pQ and pG, the weight p would press these planes perpendicularly with the forces pN and HN—plane pQ, that is, with force pN and plane pG with force HN. Therefore, if the plane pQ is removed, so that the weight stretches the cord, then—since the cord, in sustaining the weight, now takes the place of the plane which has been removed—the cord will be stretched by the same force pN with which the plane was formerly pressed. Thus the tension of this oblique cord will be to the tension of the other, and perpendicular, cord PN as pN to pH. Therefore, if the weight p is to the weight A in a ratio that is compounded of the inverse ratio of the least distances of their respective cords pN and AM from the center of the wheel and the direct ratio of pH to pN, the weights will have the same power to move the wheel and so will sustain each other, as anyone can test.

Now, the weight p, lying on those two oblique planes, has the role of a wedge between the inner surfaces of a body that has been split open; and hence the forces of a wedge and hammer can be determined, because the force with which the weight p presses the plane pQ is to the force with which weight p is impelled along the line pH toward the planes, whether by its own gravity or by the blow of a hammer, as pN is to pH, and because the force with which p presses plane pQ is to the force by which it presses the other plane pG as pN to NH. Furthermore, the force of a screw can also be determined by a similar resolution of forces, inasmuch as it is a wedge impelled by a lever. Therefore, this corollary can be used very extensively, and the variety of its applications clearly shows its truth, since the whole of mechanics—demonstrated in different ways by those who have written on this subject—depends on what has just now been said. For from this are easily derived the forces of machines, which are generally composed of wheels, drums, pulleys, levers, stretched strings, and weights, ascending directly or obliquely, and the other mechanical powers, as well as the forces of tendons to move the bones of animals.

Corollary 3 The quantity of motion, which is determined by adding the motions made in one direction and subtracting the motions made in the opposite direction, is not changed by the action of bodies on one another.

For an action and the reaction opposite to it are equal by law 3, and thus by law 2 the changes which they produce in motions are equal and in opposite directions. Therefore, if motions are in the same direction, whatever is added to the motion of the first body [lit. the fleeing body] will be subtracted from the motion of the second body [lit. the pursuing body] in such a way that the sum remains the same as before. But if the bodies meet head-on, the quantity subtracted from each of the motions will be the same, and thus the difference of the motions made in opposite directions will remain the same.

For example, suppose a spherical body A is three times as large as a spherical body B and has two parts of velocity, and let B follow A in the same straight line with ten parts of velocity; then the motion of A is to the motion of B as six to ten. Suppose that their motions are of six parts and ten parts respectively; the sum will be sixteen parts. When the bodies collide, therefore, if body A gains three or four or five parts of motion, body B will lose just as many parts of motion and thus after reflection body A will continue with nine or ten or eleven parts of motion and B with seven or six or five parts of motion, the sum being always, as originally, sixteen parts of motion. Suppose body A gains nine or ten or eleven or twelve parts of motion and so moves forward with fifteen or sixteen or seventeen or eighteen parts of motion after meeting body B; then body B, by losing as many parts of motion as A gains, will either move forward with one part, having lost nine parts of motion, or will be at rest, having lost its forward motion of ten parts, or will move backward with one part of motion, having lost its motion and (if I may say so) one part more, or will move backward with two parts of motion because a forward motion of twelve parts has been subtracted. And thus the sums, 15 + 1 or 16 + 0, of the motions in the same direction and the differences, 17 − 1 and 18 − 2, of the motions in opposite directions will always be sixteen parts of motion, just as before the bodies met and were reflected. And since the motions with which the bodies will continue to move after reflection are known, the velocity of each will be found, on the supposition that it is to the velocity before reflection as the motion after reflection is to the motion before reflection. For example, in the last case, where the motion of body A was six parts before reflection and eighteen parts afterward, and its velocity was two parts before reflection, its velocity will be found to be six parts after reflection on the basis of the following statement: as six parts of motion before reflection is to eighteen parts of motion afterward, so two parts of velocity before reflection is to six parts of velocity afterward.

But if bodies that either are not spherical or are moving in different straight lines strike against each other obliquely and it is required to find their motions after reflection, the position of the plane by which the colliding bodies are touched at the point of collision must be determined; then (by corol. 2) the motion of each body must be resolved into two motions, one perpendicular to this plane and the other parallel to it. Because the bodies act upon each other along a line perpendicular to this plane, the parallel motions [i.e., components] must be kept the same after reflection; and equal changes in opposite directions must be attributed to the perpendicular motions in such a way that the sum of the motions in the same direction and the difference of the motions in opposite directions remain the same as before the bodies came together. The circular motions of bodies about their own centers also generally arise from reflections of this sort. But I do not consider such cases in what follows, and it would be too tedious to demonstrate everything relating to this subject.

Corollary 4 The common center of gravity of two or more bodies does not change its state whether of motion or of rest as a result of the actions of the bodies upon one another; and therefore the common center of gravity of all bodies acting upon one another (excluding external actions and impediments) either is at rest or moves uniformly straight forward.

For if two points move forward with uniform motion in straight lines, and the distance between them is divided in a given ratio, the dividing point either is at rest or moves forward uniformly in a straight line. This is demonstrated below in lem. 23 and its corollary for the case in which the motions of the points take place in the same plane, and it can be demonstrated by the same reasoning for the case in which those motions do not take place in the same plane. Therefore, if any number of bodies move uniformly in straight lines, the common center of gravity of any two either is at rest or moves forward uniformly in a straight line, because any line joining these bodies through their centers—which move forward uniformly in straight lines—is divided by this common center in a given ratio. Similarly, the common center of gravity of these two bodies and any third body either is at rest or moves forward uniformly in a straight line, because the distance between the common center of the two bodies and the center of the third body is divided in a given ratio by the common center of the three. In the same way, the common center of these three and of any fourth body either is at rest or moves forward uniformly in a straight line, because that common center divides in a given ratio the distance between the common center of the three and the center of the fourth body, and so on without end. Therefore, in a system of bodies in which the bodies are entirely free of actions upon one another and of all other actions impressed upon them externally, and in which each body accordingly moves uniformly in its individual straight line, the common center of gravity of them all either is at rest or moves uniformly straight forward.

Further, in a system of two bodies acting on each other, since the distances of their centers from the common center of gravity are inversely as the bodies, the relative motions of these bodies, whether of approaching that center or of receding from it, will be equal. Accordingly, as a result of equal changes in opposite directions in the motions of these bodies, and consequently as a result of the actions of the bodies on each other, that center is neither accelerated nor retarded nor does it undergo any change in its state of motion or of rest. In a system of several bodies, the common center of gravity of any two acting upon each other does not in any way change its state as a result of that action, and the common center of gravity of the rest of the bodies (with which that action has nothing to do) is not affected by that action; the distance between these two centers is divided by the common center of gravity of all the bodies into parts inversely proportional to the total sums of the bodies whose centers they are, and (since those two centers maintain their state of moving or of being at rest) the common center of all maintains its state also—for all these reasons it is obvious that this common center of all never changes its state with respect to motion and rest as a result of the actions of two bodies upon each other. Moreover, in such a system all the actions of bodies upon one another either occur between two bodies or are compounded of such actions between two bodies and therefore never introduce any change in the state of motion or of rest of the common center of all. Thus, since that center either is at rest or moves forward uniformly in some straight line, when the bodies do not act upon one another, that center will, notwithstanding the actions of the bodies upon one another, continue either to be always at rest or to move always uniformly straight forward, unless it is driven from this state by forces impressed on the system from outside. Therefore, the law is the same for a system of several bodies as for a single body with respect to perseverance in a state of motion or of rest. For the progressive motion, whether of a single body or of a system of bodies, should always be reckoned by the motion of the center of gravity.

Corollary 5 When bodies are enclosed in a given space, their motions in relation to one another are the same whether the space is at rest or whether it is moving uniformly straight forward without circular motion.

For in either case the differences of the motions tending in the same direction and the sums of those tending in opposite directions are the same at the beginning (by hypothesis), and from these sums or differences there arise the collisions and impulses [lit. impetuses] with which the bodies strike one another. Therefore, by law 2, the effects of the collisions will be equal in both cases, and thus the motions with respect to one another in the one case will remain equal to the motions with respect to one another in the other case. This is proved clearly by experience: on a ship, all the motions are the same with respect to one another whether the ship is at rest or is moving uniformly straight forward.

Corollary 6 If bodies are moving in any way whatsoever with respect to one another and are urged by equal accelerative forces along parallel lines, they will all continue to move with respect to one another in the same way as they would if they were not acted on by those forces.

For those forces, by acting equally (in proportion to the quantities of the bodies to be moved) and along parallel lines, will (by law 2) move all the bodies equally (with respect to velocity), and so will never change their positions and motions with respect to one another.

Scholium The principles I have set forth are accepted by mathematicians and confirmed by experiments of many kinds. By means of the first two laws and the first two corollaries Galileo found that the descent of heavy bodies is in the squared ratio of the time and that the motion of projectiles occurs in a parabola, as experiment confirms, except insofar as these motions are somewhat retarded by the resistance of the air. ^aWhen a body falls, uniform gravity, by acting equally in individual equal particles of time, impresses equal forces upon that body and generates equal velocities; and in the total time it impresses a total force and generates a total velocity proportional to the time. And the spaces described in proportional times are as the velocities and the times jointly, that is, in the squared ratio of the times. And when a body is projected upward, uniform gravity impresses forces and takes away velocities proportional to the times; and the times of ascending to the greatest heights are as the velocities to be taken away, and these heights are as the velocities and the times jointly, or as the squares of the velocities. And when a body is projected along any straight line, its motion arising from the projection is compounded with the motion arising from gravity.

For example, let body A by the motion of projection alone describe the 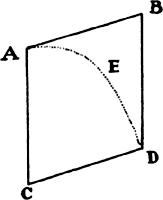straight line AB in a given time, and by the motion of falling alone describe the vertical distance AC in the same time; then complete the parallelogram ABDC, and by the compounded motion the body will be found in place D at the end of the time; and the curved line AED which the body will describe will be a parabola which the straight line AB touches at A and whose ordinate BD is as AB².^a

What has been demonstrated concerning the times of oscillating pendulums depends on the same first two laws and first two corollaries, and this is supported by daily experience with clocks. From the same laws and corollaries and law 3, Sir Christopher Wren, Dr. John Wallis, and Mr. Christiaan Huygens, easily the foremost geometers of the previous generation, independently found the rules of the collisions and reflections of hard bodies, and communicated them to the Royal Society at nearly the same time, entirely agreeing with one another (as to these rules); and Wallis was indeed the first to publish what had been found, followed by Wren and Huygens. But Wren additionally proved the truth of these rules before the Royal Society by means of an experiment with pendulums, which the eminent Mariotte soon after thought worthy to be made the subject of a whole book.

However, if this experiment is to agree precisely with the theories, 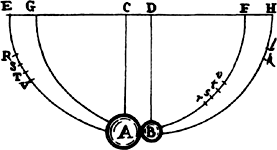account must be taken of both the resistance of the air and the elastic force of the colliding bodies. Let the spherical bodies A and B be suspended from centers C and D by parallel and equal cords AC and BD. With these centers and with those distances as radii describe semicircles EAF and GBH bisected by radii CA and DB. Take away body B, and let body A be brought to any point R of the arc EAF and be let go from there, and let it return after one oscillation to point V. RV is the retardation arising from the resistance of the air. Let ST be a fourth of RV and be located in the middle so that RS and TV are equal and RS is to ST as 3 to 2. Then ST will closely approximate the retardation in the descent from S to A. Restore body B to its original place. Let body A fall from point S, and its velocity at the place of reflection A, without sensible error, will be as great as if it had fallen in a vacuum from place T. Therefore let this velocity be represented by the chord of the arc TA. For it is a proposition very well known to geometers that the velocity of a pendulum in its lowest point is as the chord of the arc that it has described in falling. After reflection let body A arrive at place s, and body B at place k. Take away body B and find place v such that if body A is let go from this place and after one oscillation returns to place r, st will be a fourth of rv and be located in the middle, so that rs and tv are equal; and let the chord of the arc tA represent the velocity that body A had in place A immediately after reflection. For t will be that true and correct place to which body A must have ascended if there had been no resistance of the air. By a similar method the place k, to which body B ascends, will have to be corrected, and the place l, to which that body must have ascended in a vacuum, will have to be found. In this manner it is possible to make all our experiments, just as if we were in a vacuum. Finally body A will have to be multiplied (so to speak) by the chord of the arc TA, which represents its velocity, in order to get its motion in place A immediately before reflection, and then by the chord of the arc tA in order to get its motion in place A immediately after reflection. And thus body B will have to be multiplied by the chord of the arc Bl in order to get its motion immediately after reflection. And by a similar method, when two bodies are let go simultaneously from different places, the motions of both will have to be found before as well as after reflection, and then finally the motions will have to be compared with each other in order to determine the effects of the reflection.

On making a test in this way with ten-foot pendulums, using unequal as well as equal bodies, and making the bodies come together from very large distances apart, say of eight or twelve or sixteen feet, I always found—within an error of less than three inches in the measurements—that when the bodies met each other directly, the changes of motions made in the bodies in opposite directions were equal, and consequently that the action and reaction were always equal. For example, if body A collided with body B, which was at rest, with nine parts of motion and, losing seven parts, proceeded after reflection with two, body B rebounded with those seven parts. If the bodies met head-on, A with twelve parts of motion and B with six, and A rebounded with two, B rebounded with eight, fourteen parts being subtracted from each. Subtract twelve parts from the motion of A and nothing will remain; subtract another two parts, and a motion of two parts in the opposite direction will be produced; and so, subtracting fourteen parts from the six parts of the motion of body B, eight parts will be produced in the opposite direction. But if the bodies moved in the same direction, A more quickly with fourteen parts and B more slowly with five parts, and after reflection A moved with five parts, then B moved with fourteen, nine parts having been transferred from A to B. And so in all other cases. As a result of the meeting and collision of bodies, the quantity of motion—determined by adding the motions in the same direction and subtracting the motions in opposite directions—was never changed. I would attribute the error of an inch or two in the measurements to the difficulty of doing everything with sufficient accuracy. It was difficult both to release the pendulums simultaneously in such a way that the bodies would impinge upon each other in the lowest place AB, and to note the places s and k to which the bodies ascended after colliding. But also, with respect to the pendulous bodies themselves, errors were introduced by the unequal density of the parts and by irregularities of texture arising from other causes.

Further, lest anyone object that the rule which this experiment was designed to prove presupposes that bodies are either absolutely hard or at least perfectly elastic and thus of a kind which do not occur ^bnaturally,^b I add that the experiments just described work equally well with soft bodies and with hard ones, since surely they do not in any way depend on the condition of hardness. For if this rule is to be tested in bodies that are not perfectly hard, it will only be necessary to decrease the reflection in a fixed proportion to the quantity of elastic force. In the theory of Wren and Huygens, absolutely hard bodies rebound from each other with the velocity with which they have collided. This will be affirmed with more certainty of perfectly elastic bodies. In imperfectly elastic bodies the velocity of rebounding must be decreased together with the elastic force, because that force (except when the parts of the bodies are damaged as a result of collision, or experience some sort of extension such as would be caused by a hammer blow) is fixed and determinate (as far as I can tell) and makes the bodies rebound from each other with a relative velocity that is in a given ratio to the relative velocity with which they collide. I have tested this as follows with tightly wound balls of wool strongly compressed. First, releasing the pendulums and measuring their reflection, I found the quantity of their elastic force; then from this force I determined what the reflections would be in other cases of their collision, and the experiments which were made agreed with the computations. The balls always rebounded from each other with a relative velocity that was to the relative velocity of their colliding as 5 to 9, more or less. Steel balls rebounded with nearly the same velocity and cork balls with a slightly smaller velocity, while with glass balls the proportion was roughly 15 to 16. And in this manner the third law of motion—insofar as it relates to impacts and reflections—is proved by this theory, which plainly agrees with experiments.

I demonstrate the third law of motion for attractions briefly as follows. Suppose that between any two bodies A and B that attract each other any obstacle is interposed so as to impede their coming together. If one body A is more attracted toward the other body B than that other body B is attracted toward the first body A, then the obstacle will be more strongly pressed by body A than by body B and accordingly will not remain in equilibrium. The stronger pressure will prevail and will make the system of the two bodies and the obstacle move straight forward in the direction from A toward B and, in empty space, go on indefinitely with a motion that is always accelerated, which is absurd and contrary to the first law of motion. For according to the first law, the system will have to persevere in its state of resting or of moving uniformly straight forward, and accordingly the bodies will urge the obstacle equally and on that account will be equally attracted to each other. I have tested this with a lodestone and iron. If these are placed in separate vessels that touch each other and float side by side in still water, neither one will drive the other forward, but because of the equality of the attraction in both directions they will sustain their mutual endeavors toward each other, and at last, having attained equilibrium, they will be at rest.

^cIn the same way gravity is mutual between the earth and its parts. Let the earth FI be cut by any plane EG into two parts EGF and EGI; then their 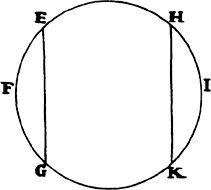weights toward each other will be equal. For if the greater part EGI is cut into two parts EGKH and HKI by another plane HK parallel to the first plane EG, in such a way that HKI is equal to the part EFG that has been cut off earlier, it is manifest that the middle part EGKH will not preponderate toward either of the outer parts but will, so to speak, be suspended in equilibrium between both and will be at rest. Moreover, the outer part HKI will press upon the middle part with all its weight and will urge it toward the other outer part EGF, and therefore the force by which EGI, the sum of the parts HKI and EGKH, tends toward the third part EGF is equal to the weight of the part HKI, that is, equal to the weight of the third part EGF. And therefore the weights of the two parts EGI and EGF toward each other are equal, as I set out to demonstrate. And if these weights were not equal, the whole earth, floating in an aether free of resistance, would yield to the greater weight and in receding from it would go off indefinitely.^c

As bodies are equipollent in collisions and reflections if their velocities are inversely as their inherent forces [i.e., forces of inertia], so in the motions of machines those agents [i.e., acting bodies] whose velocities (reckoned in the direction of their forces) are inversely as their inherent forces are equipollent and sustain one another by their contrary endeavors. Thus weights are equipollent in moving the arms of a balance if during oscillation of the balance they are inversely as their velocities upward and downward; that is, weights which move straight up and down are equipollent if they are inversely as the distances between the axis of the balance and the points from which they are suspended; but if such weights are interfered with by oblique planes or other obstacles that are introduced and thus ascend or descend obliquely, they are equipollent if they are inversely as the ascents and descents insofar as these are reckoned with respect to a perpendicular, and this is so because the direction of gravity is downward. Similarly, in a pulley or combination of pulleys, the weight will be sustained by the force of the hand pulling the rope vertically, which is to the weight (ascending either straight up or obliquely) as the velocity of the perpendicular ascent to the velocity of the hand pulling the rope. In clocks and similar devices, which are constructed out of engaged gears, the contrary forces that promote and hinder the motion of the gears will sustain each other if they are inversely as the velocities of the parts of the gears upon which they are impressed. The force of a screw to press a body is to the force of a hand turning the handle as the circular velocity of the handle, in the part where it is urged by the hand, is to the progressive velocity of the screw toward the pressed body. The forces by which a wedge presses the two parts of the wood that it splits are to the force of the hammer upon the wedge as the progress of the wedge (in the direction of the force impressed upon it by the hammer) is to the velocity with which the parts of the wood yield to the wedge along lines perpendicular to the faces of the wedge. And the case is the same for all machines.

The effectiveness and usefulness of all machines or devices consist wholly in our being able to increase the force by decreasing the velocity, and vice versa; in this way the problem is solved in the case of any working machine or device: “To move a given weight by a given force” or to overcome any other given resistance by a given force. For if machines are constructed in such a way that the velocities of the agent [or acting body] and the resistant [or resisting body] are inversely as the forces, the agent will sustain the resistance and, if there is a greater disparity of velocities, will overcome that resistance. Of course the disparity of the velocities may be so great that it can also overcome all the resistance which generally arises from the friction of contiguous bodies sliding over one another, from the cohesion of continuous bodies that are to be separated from one another, or from the weights of bodies to be raised; and if all this resistance is overcome, the remaining force will produce an acceleration of motion proportional to itself, partly in the parts of the machine, partly in the resisting body.^d

But my purpose here is not to write a treatise on mechanics. By these examples I wished only to show the wide range and the certainty of the third law of motion. For if the action of an agent is reckoned by its force and velocity jointly, and if, similarly, the reaction of a resistant is reckoned jointly by the velocities of its individual parts and the forces of resistance arising from their friction, cohesion, weight, and acceleration, the action and reaction will always be equal to each other in all examples of using devices or machines. And to the extent to which the action is propagated through the machine and ultimately impressed upon each resisting body, its ultimate direction will always be opposite to the direction of the reaction.