6 An Impoverished Language?
What does quantum mechanics say about spin? I like to think of quantum theory as a kind of language. It is a strange, abbreviated tongue. Nothing in it seems to correspond to anything that we have ever experienced, and it is utterly incapable of expressing many things. Perhaps this is not surprising: it was designed to fit the strange new world of submicroscopic entities such as electrons and photons, not normal life.
One entity in this new form of discourse is something known as a matrix. It describes the electron’s spin. A matrix like this
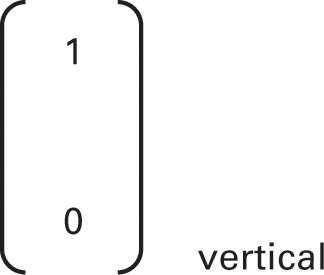
Figure 6.1
represents an electron whose spin lies upward along the vertical direction. A matrix with the “zero” on top and the “one” on the bottom represents the opposite case of a spin pointing downward against the vertical. Similar matrices describe other directions—horizontal, say, or tilted. We can add such matrices, each multiplied by a number from which can be calculated the probability that a detector will yield the corresponding result.
All in all, it is a peculiar language, and one far removed from normal experience. This is what was giving me so much trouble when I was first introduced to it as a student. Nothing in this language corresponds to our customary, everyday notion of spin. And if we search through quantum theory, looking for the slightest mention of that notion, we will not find it. We will find no rotating bodies, no axes pointing off in definite directions. Rather, what we find are matrices—utterly foreign, and utterly abstract.
If you are of a certain frame of mind, such a way of thinking will be good enough for you. Mathematicians, for instance, are perfectly comfortable speaking in terms of abstractions with no counterpart in experience. (I once met a mathematician who mentioned that she was studying non-Euclidian geometry. “What a joy! It is so delightfully concrete!”) For example, a mathematician is just as happy speaking of a negative number as a positive one. Maybe you are too. But should you be? We all know what four apples look like—but what do minus four apples look like?
The difficulty is that our normal way of thinking about a situation brings with it a mental picture of what is going on—but abstract thinking like this does not. Suppose, for instance, we ask “If there are ten apples in a bag, and four are removed, how many will be left?” Normally we would subtract to find the answer. But if you are of a mathematical bent of mind you might want to play with a second way of answering that question: that of adding a negative number of apples to the original ten. You will get the right answer. Notice, however, that this alternate way of dong the calculation fails to carry with it any such picture. Nobody has ever tossed a negative number of apples into a bag. Not even a mathematician.
In the same way, the language of quantum mechanics fails to carry with it a description of what might really be going on. Nothing in the matrices that constitute the quantum-mechanical description of spin corresponds to the sort of intuitive picture of figure 5.1. Do you find this a defect? Are you looking for more than matrices? If so, then you are looking for something that goes beyond quantum mechanics, something not contained within the theory and that encapsulates our normal conception of spin, our normal metaphysical assumption about reality.
Which is to say that you are looking for a theory better than quantum mechanics. You believe that quantum mechanics is incomplete. You are saying that it is half a theory, and it is not enough for you.
I don’t want to give the wrong impression here. Many areas of physics use abstract mathematics. You will find the square root of minus one all over the place in the theory of electromagnetism, and non-Euclidian geometry in relativity. The point is that, in all these other areas, the math is about something that can be pictured.
In chapter 2 I spoke of the “reticence” of the Great Predictor, and of his “refusal” to answer my questions. In truth it is not really a question of reticence or refusal. Rather it is a question of his being incapable of speaking. The language that the Predictor speaks simply has no means of expressing all those things that constitute the reality concerning which Einstein wanted him to speak.
But maybe you—and Einstein—are wrong in your wish. For notice that, for all its abstractness, quantum mechanics makes perfectly definite predictions about the results of experiments. It predicts the probability that such-and-such a measurement will yield such-and-such a result. And if I make that measurement, I find that the prediction was correct. Isn’t that enough? The Great Predictor got it right yet again: why isn’t that good enough? If a theory predicts what I will find when I do something, is that not everything I should want of a theory?
There are times when I think that the language of quantum mechanics is not impoverished at all. To the contrary, it is perfectly adapted to the microworld—a realm utterly different than that of everyday experience, a realm in which our old ways of thinking are no longer appropriate. As with the uncertainty principle, perhaps the strange new language that the Predictor speaks is not a problem but a discovery—a profound insight into the very nature of physical reality.
I understand that Eskimos have many different words for snow. Quantum mechanics is like a language that has no words for snow. And the question is whether this is a failing of that language. Maybe not! Perhaps we should recognize it as a positive benefit of this way of speaking. For after all—maybe there is no such thing as snow. Maybe snow is like Santa Claus: a fiction that we are so accustomed to that we have mistaken it for the truth.
In this view, the image in figure 5.1 and the desire we may feel for a fuller description of what is really going on are instances of a naive, outmoded way of thinking. They are relics from an earlier time, from an earlier metaphysics, a metaphysics not yet informed by the wonderful discovery that is quantum theory. Better we should grow up.