SALV. Eccolo là. Vi fu messo subito che cominciaste a guardare le minuzie, e non ve ne sete accorto, sì grande è stato l’accrescimento del lume nel resto della parete. Or tolgasi via lo specchio piano. Eccovi levata via ogni reflessione, ancorché vi sia rimasto il grande specchio convesso. Rimuovasi questo ancora, e poi vi si riponga quanto vi piace: voi non vedrete mutazione alcuna di luce in tutto il muro. Eccovi dunque mostrato al senso come la reflessione del Sole fatta in ispecchio sferico convesso non illumina sensibilmente i luoghi circonvicini. Ora che risponderete voi a questa esperienza?

SIMP. Io ho paura che qui non entri qualche giuoco di mano. Io veggo pure, nel riguardar quello specchio, uscire un grande splendore, che quasi mi toglie la vista, e, quel che più importa, ve lo veggo sempre da qualsivoglia luogo ch’io lo rimiri, e veggolo andar mutando sito sopra la superficie dello specchio, secondo ch’io mi pongo a rimirarlo in questo o in quel luogo: argomento necessario, che il lume si reflette vivo assai verso tutte le bande, ed in conseguenza così potente sopra tutta quella parete come sopra il mio occhio.

SALV. Or vedete quanto bisogni andar cauto e riservato nel prestare assenso a quello che il solo discorso ci rappresenta. Non ha dubbio che questo che voi dite ha assai dell’apparente; tuttavia potete vedere come la sensata esperienza mostra in contrario.

SIMP. Come dunque cammina questo negozio?

SALV. Io vi dirò quel che ne sento, che non so quanto vi sia per appagare. E prima, quello splendore così vivo che voi vedete sopra lo specchio, e che vi par che ne occupi assai buona parte, non è così grande a gran pezzo, anzi è piccolo assai assai; ma la sua vivezza cagiona nell’occhio vostro, mediante la reflessione fatta nell’umido de gli orli delle palpebre, la quale si distende sopra la pupilla, una irradiazione avventizia, simile a quel capillizio che ci par di vedere intorno alla fiammella di una candela posta alquanto lontana, Corpicello delle
stelle irraggiato
apparisce mille
volte maggiore
che nudo.o vogliate assimigliarla allo splendore avventizio di una stella; che se voi paragonerete il piccolo corpicello, v. g., della Canicola, veduto di giorno col telescopio, quando si vede senza irradiazione, col medesimo veduto di notte coll’occhio libero, voi fuor di ogni dubbio comprenderete che l’irraggiato si mostra più di mille volte maggiore del nudo e real corpicello: ed un simile o maggior ricrescimento fa l’immagine del Sole che voi vedete in quello specchio; dico maggiore, per esser ella più viva della stella, come è manifesto dal potersi rimirar la stella con assai minor offesa alla vista, che questa reflession dello specchio. Il reverbero dunque, che si ha da participare sopra tutta questa parete, viene da piccola parte di quello specchio; e quello che pur ora veniva da tutto lo specchio piano, si participava e ristrigneva a piccolissima parte della medesima parete: qual meraviglia è dunque che la reflessione prima illumini molto vivamente, e che quest’altra resti quasi impercettibile?

SIMP. Io mi trovo più inviluppato che mai, e mi sopraggiugne l’altra difficultà, come possa essere che quel muro, essendo di materia così oscura e di superficie così mal pulita, abbia a ripercuoter lume più potente e vivace che uno specchio ben terso e pulito.

SALV. Più vivace no,⁷⁶ ma ben più universale; ché, quanto alla vivezza, voi vedete che la reflessione di quello specchietto piano, dove ella ferisce là sotto la loggia, illumina gagliardamente, ed il restante della parete, che riceve la reflession del muro, dove è attaccato lo specchio, non è a gran segno illuminato come la piccola parte doveLume reflesso de i
corpi asperi più
universale che quello
de i tersi, e perché. arriva il reflesso dello specchio. E se voi desiderate intender l’intero di questo negozio, considerate come l’esser la superficie di quel muro aspra, è l’istesso che l’esser composta di innumerabili superficie e piccolissime, disposte secondo innumerabili diversità di inclinazioni, tra le quali di necessità accade che ne sieno molte disposte a mandare i raggi, reflessi da loro, in un tal luogo, molte altre in altro; ed in somma non è luogo alcuno al quale non arrivino moltissimi raggi reflessi da moltissime superficiette sparse per tutta l’intera superficie del corpo scabroso, sopra il quale cascano i raggi luminosi: dal che segue di necessità che sopra qualsivoglia parte di qualunque superficie opposta a quella che riceve i raggiLuna se fosse tersa
e liscia sarebbe
invisibile. primarii incidenti, pervengano raggi reflessi, ed in conseguenza l’illuminazione. Seguene ancora, che il medesimo corpo sul quale vengono i raggi illuminanti, rimirato da qualsivoglia luogo, si mostri tutto illuminato e chiaro: e però la Luna, per esser di superficie aspra e non tersa, rimanda la luce del Sole verso tutte le bande, ed a tutti i riguardanti si mostra egualmente lucida. Che se la superficie sua, essendo sferica, fusse ancora liscia come uno specchio, resterebbe del tutto invisibile, atteso che quella piccolissima parte dalla quale potesse venir reflessa l’immagine del Sole, all’occhio di un particolare, per la gran lontananza, resterebbe invisibile, come già abbiam detto.

SIMP. Resto assai ben capace del vostro discorso; tuttavia mi par di poter risolverlo con pochissima fatica, e mantener benissimo che la Luna sia rotonda e pulitissima e che refletta il lume del Sole a noi al modo di uno specchio: né perciò l’immagine del Sole si deve veder nel suo mezo; avvengaché «non per le spezie⁷⁷ dell’istesso Sole possa vedersi in sì gran distanza la piccola figura del Sole, ma sia compresa da noi per il lume prodotto dal Sole l’illuminazione di tutto il corpo lunare. Una tal cosa possiamo noi vedere in una piastra dorata e ben brunita, che, percossa da un corpo luminoso, si mostra, a chi la guarda da lontano, tutta risplendente; e solo da vicino si scorge nel mezo di essa la piccola immagine del corpo luminoso».

SALV. Confessando ingenuamente la mia incapacità, dico che non intendo di questo vostro discorso altro che di quella piastra dorata; e se voi mi concedete il parlar liberamente, ho grande opinione che voi ancora non l’intendiate, ma abbiate imparate a mente quelle parole scritte da qualcuno per desiderio di contraddire e mostrarsi più intelligente dell’avversario, mostrarsi, però, a quelli che, per apparir eglino ancora intelligenti, applaudono a quello che e’ non intendono, e maggior concetto si formano delle persone secondo che daAlcuni scrivono
quel che non
intendono, e però
non s’intende
quel che essi
scrivono. loro son manco intese; e pur che lo scrittore stesso non sia (come molti ce ne sono) di quelli che scrivono quel che non intendono, e che però non s’intende quel che essi scrivono. Però, lasciando il resto, vi rispondo, quanto alla piastra dorata, che quando ella sia piana e non molto grande, potrà apparir da lontano tutta risplendente, mentre sia ferita da un lume gagliardo, ma però si vedrà tale quando l’occhio sia in una linea determinata, cioè in quella de i raggi reflessi; e vedrassi più fiammeggiante che se fusse, v. g., d’argento, mediante l’esser colorata ed atta, per la somma densità del metallo, a ricevere brunimento perfettissimo: e quando la sua superficie, essendo benissimo lustrata, non fusse poi esattamente piana, ma avesse varie inclinazioni, allora anco da più luoghi si vedrebbe il suo splendore, cioè da tanti a quanti pervenissero le varie reflessioni fatte dalle diverse superficie; che però si lavorano i diamanti a molte facce, acciò il lor dilettevol fulgore si Diamanti si lavorano
a molte facce,
e perché.scorga da molti luoghi: ma quando la piastra fusse molto grande, non però da lontano, ancorché ella fusse tutta piana, si vedrebbe tutta risplendente. E per meglio dichiararmi, intendasi una piastra dorata piana e grandissima esposta al Sole: mostrerassi a un occhio lontano l’immagine del Sole occupare una parte di tal piastra solamente, cioè quella donde viene la reflessione de i raggi solari incidenti; ma è vero che per la vivacità del lume tal immagine apparirà inghirlandata di molti raggi, e però sembrerà occupare maggior parte assai della piastra che veramente ella non occuperà. E che ciò sia vero, notato il luogo particolare della piastra donde viene la reflessione, e figurato parimente quanto grande mi si rappresenta lo spazio risplendente, cuoprasi di esso spazio la maggior parte, lasciando solamente scoperto intorno al mezo: non però si diminuirà punto la grandezza dell’apparente splendore a quello che di lontano lo rimira, anzi si vedrà egli largamente sparso sopra il panno o altro con che si ricoperse. Se dunque alcuno Argento brunito
apparisce più
oscuro che il non
brunito, e perché. col vedere una piccola piastra dorata da lontano tutta risplendente, si sarà immaginato che l’istesso dovesse accadere anco di piastre grandi quanto la Luna, si è ingannato non meno che se credesse, la Luna non esser maggiore di un fondo di tino. Quando poi la piastra fusse di superficie sferica, vedrebbesi in una sola sua particella il reflesso gagliardo, ma ben, mediante la vivezza, si mostrerebbe inghirlandato di molti raggi assai vibranti: il resto della palla si vedrebbe come colorato, e questo anco solamente quando e’ non fusse in sommo grado pulito; che quando e’ fusse brunito perfettamente, apparirebbe oscuro. Esempio di questo aviamo giornalmente avanti gli occhi ne i vasi d’argento, li quali, mentre sono solamente bolliti nel bianchimento, son tutti candidi come la neve, né punto rendono l’immagini; ma se in alcuna parte si bruniscono, in quella subito diventano oscuri, e di lì rendono l’immagini come specchi: e quel divenire oscuro non procede da altro che dall’essersi spianata una finissima grana che faceva la superficie dell’argento scabrosa, e però tale che rifletteva il lume verso tutte leAcciaio brunito da
alcune vedute appar
chiarissimo e da
altre oscurissimo. parti, per lo che da tutti i luoghi si mostrava egualmente illuminata; quando poi, col brunirla, si spianano esquisitamente quelle minime inegualità, sì che la reflessione de i raggi incidenti si drizza tutta in luogo determinato, allora da quel tal luogo si mostra la parte brunita assai più chiara e lucida del restante, che è solamente bianchito, ma da tutti gli altri luoghi si vede molto oscura. È noto che la diversità delle vedute, nel rimirar superficie brunite, cagiona differenze tali di apparenze, che per imitare e rappresentare in pittura, v. g., una corazza brunita, bisogna accoppiare neri schietti e bianchi, l’uno a canto all’altro, in parti di essa arme dove il lume cade egualmente.

SAGR. Adunque, quando questi Signori filosofi si contentassero di conceder che la Luna, Venere e gli altri pianeti fussero di superficie non così lustra e tersa come uno specchio, ma un capello manco, cioè quale è una piastra di argento bianchita solamente, ma non brunita, questo basterebbe a poterla far visibile ed accomodata a ripercuoterci il lume del Sole?

SALV. Basterebbe in parte; ma non renderebbe un lume così potente, come fa essendo montuosa ed in somma piena di eminenze e cavità grandi. Ma questi Signori filosofi non la concederanno mai pulita meno di uno specchio, ma bene assai più, se più si può immaginare, perché stimando eglino che a’ corpi perfettissimi si convengano figure perfettissime, bisogna che la sfericità di quei globi celesti sia assolutissima; oltre che, quando e’ mi concedessero qualche inegualità, ancorché minima, io me ne prenderei senza scrupolo alcuno altra assai maggiore, perché consistendo tal perfezione in indivisibili, tanto la guasta un capello quanto una montagna.

SAGR. Qui mi nascono due dubbi: l’uno è l’intendere, perché la maggior inegualità di superficie abbia a far più potente reflession di lume; l’altro è, perché questi Signori Peripatetici voglian questa esatta figura.

SALV. Al primo risponderò io, ed al Sig. Simplicio lascerò la cura di Superficie più scabrosa
fa maggior reflessione
di lume che la meno
scabrosa. rispondere al secondo. Devesi dunque avvertire che le medesime superficie vengono dal medesimo lume più e meno illuminate, secondoché i raggi illuminanti vi cascano sopra più o meno obliquamente, sì che la massima illuminazione è dove i raggi son perpendicolari. Ed ecco ch’io ve lo mostro al senso. Io piego questo foglio tanto che una parte faccia angolo sopra l’altra; ed esponendoleRaggi perpendicolari
illuminano più che gli
obbliqui, e perché. alla reflession del lume di quel muro opposto, vedete come questa faccia, che riceve i raggi obliquamente, è manco chiara di quest’altra, dove la reflessione viene ad angoli retti; e notate come secondo che io gli vo ricevendo più e più obliquamente, l’illuminazione si fa più debole.

SAGR. Veggo l’effetto, ma non comprendo la causa.

SALV. Se voi ci pensaste un centesimo d’ora, la trovereste; ma per non consumare il tempo, eccovene un poco di dimostrazione in questa figura.

SAGR. La sola vista della figura mi ha chiarito il tutto, però seguite.

SIMP. Dite in grazia il resto a me, che non sono di sì veloce apprensiva.

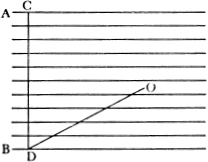
SALV. Fate conto che tutte le linee parallele che voi vedete partirsi da i termini A, B, sieno i raggi che sopra la linea CD vengono ad angoli retti: inclinate ora la medesima CD, I raggi più obbliqui
illuminano meno,
e perché.sì che penda come DO: non vedete voi che buona parte di quei raggi che ferivano la CD, passano senza toccar la DO? Adunque se la DO è illuminata da manco raggi, è ben ragionevole che il lume ricevuto da lei sia più debole. Torniamo ora alla Luna, la quale, essendo di figura sferica, quando la sua superficie fusse pulita quanto questa carta, le parti del suo emisferio illuminato dal Sole che sono verso l’estremità, riceverebbero minor lume assaissimo che le parti di mezo, cadendo sopra quelle i raggi obliquissimi, e sopra queste ad angoli retti; per lo che nel plenilunio, quando noi veggiamo quasi tutto l’emisferio illuminato, le parti verso il mezo ci si dovrebbero mostrare più risplendenti, che l’altre verso la circonferenza: il che non si vede. Figuratevi ora la faccia della Luna piena di montagne ben alte: non vedete voi come le piagge e i dorsi loro, elevandosi sopra la convessità della perfetta superficie sferica, vengono esposti alla vista del Sole, ed accomodati a ricevere i raggi, assai meno obliquamente, e perciò a mostrarsi illuminati quanto il resto?

SAGR. Tutto bene: ma se vi sono tali montagne, è vero che il Sole le ferirà assai più direttamente che non farebbe l’inclinazione di una superficie pulita, ma è anco vero che tra esse montagne resterebbero tutte le valli oscure, mediante l’ombre grandissime che in quel tempo verrebber da i monti; dove che le parti di mezo, benché piene di valli e monti, mediante l’avere il Sole elevato, rimarrebbero senz’ombre, e però più lucide assai che le parti estreme, sparse non men di ombre che di lume: e pur tuttavia non si vede tal differenza.

SIMP. Una simil difficultà mi si andava avvolgendo per la fantasia.

SALV. Quanto è più pronto il Sig. Simplicio a penetrar le difficultà che favoriscono le opinioni d’Aristotile, che le soluzioni! Ma io ho qualche sospetto che a bello studio e’ voglia anco talvolta tacerle: e nel presente particulare, avendo da per sé potuto veder l’obbiezione, che pure è assai ingegnosa, non posso credere che e’ non abbia ancora avvertita la risposta, ond’io voglio tentar di cavargliela (come si dice) di bocca. Però ditemi, Sig. Simplicio: credete voi che possa essere ombra dove feriscono i raggi del Sole?

SIMP. Credo, anzi son sicuro, che no, perché essendo egli il massimo luminare, che scaccia con i suoi raggi le tenebre, è impossibile che dove egli arriva resti tenebroso; e poi aviamo la definizione, che tenebrae sunt privatio luminis.⁷⁸

SALV. Adunque il Sole, rimirando la Terra o la Luna o altro corpo opaco, non vede mai alcuna delle sue parti ombrose, non avendo altri occhi da vedere che i suoi raggi apportatori del lume; ed in conseguenza uno che fusse nel Sole, non vedrebbe mai niente di adombrato, imperocché i raggi suoi visivi⁷⁹ andrebbero sempre in compagnia de i solari illuminanti.

SIMP. Questo è verissimo, senza contradizione alcuna.

SALV. Ma quando la Luna è all’opposizion del Sole, qual differenza è tra il viaggio che fanno i raggi della vostra vista, e quello che fanno i raggi del Sole?

SIMP. Ora ho inteso; voi volete dire che caminando i raggi della vista e quelli del Sole per le medesime linee, noi non possiamo scoprir alcuna delle valli ombrose della Luna. Di grazia, toglietevi giù di questa opinione, ch’io sia simulatore o dissimulatore; e vi giuro da gentiluomo che non avevo penetrata cotal risposta, né forse l’avrei ritrovata senza l’aiuto vostro o senza lungo pensarvi.

SAGR. La soluzione che fra tutti due avete addotta circa quest’ultima difficultà, ha veramente soddisfatto a me ancora; ma nel medesimo tempo questa considerazione del camminare i raggi della vista con quelli del Sole, mi ha destato un altro scrupolo circa l’altra parte: ma non so se io lo saprò spiegare, perché, essendomi nato di presente, non l’ho per ancora ordinato a modo mio; ma vedremo fra tutti di ridurlo a chiarezza. È non è dubbio alcuno che le parti verso la circonferenza dell’emisferio pulito, ma non brunito, che sia illuminato dal Sole, ricevendo i raggi obliquamente, ne ricevono assai meno che le parti di mezo, le quali direttamente gli ricevono; e può essere che una striscia larga, v. g., venti gradi, che sia verso l’estremità dell’emisferio, non riceva più raggi che un’altra verso le parti di mezo, larga non più di quattro gradi; onde quella veramente sarà assai più oscura di questa, e tale apparirà a chiunque le rimirasse amendue in faccia o vogliam dire in maestà. Ma quando l’occhio del riguardante fusse costituito in luogo tale che la larghezza de i venti gradi della striscia oscura se gli rappresentasse non più lunga d’una di quattro gradi posta sul mezo dell’emisferio, io non ho per impossibile che se gli potesse mostrare egualmente chiara e luminosa come l’altra, perché finalmente dentro a due angoli eguali, cioè di quattro gradi l’uno, vengono all’occhio le reflessioni di due eguali moltitudini di raggi, di quelli, cioè, che si reflettono dalla striscia di mezo, larga gradi quattro, e de i reflessi dall’altra di venti gradi, ma veduta in iscorcio sotto la quantità di gradi quattro: ed un sito tale otterrà l’occhio, quando e’ sia collocato tra ’l detto emisfero e ’l corpo che l’illumina, perché allora la vista e i raggi vanno per le medesime linee. Par dunque che non sia impossibile che la Luna possa esser di superficie assai bene eguale, e che non dimeno nel plenilunio si mostri non men luminosa nell’estremità che nelle parti di mezo.

SALV. La dubitazione è ingegnosa e degna d’esser considerata: e comeché ella vi è nata pur ora improvisamente, io parimente risponderò quello che improvisamente mi cade in mente, e forse potrebb’essere che col pensarvi più mi sovvenisse miglior risposta. Ma prima che io produca altro in mezo, sarà bene che noi ci assicuriamo con l’esperienza se la vostra opposizione risponde così in fatto, come par che concluda in apparenza. E però, ripigliando la medesima carta, inclinandone, col piegarla, una piccola parte sopra il rimanente, proviamo se esponendola al lume, sì che sopra la minor parte caschino i raggi del lume direttamente, e sopra l’altra obliquamente, questa che riceve i raggi diretti si mostri più chiara: ed ecco già l’esperienza manifesta, che l’è notabilmente più luminosa. Ora, quando la vostra opposizione sia concludente, bisognerà che, abbassando noi l’occhio tanto che, rimirando l’altra maggior parte, meno illuminata, in iscorcio, ella ci apparisca non più larga dell’altra più illuminata, e che in conseguenza non sia veduta sotto maggior angolo che quella, bisognerà, dico, che il suo lume si accresca sì, che ci sembri così lucida come l’altra. Ecco che io la guardo, e la veggo sì obliquamente che la mi apparisce più stretta dell’altra; ma con tutto ciò la sua oscurità non mi si rischiara punto. Guardate ora se l’istesso accade a voi.

SAGR. Ho visto, né, perché io abbassi l’occhio, veggo punto illuminarsi o rischiararsi davvantaggio la detta superficie; anzi mi par più tosto che ella si imbrunisca.

SALV. Siamo dunque sin ora sicuri dell’inefficacia dell’opposizione. Quanto poi alla soluzione, credo che, per esser la superficie di questa carta poco meno che tersa, pochi sieno i raggi che si reflettano verso gl’incidenti, in comparazione della moltitudine che si reflette verso le parti opposte, e che di quei pochi se ne perdano sempre più quanto più si accostano i raggi visivi a essi raggi luminosi incidenti; e perché non i raggi incidenti, ma quelli che si reflettono all’occhio, fanno apparir l’oggetto luminoso, però, nell’abbassar l’occhio, più è quello che si perde che quello che si acquista, come anco voi stesso dite apparirvi nel vedere il foglio più oscuro.

SAGR. Io dell’esperienza e della ragione mi appago. Resta ora che ’l Sig. Simplicio risponda all’altro mio quesito, dichiarandomi quali cose muovano i Peripatetici a voler questa rotondità ne i corpi celesti tanto esatta.

SIMP. L’essere i corpi celesti ingenerabili, incorruttibili, Sfericità perfetta
perché si ponga ne’
corpi celesti da i
Peripatetici.inalterabili, impassibili, immortali etc., fa che e’ sieno assolutamente perfetti; e l’essere assolutamente perfetti si tira in conseguenza che in loro sia ogni genere di perfezione, e però che la figura ancora sia perfetta, cioè sferica, e assolutamente e perfettamente sferica, e non aspera ed irregolare.

SALV. E questa incorruttibilità da che la cavate voi?

SIMP. Dal mancar di contrari immediatamente, e mediatamente dal moto semplice circolare.

SALV. Talché, per quanto io raccolgo dal vostro discorso, nel costituir l’essenza de i corpi celesti incorruttibile, inalterabile etc., non v’entra, come causa o requisito necessario, la rotondità; che quando questa cagionasse l’inalterabilità, noi potremo ad arbitrio nostro far incorruttibile il legno, la cera ed altre materie elementari, col ridurle in figura sferica.

SIMP. E La figura non è
causa dell’incorrutt
ibilità, ma di più
lunga durazione.non è egli manifesto che una palla di legno meglio e più lungo tempo si conserverà che una guglia o altra forma angolare, fatta di altrettanto del medesimo legno?

SALV. Cotesto è verissimo, ma non però di corruttibile diverrà ella incorruttibile; anzi resterà pur corruttibile, ma ben di più lunga durata. Però è da notarsi che il corruttibile è capace diIl corruttibile riceve
il più e ’l meno, ma
non l’incorruttibile. più e di meno tale, potendo noi dire: «Questo è men corruttibile di quello», come, per esempio, il diaspro è men corruttibile della pietra serena; ma l’incorruttibile non riceve il più e ’l meno, sì che si possa dire: «Questo è più incorruttibile di quell’altro», se amendue sono incorruttibili ed eterni. La diversità La perfezion di figura
opera nei corpi
corruttibili, ma non
già negli eterni.dunque di figura non può operare se non nelle materie che son capaci del più o del meno durare; ma nelle eterne, che non posson essere se non egualmente eterne, cessa l’operazione della figura. E per tanto, già che la materia celeste non per la figura è incorruttibile, ma per altro, non occorre esser così ansioso di questa perfetta sfericità, perché, quando la materia sarà incorruttibile, abbia pur che figura si voglia, ella sarà sempre tale.

SAGR. Ma io vo considerando qualche cosa di più, e dico che, conceduto che la figura sferica avesse facultà di conferire l’incorruttibilità, tutti i corpi, di qualsivoglia Se la figura sferica
conferisse l’eternità,
tutti i corpi
sarebbero eterni.figura, sarebbero eterni e incorruttibili. Imperocché, essendo il corpo rotondo incorruttibile, la corruttibilità verrebbe a consistere in quelle parti che alterano la perfetta rotondità: come, per esempio, in un dado vi è dentro una palla perfettamente rotonda, e come tale incorruttibile; resta dunque che corruttibili sieno quelli angoli che ricuoprono ed ascondono la rotondità; al più dunque che potesse accadere, sarebbe che tali angoli e (per così dire) escrescenze si corrompessero. Ma se più internamente andremo considerando, in quelle parti ancora verso gli angoli vi son dentro altre minori palle della medesima materia, e però esse ancora, per esser rotonde, incorruttibili; e così ne’ residui che circondano queste otto minori sferette, vi se ne possono intendere altre; talché finalmente, risolvendo tutto il dado in palle innumerabili, bisognerà confessarlo incorruttibile. E questo medesimo discorso ed una simile resoluzione si può far di tutte le altre figure.

SALV. Il progresso cammina benissimo: sì che quando, v. g., un cristallo sferico avesse dalla figura l’esser incorruttibile, cioè la facultà di resistere a tutte le alterazioni interne ed esterne, non si vede che l’aggiugnerli altro cristallo e ridurlo, v. g., in cubo l’avesse ad alterar dentro, né anco di fuori, sì che ne divenisse meno atto a resistere al nuovo ambiente, fatto dell’istessa materia, che non era all’altro di materia diversa, e massime se è vero che la corruzione si faccia da i contrari, come dice Aristotile; e di qual cosa si può circondare quella palla di cristallo, che gli sia manco contraria del cristallo medesimo? Ma noi non ci accorgiamo del fuggir dell’ore, e tardi verremo a capo de’ nostri ragionamenti, se sopra ogni particulare si hanno da fare sì lunghi discorsi; oltre che la memoria si confonde talmente nella multiplicità delle cose, che difficilmente posso ricordarmi delle proposizioni che ordinatamente aveva proposte il Sig. Simplicio da considerarsi.

SIMP. Io me ne ricordo benissimo; e circa questo particulare della montuosità della Luna, resta ancora in piede la causa che io addussi di tale apparenza, potendosi benissimo Salvare con dir ch’ella sia un’illusione procedente dall’esser le parti della Luna inegualmente opache e perspicue.

SAGR. Poco fa, quando il Sig. Simplicio attribuiva le apparenti inegualità della Luna, conforme all’opinione di certo Peripatetico amico suo, alle parti di essa Luna diversamente opache e perspicue, conforme a che simili illusioni si veggono in cristalli e gemme di più sorti, mi sovvenne una materia molto più Madreperle atte a
imitar l’apparente
inegualità della
superficie della
Luna.accomodata per rappresentar cotali effetti, e tale che credo certo che quel filosofo la pagherebbe qualsivoglia prezo; e queste sono le madreperle, le quali si lavorano in varie figure, e benché ridotte ad una estrema liscezza, sembrano all’occhio tanto variamente in diverse parti cave e colme, che appena al tatto stesso si può dar fede della loro egualità.

SALV. Bellissimo è veramente questo pensiero; e quel che non è stato fatto sin ora, potrebbe esser fatto un’altra volta, e se sono state prodotte altre gemme e cristalli, che non han che fare con l’illusioni delle madreperle,Le apparenti
inegualità della
Luna non si possono
imitar per via di
più e meno opaco e
perspicuo. saran ben prodotte queste ancora. Intanto, per non tagliar l’occasione ad alcuno, tacerò la risposta che ci andrebbe, e solo procurerò per ora di sodisfare alle obbiezioni portate dal Sig. Simplicio. Dico per tanto che questa vostra è una ragion troppo generale, e come voi non l’applicate a tutte le apparenze ad una ad una che si veggono nella Luna, e per le quali io ed altri si son mossi a tenerla montuosa, non credo che voi siate per trovare chi si soddisfaccia di tal dottrina; né credo che voi stesso né l’autor medesimo trovi in essa maggior quiete, che in qualsivogliaVedute varie della
Luna imitabili con
qualsivoglia materia
opaca. altra cosa remota dal proposito. Delle molte e molte apparenze varie che si scorgono di sera in sera in un corso lunare, voi pur una sola non ne potrete imitare col fabbricare una palla a vostro arbitrio di parti più e meno opache e perspicue e che sia di superficie pulita; dove che, all’incontro, di qualsivoglia materia solida e non trasparente si fabbricheranno palle le quali, solo con eminenze e cavità e col ricevere variamente l’illuminazione, rappresenteranno l’istesse viste e mutazioni a capello, che d’ora in ora si scorgono nella Luna. In esse vedrete i dorsi dell’eminenze esposte al lume del Sole chiari assai, e doppo di loro le proiezioni dell’ombre oscurissime; vedrete le maggiori e minori, secondo che esse eminenze si troveranno più o meno distanti dal confine che distingue la parte della Luna illuminata dalla tenebrosa; vedrete l’istesso termine e confine, non Apparenze varie
dalle quali si
argomenta la
montuosità nella
Luna. egualmente disteso, qual sarebbe se la palla fusse pulita, ma anfrattuoso e merlato; vedrete, oltre al detto termine, nella parte tenebrosa, molte sommità illuminate e staccate dal resto già luminoso; vedrete l’ombre sopradette, secondoché l’illuminazione si va alzando, andarsi elleno diminuendo, sinché del tutto svaniscono, né più vedersene alcuna quando tutto l’emisferio sia illuminato; all’incontro poi, nel passare il lume verso l’altro emisfero lunare, riconoscerete l’istesse eminenze osservate prima, e vedrete le proiezioni dell’ombre loro farsi al contrario ed andar crescendo: delle quali cose torno a replicarvi che voi pur una non potrete rappresentarmi col vostro opaco e perspicuo.

SAGR. Anzi pur se ne imiterà una, cioè quella del plenilunio, quando, per esser il tutto illuminato, non si scorge più né ombre né altro che dalle eminenze e cavità riceva alcuna variazione. Ma di grazia, Sig. Salviati,, non perdete più tempo in questo particolare, perché uno che avesse avuto pazienza di far l’osservazioni di una o due lunazioni e non restasse capace di questa sensatissima verità, si potrebbe ben sentenziare per privo del tutto di giudizio; e con simili, a che consumar tempo e parole indarno?

SIMP. Io veramente non ho fatte tali osservazioni, perché non ho avuta questa curiosità, né meno strumento atto a poterle fare; ma voglio per ogni modo farle: e intanto possiamo lasciar questa questione in pendente e passare a quel punto che segue, producendo i motivi per i quali voi stimate che la Terra possa reflettere il lume del Sole non men gagliardamente che la Luna, perché a me par ella tanto oscura ed opaca, che un tale effetto mi si rappresenta del tutto impossibile.

SALV. La causa per la quale voi reputate la Terra inetta all’illuminazione, non è altramente cotesta, Sig. Simplicio. E non sarebbe bella cosa che io penetrassi i vostri discorsi meglio che voi medesimo?

SIMP. Se io mi discorra bene o male, potrebb’esser che voi meglio di me lo conosceste; ma, o bene o mal ch’io mi discorra, che voi possiate meglio di me penetrar il mio discorso, questo non crederò io mai.

SALV. Anzi vel farò io creder pur ora. Ditemi un poco: quando la Luna è presso che piena, sì che ella si può veder di giorno ed anco a meza notte, quando vi par ella più splendente, il giorno o la notte?

SIMP. La notte, senza comparazione, e parmi che la Luna Luna apparisce più
risplendente la
notte che ’l giorno. imiti quella colonna di nugole e di fuoco che fu scorta a i figliuoli di Isdraele, che alla presenza del Sole si mostrava come una nugoletta, ma la notte poi era splendidissima. Così ho io osservato alcune volte di giorno tra certe nugoletteLuna veduta di giorno
simile a una nugoletta. la Luna non altramente che una di esse biancheggiante; ma la notte poi si mostra splendentissima.

SALV. Talché quando voi non vi foste mai abbattuto a veder la Luna se non di giorno, voi non l’avreste giudicata più splendida di una di quelle nugolette.

SIMP. Così credo fermamente.

SALV. Ditemi ora: credete voi che la Luna sia realmente più lucente la notte che ’l giorno, o pur che per qualche accidente ella si mostri tale?

SIMP. Credo che realmente ella risplenda in sé stessa tanto di giorno quanto di notte, ma che ’l suo lume si mostri maggiore di notte perché noi la vediamo nel campo oscuro del cielo; ed il giorno, per esser tutto l’ambiente assai chiaro, sì che ella di poco lo avanza di luce, ci si rappresenta assai men lucida.

SALV. Or ditemi: avete voi veduto mai in su la meza notte il globo terrestre illuminato dal Sole?

SIMP. Questa mi pare una domanda da non farsi se non per burla, o vero a qualche persona conosciuta per insensata affatto.

SALV. No, no, io v’ho per uomo sensatissimo, e fo la domanda sul saldo: e però rispondete pure, e poi se vi parrà che io parli a sproposito, mi contento d’esser io l’insensato; ché bene è più sciocco quello che interroga scioccamente, che quello a chi si fa interrogazione.

SIMP. Se dunque voi non mi avete per semplice affatto, fate conto ch’io v’abbia risposto, e detto che è impossibile che uno che sia in Terra, come siamo noi, vegga di notte quella parte della Terra dove è giorno, cioè che è percossa dal Sole.

SALV. Adunque non vi è toccato mai a veder la Terra illuminata se non di giorno; ma la Luna la vedete anco nella più profonda notte risplendere in cielo: e questa, Sig. Simplicio, è la cagione che vi fa credere che la Terra non risplenda come la Luna; che se voi poteste veder la Terra illuminata mentreché voi fuste in luogo tenebroso come la nostra notte, la vedreste splendida più che la Luna. Ora, se voi volete che la comparazione proceda bene, bisogna far parallelo del lume della Terra con quel della Luna veduta di giorno, e non con la Luna notturna, poiché non ci tocca a veder la Terra illuminata se non di giorno. Non sta così?

SIMP. Così è dovere.

SALV. E perché voi medesimo avete già confessato d’aver veduta la Luna di giorno tra nugolette biancheggianti e similissima, quanto all’aspetto, ad una di esse, già primamente venite a confessare che quelle nugolette, che pur son materie elementari, son atte a riceverNugole atte ad
essere illuminate dal
Sole non meno che
la Luna. l’illuminazione quanto la Luna, ed ancor più, se voi vi ridurrete in fantasia d’aver vedute talvolta alcune nugole grandissime, e candidissime come la neve; e non si può dubitare che se una tale si potesse conservar così luminosa nella più profonda notte, ella illuminerebbe i luoghi circonvicini più che cento Lune. Quando dunque noi fussimo sicuri che la Terra si illuminasse dal Sole al pari di una di quelle nugolette, non resterebbe dubbio che ella fusse non meno risplendente della Luna. Ma di questo cessa ogni dubbio, mentre noi veggiamo le medesime nugole, nell’assenza del Sole, restar la notte così oscure come la Terra; e, quel che è più, non è alcuno di noi al quale non sia accaduto di veder più volte alcune tali nugole basse e lontane, e stare in dubbio se le fussero nugole o montagne: segno evidente, le montagne non esser men luminose di quelle nugole.

SAGR. Ma che più altri discorsi? Eccovi là su la Luna, che è più diMuro illuminato dal Sole,
e paragonato con la Luna,
lucido non meno di quella? meza; eccovi là quel muro alto, dove batte il Sole; ritiratevi in qua, sì che la Luna si vegga accanto al muro; guardate ora: che vi par più chiaro? non vedete voi che, se vantaggio vi è, l’ha il muro? Il Sole percuote in quella parete; di lì si reverbera nelle pareti della sala; da quelle si reflette in quella camera, sì cheIllumina più la terza
reflessione d’un muro
che la prima della Luna. in essa arriva con la terza reflessione: e ad ogni modo son sicuro che vi è più lume, che se direttamente vi arrivasse il lume della Luna.

SIMP. O questo non credo io, perché quel della Luna, e massime quando ell’è piena, è un grande illuminare.

SAGR. Par grande per l’oscurità de i luoghi circonvicini ombrosi, ma assolutamente non è molto, ed è minore che Lume della Luna
più debole di quel
del crepuscolo.quel del crepuscolo di mez’ora doppo il tramontar del Sole; il che è manifesto, perché non prima che allora vedrete cominciare a distinguersi in Terra le ombre de i corpi illuminati dalla Luna. Se poi quella terza reflessione in quella camera illumini più che la prima della Luna, si potrà conoscere andando là, col legger quivi un libro, e provar poi stasera al lume della Luna se si legge più agevolmente o meno, che credo senz’altro che si leggerà meno.

SALV. Ora, Sig. Simplicio (se però voi sete stato appagato), potete comprender come voi medesimo sapevi veramente che la Terra risplendeva non meno che la Luna, e che il ricordarvi solamente alcune cose sapute da per voi, e non insegnate da me, ve n’ha reso certo:⁸⁰ perché io non vi ho insegnato che la Luna si mostra più risplendente la notte che ’l giorno, ma già lo sapevi da per voi, come anco sapevi che tanto si mostra chiara una nugoletta quanto la Luna; sapevi parimente che l’illuminazion della Terra non si vede di notte, ed in somma sapevi il tutto, senza saper di saperlo. Di qui non doverà di ragione esservi difficile il conceder che la reflessione della Terra possa illuminar la parte tenebrosa della Luna, con luce non minor di quella con la quale la Luna illustra le tenebre della notte, anzi tanto più, quanto che la Terra è quaranta volte maggior della Luna.

SIMP. Veramente io credeva che quel lume secondario fosse proprio della Luna.

SALV. E questo ancora sapete da per voi, e non v’accorgete I corpi illuminati
appariscono più
chiari nell’ambiente
oscuro.di saperlo. Ditemi: non avete voi per voi stesso saputo che la Luna si mostra più luminosa assai la notte che il giorno, rispetto all’oscurità del campo ambiente? ed in conseguenza non venite voi a sapere in genere, che ogni corpo lucido si mostra più chiaro quanto l’ambiente è più oscuro?

SIMP. Questo so io benissimo.

SALV. Quando la Luna è falcata⁸¹ e vi mostra assai chiaro quel lume secondario, non è ella sempre vicina al Sole, ed in conseguenza nel lume del crepusculo?

SIMP. Èvvi; e molte volte ho desiderato che l’aria si facesse più fosca per poter veder quel tal lume più chiaro, ma l’è tramontata avanti notte oscura.

SALV. Voi dunque sapete benissimo che nella profonda notte quel lume apparirebbe più?

SIMP. Signor sì, ed ancor più se si potesse tor via il gran lume delle corna tocche dal Sole, la presenza del quale offusca assai l’altro minore.

SALV. Oh non accad’egli talvolta di poter vedere dentro ad oscurissima notte tutto il disco della Luna, senza punto essere illuminato dal Sole?

SIMP. Io non so che questo avvenga mai, se non ne gli eclissi totali della Luna.

SALV. Adunque allora dovrebbe questa sua luce mostrarsi vivissima, essendo in un campo oscurissimo e non offuscata dalla chiarezza delle corna luminose: ma voi in quello stato come l’avete veduta lucida?

SIMP. Holla veduta talvolta del color del rame ed un poco albicante; ma altre volte è rimasta tanto oscura, che l’ho del tutto persa di vista.

SALV. Come dunque può esser sua propria quella luce, che voi così chiara vedete nell’albor del crepuscolo, non ostante l’impedimento dello splendor grande e contiguo delle corna, e che poi nella più oscura notte, rimossa ogni altra luce, non apparisce punto?

SIMP. Intendo esserci stato chi ha creduto cotal lume venirle participato dall’altre stelle, ed in particolare da Venere,⁸² sua vicina.

SALV. E cotesta parimente è una vanità, perché nel tempo della sua totale oscurazione dovrebbe pur mostrarsi più lucida che mai, ché non si può dire che l’ombra della Terra gli asconda la vista di Venere né dell’altre stelle; ma ben ne riman ella del tutto priva allora, perché l’emisferio terrestre che in quel tempo riguarda verso la Luna è quello dove è notte, cioè un’intera privazion del lume del Sole. E se voi diligentemente andrete osservando, vedrete sensatamente che, sì come la Luna, quando è sottilmente falcata, pochissimo illumina la Terra, e secondoché in lei vien crescendo la parte illuminata dal Sole, cresce parimente lo splendore a noi, che da quella vienci reflesso; così la Luna, mentre è sottilmente falcata e che, per esser tra ’l Sole e la Terra, scuopre grandissima parte dell’emisferio terreno illuminato, si mostra assai chiara, e discostandosi dal Sole e venendo verso la quadratura, si vede tal lume andar languendo, ed oltre la quadratura si vede assai debile, perché sempre va perdendo della vista della parte luminosa della Terra: e pur dovrebbe accadere il contrario quando tal lume fusse suo o comunicatole dalle stelle, perché allora la possiamo vedere nella profonda notte e nell’ambiente molto tenebroso.

SIMP. Fermate, di grazia, ché pur ora mi sovviene aver letto in un libretto moderno di conclusioni,⁸³ pieno di molte novità, «che questo lume secondario non è cagionato dalle stelle né è proprio della Luna e men di tutti comunicatogli dalla Terra, ma che deriva dalla medesima illuminazion del Sole, la quale, per esser la sustanza del globo lunare alquanto trasparente, penetra per tutto il suo corpo,Luce secondaria
della Luna cagionata
dal Sole, secondo
alcuni. ma più vivamente illumina la superficie dell’emisfero esposto a i raggi del Sole, e la profondità, imbevendo e, per così dire, inzuppandosi di tal luce a guisa di una nugola o di un cristallo, la trasmette e si rende visibilmente lucida. E questo (se ben mi ricorda) prova egli con l’autorità, con l’esperienza e con la ragione, adducendo Cleomede, Vitellione, Macrobio e qualch’altro autor moderno,⁸⁴ e soggiugnendo, vedersi per esperienza ch’ella si mostra molto lucida ne i giorni prossimi alla congiunzione, cioè quando è falcata, e massimamente risplende intorno al suo limbo; e di più scrive che negli eclissi solari, quando ella è sotto il disco del Sole, si vede tralucere, e massime intorno all’estremo cerchio: quanto poi alle ragioni, parmi ch’e’ dica che non potendo ciò derivare né dalla Terra né dalle stelle né da sé stessa, resta necessariamente ch’e’ venga dal Sole; oltreché, fatta questa supposizione, benissimo si rendono accomodate ragioni di tutti i particulari che accascano. Imperocché del mostrarsi tal luce secondaria più vivace intorno all’estremo limbo, ne è cagione la brevità dello spazio da esser penetrato da i raggi del Sole, essendoché delle linee che traversano un cerchio, la massima è quella che passa per il centro, e delle altre le più lontane da questa son sempre minori delle più vicine. Dal medesimo principio dice egli derivare che tal lume poco diminuisce. E finalmente, per questa via si assegna la causa onde avvenga che quel cerchio più lucido intorno all’estremo margine della Luna si scorga nell’eclisse solare in quella parte che sta sotto il disco del Sole, ma non in quella che è fuor del disco; provenendo ciò, perché i raggi del Sole trapassano a dirittura al nostro occhio per le parti della Luna sottoposte, ma per le parti che son fuori, cascano fuori dell’occhio».

SALV. Se questo filosofo fusse stato il primo autore di tale opinione, io non mi maraviglierei che e’ vi fusse talmente affezionato, che e’ l’avesse ricevuta per vera; ma ricevendola da altri, non saprei addur ragione bastante per iscusarlo dal non aver comprese le sue fallacie, e massime doppo l’aver egli sentita la vera causa di tale effetto, ed aver potuto con mille esperienze e manifesti riscontri assicurarsi, ciò dal reflesso della Terra, e non da altro, procedere; e quanto questa cognizione fa desiderar qualche cosa nell’accorgimento di questo autore e di tutti gli altri che non le prestano l’assenso, tanto il non l’avere intesa e non esser loro sovvenuta mi rende scusabili quei più antichi, i quali son ben sicuro che se adesso l’intendessero, senza una minima repugnanza l’ammetterebbero. E se io vi devo schiettamente dire il mio concetto, non posso creder che quest’autor moderno internamente non la creda, ma dubito che il non potersen’egli fare il primo autore, lo stimoli un poco a tentare di supprimerla o smaccarla almanco appresso a i semplici, il numero de i quali sappiamo esser grandissimo; e molti sono che godono assai più dell’applauso numeroso del popolo, che dell’assenso de i pochi non vulgari.

SAGR. Fermate un poco, Sig. Salviati,, ché mi par di vedere che voi non andiate drittamente al vero punto nel vostro parlare; perché questi, che tendono le pareti al comune, si sanno anco fare autori dell’invenzioni di altri, purché non sieno tanto antiche e fatte pubbliche per le cattedre e per le piazze, che sieno più che notorie a tutti.

SALV. Oh io son più cattivo di voi. Che dite voi di pubbliche o di notorie? non è egli l’istesso l’esser l’opinioni e l’invenzioni nuove a gli uomini, che l’esser gli uomini nuovi a loro? se voi vi contentaste della stima de’ È l’istesso esser
le opinioni nuove a
gli uomini, ed esser
gli uomini nuovi
alle opinioni.principianti nelle scienze, che vengon su di tempo in tempo, potreste farvi anco inventore sin dell’alfabeto, e così rendervi ad essi ammirando; e se ben poi col progresso del tempo si scoprisse la vostra sagacità, ciò poco pregiudica al vostro fine, perché altri sottentrano a mantenere il numero de i fautori. Ma torniamo a mostrare al Sig. Simplicio la inefficacia de i discorsi del suo modernoLuce secondaria della
Luna apparisce in
forma di anello,
cioè chiara nell’estrema
circonferenza e non
nel mezo, e perché. autore, ne i quali ci sono falsità e cose non concludenti ed inopinabili. E prima, è falso che questa luce secondaria sia più chiara intorno all’estremo margine che nelle parti di mezo, sì che si formi quasi un anello o cerchio Modo di osservar la
luce secondaria
della Luna.più risplendente del resto del campo. Ben è vero che guardando la Luna posta nel crepuscolo, si mostra, nel primo apparire, un tal cerchio, ma con inganno che nasce dalla diversità de i confini con i quali termina il disco lunare, sparso di questa luce secondaria: imperocché dalla parte verso il Sole confina con le corna lucidissime della Luna, e dall’altra ha per termine confinante il campo oscuro del crepuscolo, la relazion del quale ci fa parere più chiaro l’albore del disco lunare, il quale nella parte opposta viene offuscato dallo splendor maggiore delle corna. Che se l’autor moderno avesse provato a farsi ostacolo tra l’occhio e lo splendor primario col tetto di qualche casa o con altro tramezzo, sì che visibile restasse solamente la piazza della Luna fuori delle corna, l’avrebbe veduta tutta egualmente luminosa.

SIMP. Mi par pur ricordare che egli scriva d’essersi servito di un simile artifizio per nascondersi la falce lucida.

SALV. Oh come questo è, la sua, che io stimava inavvertenza, diventa bugia; la quale pizzica anco di temerità, poiché ciascheduno ne può far frequentemente la riprova. Disco della Luna
nell’eclisse del
Sole non può vedersi
se non per privazione.Che poi nell’eclisse del Sole si vegga il disco della Luna in altro modo che per privazione, io ne dubito assai, e massime quando l’eclisse non sia totale, come necessariamente bisogna che siano state le osservate dall’autore; ma quando anco e’ si scorgesse come lucido, questo non contraria, anzi favorisce, l’opinion nostra, avvengaché allora si oppone alla Luna tutto l’emisferio terrestre illuminato dal Sole, ché se bene l’ombra della Luna ne oscura una parte, questa è pochissima in comparazione di quella che rimane illuminata. Quello che aggiugne di più, che in questo caso la parte del margine che soggiace al Sole si mostri assai lucida, ma non così quella che resta fuori, e ciò derivare dal venirci direttamente per quella parte i raggi solari all’occhio, ma non per questa, è bene una di quelle favole che manifestano le altre finzioni di colui che le racconta; perché, se L’autor del libretto
delle conclusioni va
accomodando le cose
a i suoi propositi, e
non i propositi alle cose.per farci visibile di luce secondaria il disco lunare bisogna che i raggi del Sole vengano direttamente al nostro occhio, non vede il poverino che noi mai non vedremmo tal luce secondaria se non nell’eclisse del Sole? e se l’esser una parte della Luna remota dal disco solare solamente manco assai di mezo grado può deviare i raggi del Sole, sì che non arrivino al nostro occhio, che sarà quando ella se ne trovi lontana venti e trenta, quale ella ne è nella sua prima apparizione? e come verranno i raggi del Sole, che hanno a trapassar per il corpo della Luna, a trovar l’occhio nostro? Quest’uomo si va di mano in mano figurando le cose quali bisognerebbe ch’elle fussero per servire al suo proposito, e non va accomodando i suoi propositi di mano in mano alle cose quali elle sono. Ecco: per far che lo splendor del Sole possa penetrar la sustanza della Luna, ei la fa in parte diafana, quale è, v. g., la trasparenza di una nugola o di un cristallo; ma non so poi quello ch’ei si giudicasse, circa una tal trasparenza, quando i raggi solari avessero a penetrare una profondità di nugola di più di dua mila miglia. Ma ammettasi che egli arditamente rispondesse, ciò potere esser benissimo ne i corpi celesti, che sono altre faccende che questi nostri elementari, impuri e fecciosi, e convinchiamo l’error suo con mezi che non ammettono risposta o, per dir meglio, sutterfugii. Quando ei voglia mantenere che la sustanza della Luna sia diafana, bisogna ch’ei dica che ella è tale mentreché i raggi del Sole abbiano a penetrar tutta la sua Burla fatta a uno
che voleva vender
certo segreto da poter
parlar con uno in
lontananza di mille
miglia.profondità, cioè ne abbiano a penetrar più di dua mila miglia, ma che opponendosigliene solo un miglio ed anco meno, non la penetreranno più che e’ si penetrino una delle nostre montagne.

SAGR. Voi mi fate sovvenire di uno⁸⁵ che mi voleva vendere un segreto di poter parlare, per via di certa simpatia di aghi calamitati, a uno che fusse stato lontano due o tre mila miglia; e dicendoli io che volentieri l’avrei comprato, ma che volevo vederne l’esperienza, e che mi bastava farla stando io in una delle mie camere, ed egli in un’altra, mi rispose che in sì piccola distanza non si poteva veder ben l’operazione: onde io lo licenziai, con dire che non mi sentivo per allora di andare nel Cairo o in Moscovia per veder tale esperienza; ma se pure voleva andare esso, che io arei fatto l’altra parte, restando in Venezia. Ma sentiamo come va la conseguenza dell’autore, e come bisogni ch’egli ammetta, la materia della Luna esser permeabilissima da i raggi solari nella profondità di dua mila miglia, ma opacissima più di una montagna delle nostre nella grossezza di un miglio solo.

SALV. L’istesse montagne appunto della Luna ce ne fanno testimonianza, le quali, ferite da una parte dal Sole, gettano dall’opposta ombre negrissime, terminate e taglienti più assai dell’ombre delle nostre; che quando elle fussero diafane, mai non avremmo potuto conoscere asprezza veruna nella superficie della Luna, né veder quelle cuspidi luminose staccate dal termine che distingue la parte illuminata dalla tenebrosa; anzi né meno vedremmo noi questo medesimo termine così distinto, se fusse vero che ’l lume del Sole penetrasse la profondità della Luna; anzi, per il detto medesimo dell’autore, bisognerebbe vedere il passaggio e confine tra la parte vista e la non vista dal Sole assai confuso e misto di luce e tenebre, ché bene è, necessario che quella materia che dà il transito a i raggi solari nella profondità di dua mila miglia, sia tanto trasparente che pochissimo gli contrasti nella centesima o minor parte di tal grossezza: tuttavia il termine che separa la parte illuminata dalla oscura è tagliente e così distinto quanto è distinto il bianco dal nero, e massime dove il taglio passa sopra la parte della Luna naturalmente più chiara e più aspra; ma dove sega le macchie antiche,⁸⁶ le quali sono pianure, per andare elle sfericamente inclinandosi, sì che ricevono i raggi del Sole obliquissimi, quivi il termine non è così tagliente, mediante la illuminazione più languida. Quello finalmente ch’ei dice del non si diminuire ed abbacinare la luce secondaria secondo che la Luna va crescendo, ma conservarsi continuamente della medesima efficacia, è falsissimo; anzi, poco si vede nella quadratura, quando, per l’opposito, ella dovrebbe vedersi più viva, potendosi vedere fuor del crepuscolo, nella notte La Terra può
reciprocamente
operare ne’ corpi
celesti col lume.più profonda. Concludiamo per tanto, esser la reflession della Terra potentissima nella Luna; e, quello di che dovrete far maggiore stima, cavatene un’altra congruenza bellissima: cioè, che se è vero che i pianeti operino sopra la Terra col moto e col lume, forse la Terra non meno sarà potente a operar reciprocamente in loro col medesimo lume e per avventura col moto ancora; e quando anco ella non si movesse, pur gli può restare la medesima operazione, perché già, come si è veduto, l’azione del lume è la medesima appunto, cioè del lume del Sole reflesso, e ’l moto non fa altro che la variazione de gli aspetti, la quale segue nel modo medesimo facendo muover la Terra e star fermo il Sole, che se si faccia per l’opposito.

SIMP. Non si troverà alcuno de i filosofi che abbia detto che questi corpi inferiori operino ne i celesti, ed Aristotile dice chiaro il contrario.

SALV. Aristotile e gli altri che non han saputo che la Terra e la Luna si illuminino scambievolmente, son degni di scusa; ma sarebber ben degni di riprensione se, mentre vogliono che noi concediamo e crediamo a loro che la Luna operi in Terra col lume, e’ volessin poi a noi, che gli aviamo insegnato che la Terra illumina la Luna, negare l’azione della Terra nella Luna.

SIMP. In somma io sento in me un’estrema repugnanza nel potere ammettere questa società che voi vorreste persuadermi tra la Terra e la Luna, ponendola, come si dice, in ischiera con le stelle; ché, quando altro non ci fusse, la gran separazione e lontananza tra essa e i corpi celesti mi par che necessariamente concluda una grandissima dissimilitudine tra di loro.

SALV. Vedete, Sig. Simplicio, quanto può un inveterato affetto ed una radicata opinione; poiché è tanto gagliarda, che vi fa parer favorevoli quelle cose medesime che voi stesso producete contro di voi. Che se la separazione e lontananza sono accidenti validi per persuadervi una gran diversità di nature, convien che per l’opposito la vicinanza eAffinità tra la
Terra e la Luna
rispetto alla
vicinanza. contiguità importino similitudine: ma quanto è più vicina la Luna alla Terra che a qualsivoglia altro de i globi celesti? Confessate dunque, per la vostra medesima concessione (ed averete anco altri filosofi per compagni),⁸⁷ grandissima affinità esser tra la Terra e la Luna. Or seguitiamo avanti, e proponete se altro ci resta da considerare circa le difficultà che voi moveste contro le congruenze tra questi due corpi.

SIMP. Ci resterebbe non so che in proposito della solidità della Luna, la quale io argumentava, dall’esser ella sommamente pulita e liscia, e voi dall’esser montuosa. Un’altra difficultà mi nasceva per il credere io che la reflession del mare dovesse esser, per l’egualità della sua superficie, più gagliarda che quella della terra, la cui superficie è tanto scabrosa ed opaca.

SALV. Quanto al primo dubbio, dico che, sì come nelle parti della Terra, che tutte per la lor gravità conspirano ad approssimarsi quanto più possono al centro, alcune tuttavia ne rimangono più remote che l’altre, cioè le montagne più delle pianure, e questo per la lor solidità e durezza (ché se fusser di materia fluida si spianerebbero), così il Solidità del globo
lunare si argomenta
dall’esser montuoso. veder noi alcune parti della Luna restare elevate sopra la sfericità delle parti più basse arguisce la loro durezza, perché è credibile che la materia della Luna si figuri in forma sferica per la concorde conspirazione di tutte le sue parti al medesimo centro.⁸⁸ Circa l’altro dubbio, parmi che per le cose che aviamo considerate accader negli specchi, possiamo intender benissimo che la reflession del lume che vien dal mare sia inferiore assai a quella che vien dalla terra, intendendo peròReflession del lume
più debile dal mare
che dalla terra. della reflessione universale; perché quanto alla particolare che la superficie dell’acqua quieta manda in un luogo determinato, non ha dubbio che chi si constituirà in tal luogo, vedrà nell’acqua un reflesso potentissimo, ma da tutti gli altri luoghi si vedrà la superficie dell’acqua più oscura di quella della terra. E per mostrarlo al senso, andiamo qua in sala e Esperienza che
mostra la reflession
dell’acqua men chiara
di quella della terra.versiamo un poco di acqua sul pavimento: ditemi ora, non si mostr’egli questo mattone bagnato più oscuro assai degli altri asciutti? Certo sì, e tale si mostrerà egli rimirato da qualsivoglia luogo, eccettuatone un solo, e questo è quello dove arriva il reflesso del lume che entra per quella finestra: tiratevi adunque indietro pian piano.

SIMP. Di qui veggo io la parte bagnata più lucida del resto del pavimento, e veggo che ciò avviene perché il reflesso del lume, che entra per la finestra, viene verso di me.

SALV. Quel bagnare non ha fatto altro che riempier quelle piccole cavità che sono nel mattone e ridur la sua superficie a un piano esquisito, onde poi i raggi reflessi vanno uniti verso un medesimo luogo: ma il resto del pavimento asciutto ha la sua asprezza, cioè una innumerabil varietà di inclinazioni nelle sue minime particelle, onde le reflessioni del lume vanno verso tutte le parti, ma più debili che se andasser tutte unite insieme; e però poco o niente si varia il suo aspetto per riguardarlo da diverse bande, ma da tutti i luoghi si mostra l’istesso, ma ben men chiaro assai che quella reflession della parte bagnata. Concludo per tanto che la superficie del mare, veduta dalla Luna, sì come apparirebbe egualissima (trattone le isole e gli scogli), così Luce secondaria
della Luna più
chiara innanzi la
congiunzione che
doppo.apparirebbe men chiara che quella della terra, montuosa e ineguale. E se non fusse ch’io non vorrei parer, come si dice, di volerne troppo, vi direi d’aver osservato nella Luna quel lume secondario, ch’io dico venirle dalla reflession del globo terrestre, esser notabilmente più chiaro due o tre giorni avanti la congiunzione che doppo, cioè quando noi la veggiamo avanti l’alba in oriente che quando si vede la sera, doppo il tramontar del Sole, in occidente; della qual differenza ne è causa che l’emisferio terrestre che si oppone alla Luna orientale ha poco mare ed assaissima terra, avendo tutta l’Asia, doveché, quando ella è in occidente, riguarda grandissimi mari, cioè tutto l’Oceano Atlantico sino alle Americhe: argomento assai probabile del mostrarsi meno splendida la superficie dell’acqua che quella della terra.

SIMP. Ma credete voi forse che quelle gran macchie che si veggono nella faccia della Luna, siano mari, e ’l resto più chiaro, terra o cosa tale?⁸⁹

SALV. Questo che voi domandate è il principio delle incongruenze ch’io stimo esser tra la Luna e la Terra, dalle quali sarà tempo che noi ci sbrighiamo, ché pur troppo siamo dimorati in questa Luna. Dico dunque che quando in natura non fusse Le parti più oscure
della Luna son piane,
e le più chiare
montuose.altro che un modo solo per far apparir due superficie, illustrate dal Sole, una più chiara dell’altra, e che questo fosse per esser una di terra e l’altra di acqua bisognerebbe necessariamente dire che la superficie della Luna fosse parte terrea e parte aquea; ma perché vi sono più modi conosciuti da noi, che posson cagionare il medesimo effetto, ed altri per avventura ne posson essere incogniti a noi, però io Intorno alle macchie
della Luna sono lunghe
tirate di montagne.non ardirei di affermare, questo più che quello esser nella Luna. Già si è veduto di sopra come una piastra d’argento bianchito, col toccarlo col brunitoio, di candido si rappresenta oscuro; la parte umida della Terra si mostra più oscura della arida; ne i dorsi delle montagne, le parti silvose appariscono assai più fosche delle nude e sterili; ciò accade, perché tra Nella Luna non si
generano cose simili alle
nostre, ma diversissime,
quando pur vi sia
generazione.le piante casca gran quantità di ombra, ed i luoghi aprici son tutti illuminati dal Sole; e questa mistione di ombre opera tanto, che voi vedete ne i velluti a opera il color della seta tagliata mostrarsi molto più oscuro che quel della non tagliata, mediante le ombre disseminate tra pelo e pelo, ed il velluto piano parimente assai più fosco che un ermisino fatto Luna non composta
di terra e d’acqua.della medesima seta: sì che quando nella Luna fossero cose che imitassero grandissime selve, l’aspetto loro potrebbe rappresentarci le macchie che noi veggiamo; una tal differenza farebbero s’elle fusser mari; e finalmente non repugna che potesse esser che quelle macchie fosser realmente di color più oscuro del rimanente, ché in questa guisa la neve fa comparir le montagne più chiare. Quello che si vede manifestamente nella Luna è che le parti più oscure son tutte pianure, con pochi scogli e argini dentrovi, ma pur ve ne son alcuni: il restante più chiaro è tutto pieno diAspetti del Sole,
necessarii per le
nostre generazioni,
non sono tali
nella Luna. scogli, montagne, arginetti rotondi e di altre figure; ed in particolare intorno alle macchie sono grandissime tirate di montagne. Dell’esser le macchie superficie piane, ce ne assicura il veder come il termine che distingue la parte illuminata dall’oscura, nel traversar le macchie fa il taglio eguale, ma nelle parti chiare si mostra per tutto anfrattuoso e merlato. Ma non so già se questa egualità di superficie possa esser bastante per sé sola a far apparir l’oscurità, e credo più tosto di no. Reputo, oltre a questo, la Luna differentissima dalla Terra, perché, se bene io mi immagino che quelli non sien paesi oziosi e morti, non affermo però che vi sieno movimenti e vita, e molto meno che vi si generino piante, animali o altre cose Giorni naturali
nella Luna sono di
un mese l’uno.simili alle nostre, ma, se pur ve n’è, fussero diversissime, e remote da ogni nostra immaginazione: e muovomi a così credere, perché, primamente, stimo che la materia del globo lunare non sia di terra e di acqua, e questo solo basta a tor via le generazioni e alterazioni simili alle nostre; ma, posto anco che lassù fosse acqua e terra, ad ogni modo non vi nascerebbero piante ed animali simili a i nostri, e questo per due ragioni principali. La prima è, che per le nostre generazioni son tanto necessarii gli aspetti variabili del Sole, che senza essi il tutto mancherebbe:⁹⁰ ora le abitudini del Sole verso la Terra son molto differenti da quelle verso Alla Luna il Sole
s’abbassa ed alza con
diversità di gradi 10,
ed alla Terra di
gradi 47.la Luna. Noi, quanto all’illuminazion diurna, abbiamo nella maggior parte della Terra ogni ventiquattr’ore parte di giorno e parte di notte, il quale effetto nella Luna si fa in un mese; e quello abbassamento ed alzamento annuo per il quale il Sole ci apporta le diverse stagioni e la disegualità de i giorni e delle notti, nella Luna si finisce pur in un mese; e dove il Sole a noi si alza ed abbassa tanto, che dalla massima alla minima altezza vi corre circa quarantasette gradi di differenza, cioè quanta è la distanza dall’uno all’altro tropico, nella Luna non importa altro che gradi dieci o poco più, ché tanto importano le massime latitudini del dragone di qua e di là dall’eclittica.⁹¹ Considerisi ora qual sarebbe l’azion del Sole dentro alla zona torrida quando e’ durasse quindici giorni continui a ferirla con i suoi raggi, che senz’altro s’intenderà che tutte le piante le erbe e gli animali si dispergerebbero; e se pur vi siNella Luna non
sono piogge. facessero generazioni, sarebber di erbe piante ed animali diversissimi da i presenti. Secondariamente, io tengo per fermo che nella Luna non siano piogge, perché quando in qualche parte vi si congregassero nugole, come intorno alla Terra, ci verrebbero ad ascondere alcuna di quelle cose che noi col telescopio veggiamo nella Luna, ed in somma in qualche particella ci varierebber la vista; effetto che io per lunghe e diligenti osservazioni non ho veduto mai, ma sempre vi ho scorto una uniforme serenità purissima.

SAGR. A questo si potrebbe rispondere, o che vi fossero grandissime rugiade, o che vi piovesse ne i tempi della lor notte, cioè quando il Sole non la illumina.

SALV. Se per altri riscontri noi avessimo indizii che in essa si facesser generazioni simili alle nostre, e solo ci mancasse il concorso delle piogge, potremmo trovarci questo o altro temperamento che supplisse in vece di quelle, come accade nell’Egitto dell’inondazione del Nilo; ma non incontrando accidente alcuno che concordi co i nostri, de’ molti che si ricercherebbero per produrvi gli effetti simili, non occorre affaticarsi per introdurne un solo, e quello anco non perché se n’abbia sicura osservazione, ma per una semplice non repugnanza. Oltre che, quando mi fosse domandato quello che la prima apprensione ed il puro naturale discorso mi detta circa il prodursi là cose simili o pur differenti dalle nostre, io direi sempre, differentissime ed a noi del tutto inimmaginabili, ché così mi pare che ricerchi la ricchezza della natura e l’onnipotenza del Creatore e Governatore.⁹²

SAGR. Estrema temerità mi è parsa sempre quella di coloro che voglion far la capacità umana misura di quanto possa e sappia operar la natura, dove che, all’incontro, e’ non è effetto alcuno in natura, per minimo che e’ sia, all’interaIl non aver
mai inteso nulla
perfettamente fa
che alcuni credono
d’intender il tutto. cognizion del quale possano arrivare i più specolativi ingegni. Questa così vana prosunzione d’intendere il tutto non può aver principio da altro che dal non avere inteso mai nulla, perché, quando altri avesse esperimentato una volta sola a intender perfettamente una sola cosa ed avesse gustato veramente come è fatto il sapere, conoscerebbe come dell’infinità dell’altre conclusioni niuna ne intende.

SALV. Concludentissimo è il vostro discorso; in confermazion del quale abbiamo l’esperienza di quelli che intendono o hanno inteso qualche cosa, i quali quanto più sono sapienti, tanto più conoscono e liberamente confessano di saper poco; ed il sapientissimo della Grecia, e per tale sentenziato da gli oracoli, diceva apertamente conoscer di non saper nulla.

SIMP. Convien dunque dire, o che l’oracolo, o l’istesso Socrate, fusse bugiardo, predicandolo quello per sapientissimo, e dicendo questo di conoscersi ignorantissimo.

SALV. Non ne séguita né l’uno né l’altro, essendo che amendue i pronunziati posson esser veri. Giudica l’oracolo sapientissimo Socrate sopra gli altri uomini, la sapienza de i quali è limitata; si conosce Socrate non saper nulla in relazione Responso dell’oracolo
vero in giudicar Socrate
sapientissimo.alla sapienza assoluta, che è infinita; e perché dell’infinito tal parte n’è il molto che ’l poco e che il niente (perché per arrivar, per esempio, al numero infinito tanto è l’accumular migliaia, quanto decine e quanto zeri), però ben conosceva Socrate, la terminata sua sapienza esser nulla all’infinita, che gli mancava. Ma perché pur tra gli uomini si trova qualche sapere, e questo non egualmente compartito a tutti, potette Socrate averne maggior parte de gli altri, e perciò verificarsi il responso dell’oracolo.

SAGR. Parmi di intender benissimo questo punto. Tra gli uomini, Sig. Simplicio, è la potestà di operare, ma non egualmente participata da tutti: e non è dubbio che la potenza d’un imperadore è maggiore assai che quella d’una persona privata; ma e questa e quella è nulla in comparazione dell’onnipotenza Saper divino infinite
volte infinito.divina. Tra gli uomini vi sono alcuni che intendon meglio l’agricoltura che molti altri; ma il saper piantar un sermento di vite in una fossa, che ha da far col saperlo far barbicare, attrarre il nutrimento, da quello scierre questa parte buona per farne le foglie, quest’altra per formarne i viticci, quella per i grappoli, quell’altra per l’uva, ed un’altra per i fiocini, che son poi l’opere della sapientissima natura? Questa è una sola opera particolare delle innumerabili che fa la natura, ed in essa sola si conosce un’infinita sapienza, talché si può concludere, il saper divino esser infinite volte infinito.

SALV. Eccone un altro esempio. Non direm noi che ’l sapere scoprire in un marmo una bellissima statua ha sublimato l’ingegno del Buonarruoti assai assai sopra gli ingegni Buonarruoti
d’ingegno subblime.comuni degli altri uomini? E questa opera non è altro che imitare una sola attitudine e disposizion di membra esteriore e superficiale d’un uomo immobile; e però che cosa è in comparazione d’un uomo fatto dalla natura, composto di tante membra esterne ed interne, de i tanti muscoli, tendini, nervi, ossa, che servono a i tanti e sì diversi movimenti? Ma che diremo de i sensi, delle potenze dell’anima, e finalmente dell’intendere? non possiamo noi dire, e con ragione, la fabbrica d’una statua cedere d’infinito intervallo alla formazion d’un uomo vivo, anzi anco alla formazion d’un vilissimo verme?

SAGR. E qual differenza crediamo che fusse tra la colomba d’Archita⁹³ ed una della natura?

SIMP. O io non sono un di quegli uomini che intendano, o ’n questo vostro discorso è una manifesta contradizione. Voi tra i maggiori encomii, anzi pur per il massimo di tutti, attribuite all’uomo, fatto dalla natura, questo dell’intendere; e poco fa dicevi con Socrate che ’l suo intendere non era nulla; adunque bisognerà dire che né anco la natura abbia inteso il modo di fare un intelletto che intenda.

SALV. Molto acutamente opponete; e per rispondere all’obbiezione, convien ricorrere a una distinzione filosofica, dicendo che l’intendere si può pigliare in due modi, cioè intensive o vero extensive: e che extensive, cioè quanto alla moltitudine degli intelligibili, che sono infiniti, l’intender umano è come nullo, quandoL’uomo intende
assai intensive, ma
poco extensive. bene egli intendesse mille proposizioni, perché mille rispetto all’infinità è come un zero; ma pigliando l’intendere intensive, in quanto cotal termine importa intensivamente, cioè perfettamente, alcuna proposizione, dico che l’intelletto umano ne intende alcune così perfettamente, e ne ha così assoluta certezza, quanto se n’abbia l’istessa natura; e tali sono le scienze matematiche pure, cioè la geometria e l’aritmetica, delle quali l’intelletto divino ne sa bene infinite proposizioni di più, perché le sa tutte, ma di quelle poche intese dall’intelletto umano credo che la cognizione agguagli la divina nella certezza obiettiva, poiché arriva a comprenderne la necessità, sopra la quale non par che possa esser sicurezza maggiore.

SIMP. Questo mi pare un parlar molto resoluto ed ardito.

SALV. Queste son proposizioni comuni e lontane da ogni ombra di temerità o d’ardire⁹⁴ e che punto non detraggono di maestà alla divina sapienza, sì come niente diminuisce la Sua onnipotenza il dire che Iddio non può fare che il fatto non sia fatto. Ma dubito, Sig. Simplicio, che voi pigliate ombra per esser state ricevute da voi le mie parole con qualche equivocazione. Però,Modo di conoscere di
Dio diverso da quello
de gli uomini. per meglio dichiararmi, dico che quanto alla verità di che ci danno cognizione le dimostrazioni matematiche, ella è l’istessa che conosce la sapienza divina; ma vi concederò bene che il modo col quale Iddio conosce le infinite proposizioni, delle quali noi conosciamo alcune poche, è sommamente più eccellente del nostro, il quale procede con discorsi e con passaggi di conclusione in conclusione, dove il Suo è di Intendere umano
fatto per discorso.un semplice intuito: e dove noi, per esempio, per guadagnar la scienza d’alcune passioni del cerchio, che ne ha infinite, cominciando da una delle più semplici e quella pigliando per sua definizione, passiamo con discorso ad un’altra, e da questa alla terza, e poi alla quarta etc., l’intelletto divino con la semplice apprensione della sua essenza comprende, senza temporaneo Definizioni comprendono
virtualmente tutte le
passioni delle cose
definite.discorso, tutta la infinità di quelle passioni; le quali anco poi in effetto virtualmente si comprendono nelle definizioni di tutte le cose, e che poi finalmente, per esser infinite, forse sono una sola nell’essenza loro e nella mente divina. Il che né anco all’intelletto umano è del tutto incognito, ma ben da profonda e densa caligine adombrato, la qual viene in parte assottigliata e chiarificata quando ci siamo fatti padroni di alcune conclusioni fermamente dimostrate tanto speditamente possedute da noi, che tra esse possiamo velocemente trascorrere: perché in somma, che Passioni infinite
sono forse una sola.altro è l’esser nel triangolo il quadrato opposto all’angolo retto eguale a gli altri due che gli sono intorno, se non l’esser i parallelogrammi sopra base comune e tra le parallele, tra loro eguali? e questo non è egli finalmente il medesimo, che essere eguali quelle due superficie che adattate insieme non si avanzano, ma si racchiuggono dentro al medesimo termine?⁹⁵ Or questi passaggi, che l’intelletto nostro fa Passaggi fatti con
tempo dal discorso
umano, l’intelletto
divino fa in
instanti, cioè gli
ha sempre presenti.con tempo e con moto di passo in passo, l’intelletto divino, a guisa di luce, trascorre in un instante, che è l’istesso che dire, gli ha sempre tutti presenti. Concludo per tanto, l’intender nostro, e quanto al modo e quanto alla moltitudine delle cose intese, esser d’infinito intervallo superato dal divino; ma non però l’avvilisco tanto, ch’io lo reputi assolutamente nullo; anzi, quando io vo considerando quante e quanto maravigliose cose hanno intese investigate ed operate gli uomini, pur troppo chiaramente conosco io ed intendo, esser la mente umana opera di Dio, e delle più eccellenti.

SAGR. Io son molte volte andato meco medesimo considerando, in proposito di questo che di presente dite, quanto grande sia l’acutezza dell’ingegno umano; e mentre io discorro per tante e tanto maravigliose invenzioni trovate da gli uomini, sì nelle arti come nelle lettere, e poi fo reflessione sopra il saper mio, tanto lontano dal potersi promettere non solo di ritrovarne alcuna di nuovo, ma anco di apprendere delle già ritrovate, confuso dallo stupore ed afflitto dallaIngegno umano
mirabile in acuteza. disperazione, mi reputo poco meno che infelice. S’io guardo alcuna statua delle eccellenti, dico a me medesimo: «E quando sapresti levare il soverchio da un pezzo di marmo, e scoprire sì bella figura che vi era nascosa? quando mescolare e distendere sopra una tela o parete colori diversi, e con essi rappresentare tutti gli oggetti visibili, come un Michelagnolo, un Raffaello, un Tiziano?» S’io guardo quel che hanno ritrovato gli uomini nel compartir gl’intervalli musici, nello stabilir precetti e regole per potergli maneggiar con diletto mirabile dell’udito, quando potrò io finir di stupire? Che dirò de i tanti e sì diversi strumenti? La lettura de i poeti eccellenti di qual meraviglia riempie chi attentamente considera l’invenzion de’ concetti e la spiegatura loro? Che diremo dell’architettura? cheL’invenzione dello
scrivere stupenda sopra
tutte l’altre. dell’arte navigatoria? Ma sopra tutte le invenzioni stupende, qual eminenza di mente fu quella di colui che s’immaginò di trovar modo di comunicare i suoi più reconditi pensieri a qualsivoglia altra persona, benché distante per lunghissimo intervallo di luogo e di tempo? parlare con quelli che son nell’Indie, parlare a quelli che non sono ancora nati né saranno se non di qua a mille e dieci mila anni? e con qual facilità? con i vari accozzamenti di venti caratteruzzi sopra una carta. Sia questo il sigillo di tutte le ammirande invenzioni umane, e la chiusa de’ nostri ragionamenti di questo giorno: ed essendo passate le ore più calde, il Sig. Salviati, penso io che avrà gusto di andare a godere de i nostri freschi in barca; e domani vi starò attendendo amendue per continuare i discorsi cominciati, etc.

 

---

¹ Aristotele (384-322 a.C.) era considerato il filosofo per eccellenza. In questa sede però importa soprattutto che elaborò una cosmologia, basata sugli omocentrici di Eudosso di Cnido e sviluppata sulle fondamenta della propria fisica. In quest’ambito le sue idee, sebbene molto modificate e ampliate dai suoi seguaci, furono superate soltanto nel XVII secolo, e nelle opere di Galileo Aristotele, e soprattutto l’aristotelismo, appaiono sempre come il grande nemico da sconfiggere.

² Claudio Tolomeo fu il massimo astronomo dell’antichità classica. Con i contributi geometrici di Apollonio e Ipparco, il sistema di deferentiepicicli ed eccentrici, e con l’equante di sua invenzione, sviluppò quella che era destinata a diventare la teoria astronomica dominante fino a Copernico. Il suo sistema è ovviamente geocentrico e geostatico, come quello di Aristotele, e tanto lui quanto i suoi seguaci si avvalsero della fisica aristotelica per sostenere la loro astronomia matematica.

³ Copernico (1473-1543) fu il primo capace di elaborare una cosmologia che costituiva un’alternativa totale a quella di Aristotele, e il cui sistema astronomico risultò tale da competere sul piano tecnico con quello di Tolomeo. La sua teoria forniva un’elegante soluzione all’eterno problema della retrogradazione dei pianeti, dimostrando che si trattava di pura apparenza. I suoi strumenti sia geometrici sia concettuali erano in grande misura quelli classici, ma il suo eliocentrismo e la concezione della Terra come uno tra i pianeti, e in movimento, poneva problemi fondamentali, non solo nel campo della fisica del tempo ma anche, per certuni, in campo religioso. Per tale ragione nel 1616 le opere di Copernico vennero incluse nell’Indice dei libri proibiti.

⁴ Per quanto riguarda la differenza tra il mondo sublunare e quello sovralunare, tra l’etere celeste e gli elementi acqua, aria, terra e fuoco, si veda Aristotele, De caelo, I, 2 e 3, specialmente 270b 20-25.

⁵ Tutto questo paragrafo e i «testi» ai quali allude Simplicio corrispondono a De caelo, I, 1, 268a 1-268b 10, e sono una parafrasi del testo aristotelico. L’espressione latina «ad pleniorem scientiam» significa «per una conoscenza più completa».

⁶ L’aneddoto relativo è riferito in Macrobio, Saturnalia, I, 6, 18-26. Macrobio sta spiegando l’origine dell’indumento chiamato praetexta e i significati assunti dal termine, riportando la storia di Papirio che ai nostri fini può riassumersi così: i senatori avevano l’abitudine di portare i loro figli alla curia, e Papirio vi fu condotto da suo padre. Quel giorno il senato aveva deciso che la questione che si stava dibattendo non venisse menzionata finché non fosse stata decisa nella sessione successiva. La madre di Papirio chiese a questi che cosa si era discusso durante la seduta, e Papirio le rispose che non poteva dirglielo; ma, di fronte alla cocciuta insistenza della madre, inventò che la discussione riguardava il problema se fosse più utile all’interesse dello stato che gli uomini si sposassero con due donne o le donne con due uomini. Il giorno dopo, la madre organizzò una manifestazione di madri di famiglia che avvicinò i membri del senato che si recavano in curia supplicandoli, piangendo, che decidessero che una donna poteva sposarsi con due uomini. Papirio dovette spiegare ai senatori sbalorditi che aveva inventato la faccenda per rispettare la decisione del silenzio. Da quel momento, venne vietato l’ingresso in senato dei bambini, eccezion fatta per Papirio che, per la sua prudenza, ricevette il nome di Praetextatus.

⁷ È questo il primo dei numerosi riferimenti fatti da Galileo, nel Dialogo, alla dottrina platonica della anamnesi, ovvero conoscenza come ricordo.

⁸ È questa la prima delle numerosissime occasioni in cui Simplicio, di fronte all’atteggiamento consueto di Salviati, che in fatto di filosofia naturale si richiama continuamente alla geometria, mette in discussione la pertinenza delle matematiche nello studio della natura. È una tesi tipica dell’aristotelismo che, ai tempi di Galileo, costituiva un fattore di dissenso e disputa con il platonismo nel campo della filosofia naturale.

⁹ Il testo aristotelico suona: «Tutti i corpi e le grandezze naturali, noi diciamo, sono per se stessi mobili secondo il luogo; diciamo infatti che la natura è principio di movimento in essi» De caelo, I, 2, 268b 15-17, trad. it. di Oddone Longo, 1962, p. 7.

¹⁰ Il significato delle parole di Sagredo non è chiaro, ma un altro luogo o testo aristotelico pertinente, oltre a quello già citato nella nostra nota 9, è il seguente: «La natura è un principio e una causa del movimento e della quiete in tutto ciò che esiste di per sé e non per accidente», Fisica, II, 1, 192b, 22-23, trad. it. di Antonio Russo, 1968, p. 29.

¹¹ Tra i Frammenti scritti da Galileo in relazione al Dialogo, che Favaro riunì e pubblicò di seguito a questo, se ne trova uno che sviluppa tale idea, però mettendolo in bocca a Salviati. Il passo suona: «Tu, Aristotile, determini i moti semplici esser quelli che si fanno per linee semplici, e chiami linee semplici la retta e la circolare. Ora, se la simplicità si deve attendere dalla simplicità della linea, il moto per una retta che passi per il centro sarà semplice, e come tale potrà esser naturale di qualche corpo semplice; e tale ancora sarà quello che traversi il cerchio senza passar per il centro: tuttavia poi tu dirai che il moto per la medesima retta sino al centro sarà contrario al conseguente per la medesima retta oltre al centro; e non vorrai più che il medesimo moto che tu chiamavi semplice, mercé dell’esser fatto per una stessa retta semplice, convenga al medesimo corpo semplice, e non vorrai che nell’istessa retta semplice siano moti contrarii.
«Il convenirsi il moto semplice al corpo semplice bisogna che sia un moto la cui simplicità si attenda da altro che dalla simplicità della linea; perché così il moto al centro non sarebbe proprio e naturale de i gravi più che il moto del centro…» (Opere, VII, p. 546).

¹² Così è perché, nell’universo aristotelico, gli unici moti retti e naturali che possono esistere sono i moti verso l’alto o verso il basso dei corpi leggeri o pesanti, rispettivamente verso il loro luogo naturale e questi, secondo Aristotele (De caelo, I, 8, 277a 28-30), sono accelerati.

¹³ Galileo allude qui ad Aristotele, De caelo, I, 2; si noti però che queste argomentazioni e tesi sono reperibili anche in Fisica, VIII, 8-9, 265 a e b.

¹⁴ Vale a dire l’etere, che è la materia di cui nella cosmologia aristotelica si compone il mondo celeste.

¹⁵ Vale a dire i corpi del mondo sublunare costituiti dai quattro elementi.

¹⁶ Senza dubbio il riferimento è al termine greco «kosmos», con il quale i greci ci hanno indotti a pensare all’universo come ordinato. Comunque, Aristotele ritiene che un universo disordinato sia un controsenso (si veda De caelo, III, 2, 301a), e Galileo condivide con lui questa premessa.

¹⁷ Tutta questa argomentazione assomiglia straordinariamente al tipo di argomento logico e sistematico di Aristotele, che Galileo ha appena criticato. È ovvio che Galileo, come qualsiasi scienziato mai esistito, dà per scontato che il mondo sia naturalmente ordinato. Ma, come cristiano, ritiene più adeguata la metafisica creazionista di quella eternista. Risulta del resto chiaro che egli era affascinato, come tutti i suoi predecessori, dalla priorità del movimento circolare che solo Keplero, dopo una lunga lotta, avrebbe respinto. Per quanto riguarda i precedenti più immediati, è evidente che qui Galileo è del tutto copernicano e fa proprio un argomento già sviluppato da Copernico nel suo De revolutionibus, I, 8, dove si legge: «Dunque, come dicono, a un corpo semplice appartiene un movimento semplice (il che si verifica in primo luogo a proposito del circolare), tanto a lungo quanto il corpo semplice resta nel suo luogo naturale e nella sua unità. Infatti, in questo luogo il movimento non è altro che circolare, ed esso rimane interamente in sé, simile allo stato di quiete. Invece il movimento rettilineo sopravvive in quelle cose che si muovono fuori del loro luogo naturale, si che ne siano cacciate, sia che in qualche modo ne siano fuori. Ora nulla repugna tanto all’ordine del tutto e alla forma del mondo quanto il fatto che qualcosa sia fuori dal suo posto. Dunque il movimento rettilineo non accade se non alle cose che non si trovano a posto, e non sono perfette secondo natura, ma si separano dal loro tutto e abbandonano la loro unità».

¹⁸ Come ha reso evidente Sambursky, «Galileo’s Attempt at a Cosmogony», in Isis, LIII (1962), pp. 460-463, dal momento che questa idea si trova in Platone, Galileo si riferisce qui al testo del Timeo 38a-39b, sebbene il testo platonico sia ben lungi dall’affermare ciò che gli attribuisce Galileo. Come fa notare A. Koyré, gli autori del tempo di Galileo nutrirono grande interesse per questa concezione platonica. Mersenne, che non era riuscito a imbattersi in questa dottrina in Platone, scrisse a Peiresc perché consultasse in merito Gassendi, ma tutto fu inutile. Non maggior fortuna hanno avuto gli studiosi moderni. «È stato così necessario arrendersi di fronte all’evidenza: per quanto sublime possa essere, la teoria in questione non si trova in Platone» (Koyré, 1972, p. 242).
D’altro canto, in una lettera a Carcavy del giugno 1637 (Opere, XVII, p. 89), Galileo parla della sua speculazione come di «un capriccio et una bizzarria, cioè jocularis quaedam audacia». Ciò è parso legittimare l’ipotesi che in realtà Galileo non prendesse molto sul serio tale speculazione cosmologica. Sta però di fatto che, sia che si rifaccia a una lettura di Platone, sia che si tratti di una sua invenzione, qui ne fa due volte menzione, nella Giornata prima del Dialogo, e nei Discorsi torna a riprenderla, riferendosi a essa come a un concetto «degno di Platone; ed è tanto più da stimarsi, quanto i fondamenti taciuti da quello e scoperti dal nostro Autore, con levargli la maschera o sembianza poetica, lo scuoprono in aspetto di verace istoria» (Opere, VIII, p. 284). Tutto questo induce a credere che si tratti di qualcosa di più di un mero ornamento letterario (si veda in proposito Koyré, 1972, pp. 228-244). Umberto Barcaro ha avanzato più di recente l’ipotesi che il testo galileiano debba esser letto in una chiave simile a quella riservata, nell’opera di Platone, ai miti mediante i quali una dottrina filosofica risulta illustrata con particolare efficacia in forma figurata («Riflessioni sul mito platonico del “Dialogo”», in Galluzzi, a cura di, 1984, pp. 117-128, specialmente p. 117).
Si può inoltre aggiungere un ulteriore aspetto, anch’esso di carattere speculativo. Quando si rifletta in teoria sulla formazione della Terra a partire dal «primo caos», come dice anche Galileo, nel contesto del mito giudaico-cristiano della creazione, studiato da autori come Cartesio (Principi, IV, 2-3) e soprattutto dagli immediatamente successivi «teorici della Terra», da Thomas Burnet in poi, non sembra troppo azzardato ritenere che Galileo attribuisse una certa verosimiglianza alla sua idea platonica. Soprattutto perché, nel De motu, Galileo aveva già fatto certe riflessioni in merito. Si veda a questo proposito la mia Introduzione. Per quanto attiene ad altri aspetti della speculazione platonica di Galileo, si veda più avanti la nostra nota 28.

¹⁹ Si riferisce, ovviamente, allo stesso Galileo che era il massimo protagonista dell’Accademia dei Lincei fondata poco prima e patrocinata dal principe Federico Cesi. L’Accademia riuniva i più validi difensori di una nuova e rinnovatrice politica culturale e scientifica. Galileo, sia detto di passaggio, si serviva appunto di questo espediente dell’autoriferimento, ogni volta che voleva rivendicare la proprietà o priorità di un’idea.

²⁰ Il termine grado, in italiano come in spagnolo, equivale al latino gradus, che fu introdotto e ampiamente usato dagli scolastici nella loro trattazione del problema «de intensione et remissione formarum», vale a dire del crescere e del decrescere della qualità o forme in senso aristotelico. Lasciando da parte i possibili antecedenti, gli autori che svilupparono la cinematica del Merton College, fra cui Heytesbury, Bradwardine e Swineshead, affermarono che l’aumento o il decrescere dell’intensità qualitativa aveva luogo per gradi di intensità. Questi filosofi applicarono immediatamente queste idee e le regole numeriche sviluppate, al caso del movimento locale e, in particolare, al movimento accelerato. Questo era inteso come una variazione positiva o negativa della velocità del movimento, intensio et remissio motus. Il grado di velocità (gradus velocitatis) o grado di movimento (gradus motus) designava la misura della qualità e intensità del movimento e, nel caso di movimenti non uniformi, la velocità istantanea. Uno dei loro grandi risultati, a partire da queste definizioni, fu la formulazione del teorema del «grado medio» o «velocità media» con il quale si riduceva un movimento accelerato a un movimento di velocità uniforme. È ben noto che Galileo introduce tale teorema, con una formulazione quasi identica, come Teorema primo, Proposizione I del Libro secondo, sul movimento accelerato dei Discorsi (Opere, VIII, p. 208). D’altra parte, l’uso continuato di questa terminologia medievale nei Discorsi rivela quanto fosse difficile, per Galileo, liberarsi completamente di questi presupposti e di questa concezione della velocità, che ancora non è quella della scienza moderna. Si veda in proposito l’articolo di Kuhn, «A function for Thought Experiments», in Kuhn, 1977, pp. 240-265.
Questa e altre coincidenze indussero Duhem a vedere in Galileo un «mero continuatore» degli autori medievali. Oggi la tesi continuista ha tuttora difensori, a volte in termini assai più sfumati, per esempio in uno storico come M. Clagett (Clagett, 1959), altre volte invece in senso più radicale come nel caso di W.A. Wallace, uno dei grandi studiosi dell’attualità delle fonti del giovane Galileo (si veda per esempio Wallace, 1977, 1981 e 1984). Oggi però, come negli anni Cinquanta, la polemica che divide i continuisti da coloro che postulano una rottura tra le idee di quegli autori medievali e quelle di Galileo, tra la scienza medievale e quella moderna, non è vista soltanto – a volte in senso assoluto – quale un disaccordo circa i dati di fatto.
In ogni caso, per quanto riguarda l’espressione grado di velocità, Galluzzi richiama l’attenzione sul fatto che quest’espressione appare per la prima volta in Galileo non nel suo periodo giovanile, «più medievale», di Pisa, ma già nel periodo padovano, nella famosa lettera del 1604 a Paolo Sarpi, dove egli riferisce la velocità raggiunta da un corpo in caduta a una determinata distanza dal suo punto di partenza (Opere, X, p. 115).

²¹ Come risulta evidente dallo sviluppo dell’argomento, il termine «accelerazione» si riferisce qui al processo di aumento della velocità, che è l’opposto o inverso del «rallentamento» o perdita di velocità. Non si tratta dunque della «grandezza» fisica che il termine acquista nella fisica newtoniana, e che Galileo non giunse a concepire. Va detto, d’altra parte, che la caratterizzazione dell’accelerazione proposta qui da Galileo è assai vicina a quella animistica di Aristotele: la terra si muove tanto più rapidamente quanto più è vicina al centro» (De caelo, I, 8, 277a 28-30), ed è completamente diversa dalle linee di riflessione di Galileo, palesi in tutta la sua opera, circa la natura o proprietà dell’accelerazione dei corpi di caduta. Alla luce di queste considerazioni, è stata avanzata l’ipotesi (Galluzzi, 1979, p. 327, nota 45) che Galileo se ne serva semplicemente perché si sposa bene con il «mito platonico», e che non si deve attribuirle eccessiva importanza. Infatti, nei Discorsi (Opere, VIII, p. 202) Galileo menziona la causa dell’accelerazione, definendo «fantasie» le varie spiegazioni che «da varii filosofi […] sono state prodotte». Finocchiaro, invece, attribuisce grande importanza a queste tesi di Galileo sull’accelerazione (si veda Finocchiaro, 1980, pp. 80 ss.).

²² Nella sua edizione, Favaro ha utilizzato anche un esemplare dell’edizione originale del Dialogo appartenuta a Galileo, che contiene annotazioni e correzioni di sua mano, e oggi è conservata nella Biblioteca del Seminario di Padova. In tale esemplare, dopo «miracolosa» prima della replica di Sagredo, si legge la seguente aggiunta, vergata dallo stesso Galileo. «Muovasi con qual si voglia velocità qual si sia poderosissimo mobile, ed incontri qualsivoglia corpo costituito in quiete, ben che debolissimo e di minima resistenza; quel mobile, incontrandolo, già mai non gli conferirà immediatamente la sua velocità: segno evidente di che ne è il sentirsi il suono della percossa, il quale non si sentirebbe, o per dir meglio non sarebbe, se il corpo che stava in quiete ricevesse, nell’arrivo del mobile, la medesima velocità di quello.»

²³ Il termine italiano «impeto», con cui Galileo traduce il termine tecnico impetus, ha una sfera semantica diversa. Qui è importante capire fino a che punto Galileo conoscesse, e se ne servisse, concezioni anteriori e in che misura elaborasse la propria concezione indipendentemente, pur servendosi degli stessi termini. Potremmo sintetizzare la storia in questione come segue.
Assodato il principio secondo cui «tutto ciò che si muove è mosso da qualcosa» (Fisica, VII, 1, 2, 241b 34), Aristotele incontrò gravi difficoltà nello spiegare la continuità del movimento dei proietti, una volta che cessavano di essere in contatto con il proiciente (Fisica, VIII, 10, 266b 27 ss.). Ma, anche nel caso dell’accelerazione dei gravi in caduta, la sua spiegazione risentiva di grandi difficoltà o insufficienze e fu assai presto oggetto di critiche. Secondo Simplicio (si veda Clagett, 1972, p. 579), il famoso astronomo Ipparco aveva introdotto una teoria alternativa che unificava la spiegazione del movimento naturale e di quello violento. Secondo tale teoria, quando lanciamo una pietra all’insù, le imprimiamo una virtù o forza che fa sì che si muova verso l’alto, a patto che tale virtù sia più forte della tendenza naturale del corpo verso il basso. A mano a mano che diminuisce la virtù motrice impressa al corpo, questo rallenta la propria ascesa e quando la gravità della pietra è in equilibrio con tale virtù, la pietra si ferma e immediatamente comincia a cadere. In questo momento, però, la virtù motrice impressa non è ancora uguale a zero, ma solo minore della tendenza verso il basso dovuta al peso della pietra. Così dunque la velocità della pietra nella sua caduta aumenta nella misura in cui la virtù impressa, che adesso agisce ritardando la velocità di caduta, si va riducendo e quando essa scompare, la pietra raggiunge il massimo di accelerazione nella sua caduta. Questa teoria della virtù motrice impressa fu ripresa o reintrodotta da Filopono nel VI secolo d.C., nel secolo XII da alcuni autori arabi, che la denominarono mail, e da costoro passò in Europa nel XIV secolo a opera di Francesco di Marchia che la chiamò virtus derelicta. Forse ispirandosi a questa, Buridano, nel secolo XIV, elaborò una teoria diversa, la «teoria dell’impetus». A differenza della virtus impressa, che si consumava da sé, l’impetus, comunicato al proietto e responsabile della continuità del suo movimento, aveva carattere permanente e si consumava soltanto a causa della resistenza dell’aria e del peso del corpo che lo portava verso il basso. Inoltre, l’impetus poteva essere misurato in funzione della quantità di materia del proietto e della velocità che gli era stata impartita. La teoria dell’impetus fu usata anche per spiegare l’accelerazione dei gravi in caduta: la gravità fa sì che un corpo pesante allontanato dal suo luogo naturale acquisisca, non solo movimento, ma anche un certo impetus che ha anch’esso la virtù di muovere e che si accresce a mano a mano che aumenta la velocità del movimento, col che viene a crearsi un circolo vizioso di maggior impetus, maggior velocità, vale a dire accelerazione. (Si veda M. Clagett, 1972, capp. 8 e 9.)
Verso la fine del decennio 1930-1940, prima che storici come E. Moody e M. Clagett chiarissero le differenze tra le teorie della virtus impressa e dell’impetus, Koyré sostenne che Galileo aveva conosciuto la teoria dell’«impetus» tramite l’opera di G.B. Benedetti, e l’aveva inclusa nel suo De motu pisano. Effettivamente, in quest’opera Galileo si serve indistintamente delle espressioni virtus impressa e impetus, ma tanto con l’una come con l’altra si riferisce alla virtus impressa quale fu intesa da Ipparco e Francesco di Marchia e in nessun caso all’impetus quale lo intendeva Buridano e lo riprese Benedetti. Moody (Moody, 1951) sostenne che Galileo l’avesse ripresa da Avempace. Lo stesso Galileo ci dice che, dopo concepito personalmente la teoria, lui stesso aveva dimostrato che Ipparco l’aveva parzialmente formulata (Opere, I, pp. 319-320). In ogni caso, oltre a distinguere le due teorie medievali, adesso si sostenne che, nel suo periodo iniziale, Galileo aveva ripreso da autori medievali quella della virtusimpressa, laddove la teoria dell’impetus di Buridano avrebbe influito in periodi successivi sul suo sviluppo. Ma, sebbene non manchino casi (per esempio, Opere, VIII, p. 279) in cui Galileo interpreta l’impetus come causa del movimento, è certo che nella sua opera della maturità è molto lontano dalla concezione di Buridano e, al contrario di questi, concepisce l’impetus o impeto come un effetto del moto e della velocità. Un esempio di quanto andiamo dicendo si trova proprio nel testo che ha dato motivo a questa nota. I gradi di impetus aumentano nella stessa proporzione dei gradi di velocità. Inoltre, questo aumento di impetus non influisce a sua volta sulla velocità, come invece succedeva nel circolo vizioso implicito nella concezione di Buridano. A volte Galileo parla indistintamente di grado di velocità e di impeto, nonché di grado di impeto, che sembra essere la contropartita dinamica del grado di velocità.

²⁴ Nella Giornata terza dei Discorsi, questo viene enunciato come l’unico principio del movimento accelerato (Opere, VIII, p. 205) e poco più avanti lo si dimostra in termini di teorema: «I gradi di velocità d’un mobile descendente con moto naturale dalla medesima sublimità per piani in qualsivoglia modo inclinati, all’arrivo all’orizonte son sempre eguali, rimossi gl’impedimenti» (Opere, VIII, p. 218).

²⁵ «Le cose hanno la stessa velocità se in un tempo uguale attraversano la stessa magnitudine» (Aristotele, Fisica, VII, 294a 19).

²⁶ Nei Discorsi, Galileo dà la seguente definizione: «Aequalem, seu uniformem, motum intelligo eum, cuius partes quibuscunque temporibus aequalibus a mobili peractae, sunt inter se aequales» («Moto eguale o uniforme intendo quello in cui gli spazi percorsi da un mobile in tempi eguali, comunque presi, risultano tra di loro eguali», Opere, VIII, p. 191, trad. it. di Adriano Carugo, in Galilei [1958], p. 169).

²⁷ Questo testo comporta una nuova definizione del concetto di velocità, come segnala Kuhn, 1977.

²⁸ Anche questa parte della cosmogonia platonica di Galileo è assai problematica. Infatti non si trova traccia di tali calcoli, non solo in nessuna pubblicazione posteriore, ma neppure nella corrispondenza di Galileo, cosa che per molto tempo ha giustificato l’asserzione che mai li fece. C’erano anche altri elementi che inducevano a pensarlo. Per esempio, il suo contemporaneo Mersenne eseguì effettivamente questi «lunghi e difficili calcoli» (Harmonie universelle. Seconde Partie. Traités de la nature des sons et des mouvements de toutes sortes des corps, Parigi 1637, pp. 103-107) mostrando che non coincidevano affatto con l’ipotesi galileiana secondo la quale tutti i pianeti provengono da uno stesso luogo. Successivamente Newton che, come è ben noto, era molto interessato a dimostrare la necessità dell’azione di Dio nel mondo, si occupò della speculazione galileiana. Innanzitutto, fece notare che l’accelerazione costante supposta da Galileo, nei pianeti che cadano dallo stesso punto, era incompatibile con il comportamento di questi e delle loro orbite. Naturalmente, in accordo con la sua teoria della gravitazione universale, Newton ipotizzò che l’accelerazione variasse in proporzione inversa al quadrato della distanza. Ne deriva però che i pianeti giungerebbero alle loro rispettive orbite a velocità doppia di quella necessaria per mantenersi in esse. (Si veda in proposito l’analisi di I.B. Cohen, «Galileo, Newton and the Divine Order of the Solar System», in E.A. McMullin, a cura di, 1967, pp. 207-231.)
Una svolta decisiva al problema è stata data da Drake che nel 1973 riportò alla luce una serie di manoscritti da lui datati al primo decennio del XVII secolo. Essi contengono solo operazioni matematiche e alcune circonferenze concentriche. Dal loro esame sembra però risultare evidente che Galileo eseguì effettivamente i calcoli in questione, utilizzando le distanze dal Sole attribuite da Keplero ai pianeti nel capitolo 20 della sua opera Harmonice mundi, pubblicata a Linz nel 1619, e di cui gli aveva inviato un esemplare. Nel suo entusiasmo filogalileiano e con notevole azzardo interpretativo, Drake non solo afferma che Galileo compì con buon esito i calcoli menzionati ma arriva a dire che, con questo lavoro, Galileo scoprì la terza legge di Keplero. L’articolo in questione è «Galileo’s “Platonic” Cosmogony and Kepler’s Prodromus», in Journal for the History of Astronomy, 4 (1973), pp. 174-191. (Si può vedere anche Drake, 1990, pp. 90 e 128-129.) Un’interpretazione più prudente, pur nella sua necessaria audacia, è quella di Eric Meyer, 1989. Dal suo lavoro, che rende evidenti alcuni errori fondamentali contenuti nell’interpretazione di Drake, si può dedurre che Galileo aveva già compiuto i calcoli che nel Dialogo dichiara di rimandare a un’altra occasione. Tuttavia le prove disponibili, nella misura in cui i manoscritti possono considerarsi tali, confermano che questi calcoli sono completamente errati e che in nessun caso si può affermarsi che la loro coincidenza con i dati di fatto risulti «cosa meravigliosa», come dice Galileo.

²⁹ Il testo in parentesi quadra che qui comincia corrisponde a un’aggiunta scritta, a questo punto, dallo stesso Galileo nell’esemplare menzionato di sua proprietà.

³⁰ Galileo scrive le «sensate esperienze» al plurale. Di qui un problema di difficile soluzione, in relazione alle due grandi interpretazioni classiche dell’opera galileiana, quella «sperimentalista», oggi rappresentata in termini radicali da Stillman Drake, e quella «razionalista» di Alexandre Koyré. La forma plurale dell’espressione sembra che ci autorizzi, o forse ci obblighi a interpretarla, non già nel senso di «esperienza», bensì in quello di «esperimento». Credo che, in altri casi, sia questa una versione possibile e corretta. Orbene, dato che oggi si è già introdotta una assai chiara distinzione tra «esperienza» ed «esperimento» (Koyré, 1977, p. 275), molte delle osservazioni o situazioni sperimentali descritte da Galileo nel corso della sua opera, ben difficilmente possono considerarsi esperimenti in senso stretto, bensì semplicemente osservazioni acute e, dal momento che Galileo usa un unico termine, credo sia meglio interpretare il termine «esperienze» appunto come tali. Del resto, in generale il contesto indica, con sufficiente chiarezza, il senso più attendibile. Ciò detto, a mio parere è chiaro che, nel testo in esame, Galileo si riferisce alla [evidenza del]la esperienza sensibile e che questo è anche il significato dell’espressione «il senso». È questa, in effetti, l’«esperienza» rivendicata da Aristotele e dall’aristotelismo, quella che, non dimentichiamolo, è difesa da Simplicio, che è colui che in questo passo sta parlando. Ritengo inoltre che sarebbe oltretutto contraddittorio mettere in bocca a Simplicio la difesa degli «esperimenti». Nel corso dell’opera, è quasi sempre questi a rivendicare il valore dell’esperienza nel senso di un’informazione immediata fornita dai sensi, mentre Salviati, vale a dire Galileo, pur rivendicando, come è evidente, la necessità dell’esperienza, mette in discussione questa immediatezza e insiste sulla complessità del rapporto esperienzateoria e sull’ingenuità di questo empirismo aristotelico. Mi permetto di rinviare, per lo sviluppo di questo problema, ad A. Beltrán, 1983, pp. 111-138.

³¹ Versione latina del principio che si può trovare già formulato in Aristotele, De caelo, I, 3, 270a 11. Lo si può interpretare come «lo stesso ragionamento si applica al tutto e alle sue parti». In questo contesto, tale principio dimostrerebbe che ciò che è certo quanto alle parti dei due elementi terra e fuoco – che cioè il loro movimento naturale è rettilineo rispettivamente verso il basso (o verso il centro) e verso l’alto (o dal centro) – lo sarà anche per tali elementi in quanto parti di un tutto.
Per quanto riguarda le altre espressioni latine, deorsum significa «verso il basso»; sursum «verso l’alto»; ad medium «verso il centro»; e a medio «in allontanamento dal centro».

³² È impossibile vedere qui un’anticipazione di idee newtoniane, quanto piuttosto la continuazione di una tradizione che potremmo considerare platonica. Nel Timeo, 63, Platone sembra proporre una teoria secondo la quale la gravità consisterebbe in un caso del principio generale secondo il quale «il simile attrae il simile». Aristotele infatti aveva pensato la possibilità esposta più avanti da Galileo il quale, naturalmente, la respingeva perché, come abbiamo visto, il luogo naturale, in questo caso il centro dell’universo, è dotato di certi poteri: «… il muoversi verso il proprio luogo è per ogni corpo come un muoversi verso la propria forma; e così andrebbe inteso il detto degli antichi che il simile tende verso il suo simile. Ma non è che accada sempre così: se infatti si trasferisse la Terra dove si trova la Luna, ogni sua parte si muoverebbe non verso il proprio luogo, bensì verso la Terra dove ora si trova» (De caelo, IV, 3, 310b 1-5). In Aristotele, come abbiamo già detto, la Terra si trova al centro dell’universo perché è questo il luogo naturale dei corpi pesanti. Ne deriva che, indipendentemente dal fatto che la Terra fosse spostata dal suo sito, il corpo pesante, in concreto quello costituito dall’elemento Terra, continuerebbe a tendere verso il centro dell’universo. La gravità, pertanto, è un rapporto di inclinazione di una determinata categoria di corpi – i pesanti – verso un determinato sito o luogo. Durante il Medioevo, soprattutto dopo le condanne del 1277, e in rapporto a questioni teologiche, la discussione circa l’ipotesi della pluralità o infinità dei mondi, coesistenti con il nostro, indusse autori come Oresme a ipotizzare la possibilità che gli elementi pesanti di ogni mondo avessero inclinazione a muoversi verso il centro di gravità del loro proprio mondo, o anche verso il centro di gravità del mondo più vicino, indipendentemente dalla loro provenienza (Oresme, Le livre du Ciel et du Monde, a cura di A.D. Menut e A.J. Denomy, in Medieval Studies, 1941, pp. 243-244). Oresme infatti era qui propenso ad accettare il principio che il simile attrae il simile (inclinatio ad suum simile), e pertanto spiegava la gravità come un rapporto tra parti simili di uno stesso corpo. Anche in Copernico si ritrova questa idea, però con nuove e importanti implicazioni. Dopo aver fatto notare che i movimenti apparenti dei pianeti e le loro distanze variabili mostrano che la Terra non è il centro di tutte le loro rivoluzioni, aggiunge: «Poiché esistono, dunque, vari centri, anche per quel che riguarda il centro del mondo non sarà azzardato dubitare che esso sia quello della gravità terrestre o un altro. Per parte mia, credo che la gravità non sia altro che una certa brama naturale, attribuita alle parti dalla divina provvidenza dell’artefice di tutte le cose, affinché si riuniscano nella loro unità e integrità congiungendosi in forma di globo. E questa inclinazione è credibile sia insita anche nel Sole, nella Luna e negli altri splendori erranti, cosicché per la sua efficacia essi restano in quella rotondità con cui si presentano, sebbene in molti modi effettuino i loro circuiti. (De revolutionibus, I, 9; trad. it. di C. Vivanti, in Copernico, 1975, p. 83). Se esaminiamo la formulazione di Galileo potremmo pensare che vi sia citato, pur senza menzionarlo, il testo di Copernico. Sta di fatto che con la tesi copernicano-galileiana ci ritroviamo, per così dire, nella tradizione platonica che si basa sul principio dell’attrazione del simile a opera del simile e non nella tradizione newtoniana secondo la quale la gravitazione è un’attrazione tra qualsivoglia categoria di corpi. Sicché, la teoria di Newton è completamente diversa sia da quella aristotelica sia da quella galileiana.

³³ Tra i Frammenti ce n’è uno assai esplicito in proposito: «Le parti della Terra hanno tal propensione al centro di essa, che quando ella cangiasse luogo, le dette parti (benché lontane dal globo nel tempo della mutazione di esso) la seguirebbero per tutto: esempio di ciò sia il seguito perpetuo delle Medicee, ancor che separate continuamente da Giove.
«L’istesso si deve dir della Luna, obbligata a seguir la Terra: il che serva per i semplici, che hanno renitenza a capire come questi 2 globi, non sendo legati insieme con una catena o infilzati ’n un’asta, si conseguitino l’un l’altro, sì che all’incitarsi o ritardarsi dell’uno, si acceleri o ritardi l’altro» (Opere, VII, p. 544).

³⁴ «Con chi nega i principi non si deve discutere», affermazione che proviene da Aristotele, Fisica, I, 2, 185a 1 ss.: «Esattamente come un geometra non ha nulla da dire a chi neghi i principi della sua scienza…, così un uomo che indaghi i principi non può discutere con uno che nega la loro esistenza». Si tratta di un principio che i critici aristotelici di Galileo gli rinfacciarono più volte scandalizzati. È chiaro che, oltre a illustrare una volta di più la fedeltà degli aristotelici alle formule e al formalismo del Maestro e in generale della tradizione, il principio illustra chiaramente la difficoltà di comunicazione tra i metodi di Galileo da un lato e quelli dello scienziato tradizionale dall’altro. L’assenza di comunicazione è tanto radicale da far sembrare che non possano mettersi d’accordo neppure circa la cosa più elementare, la più sicura e solida, sulla quale poggia tutta la teoria: i fatti, l’esperienza, l’evidenza dei sensi.

³⁵ De caelo, IV, 4-5, 311a 15-312b.

³⁶ «Accidentalmente», «per caso». L’affermazione deriva da Aristotele, De caelo, II, 13, 296b 15-16: «Si dà comunque il caso che il centro della Terra e il centro del tutto coincidano. I corpi gravi, infatti, si muovono verso il centro della Terra, ma accidentalmente, in virtù del fatto che il centro della Terra si trova nel centro del tutto».

³⁷ Galileo qui gioca con il titolo collettivo delle opere di logica di Aristotele, Organon, l’organo come parte funzionale del corpo e l’organo come strumento musicale. Quanto a ciò che segue, Aristotele ha scritto anche un’opera intitolata Poetica.

³⁸ Qui Galileo non solo denuncia l’errore di confondere senz’altro il centro della Terra con il centro dell’universo, ma almeno in parte si oppone direttamente al finalismo e animismo della concezione aristotelica dei «luoghi naturali». Aristotele attribuisce esplicitamente una certa «facoltà» ai «luoghi naturali» e, in concreto, al centro del mondo, laddove dice che alto e basso non si distinguono solo in rapporto a noi, ma in senso assoluto perché è la natura a distinguerli. «Il moto locale dei corpi naturali elementari – vale a dire, fuoco, aria, ecc. – mostra non solo che il luogo è un qualcosa, ma che esercita una certa influenza… “In alto” non indica una qualunque direzione casuale, bensì quella in cui si dirigono il fuoco e ciò che è leggero. Allo stesso modo, neppure “in basso” indica qualsivoglia direzione, bensì il luogo dove si dirigono le cose che pesano e quelle che sono fatte di terra. Ne deriva che tali luoghi, non solo differiscono per la loro posizione, ma anche perché sono dotati di diversi poteri» (Fisica IV, 1, 208b 8-22). D’altro canto, questa è una delle numerose occasioni in cui Galileo lascia in sospeso la questione della finitezza o infinità dell’universo. Si veda l’Introduzione, pp. 79-82.

³⁹ Si veda De caelo, I, 2-3, 269a-270b.

⁴⁰ È evidente che Galileo era in dubbio circa il tipo e la messa a fuoco dell’opportuna risposta a questa accusa che fu di fatto frequente nella disputa tra difensori della tradizione e protagonisti della controriforma da un lato e i «novatori», i «virtuosi», i «curiosi» dall’altro; con il suo Saggiatore, Galileo aveva sfidato apertamente e clamorosamente questa cultura ufficiale (si veda Redondi, 1983, specialmente cap. 3 che descrive in maniera brillante lo scontro tra le due correnti). I dubbi di Galileo risultano chiaramente palesi in vari Frammenti: da due di essi emerge che egli era tentato di dare una risposta polemica, quasi aggressiva. Il primo suona: «In materia dell’introdur novità.
«E chi dubita che la nuova introduzzione, del voler che gl’intelletti creati liberi da Dio si facciano schiavi dell’altrui volontà, non sia per partorire scandoli gravissimi?
«e che il volere che altri neghi i proprii sensi e gli posponga all’arbitrio di altri
«e che l’ammettere che persone ignorantissime d’una scienza o arte abbiano ad esser giudici sopra gl’intelligenti, e per l’autorità concedutagli siano potenti a volgergli a modo loro
«Queste sono le novità potenti a rovinare le repubbliche e sovvertire gli stati» (Opere, VII, p. 540). Il secondo, con alcune lacune che a volte Favaro si prova a colmare, suona: «dottrine nuove, che progiudicano, sono le vostre, che volete con non mai più… costringer l’intelletto e i sensi a non intendere e non vedere, etc. [che facendo il] moto o la quiete etc. materia di fede, tu metti Santa Chiesa in… pericolo che po[ssa accadere una] volta… [eretic]i quelli [che tene]ssero la Terra… sta[bile] e ’l Sole mobile… con le novità cagionate gran rovine nella religione etc.: né troverete astronomo o filo[so]fo alcuno (per eretico che sia in altri articoli), che mai abbia derogato la fede alle Scritture… predicatole per false, perché dicano che il Sole si muove etc.; [m]a con usitatissima maniera scu[san] lo scrittore, che [parla] conforme alle capacità del vulgo etc.: e voi sete che cagionate l’ere[sia], mentre, senza cagione alcuna, volete che il senso delle Scritture sia quello che piace a voi, [e che] i sapienti neghino i sensi proprii e le dimostrazioni necessarie… ti stimi di giudizio tanto eminente sopra gli antichi, che dove essi ponevano tra i [De]i i trovatori di cose nuove, [tu, co]me più savio, gli s[e]ntenzi degni d’esser banditi dalla repubblica?» (Opere, VII, p. 544.) (Le parentesi quadre e i corsivi, che indicano lacune e aggiunte, si trovano nel testo di Favaro, e io mi sono sforzato di riprodurli con la maggiore fedeltà possibile.) C’è anche un altro frammento che riguarda direttamente questo tema, ma in esso Galileo si mostra più cauto. Si muove nel campo puramente teorico, e invece di polemizzare ribaltando le accuse che gli vengono mosse, insiste sull’ambito limitato della «sua novità» indicando un campionario degli ambiti che potrebbero ugualmente presentarsi:
«Per quelli che si perturbano per avere a mutar tutta la filosofia, mostrar come non è così, e che resta la medesima dottrina dell’anima, della generazione, delle meteore, degli animali» (Opere, VII, p. 541).
È chiaro che Galileo non elaborò mai teorie alternative a proposito dei temi segnalati e, da questo punto di vista, possiamo accettare la sua affermazione che potrebbero rimanere come sono. Orbene, una delle qualità della cosmologia e della filosofia aristotelica in generale era la sua coerenza interna. I concetti centrali sono gli stessi nella metafisica, nella psicologia e nella fisica, biologia compresa. Era una delle sue grandi qualità, la quale d’altra parte implicava che il crollo di una delle sue parti poteva causare quello dell’intero sistema. E, se teniamo conto della critica all’apparato categoriale aristotelico sviluppata in questa Giornata prima e, soprattutto, nel Saggiatore – la critica all’essenzialismo, la proposta di un’ontologia di carattere atomistico o corpuscolare, e la distinzione tra qualità primarie e secondarie, con la conseguente rielaborazione delle categorie di «soggetto» e «oggetto», il riordinamento delle scienze e dei loro rapporti – risulta difficile pensare che gli ambiti menzionati potessero uscirne incolumi. In ogni caso è possibile che Galileo, che la sua affermazione sia sincera o puramente diplomatica, non avesse alcuna intenzione di proporre teorie alternative nelle scienze in oggetto, e d’altra parte è anche certo e palese in tutta la sua opera che era consapevole di proporre un’alternativa globale.

⁴¹ Questo testo è una parafrasi di quello di Aristotele in De caelo, I, 3, 270a, 14-17: «Poiché tutto ciò che si genera è generato a partire da un opposto e da un qualche sostrato, nello stesso modo si distrugge in un sostrato per l’azione di un opposto verso un altro contrario». Per lo sviluppo di questi temi, si può anche vedere Fisica, I, 5, 188b, 21-26; e Fisica I, 7-9, 190a-200b.

⁴² La credenza nella generazione spontanea, ossia nella possibilità che si generassero esseri viventi, di solito piuttosto elementari, a partire da varie categorie di materia inerte, è unanime fin dall’antichità classica. Solo a partire dalla seconda metà del XVII secolo, grazie a esperienze come quelle di Redi, Malpighi, Leeuwenhoek, Swammerdam e altri, andarono progressivamente diminuendo gli animalcula che si supponevano così generati. Ma il mondo microscopico, che si cominciò a scoprire allora, complicò alquanto la problematica e, fino al XIX secolo, con Pasteur, la teoria non venne totalmente liquidata.

⁴³ Galileo voleva così evitare di rimanere impigliato nel misterioso dogma della transustanziazione dell’eucarestia. Pietro Redondi ha sostenuto (Redondi, 1983) che Galileo era caduto in quel pericolo nel Saggiatore che, con la sua teoria atomistica della materia, metteva in discussione tale dogma e, a partire da ciò, ha ipotizzato che fosse stato questo l’autentico motivo della condanna di Galileo. La difesa del copernicanesimo sarebbe stata un mero pretesto di cui si sarebbe servito papa Urbano VIII per nascondere l’autentico problema sollevato dal suo antico protetto. La tesi del libro di Redondi è stata duramente ed efficacemente criticata, ma ciò non toglie che l’opera di Redondi continui a risultare appassionante.

⁴⁴ A questo punto c’è una lacuna nel testo.

⁴⁵ Abila o Abilix e Calpe sono i nomi antichi delle alture, la prima in Africa (Ceuta), l’altra in Europa (Gibilterra), che formavano le mitiche colonne erette da Ercole ai limiti dello Stretto. Secondo una versione del mito, sarebbe stato anzi Ercole ad aprire lo Stretto, e un’altra versione ancora vuole che lo abbia reso più angusto di quanto fosse per impedire il passaggio di balene e altri mostri. In entrambi i casi, avrebbe unito l’Atlantico e un già esistente Mediterraneo. Un altro mito trasmesso da Plinio (Naturalis historia, VI, 1), al quale si riferisce Simplicio, racconta che l’oceano, dopo aver separato Calpe dall’Africa, invase le terre dando origine al Mediterraneo e più avanti al Ponto Eusino (il Mar Nero).

⁴⁶ Galileo fu il primo selenografo con le mappe lunari che pubblicò nel Sidereus nuncius nel 1610. La storia secondo la quale Dio avrebbe condannato Caino ad accumulare spini per la Luna, è accennata da Dante nella Divina Commedia, Inferno, XX, 126 e Paradiso, II, 49-51.

⁴⁷ Si tratta delle due «novae», vale a dire quelle che a partire da allora sarebbero state identificate come «stelle nuove», apparse in cielo in quest’epoca. Quella comparsa nel 1572 (pare che fosse anzi una supernova) nella costellazione di Cassiopea splendeva quanto Venere nei suoi momenti di massima luminosità. Restò visibile per diciotto mesi durante i quali andò progressivamente impallidendo fino a scomparire. Fu meticolosamente studiata, anche dal punto di vista astrologico, da Tycho Brahe, che convinse la maggior parte dei migliori astronomi del tempo che senza dubbio si trovava nel mondo sopralunare. Maestlin e Digges se ne servirono come argomento in favore del copernicanesimo. Ma fu soprattutto in combinazione con gli studi della cometa del 1577, da Tycho collocata del pari nel mondo sopralunare, che ebbe maggior effetto. Queste scoperte esigevano l’abbandono della teoria dell’ingenerabilità e immutabilità del mondo celeste. Se quella del 1572 è la nova di Tycho, quella del 1604, che apparve prossima alla congiunzione di vari pianeti e in coincidenza con essa, è la nova di Keplero, che la studiò particolareggiatamente, confrontandola con quella del 1572. Cosa interessante per noi, la nova del 1604 fu praticamente il primo fatto astronomico su cui Galileo intervenne direttamente. Su di essa tenne tre lezioni e scrisse alcune lettere, ma a noi sono giunti soltanto due brevi frammenti (Opere, II, pp. 277-288, 281 e X, pp. 134-155). Ci consta che, oltre a conoscere l’apparizione della nova del 1604, Galileo chiese informazioni ad astronomi in altre città italiane nel tentativo di stabilire se la nuova stella presentasse parallasse, senza però riuscire a stabilirlo. Di solito si era dato per scontato che quella nova avesse rafforzato le convinzioni copernicane che Galileo aveva già affermato di aver fatto proprie; ma Drake, al termine di una delle sue ricostruzioni, ipotizza che quell’insuccesso abbia fatto perdere a Galileo la fede nel copernicanesimo fino al 1610 (Drake, 1988, p. 167).

⁴⁸ Antitichone – vale a dire Anti-Tycho o Contro Tycho Brahe – è un’opera di Scipione Chiaramonti (1565-1652) pubblicata nel 1621, nella quale egli contestava la tesi di Tycho Brahe e l’opinione del gesuita Orazio Grassi che la accoglieva, che le comete si muovessero sopra la sfera della luna. Circa l’opera di Chiaramonti e la sua importanza nella genesi del Dialogo, si veda la mia Introduzione, pp. 68 ss.

⁴⁹ La parallasse è l’angolo sotto il quale si vede un corpo celeste osservato da vari punti della superficie terrestre (parallasse diurna) o da vari punti dell’orbita terrestre (parallasse annua).

⁵⁰ Nel 1618 apparvero tre comete, che furono fatte oggetto di numerosi studi e pubblicazioni. In una delle sue lezioni pubblicata anonima, il gesuita Orazio Grassi, professore di matematiche del Collegio Romano, faceva sue le tesi di Tycho Brahe circa la cometa del 1577 e collocava la più luminosa delle tre, quella del 1618, nel mondo celeste, tra la Luna e il Sole. Si mormorava che i gesuiti vedessero in quegli astri una confutazione del sistema copernicano, e a Galileo era stato chiesto di esprimere la sua opinione in merito. E così, sebbene nel momento dell’apparizione delle comete Galileo fosse malato e non in grado di compiere osservazioni, dettò al suo discepolo Mario Guiducci il Discorso delle comete. Esso fu contestato da Grassi nella Libra Astronomica ac Philosophica, pubblicata nel 1619 con lo pseudonimo di Lotario Sarsi. Fu allora che Galileo replicò scrivendo il Saggiatore; per difendere il copernicanesimo, affermava che le comete erano fenomeni ottici causati dalla rifrazione della luce del Sole in vapori atmosferici, in altre parole affermava che erano sublunari: uno sfortunato errore che collocava Galileo accanto ad Aristotele e lo sprofondava in un mare di contraddizioni. Sembrerebbe che qui, focalizzandosi sul tema della «corruttibilità» o «incorruttibilità» dei cieli, Galileo prenda le distanze da quella tesi. Ma la marginalità dell’indecisione o indifferenza nei confronti dell’una o dell’altra tesi, qui palesata da Galileo, non induce a darle l’importanza che altrimenti potrebbe avere. Anche più avanti Galileo continua a mantenere aperto il problema (Opere, VII, p. 82. Vedasi però anche Opere, VII, p. 264).

⁵¹ Tycho Brahe (1546-1601) fu l’astronomo più importante della seconda metà del secolo XVI. Le sue osservazioni, assai più precise di quelle dei suoi predecessori e contemporanei, per la prima volta eseguite ripetutamente e sistematicamente, fornirono i dati d’osservazione necessari alla spiegazione di qualsiasi teoria astronomica, sostituendo il caos di osservazioni accumulate e molte volte erronee, dal quale dipendevano fino allora gli astronomi. Se ne avvalse Keplero per giungere alla soluzione del movimento planetario. Le scoperte delle novae del 1572 e del 1604, nelle costellazioni di Cassiopea e del Serpentario, che, grazie alla sua precisione, Tycho collocò al di là di Saturno, e lo studio delle traiettorie di varie comete che, come dedusse, attraversarono le orbite dei pianeti, contribuirono in maniera decisiva all’abbandono della credenza nell’inalterabilità rispettivamente dei cieli e delle sfere celesti. Nel suo sistema astronomico, i pianeti orbitano intorno al Sole che, a sua volta compie come la Luna la sua rivoluzione intorno alla Terra, situata al centro dell’universo e immobile. Questo sistema geo-eliocentrico assicurava cospicui vantaggi ed ebbe notevole successo. In realtà, il sistema di Tycho era quello che poteva rappresentare, ed effettivamente costituì, soprattutto nei paesi cattolici, un’autentica alternativa al copernicanesimo, sia in senso storico che teorico. Da un lato era infatti il sistema che, per varie ragioni, tra cui la condanna del copernicanesimo nel 1616, era stato adottato effettivamente da molti astronomi, specialmente cattolici; dall’altro, non era esposto alle grandi difficoltà fisiche alle quali doveva far fronte il sistema eliocentrico e, dal punto di vista astronomico, si sottraeva anche all’argomento della parallasse, grande scoglio del sistema copernicano.
Il silenzio di Galileo nei confronti del sistema tychonico può sembrare sorprendente e, in un certo senso, senza dubbio lo è. Ma le differenze e i vantaggi del sistema di Tycho apparivano manifesti solo nell’ambito dell’astronomia tecnica e Galileo, nel Dialogo, in nessun momento vuole metter becco nelle questioni astronomiche tecniche. Inoltre, era convinto che il telescopio avesse reso evidenti certi fondamentali errori nelle osservazioni di Tycho. Nei suoi calcoli e argomenti anticopernicani, Tycho si era lasciato ingannare dalla grandezza apparente delle stelle. Ma il telescopio eliminava l’irradiazione stellare, riducendo in misura enorme la loro grandezza e invalidando gli argomenti di Tycho. Lo affermava Galileo in una lettera del 30 dicembre 1610 a Clavio (Opere, X, p. 500; si vedano anche le sue argomentazioni nel Saggiatore, Opere, VI, pp. 271 ss.). Inoltre, il fatto che Tycho attribuisse una traiettoria ovale, e quindi una linea «irregolare», «indefinibile», alle comete, a Galileo sembrava che una spiegazione fondata su linee irregolari non fosse «punto migliore delle simpatie, antipatie, proprietà occulte» ecc. Ovviamente, Galileo censura Grassi, ma la tesi era di Tycho (Opere, VI, pp. 243-244). La cosa più importante è però che nel Dialogo Galileo si pone, con vivo interesse, il problema del moto della Terra, ed è questo senza dubbio il punto fondamentale che contrappone il sistema copernicano agli altri; sotto questo profilo, il sistema di Tycho non si differenziava assolutamente dal geocentrismo più tradizionale. Una tesi assai più azzardata e contorta è reperibile in Howard Margolis, 1991, secondo il quale, sebbene Galileo si riferisca costantemente a Tolomeo, in realtà contrappone il sistema copernicano a quello di Tycho, ma vuole farlo nascostamente. I gesuiti e la Chiesa si erano dichiarati per il sistema tychonico e Galileo non avrebbe ottenuto l’imprimatur se lo avesse attaccato apertamente.

⁵² Nel novembre e dicembre del 1611, il gesuita Cristoforo Scheiner scrisse tre lettere a Marcus Welser per informarlo che aveva scoperto delle macchie sulla superficie solare, e ne spiegava la natura. Dopo aver preso in considerazione altre ipotesi, nella terza epistola affermava che le macchie solari erano stelle – vale a dire pianeti o corpi opachi – vicini al Sole, cosa questa che era la migliore salvaguardia della incorruttibilità e ingenerabilità del Sole e, per estensione, del mondo celeste. Poiché i gesuiti non volevano esporsi a possibili errori che li screditassero in seno alla Compagnia, le Tres epistolae de maculis solaribus furono pubblicate nel 1612 con lo pseudonimo di Apelles Latens post tabulam, e Welser le inviò a Galileo. Nel maggio del 1612, questi rispose con due lettere successive contestando la tesi di Apelles, che aveva capito essere un gesuita, ed esponendo la sua interpretazione. Dal canto suo, Scheiner scrisse un trattatello che fu pubblicato nell’inverno del 1612, con il titolo di De maculis solaribus et stellis circa Jovem errantibus accuratior disquisitio, nel quale enumerava le auctoritates a suo favore, annunciava la scoperta di un quinto satellite di Giove e spiegava la luce secondaria della Luna come frutto della sua trasparenza. Galileo replicò con una terza lettera a Welser nella quale rivendicava per sé, pubblicamente, la priorità della scoperta delle macchie. Le tre lettere di Galileo furono pubblicate nel 1613 dall’Accademia dei Lincei con il titolo di Istoria e dimostrazioni intorno alle macchie solari e loro accidenti. È difficile verificare la fondatezza della rivendicazione della priorità di Galileo. In ogni caso sembra che tanto lui, quanto Scheiner o Johannes Fabricius a Wittenberg, Thomas Harriot in Inghilterra e Domenico Passignani in Italia, abbiano osservato le macchie indipendentemente l’uno dall’altro. Le lettere e i trattati menzionati sono contenuti nel volume V delle Opere di Galileo.

⁵³ Non si dimentichi che, secondo la cosmologia aristotelico-tolemaica, noi, trovandoci al centro, guardiamo il Sole «dal basso». Sicché, se vediamo macchie «davanti» al Sole, è perché si trovano «al di sotto» di esso.

⁵⁴ A prima vista i moti del Sole e della Luna sembrano meno complicati, e più facilmente spiegabili, mediante moti circolari, di quelli degli altri pianeti. Potrebbe effettivamente sembrare che sarebbe sufficiente collocarli su un circolo che girasse attorno alla Terra a determinate velocità; ma, quando lo si verifica, si scoprono altre irregolarità che complicano enormemente il problema. Per trovare la soluzione a queste irregolarità, Tolomeo si servì di tre tipi di espedienti geometrici, il sistema di epiciclo-deferente (del quale parleremo più avanti), l’eccentrico e l’equante. L’eccentrico è un espediente geometrico mediante il quale si colloca il pianeta – in questo caso il Sole – in un cerchio il cui centro non coincide con la Terra. Nell’eccentrico, il pianeta si muove in cerchio con moto uniforme intorno al centro geometrico, e il metodo serve a spiegare apparenti irregolarità nella velocità o nella circolarità delle orbite planetarie. Tolomeo si serviva di questo espediente per spiegare, per esempio, il fatto che il Sole tarderebbe sei giorni di più per spostarsi dall’equinozio di primavera all’equinozio di autunno – a 180° se il moto avesse per centro la Terra –, che per passare dall’equinozio d’autunno a quello di primavera – altri 180° nell’ipotesi geocentrica. L’equante è un punto eccentrico rispetto al centro geometrico dell’orbita planetaria. In questo caso, però, il pianeta si muove di moto uniforme rispetto al centro equante e non rispetto al centro geometrico come accade nel caso dell’eccentrico.
In realtà, fin da Aristotele con la sua cosmologia omocentrica e da Tolomeo con le Ipotesi dei pianeti, le sfere dei pianeti presentano uno spessore – che possiamo immaginare composto di strati – che può essere maggiore del diametro del pianeta in modo da permettergli di avvicinarsi o allontanarsi dalla Terra, nella misura in cui lo esiga il suo apparente cambiamento di grandezza o di luminosità. Per questo possono aversi strati della sfera tra il pianeta, in questo caso il Sole, e noi, e in tali strati si collocherebbero, secondo tali ipotesi, gli astri-macchie solari. Perciò, se il periodo orbitale delle macchie è diverso da quello degli strati che avvolgono il corpo del Sole, esse possono apparire e scomparire sullo sfondo del Sole stesso.

⁵⁵ Si tratta delle lettere pubblicate con il titolo di Istoria e dimostrazioni intorno alle macchie solari…, di cui abbiamo parlato nella nota 52.

⁵⁶ Edificio ateniese dove si mantenevano, a spese del pubblico erario, i cittadini meritevoli.

⁵⁷ Ironia a parte, non c’è qui nessuna esagerazione. Come si può vedere nell’Introduzione, pp. 18 ss., i gesuiti, massimi protagonisti della politica culturale controriformistica, tramite la loro Ratio studiorum avevano stabilito una duplice identità tra filosofia e difesa della fede, e tra filosofia e scolastica aristotelica. Nella lezione inaugurale del corso del 1623-1624 – e possiamo pensare che il messaggio avesse qualche rapporto con la nuova filosofia proposta nel Saggiatore di Galileo recentemente pubblicato – il Collegio Romano proclamava, come racconta Virginio Cesarini a Galileo, che «fuori di Aristotele non c’è verità alcuna» (Opere, XIII, p. 107). Nella lezione inaugurale del seguente anno accademico, il padre Spinola aveva proclamato che «la filosofia degna dell’uomo cristiano è pertanto quella posta al servizio della Teologia», e nella quale bisognava «abbandonare le invenzioni delle opinioni nuove e abbracciare il parere confermato dalla testimonianza degli autori». Il primo di questi era naturalmente Aristotele, e Spinola condannava con forza la pretesa di costruire «una nuova fabbrica dell’umana sapienza» (cit. da Redondi, 1983, pp. 162-166). Appare difficile non collegare il testo di Galileo con quello che ho appena citato. Quest’immagine architettonica riapparirà però in bocca ai nemici di Galileo. Poco prima che si pubblicasse il Dialogo, era stata usata dal padre Orazio Grassi con un tono che non si prestava assolutamente a ironie. Nel suo sermone del Venerdì Santo del 18 aprile 1631, pronunciato nella Cappella Sistina, Grassi, rappresentante delle tendenze più conservatrici della Controriforma, rimproverava al papa la sua eccessiva tolleranza verso i nemici della fede. «Dobbiamo piangere, Beatissimo Padre, un’immane distruzione e un’immensa rovina. L’edificio che con le sue mani la Sapienza Divina aveva eretto, quel tempio eterno della pace fra Dio e gli uomini è demolito da empi predoni, distrutto, raso al suolo. Quanto è veramente atroce assistere alla scena dell’imminente rovina. Quegli strumenti, quelle leve, quelle macchine, gli operai, tutto è apparecchiato e pronto per l’immane opera distruttiva […]. I custodi del Tempio, nuovi Leviti, dormono un sonno profondo […]. Ma il terrore li scuote ora dal loro sonno profondo. La turba dei furibondi predoni si avanza […]. Già il velo del tempio, al separarsi dell’anima dal corpo di Cristo, è strappato: già la struttura tutta si inclina ed essi da tanto fragore come di morte, anche se addormentati ora sono spinti a svegliarsi […]. Le cose sacre sono calpestate, gli altari rovesciati, il tempio in rovina: dove ci rifugeremo, dove, io dico?» (cit. da Redondi, 1983, p. 288, p. 269, con un ampio commento). Mettere l’una accanto all’altra l’immagine architettonica del tono giocoso di Galileo e la sua contropartita apocalittica non può non dare i brividi.

⁵⁸ Possiamo accettare che Galileo abbia affidato a Dio il compito di rifare i cervelli, e d’altro canto tentò di rifare le menti dei suoi oppositori. In altre parole, tentò di insegnare loro a pensare a partire da alcuni «principi della scienza» diversi da quelli che ritenevano sacri. Ed è appunto quello che tenta di fare in quest’opera, rendendo manifesta la chiara consapevolezza della rottura della sua posizione rispetto alla loro filosofia naturale. È difficile stabilire se in questo passo a dominare sia l’ironia o il disincanto.

⁵⁹ All’inizio del XVI secolo era un luogo comune tra gli aristotelici essere «evidente che la forza degli astri e dell’aria intervengono nella generazione e corruzione dei corpi viventi» (Sisinius, De natura foetus, Roma, 1615, p. 13). Del resto, nello stesso Aristotele ci si imbatte in passi che non si prestano a equivoci in merito. Si veda la nostra nota 90 a questa Giornata prima.

⁶⁰ «La natura non fa nulla invano». È un’espressione classica del finalismo, un principio formulato abbondantemente in Grecia e in seguito da Aristotele che lo sviluppa in Fisica, II, 198b 10-199b 33, e lo formula in testi come De caelo, I, 271a 33, come pure in numerosi passi della metafisica e dei trattati di «biologia». La formulazione latina è forse tratta da Galeno (De usu partium, X, 14).

⁶¹ Quando la Luna e il Sole, visti dalla Terra, si trovano a 180° l’uno dall’altra. Si veda più avanti la nota 63.

⁶² Questi argomenti sono esattamente analoghi a quelli usati da Tolomeo per affermare la sfericità della Terra (Almagesto, I, 4).

⁶³ Gli «aspetti» sono gli angoli (o archi di ellittica) che formano le linee visive che dalla Terra si dirigono ai vari pianeti. Galileo allude continuamente a tre di essi, riferendosi alla Luna e al Sole: la congiunzione in cui la Luna e il Sole coincidono nella stessa linea visiva e senza formare angolo; l’opposizione, nella quale si trovano a lati opposti dell’osservatore e separati da 180°; le due quadrature, nelle quali sono separati da 90°. Come risulta evidente, la congiunzione corrisponde alla Luna nuova, e la si ha quando possono prodursi eclissi solari, e l’opposizione corrisponde alla Luna piena, e la si ha quando possono prodursi eclissi lunari. Le quadrature corrispondono al primo quarto (Luna crescente) all’ultimo quarto (Luna calante).

⁶⁴ Cosa questa che è possibile perché sebbene nella congiunzione il Sole e la Luna si trovino alla stessa longitudine celeste, non stanno esattamente nella stessa latitudine. Se infatti la Luna si trovasse sempre nel medesimo piano dell’ellittica ogni qualvolta fosse in opposizione e in congiunzione, si produrrebbe rispettivamente un’eclisse di Luna e di Sole. In realtà, però, la Luna oscilla costantemente – di circa 5° – a nord e a sud dell’eclittica e ciò fa sì che le eclissi visibili da una determinata posizione della Terra, siano fenomeni piuttosto rari.

⁶⁵ I greci non riuscivano a concepire che i corpi celesti potessero muoversi se non circolarmente. Con questa premessa – dalla quale, come abbiamo visto, Galileo non si è ancora liberato – il movimento dei pianeti, specialmente di Mercurio, Venere, Marte, Giove e Saturno, è assai irregolare e irrazionale. Effettivamente, nel loro moto normale verso est, sullo sfondo delle stelle, questi pianeti di tanto in tanto sembrano fermarsi, retrocedere verso ovest e quindi ricominciare il loro movimento verso est. Per spiegare questi strani fatti, per «salvare queste apparenze», Tolomeo fece ricorso a un espediente geometrico consistente nel supporre che il pianeta fosse situato sopra un cerchio, il cosiddetto epiciclo, che si muoveva sulla circonferenza di un altro cerchio, deferente, che a sua volta si muoveva in cerchio intorno alla Terra. Copernico non aveva bisogno di questi epicicli maggiori, perché nel suo sistema la retrogradazione era solo apparente e spiegabile con le velocità e posizioni relative della Terra e dei pianeti. Ma anch’egli condivideva il dogma della circolarità, e si servì di epicicli minori per spiegare anomalie meno palesi. Così per esempio, nel caso della Luna, Copernico critica l’uso che Tolomeo aveva fatto dell’equante e utilizza non uno, bensì due epicicli, sovrapposti l’uno all’altro (Copernico, De revolutionibus, libro IV, cap. 3 ss.). Ciò detto, la tesi di Sagredo consiste nel sostenere, che se la Luna è fissa in un deferente, dalla Terra posta al centro ne vedremo sempre la stessa faccia. La tesi di Salviati è che, se ciò accade, è perché la Luna è fissa in un epiciclo minore che si muove in cerchio su un deferente nel cui centro sta la Terra. Se l’epiciclo ruota su se stesso alla stessa velocità con cui il deferente compie un giro intorno alla Terra, anche allora vedremo sempre la stessa faccia della Luna. Noi diremmo semplicemente che la Luna gira su se stessa alla stessa velocità che intorno alla Terra.

⁶⁶ Si attribuisce ai pitagorici, e più precisamente a Filolao, la creazione di un sistema nel quale la Terra, la Luna, il Sole, Mercurio, Venere, Marte, Giove, Saturno e la sfera delle stelle fisse giravano, in quest’ordine, intorno a un fuoco centrale chiamato Estia, il quale comprendeva nove corpi rotanti attorno al centro, cosa che, a quanto sembrava, costituiva una qualche imperfezione impossibile, uno scarto che bisognava correggere: la perfezione del numero dieci esigeva l’esistenza di un decimo corpo. Identificato come Anticton o anti-Terra e situato tra la Terra e il fuoco centrale, esso avrebbe completato il sistema. Il periodo di rivoluzione della Terra intorno al fuoco centrale sarebbe di ventiquattro ore e coinciderebbe con la durata della sua rotazione sul proprio asse. Questa rotazione legata farebbe sì che una delle sue facce, precisamente quella abitata dai greci e da noi, guardasse sempre il lato opposto del fuoco centrale, sicché questo resterebbe invisibile. Inoltre, dato che l’anti-Terra avrebbe lo stesso periodo di rivoluzione della Terra, si troverebbe sempre situata esattamente tra la Terra e il fuoco centrale e pertanto ci risulterebbe anch’essa invisibile. Lo stesso Aristotele (De caelo, XIII, 293a 20-25, e Metafisica, I, 5, 986a 10) considerava questa teoria altamente speculativa. In ogni caso risulta ovvia l’analogia tra le rotazioni legate della Terra secondo il sistema pitagorico e della nostra Luna, e pertanto le possibilità di visione degli abitanti della Terra pitagorica e della nostra Luna, cosa che giustifica la boutade di Galileo.

⁶⁷ Sarebbe questo l’unico caso nel quale l’osservatore si troverebbe esattamente nel punto della superficie terrestre per il quale passerebbe la linea che unisce i centri lunare e terrestre. L’argomento di Galileo somiglia assai da vicino alla spiegazione data da Tolomeo della parallasse lunare in Almagesto, IV, 1.

⁶⁸ Come ho già detto, la Luna non si muove esattamente nel piano dell’eclittica, cioè non esattamente sullo stesso piano dell’orbita terrestre dal quale si discosta di poco più di 5° verso nord e verso sud. I due punti nei quali la sua orbita interseca l’eclittica o orbita terrestre si chiamano nodi o punti draconici – ascendente quello nel quale transita da sud a nord, e discendente il contrario – che nella tradizione astrologica corrispondevano alla testa e alla coda di un drago. Mentre i punti di massima latitudine nord e sud dell’orbita lunare, sono quelli che Galileo chiama ventri del suo dragone. Orbene, i nodi non sono fissi bensì retrogradi, poiché si muovono verso occidente, ed è questa la causa per cui il tempo che occorre alla Luna per giungere nuovamente a un nodo è leggermente minore, di circa 1/10, del mese sidereo. Ancora oggi chiamiamo periodo o mese draconico il tempo che trascorre tra due passaggi successivi della Luna per un nodo. Periodo o mese sidereo è il tempo che occorre alla Luna per percorrere 360° sullo sfondo delle stelle, pari approssimativamente a 27,3 giorni. Il periodo o mese sinodico – synodus significa riunione o congiunzione, in questo caso del Sole o della Luna – è il tempo corrispondente a un intero ciclo di fasi lunari, cioè da una luna nuova a un’altra, ed è di circa 29,5 giorni. È detto anche lunazione. La differenza tra mese sidereo e sinodico è dovuta al movimento della Terra. Si tratta in tutti i casi di tempi medi.
La retrogradazione dei nodi ha per effetto che il dragone serpeggi lungo il suo percorso, in altre parole che l’orbita lunare oscilli sullo sfondo delle stelle. Così per esempio, i punti massimi della latitudine lunare – nord e sud – rispetto all’ellittica non coincidono sullo stesso sfondo delle stelle in ogni orbita della Luna, ma oscillano, sullo stesso sfondo, come il ventre del dragone. Galileo aveva fatto riferimento al drago della Luna nel suo Trattato della Sfera ovvero Cosmografia (Opere, II, p. 245).

⁶⁹ L’intera volta stellata compie una rotazione apparente in ventiquattr’ore intorno alla Terra su un determinato asse che passa per i poli celesti, nord e sud. Un meridiano è, per definizione, qualsiasi cerchio massimo che passi per questi poli. Orbene, in ogni punto della superficie terrestre la direzione della gravità, determinata dal filo a piombo, interseca la sfera celeste in due punti: lo zenit situato al di sopra dell’osservatore e il nadir, situato al di sotto. Il cerchio massimo che passa per i poli e per lo zenit e il nadir si chiama meridiano locale. È caratterizzato dal fatto di dividere in due parti uguali l’orizzonte, l’equatore e i paralleli, a cui è perpendicolare. L’asse del mondo lo divide in due parti uguali; quella che contiene lo zenit si chiama meridiano superiore, quella contenente il nadir si chiama meridiano inferiore. L’istante in cui un corpo celeste attraversa il meridiano locale divide in due parti uguali il tempo del suo percorso dal momento che comincia a est fino a quello in cui si conclude a ovest. Il passaggio di un corpo celeste per questo punto è detto culminazione. Se nell’anti-chità il meridiano era noto anche come cerchio mesembrino (dal greco mesembrìa, «mezzogiorno») era perché ovviamente segnava il mezzogiorno e la mezzanotte locali.

⁷⁰ Galileo scopre e descrive qui il fenomeno che chiamiamo librazione. Comincia col definire gli effetti della cosiddetta librazione diurna: dalla superficie terrestre l’osservatore vede un orlo che non vedrebbe dal centro della Terra. Galileo passa poi a descrivere la librazione in latitudine, dovuta all’inclinazione dell’orbita lunare rispetto all’eclittica ovvero orbita terrestre, la quale fa sì che vediamo la Luna «da più in basso» o «da più in alto», con la conseguente variazione del suo apparente contorno lunare. Esiste però una terza librazione che Galileo non menziona, ed è la librazione in longitudine. La Luna descrive in realtà un’orbita leggermente ellittica – la sua eccentricità è di 1/18 – cosicché, in forza della seconda legge di Keplero, la velocità lungo la sua orbita varia nel senso che la Luna si muove più lentamente all’apogeo ovvero punto dell’orbita più lontano dalla Terra, che non al perigeo o punto più vicino. Ciò nonostante, la velocità di rotazione della Luna si mantiene costante, e ciò ha per effetto un’oscillazione apparente verso est e ovest, in conseguenza della quale possiamo vedere un’ulteriore fetta a destra e a sinistra. La librazione diurna rappresenta ±1,2°, quella in longitudine ±8° e quella in latitudine ±6,7°. Si potrebbe pensare che, quando Galileo descrive gli effetti della librazione diurna, nel modo in cui lo fa, cioè con variazioni a seconda che la Luna sia situata a oriente o a occidente, non distingua la librazione diurna da quella in longitudine; certo è però che Galileo non parla della librazione in longitudine. In qualunque caso, è senz’altro certo che si deve alla combinazione delle librazioni se vediamo, non un 50% bensì un 59% della superficie lunare.

⁷¹ Si tratta della luce secondaria o luce cinerea che Galileo aveva spiegato già nel Sidereus nuncius. Si veda Galilei (1948), pp. 29-37.

⁷² Secondo Drake, si tratta di Cesare Cremonini, celebre rappresentante dell’aristotelismo padovano, che in diversi momenti fu oggetto di accuse e sospetti di eresia. Può darsi che le comuni afflizioni siano state il fondamento dell’amicizia tra Cremonini e Galileo i quali, nonostante le radicali differenze filosofiche, in molte occasioni si aiutarono e sostennero a vicenda.

⁷³ Si veda Opere, VI, pp. 283, ss.

⁷⁴ Ritengo opportuno citare alcuni testi medievali relativi a queste questioni. Fin dall’antichità classica si era osservata «la macchia della Luna» e, per spiegarla, si erano formulate numerose ipotesi circa la natura dell’astro, l’origine della sua luce, la sua densità o rarità, la capacità di assorbire la luce e rifletterla, ecc. Plutarco e Averroè hanno ruoli importanti in questa storia. Qui però mi limiterò a citare un passo di Buridano il quale, dopo aver alluso al fatto che la Luna non riflette la luce come uno specchio, perché la rinvia in tutte le direzioni, prosegue: «Alcuni hanno voluto salvare questo ragionamento dicendo: la Luna è come un muro; quando i raggi del Sole cadono su un muro, questo appare illuminato nella sua totalità e non soltanto secondo le linee lungo le quali il raggio incidente e il raggio riflesso formano angoli uguali. E così accade con la Luna.
«Ma questa soluzione è insufficiente. Se si ha riflessione al nostro occhio da tutte le parti del muro è, diciamo noi, a causa della rugosità del muro, alla quale si deve se tutti i raggi sono rifratti in tutti i sensi. Se al contrario il muro fosse perfettamente liscio, come uno specchio di acciaio, non si avrebbe una grande luminosità diffusa in tutto il muro, ma la si vedrebbe unicamente nella parte che abbiamo detto.
«Lo si vede chiaramente in un’acqua tranquilla: solo una piccola parte di quest’acqua ci rimanda intensamente la luce del Sole o di altri astri; ma se si agita un po’ l’acqua, in modo che la superficie non sia liscia, la stessa luce si diffonde sopra una vasta estensione dell’acqua stessa. «Ora, noi supponiamo che la Luna sia perfettamente liscia e non presenti nessuna asperità. E infatti Aristotele pensò che tutti i corpi celesti fossero fatti così.
«Altri suppongono, con maggiore probabilità, che la Luna non sia luminosa in modo attuale, e che non sia in grado di mettere in movimento da se stessa un mezzo trasparente. Ma grazie alla sua disposizione naturale, potenzialmente è prossima a trasformarsi in luminosa, e quando la luce del sole cade su di essa, eccola costretta a brillare in modo attuale», Buridano, Quaestiones super libris de caelo et mundo, Cod. lat. 19.551, folio 97 col. B., cit. da Duhem, 1958, vol. IX, pp. 420-421. Buridano si rifà ad Averroè e alla fine propende anche verso la sua ipotesi della fluorescenza della Luna, alla quale allude a conclusione del testo citato. La somiglianza della sua argomentazione con quella di Galileo, così personale, è tanto più indicativa dal momento che le loro conclusioni sono contrapposte, come tanto spesso accade con Buridano e Oresme, rispetto a Copernico e a Galileo.

⁷⁵ Finora nessuno ha identificato il riferimento, evidentemente letterario se teniamo conto delle virgolette. In ogni caso, Galileo molto spesso mescola parafrasi o sintesi dei testi che cita invece dei testi veri e propri, cosa che ne rende più ancora difficile l’identificazione.

⁷⁶ Nell’edizione originale, a conclusione dell’intervento di Simplicio, si ha: «abbia a ripercuoter maggior lume che uno specchio terso e pulito. SALV. Maggior lume no», ma nel suo già menzionato esemplare, Galileo corresse la frase di mano propria, scrivendo quanto appare nel nostro testo.

⁷⁷ Galileo trascrive qui, intenzionalmente, un testo alquanto oscuro, di autore non identificato, come del resto quello tra virgolette di qualche pagina più sopra. In ogni caso, il termine «spezie» si rifà a una delle teorie della visione secondo la quale questa consisteva nella ricezione da parte dell’occhio delle «specie» o «simulacri», vale a dire «immagini» di se stesse emesse dalle cose. Nonostante il suo uso e perfezionamento tecnico del telescopio, Galileo non dà mai a vedere di avere conosciuto le nuove idee di Keplero (Ad Vitellionem paralipomena del 1604 e la Dioptrice del 1611) che inaugurarono l’ottica moderna. In realtà, nonostante l’ironia con cui replica all’aristotelico, Galileo personalmente non riuscì mai a superare l’ottica delle «specie».

⁷⁸ «Le tenebre sono privazione di luce». È una definizione che deriva dalle idee formulate da Aristotele nel De anima, II, 7, 418b 18 ss.; e, più letteralmente, nel De sensu, 439a 20.

⁷⁹ L’espressione «raggi visivi» o «raggi della vista», come Galileo dice più sotto, ci riporta ancora una volta alla teoria ottica tradizionale. Inizialmente, nel mondo greco si ebbero due grandi schemi esplicativi del meccanismo della visione. Una teoria, cui abbiamo già accennato, era quella che, prendendo le mosse dai filosofi atomisti per i quali ogni percezione sensibile era tattile, spiegava la visione come percezione, da parte dell’occhio, delle «specie», «immagini» o «simulacri» emessi dagli oggetti. L’altra era quella inaugurata dai pitagorici e sviluppata da matematici come Euclide o Tolomeo, secondo la quale l’occhio emetteva un fuoco identificabile con alcuni raggi visivi o della vista, che toccavano gli oggetti trasmettendo all’anima la sensazione della visione. Tuttavia, ben presto sarebbe stata proposta una sorta di sintesi tra le emissioni degli oggetti e gli effluvi dell’occhio. Così Platone nel Timeo, 45 ss., in un passo alquanto confuso, e nel Teeteto, 156 ss., in termini un po’ più chiari, avanza una proposta appunto di questo tipo. Neanche Aristotele si mostra più preciso sull’argomento, ma critica chiaramente tutte quelle idee, soprattutto nel De sensu, II e III, proponendo quella che potrebbe essere considerata una volta ancora una sorta di sintesi: «In ogni caso dobbiamo quindi spiegare la percezione sensibile tramite il tatto, ragion per cui sarebbe meglio dire una volta per tutte che la percezione visiva è dovuta a un processo originato dall’oggetto percepito nel mezzo che sta tra quell’oggetto e l’organo sensitivo; vale a dire, dovuta al contatto, non alle emanazioni» (De sensu, 440a 15-20). Comunque, sul finire del XVI secolo era frequente la tesi che le «specie» avanzavano lungo la piramide formata dai raggi della vista. Come si vede, Galileo resta nell’ambito teorico tradizionale, servendosi dei concetti centrali dell’una o dell’altra teoria, sebbene in nessun momento giunga a pronunciarsi a favore dell’una o dell’altra sintesi.

⁸⁰ Si ha qui un ulteriore riferimento alla teoria platonica della conoscenza come reminiscenza.

⁸¹ Nel primo quarto.

⁸² Fu Tycho Brahe a difendere questa teoria nel libro II dei suoi Astronomiae instauratae progymnasmata, come afferma Keplero in Ad Vitellionem Paralipomena, VI, 10.

⁸³ È il libro scritto da Johannes Locher sotto la direzione del gesuita Christopher Scheiner, come indica il lungo titolo: Disquisitiones mathematicae de controversiis et novitatibus astronomicis. Quas sub Praesidio Christophori Scheineri, de Societate Jesu, Sacrae linguae et matheseos in Alma Ingolstadiensi universitate, Professori Ordinarii, Publice Disputandas posuit propugnavitque Mense Septembri, […] Nobilis et Doctissimus iuvenis, Johannes Georgius Locher, Boius Monacensis, Artium et Philosophiae Baccalaureus, Magisterii Candidatus, Iuris Studiosus, Ingolstadii, 1614. Nella Giornata seconda vedremo Galileo criticare con mordace ironia alcune sue tesi. Inoltre, nel De maculis solaribus… accuratior disquisitio del 1612, Scheiner aveva affermato che la luce secondaria è dovuta alla trasparenza del corpo lunare (si veda Opere, V, p. 67).

⁸⁴ Cleomede, astronomo del II secolo d.C., fu autore di un’opera uscita nel 1539 col titolo di Cyclica consideratio meteorum in cui compendiò gli studi di vari autori greci fra cui Posidonio. Quanto a Witelo, che visse verso la fine del secolo XIII fu autore di un trattato di ottica – che copiava Alhazen senza menzionarlo – ampiamente studiato, durante il Medioevo, da copie manoscritte e finalmente stampato su richiesta di Petrus Ramus, insieme al manoscritto di Alhazen, nel 1572. Keplero si riferì a tale trattato in una delle sue opere di ottica, gli Ad Vitellionem paralipomena. Macrobio, vissuto nel IV secolo d.C., fu autore di un celeberrimo commento a Cicerone intitolato Somnium Scipionis, nel quale esponeva alcune delle idee qui menzionate. Quanto all’«autore moderno» si tratterebbe, secondo Drake, di Franciscus Aquilonius che nel 1604 pubblicò un trattato di ottica. Comunque, la tesi che la luce della Luna proviene dal Sole e che la Luna se ne imbeve, derivava da Averroè e da Abraham ben Ezra, ed ebbe ampia diffusione in seguito, giungendo come si è visto fino a Buridano (si veda Duhem, 1958, vol. IX, pp. 411 ss.). Comunque, qui la teoria viene usata per spiegare non la luce della Luna, bensì solo la luce secondaria.

⁸⁵ Favaro ha pensato che potesse trattarsi di Giovanni Battista della Porta, rifacendosi alla Magia naturalis, 1589, p. 128. Sosio ha avanzato l’ipotesi che possa trattarsi di Martin Horky che infatti, in una lettera a Keplero del 24 maggio 1610, lo informava di disporre di uno strumento mediante il quale, non solo si poteva vedere meglio che con il telescopio di Galileo, ma che permetteva anche di parlare con chiunque si trovasse a una distanza di 15 miglia (Opere, X, p. 359).

⁸⁶ «Macchie antiche», dice Galileo, ma non si trattava di una attribuzione di antichità diversa a queste o a quelle macchie, bensì del fatto che alcune erano «note fin dall’antichità» come spiega nel Sidereus nuncius. Là dove in quel testo comincia a parlare delle osservazioni della Luna, commenta che, per comodità, divide la faccia dell’astro in due parti, la più chiara e la più scura. Qui per l’esattezza si riferisce a una distinzione che può applicarsi alla Luna piena e pertanto non si riferisce alla divisione che introduce, al termine, tra la parte illuminata e la oscura della Luna, che ha ampiamente commentato nel nostro testo. Nel Sidereus nuncius dice: «la più oscura tinge, a guisa di nuvola, l’istessa faccia lunare e la dimostra macchiata. Ma queste parti, men lucide e così grandi, facilmente si appresentano alla vista d’ognuno, e da tutti gli antichi son state eternamente vedute; e perciò io le chiamo con nome di grandi, o antiche, a differenza d’altre macchie, minori ma bensì spesse, che riempiono tutta la superficie lunare, e principalmente la parte più lucida», Sidereus nuncius, dalla trad. it. parziale di Vincenzo Viviani, in Galileo Galilei, La prosa, a cura di Isidoro Del Lungo e Antonio Favaro, Sansoni, Firenze, 1957, pp. 63-64.

⁸⁷ Già tra i presocratici c’era chi, come Filolao e Anassagora, sosteneva il carattere terrestre della Luna (Diels-Kranz, Die Fragmente der Vorsokratiker, 44 A 20; 59 A 35; 59 A 77). Plutarco fece lo stesso nel suo famoso opuscolo De facie in orbe Lunae, VI, 932c, e Averroè avrebbe attribuito allo stesso Aristotele l’affermazione della «natura terrestre della Luna» (In libris Aristotelis De Caelo commentarii, lib. II, summa II, quaestio III, comm. 32. Cit. da Duhem, 1958, IX, p. 410) Come ricorda Sosio, a partire dal Rinascimento questa tesi fu difesa da autori come Leonardo, Bruno e lo stesso Sarpi.

⁸⁸ Su questo tema si veda la nota 32 della Giornata prima. Si ritrova qui il principio generale del simile che attrae il simile, da Galileo esteso dalla Terra alla Luna. Ma, come abbiamo detto nell’Introduzione, è chiaro che l’affermazione pone più problemi di quanti non ne risolva. Da un lato, data la struttura elementare del mondo sublunare, non risulta chiaro quale rapporto e comportamento abbiano le sfere elementari rispetto alla Luna con la quale confinano. Inoltre, è ovvio che Galileo si imbatte qui in molti dubbi. Si veda l’Introduzione, pp. 83-86.

⁸⁹ Favaro informa che questo intervento di Simplicio era stato omesso per errore nell’edizione originale. Ragion per cui in molti esemplari di questa fu aggiunto in un cartoncino a stampa incollato al margine sinistro della pagina. Tuttavia, nel già menzionato esemplare di Galileo, sta scritto per mano di questi: «SIMP. Adunque, per vostro credere, ella farebbe un aspetto simile a quello che noi veggiamo nella Luna, delle 2 parti massime», per poi continuare con l’intervento di Simplicio che compare nel testo.

⁹⁰ Qui Galileo formula una tesi aristotelica che del resto nel secoli XVI e XVII era accolta praticamente da tutti i filosofi o scienziati, quale che fosse la loro tendenza, sebbene i particolari suscitassero enormi discussioni. Secondo Aristotele, infatti, era per esempio chiaro che, tanto nella generazione spontanea quanto in quella sessuata, interveniva come elemento fondamentale il «calore vitale» presente nel seme del maschio e che era «analogo all’elemento delle stelle». Non era «fuoco», puntualizzava Aristotele, che «non genera nessun… essere vivente…», mentre a generarli sono «il calore del Sole e quello degli animali» (De generatione animalium, V, 10, 777b 24-31).

⁹¹ L’asse di rotazione terrestre, pur restando parallelo a se stesso, è inclinato nella teoria eliocentrica di 23,5° rispetto al piano dell’orbita terrestre ovvero piano dell’eclittica. Questa inclinazione provoca l’apparente salita o discesa del Sole nel suo moto annuo apparente. Lo spostamento dal piano dell’elittica è di 23,5° verso nord in giugno e verso sud in dicembre, con un’escursione annua complessiva di 47°. Anche l’asse di rotazione della Luna si mantiene parallelo a se stesso, ma la sua inclinazione rispetto all’eclittica è di quasi 90°, cioè quasi perpendicolare all’asse dell’eclittica. La sua variazione stagionale si deve pertanto quasi unicamente all’inclinazione della sua orbita rispetto al piano dell’eclittica, che è di circa 5°. Abbiamo già accennato a questa «deambulazione» del ventre del dragone in una precedente nota. In realtà, come si vede, Galileo parla qui in termini geocentrici. Visto dalla Terra apparentemente immobile, il Sole non «sorge» né «tramonta» per gli stessi punti rispettivamente dell’est e dell’ovest, ma, nel corso dell’anno, si sposta «salendo» e «scendendo» verso il nord e verso il sud entro un angolo di circa 47°, spostamento che corrisponde all’angolo compreso tra il punto più a nord e il punto più a sud dell’eclittica (o percorso annuo del Sole), che è inclinata rispetto all’equatore di circa 23,5°.

⁹² Questo passo potrebbe essere interpretato come un’espressione del principio di pienezza, il quale afferma che tutto ciò che è possibile è reale, e che non esiste potenzialità dell’essere che non si attualizzi; perciò esisterebbero, per esempio, tutte le possibili varianti dei generi di esseri viventi. Nel pensiero cristiano, com’è ovvio, questo principio diventa un prodotto dell’onnipotenza e bontà divine. Si veda Lovejoy, 1966, pp. 73 e 169 ss.

⁹³ Archita di Taranto, famoso filosofo e uomo politico pitagorico del IV secolo a.C., che fu amico di Platone. Nelle Noctes atticae, Aulo Gellio, dopo aver rifiutato alcuni prodigi attribuiti ad autori antichi, o da loro menzionati cita questa meraviglia meccanica che molti filosofi greci, e soprattutto Favorino, attribuivano ad Archita. La citazione di Favorino riferita da Aulo Gellio, suona: «Archita di Taranto, che tra le altre cognizioni padroneggiava la meccanica, fece una colomba di legno che volava e che, quando si posava, non tornava più a levarsi in volo» (Aulo Gellio, Le notti attiche, a cura di Luigi Rusca, Rizzoli, Milano, 1968, lib. X, cap. 12, p. 279).

⁹⁴ È certo che questo paragone tra la comprensione umana e la divina fu uno dei luoghi che la commissione speciale nominata da papa Urbano VIII, dopo la pubblicazione del Dialogo nel 1632, consegnò per un esame al Sant’Uffizio (Opere, XIX, p. 327).

⁹⁵ Per un’esatta comprensione di questo passo, si dovrebbe riportare la dimostrazione del cosiddetto teorema di Pitagora, esposta da Euclide negli Elementi, Libro I, Proposizione 47, come pure l’enunciato delle proposizioni 35 ss. Possiamo comunque fare le seguenti osservazioni. In primo luogo, come è ovvio, il termine «quadrato» va inteso nell’accezione geometrica, predecessore storico del significato algebrico o aritmetico di «seconda potenza». In secondo luogo, è opportuno ricordare che le proposizioni 35 ss. con le relative dimostrazioni stabiliscono l’equivalenza di varie figure piane. Così per esempio, la 35 afferma che «Parallelogrammi che siano [posti] sulla stessa base e fra le stesse parallele sono uguali fra loro» – il termine greco è íson, che qui ha il significato, non di uguaglianza di forma, bensì di uguaglianza di superficie. Lo stesso si potrebbe precisare circa la proposizione 37 secondo la quale «Triangoli che siano posti sulla stessa base e tra le stesse parallele sono uguali fra loro». Orbene, la dimostrazione del teorema di Pitagora si basa, precisamente, su questi teoremi che, in ultima istanza, costituiscono casi particolari del principio più generale che Galileo formula per ultimo, quello dell’uguaglianza delle figure con la stessa area. Questo potrebbe forse essere inteso come un’illustrazione dei passi via via più elementari, che ci porterebbero a quelle che Euclide chiama «nozioni comuni» le quali, insieme ai postulati, costituiscono il passo precedente e la base delle successive proposizioni. In altre parole, Galileo sembra qui esporre un esempio dei successivi passi o «transiti», come dice più avanti, che la mente umana deve compiere nella conoscenza della geometria. (Le citazioni sono tratte da Euclide, 1970, pp. 131, 133.)