Use when there is an unknown in the question stem and numbers in the answer choices. Plug one of the choices into the question stem and see if the result is too large, too small, or just right. If the answer choices are arranged in numerical order, start with (B) or (C).
Use when (1) there are variables in the question stem and variables in the choices or (2) there’s a number (other than the answer) that the test maker doesn’t provide and that would be helpful in solving the problem. Pick numbers that are permissible (allowed, given the problem) and manageable (easy to work with).
Use when the answer choice has to have a certain property (such as being a perfect square, or being below a certain value). Eliminate answer choices that do not display that property.
Remember PEMDAS: Parentheses, Exponents and radicals, Multiplication and Division, Addition and Subtraction. Work fromleft to right.
9 − 2 × (5 − 3)2 + 6 ÷ 3 =
9 − 2 × (2)2 + 6 ÷ 3 =
9 − 2 × 4 + 6 ÷ 3 =
9 − 8 + 2 =
1 + 2 = 3
Find a common denominator.
Multiply the numerators, then the denominators. To divide, invert the second fraction before multiplying.
| Divisor | Divisibility Rule |
| 2 | All even numbers are divisible by 2. |
| 3 | Add up the individual digits of the number. If the total is divisible by 3, then the number itself is divisible by 3; for example, 243 is divisible by 3 because the sum of its digits is 2 + 4 + 3 = 9. However, 367 is not divisible by 3 because the sum of its digits is 3 + 6 + 7 = 16 and 16 is not a multiple of 3. |
| 4 | Take the last two digits and divide them by 2. If the result is even, the number is divisible by 4. If the result is odd, then the number is not divisible by 4. |
| 5 | All numbers ending in 5 or 0 are divisible by 5. |
| 6 | All even numbers that meet the test for divisibility by 3 are divisible by 6. |
| 8 | Divide the number by 2 twice; if the result is even, then the number is divisible by 8. |
| 9 | Add up the digits of the number; if the total is divisible by 9, then the number is divisible by 9. |
To multiply decimals, multiply both numbers. Count how many digits are to the right of the decimal in both numbers and move the decimal over to the left that number of spaces in the result.
To divide decimals, move the decimal to the right in both numbers until each is a whole number.
To solve 3.11 × 2.2, multiply 311 × 22 = 6842 Then move the decimal to the left three places: 6.842
To divide 5.12 by 6.4, move the decimal in both numbers over to make 5.12 into a whole number: 5.12 ÷ 6.4 = 512 ÷ 640 = 0.8
To express a fraction as a decimal, divide the numerator by the denominator. Multiply that by 100 to express as a percent. Remember these common fraction-decimal equivalencies:
(ax)y = axy
(ax)(bx) = (ab)x
When a negative number is raised to an even exponent, the result is positive. When a negative number is raised to an odd exponent, the result is negative.
When multiplying a number by a power of 10, as in scientific notation, the exponent simply represents the number of places to move the decimal. For example:
1.75 × 105 = 175,000
2.4 × 10−4 = 0.00024
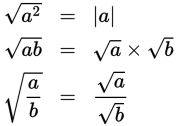
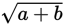does NOT equal
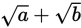(and the same applies to subtraction)
Look for factors of the number under the radical sign that are perfect squares; then find the square root of those perfect squares. Pull those roots outside of the radical sign.
Multiply the number by each positive integer smaller than that number.
8! = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 40,320
Begin by identifying one prime factor, and then break the number down into smaller and smaller factors until only primes remain. For example, to find the prime factorization of 60:
60 = 30 × 2 = 15 × 2 × 2 = 5 × 3 × 2 × 2
pos + pos = pos
pos + neg = (outcome will take
the sign of whichever addend
has the larger absolute value)
pos × or ÷ pos = pos
pos × or ÷ neg = neg
neg × or ÷ neg = pos
odd ± odd = even
even ± even = even
even ± odd = odd
odd × odd = odd
even × even = even
even × odd = even
(There are no rules for predicting whether the result of division will be even or odd, since division does not always result in a whole number, and only whole numbers are even or odd.)
The mean (arithmetic average) of 3, 4, 4, 6, and 8:
largest number − smallest number The range of 3, 4, and 8: 8 − 3 = 5
Find the middle number or (if the set has an even number of items) the mean of the two middle numbers.
The median of 3, 4, 4, 6, and 8: 4
The median of 3, 5, 8, and 9:
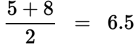
Find the number that repeats most often. The mode of 3, 4, 4, 6, and 8: 4
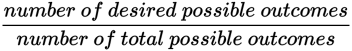
To calculate the probability that two events will occur, multiply the probabilities of each.
To calculate the probability that at least one of two independent events will occur, add the probabilities of each.
whole × percent (expressed as a decimal or fraction) = part
Given two parts of that equation, you can solve for the third. E.g., 18 is 60% of what number?
whole × .6 = 18
whole = 18 ÷ .6 = 30
distance = rate (that is, speed) × time
work performed = rate of work × time
Given two parts of that equation, you can solve for the third.
Given incomplete information and two journeys or work projects, set up a proportion to solve for the unknowns. For example, Joe can travel 62 miles on his bike in 5 hours. At that rate, how far could he travel in 7 hours?
Cross-multiply to solve for x.
total distance = average rate × total time
Remember FOIL: first, outer, inner, last.
(x + 3)(x − 2) = x2 − 2x + 3x − 6 = x2 + x − 6
Manipulate the quadratic so that it is in the form ax2 + bx + c= 0 (where a, b, and ccan be positive or negative numbers). Then perform reverse-FOIL: that is, find two binomials that multiply to make the quadratic. This will usually yield two possible values for x. For example:
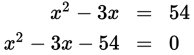
Find two numbers that add to −3 and multiply to −54.
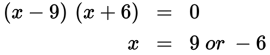
These shortcuts may help on some quadratics:
a2 − b2 = (a + b)(a − b)
a2 + 2ab + b2 = (a + b)(a + b) = (a + b)2
a2 − 2ab + b2 = (a − b)(a − b) = (a − b)2
Isolate the variable you’re solving for on one side of the equation. You may add, subtract, multiply, or divide both sides of the equation by variables or numbers, as long as you do the same thing to both sides.
Follow the same steps as solving a linear equation, but remember these two rules:
(1) If you multiply or divide both sides of an inequality by a negative number, you must reverse the inequality sign.
(2) You cannot multiply or divide both sides of an inequality by a variable (since you do not know the sign of the variable).
angle measure = 90: right
angle measure < 90: acute
90 < angle measure < 180: obtuse
angle measure = 180: straight
angle measure > 180: reflex
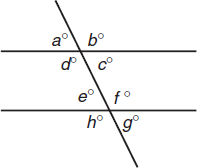
Corresponding angles are equal. For example, a = e. Same-side interior angles are supplementary. For example, c + f = 180.
Opposite angles are equal, and alternate interior angles are equal. For example,
b = d = f.
All four acute angles are equal. All four obtuse angles are equal.
perimeter = 2(length) + 2(width) area = length × width
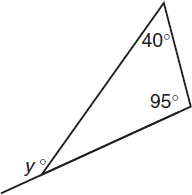
Find the measure of an interior or exterior angle of a triangle:
The interior angles of a triangle add to 180. An exterior angle of a triangle is equal to the sum of the two opposite interior angles.
x + 40 + 95 = 180
y = 40 + 95
perimeter: side + side + side
area:
, where b is the base of the triangle and h is the height (which is the perpendicular distance between the base and the vertex opposite the base)
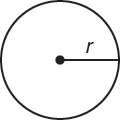
radius: half the distance across the middle of the circle
diameter: the distance across the middle of the circle, or 2r
circumference: C = 2πr
area: A = πr2
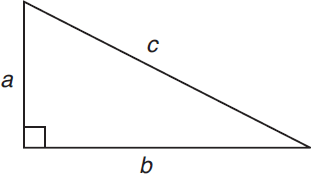
if you know the lengths of two sides of a right triangle (that is, a triangle with a 90 degree angle), you can calculate the third side.
a2 + b2 = c2
Memorize these ratios, often (but not always) displayed by the sides of right triangles:
3:4:5
5:12:13
Also, remember these proportions displayed by some right triangles:
The legs of a right triangle with angle measures 45:45:90 display this proportion: x:x:x
The legs of a right triangle with angle measures 30:60:90 display this proportion: x: x
:2x
Similar triangles have the same angle measures as each other. Corresponding sides of these triangles are proportional.
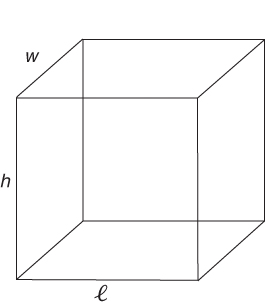
V = lwh
SA = 2lw + 2wh + 2lh
V = πr2h
SA = 2πr2 + 2πrh
y = mx + b, where m is the slope and b is the y-intercept
A horizontal line has a slope of zero.
The slope of a vertical line is undefined.
Use the Pythagorean theorem. For example, to find the distance between points A and B below, first draw a right triangle with A and B as the two ends of the hypotenuse.
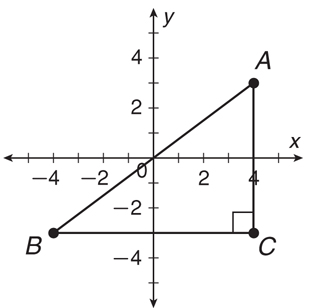
Find the distance from A to C and from B to C, and plug those distances into the Pythagorean theorem:
