Answers and Explanations

Part 2: Arithmetic Reasoning (AR)

1. C

   This question asks you to determine the sale price of a camera that normally sells at $160 and is discounted 20%. To solve, determine what 20% of $160 equals. Rewrite 20% as a decimal. 20% = 0.20. So 20% of $160 = 0.20 × $160 = $32The sale price of the camera would be $160 – $32 = $128, choice (C).

2. B

   First, set up the rate as a proportion, where x is the number of stations.

   

   Then, convert the units.

   

   Cross multiply and solve for x.

   180 = 10x

   18 = x

3. B

   In this question, the ratio is implied: for every 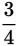inch of map there is 1 real mile, so the ratio of inches to the miles they represent is always 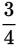to 1. Therefore, you can set up the proportion:

   

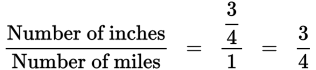
   Now inches = inches.

   Set up a proportion:

   inches

   

   Cross-multiply:

   

4. D

   You can express the ratio of baseballs to golf balls as 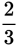. Since you know the number of baseballs, you can set up a proportion: where x is the number of golf balls. To solve, cross-multiply to get 2x = 90, or x = 45.

5. D

   The total cost of the taxi ride equals $36 + (25% of $36), or $36 + (.25 × $36) = $36 + $9 = $45. If four people split the cost equally, then each person paid 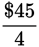, or $11.25 each.

6. A

   Find the number of seconds in an hour and then multiply this by the distance the car is traveling each second. There are 60 seconds in a minute and 60 minutes in one hour; therefore, there are 60 × 60, or 3,600, seconds in an hour. In one second the car travels kilometers; in one hour the car will travel 3,600 × or 36 kilometers.

7. B

   Subtracting a negative number is the same as addition, so 20 − (−5) is really 20 + 5 = 25.

8. C

   If Ms. Smith’s car averages 35 miles per gallon, she can go 35 miles on 1 gallon. To go 700 miles she will need , or 20 gallons of gasoline. The price of gasoline was $1.25 per gallon, so she spent 20 × $1.25, or $25, for her trip.

9. D

   Be careful with a question like this one. You’re given the percent decrease (25%) and the new number (72), and you’re asked to reconstruct the original number. Don’t just take 25% of 72 and add it on. That 25% is based not on the new number, 72, but on the original number—the number you’re looking for. The best way to do a problem like this is to set up an equation:

   

   Alternatively, you can use the answer choices to determine the correct answer. The original number of jelly beans has to be reducible by 25%, or . That means the original number of jelly beans has to be a multiple of 4 (or else you'd be reducing by pieces of jelly beans). Only the correct answer, 96, is a multiple of 4.

10. B

    The time it takes to complete the entire exam is the sum of the time spent on the first half of the exam and the time spent on the second half. The time spent on the first half is of the time spent on the second half. If S represents the time spent on the second half, then the total time spent is . You know this total time is one hour, or 60 minutes. Set up a simple equation and solve for S.

    

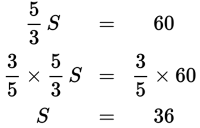
    So the second half takes 36 minutes. The first half takes 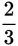of this, or 24 minutes. You could also find the first half by subtracting 36 minutes from the total time, 60 minutes.

11. A

    You’re asked what percent of the new solution is alcohol. The part is the number of ounces of alcohol; the whole is the total number of ounces of the new solution. There were 25 ounces originally. Then 50 ounces were added, so there are 75 ounces of new solution. How many ounces are alcohol? 20% of the original 25-ounce solution was alcohol. 20% is , so of 25, or 5 ounces are alcohol. Now you can find the percent of alcohol in the new solution:

    

12. A

    To find probability, determine the number of desired outcomes and divide that by the number of possible outcomes. The probability formula looks like this:

    

    In this case, Marty is pulling one pen at random from his knapsack, and you want to determine the probability that the pen is either red or black. There are 5 blue pens, 6 black pens, and 4 red pens in the knapsack. Let’s return to the probability formula:

    

13. D

    Be careful with combined percent increase. You cannot just add the two percents, because they’re percents of different bases. In this instance, the 100% increase is based on the 1980 population, but the 50% increase is based on the larger 1990 population. If you just added 100% and 50% to get 150%, you would have chosen a wrong answer.

    The best way to do a problem like this one is to pick a number for the original whole and just see what happens. The best number to pick here is 100. (That may be a small number for the population of a country, but reality is not important—all that matters is the math.)

    If the 1980 population was 100, then a 100% increase would put the 1990 population at 200. And a 50% increase over 200 would be 200 + 100 = 300.

    Since the population went from 100 to 300, that’s a percent increase of 200%.

    

14. B

    To learn the man’s overtime rate of pay, first figure out his regular rate of pay. Divide the amount of money made, $200, by the time it took to make it, 40 hours. $200 ÷ 40 hours = $5 per hour. That is the normal rate. The man is paid times his regular rate during overtime, so when working more than 40 hours he makes × $5 per hour = $7.50 per hour. Now figure out how long it takes the man to make $230. It takes him 40 hours to make the first $200. The last $30 are made at the overtime rate. Since it takes the man one hour to make $7.50 at this rate, you can figure out the number of extra hours by dividing $30 by $7.50 per hour. $30 ÷ $7.50 per hour = 4 hours. The total time needed is 40 hours plus 4 hours, or 44 hours.

15. A

    The calculations aren’t too bad on this one. The most important thing to keep in mind is that you’re solving for 75% of x and not for x itself. First, you are told that 50% of x is 150. That means that half of x is 150, and that x is 300. So 75% of x = 0.75 × 300 = 225.

16. D

    This is a question where Backsolving (plugging in an answer choice to see if it’s correct) can save you a lot of time. Let’s start with choice (B) and see if it works. If (B) is correct, an adult’s ticket would cost $3.00, and a child’s ticket would cost $1.50. The total fare you're asked for is for two adults and three children. If an adult’s fare was $3.00, that total fare would be 2($3.00) + 3($1.50) = $6.00 + $4.50 = $10.50. That’s too low since the question states that the total fare is $14.00.

    Now see what happens if an adult fare was more expensive. If (D) was correct, an adult’s ticket would cost $4.00 and a child’s ticket would cost $2.00. The total fare would equal 2($4.00) + 3($2.00) = $8.00 + $6.00 = $14.00. That’s the total fare you’re looking for, so (D) is correct.

17. C

    To find the prime factorization of a number, find one prime that will go into the number (here 2 is a good place to start). Express the number as that prime multiplied by some other number.

    140 = 2 × 70

    Then keep breaking down the larger factor until you are left with only prime numbers.

    140 = 2 × 2 × 35

    140 = 2 × 2 × 5 × 7

18. A

    When the painter and his son work together, they charge the sum of their hourly rates, $12 + $6, or $18 per hour. Their bill equals the product of this combined rate and the number of hours they worked. Therefore $108 must equal $18 per hour times the number of hours they worked. Divide $108 by $18 per hour to find the number of hours. $108 ÷ $18 = 6.

19. C

    The exclamation mark indicates a factorial. A factorial is an integer multiplied by every smaller integer, down to the number 1, like this: 4! = 4 × 3 × 2 × 1 = 24

20. B

    Compute the cost of parking a car for 5 hours at each garage. Since the two garages have a split-rate system of charging, the cost for the first hour is different from the cost of each remaining hour.

    The first hour at garage A costs $8.75

    The next 4 hours cost 4 × $1.25 = $5.00

    The total cost for parking at garage A = $8.75 + 5.00 = $13.75

    The first hour at garage B costs $5.50

    The next 4 hours cost 4 × $2.50 = $10.00

    The total cost for parking at garage B = $5.50 + $10.00 = $15.50

    So the difference in cost = $15.50 − $13.75 = $1.75, (B).

21. C

    Set up a proportion:

    

    An hour is 60 minutes; one third of that is 20 minutes. So 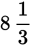hours is 8 hours and 20 minutes.

22. B

    This problem sets up relationships among large, medium, and small sodas—2 large sodas are equal to 3 medium sodas, and 2 medium sodas are equal to 3 small sodas. How many small sodas equal 8 large sodas? Well, 2 larges equal 3 mediums, so 12 mediums must equal 4 × 2 or 8 large sodas. You now can find how many small sodas represent 12 mediums. Since 2 mediums are the same as 3 small sodas, 12 mediums must equal 6 × 3 or 18 small sodas.

23. D

    If you change each digit 5 into a 7 in the number 258,546, the new number would be 278,746. The difference between these two numbers would be 278,746 − 258,546 = 20,200.

24. B

    Since 1 pound of lumber costs $4.00, 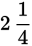pounds of lumber cost 2.25 × $4.00 = $9.00. Then add 7% sales tax to $9.00. Find 7% of $9.00 by multiplying 0.07 × $9.00 = $0.63. Add $0.63 to $9.00 to get $9.63, choice (A).

25. D

    The question asks which of five ratios is equivalent to the ratio of to . Since the ratios in the answer choices are expressed in whole numbers, turn this ratio into whole numbers. Start by turning the ratio into improper fractions:

    

    Multiply both sides of the ratio by 4.

    = 13 : 21

26. D

    Set up the proportion.

    

    Cross multiply.

    x = 72

      x = 72 ×

      x = 192

27. C

    You can save valuable time by estimating on this one. Pay special attention to how much you have left and how much you’ve already spent. If a man spent 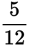of his salary and was left with $420, that means that he had left, and if the man’s salary is x dollars, then x = $420 That means that $420 is a little more than half of his salary. So his salary would be a little less than 2($420) = $840. Choice (C), $720 is a little less than $840. So (C) works perfectly, and it’s the correct answer here.

28. C

    The key to this question is that while the value of the stock decreases and increases by the same amount, it doesn’t decrease and increase by the same percent. When the stock first decreases, that amount of change is part of a larger whole. If the stock were to increase to its former value, that same amount of change would be a larger percent of a smaller whole.

    Pick a number for the original value of the stock, such as $100. (Since it’s easy to take percents of 100, it’s usually best to choose 100.) The 20% decrease represents $20, so the stock decreases to a value of $80. Now in order for the stock to reach the value of $100 again, there must be a $20 increase. What percent of $80 is $20? It’s × 100%, or × 100%, or 25%.

29. C

    This is a combined work problem. Joan can shovel the whole driveway in 50 minutes, so each minute she does of the driveway. Mary can shovel the whole driveway in 20 minutes; in each minute she does 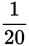of the driveway. In one minute they do:

    

    If they do 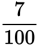of the driveway in one minute, they do the entire driveway in 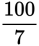minutes. (If you do of a job in 1 minute, you do the whole job in the reciprocal of , or 2 minutes.) So all that remains is to round off to the nearest integer. Since = , is approximately 14. It takes about 14 minutes for both of them to shovel the driveway.

30. B

    You’re told that Eileen earns $280 per week. Kelly earns $50 more than Eileen, so Kelly earns $280 + $50 = $330 per week. June’s salary is $70 less than Kelly’s, so June earns $330 − $70 = $260 per week, and (B) is correct.