Answers and
Explanations
Math Strategies for the ASVAB Practice Questions
-
Combination of Approaches This problem includes some unwieldy numbers, but rounding them for estimation should
get you an approximate answer. Find 80% of 1,000 gallons to determine how many gallons
are used for the first trip (80% × 1,000 = 800 gallons). Then, round 1,496 to 1,500
and round 3,016 to 3,000. Notice that the question really asks, “How many gallons
of fuel would the airplane use to fly about twice as far as the first trip?” Just
multiply 800 × 2 = 1,600 gallons and find the answer choice closest to 1,600. In other
words, combining a little calculation with some estimation works well here.
-
Backsolving Even without a question stem, you can see that all the answer choices are numbers.
That makes this an excellent candidate for Backsolving. Start by trying (B) or (C).
-
Picking Numbers There are variables in the answer choices. Picking Numbers will make the problem
more concrete, and plugging the numbers you picked into the answer choices will allow
you to find your target number.
-
Strategic Guessing Using Logic Although these fractions might look intimidating at first, closer examination will
show that they are quite spread out. (A) is very tiny, (B) is about
 , (C) is about
, (C) is about
 , and (D) is close to
, and (D) is close to
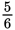 . Depending on the question asked, you can probably get a rough idea of which answer
choice is the right answer without doing a lot of complex calculating.
. Depending on the question asked, you can probably get a rough idea of which answer
choice is the right answer without doing a lot of complex calculating.
-
Backsolving Quickly plug answer choices into the equation to eliminate choices that are too large
or too small.
-
Picking Numbers A problem with percents and no amount given for Jim’s paycheck makes this a perfect
opportunity for Picking Numbers. Use $100 for the amount of Jim’s paycheck and then
apply the percentages in the problem. He spends 30% of $100, or $30, on rent. This
leaves him $70, of which he spends 40% on his car, or 40% × $70 = $28. Subtract $30
for rent and $28 for the car repairs from his $100 paycheck, and he has $42 left.
Since $100 represents the full paycheck, the dollar amount left is the same as the
percent left, 42%.
 , (C) is about
, (C) is about
 , and (D) is close to
, and (D) is close to
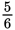 . Depending on the question asked, you can probably get a rough idea of which answer
choice is the right answer without doing a lot of complex calculating.
. Depending on the question asked, you can probably get a rough idea of which answer
choice is the right answer without doing a lot of complex calculating.