It is a truth universally acknowledged that a single man in possession of a good fortune must be in want of a wife. So runs a famous first sentence, full of statements about One. It claims a universal truth, but there is an ironic touch in the grandeur of Jane Austen’s opening, bound as it so obviously is by human pride and prejudice, and specific to the English bourgeoisie of the early nineteenth century. Even so, a modern reader finds it a good story-starter. It is well wired into human brains, tastefully pressing the buttons labelled ‘sex’ and ‘money’ in unison.
A chapter about the number One itself cannot count on any such welcome mat. Numbers do not make light conversation, and are gatecrashers at the great party of the human arts. They seem devoid of that sympathetic wit and irony which smooths the passage of letters and life. Indeed, the numbers can hardly join in the human party at all, being abstractions unable to shake hands or flirt. Where did Page One go to?—this is already Page Two, and Page One exists only by implication, possessing a One-ness only in one’s mind’s eye.
Even more annoying to the party-goers is that the numbers adopt unappetising manners whenever they get the upper hand, dictating bossy, tedious and incomprehensible regulations. This is a book about the inner life of these unwelcome guests. It is, more or less, the tale as told by the mathematicians who get to know them. I hesitate to generalise because mathematicians are an un-unionised bunch, with the solidarity of a plate of spaghetti. But the assumption implicit in mathematics is one of universal truths deeper than any Jane Austen would have countenanced as an opening gambit in polite conversation.
Numbers, to mathematicians, are the same for Cleopatra or Moctezuma, for the Neanderthals and the dinosaurs, true in any galaxy, past or future. They tell stories which could be shared with extraterrestrial intelligences. When Dante wanted something for the happy inhabitants of the Paradiso to do with eternal life, he took from Platonic tradition the contemplation of mathematical truth. Not everyone would welcome this connection: the British mathematician G. H. Hardy, who as an atheist wouldn’t be seen dead in the One to Nine of Dante’s heaven, made a famous declaration of mathematical idealism which had nothing to do with religion.
Hardy expressed this other-worldliness by using the concept of a prime number. Any number n can be represented as a multiplication of 1 × n. Put another way, 1 and n are always divisors of n. The prime numbers are those numbers which have only those two divisors, and so enjoy a special relationship with One. The numbers 2, 3, 5, 7 and 11, for instance, are prime. The number 6 is not. The distinction can be seen as a picture. Six objects can be arranged in a rectangle, but seven must lie on a line.
Even the United States is powerless to change the régime of the primes, and as the stars have swelled from 13 to 50, ingenious means have been necessary to deal with this fundamental problem. In 1940, as those then neatly 6 × 8 states were about to face their transformation into a superpower, Hardy published a short book, A Mathematician’s Apology, with a statement of superhuman Number: ‘317 is a prime, not because we think so, or because our minds are shaped in one way rather than another, but because it is so …’
What view was Hardy arguing against? His scorn was reserved for the profilic British polymath biologist Lancelot Hogben, author in 1936 of a major popular book, Mathematics for the Million. Holding his nose, Hardy quoted Hogben’s characterisation of mathematics as ‘the grammar of size and order’, needed for the planning of ‘the rational society’. Hogben was expressing the Marxism of the 1930s, which saw all cultural manifestations as the outcomes of relations of production, and thus mathematics as based in human practice. Hardy was no conservative élitist, and in fact had rather radical views. He recognised that mathematics might be useful, but insisted that its utility did not explain why mathematicians did it.
Mathematicians have largely maintained a discreet radio silence, and Hardy was unusual for striking a dissonant note in public. Someone who knew him, novelist C. P. Snow, wrote that Hardy ‘didn’t give a damn’. Snow himself became famous in the 1960s for trying to combine Jane Austen’s legacy with insight into twentieth-century science. It is doubtful whether Snow had much success with his unifying vision, and his books are neglected now. But his expression ‘Two Cultures’ has stuck as an awkward reminder of the fact that those who run the human world and dominate its discourse are generally unaware of its base in the physical world, and of the mathematics that is the only language for expressing that world. Snow used the Second Law of Thermodynamics as his example of what ought to be well known, but he might as well have used the First Law, or indeed the Zeroth Law, as his examples: it is as true now as it was in the 1960s that none of these can be referred to in polite society.
There is now an extra reason for presenting an unwelcome message about the inescapable properties of numbers, summarised in Al Gore’s expression of ‘inconvenient truth’. Although the question of recent, anthropogenic climate change involves many physical sciences—including all those laws of thermodynamics—the power of mathematics to predict is at the heart of the developing theory. The calculation of climate change certainly falls into Hogben’s realm of the relations of human production, but the phrase ‘inconvenient truth’ could have come from the inconvenient Hardy himself. The Earth’s atmosphere lacks the simplicity of 317: there are even more factors involved in climate science than in cosmology, where notable corrections have been made, and there are bound to be revisions to current models. And yet those models are essentially mathematical. Environmental campaigners who want to disrupt airports say that ‘the science tells us’ in terms that they feel put their case above the law, words that recall Hardy’s ‘it is so’. Whether one takes Hogben’s viewpoint or Hardy’s, the question of the potential of mathematics is newly vital.
In the 1990s, I wrote a weekly column on mathematical topics for a British newspaper, the Observer. The editor, Rebecca Nicolson, contacted me again in 2005 and suggested a short book with the title One to Ten. I saw a point of departure. For this had been done before, in a classic book by Constance Reid, From Zero to Infinity (1956), still in print 50 years later. Her ten chapters were headed by the numbers from Zero to Nine, each used to spark off an elegant exposition of some substantial feature of the theory of numbers. Anything I wrote was bound to resemble her plan.
I remembered her book well because I learnt so much from it, perhaps most of all because through Constance Reid I had absorbed Hardy’s view of other-worldly mathematics, communicated with all his charm but without his awkward-squad agenda. Her succinct and lucid pages now convey a 1950s America, fortress of world culture, but not much given to airing controversies. It is compelling in its commitment to the fascination of numbers for their own sake. Questions of motivation or usefulness hardly arise in her account. These, however, poured from another book of my childhood: this was Man Must Measure (1955) by none other than Lancelot Hogben. In the 1950s he blazed a new trail, using extensive graphics and photographs to pour out an encyclopedic knowledge. In his enthusiastic account, mathematical advance was as anthropogenic as carbon dioxide, the fruit of human industry, interwoven with every kind of human skill and argument. So between them, these books exposed me to two different points of view, echoing the 1930s political conflict. Fifty years later, I find myself having to re-echo them.
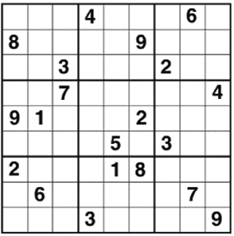
Given the publisher’s suggestion of One to Ten, and the classic example of Reid’s sequence from zero to nine, my decision was for One to Nine. The clinching factor was, of course, the worldwide popularity of the Sudoku square. In case you’ve been away from the solar system for a while, here is an example of the basic 3 × 3 Sudoku puzzle. The grid must be completed so that every row, column and subsquare contains just the numbers One to Nine.
A TOUGH problem, with no obvious first step. Hint: there is only one place where the 3 can go in the central square.
The numbers entered this book saying that they made no light conversation. But if numbers did make light conversation, Sudoku shows how they would talk. What’s more, it shows they can tell a joke. It is this: although The Times of London and other newspapers insist that the puzzle ‘needs no maths’, the process of solving it is an elegant miniature version of the experience of real, adult, mathematics. What The Times means is that it needs no school maths, reflecting the legacy of fear and anxiety generated by schools, which leaves most of their victims with a lifetime of mumbling apologetically about ‘my worst subject’.
Sudoku problems are Hardy-ish in having no use whatsoever, apart from helping to keep Alzheimer’s at bay. They do nothing for the once-planned society of the future, nor for the market economy which has replaced it. In fact they must have subtracted millions of person-hours from the duties of profit-making. They have none of the cosy linguistic clubbiness of cryptic crosswords. The problems need up to an hour of concentrated thought. Yet the demand for them appears insatiable.
In contrast, school mathematics teaching seems to be in a particular state of crisis. The Guardian, the leading British newspaper for the education business, describes it as ‘needing a makeover, to make it sexy again’. Mathematicians, its writer explains, ‘are bald, overweight with beards and glasses and eternally single, leading little or no social life’. Jane Austen’s efforts would clearly have been doomed had she opened with such a character, and curiously, the writer for this progressive newspaper—long a leading voice for feminism—tacitly and unrealistically assumes mathematicians to be male. Another Guardian Education feature helpfully describes all science as ‘boring, prohibitively hard, too abstract and too male, in a spoddy, won’t-get-a-girlfriend kind of way’. These artless articles reveal an unlovely truth: that mass, compulsory, school maths has enjoyed about the same success as the War on Drugs.
In stark contrast to these effusions, Sudoku gains cool customers without any need for sexing up, and the Times champion is, as it happens, a young woman. The reason, perhaps, is that Sudoku encapsulates some of the most fascinating elements of adult mathematics: elegant geometry and pure logic. You can try to solve a puzzle by guessing—but pencilling in trial solutions and rubbing them out again is likely to be a losing battle. Faith, hope, fantasy and bluster are prominent in the planning of world domination, but are powerless to solve the Sudoku square—or mathematical problems.
Although we are following Sudoku with One to Nine, we cannot ignore the Zero with which Constance Reid chose to begin. There is a difficulty about her choice. She says that Zero, ‘first of the numbers, was the last to be discovered.’ This makes One her second number, and Two her third. This seems very odd, but it makes sense if you distinguish cardinal and ordinal numbers. Word roots show how human culture has thought of ‘one’ in more than one way. The root one, un, uno, ein … answers the question of ‘how many’. It is the cardinal number which counts. But the root that shows in prime, prince, Fürst, first, evoking the social relationships of primitive primates, with their prima donnas and prime ministers, is the ordinal number. It is the difference between ‘one page’ and ‘Page One’. So the apparent contradiction can be explained; Constance Reid took the cardinal Zero to correspond to the ordinal ‘first’.
She could have avoided this by describing Zero as the noughth number. The words ‘noughth’ or ‘zeroth’ do have a shadowy existence in language, used for something that has to be placed before something that has already been called ‘first’. After the First Law of Thermodynamics (the conservation of energy) had been established, the Zeroth Law (temperature exists) was recognised as more primitive. Oxford University has a Noughth Week before the first week of term, but no Noughth Class degrees better than a First. There are other grey areas where language calls for starting a list with zero: the Dewey decimal classification, the Noughties for this first decade. However, having to explain the ordinal ‘noughth’ probably causes more problems than it solves.
With cardinal numbers, at least there is no doubt about what Zero means, and Constance Reid argued that it (probably) answers the question, ‘How many elephants are there in the room where you are reading this book?’ Nevertheless, we do not normally start counting until there is something to count. A queue of zero people is not a queue at all. For this reason, the numbers 1, 2, 3, 4 … are usually called the natural numbers by mathematicians. One banana, two bananas, three bananas, four … shows the naturalness of the definition. Yes we have no bananas, although comprehensible, shows the oddness of offering zero bananas for sale.
Nought-words go far back in Indo-European languages, with thousands of years of clicking tongue against palate to deny, negate or undo. We show no reluctance to make a positive assertion of nothing. Yet counting zero is not like counting one or two. What is or are nought bananas? Nothing at all? If so, then ‘We have no bananas’ would mean the same as ‘We have no sour grapes’—which it does not. The difficulty about asserting nought of something is that it seems to assert a potential existence of the very thing of which there are none. This is not problematic for greengrocers—but it is for atheists. ‘I have zero pet unicorns’ is a true statement, but it seems to assert the possibility of a very untrue one.
Ambivalence and awkwardness about Nought pervades English grammar. Sticklers for accuracy insist that Messrs. Blair and Bush should have said that ‘none of the terrorist threats is caused by the occupation of Iraq’ because ‘none’ is short for ‘not one’ and therefore takes a singular verb. Yet Nought takes a plural. Join MySpace and read that you have 0 friends. (Or read the Guardian report that ‘poor old mathematicians’ have no friends except other mathematicians.) When giving her illustration, Constance Reid was unaware that 50 years later computers would announce ‘there are 0 people in this chat-room’, in conspicuously unnatural language.
Zero is not natural language. How many E, man? O, please! Got any change? Sure, here’s 0p! Media intern: salary $0. Yo emperor kewl kit:-) Yo m8 got 0 on. Supermodels inspire Susie Orbach to say that ‘size zero means you don’t exist!’ This plays exactly on the puzzle of Nought, the puzzle of observing something that is not there, and perhaps this puzzle explains why it took so long for zero to acquire a symbol, and so was ‘the last to be discovered’.
The odd thing is that in the world of Greek mathematics, an abacus or its equivalent was used to do calculations. On an abacus, an empty wire or box plays the role of a zero. Yet the small step to a written symbol, corresponding to that empty space, was apparently never made. The innovation arose in India; a zero was used there by the ninth century CE, and used in just the same way as it is used today. The number 2007 means two thousands, zero hundreds, zero tens and seven. The value to be attached to the 2 and the 7 depends on their position: this is place-notation and it makes a zero essential.
The innovation was attested by the treatise of the leading Persian mathematician al-Khwarizmi: On the Calculation with Hindu Numerals, written in about 825CE. A decimal inscription of 870 at the temple in Gwalior, central India, is the earliest that now survives. Zeroes spread into common Arabic use. Gerbert, who became pope in 999, explained the Arabic advance in a Latin treatise. There was no equivalent of the dot-com boom in that millennial year, however; for it was not until 1202 that Leonardo of Pisa, usually known as Fibonacci, successfully urged it in his Liber Abacus for practical use in backward Europe. Slowly, thereafter, the Arabic (or perhaps more accurately, Eurabian) numerals became used in commerce. One argument advanced against them was that place-notation makes it easy to defraud by adding on a nought, and even now cheques must be written in words, a long-term legacy of the suspicion of zero.
In the tenth century, Arab mathematicians had developed place-notation into expressing fractions, which now seem naturally bound up with zeroes and the decimal point. Yet the Babylonians had much earlier managed fractions in their system, even evaluating the square root of two to a remarkable accuracy, without a zero. It is hard to see how they could have developed one abstraction without the other. It is certainly hard now to imagine how feats such as the recently discovered classical astrolabe, gear wheels imitating accurately the motion of the Moon, could have been carried out without writing down zeroes—if only to note down the state of an abacus in mid-calculation.
Perhaps the abacus workers of the ancient world did sometimes jot down dots and dashes, but were deterred by grander literary personages from using such sad and spoddy scribbles in official writing. The problem of the calendar also gives an example of how close you can come to a concept of zero without actually getting there. The sixth-century Byzantine monk Dionysius Exiguus famously defined the Christian era with an AD1. But his method for defining the date of Easter calls for writing down the remainder when the year is divided by 19. When there is no remainder, this cries out for a zero symbol, to be regarded as on a par with the symbols for other numbers. But the Hellenic world still didn’t get it. In contrast, Hindu calendars happily began with a Year Zero.
Was the Indian zero discovered or invented? Was it there all the time, as in Hardy’s world of absolute truth—or was it an example of what Hogben called ‘Mathematics in the Making’? A better word perhaps is realised, with its double meaning: both seeing a truth, and making it physically concrete.
Although I have made a fuss about the puzzle of zero being called the ‘first’ number, I should not leave the impression that this is a major issue. It is only for counting and ordering the infinite that the question of cardinals and ordinals acquires serious substance. For bananas and for book chapters, these are essentially questions of names and conventions, and a much more important point is that mathematics is a world where names and conventions do not matter, as long as they are clear. As an example, time is often described as a fourth dimension, coming after the three dimensions of space. But it is the usual convention now to place time before space as the noughth dimension.
This brings us to an important distinction, on which Constance Reid was wonderfully clear. The numerals, the symbols 0 1 2 3 4 5 6 7 8 9, are not numbers, but the names of numbers. Originally, telephones had dials physically sending ten clicks for a 0, and so made it made sense to put the symbols in the order 1234567890. (You cannot send zero clicks, because sending zero clicks can’t be distinguished from not-sending: this is exactly the unnaturalness of nought.) Nowadays, the 0 on a telephone is just an arbitrary symbol, and telephone numbers could be as freely assigned as internet names.
The properties of numbers don’t depend on the numerals used to describe them. There are many ways in which they can be described. The simplest way to write the natural numbers is by the unary notation of a prisoner scratching  on a cell wall. This shows the problem of unnatural Zero again: you cannot scratch nought marks on a prison wall to show you have not been inside.
on a cell wall. This shows the problem of unnatural Zero again: you cannot scratch nought marks on a prison wall to show you have not been inside.
Roman numerals can be thought of as an extension of unary notation, with a shorthand for I’s in handfuls of five: V for IIIII, X for IIIII IIIII and then going on to fifties, hundreds, five-hundreds and thousands. (Thus the famous number 666, which is 500 + 100 + 50 + 10 + 5 +1, is represented as DCLXVI.) Roman usage shortened IIII to IV, VIIII to IX, a striking fact because it introduced the idea that when placed before a V or X, an I serves an an instruction to subtract one, not to add one; likewise for X and C. Thus, film copyrights dated MCMXCIX (but not MIM) preceded MM. Having conceded that the meaning of symbols may change according to their placement, it is hard to see why it took so long for the Indian place-notation to be accepted in Europe. It seems that it was the symbol 0 that was the critical factor.
But using a zero does not in any way oblige a counting in tens. The logic of place-notation works just as well if some other number is used as a base. It is not obvious why all human cultures seem to have marked off numbers in tens. The exceptions, as in the sixties of the Babylonians, still build on tens. You have to look hard to find the Amazonian Pirahã people, said to live without abstraction or numbers at all. The universality of ten is not fully explained by the form of human hands. It would surely have been just as natural to use the eight fingers, not including thumbs. Eight-based counting would have been better suited to the repeated splitting of differences which is so natural for sharing and trading, as indeed for music.
If the use of the eight fingers had been adopted for counting, then only the numerals 1234567 would be needed in addition to the 0. Eight would be written as 10, and what we call sixty-four would be 100. In this octal system, adding a 0 means multiplying by eight. The multiplication table is mercifully reduced to:

You should not read ‘43’ as ‘forty-three’, short for four-tens and three, because here it means four eights plus three, or thirty-five. With a little practice you could acclimatise to this system. People readily cope with interpreting symbols according to context, reading a digital clock’s 16.03 as meaning ‘three minutes past four’, reading 4/3 as 4 March or 3 April as appropriate, and coping with bases of threes, elevens, twelves, fourteens and sixteens in the antique British system of weights and measures. There is a price to pay for the smaller octal table: multiplication by nine (written 11) needs long multiplication, and so does multiplying by ten (written 12).
Throughout this book I am offering some puzzles which, like Sudoku, depend only on logic and counting. Some are easy; some are not. Here is a first:
GENTLE: Why is 12 × 12 = 144 true in octal notation?
Any integer greater than 1 could be used as a base in the same way. With base n, a zero and (n—1) other distinct symbols are needed. So with base 2, the numerals 0 and 1 suffice. In the binary system, 1001 nights mean not a thousand and one, but nine nights, because they stand for 1 × 8 + 0 × 4 + 0 × 2 + 1 × 1.
MODERATE: In binary notation, nine weeks have 1001 × 111 = 111111 days.
The binary representation of numbers (actually a seventeenth-century idea) got a good press in the 1950s as brightly modernistic, needed for computers. Constance Reid devoted Chapter 2 of her book to it. Lancelot Hogben’s Man Must Measure illustrated binary numbers by using the symbols—and + instead of 0 and 1, connecting them with electronic computer storage. I remember this vividly, because oddly enough, Hogben’s bright illustration of technological application was the very thing that fascinated me by showing the Hardy-ish independence of pure number from symbol.
The Sudoku numbers are arbitrary symbols: they could be 0 to 8, they could be letters, they could be coloured squares. Given a puzzle, you can generate many other puzzles by permuting the symbols—changing the symbols 123456789 to (say) 783651294. But a permuted puzzle is the same puzzle: the logic is the same, the work of solving it is the same, and only the symbols have changed. In Killer Sudoku the 81 squares are broken up into subsets, in each of which the sum of the entries is specified. There is an extra rule, which is that in each of these subsets, no digit ever appears twice.
The symbols therefore actually stand for numbers and are not merely numerals. It is not always easy to untangle symbols from substance, medium from message. The principle of daylight-saving time relies on the names of the times of day retaining their cultural force and outweighing the effect of the changed position of the sun. Prices, house numbers, passwords and PINs, car number plates, all have their mix of purely symbolic and actual meaning. The numeral 1 is itself clearly entangled with its meaning: whether in Arabic, Roman, Chinese, Mayan or Babylonian systems, a single stroke gives a picture of One-ness.
People respond eagerly to brands, images and titles. Mathematics is unnatural to word-based culture, because its substance does not depend on names. In quiz shows, a typical question on mathematics is ‘what is the name for a five-sided figure?’ But this is really a question about English and Greek, not about mathematics. Numbers have no manners, and when introduced at the party rudely say, ‘What the hell does it matter what my name is?’ The impoliteness of numbers has already taken its toll on the literary consistency of this chapter. Although its subject has been grandly introduced as One, the number is a shifty character, sliding into a more informal ‘one’ when in use, and then, when involved in arithmetic, compelling the use of a 1 foreign to English prose.
Dividing by 1 has already made its unsociable entrance in defining the prime numbers. It is now time for some more steps in what is called the Theory of Numbers, which has its own quite different, and unliterary, elegance.
But first, here is a Richard Dawkins-style mini-lecture on the word ‘theory’. It is used in different ways: theory as opposed to something verified, as in a detective story; theory as opposed to practice, as in Marxism or music. But in science a ‘theory’ may simply mean a body of knowledge. In the case of the Theory of Numbers it is just this usage, and in fact the most certain knowledge of anything that we could possibly have. So much for being ‘only a theory’.
The prime numbers form a sequence beginning 2, 3, 5, 7, 11 … We don’t count 1 as a prime, for reasons we come to later. Every number is then either prime, or can be factorised into a product of primes. Thus, 42 = 2 × 3 × 7. This follows at EASY Sudoku level from the definition of a prime; given a number, either it is prime, and we are finished, or it has factors, in which case either they are prime or they break down into smaller factors. However, part of the argument has been hidden in the words ‘break down’. It is crucial that if a number has factors then they will be smaller than that number: this guarantees that the process cannot go on for ever.
More subtle—in fact a classic of Greek mathematical elegance—is a proof that there is no greatest prime number, or equivalently, that there are infinitely many primes. This is decidedly at the TRICKY level, and needs a creative step. First, suppose we have some (finite) collection of prime numbers. If we multiply them all together, and add one, we get a new number. For instance, the collection (2, 3, 7) gives 2 × 3 × 7 + 1 = 43, and the collection (11, 13) gives 11 × 13 + 1 = 144. What we know about this new number is that it cannot be divided by any of the primes in the collection, for if we attempt the division, we shall obtain a remainder of 1. So the new number is either a prime, larger than any in our collection, or it has prime factors, which are different from the primes in the collection. (43 is prime, whilst 144 has prime factors 2 and 3, which were not in the collection.) Now, if there were only finitely many primes, we could take the whole lot of them as our collection. But this would contradict what we have established. Therefore there are infinitely many primes.
More awkward—perhaps even FIENDISH—is the proof of the unique factorisation of numbers, an important Oneness of numbers. It is not obvious that the process which tells you there must be some factorisation will always give the same factorisation. Suppose you are told that
145703 × 8473181 and 91457 × 13498889
are both prime factorisations of the same number. You can check directly that this is not true. (The numbers being multiplied are indeed prime, but the first product is 1234567891243, whilst the second is 1234567891273.) But could you check that there could never be different factorisations, even for numbers with millions of factors, all with millions of digits? It is not so easy.
Here’s a smart way to approach the question. If those numbers were really the same, then we could subtract 91457 × 8473181 from both of them, to obtain:
If true (which it is not!) this would give a smaller example of a number with two prime factorisations. A little thought shows that given any putative example of a number with two prime factorisations, you could always derive a smaller example in this way. So there can be no smallest example. Therefore there are no such numbers. This is called the Fundamental Theorem of Arithmetic.
You might argue that 1 itself should be called a prime number, since it cannot be broken down. This question illustrates the insignificance of names. If you liked, you could use the word ‘prime’ to include 1, but then the Fundamental Theorem of Arithmetic would say that every number has a unique factorisation into primes-other-than-1. It is purely as a matter of verbal convenience that modern mathematicians have chosen to define ‘prime’ as they do. The numbers themselves are as indifferent to names as to branding, makeovers and sexing up.
The numerals, as names of numbers, might be compared with the line and blobs of musical notation. People who naturally play and compose by ear can find it difficult to see the blobs as music, whilst those who have been taught to play from written scores are lost without them. Does a piece of music consist of the score, interpreted by performers, or does it consist of a performance, to which the composer’s notes are a guide? A composed score is basically an elaborate sequence of numbers, representing pitches and durations, with the blobs of music notation as its numerals. But a performance is a continuous physical effect in space and time. Music involves a discrete abstract plan and a continuous interpretation. Music obliges counting, but also measuring. Those arbitrarily variable volumes, pitches, and time-lengths need the continuum.
The relationship between counting and measuring opens up much more difficult aspects of mathematics, which bedevil those unloved school lessons. It’s worth looking at the edicts emanating in 2006 from Britain’s Secretary of State for Education, in the light of the current panic over the unpopularity of maths in schools. One dictated that multiplication tables must be learnt by eight-year-olds: for some reason this rote-learning chore is held to be of vital significance. (Using the binary multiplication table would make it much easier to attain: a ritual chant of ‘one one is one’ would suffice.) But in order to make school maths cool, with ‘fashion, football, and the Olympics’ as key themes, the Education Secretary stated that a suitable school problem would involve ‘youngsters being asked to design a dress and then estimate how many yards of material will be necessary to produce it for, say, 100 girls’.
This surprises me. Multiplication by 100 seems very easy, and hardly requires any more than understanding the way numbers are written in base ten, or the relationship of a penny to a pound. But designing a dress, from a mathematical point of view, seems extremely difficult. Since the whole question is now also one of considerable religious controversy, it would be better to take the simplified fashion problem of boys’ trousers: where best to draw the line in deciding how much of the top of the bottom to show. Even this simplified problem is still one of finding the maximum of a continuous function:
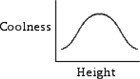
This calls for the much more advanced mathematics of the differential calculus. Anything to do with using figures for measurements brings in questions of approximations, in which the continuum is modelled by the discrete. It brings in errors and difficult questions of judgment, going well beyond the counting of One to Nine. These are difficult at school, and remain difficult in the most advanced questions of climate prediction. I am not sure that the education minister had completely thought out what was involved in the mathematics of fashion, football and the Olympics.
Civilisation and language cope with the continuity of the real world by dividing it up arbitrarily into discrete sets. Integers claim to distingush child and adult, for purposes of alcohol, sex, driving, killing. Astrological signs, or the enneagram—another fascinating One to Nine—claim to define personality types. Integers rule, from nul point in the Eurovision Song Contest, to pass-or-fail drug tests, to parliamentary votes. Critical phenomena—like a ball hitting the crossbar of a goal—squeeze a spectrum of continuous possibilities into discrete win-or-lose compartments.
Digitalisation has added excitement to this relationship. Music has a new relationship with the integers, because the sound of a performance can be captured on a CD or DVD by what is effectively a gigantic integer. The fact that these integers can be copied with amazing ease and reliability gives rise to all the associated problems of communication and copyright. But underneath the simplicities of digital files, there always lies a complex question of the relationship with the continuous or ‘analogue’ world. Moving images, for instance, depend on an illusion based on the speed at which the brain can process them. The opticians Vision Express insist that eyes register 24 million images in a lifetime. This seems an oddly low figure—about one image for each waking minute—but a deeper problem is how visual images can be discretely counted at all.
In 2006 one of the best-known examples of One to Nine was abandoned. It had long been known that the so-called ninth planet, Pluto, had no better claim to planetary status than Ceres, the largest of the asteroids, and the first to be identified. The fuss about the reclassification, dropping Pluto as a planet, but defining a new class of smaller objects, showed how much names matter to people. In fact the observation of Ceres on Day One of the nineteenth century, 1 January 1801, could be regarded as the beginning of the modern understanding of the Earth’s history, with its wide spectrum of collisions from catastrophic to imperceptible. The solar system has big planets, little planets, large asteroids, small asteroids, asteroids breaking up like Shoemaker-Levy, big rocks, tiny rocks, dust, molecules, protons, with no particular place to draw discrete dividing lines.
The relationship of the discrete to the continuous becomes even more problematic when this thought is pursued further. At the atomic level, particles need a quantum description. Centuries of puzzling as to whether light is wave-like or particle-like—continuous or discrete—were resolved in the twentieth century by a new kind of description which involves both. The year 1900 is important for the definition of the quantum as a unit of existence—a discovery about the number One, whose meaning is still far from fully understood.
Pedants say that ‘less’ is to be used with measured quantities, ‘fewer’ with those that are counted. But this distinction is not always clear, even in ordinary life. Do you get fewer bangs for fewer bucks or for less bucks? As extinctions continue, will the oceans have less fish or fewer fish? And looking on the dark side, will we have less light, or fewer photons?
Mary Ann Singleton, who starts page 1 of Armistead Maupin’s Tales of the City, reminds us of yet another word root for One-ness: the Latin semel that gives us simplicity. This is not the One-ness of counting or measuring objects, but the abstract One-ness behind the ideas of unity, integrity, and consistency—concepts as important in mathematics as in life.
Being single is not so simple (even though in German, the word einfach, one-fold, means ‘easy’). I am not just thinking of the common confusions over the plurality of data, media, criteria, or the arbitrariness that makes French la politique singular, les mathématiques plural. More genuinely ambivalent is the singularity of collective nouns. The public that believes what the government says, is both one and many. E pluribus unum, the United States is generally singular but sometimes ‘these United States’ are more grandly referred to. Yet the Nation of Nations is not united, nor is, or are, the United Nations. John Bolton, the former US ambassador to the UN, and its ex-secretary general, Kofi Annan, have both said, for different motives, that there is no such thing as the United Nations.
‘The cultivated banana’ is singular, ‘cultivated bananas’ are plural (although in fact all cultivated bananas are genetically identical, giving the singular a more concrete meaning). Abstraction is counted differently in different languages: The line of beauty, in French, would go further to suggest the singularity of la beauté. The title of Alan Hollinghurst’s prize-winning novel alludes to the line of coke and the (male) bottom line as well as to Hogarth’s aesthetics. Which is singular and which are plural, the drug, the sex, the rock or the roll?
Higher abstractions raise greater difficulties. The most elaborated claim for simplicity lies in monotheistic religion, distinguished by the idea of the one and only one god. In fact, this subject must have given rise to more human thought on One-ness than anything else. Islam asserts existence and uniqueness with particular insistence, and Islam is perhaps closest to mathematics, with its images from the natural world, and its geometrical patterns. Christianity, with its anthropic images, has involved enormous conflict over the meaning of one. The Nicene Creed, committee work intended by Constantine for political unification, skated over the full difficulty. It was left for the Athanasian formula—that the three persons of the Trinity are not three incomprehensibles, but one incomprehensible—to define the distinctive Christian problem with singularity and plurality.
In Bach’s Mass in B minor, the Nicene Credo in unum Deum is based on a theme which emphasises the number One: Bach reached back into medieval music for a unison chant predating polyphony, and also used the antique notation of the breve, virtually extinct by the classical period, as the fundamental unit of time. (Originally the breve was a short note, as its name indicates, but by Bach’s time a sort of musical inflation had made it unfeasibly long.) Yet even Bach’s staggering choral and orchestral counterpoint could not make sense of that word et with which soprano and alto open the next section, and so coolly contradict the unum.
Even leaving aside the problem of the continuum, there is a deep problem posed by the integers. It is that problem of their simplicity, integrity or consistency—their logical Oneness. How can you be sure that alleged proofs, for instance of the infinite number of primes, are fool-proof? How can you know that a long and difficult proof will never lead to the conclusion that 1=3? In human affairs, apparently authoritative ‘proof’ can be overturned, as countless miscarriages of justice testify. If mathematical argument is a human invention, why should it not be equally fallible? On the other hand, if it is something above and beyond the merely human, what are the superhuman features that guarantee its consistency, even for statements about infinitely many numbers?
The dream can be traced back at least to seventeenth-century Leibniz, who hoped to find in mathematics an unassailable logical structure for all knowledge. But it surfaced most prominently at the beginning of the twentieth century in Bertrand Russell’s work. Russell hoped to derive the numbers from something simpler: logic. This meant finding a logical definition of One to guarantee unity and consistency.
Sudoku gives an analogy. A Sudoku-setter must create a puzzle with a selection of numbers allowing one and only one solution. This gives rise to questions which are more difficult and more abstract than that of solving a particular Sudoku puzzle. What is the smallest selection of numbers that will have a unique solution? The answer to this question is currently unknown (it is at most seventeen). How can one be sure that the given starting numbers are sufficient to solve the puzzle? How can one be sure that they do not give rise to an inconsistency? Both these things must be settled to create a valid puzzle. In practice, a setter can simply work through the puzzle step by step and ensure that every square can be filled in uniquely. But mathematics is like an infinite Sudoku, with no way to fill in all the squares. Logicians needed a theory that would establish consistency in some other way.
What is the analogue in mathematics of those start-off numbers in a Sudoku puzzle? They are the axioms, and a great deal of sorting-out work in the late nineteenth century had arrived at sets as the right place to find suitable underlying axioms. At first sight, or noughth sight, the idea of a set is simple: a book is a set of words, and if you open the book, you see what the words are. But the simplicity is deceptive, involving all those questions of collective nouns and abstractions—and worse.
Chapter 0 of Constance Reid’s From Zero to Infinity referred to this foundation in sets, saying that One is ‘the number of all those sets which contain a single member’. But this looks suspiciously like a circular definition. How do you know what ‘containing a single member’ means, without knowing the meaning of One?
The ingenuity of Russell’s definition lay in characterising single-element sets without using the concept of One. Given a set, we can say it is a single-element set if (1) it is not empty and (2) if you ask any question of an element of the set, you will get the same answer whichever element you take. But only after 344 pages of Principia Mathematica could Russell define a single-element set in this way. Those pages involved defining such concepts as ‘any’, ‘same’ and ‘the’, which was a far from easy task. The word ‘the’, for instance, may seem simple, but it conceals an assertion of existence which has to be made explicit. ‘The madness of King George was incurable’ is probably a true proposition, but ‘Mr Blair was loyal to the King of the United States’ is not, and neither is ‘Mr Blair was not loyal to the King of the United States’, for there is no such King.
Russell’s principle was that 1 could then be defined as the set of all single-member sets. This is not quite what you might expect. One is not the property common to all single-member sets, but is defined to be a set of sets.
Unfortunately, the concept of ‘a set of sets’ turns out to be even more problematic than the United Nations. Here is one way of seeing why. School maths has unwisely dipped into set theory in an attempt to look modern, and I have seen it said that ‘The universal set is the set of all sets’. But the concept of ‘the set of all sets’ is self-contradictory. Suppose that ‘the set of all sets’ is a consistent idea. It is itself a set, therefore it is an example of a set which is a member of itself. So there are two kinds of sets: those that are members of themselves, and those that are not. Now consider the set of all sets which are not members of themselves. Which kind of set is it? If it is a member of itself then it isn’t a member of itself. Both possible answers are self-contradictory. The idea of defining the number One as a ‘set of all sets’ cannot be used without resolving this problem.
Russell had ingenious ways of escaping this difficulty, but they required very questionable further assumptions. One striking aspect of the theory was that it seemed to be more complicated than the numbers that it was trying to explain, so that it did become circular: you could not understand the logical theory unless you already understood what numbers meant. Without an understanding of One, how could you speak of ‘a’ set? This is the key difficulty that was crystallised in 1931 by the discovery made by the young central European logician, Kurt Gödel.
Gödel showed that there was no hope of regarding mathematics as a puzzle like Sudoku. The analogy fails. The difficulty is essentially this. A question about Sudoku such as ‘What is the smallest selection of numbers that will have a unique solution?’ is not itself a Sudoku puzzle: it is on a distinctly higher and different level. In contrast, a question about mathematics is itself a question within mathematics. The levels are inextricably mixed up. This follows simply from the business of putting all mathematical arguments into symbols. It is not possible to capture the truth of mathematical statements in terms of a Sudoku-like puzzle of proving them from starting axioms.
Gödel’s argument had a punchline involving a mathematical statement which referred to its own proof. It was closely related to the problem arising from a set being a member of itself. These and many other developments in twentieth-century logic have emerged like a strange joke at the solemn heart of formality. Good jokes depend on seeing something at a higher level, and then the levels being mixed up. ‘Hurt me,’ says the masochist; ‘No,’ says the sadist. In The Life of Brian, Jesus’s alter ego urges the enlightened axiom of thinking for oneself, only for his disciples to repeat obediently, ‘We’ve all got to work it out for ourselves’, illustrating the one thing you cannot teach by instruction. Parallel intractable difficulties may be involved in real life logic. ‘You must conform to our liberal values’ is an example.
If Russell’s plan had prevailed, there would be a highly technical definition of One in terms of symbols which only a sort of élite Brains Trust could understand. But in fact, the number One cannot be captured in symbols and there is no better definition than what you can see for yourself. It is an open question as to what this discovery means. Gödel himself seems to have considered that this meant human minds, thinking for themselves, could do something beyond anything that could be achieved by a computer. Other leading people say that this is illusory. For fifty years after Gödel’s discovery this remained a rather abstruse argument. But in 1979, the computer scientist and philosopher Douglas Hofstadter published Gödel, Escher, Bach, and opened it up with a flood of scientific and cultural ramifications, wonderfully illustrated.
One aspect of Hofstadter’s work was that he saw the potential of computers in communication, fifteen years before ‘New Media’ caught on. He swept these central problems of logic into the enormously expanded symbolic systems made possible by the 1970s, giving an early vision of the scale and quality of what would be possible for the public of the 1990s. Computer science has given logic a new home. The logic that Russell pioneered in Principia Mathematica is now the background to database querying. The puzzles that he found are alive and well in that home, and an example came at the opening of this chapter. Originally I wrote the words ‘This is Page One’, knowing that a statement referring to its own page was just asking for trouble, as indeed it was. Computer typesetting, of which Hofstadter was also a pioneer, gives a miniature picture of the possible tangles of logical typesetting.
This technological connection is not what the logicians of 1900 had in mind: they were hoping to give a complete foundation for knowledge and truth, and might be surprised that the twenty-first century would open with this universal ambition largely abandoned.
In contrast, physics has never given up hope of supplying a complete explanation, and has undiminished ambitions for a single ‘theory of everything’. A better word for this ambition might be a monolithic theory, for ‘monolith’, Greek for ‘one stone’, is translated into German as Einstein. It is a tantalising possibility that logic will have to come back into the picture, to make true sense of ‘everything’. There may yet be something completely new to be found out about One.
There is one completely simple and definite thing to be said about One. It concerns that noughth dimension, time. Time has just one dimension.
It is this which makes the clear separation between past and future. Two dimensions would give something utterly different; not even science fiction could describe it since even the idea of fiction needs a one-dimensional storytelling. That the dimension of time in the real world is just one, is a first fundamental fact that a true theory of everything must explain.
Consciousness seems closely related to the one-dimensionality of time: we seem only to be able to concentrate on one thing at one time. Explicitly in music, drama, novels, but implicitly even in painting and architecture, consciousness needs a linear narrative, ordered in time, with a first page. Writing is the business of turning multi-dimensional facts and ideas into a one-dimensional string of symbols.
English uses almost the same symbol for I, the first person, as for One; and its pronoun ‘one’ stands for the impersonal I. We look after Number One: the sole soul. But the individual’s One-ness is not a static quality, but a process, a dialogue, perhaps an intense struggle. Walt Whitman wrote: One’s self I sing, a simple separate person, Yet utter the word Democratic, the word En-Masse. Real concentration on real mathematics—as with any concentrated artistic or athletic effort—means shutting out many demands of society. But it depends on a social network. It is an intensely individual process and yet, when mathematical ideas are absorbed, the original individuals become anonymous, forgotten atoms in the fabric.
There are dark sides to the En-Masse, and ideals of Oneness can bring them out. When governments make a disastrous mess they call for national unity: all criticism must cease. The word ‘united’ too often suggests the dead body over which some past takeover was forced through. The ‘United’ Kingdom (so flatteringly considered as Airstrip One by George Orwell), arrived with the asteroids in 1801 to crush Irish identity as that of Scotland had already been. The plurality that is Germany has suffered even more from Oneness, the ideal of unity or Einheit. The story ran from the Zollverein (customs union), to ein Volk, ein Reich, ein Führer. (Unity Mitford, one of the few people, with Zero Mostel, to have a number as a name, famously adhered to this vision.) Fortunately the Wiedervereinigung (reunification) has been a more mixed curse. The Pet Shop Boys end Fundamental with ‘One … one … one …’ on a menacing monotone, responding negatively to the New Labour project of digital identity cards for individuals, and questioning the whole ideal of the Integral.
But One-ness can also carry with it the ideal of integrity, as opposed to conventional duplicities. Writing in 1956, Constance Reid may well not have been aware that ONE, Inc. was then the name of a first American organisation for homosexual rights. It was an unloved One in the Eisenhower era, but since then, there have been great changes in the perception of what ‘to thine own self be true’ should mean—and contrary to Jane Austen’s supposedly universal truth, it is now acknowledged that a single man may not be in want of a wife.
One-ness, in a certain kind of extreme, also characterises autistic people. There are exceptional individuals with great powers of mental arithmetic, whose minds see a vast range of numbers in a direct, intuitive manner. These amazing feats suggest that there is far more yet to be found out about the relationship of number to the human mind, and the true potential of the individual’s contribution.
To thine own self and Walt Whitman’s careful words ‘one’s self’, ‘I and my Soul’, suggest that the one of the I is not a simple one. For some it is in Bach’s cello suites, for others in the early Bob Dylan, where a perfect solo conveys self-reflection like a dialogue. Inside the I, there is a You—perhaps too many people. To write I must read as if I were you, but if I were you, I would not be writing. The artless Guardian writer let slip that ‘the universal reader to whom I imagine I am addressing these words is, in my mind, an arts graduate’, and as she says, this points to a problem, one which C. P. Snow failed to solve. I cannot solve it either, but I must lead you on as if I could.
Indian mathematicians have a self-deprecating joke: ‘India contributed zero to mathematics.’ The joke plays on the unnatural language of zero. Contributing ‘zero’ is not the same as contributing zero: ‘zero’ is something! This joke is also the basis of a simpler approach to the logic of numbers. Take Zero to be the empty set, the set containing nothing. Then One is the set containing just one thing: namely Zero. Then, Zero and One give two things…
Underlining and highlighting simplicity shows its complexity. Numeral 1, adorned with its peaked cap and plinth, stops being a picture of One-ness and morphs into a—