© Springer Nature Switzerland AG 2019
B. Pochiraju, S. Seshadri (eds.)Essentials of Business AnalyticsInternational Series in Operations Research & Management Science264https://doi.org/10.1007/978-3-319-68837-4_14

14. Survival Analysis

Thriyambakam Krishnan1  
(1)
Chennai Mathematical Institute, Chennai, India
 
 
Thriyambakam Krishnan
Email: sridhar@illinois.edu

1 Introduction

Survival analysis is a collection of statistical techniques for the analysis of data on “time-to-event” as a response variable and its relationships to other explanatory variables. The notion of “event” depends on the context and the applications. The event in question may be dealt as may happen in a biomedical context or churning in a business context or machine failure in an engineering context. Survival methods are characterized by “censoring” by which the event in question may not have happened (at the time observations end) for certain observational units (cases) in the data; yet, such censored data are useful and are judiciously used in survival analysis. In that sense, survival analysis methods differ from techniques such as regression analysis. The topics covered in this chapter are:

  • Understanding time-to-event data and survival probabilities

  • Understanding the notion of censoring

  • Understanding the survival curve and other ways of representing survival distributions

  • Learning to compute the Kaplan–Meier survival curve

  • Learning to fit and validate a Cox proportional hazards model

  • Learning to fit and validate parametric survival models

2 Motivating Business Problems

Survival analysis can provide tremendous insights and improved understanding into patterns of customer behavior depending upon their profiles and key performance indicators, especially in regard to churning, attrition, product purchase pattern, insurance claims, credit card default, etc. It can be used to compute customer lifetime values as a function of their past behaviors and contributions to a business, which in turn can be used to fine-tune campaigns. It can also be used to study organizational behaviors like bankruptcy, etc. The data required is a set of cases (suitably selected) where “lifetime” information (even if censored, but with censoring information) and information on possible drivers of such lifetimes is available. Some specific examples of survival analysis are given below:

  • Business bankruptcy (time to bankruptcy) analysis on the basis of explanatory variables such as profitability, liquidity, leverage, efficiency, valuation ratio, etc. A firm not bankrupt at the time of end of data collection yields a censored observation that has to be interpreted in the analysis as samples of firms that have not yet failed (Lee 2014).

  • Analysis of churn pattern in the telecom industry and impact of explanatory variables like the kind of plan, usage, subscriber profile like age, gender, household size, income, etc. on churn pattern. This information may be useful to reduce churn (Lu and Park 2003).

  • Analysis of lifespan of car insurance contracts in terms of car’s age, type of vehicle, age of primary driver, etc. may be carried out using survival analysis techniques to measure profitability of such contracts.

  • Estimating a customer lifetime value (CLV) to a business on the basis of past revenue from the customer and an estimate of their survival probabilities based on their profile is a standard application of survival analysis techniques and results. This type of analysis is applicable to many types of business, this helps plan different campaign strategies depending on estimated lifetime value.

3 Methods of Survival Analysis

3.1 Time-to-Event Data and Censoring

Survival times are follow-up times from a defined starting point to the occurrence of a given event. Some typical examples are the time from the beginning of a customer-ship to churning; from issue of credit card to the first default; from beginning of an insurance to the first claim, etc. Standard statistical techniques do not apply because the underlying distribution is rarely normal; and the data are often “censored.”

A survival time is called “censored” when there is a follow-up time but the defined event has not yet occurred or is not known to have occurred. In the examples above, the survival time is censored if the following happens: at the end of the study if the customer is still transacting; the credit card customer has not defaulted; the insurance policy holder has not made a claim. Concepts, terminology, and methodology of survival analysis originate in medical and engineering applications, where the prototype events are death and failure, respectively. Hence, terms such as lifetime, survival time, response time, death, and failure are current in the subject of survival analysis. The scope of applications is wider including in business, such as customer churn, employee attrition, etc. In Engineering these methods are called reliability analysis. In Sociology it is known as event-history analysis.

As opposed to survival analysis, regression analysis considers uncensored data (or simply ignores censoring). Logistic regression models proportion of events in groups for various values of predictors or covariates; it ignores time. Survival analysis accounts for censored observations as well as time to event. Survival models can handle time-varying covariates (TVCs) as well.

3.2 Types of Censoring

The most common form of censoring is right-censoring where a case is removed from the study during the study, or the observational part of the study is complete before the event occurs for a case. An example is where in an employee attrition study, an employee dies during the observational period (case removed) or may be still employed at the end of observations (event has not occurred). An observation is left-censored if its initial time at risk is unknown, like in a medical study in which the time of contracting the disease is unknown. The same observation may be both right- and left-censored, a circumstance termed interval-censoring. Censoring complicates the estimation of survival models and hence special techniques are required. If for a case (observational unit) the event of interest has not occurred then, all we know is that the time to event is greater than the observed time. In this chapter, we only consider right-censoring. One can consult Gomez et al. (1992) for left-censoring, Lagakos (1979) for right-censoring, and Sun (2006) for interval-censoring.

Observations that are censored give us no information about when the event occurs, but they do give us a bound on the length of their survival. For such observations, we know that they survived at least up to some observed time t c and that their true lifetime is some t ∗≥ t c. In the dataset, for each observation, a censoring indicator c i is created such that
$$\displaystyle \begin{aligned} c_i = \left\{ \begin{array}{ll} 1 & \mbox{if } \text{not }\ \text{censored} \\ 0 & \mbox{if } \text{censored.} \end{array} \right. \end{aligned}$$

Censored observations are incorporated into the likelihood (or for that matter, in other approaches as well) as probability t ∗≥ t c, whereas uncensored observations are incorporated into the likelihood through the survivor density. This idea is illustrated below.

Suppose the lifetime (T) distribution is exponential (λ) with density function f(t|λ) = λe −λt. Suppose an observation t is a censored observation. Then the contribution to the likelihood is P(T ≥ t) = e −λt. Suppose an observation t is an uncensored observation. Then the contribution to the likelihood is λe −λt. Suppose t 1, t 2 are censored, and u 1, u 2, u 3 are uncensored, then the likelihood function is
$$\displaystyle \begin{aligned} L(\lambda) = e^{-\lambda t_1} \times e^{-\lambda t_2} \times \lambda e^{-\lambda u_1} \times \lambda e^{-\lambda u_2} \times \lambda e^{-\lambda u_3}, \end{aligned}$$
$$\displaystyle \begin{aligned} \log(L(\lambda)) = -\lambda (t_1+t_2+u_1+u_2+u_3)+ 3\log(\lambda), \end{aligned}$$
maximizing which gives the maximum likelihood estimates of the parameters of the survival density.

3.3 Survival Analysis Functions

Survival time or lifetime T is regarded as a positive-valued continuous variable. Let f(t): probability density function (pdf) of T.

Let F(t): cumulative distribution function (CDF) of T = P(T ≤ t). S(t): Survival function of T defined as S(t) = 1 − F(t) = P(T > t).

The hazard function plays an important role in modeling exercises in survival analysis. It is defined below:

Let h(t): hazard function or instantaneous risk (of death) function. It is defined as
$$\displaystyle \begin{aligned} h(t) = \displaystyle\lim_{dt \rightarrow 0} \frac{P(t \leq T \leq t + dt|T \geq t)}{dt} = \frac{f(t)}{S(t)} = -\frac{d}{dt} \log(S(t)). \end{aligned}$$
It can be seen that
$$\displaystyle \begin{aligned} S(t) = e^{-\int_0^t h(x) dx}. \end{aligned}$$
The function $$H(t) = \int _0^t h(x)dx$$ is called the cumulative hazard and is the aggregate of risks faced in the interval 0 to t. It can be shown that the mean (or expected) life $$\int _0^{\infty } tf(t) dt$$ is also $$\int _0^{\infty } S(t) dt$$ . The hazard function has the following interpretation:
If a customer has been with a provider for 2 years, what is the probability he will attrite in the next year? Such questions are answered using the hazard rate. Answer: $$H(1) = \int _{2}^{3} h(t)dt$$ . The hazard rate is a function of time. Some simple types of hazard functions are:
Increasing hazard:

A customer who has continued for 2 years is more likely to attrite than one that has stayed 1 year

Decreasing hazard:

A customer who has continued for 2 years is less likely to attrite than one that has stayed 1 year

Flat hazard:

A customer who has continued for 2 years is no more or less likely to attrite than one that has stayed 1 year

3.4 Parametric and Nonparametric Methods

Once we have collected time-to-event data, our first task is to describe it—usually this is done graphically using a survival curve. Visualization allows us to appreciate temporal patterns in the data. If the survival curve is sufficiently nice, it can help us identify an appropriate distributional form for the survival time. If the data are consistent with a parametric form of the distribution, then parameters can be derived to efficiently describe the survival pattern and statistical inference can be based on the chosen distribution by specifying a parametric model for h(t) based on a particular density function f(t) (parametric function). Otherwise, when no such parametric model can be conceived, an empirical estimate of the survival function can be developed (i.e., nonparametric estimation). Parametric models usually assume some shape for the hazard rate (i.e., flat, monotonic, etc.).

3.5 Nonparametric Methods for Survival Curves

Suppose there are no censored cases in the dataset. Then let t 1, t 2, …, t n be the event-times (uncensored) observed on a random sample. The empirical estimate of the survival function, $$\hat {S}(t)$$ , is the proportion of individuals with event-times greater than t.
$$\displaystyle \begin{aligned} \hat{S}(t) = \frac{\mbox{Number of event-times}\,{>}\,t}{n}.{} \end{aligned} $$
(14.1)
When there is censoring $$\hat {S}(t)$$ is not a good estimate of the true S(t); so other nonparametric methods must be used to account for censoring. Some of the standard methods are:
  1. 1.

    Kaplan–Meier method

     
  2. 2.

    Life table method, and

     
  3. 3.

    Nelson–Aalen method

     

We discuss only the Kaplan–Meier method in this chapter. For Life table method, one can consult Diener-West and Kanchanaraksa1 and for Nelson–Aalen method, one may consult the notes provided by Ronghui (Lily) Xu.2

3.6 Kaplan–Meier (KM) method

This is also known as Product-Limit formula as will be evident when the method is described. This accounts for censoring. It generates the characteristic “stair case” survival curves. It produces an intuitive graphical representation of the survival curve. The method is based on individual event-times and censoring information. The survival curve is defined as the probability of surviving for a given length of time while considering time in intervals dictated by the data. The following assumptions are made in this analysis:

  • At any time, cases that are censored have the same survival prospects as those who continue to be followed.

  • Censoring is independent of event-time (i.e., the reason an observation is censored is unrelated to the time of censoring).

  • The survival probabilities are the same for subjects recruited early and late in the study.

  • The event happens at the time specified.

The method involves computing of probabilities of occurrence of events at certain points of time dictated by when events occur in the dataset. These are conditional probabilities of occurrence of events in certain intervals. We multiply these successive conditional probabilities to get the final estimate of the marginal probabilities of survival up to these points of time.

3.6.1 Kaplan–Meier Estimate as a Product-Limit Estimate

With censored data, Eq. (14.1) needs modifications since the number of event-times > t will not be known exactly. Suppose out of the n event-times, there are k distinct times t 1, t 2, …, t k. Let event-time t j repeat d j times. Besides the event-times t 1, t 2, …, t k, there are also censoring times of cases whose event-times are not observed. The Kaplan–Meier or Product-Limit (PL) estimator of survival at time t is
$$\displaystyle \begin{aligned} \hat{S}(t) = \displaystyle\prod_{j: t_j \leq t} \frac{(r_j-d_j)}{r_j}\ \ \text{for}\ \ 0 \leq t \leq t^{+},{}\end{aligned} $$
(14.2)
where t j, j = 1, 2, …, n is the total set of event-times recorded (with t + as the maximum event-time), d j is the number of events at time t j, and r j is the number of individuals at risk at time t j. Any case where a censoring time is a t j is included in the r j, as also cases whose event-time is t j. This estimate can be considered a nonparametric maximum likelihood estimate.

3.6.2 Kaplan–Meier Method: An Example

The aim of the study in this example is to evaluate attrition rates of employees of a company. Data were collected over 30 years over n = 23 employees. Follow-up times are different for different employees due to different starting points of employment. The number of months with company is given below where + indicates still employed (censored):
$$\displaystyle \begin{aligned} &6,12,21,27,32,39,43,43,46+,89,115+,139+,181+,211+,\\ &217+,261,263,270,295+,311,335+,346+,365+ \end{aligned} $$
The same data is named as “employ.csv” and available on the book’s website. The following is the data dictionary.

Variable

Description

ID

The unique id of the employee

att

Represent 1 if uncensored and 0 if censored

months

No. of months the employee worked in the company

Survival rates are computed as follows:

P(surviving t days)=P(surviving day t ∣ survived day t − 1).P(surviving day t − 1 ∣ survived day t − 2).P(surviving day t − 2 ∣ survived day t − 3) ⋮ P(surviving day 3 ∣ survived day 2).P(surviving day 2 ∣ survived day 1).P(surviving day 1)

Standard errors of survival probabilities are computed using Greenwood’s formula as follows:
$$\displaystyle \begin{aligned} \hat{V}(\hat{{S}(t)}) = \hat{{S}(t)^2} \displaystyle\sum_{t_i \leq t} \frac{d_i}{n_i(n_i-d_i)} \end{aligned}$$
Table 14.1 gives the survival probabilities computed by the Kaplan–Meier method. Notice that the probabilities are computed only at those time points where an event happens. In the table, n.risk is the r j and n.event is the d j in the formula, “survival” is the estimate of the survival probability s(t) at time t. This table leads to the “stair-case” survival curve presented in the graph. The curve represents the probabilities of survival (y-axis) beyond the time points marked on the x-axis. Notice that we get revised estimates only at those points where an event is recorded in the data. The little vertical lines indicate the censored times in the data (Fig. 14.1).
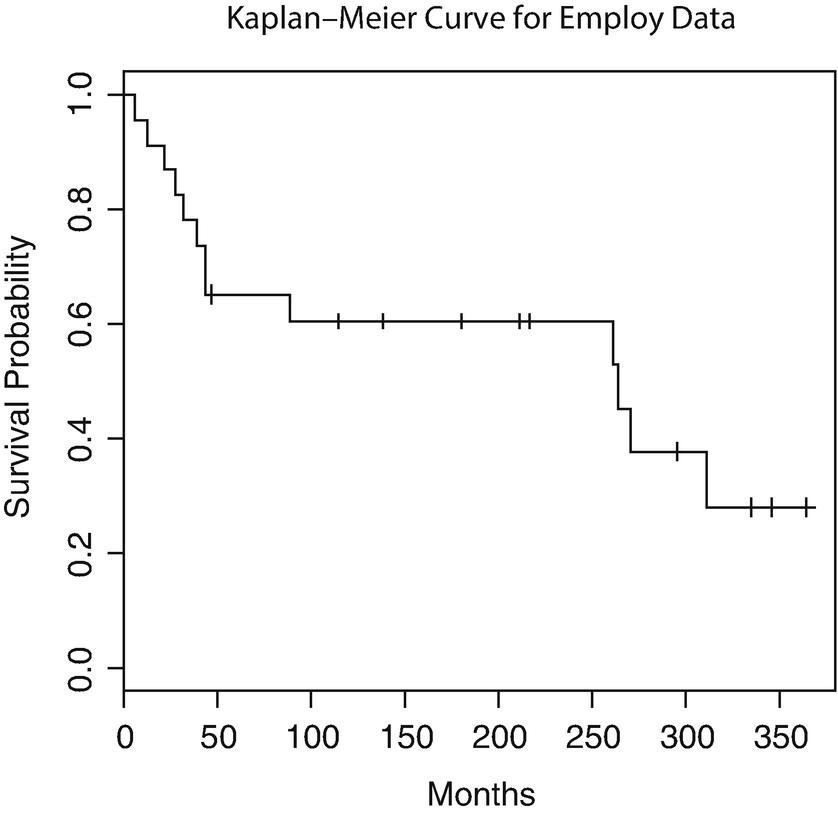
../images/428412_1_En_14_Chapter/428412_1_En_14_Fig1_HTML.png
Fig. 14.1

Kaplan–Meier Curve

../images/428412_1_En_14_Chapter/428412_1_En_14_Fig2_HTML.png
Fig. 14.2

Estimated survival function by PH method

Table 14.1

Survival probabilities using KM method

Time

n.risk

n.event

Survival

Std. err

6

23

1

0.957

0.0425

12

22

1

0.913

0.0588

21

21

1

0.870

0.0702

27

20

1

0.826

0.0790

32

19

1

0.783

0.0860

39

18

1

0.739

0.0916

43

17

2

0.652

0.0993

89

14

1

0.606

0.1026

261

8

1

0.530

0.1143

263

7

1

0.454

0.1205

270

6

1

0.378

0.1219

311

4

1

0.284

0.1228

> employsurv <- survfit(Surv(months, att)~ 1, conf.
type="none",data = employ)summary(employsurv)
> plot(employsurv,mark.time = TRUE, xlab="Months",
ylab="Survival Probability",main="Kaplan-Meier Curve
for Employ Data")

3.7 Regression Models for Survival Data: Semiparametric Models

What happens when you have several covariates that you believe contribute to survival? For example, in job attrition data, gender, age, etc. may be such covariates. In that case, we can use stratified KM curves, that is, different survival curves for different levels of a categorical covariate, possibly drawn in the same frame. Another approach is the Cox proportional hazards model.

Of all survival analysis functions, the hazard function captures the essence of the time process. Survival analysis uses a regression model-like structure into hazard function h(t). The h(t) being a rate should be positive with infinite range. To achieve this h(t) is formulated as h(t) = e β. Covariates (explanatory variables) x (a vector with components (1, x 1, x 2, …, x p)) is included by being additive in the log scale. Formulation:
$$\displaystyle \begin{aligned} \log[h(t,\boldsymbol{x})] = \boldsymbol{\beta}^T\boldsymbol{x} = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_p x_p \end{aligned}$$
or
$$\displaystyle \begin{aligned} h(t,\boldsymbol{x}) = e^{\boldsymbol{\beta}^T \boldsymbol{x}}{} \end{aligned} $$
(14.3)

Equation (14.3) can be modified by introducing a function of time with a distribution model like a Weibull model. This will then be a fully parametric hazard function model, and describe a survival time distribution as an error component of regression, and describe how this distribution changes as a function of covariates (the systematic component). Such fully parametric models help predict survival time distributions for specific covariate conditions. If only relative survival experience is required under two or more conditions after adjusting for covariates, fully parametric models may be too unwieldy with too many restrictions. If we only need parameters in the systematic component of the model, then models with fully parametric regression leaving out the dependence on time unspecified may be useful. These are called semiparametric models.

A model of the form
$$\displaystyle \begin{aligned} h(t,\boldsymbol{x},\boldsymbol{\beta}) = h_0(t)r(\boldsymbol{x},\boldsymbol{\beta}) \end{aligned}$$
is such a formulation. h 0(t) describes how the hazard function changes over time, r(x, β) describes how the hazard function changes with the covariates. It is necessary that h(t, x, β) > 0. Then h(t, x, β) = h 0(t) when r(x, β) = 1. h 0(t) is called the baseline hazard function—a generalization of intercept in regression.
The h 0(t) which is the baseline hazard rate when X = 0̱ = (0, 0, …, 0); this serves as a convenient reference point although an individual with X = 0̱ may not be a realistic one. Hazard ratio (HR) between two cases with x 1, x 2 is given by
$$\displaystyle \begin{aligned} \text{HR}(t,\boldsymbol{x}_1, \boldsymbol{x}_2)= \frac{r(x_1,\boldsymbol{\beta})}{r(x_2,\boldsymbol{\beta})} \end{aligned}$$
and does not depend on h 0(t). Cox proposed the form $$r(\boldsymbol {x}, \boldsymbol {\beta }) = e^{(\boldsymbol {x}^T \boldsymbol {\beta })}$$ so that $$h(t, \boldsymbol {x},\boldsymbol {\beta }) = h_0(t)e^{\boldsymbol {x}^T \boldsymbol {\beta }}$$ . Then HR $$(t,\boldsymbol {x}_1,\boldsymbol {x}_2) = e^{(\boldsymbol {x}_1-\boldsymbol {x}_2)^T \boldsymbol {\beta }}$$ . This is called Cox model, proportional hazards model, or Cox proportional hazards model.

3.8 Cox Proportional Hazards Model (Cox PH model)

This is a semiparametric model (part parametric, part nonparametric). It makes no assumptions about the form of h(t) (nonparametric part). It assumes a parametric form for the effect of the explanatory variables on the hazard, but makes the assumption that the hazards are proportional over follow-up time. In most situations, we are more interested in studying how survival varies as a function of explanatory variables rather than the shape of the underlying hazard function. The Cox PH model is well suited for this purpose.

Let X = (X 1, X 2, …, X p) be the explanatory variables. The model is
$$\displaystyle \begin{aligned} \log \frac{h(t|\boldsymbol{X})}{h(t)} = \boldsymbol{X}^T \boldsymbol{\beta} = \beta_1 X_1 + \beta_2 X_2 + \ldots + \beta_p X_p. \end{aligned}$$
The model can also be written as $$h(t|\boldsymbol {X}) = h(t)e^{(\boldsymbol {X}^T \boldsymbol {\beta })}$$ . The model can also be written as $$S(t|\boldsymbol {X}) = S(t|\boldsymbol {X}) = \b 0)e^{(\boldsymbol {X}^T\boldsymbol {\beta })}$$ . Predictor effects are the same for all t. No assumptions are made on the forms of S, h, f.
The hazard rate in PH models increases or decreases as a function of the covariates associated with each unit. The PH property implies that absolute differences in x imply proportionate differences in the hazard rate at each t. For some $$t = \bar {t}$$ , the ratio of hazard rates for two units i and j with vectors of covariates x i and x j is:
$$\displaystyle \begin{aligned} \frac{h(\bar{t},\boldsymbol{x}_i)}{h(\bar{t},\boldsymbol{x}_j)} = e^{(\boldsymbol{x}_i-\boldsymbol{x}_j)\boldsymbol{\beta}}. \end{aligned}$$
Because the baseline hazards drop out in the equation it indicates that the baseline hazard rate for unit i is $$e^{(\boldsymbol {X}_i-\boldsymbol {X}_j)\boldsymbol {\beta }}$$ times different from that of unit j. Importantly, the right-hand side of the equation does not depend on time, i.e., the proportional difference in the hazard rates of these two units is fixed across time. Put differently, the effects of the covariates in PH models are assumed to be fixed across time.

Estimates of the β’s are generally obtained using the method of maximum partial likelihood, a variation of the maximum likelihood method. Partial likelihood is based on factoring the likelihood function using the multiplication rule of probability and discarding certain portions that involve nuisance parameters. If a particular regression coefficient β j is zero, then the corresponding explanatory variable, X j, is not associated with the hazard rate of the response; in that case, X j may be omitted from any final model for the observed data. The statistical significance of explanatory variables is assessed using Wald tests or, preferably, likelihood ratio tests. The Wald test is an approximation to the likelihood ratio test. The likelihood is approximated by a quadratic function, an approximation which is generally quite good when the model fits the data.

In PH regression, the baseline hazard component, h(t) vanishes from the partial likelihood. We only obtain estimates of the regression coefficients associated with the explanatory variables. Notice that h(t) = h(t|x) = β 0. Take the case of a single explanatory variable X. Then $$\beta = \log \frac {h(t|x =1)}{h(t)}$$ . Thus β is the log of the relative hazard of group with X = 1 to the hazard of group with X = 0. e (β) is the relative risk of X = 1 to X = 0. So sometimes PH regression is called relative risk regression.

Concordance is a measure of goodness-of-fit of the model and defined as probability of agreement for any two randomly chosen observations. The large concordance value (possible maximum being 1) indicates a good fit.

3.9 Semiparametric vs Parametric Models

A parametric survival model completely specifies h(t) and S(t) and hence is more consistent with theoretical S(t). It enables time-quantile prediction possible. However, the specification of the underlying model S(t) makes this exercise a difficult one. On the other hand, the Cox PH model, a semiparametric one leaves the distribution of survival time unspecified and hence may be less consistent with a theoretical S(t); an advantage of the Cox model is that the baseline hazard is not necessary for estimation of hazard ratio.

A semiparametric model has only the regression coefficients as parameters and is useful if only the study of the role of the explanatory variables is of importance. In a full parametric model, besides the role of the explanatory variables, survival curves for each profile of explanatory variables can be obtained.

Some advantages of fully parameterized models are: maximum likelihood estimates (MLEs) can be computed. The estimated coefficients or their transforms may provide useful business information. The fitted values can provide survival time estimates. Residual analysis can be done for diagnosis.

Many theoretical specifications are used based on the form of S(t) (or f(t)) in survival analysis. Some of them are: Weibull, log-normal, log-logistic, generalized gamma, etc.

The regression outputs of a semiparametric and a full parametric are not directly comparable although one may compare the relative and absolute significance (p-values) of the various regressors. However, using the form of the parametric function’s h(t) it is possible to strike a relationship between the parametric model’s regression coefficients and Cox regression coefficients.

A parametric model is often called the accelerated failure time model (AFT model) because according to this model, the effect of an explanatory variable is to accelerate (or decelerate) the lifetime by a constant as opposed to say, the Cox proportional hazards model wherein the effect of an explanatory variable is to multiply hazard by a constant.

4 A Case Study

In this section, we discuss various methods of survival analysis through an example of a customer churn data of an online retail company. The observations are made up to a certain point of time only and if the customer is still there then it is censored and if the customer leaves it is denoted as uncensored. We also have many covariates which explain the activities of the customers. We are interested in analyzing the customer churn behavior with the help of survival time of a customer and dead_flag which indicates censored or uncensored along with 16 covariates. The dataset “churn.csv” and R code “Survival_Analysis.R” are available at the website. The variables chosen for the study are given in Table 14.2.
Table 14.2

Data dictionary

Variable

Definition

ptp_months

Profitable time period in months

dead_flag

Censor case or not: 0 indicates censored case

tenure_month

Tenure of user in months

unsub_flag

Email unsubscription status: 1 indicates unsubscribed

ce_score

Confidence score of user

items_home

No. of items purchased in home division

items_Kids

No. of items purchased in kids division

items_Men

No. of items purchased in men’s division

items_Women

No. of items purchased in women’s division

avg_ip_time

Average time between purchases

returns

No. of product returns

acq_sourcePaid

Has the user joined through paid channel or not

acq_sourceReferral

Has the user joined through referral channel or not

mobile_site_user

Does the user use mobile channel

business_name

First purchase division of user

redeemed_exposed

No. of offers redeemed or No. of offers given

refer_invite

No. of Referral joined or No. of invites sent

revenue_per_month

Revenue or tenure of user

4.1 Cox PH Model

We analyze the churn data to fit a Cox PH model (semiparametric model). The results are provided in Table 14.3. The output will be in two tables where the first table contains the regression coefficients, the exponentiated coefficients which are equivalent to estimated hazard ratios, standard errors, z tests, corresponding p-values and the second table contains exponentiated coefficients along with the reciprocal of exponentiated coefficients and values at 95% confidence intervals.
Table 14.3

Cox PH model output

n= 214995, number of events= 117162

 

coef

exp( coef)

se( coef)

z

Pr( >|z|)

exp( -coef)

lower .95

upper .95

ptp_months

-9.683e-02

9.077e-01

7.721e-04

-125.417

<2e-16 ***

1.1017

0.9063

0.9091

unsub_flag

3.524e-01

1.422e+00

6.529e-03

53.973

<2e-16 ***

0.7030

1.4044

1.4408

ce_score

-1.245e+00

2.879e-01

2.220e-02

-56.079

<2e-16 ***

3.4736

0.2756

0.3007

items_Home

-3.461e-02

9.660e-01

2.130e-03

-16.250

<2e-16 ***

1.0352

0.9620

0.9700

items_Kids

-7.456e-02

9.282e-01

2.521e-03

-29.570

<2e-16 ***

1.0774

0.9236

0.9328

items_Men

3.182e-03

1.003e+00

9.949e-04

3.198

0.00138 **

0.9968

1.0012

1.0051

items_Women

1.935e-03

1.002e+00

6.936e-04

2.790

0.00527 **

0.9981

1.0006

1.0033

avg_ip_time

1.427e-03

1.001e+00

9.936e-05

14.362

<2e-16 ***

0.9986

1.0012

1.0016

returns

-1.481e-01

8.624e-01

3.020e-03

-49.024

<2e-16 ***

1.1596

0.8573

0.8675

acq_sourcePaid

4.784e-02

1.049e+00

9.992e-03

4.788

1.69e-06 ***

0.9533

1.0287

1.0697

acq_sourceReferral

-2.626e-01

7.690e-01

6.354e-03

-41.333

<2e-16 ***

1.3003

0.7595

0.7787

mobile_site_user

-3.644e-01

6.946e-01

2.278e-02

-15.998

<2e-16 ***

1.4396

0.6643

0.7263

business_nameKids

5.932e-01

1.810e+00

1.371e-02

43.264

<2e-16 ***

0.5525

1.7618

1.8591

business_nameMen

-9.704e-02

9.075e-01

1.220e-02

-7.951

1.89e-15 ***

1.1019

0.8861

0.9295

business_nameWomen

-3.631e-01

6.955e-01

1.091e-02

-33.279

<2e-16 ***

1.4378

0.6808

0.7106

redeemed_exposed

-3.089e-01

7.342e-01

1.261e-02

-24.491

<2e-16 ***

1.3620

0.7163

0.7526

refer_invite

-3.870e-01

6.791e-01

8.996e-03

-43.014

<2e-16 ***

1.4725

0.6672

0.6912

avg_ip_time_sq

-5.027e-07

1.000e+00

1.970e-07

-2.552

0.01072 *

1.0000

1.0000

1.0000

revenue_per_month

1.712e-03

1.002e+00

2.555e-05

67.024

<2e-16 ***

0.9983

1.0017

1.0018

Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 . 0.1 1

Concordance= 0.814 ( se = 0.001 )

Rsquare= 0.409 ( max possible = 1 )

Likelihood ratio test= 113002 on 19 df, p=0

Wald test = 75990 on 19 df, p=0

Score ( logrank) test = 92819 on 19 df, p=0

> churncoxph <- coxph(Surv(tenure_month, dead_flag) ~
ptp_months+unsub_flag+ce_score+items_Home+items_Kids+
items_Men+items_women
+avg_ip_time+returns +acq_sourcePaid+acq_
sourceReferral+mobile_site_user+business_name+redeemed
_exposed+refer_invite+avg_ip_time_sq+revenue_per_month,
data=churn)
> summary(churncoxph)
> predict(churncoxph, newdata=churn[1:6,], type="risk")

From the output, the estimated hazard ratio for business_nameKids vs business_nameHome is under column “exp(coef)” which is 1.8098 with 95% CI (1.7618, 1.8591). Similarly, exp(-coef) provides estimated hazard rate for business_nameHome vs business_ nameKids which is 0.5525 (the reciprocal of 1.8098). For continuous variables, exp(coef) is estimated hazard ratio for one unit increment in x, “(x+1)” vs “x” and exp(-coef) provides “x” vs 1 unit increment in x, “(x+1)”. From the table the concordance is 0.814, which is large enough and thus indicating a good fit.

Besides interpreting the significance or otherwise of the explanatory variables and their relative use in predicting hazards, the output is useful in computing the relative risk of two explanatory variable profiles or relative risk with respect to the average profile, i.e., $$e^{(\boldsymbol {X}_i-\boldsymbol {X}_j)^\prime \beta }$$ , where X i contains particular observation and X j contains average values. The relative risks of the first six cases with respect to the average profile are: 3.10e-11, 0.60, 0.0389, 1.15, 0.196, and 0.182 (refer Table 14.3 for β values). We can compute the survival estimates of fitted model and obtain Cox adjusted survival curve.

> summary(survfit(churncoxph))
> plot(survfit(churncoxph),main= "Estimated Survival
Function by PH model", ylab="Proportion not churned")

4.2 Log-Logistic Model

Now we analyze the same data to fit the log-logistic parametric model. A simple way of stating the log-logistic model is by failure odds:
$$\displaystyle \begin{aligned} \frac{1-S(t)}{S(t)} = \lambda t^p \end{aligned}$$
where p is the shape parameter and λ is a function of predictor variables and regression parameters.

Following is the R code to fit the log-logistic model on the given data.

> aftloglogis<-survreg(formula = Surv(tenure_month,
dead_flag) ~ ptp_months + unsub_flag + +ce_score +
items_Home + items_Kids + items_Men +
+items_women + avg_ip_time, data = churn, dist =
"loglogistic")
> summary(aftloglogis)
> predict(aftloglogis, churn[1:10, ], type="quantile",
p=c(0.1,0.5,0.9))
The results are given in Table 14.4.
Table 14.4

Output of parametric model log-logistic

 

Value

Std. error

z

p

( Intercept)

2.484162

4.38e-03

566.79

0.00e+00

ptp_months

0.063756

4.26e-04

149.76

0.00e+00

unsub_flag

-0.269003

4.09e-03

-65.80

0.00e+00

ce_score

1.041445

1.27e-02

82.21

0.00e+00

items_Home

0.005020

8.80e-04

5.70

1.17e-08

items_Kids

-0.004644

5.57e-04

-8.34

7.73e-17

items_Men

0.002426

4.73e-04

5.12

2.99e-07

items_Women

0.013681

5.12e-04

26.74

1.67e-157

avg_ip_time

-0.000857

2.78e-05

-30.82

1.37e-208

Log logistic distribution

Loglik( model) = -458898.3 Loglik( intercept only) = -505430.2

Chisq= 93063.76 on 8 degrees of freedom, p= 0

Number of Newton-Raphson Iterations: 5

n= 214995

Coefficient estimates correspond to covariate coefficient estimates. Also of significant interest is the log-likelihood, which is used to find the Akaike information criterion (AIC), i.e., AIC $$= -2 \log L + 2 \times \ $$ number of parameters = 917,817. This is useful for comparison with any other model fitted on the same data (the lower the better).

The survival time difference for 1 month increase in tenure (ptp_months) is exp(0.063756) = 1.066 increase, and from email unsub to sub (unsub_flag) is exp (−0.269003) = 0.764 decrease.

For new data, any number of quantiles (importantly the 0.5 quantile, the median) of survival times can be predicted for input cases of regressors, effectively predicting the survival curves. The following is an example of 0.1, 0.5, 0.9 quantiles for the first ten cases in the dataset from the above model (Table 14.5). From the predicted values the median time is 2359.47 months for the first observation and for second observation it is only 33.89 months. You can similarly interpret other values.
Table 14.5

Predicting survival time using the log-logistic model

Case

0.1

0.5

0.9

[1,]

1004.83620

2359.47444

5540.3255

[2,]

14.43473

33.89446

79.5882

[3,]

43.76790

102.77221

241.3213

[4,]

18.29105

42.94956

100.8506

[5,]

26.14241

61.38547

144.1404

[6,]

28.95115

67.98072

159.6268

[7,]

143.45923

336.85927

790.9855

[8,]

89.83391

210.94067

495.3137

[9,]

5.07855

11.92504

28.0014

[10,]

52.18694

122.54111

287.7410

4.3 Weibull Model

Next, we fit a Weibull parametric model on the same data. In the Weibull model,
$$\displaystyle \begin{aligned} S(t)=e^{(-\lambda^\ast tp)} \end{aligned}$$
where p is the shape parameter and λ is a function of predictor variables and regression parameters.
We can use the following R code to fit the Weibull model:
> aftweibull<-survreg(Surv(tenure_month, dead_flag) ~
ptp_months+unsub_flag+ce_score+items_Home+items_Kids+
items_Men++items_women+avg_ip_time, data=churn, dist
= "weibull")
> summary(aftweibull)
> predict(aftweibull,
coxfulla[1:10, ],type="quantile", p=c(0.1,0.5,0.9))
Coefficient estimates in Table 14.6 correspond to covariate coefficient estimates. Also of significant interest is the log-likelihood, which is used to find the Akaike information criterion (AIC), i.e., $$\mathrm {AIC}=-2\log L+2\times $$ number of parameters = 909,304. This is useful for comparison with any other model fitted on the same data (the lower the better).
Table 14.6

Output of the Weibull parametric model

 

Value

Std. error

z

p

( Intercept)

2.806480

3.88e-03

724.10

0.00e+00

ptp_months

0.056311

4.47e-04

126.09

0.00e+00

unsub_flag

-0.192530

3.32e-03

-57.96

0.00e+00

ce_score

0.746628

1.14e-02

65.52

0.00e+00

items_Home

0.008579

1.14e-04

9.07

1.23e-19

items_Kids

-0.001338

6.23e-04

-2.15

3.18e-02

items_Men

0.001414

4.75e-04

2.98

2.92e-03

items_Women

0.014788

5.44e-04

27.19

8.25e-163

avg_ip_time

-0.000858

2.68e-05

-32.05

2.52e-225

Weibull distribution

Loglik( model) = -454641.8 Loglik( intercept only) = -498568.4

Chisq= 87853.26 on 8 degrees of freedom, p= 0

Number of Newton-Raphson Iterations: 8

n= 214995

The survival time difference for 1 month increase in tenure(ptp_months) is $$\exp (0.056311) = 1.06$$ increase, and from email unsub to sub (unsub_flag) is $$\exp (-0.192530)=0.825$$ decrease (refer Table 14.6). Here, we observe that the Weibull model is predicting better than the log-logistic model as it has lower AIC value compared to the log-logistic model.

For new data, any number of quantiles (importantly the 0.5 quantile, the median) of survival times can be predicted for input cases of regressors, effectively predicting the survival curves. The following is an example of 0.1, 0.5, 0.9 quantiles for the first ten cases in the dataset from the above model (Table 14.7). From the predicted values the median time for the first observation is 4180.3 months and for the second observation it is only 33.0 months. You can similarly interpret other values.
Table 14.7

Predicting survival time using the Weibull model

 

[,1]

[,2]

[,3]

[1,]

1603.92

4180.3

7697.2

[2,]

12.66

33.0

60.8

[3,]

33.72

87.9

161.8

[4,]

17.01

44.3

81.7

[5,]

20.52

53.5

98.5

[6,]

23.04

60.0

110.6

[7,]

105.66

275.4

507.1

[8,]

77.17

201.1

370.3

[9,]

5.34

13.9

25.6

[10,]

38.51

100.4

184.8

5 Summary

This chapter introduces the concepts and some of the basic techniques of survival analysis. It covers a nonparametric method of estimating a survival function called the Kaplan–Meier method, a semiparametric method of relating a hazard function to covariates in the Cox proportional hazards model, and a fully parametric method of relating survival time to covariates in terms of a regression as well as estimating quantiles of survival time distributions for various profiles of the covariate values. Survival analysis computations can be easily carried out in R with specialized packages such as survival, KMsurv, survreg, RPub, and innumerable other packages. Several textbooks provide the theory and explanations of the methods in detail. These include Gomez et al. (1992), Harrell (2001), Kleinbaum and Klein (2005), Hosmer et al. (2008), Klein and Moeschberger (2003), Lawless (2003), Sun (2006), Springate (2014), as well as websites given in the references.

Electronic Supplementary Material

All the datasets, code, and other material referred in this section are available in www.​allaboutanalytic​s.​net.

  • Data 14.1: churn.csv

  • Data 14.2: employ.csv

  • Data 14.3: nextpurchase.csv

  • Code 14.1: Survival_Analysis.R

Exercises

The data file nextpurchase.csv (refer website for dataset) relates to the purchase of fertilizers from a store by various customers. Each row relates to a customer. The study relates to an analysis of “time-to-next-purchase” starting from the previous purchase of fertilizers. “Censoring” is 0 if the customer has not returned for another purchase of a fertilizer since the first one. Censoring is 1 if he has returned for the purchase of a fertilizer since his earlier one. “Days” is the number of days since last purchase (could be a censored observation). “Visits” is the number of visits to the shop in the year not necessarily for the purchase of a fertilizer. “Purchase” is the amount of all purchases (in $’s) during the current year so far. “Age” is the customer’s age in completed years. “Card” is 1 if they used a credit card; else 0.

Ex. 14.1

Without taking into account the covariates, use the Kaplan–Meier method to draw a survival curve for these customers.

Ex. 14.2

Fit the Weibull parametric model and predict the 0.1 (0.1) 0.9 quantiles of a customer aged 45, who uses a credit card, who spent $100 during the year so far and who has visited the shop four times in the year so far (not necessarily to purchase fertilizers).

Ex. 14.3

Rework the parametric Weibull exercise using the log-logistic parametric model.

Ex. 14.4

Rework the parametric Weibull exercise using the Cox PH model.

Useful functions for the Weibull distribution: (You need not know these to run this model.)

Density: f(t)= $$k\lambda ^k t^{k-1}e^{-(\lambda t)^k}$$ ; Survival $$S(t) = e^{(-\lambda t)^k}$$ ; Hazard h(t) = λ kkt k−1; Cumulative Hazard:H(t) = (λt)k