Planetenwiegen für Anfänger
Form und Größe der Erde haben wir nun im Gepäck, schön und gut. Aber: Wie wiegt man denn am besten einen Planeten? Nun, erst mal brauchen wir einen in der Nähe, an dem wir es ausprobieren können. Ein handelsüblicher Gesteinsplanet müsste genügen, Fortgeschrittene könnten sich aber auch an Gas- oder Eisriesen versuchen. Ein beliebter Kalauer schlägt vor, dass wir eine Waage nehmen und sie umgedreht auf den Boden legen. Das wirft allerdings zwei Probleme auf: Zum einen können wir jetzt das Zifferblatt nicht mehr ablesen, und zum anderen hatten die meisten Wissenschaftler im 18 . Jahrhundert keine batteriebetriebenen Waagen zur Hand. Doch Spaß beiseite. Mit der genauen Form und Größe unseres Planeten im Kopf konnte man sich nun daranmachen, seine Masse herauszufinden. Selbstverständlich beruhen die zugrunde liegenden Berechnungen mal wieder auf einer von Isaac Newton aufgestellten Formel (langsam sollte klar geworden sein, wie unvorstellbar wichtig dessen Principia für die Welt der Wissenschaft geworden waren).
Wir schreiben das Jahr 1798 , als ein britischer Wissenschaftler namens Henry Cavendish in seinem Haus ein Experiment durchführt, mit dem er die Dichte der Erde bestimmen will. Die Dichte?! Wollten wir nicht das Gewicht der Erde herausfinden? Was bitte soll denn jetzt die Dichte sein? Damit wir nicht durcheinanderkommen, sollen die Begriffe Masse, Gewicht und Dichte kurz definiert werden.
Masse: Masse (m) ist eine fundamentale Eigenschaft von Objekten. Sie gibt an, wie viel Materie in einem Objekt enthalten ist. Die einzige Möglichkeit, die Masse eines Objektes zu verändern, besteht darin, dass man Materie hinzufügt oder wegnimmt. Eine Bleikugel, die auf der Erde ein Kilogramm Masse hat, hat auch auf dem Mond ein Kilogramm Masse, obwohl sie dort nur 1 /6 des Gewichts hat.
Gewicht: Gewicht, oder auch Gewichtskraft, wird bestimmt durch die Masse eines Objektes in Kombination mit der Beschleunigung der Schwerkraft, welche auf das Objekt wirkt.
Gewicht = Masse (m) × Beschleunigung der Schwerkraft (g)
Wer auf der Erde 100 Kilogramm wiegt, wiegt auf dem Mond nur 16 ,5 Kilogramm, obwohl die Masse unverändert bleibt. Das heißt, Gewicht ist davon abhängig, wie viel Masse ein Körper hat und wie stark die Schwerkraft des Körpers, auf dem er sich befindet, auf ihn wirkt.
Dichte: Dichte (ρ oder griechisch Rho) wiederum gibt an, wie viel Masse pro Volumen ein Körper besitzt. Die Formel dafür lautet
Ρ = Masse / Volumen
Die Dichte von Wasser beträgt bei knapp vier Grad Celsius zum Beispiel 1 g/cm3 .
Das heißt: Wenn wir die Dichte und das Volumen eines Körpers kennen, können wir auch dessen Masse ausrechnen. Aufgrund der physikalischen Definition von »Gewicht« würde man niemals fragen: »Wie viel wiegt die Erde?«, sondern: »Welche Masse hat die Erde?« Ich werde aber die Begriffe »Gewicht« und »Masse« im Folgenden synonym verwenden, damit es nicht zu kompliziert wird.
Nun also zurück zu Mr. Cavendish. Er war ein begnadeter Wissenschaftler seiner Zeit und, wie kann es anders sein, ein echt komischer Kauz. Im Jahr 1731 in eine adelige Familie geboren, hatte er dank einer großzügigen Erbschaft genug Geld, um niemals arbeiten zu müssen. Henry Cavendish war extrem schüchtern und mied soziale Kontakte, wo es nur ging. Insbesondere vor Frauen fürchtete er sich, und so erteilte er seinen weiblichen Bediensteten die Anweisung, ihm ja nicht über den Weg zu laufen, andernfalls würde er sie feuern. 10 Als er einmal auf einer Party des damaligen Präsidenten der Royal Society als »talentierter Philosoph und Denker« vorgestellt wurde, war ihm das so unangenehm, dass er augenblicklich die Flucht ergriff: Er bahnte sich einen Weg durch die Anwesenden, stieg in seine Kutsche und fuhr nach Hause. 118
Bekannt und respektiert war Mr. Cavendish bei seinen Kollegen damals vor allem für die beeindruckende Präzision, mit der er seine naturwissenschaftlichen Experimente durchführte. Nachdem er bereits den Wasserstoff entdeckt hatte, sollte er nun auch der erste Mensch sein, der die Masse der Erde bestimmen konnte, und das, ohne auch nur einen Fuß vor die Tür zu setzen.
Für das später nach ihm benannte Cavendish-Experiment konstruierte er in seinem Haus eine hochsensible Vorrichtung, mit der er feststellen wollte, wie stark unterschiedlich große Bleikugeln einander anziehen. Denn Schwerkraft ist keine Einbahnstraße. Wie wir bereits gelernt haben, zieht sich alles im Universum gegenseitig an. Nicht nur die Erde zieht am Mond, der Mond zieht auch an der Erde. So entstehen Ebbe und Flut!
Und auch auf der Erde zieht sich alles an. Selbst dieses Buch wirkt in dem Moment, in dem ihr es in Händen haltet, im wahrsten Sinne des Wortes anziehend auf euch. Und das wollte Henry Cavendish in seinem Experiment genauer untersuchen. Dazu baute er sich eine Versuchsanordnung, die vom Prinzip her tatsächlich extrem simpel ist. Alle Physikstudierenden dürfen das Cavendish-Experiment vermutlich in ihrem ersten Semester an der Uni selbst im Hörsaal nachstellen.
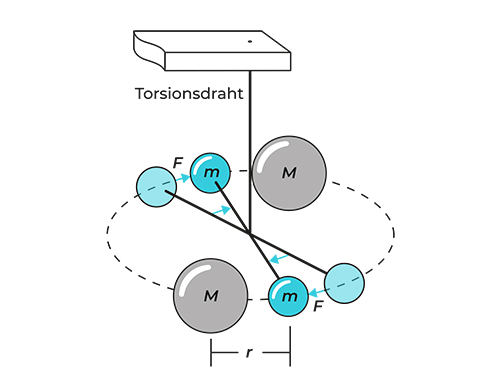
Das Kernstück von Cavendishs Vorrichtung, seiner sogenannten Torsionswaage, ist ein etwa zwei Meter langer Holzstab, der in der Luft hängt. In der Mitte ist er mit einem dünnen Draht an der Decke angebracht, sodass er frei rotieren kann. An den Enden des Holzstabs befestigte Cavendish je eine kleine Bleikugel mit einem Durchmesser von fünf Zentimetern (m), deren Gewicht (Masse) er kannte. Nun wurden zwei große, massive Bleikugeln (M), jeweils etwa 160 Kilogramm schwer, an gegenüberliegenden Seiten an der Wand angebracht. Die Idee war simpel: Die Schwerkraft der großen Kugeln sollte auf die kleinen wirken und so den Stab langsam in Bewegung setzen. So weit, so gut. Aber wie wollte Cavendish mit einer derartigen Anordnung die Masse der Erde bestimmen? Das lässt sich tatsächlich relativ einfach errechnen, wenn wir die Formel für das Gravitationsgesetz von Newton kennen:
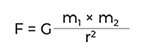
Jetzt folgt ein klein bisschen Physik, aber wir machen ganz schnell, und es tut auch fast gar nicht weh, versprochen. Dabei nehmen wir einen Haufen Abkürzungen und verstoßen mehrfach gegen die Straßenverkehrsordnung, damit niemand einschläft oder aus Protest das Buch zuschlägt.
Letzten Endes besagt Newtons Formel, dass sich zwei Körper m1 und m2 , die sich in der Entfernung r voneinander befinden, gegenseitig mit einer Kraft F anziehen.
Dröseln wir die Formel mal kurz auf und wenden sie auf Cavendishs Experiment an. Wir fangen oben im Bruch an. Die erste Variable m1 steht für die Masse einer der kleinen roten Bleikugeln. Logischerweise steht m2 dann für die Masse einer der größeren grauen Kugeln. Diese beiden Werte werden miteinander multipliziert und dann durch ihren Abstand zum Quadrat, also r2 , geteilt. Verstanden? Super. Das große G steht für die Gravitationskonstante. Konstanten sind super nice, weil sie immer denselben Wert haben und man sie deshalb nicht jedes Mal neu ausrechnen muss, sondern einfach nur den bekannten Wert in die Gleichung einsetzt. Pipifax also. Cavendishs Problem war allerdings, dass er den Wert der Konstante nicht kannte, weil sie noch nie von jemandem bestimmt worden war. Sein Experiment ist tatsächlich bis heute einer der besten Wege, um den Wert der Konstante G in Newtons Formel zu bestimmen. Nur, das ist sauschwer, weil G eine winzig kleine Zahl ist:
G ≈ 0 ,00000000006721 m³/(kg s²)
Das sind zehn Nullen nach dem Komma! Um eine so winzige Zahl messen zu können, musste Cavendish sein Experiment peinlichst genau auf Fehlerquellen überprüfen und diese möglichst beseitigen. Also baute er eine Holzbox, die etwa drei Meter breit, lang und hoch war. Damit das Experiment nicht von der Schwerkraft seines eigenen Körpers beeinflusst wurde, betätigte er Hebel und Schnüre von außerhalb der Box, um die Gewichte einzurichten, und beobachtete deren Bewegungen dann durch Teleskope, die rund um die Box angebracht waren. Und um sich wirklich sicher zu sein, führte er das Experiment nicht nur einmal, sondern gleich 17 Mal durch, bevor er seine Ergebnisse veröffentlichte. 119 Dem heute akzeptierten Wert der Gravitationskonstante G konnte Cavendish sich auf weniger als ein Prozent Abweichung nähern, 11 eine Präzision, die mal wieder absolut mind-blowing ist.
Versuchen wir also nun, die uns heute bekannte Formel des Gravitationsgesetzes so aufzulösen, dass wir am Ende die Masse der Erde rausbekommen:

In diesem Beispiel ist klein m die Masse einer uns bekannten Bleikugel und groß M die Masse der Erde, die wir noch nicht kennen. G ist die Gravitationskonstante, die Cavendish freundlicherweise für uns bestimmt hat, und r ist der durchschnittliche Radius der Erde, für dessen genaue Festlegung unsere wackeren französischen Wissenschaftler die Anden besteigen mussten. Groß F, die Gravitationskraft, ist definiert als Masse mal Beschleunigung oder auch: F=m*a. Mit anderen Worten: Jeder Körper mit einer Masse erfährt durch die Schwerkraft des Planeten, auf dem er sich befindet, eine Beschleunigung. Diese Gravitationsbeschleunigung hat den Wert a=9 ,81 m/s2 . Auch diese Zahl kann experimentell bestimmt werden. So kann groß F ersetzt werden durch m*a und unsere Formel wird zu:
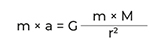
Da klein m, die Masse unserer Bleikugel, nun auf beiden Seiten auftaucht, können wir sie wegkürzen und die Formel zur Masse der Erde umstellen. Damit erhalten wir:
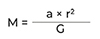
Nun fügen wir die Werte ein: a=9 ,81 m/s2 , G ist die oben beschriebene winzige Gravitationskonstante, und für r setzen wir den Radius der Erde ein, also etwa 6370 Kilometer. Das Gewicht der Erde beträgt somit
M=5 ,96 × 10 24 kg 120
Was etwa 6 Trillionen Tonnen entspricht – unsere Erde hat nun ein Gewicht. Oder besser gesagt: eine Masse!
Fun Fact: Henry Cavendish wollte mit seinem Experiment eigentlich »nur« die Dichte der Erde und damit auch ihre Masse bestimmen, fand nebenbei aber etwas weitaus Wichtigeres, worauf wir uns noch heute stützen und verlassen können: die Gravitationskonstante G. Mit der Zeit verlor die Versuchsanordnung immer mehr ihre ursprüngliche Bedeutung – ein Experiment zur Bestimmung des Gewichts der Erde – und gewann den Ruf, die wohl beste Methode zu sein, um den Wert von Newtons Gravitationskonstante herauszufinden. Heute wird teilweise sogar behauptet, Cavendish habe von vornherein versucht, G zu bestimmen, aber das ist großer Quark. Er wog die Erde und ahnte noch gar nicht, wofür sein Experiment später einmal gefeiert werden würde.