Practice Test 2: Answers and Explanations
PRACTICE TEST 2 ANSWER KEY

PRACTICE TEST 2 EXPLANATIONS
Section I: Multiple-Choice Questions
1. C
Since acceleration due to gravity is 10 m/s2, the vertical speed of the object after 2 seconds will be 20 m/s. Because the horizontal speed will not be affected, the direction will be mostly down, but slightly to the right.
2. D
Mass is not changing, so you need to consider only the changes in velocity. For each segment in order, the change in velocity is +7 m/s, 0 m/s, −4 m/s, −3 m/s, and −2 m/s. The question does not specify magnitude only, so all negatives will come before the others.
3. C
Acceleration is the change in velocity divided by the change in time. You found the changes in velocity for each segment in the previous question, and the times for each segment are, in order, 3 s, 2 s, 1 s, 3 s, and 2 s. Divide the results in the previous question by these values, and the highest result (ignoring sign because the problem specifies magnitude only) is for segment CD.
4. C
In a velocity-versus-time graph, displacement is the area beneath the curve. If the question had asked for displacement, then anything beneath the x-axis would be added as a negative displacement. However, distance cannot be negative, so there is no distinction between positive and negative velocity for this question.
Split the area into triangles and rectangles like this:
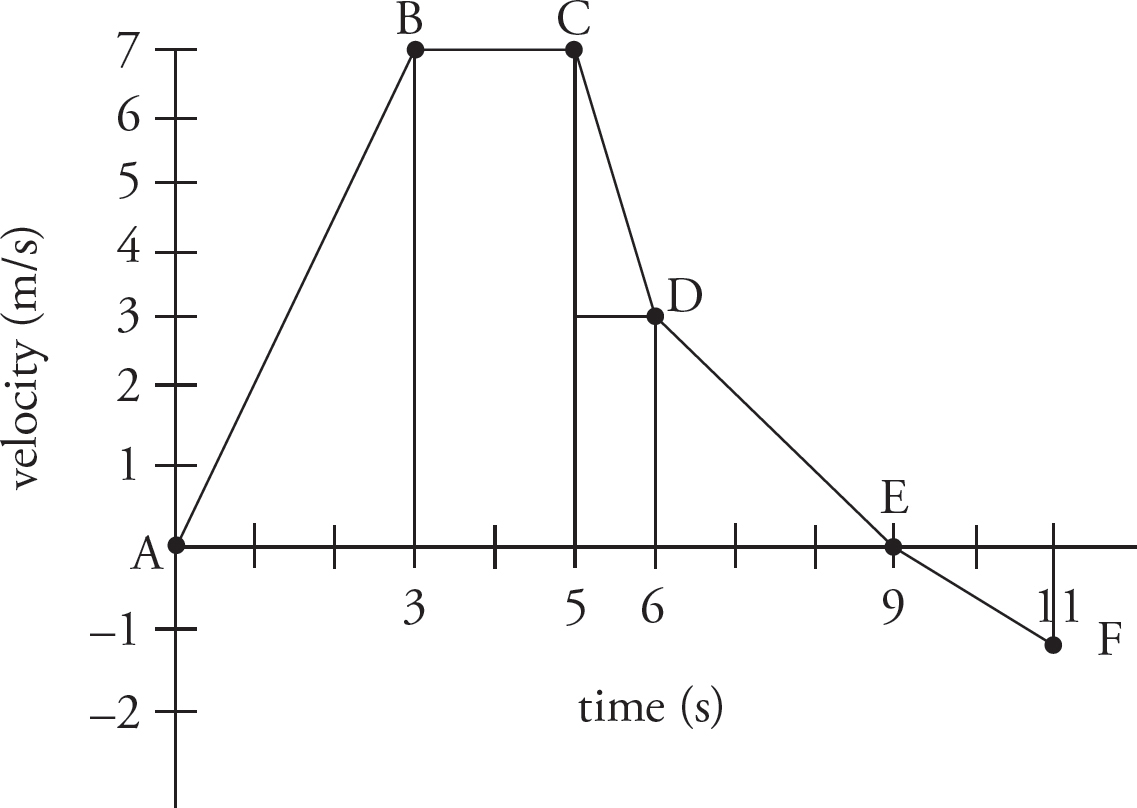
5. C
At the highest point from the ground, the ball has a vertical velocity of zero. Therefore, applying the formula vy = v0y + ayt and rearranging it for t, it becomes t = −v0y/−g. Substituting v0y = v sin θ into the equation, t = v sin θ/g.
6. B
A trick for solving problems of this nature is to make up numbers for a and t. Pretend that total time = 10 seconds, and acceleration = 2 m/s2. Then make a table:
|
Time, s |
Speed, m/s |
|
0 |
0 |
|
1 |
2 |
|
9 |
18 |
|
10 |
20 |
So in the first second, vavg = 1 m/s, and d = 1 m. In the last (tenth) second, vavg = 19 m/s, and d = 19 m. The answer to the question is 19 m − 1 m = 18 m. Which answer choice gives us 18 m?
(A) a(t + 1 s)2 = (2 m/s2)(10 s + 1 s)2 = (2 m/s2) (11 s)2 = (2 m/s2)(121 s2) = 242 m
(B) a(t − 1 s)(1 s) = (2 m/s2)(10 s − 1 s)(1 s) = (2 m/s2)(9 s)(1 s) = 18 m
(C) at2 = (2 m/s2)(10 s)2 = (2 m/s2)(100 s2) = 200 m
(D) a(t + 1 s)(1 s) = (2 m/s2)(10 s + 1 s)(1s) = (2 m/s2)(11 s)(1 s) = 22 m
Therefore, (B) is the correct answer.
If you really want to do it algebraically, here’s one way. Solve for the distance traveled in the first second.
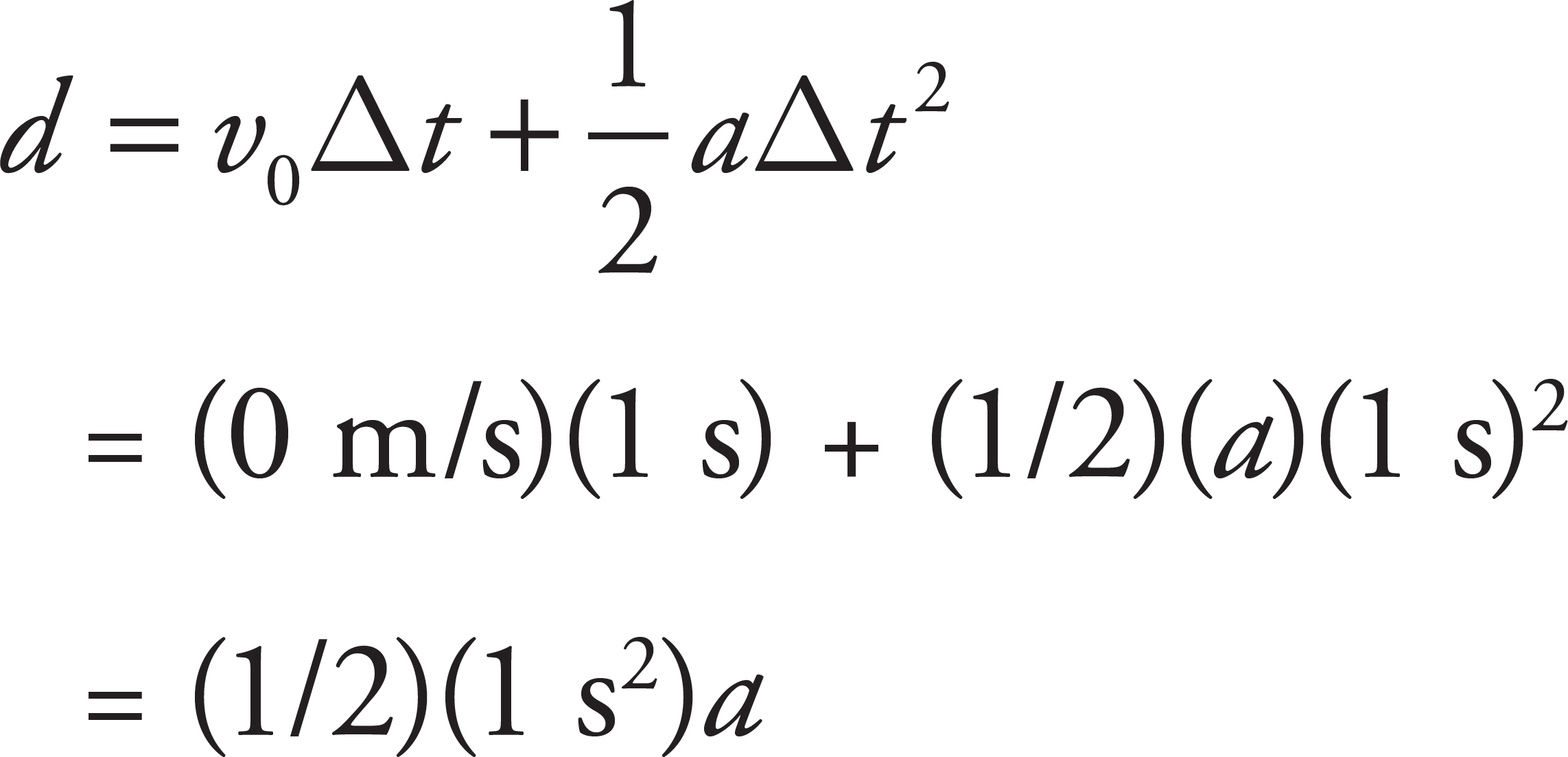
Next, solve for the distance in the final second.

The difference between the two is a(t − 1 s)(1 s) meters.
7. B
Because the floor is horizontal the weight and normal force balance each other out, so these two forces do have equal magnitudes (eliminate (C) and (D)). These two forces, however, do not form an action/reaction pair. In order to form an action/reaction pair, two forces must come from two objects acting on each other. One action/reaction pair in this situation is Earth’s gravitational pull on the person (the person’s weight) and the person’s pull on Earth. The other pair is the normal force of the floor on the person (pushing up) and the normal force of the person on the floor (pushing down).
8. C
The force of friction on a stationary object will exactly oppose the force applied to it until it reaches a maximum. This eliminates (B) and (D). Once enough force has been applied, the friction will change from static friction to kinetic friction. Kinetic friction is a constant value, so this eliminates (A).
9. B
In this situation, all variables will have the same numerical values for both forces. Therefore, it comes down to the constants. Because Coulomb’s constant (9.0 × 109) is much, much greater than the gravitational constant (6.7 × 10−11), electric force will be greater. Because the question specifies magnitude, the signs of the charges are irrelevant.
10. B
By Process of Elimination, you know you need a sine in the equation for the downward pull of the second mass down the incline of the plane, so the answer is (B).
11. D
The friction f on the block is represented by the formula f = where µkN, where N is the normal force on the block. When the force is applied 30° above the horizontal, N = mg − mg sin 30°. Since sin 30° is 0.5, N = mg − 0.5mg = 0.5mg. Substituting N into the formula for friction, it becomes f1 = μk(0.5mg). When the force is applied 30° below the horizontal, N = mg + mg sin 30° = mg + 0.5mg = 1.5mg. Substituting N into the formula for friction, it becomes f2 = μk(1.5mg) = 3f1.
12. B
Because all the masses are attached and moving as a single unit, the acceleration of any block in the system is the same as that of any other. The net force on the blocks is Fnet = (2M)g sin θ. Therefore,

13. B
At the top of the loop, the cart will remain in contact as long as the centripetal force is at least as much as the force of gravity on the cart.

14. B
The rotating platform and the object resting on it constitute an isolated system. Angular momentum must remain constant, so eliminate (A) and (C). To decide between the remaining choices, remember that a system’s rotational inertia increases as the atoms in that system get farther from the axis of rotation. For a point particle, I = mr2. To decrease rotational inertia, move the object toward the center of the platform.
15. A
If the moon and planet are treated as a single system, then the system’s total mechanical energy (kinetic energy + gravitational potential energy), linear momentum, and angular momentum are all conserved. However, that’s not necessarily true for each object individually. Let’s start with momentum. The moon is moving toward the top of the page at A but toward the bottom of the page at B. Clearly, the moon’s velocity changes a lot, so its momentum changes as well. Statement III is false. Eliminate (B), (C), and (D). The answer must be (A). (Any change in the moon’s momentum is coupled with an opposite change in the planet’s momentum, which is how total momentum stays constant. It turns out that in this situation, the lighter object contains nearly all of the system’s kinetic energy and angular momentum; the planet’s K and L are negligibly small. So not only are the system’s energy and angular momentum conserved, so is the planet’s.)
16. A
Draw out a free-body diagram of all the forces acting on the sphere:

Gravity points straight down and does affect the object but it does not provide the torque (eliminate (D)). The normal force points perpendicular to the plane and does no work on the object nor does it provide the torque (eliminate (C)). The friction in this case does provide the torque. Since the ball is rolling down the hill and not sliding down it, it is not kinetic friction (eliminate (B)). This makes sense, because when you drive a car, the tires grip the road and move you forward at one point. If there were no static friction on the road, you would never be able to go anywhere because the tires would not be able to grip onto anything.
17. B
An object’s terminal speed is the highest speed it can reach in free fall. If it has not yet reached that speed, its speed must still be increasing. This eliminates (C) and (D). The problem says that the object will experience a drag force that increases as speed increases. Therefore, the opposing force will increase over time, which means the net force will decrease (since the force from gravity will be constant). If net force decreases, so will acceleration.
18. D
The centripetal force is a name given to the net force of an object undergoing uniform circular motion. Therefore, it is not a separate force and does not have an action/reaction pair. This eliminates (A). Since the speed is constant but direction changes, acceleration must be perpendicular to velocity; eliminate (B). Not only does velocity change with time, but the acceleration also changes because the direction of the centripetal acceleration always points to the center of the circle. This eliminates (C). A satellite undergoing uniform circular motion is in fact falling (accelerating due to gravity) toward the center, but doesn’t get closer due to its tangential velocity. Its velocity is always tangent to its circular path.
19. D
To balance the seesaw you need to balance the torques. Since T = Fr sin θ, the boy currently provides double the torque. Choices (B) and (C) would double the torque on the girl’s side, and (A) would cut the boy’s torque in half. Choice (D) would cut the boy’s torque in half, but it would also increase the girl’s torque, creating a new imbalance.
20. C
Centripetal force always acts perpendicular to the object’s motion, which means it cannot ever do work.
21. B
The same two materials would be in contact, so the coefficient of friction would remain the same.
The object’s mass would also be the same, so the normal force would remain constant. Since Ff = μFN, and neither of those terms changed, the magnitude of the frictional force will also be unchanged.
22. D
Both objects begin with no kinetic energy, and they undergo the same decrease in potential energy. Therefore, they finish with the same total kinetic energy. The block doesn’t have any rotational K, so all of its K is translational. But the sphere is rotating, so some of its K is translational, and some is rotational:
Ktotal, block = Ktotal, sphere Ktrans, block + 0 = Ktrans, sphere + Krot, sphere
Thus, once they start moving, the block has more Ktrans than the sphere. Its center moves faster, so the block finishes first.
23. A
The paths all have the same horizontal displacement, x. So focus on the horizontal component of velocity, vx; don’t worry about total speed or conservation of energy. Instead, look at the normal force. On path 2, the normal force points straight up, with no x-component. Thus vx is constant the whole time. On path 1 (up first), the normal force points up and to the left at the beginning, giving it a component in the negative x direction. Thus vx decreases at the beginning, and then increases back to v0x. On path 3 (down first), the normal force points down and to the right at the beginning, giving it a component in the positive x direction. Thus vx increases at the beginning, and then decreases back to v0x. In short, path 3 not only has a higher average speed than path 2; path 3 also has a higher average forward velocity than path 2. That’s why t3 < t2.
24. D
For an elastic collision, both kinetic energy and momentum will be conserved. Writing these statements as equations gives

You’re told m1 is a given in the question, and v2,0 is also known to be 0 m/s since the object started at rest. This leaves m2, v1,0, v1,f, and v2,f as unknowns. With two equations, you can have two unknowns. Therefore, (D) is correct.
25. D
The table provides both the normal force and the frictional force. The normal will be perpendicular to the table’s surface and the frictional force will be parallel to the surface. Therefore, the total force from the table (the sum of normal and friction) will be neither parallel nor perpendicular to the surface.
26. A
The force of static friction and the force of gravity are acting down the incline in this situation. When the box just begins to move upwards, the forces in both directions are equal and the force of static friction is at its maximum. Therefore, you have the equation

27. A
First, perfectly inelastic can be immediately eliminated because the objects have different velocities after the collision. Next, recall that a collision is perfectly elastic if kinetic energy is conserved.
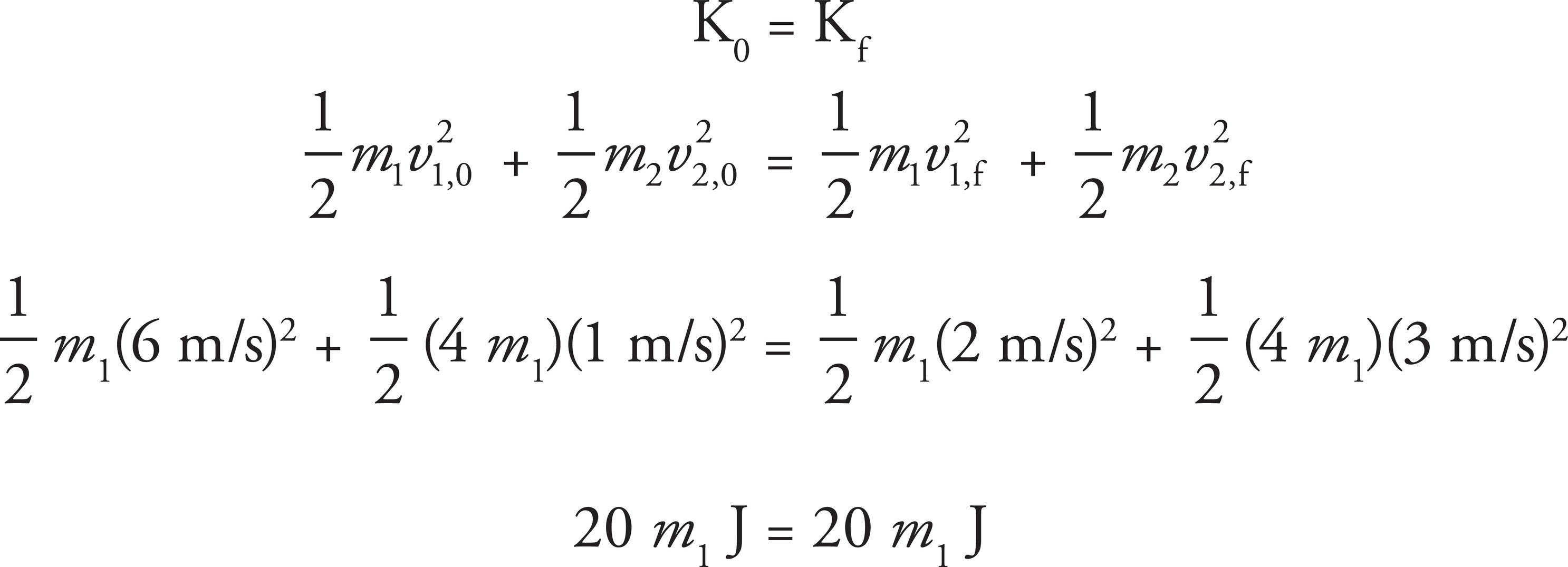
Because kinetic energy was conserved, the collision must be perfectly elastic.
28. D
In the picture, neither ball experiences any change in its horizontal motion. Ball A is originally moving down, but moves up after the collision. Therefore, the impulse it received is entirely up.
29. B
Think of the pendulum as undergoing circular motion. The centripetal force would be equal to the difference between tension and the radial component of gravity.

So long as the pendulum is in motion (as long as v > 0), tension must have a larger magnitude than the radial component of gravity. However, when v = 0 (at the maximum displacement), the two will be equal. Therefore, (B) is the correct answer.
30. C
This situation is equivalent to a spring-block system. It would start with some potential energy at one extreme edge, turn all of that energy into kinetic energy as it moved to the center, and continue to the other edge due to its momentum (turning the energy back into potential energy). This process would continue indefinitely in ideal conditions.
31. B
Since the wave speed is independent of the frequency, the speed is still v. This is Big Wave Rule #1. The wave with frequency 4f will have 1/4 the wavelength, but the wave speed will stay the same.
32. B
Kinetic energy is related to speed according to the equation  . Comparing the new kinetic energy, K’, to the original kinetic energy yields
. Comparing the new kinetic energy, K’, to the original kinetic energy yields

33. B
The forces during a collision are an example of an action/reaction pair. This means the force on the car will be equal in magnitude but opposite in direction compared to the force on the car. Because the forces are in opposite directions, the accelerations will be as well. Eliminate (A) and (C). Because the forces are equal in magnitude, Newton’s Second Law states that the acceleration of the lighter object will be double the acceleration of the heavier object. Eliminate (D). Therefore, the answer is (B).
34. D
First, draw a free-body diagram:

In order to stay in place, the force of friction needs to have a magnitude equal to the force of gravity’s.
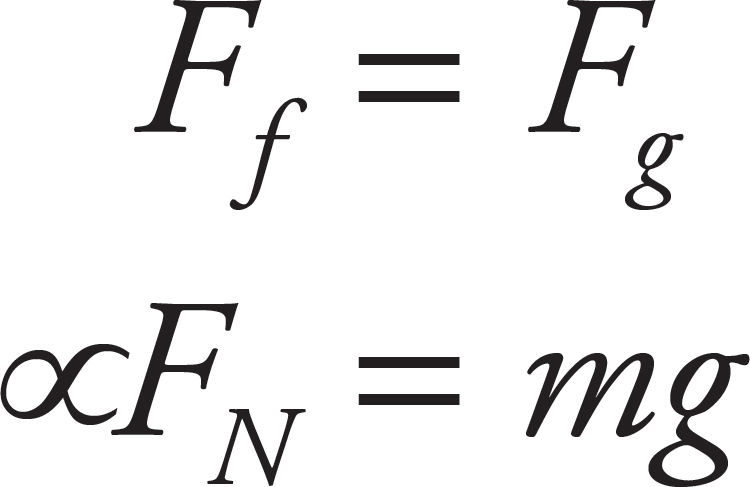
Next, solve for the normal force. This is possible because the person is undergoing uniform circular motion, so set the normal force equal to centripetal force.
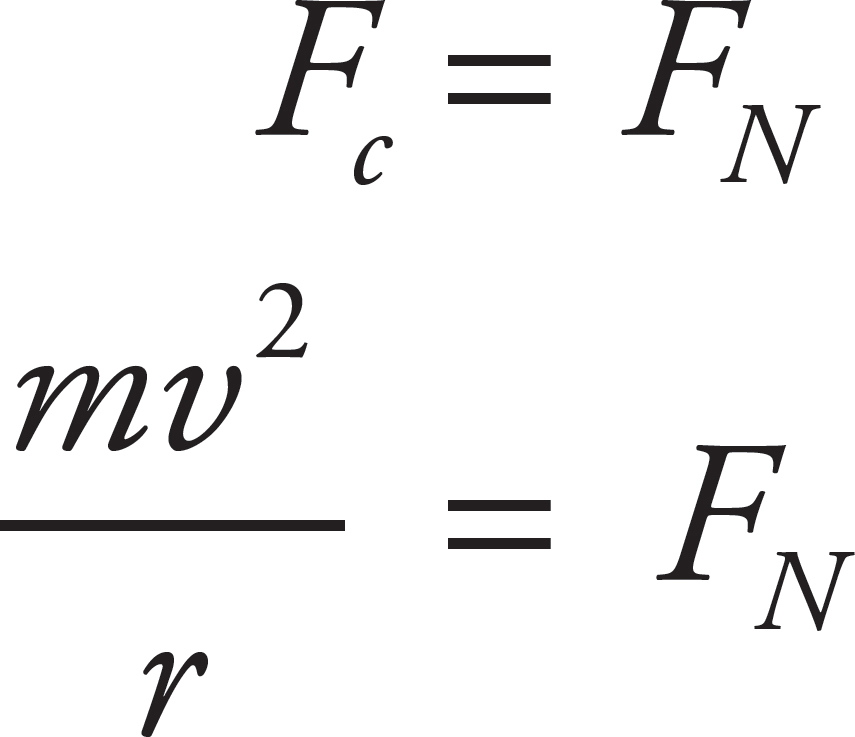
Finally, substitute this value into the previous result.

Notice that the mass actually drops out of the equation. The only variables that matter are the coefficient of friction, speed, and the radius.
35. A
Apply Conservation of Energy to compare when the block is at its equilibrium position to when the block is at greatest displacement:

36. A
First, in order for the small block to slide off, there would have to be a big force affecting the larger block. Hooke’s Law (F = −kx) states that this will happen at maximum displacement from the equilibrium position. Eliminate (B) and (D).
Second, the equation given in (C) indicates that the heavier the top block is, the more likely it is to slide off. But this is obviously not true, so (A) must be correct.
37. B
The lowest note that can be played is the fundamental frequency of the flute. For a standing wave with a node at both ends, the fundamental wavelength is twice the length of the flute, 2L. Applying the wave speed equation,

38. D
Intensity is inversely related to the square of the separation between source and detector, so the fact that the train is approaching you means the intensity (loudness) will increase. The pitch, however, is dictated by the Doppler effect. In this case, the detector is motionless, but the source is moving toward the detector. This motion results in a higher pitch at the detector. The brakes of the train (which will, of course, reduce the speed of the train) will continually diminish this effect, so the pitch will decrease.
39. D
First, replace all the resistors with an equivalent resistor.
R2 and R3 are in series, so R2 and 3, = R2 + R3.
R1 and R2 and 3 are in parallel, so  .
.
Second, calculate the current coming out of the battery,

Finally, calculate the power,

40. B
Because R1 and R2 and R3 are in parallel, the voltage across each matches the battery of 100 V. Using what you solved from problem 39 and your knowledge that current splits off in parallel, to calculate the current going into R2 and R3 use
I = V/R = V/R2 and 3 = V/(R2 + R3) = (100 V)/(80 Ω + 120 Ω) = (100 V)/(200 Ω) = 0.5 A
Now that you know the current going into this branch of the parallel circuit, you know that R2 and R3 are in series, and in series the current remains the same. So the current going across R3 is 0.5 A. Using this, you can calculate the voltage going across R3,
V3 = I3R3 = (0.5 A)(120 Ω) = 60 V
41. B
If R1 were to burn out, the total resistance in the circuit would increase. Because I = V/R, this increase in resistance would decrease the current.
42. D
At 20 s, the voltage across the resistor is 5 V, so the current is

The power at this time is given by
P = IΔV = (0.01 A)(5 V) = 0.05 W
The shape of the graph can be obtained by combining these two equations:

which shows that the power dissipated by the resistor will increase quadratically with the voltage.
43. D
The question specifies that the current through G must be 0. Recall that in parallel circuits current will distribute itself in a manner inversely proportional to the resistance in each path. Looking at the left-hand side of the configuration, you can see that the resistance on the top is half the resistance of the bottom. That means the current will distribute itself with 2/3 along the top path and 1/3 along the bottom path. For no current to pass through G, this same distribution must also be true on the right-hand side; otherwise, some current would pass through G to correct any changes to the relative resistances. The 5 Ω resistor must have the same proportional resistance to the unknown resistor that the 20 Ω resistor has to the 10 Ω resistor. Therefore, the unknown must be 2.5 Ω.
44. D
Coulomb’s Law is given by

Doubling each charge, and halving the distance between them yields

45. A
Although you do not care about the direction of the net vector in the end, you do have to take orientation into account to find the magnitude. Number the charges from the top left and go clockwise as 1, 2, 3, and 4. Drawing out the different forces on the bottom right charge (charge 3), you get

Now solve each of these force vectors:


These two are the simpler force vectors to solve. In order to solve charge 1’s force on charge 3, the distance first needs to be solved. Because they are ordered in a square, using a diagonal creates a 45°-45°-90° triangle. The distance in this case is  . So,
. So,

First, combine the F4 on 3 with F2 on 3 to get an equivalent vector that will be in the same direction as F1 on 3,

They form a 45°-45°-90° triangle when laid tail-to-end so,

This vector points in the same direction as F1 on 3, so to get the magnitude of the net force, simply add F2 and 4 on 3 with F1 on 3,

46. A, D
According to the formula v2 = v02 + 2ad, the initial velocity, v0, can be related to the stopping distance, d. If v is zero, and the equation is rearranged for d, it becomes  /2a. Since the car is decelerating, a is negative. Therefore, if v0 is doubled, the stopping distance, d, is quadrupled. To determine the relationship between v0 and t, it becomes t = −v0/a. Therefore, if v0 is doubled, the stopping time, t, is doubled.
/2a. Since the car is decelerating, a is negative. Therefore, if v0 is doubled, the stopping distance, d, is quadrupled. To determine the relationship between v0 and t, it becomes t = −v0/a. Therefore, if v0 is doubled, the stopping time, t, is doubled.
47. C, D
The period for a pendulum is 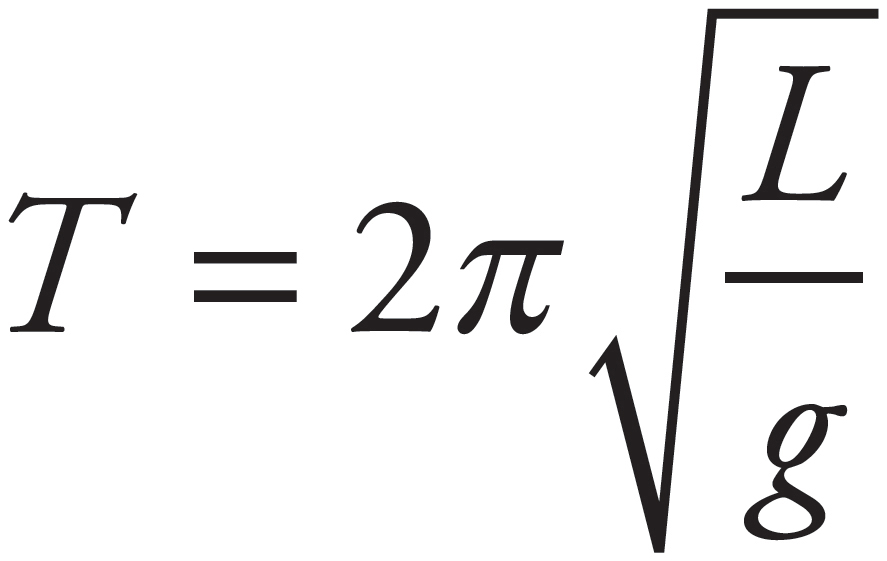 . Making changes to the length of the string or changing the acceleration of gravity (by changing the location from the Earth to the Moon) will cause changes in the period.
. Making changes to the length of the string or changing the acceleration of gravity (by changing the location from the Earth to the Moon) will cause changes in the period.
48. B, C
The resistors are all in parallel, meaning their voltage is the same across each resistor and matches the voltage of the battery. Eliminate (A). The voltage provided by the battery does not increase or decrease; the battery still maintains the same voltage. Eliminate (D). The resistors are in parallel, so eliminating one of the resistors will increase the equivalent resistance. Because I = V/R, this increase in resistance would decrease the current. The equation of power is P = IV. If the current decreases, the power decreases as well.
49. C, D
The branch of the circuit containing R1 is connected in parallel to the branch containing R2 and R3. Thus, the voltage across each branch is equal to V. R2 and R3 are connected in series, so their equivalent resistance is R2 + R3. The current through both R2 and R3 is therefore given by
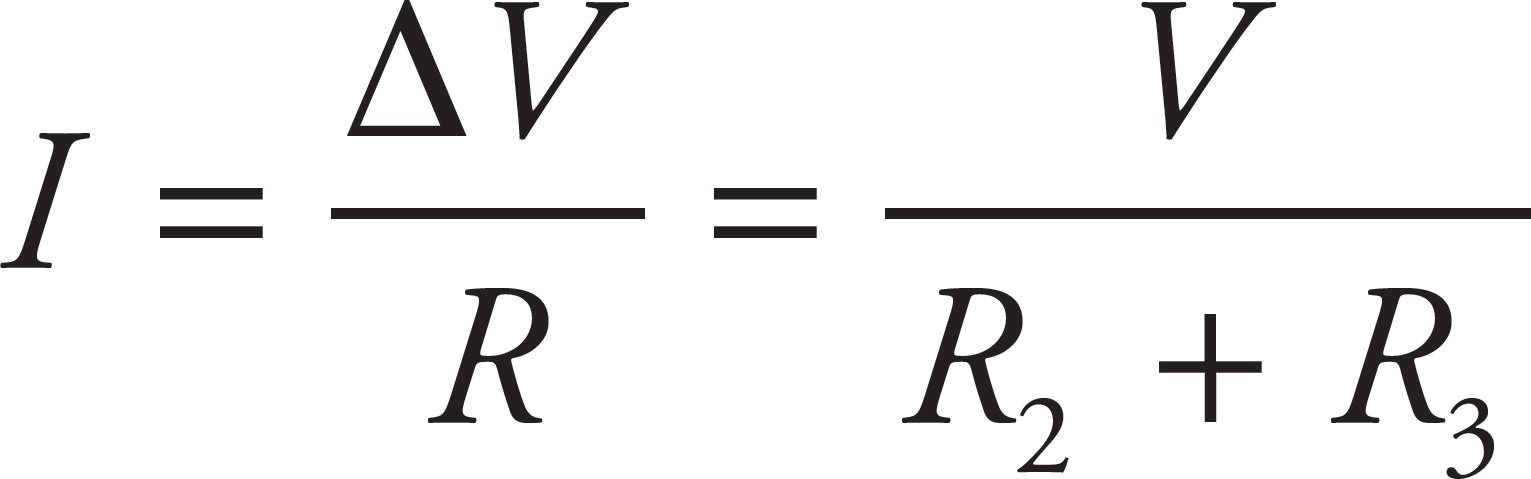
According to this equation, a decrease in V, or an increase in R2 or R3 would cause a decrease in the current through R3. Any change to R1 would not have an impact on the current through R3 because R1 has no impact on the voltage across the branch of the circuit containing R2 and R3.
50. B, D
Big Wave Rule #2 states that when a wave passes into another medium the frequency remains the same. Eliminate (A). The frequency does not change when passing into another medium; the speed and wavelength of the wave change. Choice (B) is correct.
Big Wave Rule #1 states the speed of a wave will be constant while in a single medium. So, while the sound wave is in the metal rod the speed will remain consistent. So at two different points in the rod,
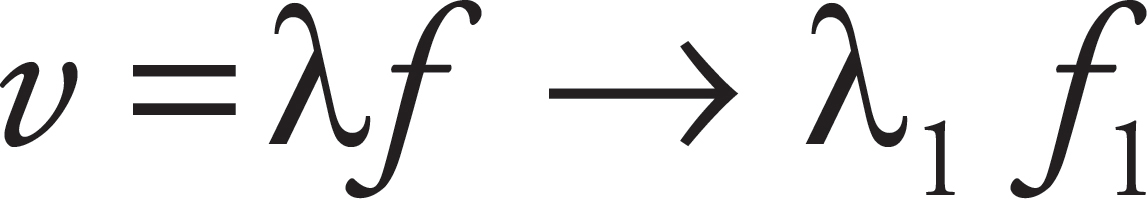
This is an inverse relationship between our wavelength, λ, and frequency, f; (D) is also correct.
Section II: Free-Response Questions
1. (a)
One such example would be to mark off two distances on the table—one for Block A before the collision, and one for the combined blocks after the collision. Push Block A to give it an initial speed. Use a stopwatch to measure the time it takes for the blocks to cross the marked distances. The speeds are the distances divided by the time.
(b)

(c)
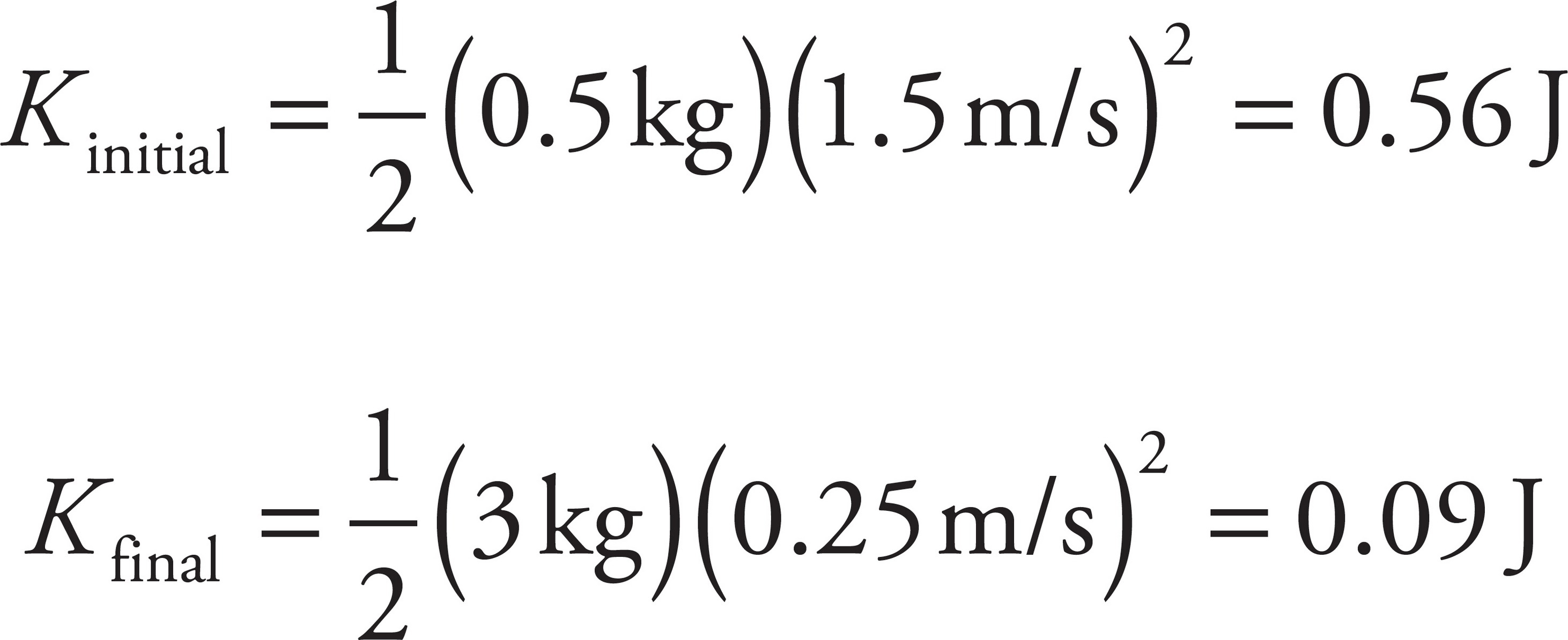
The total kinetic energy lost is equal to

2. (a)
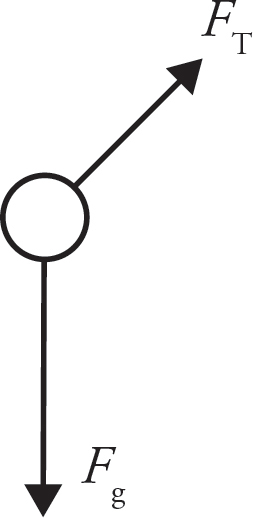
A free-body diagram would include only the tensions in the string and the force of gravity as shown below. Because the pendulum makes a horizontal circle, take some care to draw the direction of the force represented by the tension along the path of the string.
(b) Where θ is the angle between FT and the normal,
 And
And 
(c) The centripetal force is the net force in the x-direction. However, you need to use some information from the y-direction. Because the conical pendulum travels in a horizontal circle, there is no acceleration in the y-direction and so Newton’s Second Law in the y-direction becomes
FT cos θ − Fg = 0
or

Knowing this, you can solve for the centripetal acceleration. It is the same as the acceleration in the x-direction.

(d) The radius the ball travels can be found using some geometry. The length of the string is 2.2 m at an angle of 57 degrees. This means

(e) The ball will travel at a speed of
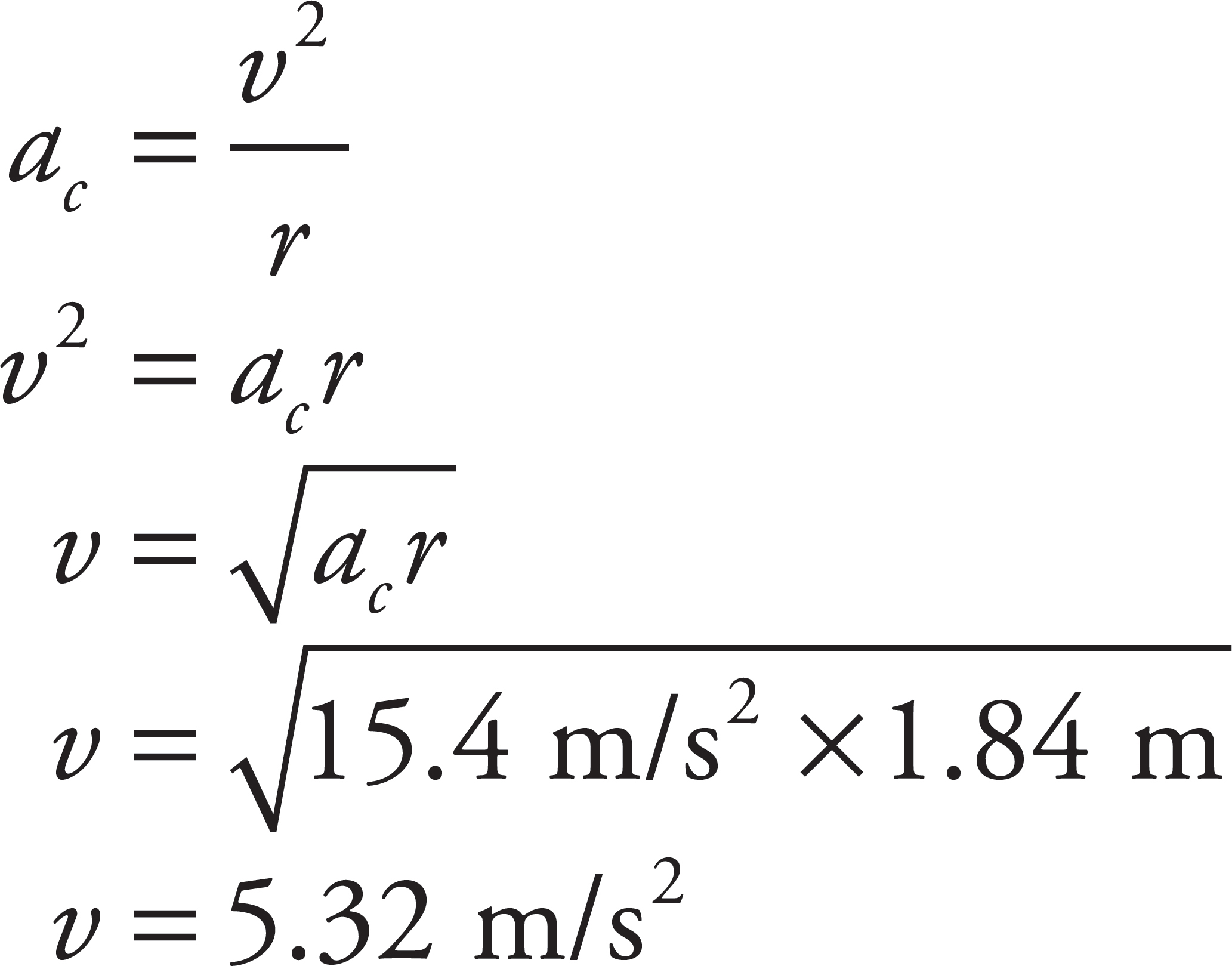
3. (a)
Because the force vector points to the left, the only logical solution is if q1 is negative and q2 is positive.
(b)
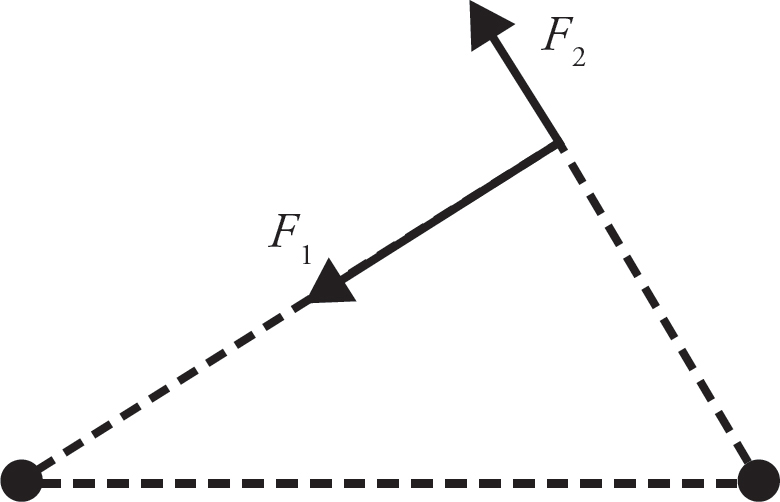
(c) Applying Coulomb’s Law to determine F1 and F2,

F is the vector sum of the two forces, F = F1 + F2. Since they are at right angles to each other, the magnitude can be found by applying the Pythagorean Theorem:

(d)
From the setup, you know that the current net force is entirely to the left. Therefore, you need to cancel this out with a force that is entirely to the right. The question specifies that you must use a positively charged particle to do this, and positive charges will create repulsive forces in this case because q3 is itself positive. So if you’re trying to repel an object and make it move right, you need to be to that object’s left. Without additional numerical information in the question, it’s impossible to determine exactly how far from q3 this charge should be placed, but it must be somewhere along the line that extends directly to the left of q3.
4. (a)
The spring observes Conservation of Mechanical Energy,

(b) (i) The value of 1/m would help in determining the spring constant when you take the slope of the line.
(ii)
1/m (kg−1)
m (kg)
h (m)
50
0.020
0.49
30
0.030
0.34
25
0.040
0.28
20
0.050
0.19
17
0.060
0.18
(c)

(d) To calculate the slope, select two points on our best-fit line. Here is one example:

From part (a),
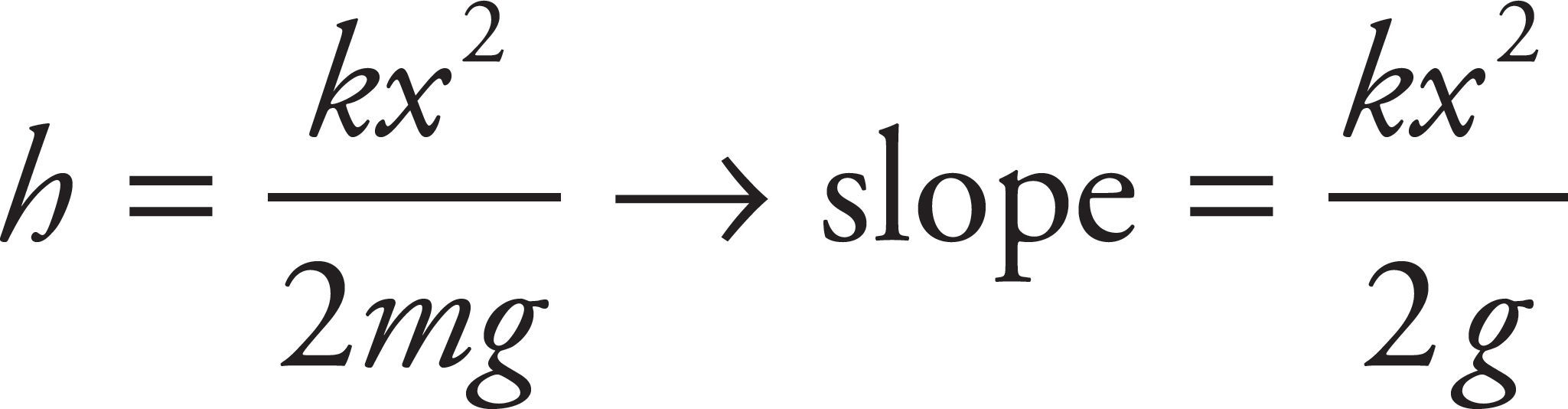
Note: Values between 450 N/m and 550 N/m are acceptable.

(e) One example would be to use a meter stick and video camera. Hold the meter stick next to the toy and allow it to jump up. Record the toy with a video camera. With this you can watch the video in slow motion later to determine its height. You can also do an alternate method of finding the height by recording the time t it takes to fall from its highest point to the lowest. Then, using kinematics equations, you can determine the height.
5. (a)
Applying Newton’s Second Law to one of the objects

(b)
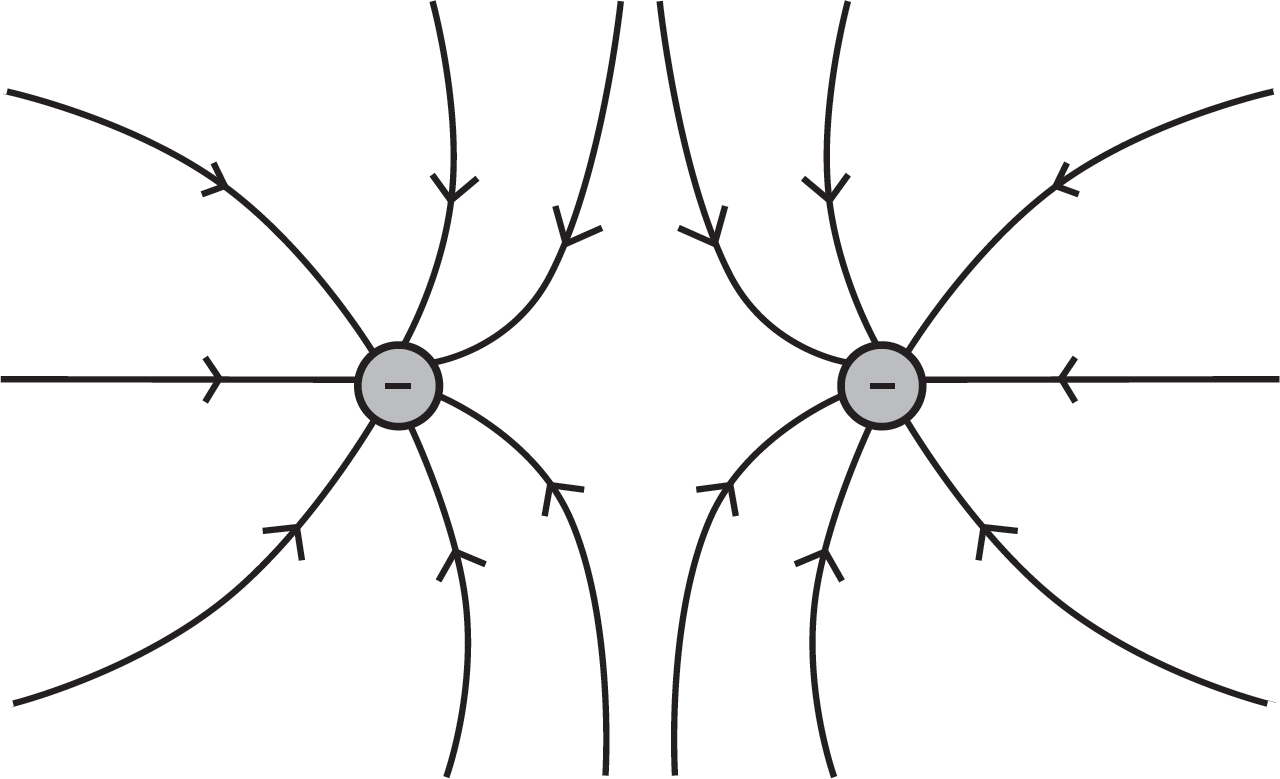
(c) The acceleration is caused by the electrostatic force, and initially that force has the same magnitude as the one calculated in part (a).
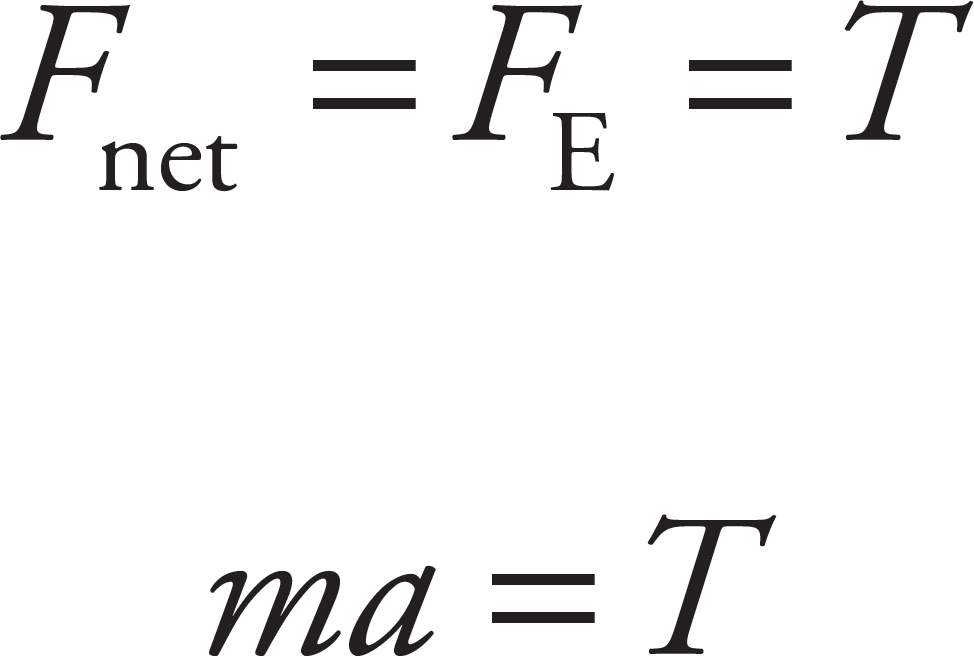
Now calculate the acceleration on each object,
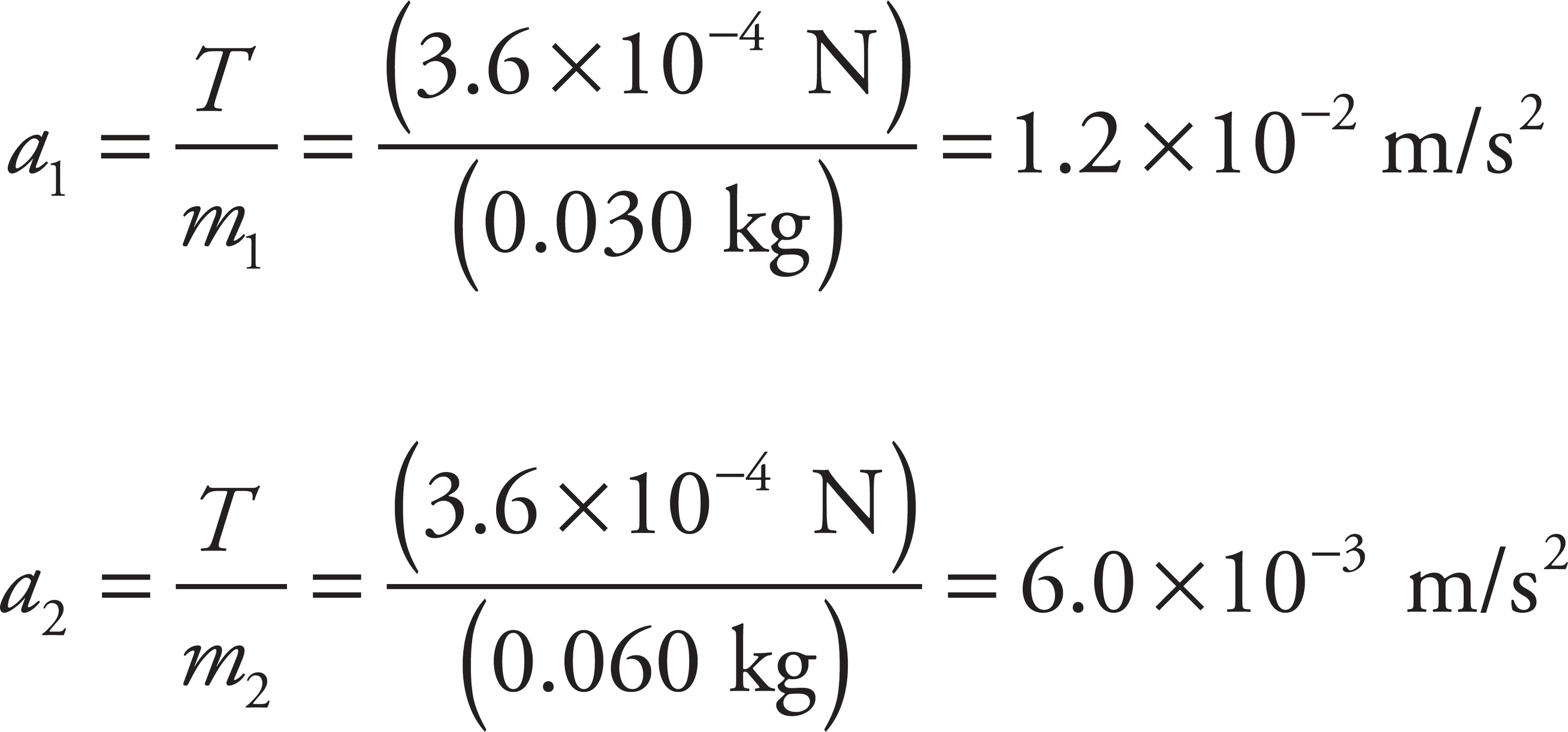
(d)

(e) As time increases, the speed of the objects increase. The objects move further apart, but their speeds increase at a slower rate. This is because the electrostatic force decreases as the objects move further apart. Hence, the acceleration also decreases. The speed approaches a constant value as the distance between the objects, d, approaches infinity.