1. B
The kayaker’s resultant velocity, v, will be the sum of the river’s velocity, vr, and the velocity of her paddling, vp:
v = vr + vp
Since the kayaker wishes to travel due east, the component of vp in the N-S direction must cancel vr, so vp,N-S = 1° m/s due N. Since the magnitude of vp is 1.5 m/s, her heading can be calculated using
2. D
The average acceleration is found using 
. Since time is a scalar that only changes the magnitude of the vector, the direction of acceleration will be defined by the change in velocity. We’ll deal with each component separately.
Δvx = v2x − v1x = 4 − (−1) = 5
Δvy = v2y − v1y = −2 − (4) = −6
It may help to draw the vector Δv. The angle this vector forms with the +x-axis can be evaluated using the equation
3. C
The student starts her journey at home and ends up at school 1.2 km away. It’s unknown if she travelled in a straight line directly to school from home, so it is unknown if the distance she travelled was 1.2 km or greater than that if she took a detour. This makes I incorrect, eliminating (A) and (D). Not knowing the distance she travels also means her average speed is also unknown since average speed = distance/time. This makes II false, eliminating (B). Although the distance travelled is unknown, displacement is an overall change in position, so her displacement is known to have a magnitude of 1.2 km. So the magnitude of her average velocity can be calculated to be
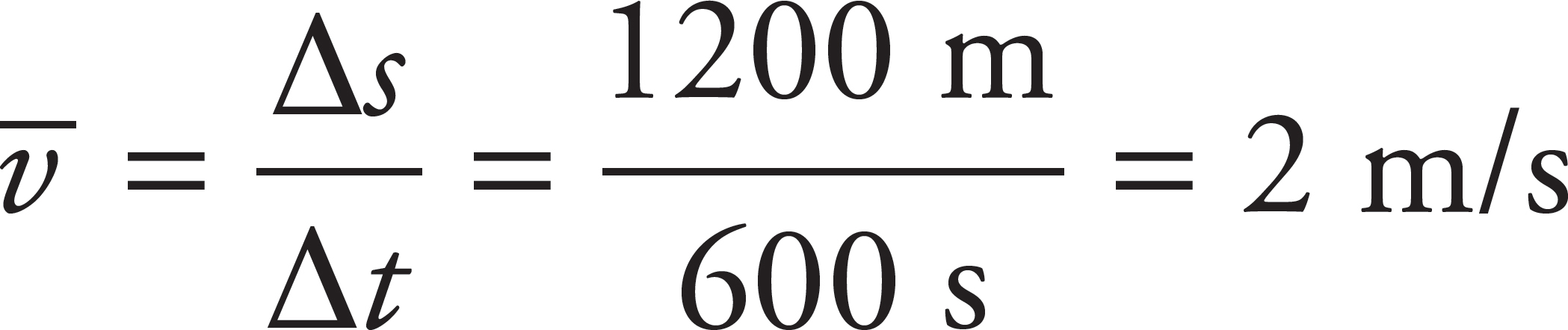
Making III, and therefore (C), correct.
4. D
The position-versus-time graphs depicted in (A) and (B) are linear, indicating constant velocity and zero acceleration. Eliminate (A) and (B). The position-versus-time graph in (C) has a negative velocity but has a positive acceleration. Eliminate (C). The position-versus-time graph in (D) has a negative velocity and a negative acceleration. Choice (D) is correct.
5. B
In section 1, the object is slowing down and moving in the positive direction. Eliminate (A). In section 3, the object is moving with constant speed in the negative direction. Eliminate (C). In section 4, the object is slowing down and moving in the negative direction. Eliminate (D). In section 2, the object is speeding up and moving in the negative direction. Choice (B) is correct.
6. C
The horizontal distance that the water travels from its drop point is given by x = v0xt. Since the water is dropped from the plane, its initial velocity will be the same as that of the airtanker, 
. Thus, v0x = 85 m/s. The time it will travel is equivalent to the water’s flight time, which can be calculated using the y-direction:
Therefore, 
.
7. B
To compare the displacement of the two cannonballs, the x- and y-components of the displacement must be calculated separately. The x-component of displacement will be given by Δx = v0xt. Since Cannonball A is fired horizontally, v0x,A = 40 m/s, and Cannonball B has an initial x-velocity of 
. Because the x-component of the initial velocities and the times will be the same, ΔxA = ΔxB. Thus, it is only differences in the displacement in the y-direction that will determine the difference in the magnitude of displacement. Applying Big Five #3 for both cannonballs yields
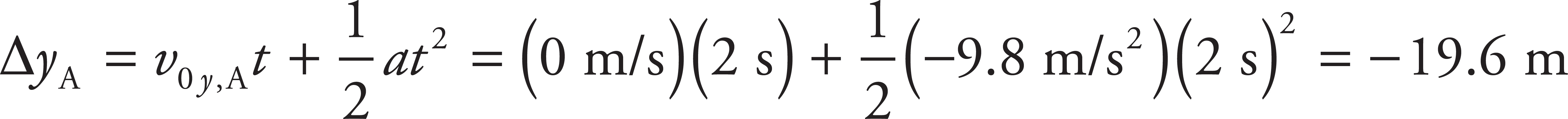
Since |ΔyA| < |ΔyB|, Cannonball B will have the greater magnitude of displacement after 2 s.
8. C
Use Big Five #1:
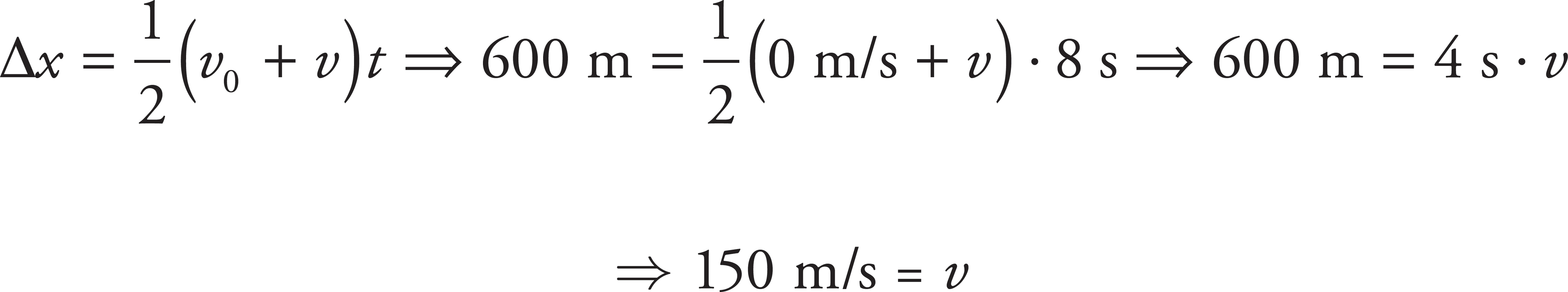
9. B
The variables involved in this question are the initial velocity (given in both cases), the acceleration (constant), final velocity (0 in both cases), and displacement (the skidding distance). As the missing variable is time, use Big Five #5 to solve for the displacement:
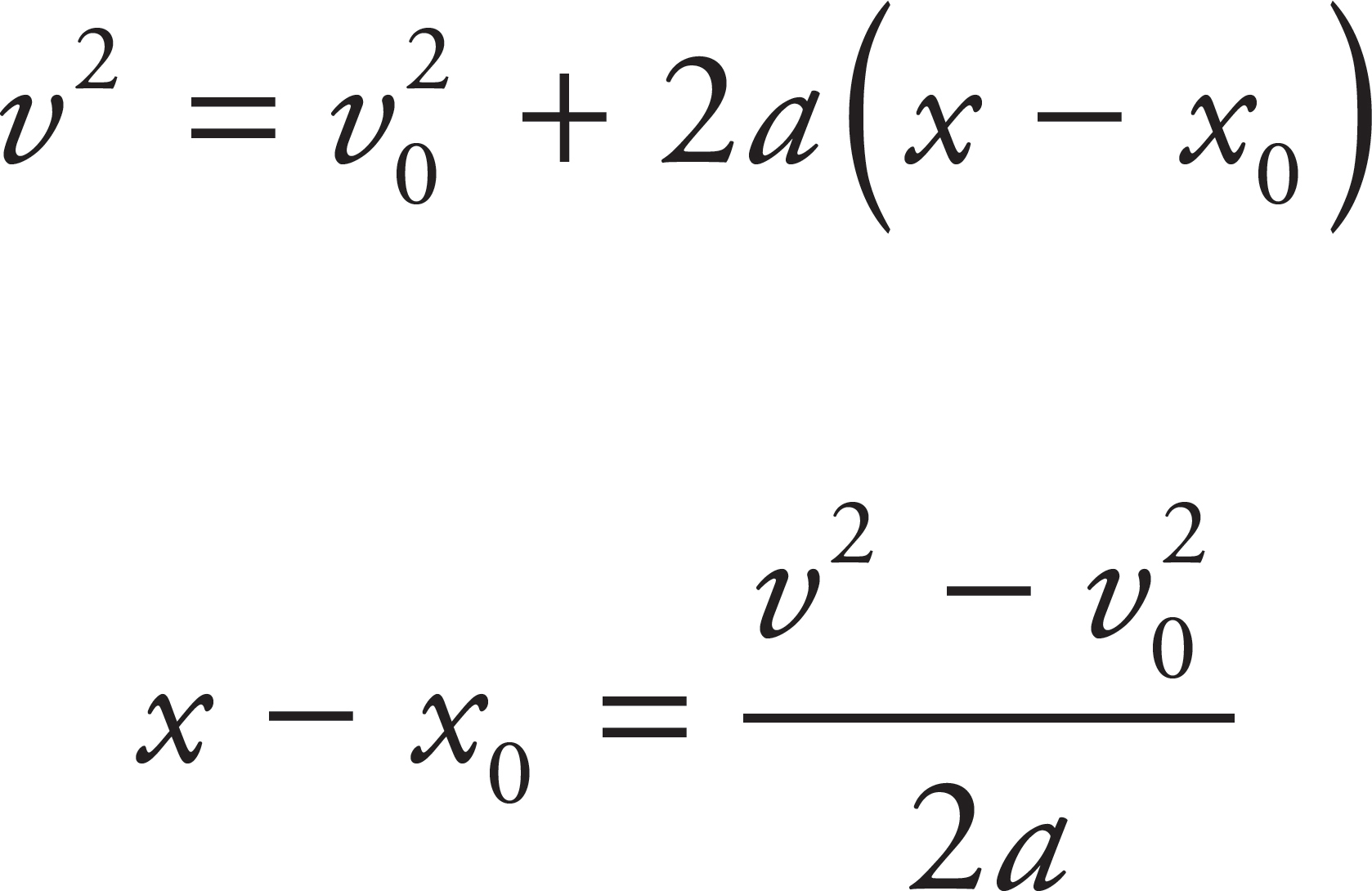
As the initial position, x0, and the final velocity, v2, are equal to 0, this equation simplifies to
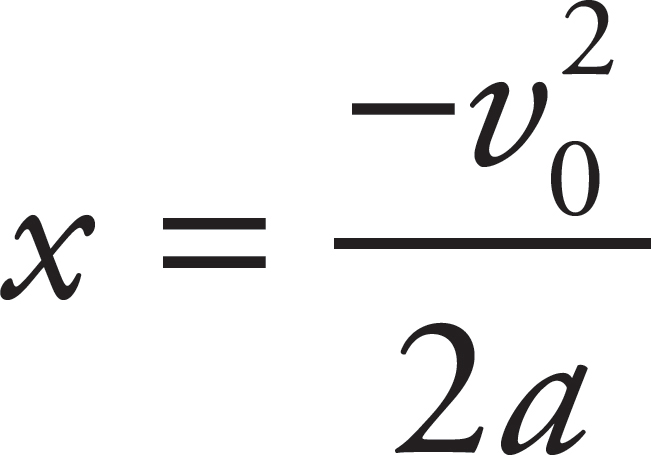
When the acceleration is doubled, the final position is halved. (Note that the acceleration in this problem is negative, as the brakes cause the car to decelerate.)
10. B
There are four forces acting on the book: the push from the student, gravity, normal force, and friction. Of these four forces, normal force and friction are forces exerted by the table on the book. The normal force is calculated from knowing that the net force in the y-direction is zero:
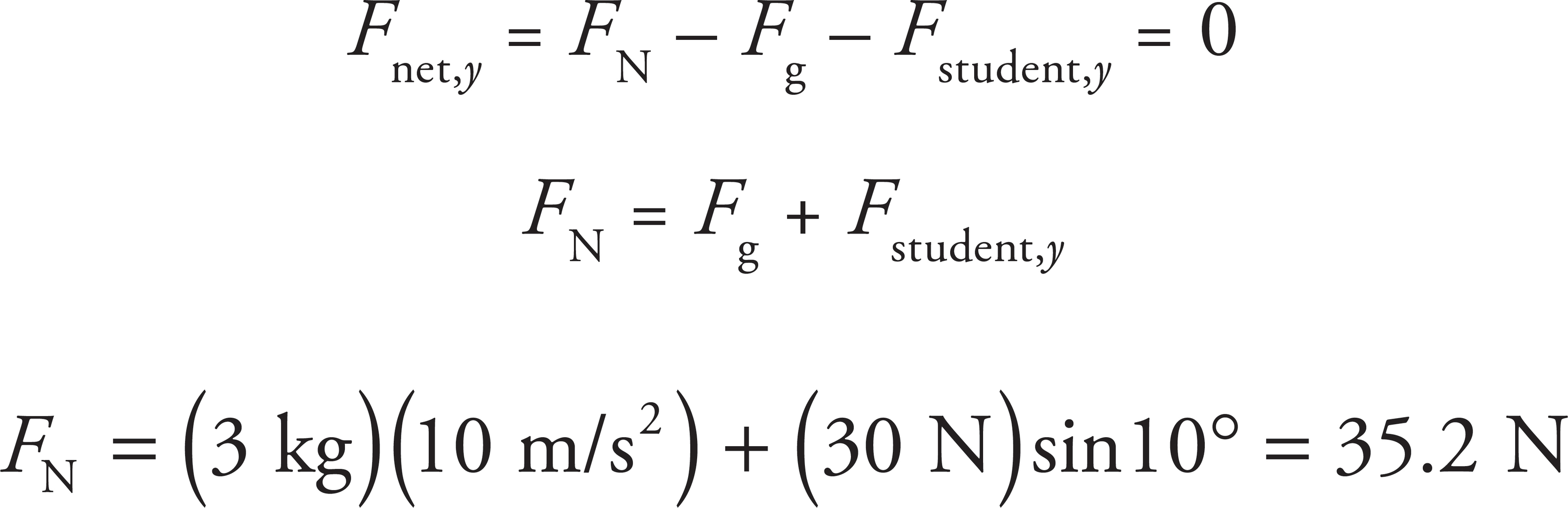
The force of friction is calculated using the normal force:
Ff = μFN = (0.3)(35.2 N) = 10.6 N
The force on the book from the table will then be the vector sum of the normal and friction forces. Since the normal force is in the y-direction, and the friction force is in the x-direction, the magnitude of their sum is found using
11. B
There are free forces acting on the box: the weight of the box, the normal force of the inclined plane on the box, and the force of friction. The weight of the box can be separated into its parallel and perpendicular components.
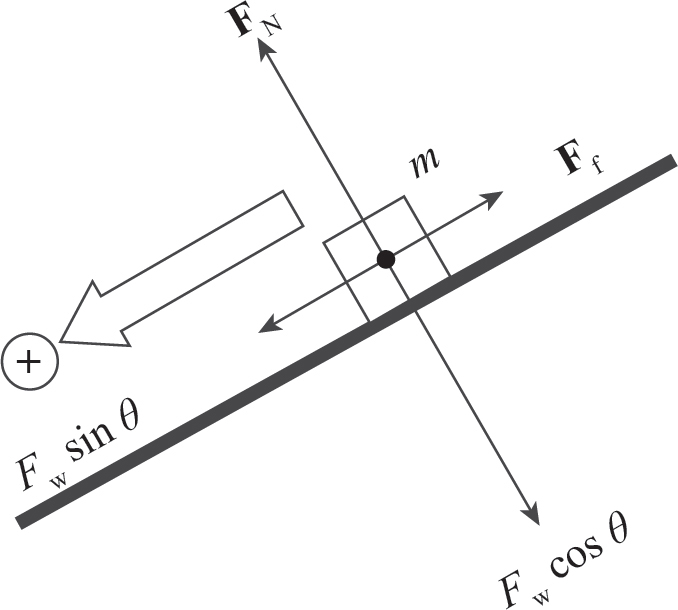
In order for the box to be at rest, the net force in both the parallel and perpendicular directions must be zero:
12. B
In both strikes, the hammer had the same initial velocity. The strike where the hammer experienced a greater force is the one where the hammer experienced a greater acceleration. As the contact time of both strikes is the same, a greater acceleration will produce a greater change in velocity. In the first strike, initial velocity (vi) was positive and the final velocity was zero. In the second strike, the initial velocity (vi) was positive and the final velocity was negative. Therefore, the second strike had a greater change in velocity and was the strike that involved a greater force on the hammer. Note that you were not given the magnitude of the final velocity. However, you can say that it has a negative value as the direction was opposite to the initial velocity.
13. C
The minimum force exerted to maintain the speed of 2 m/s will result in no acceleration. Thus, the force required will result in Fnet = 0. The friction force acting against the motion is
Thus, the force required to maintain the speed is 12.5 N, just enough to counteract the friction force.
14. C
On a force-versus-position graph, the work done is the area under the curve. At the 4 m position, the area under both student’s curves is the same:
Student A:
Student B:
0 m to 4 m: W = 30 N · 4 m = 120 J
15. A
The work done by the brakes can be calculated using the Work−Energy Theorem:
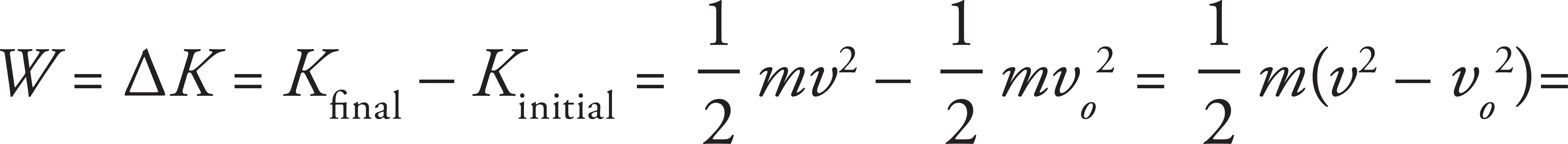
(2000 kg)(10 m/s)2 − (20 m/s)2 = (2000 kg)(100 m2/s2 − 400 m2/s2) = (1000 kg)(−300 m2/s2) = −300,000 J
Note that the work done is negative as the friction force of the brakes caused the truck to lose kinetic energy.
16. B
Apply Conservation of Mechanical Energy:
17. D
In order to maintain a constant speed, the net force on the car must be zero. This means that the car’s engine must be applying a force equal in magnitude but opposite in direction to the frictional force. The equation P = Fv then yields
P = Fv = 3500 N · 15 m/s = 52,500 W = 52.5 kW
18. D
The total work done on the rocket can be calculated using the Work–Energy Theorem:
(50 kg)(15 m/s)2 − (10 m/s)2 = (50 kg)(225 m2/s2 − 100 m2/s2) = (25 kg)(125 m2/s2) = 3,125 J
This is the total work done on the rocket. As the rocket’s secondary engines did 4,500 J of work, this means that the force of gravity must have done −1,375 J of work.
19. C
The gravitational potential energy of the rock is converted into kinetic energy. This allows you to calculate the final speed of the rock when it lands:
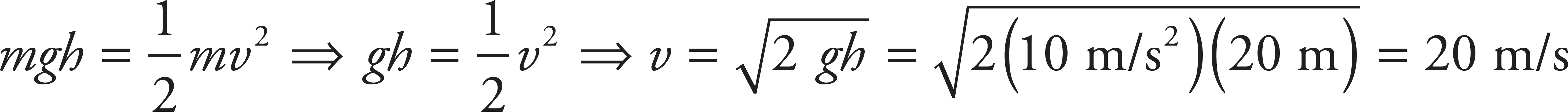
The average force experienced by the rock can be calculated using
20. A
As the plutonium atom is initially at rest, it has an initial momentum of 0. By Conservation of Linear Momentum, the total final momentum must also be equal to 0.
As the alpha particle was traveling east, the decay product must be traveling west, as its velocity is in the opposite direction.
21. A
As the collision is perfectly inelastic, the final momentum is the vector sum of the initial momentums of both vehicles. As only the truck is traveling in the north-south direction, the vertical momentum after impact is given by
py = mtruckvtruck = 2000 kg (40 m/s) = 80,000 kg·m/s north
As only the car is traveling in the north-south direction, the horizontal momentum after impact is given by
px = mcarvcar = 1500 kg (20 m/s) = 30,000 kg·m/s north
The angle of the velocity after impact can be expressed using tan(θ)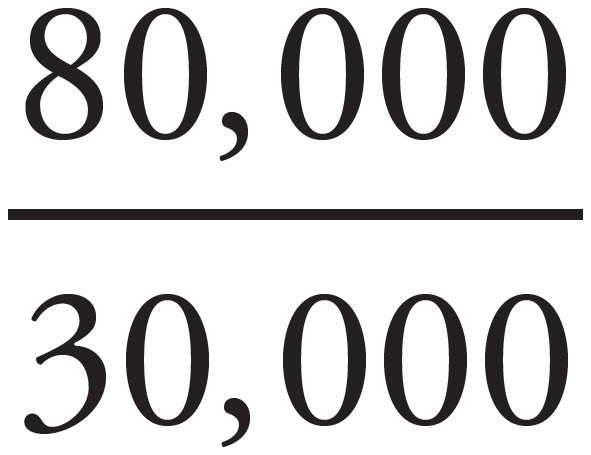 
, so θ = 
= 69.4° north of west.
22. A
The objects did not stick together after the collision, so (B) is wrong. To determine whether the collision is elastic or inelastic, calculate the total initial and final kinetic energies:
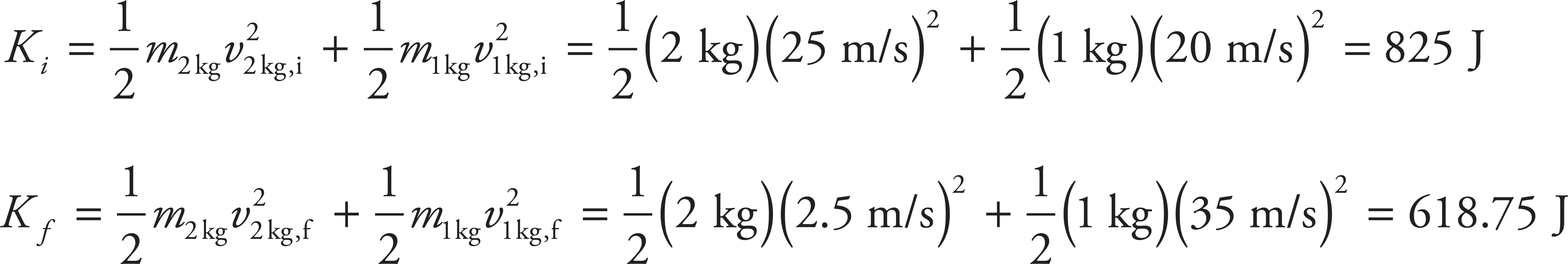
As kinetic energy was not conserved, the collision is inelastic.
23. C
Choices (A), (B), and (D) are all true statements about perfectly inelastic collisions. Choice (C) is a false statement. Kinetic energy is conserved only in elastic collisions.
24. C
Impulse can be found using J = Δp. Remembering that impulse and momentum are vectors, the magnitude of the impulse can be calculated by finding the change in the momentum in both the x- and y-directions, and finding the resulting magnitude:
≈ 12.3 N·s
25. A
Total linear momentum is conserved in the absence of external forces:
26. D
At time t = 3 s, the speed of the object is 4 m/s. The magnitude of the centripetal acceleration is given by
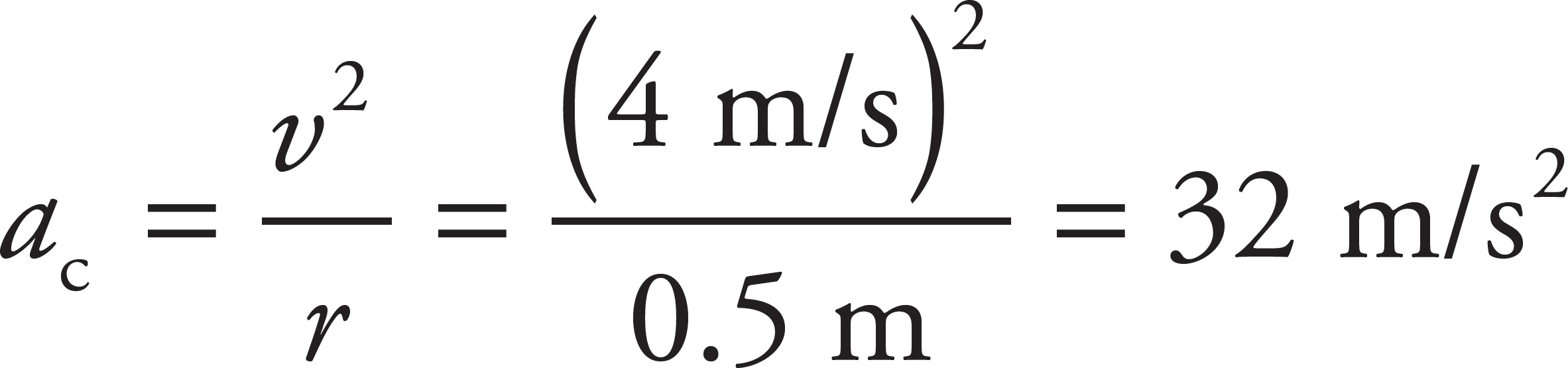
27. B
As the mass is whirled in a horizontal circle, it is the tension force that snapped the string and is equal to the breaking strength when the mass is traveling at 6 m/s. As the tension force is the only force acting in the horizontal direction, it is also producing centripetal force and can be calculated as follows:
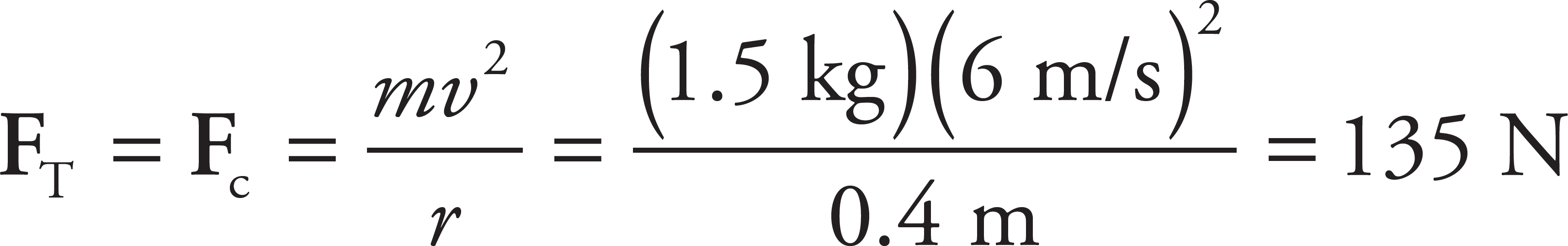
28. C
The gravitational pull of the planet provides the centripetal force on the planetoid, so
The radius between the planetoid and the planet is equal to the sum of the planet’s radius and the height of the planetoid above the planet’s surface: r = 1.6 × 105 m + 3.2 × 105 m = 4.8 × 105 m. The speed of the planetoid can then be calculated as
29. B
The magnitude of the gravitational force is given by the equation:
Doubling the mass of one object will double the magnitude of the gravitational force. Tripling the radius will decrease the magnitude of the gravitational force by a factor of nine. Combined, the new magnitude of the gravitational force is 2/9 of the original magnitude.
30. D
Apply Big Five #3 for rotational motion:
The circumference of the circle d = 2πr = 2π(2 m) = 4π m. 9π rad is equivalent to 4.5 rotations and a total distance traveled of 4.5 · 4π m = 18π m.
31. C
The position that the string can be attached to hold the bar up horizontally is the center of mass of the bar, which can be calculated using the center of mass equation with the far left side as the origin:
32. B
If the system is in equilibrium, then the net force acting on the mass is equal to 0. In the vertical direction, the forces acting on the mass are the weight of the mass and the vertical components of the two tension forces.
33. A
The frequency of the block attached to a spring is given by the equation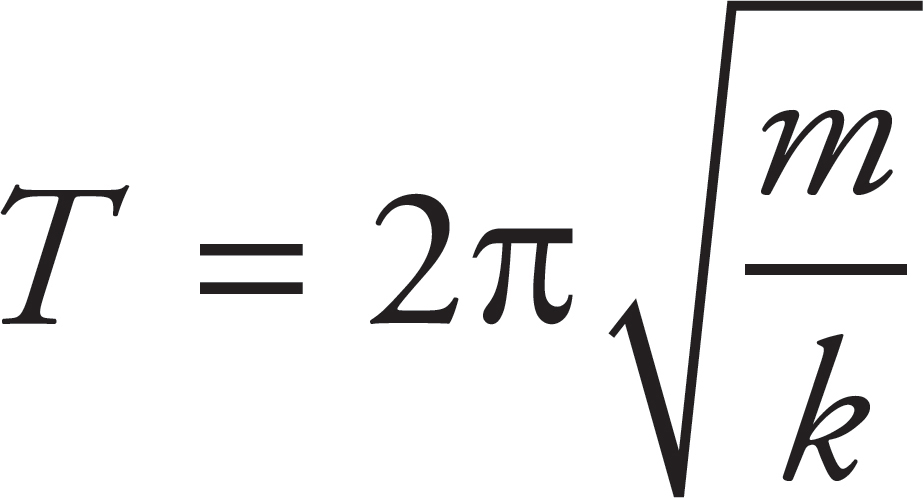 
. Changing the amplitude will not affect the period of the oscillations.
34. C
When the spring is attached to the ceiling, the spring is at its natural length when the upward force of the spring balances the weight of the block. The increase in the natural length is the distance that the spring is stretched to exert the upward force:
35. D
The magnitude of the restoring force of a simple pendulum is given by the equation:
Frestoring = mgsinθ = 3 kg (10 m/s2)(sin30°) = 15 N
36. A
By Conservation of Mechanical Energy, K + Us is a constant for the motion of the block. At the endpoints of the oscillation region, the block’s displacement, x, is equal to ±A. Since K = 0 here, all the energy is in the form of potential energy of the spring, KA2. Because KA2 gives the total energy at these positions, it also gives the total energy at any other position.
Using the equation Us(x) = kx2, find that at x = 
A,
The potential energy at this point is 1/16 of the total energy.
37. C
The distance between a crest and an adjacent trough is equal to half of a wavelength, so the wavelength of the wave is 1 m.
38. D
The speed of a transverse wave in a stretched string is given by the equation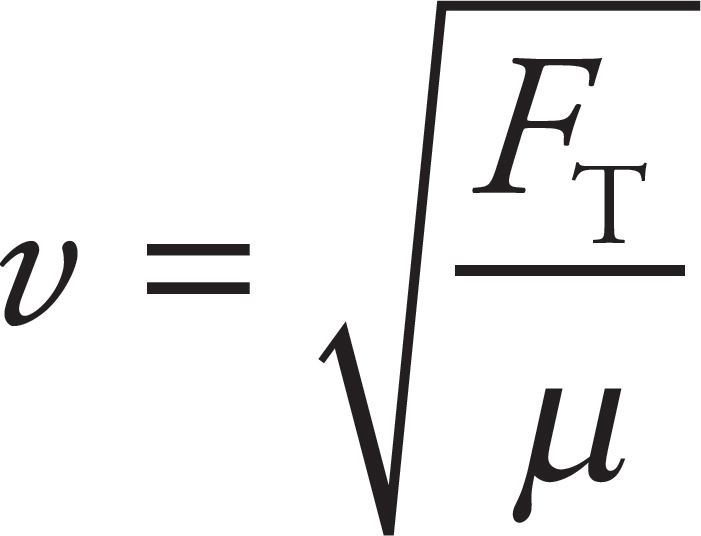 
, where FT is the tension in the string and μ is the linear mass density. Doubling FT and decreasing μ by a factor of 2 will result in an increase of v by a factor of 2.
39. C
The harmonic wavelengths of standing waves fixed at both ends are given by the equation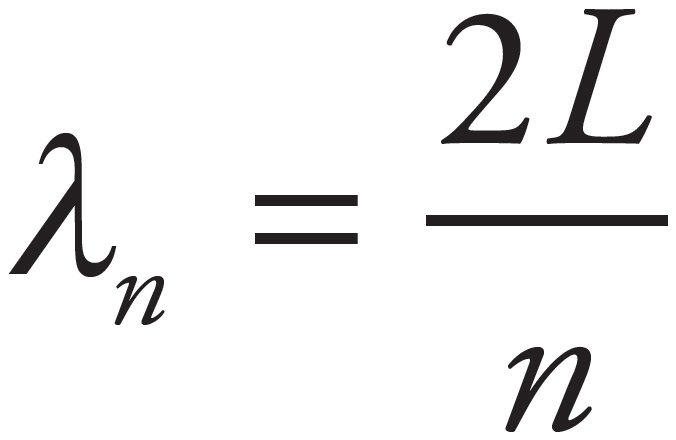 
. The wavelength of the third harmonic then is 
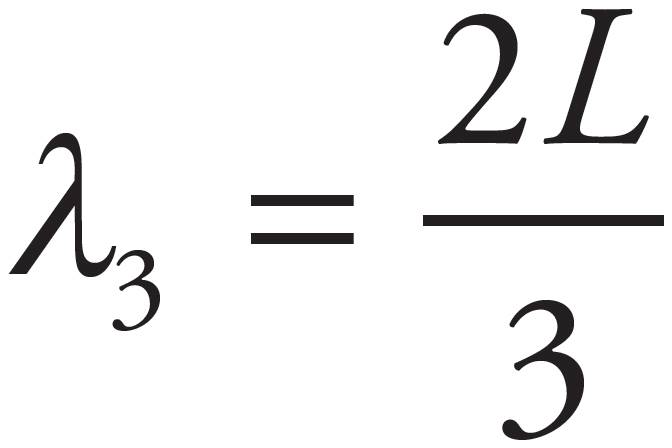, and the wavelength of the fourth harmonic is 
. The difference between the wavelengths of these two harmonics is equal to 
.
40. D
The energy of a wave is related to its amplitude, i.e., the maximum displacement of the medium from equilibrium. Since sound is a longitudinal wave, the medium it travels through will oscillate parallel to its direction of propagation. Therefore, increasing the energy of a sound wave moving in the +x-direction will result in oscillations with larger displacement in the x-direction. Note that the energy carried by a sound wave is not related to its frequency and that a wave is a propagation of energy, not the medium that carries it.
41. A
In order for the passengers of the truck to hear the music emitted from the car with no change in the frequency, there must be no relative motion between the car and the truck. This is true if the truck has the same magnitude and direction of velocity as the car.
42. A
As the train approaches the person, the person perceives the sound of the horn with a frequency higher than the original frequency emitted from the train due to the Doppler effect. As the train slows, the person still perceives a higher frequency, but it is not as high as when the train was traveling faster. As a result, the person hears a decrease in the frequency of the horn. As the train approaches, the distance between the person and the train decreases. This leads to an increase in the intensity of the horn perceived by the person.
43. D
Kirchhoff’s Loop Law can be applied to the loop containing only the battery and R1 and separately to the loop containing only the battery and R2 to show that ΔV1 = ΔV2 = Vbat. This is true with or without the addition of R3. Since I = ΔV/R and the voltages across R1 and R2 do not change with the addition of R3, the current through each of the resistors also doesn’t change. If the current through and the voltage across both R1 and R2 remain constant, the energy dissipated by each resistor per unit time also remains constant.
44. A
The equation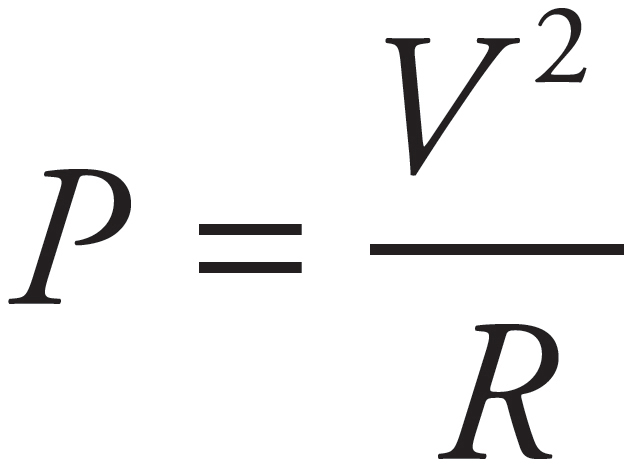 
gives
The amount of time it takes for the resistor to dissipate 100 J of energy is equal to 
.
45. C
The total resistance of two 5 Ω resistors connected in series is
Rtot = 5 Ω + 5 Ω = 10 Ω
This would produce a current of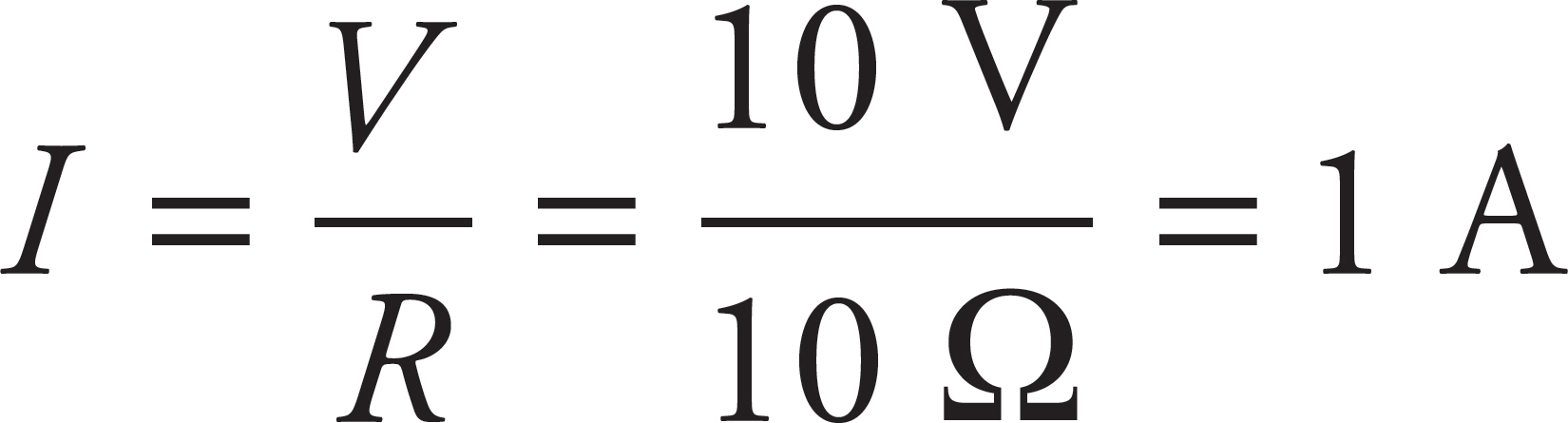 
.
The total resistance of two 5 Ω resistors connected in parallel is
This would produce a current of 
.
The difference between the current produced in the two circuits is 4 A − 1 A = 3 A.
46. A, C
The components of the vector sum A + B = C must satisfy the equation:
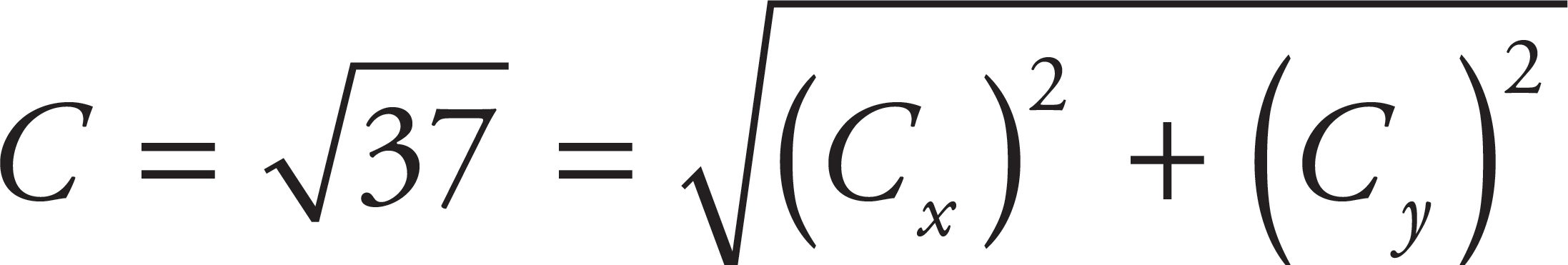
The only answer choices that satisfy the equation are (A):
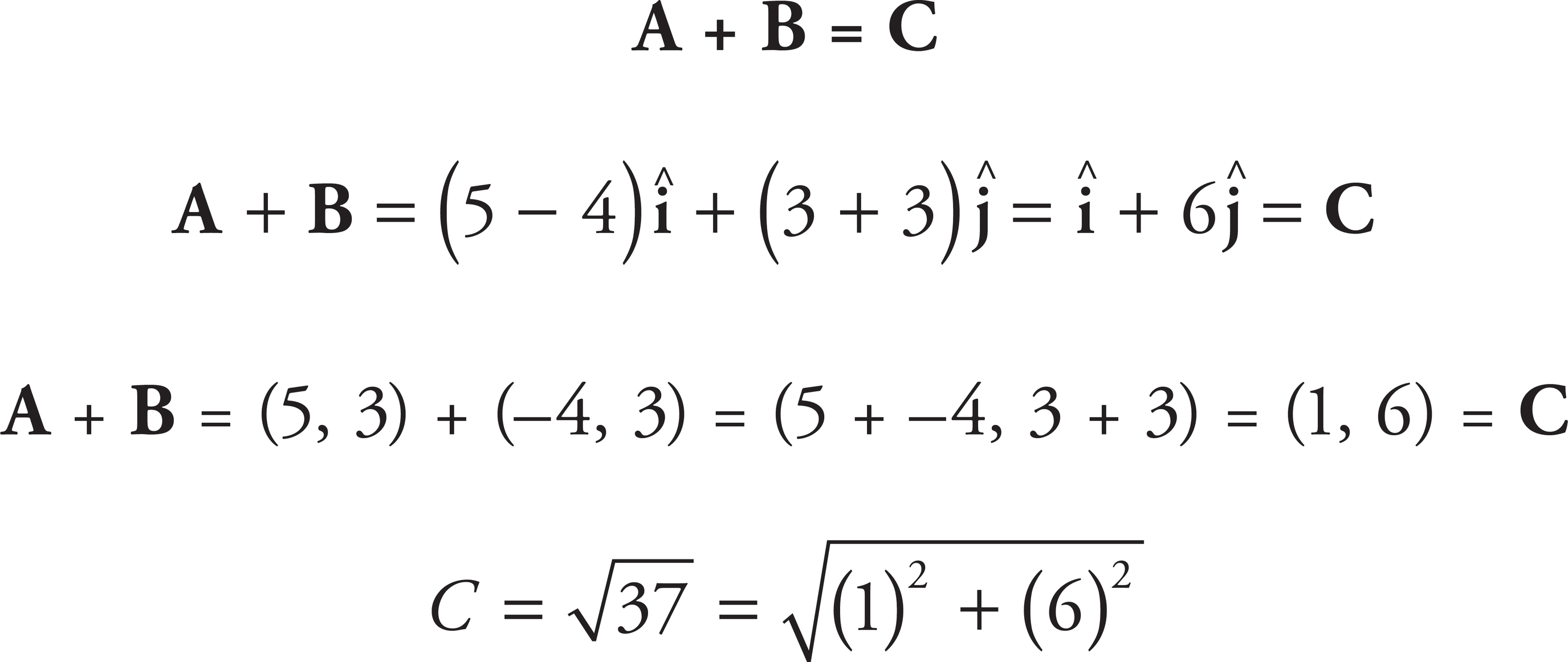
and (C):
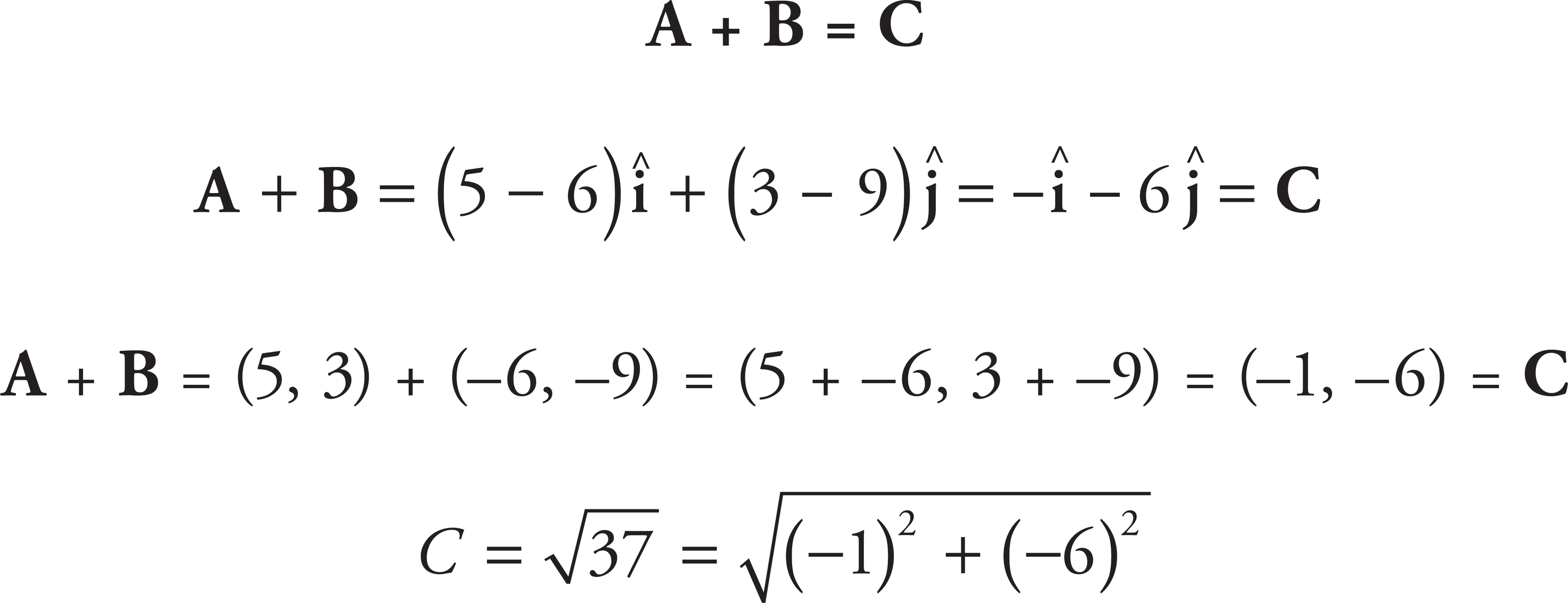
47. B, D
The direction of electric field points away from positive charges and toward negative charges. As a result, the direction of the individual electric fields produced by the two charges at their midpoint is in the same direction. Before any changes, the magnitude of the electric field at the midpoint of the two charges can be calculated as the sum of the two individual electric fields:
To double the magnitude of the electric field at the midpoint, the new electric field at the midpoint would have to have a magnitude of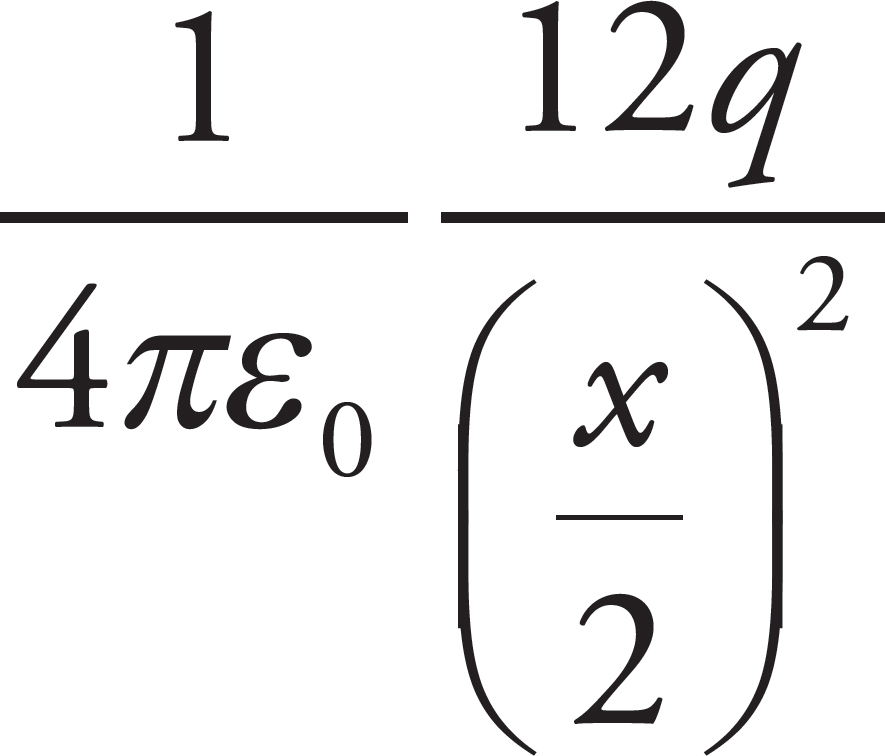 
.
This can be achieved by increasing the magnitude of the charge of q1 by a factor of 2.5:
or by increasing the magnitude of the charge of q2 by a factor of 4:
48. A, D
When springs are connected in parallel as in (A) and (B), the effective spring constant can be calculated with the equation:
keff = k1 + k2
Choice (A) is correct, as keff = k1 + k2 = k + k = 2k.
When springs are connected in series, as in (C) and (D), the effective spring constant can be calculated with the equation:
Choice (D) is correct, as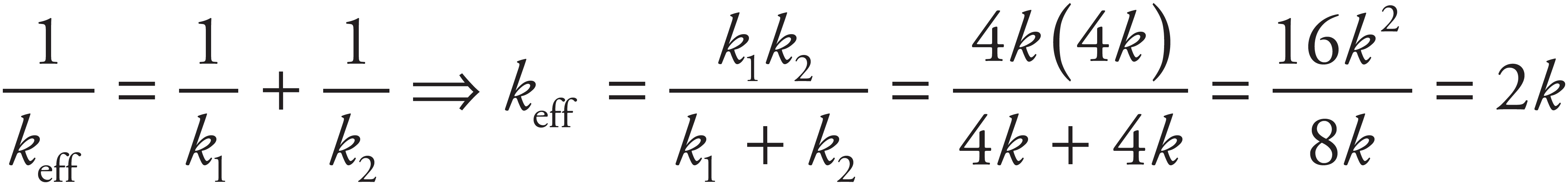 
.
49. B, C
An object is defined to be in translational equilibrium when the sum of the forces acting on it is zero. If the net force on the object is equal to 0, the object’s acceleration is also 0. An object at translational equilibrium can have a nonzero kinetic energy and net torque.
50. B, D
The frequency of the oscillations of a pendulum is given by the equation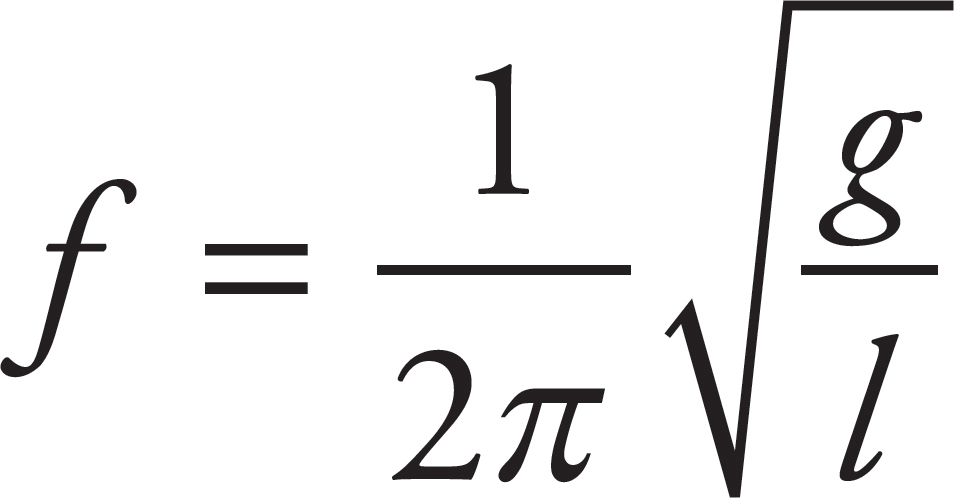 
. Based on this equation, increasing gravitational acceleration and decreasing the length of the pendulum would both increase the frequency of the pendulum.
(a)
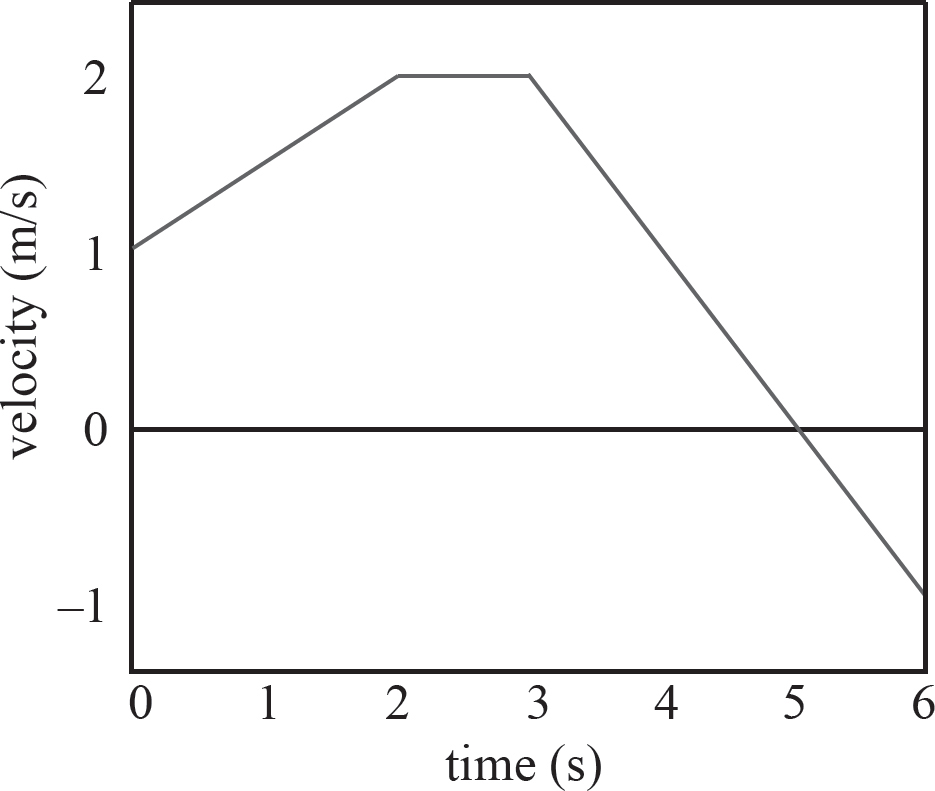
On a velocity-versus-time graph, the displacement is the area between the graph and the x-axis. Area above the x-axis is positive displacement and area below the x-axis is negative displacement. The displacement from time t = 0 s to t = 6 s can be evaluated as
t = 0 s to t = 2 s: (2 s)(1 m/s) + (2 s)(1 m/s) = 3 m
t = 2 s to t = 3 s: (1 s)(2 m/s) = 2 m
t = 3 s to t = 4 s: (1 s)(1 m/s) + (1 s)(1 m/s) = 1.5 m
t = 4 s to t = 5 s: (1 s)(1 m/s) = 0.5 m
t = 5 s to t = 6 s: (1 s)(−1 m/s) = −0.5 m
The total displacement from time t = 2 s to t = 6 s is 3 m + 2 m + 1.5 m + 0.5 m − 0.5 m = 6.5 m.
(b)
The speed of the object is increasing when the magnitude of the velocity is increasing. This occurs from time t = 0 s to t = 2 s and t = 5 s to t = 6 s.
(c)
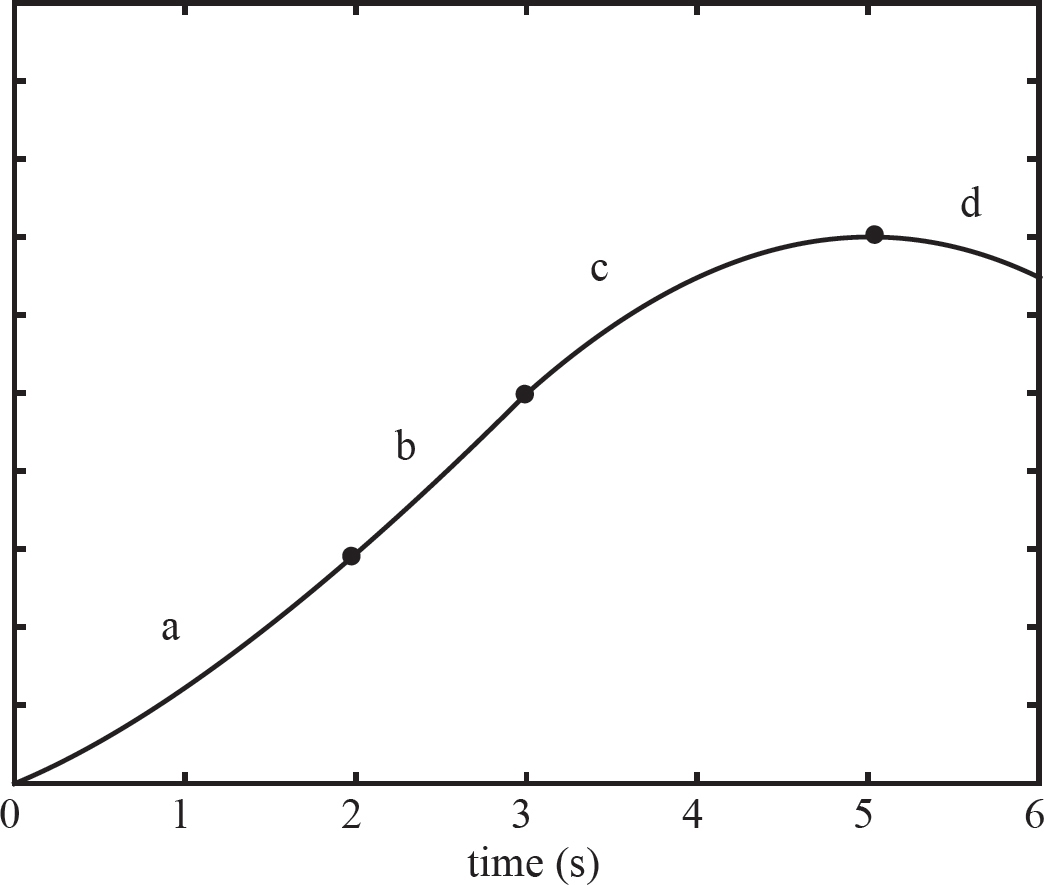
Section a tells you the object is speeding up in the positive direction (parabola with an increasingly steeper slope). Section b tells you the object is traveling with constant speed in the positive direction (linear line). Section c tells you the object is slowing down but still moving in the positive direction (parabola with a decreasingly steeper slope). Section d tells you the object is moving in the negative direction and speeding up (parabola with an increasingly steeper slope).
2. (a)
The forces acting on the small m mass are FT (the tension in the string connecting it to the 3m block), Fw (the weight of the block), FN (the normal force exerted by the inclined plane), and Ff (the force of kinetic friction).
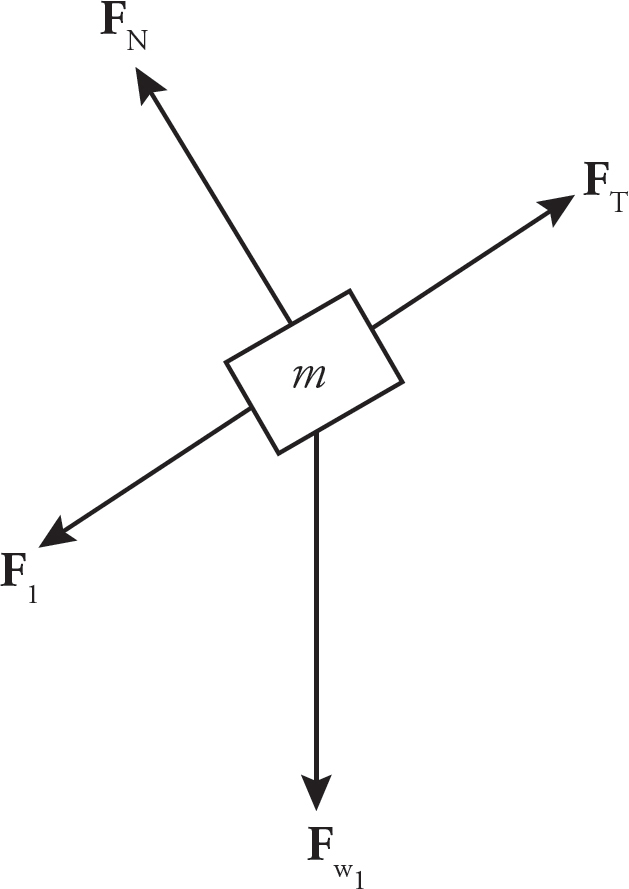
The forces acting on the larger 3m mass are FT (the tension in the string connecting it to the m block) and Fw (the weight of the block).
(b)
Newton’s Second Law applied to the 3m mass yields
Fw2 − FT = 3ma ⇒ 3mg − FT = 3ma
Newton’s Second Law applied to the m yields
FT − Ff − FN = ma ⇒ FT − μk mg cosθ
Adding these two equations together, you find that
(c)
Plugging in g = 10 m/s2, θ = 45°, and µk = 0.3, the acceleration can be calculated as follows:
Apply Big Five #3:
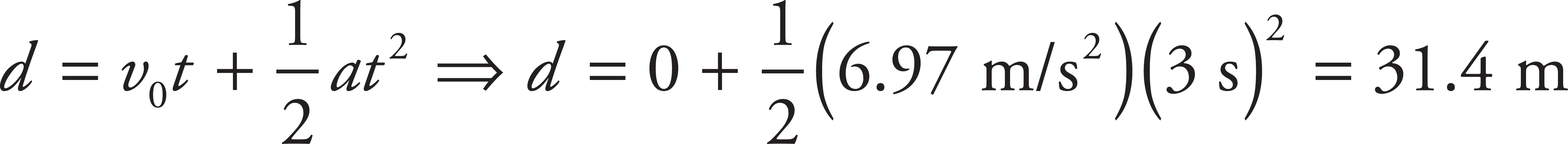
3. (a)
Apply Big Five #2, calling up the positive direction:
v = v0 + at = 80 m/s − 10 m/s2 (8 s) = 0 m/s
This means that the object is motionless at the peak of its trajectory. Since neither the wave’s source nor its detector is moving at this moment, there is no Doppler effect to consider. Therefore, the frequency is still 3 kHz.
(b)
The value of the beat frequency is given by the equation:
fbeat = |f1 − f2| = |3 kHz − 3.6 kHz| = 0.6 kHz or 600 Hz
(c)
The sound wave emitted from the speaker has a spherical wavefront and thus has an intensity proportional to 1/r2. Decreasing the distance between the detector and speaker by a factor of two will quadruple the intensity. As a result, the intensity received by the detector when the speaker is at half of its maximum height is equal to 3.2 × 10−8 W/m2.
4. (a)
First, label some points in the circuit.
There are three branches each with their own current, fabc (I1), cdef (I2), cf (I3). By the Junction Rule, I3 = I1 − I2.
By the Loop Rule, the total change around any closed loop must be zero. You can then write equations for the following loops:
abcfa:
−I1R3 − I1R4 − (I1 − I2)R2 − (I1 − I2)R1 + V1 = 0
cdefc:
V2 + (I1 − I2)R2 + (I1 − I2)R1 = 0
Substitute in the values of R1, R2, R3, R4, V1, and V2 to simplify both equations:
abcfa:
cdefc:
Adding the two equations, you get
Plugging this into the cdefc equation, you get
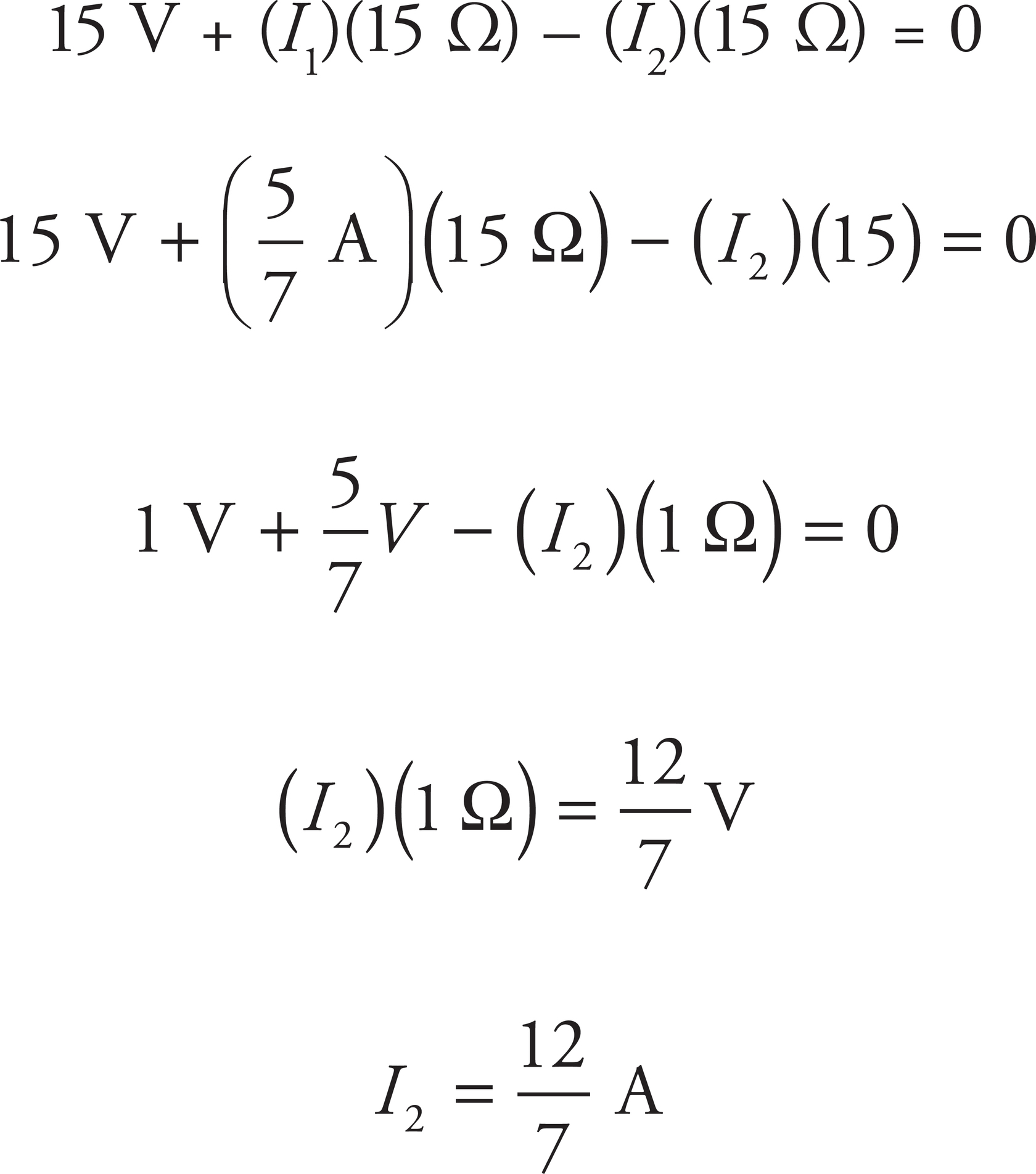
So the current through R3 is 
A and R1 is 
A.
(b)
The rate at which R4 dissipates energy is given by
P = IR2 = A(20 Ω)2 = 285.7 W
(c)
The voltmeter will read the sum of the voltage drops across R3 and R4.
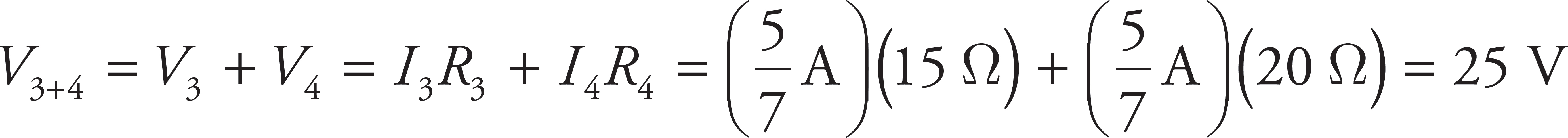
(d)
The voltmeter is connected in parallel with the circuit. To minimize the impact of the voltmeter on the circuit, the voltmeter should have a very high resistance. Consider the following calculation of the total resistance upon addition of the voltmeter:
If Rvoltmeter was very high, the Reff would be very close in value to R3+4:
5. (a)
In order for the objects to roll down the incline, there must be a force providing a torque on the two objects. A free-body diagram shows that there are three forces acting on the spheres: the weight of the sphere, the normal force, and the force of friction. Torque is given by the equation τ = rFsin(θ), where F is the magnitude of the force, r is the radius, and θ is the angle between r and F. As both the normal force and the weight of the sphere have a radius of 0, the torque must be provided by the force of friction.
(b)
As both objects have the same mass, both objects experience the same normal force and force of friction. This means both objects experience the same torque. Torque in terms of rotational inertia is given by the equation τ = Iα, where I is the rotational inertia and α is the angular acceleration. Because the mass of the hollow sphere is distributed farther from the axis that it rotates around, the hollow sphere has a greater rotational inertia than the solid sphere. With a smaller rotational inertia, the solid sphere experiences a greater angular acceleration and reaches the bottom of the inclined plane first.
(c)
As both objects have the same mass and start at the same height (on the top of the inclined plane), they both start with the same amount of potential energy. As both objects also start at rest, they both start with 0 kinetic energy. As the objects reach the bottom of the inclined plane, the potential energy of both objects is converted into kinetic energy. By conservation of energy, both objects have the same kinetic energy at the bottom of the inclined plane.