Chapter 1
Invention in antiquity
Tradition follows Aristotle in identifying the earliest physici as some gentlemen of Miletus, and in specifying half a dozen other Greek speakers as their successors. In this philo-Hellenic creation myth, no Greek physicus learned anything from a barbarian during the 250 years between the times of the eldest Milesian, Thales, and Aristotle. The story that Pythagoras, if he existed, did so partly in Egypt, suggests outside input; and studies of cuneiform texts reveal a natural knowledge among the Babylonians in some ways more advanced than that of the ancient Greeks. Still, the essential criterion that Aristotle used to identify his predecessors was not that they were Greek, but that they had conquered a paralysing prejudice. Despite robust contrary evidence, they believed that the natural world runs on law-like principles discoverable by the human mind and immune from interruption or cancellation by meddling gods and demons.
This bold departure underlies and circumscribes all forms of physica, natural philosophy, and physics. Its implications go farther even than replacing caprice by law-like behaviour. Since the gods displayed all too faithfully the behaviour of human beings, de-deifying implied (to speak Greek) de-anthropomorphizing. The progress of physics has continued to remove human quirks and qualities projected onto nature. Thus nature, or the objective world, came to lose not only benevolence, malevolence, and colour, but also such apparently indispensable attributes as space, time, and causality.
Of the four main schools of ancient philosophy, Aristotle’s paid greatest attention to physica (see Figure 1). Having a particular interest in zoology, he derived his fundamental principles with an eye to the classification of animals. Because of his emphasis on physica and because his philosophy dominated during the Middle Ages and beyond, convenience advises taking it as normative. In antiquity, however, it had to compete with Platonic, Epicurean, and Stoic philosophies. Typically, a school’s premises, library, and other assets passed from the founder to his senior disciples, and, perhaps consequently, the schools bore names suggestive more of real estate than of scholarship: the Academy (Grove) for the Platonists; Lyceum (a shrine) and Parapatos (a place for walking) for the Aristotelians; the Stoa (Porch) for the Stoics; and the Garden of Epicurus.

1. School of Athens. Raphael’s evocation of the intellectual vigor, diversity, and discursiveness of Greek Science.
During the 800 years from the founding of the Academy in Athens and its refounding in Alexandria, the four schools underwent many reversals of fortune. When operating normally, they were forums for free discussion of the sort practiced in political circles, but centred on studies pursued for personal improvement rather than for civic or financial advancement. Some students stayed with a single school for decades, others sampled each in turn. When Romans like Cicero frequented the schools of Athens they took advantage of this Lernfreiheit. The Pythagoreans did not form such a school, as they did not tolerate deviations from their doctrines and way of life.
Physica
Although physica ran from astronomy through zoology to psychology, limitation of coverage to cosmology and cosmogony, as in this book, is not unacceptably anachronistic, provided we recognize that the same principles of structure and change applied to all natural processes. This truncated physica corresponds to the books of Aristotle dealing with general principles (Physica), the heavens (De caelo), the region between the Moon and the Earth (Meteorologica), and the creation and destruction of things on or in the Earth (De generatione et corruptione). These books (and the rest of the corpus from logic to ethics) became available in a standard format edited around 60 bce from the lecture notes Aristotle bequeathed to his successors. They constitute the main parts of a theory of everything, or, as the moderns say, a TOE.
The first TOEs Aristotle stepped on belonged to the Milesian monists. He then took on more generous materialists: Leucippus and Democritus, who allowed two principles—atoms and the void; Empedocles, who accepted the three Milesian elements (water, air, fire) and added earth to complete the tetrad; and Anaxagoras, who admitted an infinite number of different sorts of stuff. There were also those whose matter had no stuff at all—Pythagoras notably, for whom number had an independent existence. The Pythagoreans’ deduction that there must be a counter-Earth circulating opposite ours around a central fire (to raise the number of heavenly bodies to the holy tetractys) proved to Aristotle both the falsity of their physica and the nonsense to which numbers can lead.
Aristotle’s teacher, Plato, inclined towards numerology. He took as his material not only mathematical abstractions but also supersensible idealizations of classes of objects: for example, the Idea ‘Horse’, in which individual horses ‘participate’ more or less, but always imperfectly. Consequently, although Plato was optimistic about the possibility of knowing the ideal world, and the supreme Good that made the Ideas and their relations intelligible, he did not allow the possibility of true knowledge of the things of this world. Since no material individual could express an Idea perfectly, our physica can never be other than fuzzy.
Physica comes from ‘physis’ meaning ‘nature’, which, according to Aristotle, ‘is the source or cause of being moved or being at rest’. What makes things move? The early physici adumbrated four causes of change that Aristotle later codified. The monists and the atomists considered only the material cause. Empedocles and Anaxagoras provided action by taking some principles to be active and others passive—vague glimpses of efficient causes. Others saw the need to explain order in a universe of change, and hinted at a teleological or final cause, such as set by a cosmic Mind. And Plato supplied a fourth cause, the formal, the Idea in which a thing participates.
Aristotle’s inventory of the cosmological ideas of his predecessors, including anticipations of the four causes of change, was not an idle retrospective. It confirmed that he had not overlooked anything fundamental. ‘Of all who have discussed principles and causes none has spoken of any kind except those which have been distinguished in [my] discourses on Physics’. Aristotle’s TOE, thus established as complete, makes use of some special concepts. A substance is any individual thing. The collection of its properties constitutes its form, which, contrary to a Platonic Idea, occurs only in union with matter. Form can be divided, although only mentally, into essence, which makes a substance the sort of thing it is, and accidents, which can change without causing the substance to alter its essence or kind. The essences of the four elements are easily stated: fire is dry, hot, and absolutely light; air is hot, moist, and relatively light; water is cold, moist, and relatively heavy; earth is cold, dry, and absolutely heavy. The elements can transform into one another, as fire evaporates water into air. Socrates may be warm or cold, but heated or cooled too much he will cease to be Socrates.
It may now be intelligible to state that a substance’s matter and essence are its material and formal causes, and that the active qualities of hotness and moistness are the principal efficient causes of change. The final cause is the purpose for the existence of a form. Heavy bodies have gravity so as to fall towards the centre of the world, and light bodies have levity so as to rise towards the heavens, thus restoring order disrupted by the activity of animate creatures or the revolutions of the celestial spheres. These spheres and the stars and planets they carry cannot be made of the four elements, whose forms require that they move when unimpeded in a straight line towards or away from the world’s centre. A fifth element, a quintessence, obeying its formal and final causes, circulates around the universal centre. With these few principles and some ad hoc adjustments, Aristotle worked his way from the Mind of the Unmoved Mover, which, as it can think only of the most sublime thing, can think only of itself, down to the mind of man, which, though no less self-centred than the Mind of the Universe, is changeable like everything else below the quintessential heavens. And where there is change, there cannot be certainty; the best a physicus can do is to find a ‘rule [that] applies to what is always true or true for the most part’.
A few deductions from Aristotle’s approximate physica that came under sustained scrutiny will give some impression of its general character. Every motion, whether change of place or colour or species, requires an external mover. In a vacuum there literally is no place (no reference material) by which a body can orient itself; hence, there can be no vacuum. The flight of an arrow implies a vortex in the air, which cedes a place to the tip while pushing in at the tail. The ambiguous role of the air, offering both resistance and propulsion, made an obvious difficulty. Another awkwardness arose from the absolute dichotomy between terrestrial and celestial physics. Because the heavens cannot change, transient phenomena that appear to take place there, like comets and meteors, must have their seat with lightning and the weather in sublunar regions.
Nothing, however, is more obvious than that the Sun influences the weather. How? Sometimes Aristotle wrote as if he thought that the Sun was hot, which would violate his proscription against terrestrial qualities in heaven. More often, he ascribed the seasonal powers of the Sun to its annual revolution, which, together with the rolling of the quintessential spheres, continually stirs up the sublunary regions. These disturbances cause moist and dry vapours to rise from the Earth. Precipitation results from the moist exhalation, winds from the dry. ‘The same stuff is wind on the earth, and earthquakes under it, and in the clouds thunder’. Lightning and thunder are dry exhalations breaking free from the clouds. The rainbow is a reflection from the clouds. Aristotle uncharacteristically described it geometrically: the Sun, the eye of the observer, and the centre of the bow lie on a straight line that cannot exceed a certain angle with the horizon. This factoid would have a long and influential history.
Despite the continuing operation of final causes, the world is not in perfect order. The frictional drag of the turning lunar sphere on the stationary region of fire below it produces such anomalies as fiery meteors in the air, mountains above sea level, and water below earth. In the big picture, however, the universe resembles an onion. Peeled from the outside in, it discloses the fixed stars, the planets and luminaries in the conventional order Saturn, Jupiter, Mars, Sun, Venus, Mercury, and Moon, and, in slight disorder, the elements fire, air, water, and earth. What is outside the skin? Here the onion analogy fails. There is literally nothing there. And just as there is no space not included in the visible universe, there was no time at which it did not exist.
Aristotle’s world picture thus lacked a creator. So did the atomic theory of Democritus, who, nevertheless, offered a creation story for the visible universe. It began to be when some atoms bouncing about in the infinite void chanced to form a great vortex. The largest fell to the centre, forming the Earth. From what remained, centrifugation produced the air, the luminaries, the planets, and the stars. Although the same dull stuff makes up everything, our sensory systems can build rich images from its few properties—the size, shape, and motion of its constituent atoms. Epicurus added a spontaneous ‘swerve’ to explain how atoms, falling in parallel through the void, occasionally collide and concatenate a world. According to him, the soul can exploit the swerve to choose to live the good life in an otherwise pointless universe. Since the Epicurean did not have to fear gods in this life or anything in the next, he could take moderate enjoyment of the flesh and free employment of the mind as the greatest goods. The inevitable erosion of all sound doctrine has transformed Epicurus’ sober happiness into selfish hedonism.
Whereas the atomists allowed for the creation of many worlds in space and time by random accretion of their parts, the Stoics supposed that the single cosmos they admitted, geocentric like Aristotle’s, is alternately destroyed and recreated. In place of disparate atoms, the Stoics put a continuous prime matter; and in place of bumps and grinds, ‘pneuma’, a self-moving elastic compound of fire and air that gives matter its cohesive and other properties. Strict causality applies everywhere, guaranteed and effected by the spatial continuity of the pneuma. The system would seem to rule out free will decisively. But since ethics required a free acceptance of fate and the mental preparation necessary to meet it, Stoics had to find a way around the strict causality of their physics. Their solution was no more plausible than the Epicurean swerve. As an alternative to strict atomism, however, the Stoic concept of a space-filling, active, elastic spirit had a future.
In contrast to the Peripatetics with their unchanging, uncreated cosmos, and the atomists and Stoics with their random and cyclical worlds, the Academics had a full cosmogony, with a creator as well as a creation story. As told by Plato’s mouthpiece, the mathematician Timaeus of Locris, the Demiurge who made the realm of Ideas used what he had left after rolling out the celestial equator and the paths of the planets to manufacture human souls. These he sent to stars in the realm of Ideas to await planting in bodies created by the lesser gods to whom he assigned the task of making the sensible world. At the end of life, the rational soul returns to its star if its human possessor has lived a good life; if not, the soul reincarnates in a lesser being. Our animal parts serve merely to keep our head, the seat of our reason, from rolling around on the ground.
Used properly, our rational soul can bring us via observation of the motions of the heavenly bodies to the discovery of number, time, and harmony, and to the contemplation of the Ideas. We might then perceive that the Ideas of the four elements and the quintessence are linked to the mathematics of the five regular solids. The plane faces of three of them (the tetra, octa, and icosahedron) are equilateral triangles, and consequently the elements corresponding to them (fire, air, and water) are interconvertible (see Figure 2). The remaining two, the cube and the dodecahedron, are the ‘Ideas’ of the Earth and the universe as a whole. We should not press the obvious difficulties. The lesser gods who created the material world were not entirely competent. ‘[I]t is fitting that we should, in these matters, accept the likely story and look for nothing further’.
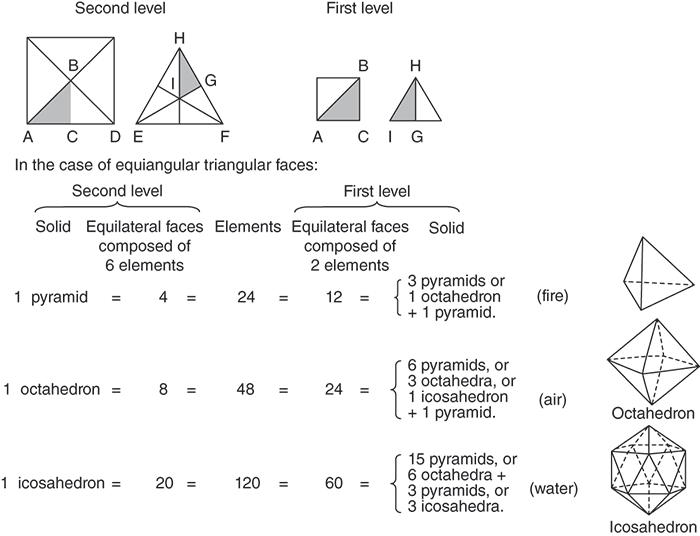
2. Geometrical foundations of the world. The faces of the cube come in aggregates of elementary isosceles right triangles ACB; those of the pyramid, octahedron, and icosahedron come in aggregates of various sizes of elementary 30-60-90 degree triangles IGH. The diagram shows how the second level aggregates from the first and, in the case of the three solids with equilateral triangles as faces, how the solids can transform into one another.
Roman worlds
Although foreign students from Rome added little of note to Greek physica, they turned much of it into useful summaries and compendia. During the last years of the Republic, Lucretius versified Epicurus’ atomism. During the reign of Caesar Augustus, the poet Ovid made a conspicuous place for Pythagoreanism in his Metamorphoses. Under the Emperor Nero, Seneca composed a meteorology on Stoic principles—cut short, unfortunately, by Nero’s invitation (which Seneca could scarcely refuse) to commit suicide. And in the years before his fatal inspection of Vesuvius during its eruption of 79 ce, Pliny the Elder crammed into one of the thirty-seven books of his Natural History a qualitative survey of the world featuring a God unpolluted by commerce with human beings; a naturalistic account of meteors, comets, and eclipses calculated to free humankind from fear of lesser gods; some hints at atomism and stoicism (physica of chance and necessity); and a few bars from Pythagorean music of the spheres.
Lucretius begins his poem with the customary invocation of a muse, in this case Venus, after which he disobligingly announces that his great purpose is to remove her and all the other gods from human concerns. The atoms cavorting in the infinite void follow the laws of necessity apart from the occasional unintelligible swerve that gives spontaneity to the world and freedom to the will. No external agency can interfere with this process. Though thou be nothing but a chance congeries of buzzing particles, be joyful, submit to fate, and fear not the impotent gods.
The exposition of Pythagorean doctrine that Ovid jams into his catalogue of beings that transform into beasts treats only briefly the founder’s physica, his teachings about
The great world’s origin, the cause of things | what nature is, what god, and whence the snow | what makes the lightning, whether thunder comes | from Jove or from the winds when clouds burst wide | why the earth quakes, what ordnance controls | the courses of the stars.
Most of Ovid’s account of Pythagorean thought concerns metempsychosis and vegetarianism, a belief and a practice indissolubly connected. If souls transmigrate, how can you tell whether your ox, your faithful brother at the plow, was not in fact your late brother?
This sound teaching fell on deaf ears. Ovid admitted as much; Seneca, writing half a century later, reported that would-be Pythagoreans could not find a teacher. But that, according to Seneca, merely mirrored the sad state to which philosophy in general had fallen: ‘Many philosophical lineages are dying out without a successor.’ His Natural Questions, an attempt to reinvigorate Stoic physica, reconstructed the meteorology of the Stoa and the Lyceum to answer the questions whose solution Ovid credited to Pythagoras—the causes of the wind and weather, thunder and lightning, and earthquakes. These had been standard problems in physica since the time of Thales. In Seneca’s meteorology, high winds, thunder, and earthquakes are explosions of previously constrained pneuma. Breaking from Stoic authority, he enrolled comets, famous for bad reputations, among the planets and toyed with the possibility that their daily motions, and those of the stars in general, arise from a revolution of the Earth rather than from the turning of the celestial vault. As his placement of comets suggests, the interconnectedness of the Stoics’ space-filling active pneuma destroyed the barrier between the heavens and the Earth characteristic of Aristotelian cosmology.
Seneca puffed up his meteorology with moral reflections that appear to be its reason and result. If you do not enquire into the material foundation of the world and the nature of its creator or guardian, or speculate whether he still creates (if he ever did) or has retired, whether he thinks only of himself, and whether he can amend fate, you enslave yourself to merely human affairs. Life would not be worth its pain and suffering were it not for the opportunity to learn that nature, fate, the world, providence, and God are different names for the same thing; that God did not make the world exclusively for human beings; that life is a sentence of death and philosophy, by dispelling fear of death, is the only healthy way to resign oneself to fate. Seneca’s eloquent combination of moralizing and meteorology made the Natural Questions the authority on the physical problems it treated for most of the Latin Middle Ages.
Had Plutarch’s dialogue on the markings on the Moon not suffered an eclipse of fifteen centuries, Seneca’s stoicism would have faced a sprightly challenge in medieval times. Plutarch proposed a question that embarrassed several ancient systems: why do we not see the Sun’s image on the Moon as we see it on the sea? Since the answer depends on knowledge of the Moon’s makeup, mathematicians could not answer it. What then did the physici have to say? The mottled lunar surface shows that the Peripatetic model of the Moon as pure quintessence is nonsense. The Stoic view—that it is made of a sort of pneuma—is worse, since air and fire cannot reflect visual rays. Plato’s model, which gives the Moon a rocky surface that acts as if composed of a great many randomly oriented mirrors, is the best option.
What then keeps the rocky Moon from falling on the Earth? ‘[T]he rapidity of its revolution, just as missiles placed in slings are kept from falling by being whirled around in a circle’. What keeps it close to Earth? A literal law of nature: ‘the position of earth lays an action against the Moon and she is legally assignable by right of propinquity and kinship to the earth’s real and personal property’. Is the Moon inhabited? Very likely, but by creatures as different from us as we are from fish, and also by disembodied souls awaiting their next incarnation. Plutarch’s ideas about the Moon, minus his metempsychosis, recur in Galileo and Kepler.
During the philosophical downturn mentioned by Seneca, the Platonic Academy did not exist. It had come to a temporary end during the Roman conquest of Athens in 86 bce after a period of intense scepticism about the possibility of achieving any secure knowledge about anything. It revived in 410 ce with a curriculum based on ‘Neoplatonism’, invented in Rome by Plotinus, who died in 270 ce, and systematized by his disciple, Porphyry. Plotinus was not a sceptic. His confident speculations rose above even the Demiurge, whose employment as creator, even if only of the rational realm and the lesser gods, seemed to him incompatible with occupying the acme of the divine pyramid. How did the Demiurge relate to the impassable God or Good that Plato had put in charge of everything? Plotinus answered that God stands immovable at the head of a chain of created and creating ‘emanations’. The first of these emanations, Intellect, contains the Ideas; the second, Soul, contains Nature; the next is the Demiurge. Plato had not supplied much information about the natural world created by the Demiurge’s collaborators, and his thesis that we cannot know such things in principle inhibited elaboration of Timaeus’ hints about polyhedra. So Neoplatonism grafted on Aristotle’s physica as its account of the visible universe created by the demigods employed by the Demiurge.
Another conflation assimilated the top Neoplatonic powers—the One, the Intellect, and the World Soul—with the Christian Trinity. In orthodox Christianity, God did not employ a vicar in his creative works. But several Christian sects still competitive in the 4th century taught that God the Father created only spiritual beings, one of whom, Jehovah, broke the chain of spiritual emanations and materialized his successors. Neoplatonism was the leading philosophy, and its co-inventor Porphyry the most effective critic, of Christianity during the late empire. His opponents, the architects of Christianity concerned to achieve standardization of belief, faced the challenges of harmonizing discrepancies among the four canonical gospels, explaining evil in the creation of a beneficent deity, and defining the relationships among the Persons of the Trinity. The most abstruse of their conundrums probably could not have been concocted without the language and concepts of Aristotelian physica and Neoplatonic philosophy.
Applications
The speculations of Physici were less useful to princes than the advice of applied mathematicians. The greatest of them all, Archimedes, worked for a tyrant of Syracuse. Although best known now for his detection of a counterfeit crown and his legendary feats in defence of Syracuse, Archimedes preferred to be remembered in the manner of a physicus, as a liberal artist. According to Plutarch, he regarded his practical accomplishments as ‘mere accessories of geometry practiced for amusement’ and ‘every act that ministers to the needs of life as ignoble and vulgar’. Plutarch added that Plato had chastised two clever mathematicians, Eudoxus and Archytas, for turning their hands to practical things, and becoming ‘corruptors and destroyers of the pure excellence of geometry’.
In contrast to the many useful applications of geometry, physica could do little more for the practical man than veneer him. Vitruvius recommends in his Ten Books of Architecture, which dates from the early Roman Empire, that the student learn physica to be able to judge excellence, to achieve authority, and to grow ‘courteous, just, and honest’. More obviously, knowledge of ‘the principles of physics [as taught] in philosophy’ was needed for constructing waterworks; of the principles of musical intervals, for tuning catapults; of astronomy, for choosing sites for buildings; of meteorology, for avoiding places exposed to winds, lightning, and earthquakes. None of this related to the main business of construction, and for good reason. Physica knew nothing about the strength of materials. When it came to foundations, Vitruvius could only advise to ‘dig down …as deep as the magnitude of the proposed work seems to require’.
A more lasting application of physical principles occurs in the writings of Ptolemy of Alexandria. He distinguished his astronomy, enshrined in the thirteen books of his Syntaxis mathematica or Almagest (as it is usually named after its Arabic translation), from his four books of astrological interpretation, the Tetrabiblos. The Almagest considers planets only as moving points; the Tetrabiblos ascribes to them the active elemental qualities that bring their influence down to Earth. The planets are warm, moist, cold, and dry in different degrees depending upon their distances from warm Sun, moist Moon, and cold and dry Earth. Judged by temperature and humidity, Jupiter, Venus, and Moon are beneficent; Mars and Saturn evildoers; and Sun and Mercury ambiguous. From this astrophysics, Ptolemy derived a physical anthropology that explained why Ethiopians are black; Scythians white; inhabitants of the temperate region medium in colour, civilized, and sagacious; and himself mathematical.
Although the astrophysics of the Tetrabiblos admitted earthly qualities into the celestial regions, Ptolemy’s astronomy revolved in the quintessence of the Aristotelian universe. According to Aristotelian celestial mechanics, each planet and luminary travels on a sphere concentric with the Earth. But none of the Peripatetics, including that Eudoxus whom Plato criticized for doing carpentry instead of geometry, could ‘save the phenomena’ consistently with the concentric principle. The obvious explanation of the notable alterations in brightness of the Moon and the planets is their changing distance from Earth. So mathematicians dismissed Aristotle’s spheres in favour of non-concentric circles on which to mount celestial objects.
Ptolemy’s Almagest saves the phenomena by displacing Earth from the centre of the Sun’s circular orbit, thus representing phenomena arising from the ellipticity of Earth’s orbit as an effect of perspective (see Figure 3a). Moon and planets likewise require circles (‘eccentrics’) with centres displaced, though in different directions and magnitudes, from Earth’s. They also require a second circle (‘epicycle’) to model the effects of Earth’s revolution around the Sun, during which a ‘superior’ planet (Mars, Jupiter, or Saturn) appears to reverse directions periodically in its orbit around Earth (see Figure 3b). A splendid refinement, mimicking the effects of ellipticity almost perfectly, made the centre of the epicycle rotate with constant velocity around an ‘equant’ point placed as far on one side of the centre of the eccentric as the Earth was on the other (see Figure 3c).
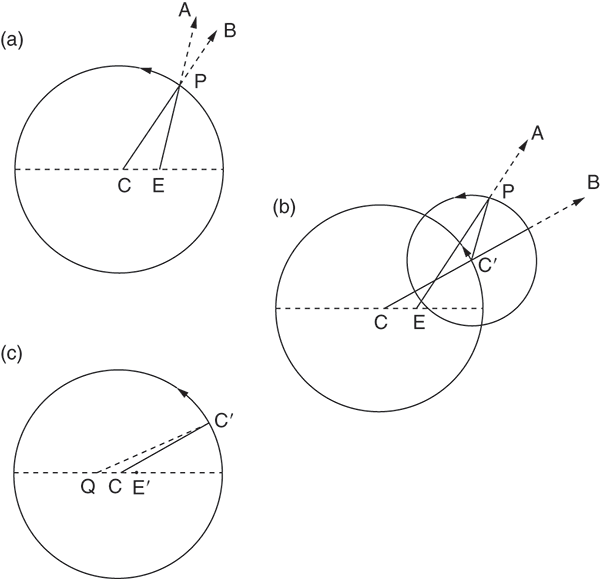
3. Ptolemaic bric-a-brac. (a) Saving the first anomaly: P, the planet orbiting at constant velocity on a circle centered at C (‘the eccentric’); EA, CB, directions of P as seen from E and C, respectively. (b) Saving the second anomaly: C′, the center of P’s epicycle, moves cc (counterclockwise) on eccentric C as P moves cc around it, both motions at constant velocity. (c) The equant: C′ moves cc with constant velocity around Q (‘the equant point’) where QC = CE′ = CE/2.
This brilliant, complex bric-a-brac violated good physics by postulating revolutions around unoccupied points without giving any physical reason for their position or motion. They were fictions introduced for description, not explanation. Ptolemy was not content with the division of labour by which physici aimed at the truth about substance and mathematicians at description of its accidents. Reversing the usual precedence, he declared the priority of mathematics over physics in the Almagest and exemplified it in the astrophysics of his Hypotheses of the Planets. Here he made the Sun run in a groove between two concentric spheres whose common centre is offset from the centre of the Earth. Each superior planet rides on a marble (a reified epicycle) running in a similar groove between another pair of eccentric spheres. Accepting the Aristotelian (and Stoic) prohibition of a vacuum, Ptolemy close-packed his system so that the apogee of one celestial body coincides with the perigee of the next, and the greatest distance of Saturn lies in the vault of the stars. Knowing from eclipse observations the average lunar distance in terms of the Earth’s radius r and, from his astronomical calculations, the ratios of the radii of the epicycles and eccentrics of each planet in his close-packed system, Ptolemy worked out the distance to the stars to be just shy of 20,000r.
This number, though vastly less than the true radius of Saturn’s orbit, was large enough to suggest the insignificance of humankind, especially when expressed in miles. Eratosthenes of Cyrene, one-time head of the Library of Alexandria, converted r to human measure by determining the angle α between the vertical and the direction of the Sun’s rays at Alexandria at noon at the same instant that it stood overhead at Aswan, 5,000 stadia due south. Since α equals the difference in latitude between the two places, Eratosthenes could calculate, from 2πr:5,000 = 360°:α, that r ≈ 4,000 miles (see Chapter 2, Figure 8). The radius of the visible world would then be eighty million miles. These numbers were scarcely bettered before the 17th century.
Among other enduring pieces of mixed mathematics from the Hellenistic period are Archimedes’ demonstration of the law of the balance, his hydrostatics with its associated concept of specific gravity, an anonymous treatise on mechanics incorrectly attributed to Aristotle, and parts of texts on optics by Euclid and Ptolemy. The optical works, although mainly geometry, presuppose at least three physical principles of interest: the rays responsible for vision originate from the eye, change direction abruptly at the surface between media of different density, and take the shortest path between eye and object. Thus the angles of incidence and reflection are equal. A treatise perhaps written by Ptolemy offers measurements of the breaking of visual rays when they strike an air–water surface. The method gave results that differ insignificantly from Snell’s law for angles of incidence up to 40°. The Ptolemaic author observed that refraction must also occur at the boundary between air and ether (or fire or quintessence) and, although he could not calculate the amount, rightly stated that the effect makes celestial objects near the horizon look higher in the sky than they are.
The pseudo-Aristotelian Mechanica exceeds the scope of physica in being addressed to mechanical problems. But it begins with some physics talk about the paradoxical marvels of circular motion. In a spinning wheel, the highest point moves forward and downward as the lowest point moves backward and upward; and the rim, though larger than the hub, moves faster. Pseudo-Aristotle explains that the shorter the spoke, the closer its extremity to the stationary centre. By an assumed principle of continuity, the proximity inhibits the motion. On the principle that longer radii are moved more easily through a given angle than shorter ones, the author delivers the law of the lever and deftly applies it to oars, rudders, sails, wheels, pulleys, capstans, wedges, tooth extractors, and nutcrackers. From the nutcracker he proceeds to the headcracker later known as ‘Aristotle’s wheel’. Two circles fixed together concentrically roll horizontally. Although the larger lays down a longer path than the smaller, they stay together. Why? ‘It is strange …and wonderful’. The wonder rolled all the way to Galileo, who took many hints and problems from the Mechanica believing that they came from Aristotle.
Ancient applications of what today would be deemed engineering physics included the hydraulics of the magnificent system of aqueducts, tunnels, and fountains that supplied Rome’s water. ‘There was never any desseine in the whole world enterprised and effected, more admirable than this’, so said Pliny, the expert on marvels. The ancients also knew of the suction pump and waterwheel but made little use of either. Perhaps the best known of their waterworks apart from aqueducts push water around for theatrical effects. The greatest impresario in this line, the military engineer, Hero of Alexandria, opened his treatise on ingenious devices with proofs that air is corporeal and that, in union with the other elements and principles, it could amaze the most jaded. For example, concealed hollow tubes running inside a wine-filled altar brought wine to the altar when a fire was kindled on it. Another mechanism allowed the sacred fire to open temple doors (see Figure 4). Such games did not lead to steam engines.
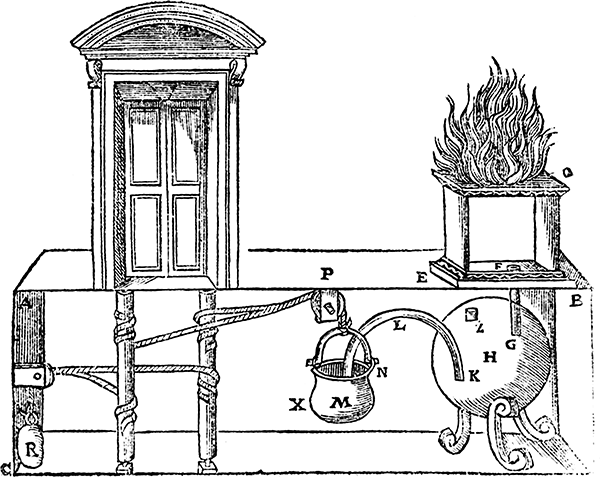
4. Sabbath machinery. Air heated by the fire on the altar pushes water and steam from the vessel H into the pot M, which, in descending, pulls ropes that cause the axles they encircle to rotate and open the temple door.
Dumbing down
Owing to lack of interest, disturbances, or the rise of Christianity, Latin speakers gradually ceased frequenting Greek schools and cultivated Greek slaves, who taught their owners their language, became scarce. Knowledge of Greek, and the copying of Greek texts, dwindled, to arrive functionally at zero by the time the Ostrogoth Theodoric became King of Italy in 493. Curiously, Theodoric knew more Greek than his learned Latin subjects, having been reared as a hostage in Byzantium.
Christian education beyond the Latin schools that taught skills useful to orators and bureaucrats was haphazard and, in the higher reaches of biblical interpretation, Christians were largely self-taught. That might help account for the breadth of opinion, and frequency of heresy, among the early self-made theologians. Many of them conveyed snippets of the physica they knew in their Bible commentaries, particularly on the six days of creation (Hexaemeron). Unfortunately, Augustine’s call in his De Doctrina Christiana for a dictionary of ancient science to assist understanding of Scripture met with only partial success.
Lacking such a text in the 5th century, Latin admirers of physica resorted to the many compendia copied or composed during the time of troubles. Of first importance was Pliny’s Natural History. Drawing on him and others, Macrobius Theodosius, perhaps a Greek-speaker in Theodoric’s service, sugarcoated the liberal arts in a Commentary on the Dream of Scipio that would suit the taste of the Middle Ages. In this dream, Cicero describes a visit of the deceased Scipio Africanus, the scourge of Carthage, to Scipio’s grandson. Africanus reports that the souls of true statesmen dwell in the Milky Way between incarnations, and he transports young Scipio there to compare the vastness of the heavens and their harmonious revolutions with the pettiness and discord of the greatest terrestrial empires.
Proceeding downwards from the soul emporium of the Milky Way, Macrobius defines the usual reference circles of astronomers (equator, ecliptic, and so on), describes the apparent motions of Sun, Moon, and planets; and surveys Earth’s five climes, impenetrable torrid zone, and surrounding ocean. Earth is so small a speck compared with the heavens that the pressure of the surrounding air easily sustains it in the world’s centre. Thus suspended, its inhabitants can descry that the Demiurge gave the planets and luminaries distances and periods keyed to the intervals Pythagoras had discovered by plucking lute strings on Earth. If Macrobius knew that these intervals differed altogether from the planetary parameters calculated by Ptolemy, the discrepancy did not bother him. He referred quantitative details to people ‘disengaged from serious matters’.
While descending from the Milky Way to its temporary abode on Earth, the pure soul acquires reason from Saturn’s sphere, power to act from Jupiter’s, boldness from Mars’, sense perception and imagination from the Sun’s, passion from Venus’, speech and analytical capacity from Mercury’s, and, from the Moon’s, the ability to perform the physical functions incident to life among the dregs of creation. Macrobius conveys much interesting misinformation in describing this journey: for example, that the planets shine by their own light, the Earth does not reflect sunlight, and Venus and Mercury lie between the Sun and Mars. Giving Plotinus as his authority, Macrobius makes the planets and luminaries merely the signs, not the movers, of future events.
Macrobius’ blend of physica, Neoplatonism, numerology, metempsychosis, moralizing, and misinformation was not the only vehicle of transmission of ancient texts produced by high-level civil servants (if such he was) at the court of Theodoric. Theodoric’s chief advisor, the Catholic Boethius, knew Greek. Concerned that his employer’s friends and enemies threatened the survival of philosophy, he undertook to translate all of Aristotle’s works. He began with the Organon (Aristotle’s logical treatises), which, being useful in religious controversy, served as a Trojan horse for the rest of Peripatetic philosophy. Boethius did not complete much of his project, however, before Theodoric, believing him a traitor, had him killed. While awaiting execution, Boethius wrote his famous Consolations of Philosophy grounded on a Christian Neoplatonic world view that supported his Stoic resolve. Together with his Consolations and Aristotle’s logic, Boethius bequeathed to medieval letters a short tract on music, which covered the terrestrial and celestial types, and the harmony of the soul. His successor as Theodoric’s minister was a lawyer, Cassiodorus, who also laboured to preserve ancient learning for Christians. He set up a monastery for whose inmates he rendered the seven liberal arts in a manner suitable to Christians struggling to preserve some remnants of Roman culture in an increasingly barbarous world.
The most popular rendition of the seven liberal arts bequeathed to the Latin Middle Ages was a work of the 5th century, the Wedding of Mercury and Philology. Its author, Martianus Capella, set forth what little he knew about the liberal arts in lectures by philology’s bridesmaids. Much of what they say is unintelligible. Thus Astronomy, having stepped from her ball of heavenly light, declared that during the 40,000 years she spent in Egypt studying her subject she learned that celestial natures, ‘circling by their own surging, are diffused the entire way around in globular belts and circles’. After this venture into physica she described the apparent motions of the planets and luminaries, defined the equator and zodiac, tried to explain how to measure the Earth, climbed back into her ball, and, like the antiquity she represented, flew away.