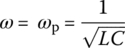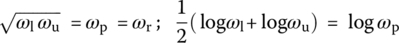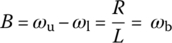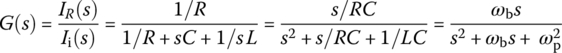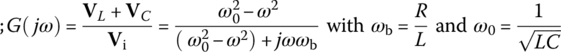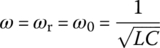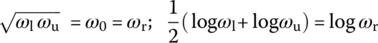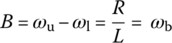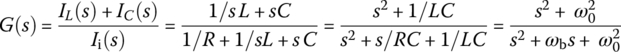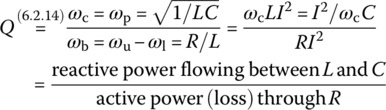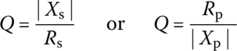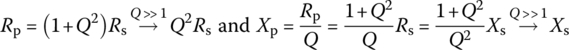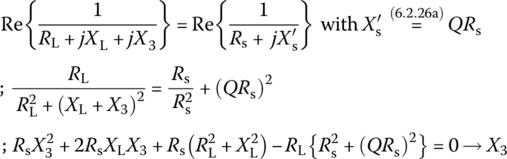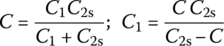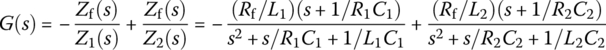6
Analog Filter
This chapter discusses how to design and realize analog filters in the form of passive filters and active filters.
6.1 Analog Filter Design
Figure 6.1(a)‐(d) shows typical low‐pass/band‐pass/band‐stop/high‐pass filter (LPF/BPF/BSF/HPF) specifications on their log magnitude, 20log10|G(jω)| [dB], of frequency response. The filter specification can be described as follows:
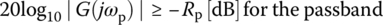
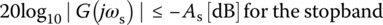
where ωp, ωs, Rp, and As are referred to as the passband edge frequency, the stopband edge frequency, the passband ripple, and the stopband attenuation, respectively. The most commonly used analog filter design techniques are the Butterworth, Chebyshev I, II, and elliptic ones ([K-2], Chapter 8). MATLAB has the built‐in functions ‘butt()’, ‘cheby1()’, ‘cheby2()’, and ‘ellip()’ for designing the four types of analog/digital filter. As summarized below, ‘butt()’ needs the 3 dB cutoff frequency while ‘cheby1()’ and ‘ellip()’ take the critical passband edge frequency and ‘cheby2()’ the critical stopband edge frequency as one of their input arguments. The parametric frequencies together with the filter order can be predetermined using ‘buttord()’, ‘cheb1ord()’, ‘cheb2ord()’, and ‘ellipord()’. The frequency input argument should be given in two‐dimensional vector for designing BPF or BSF. Also for HPF/BSF, the string 'high'/'stop' should be given as an optional input argument together with 's' for analog filter design.
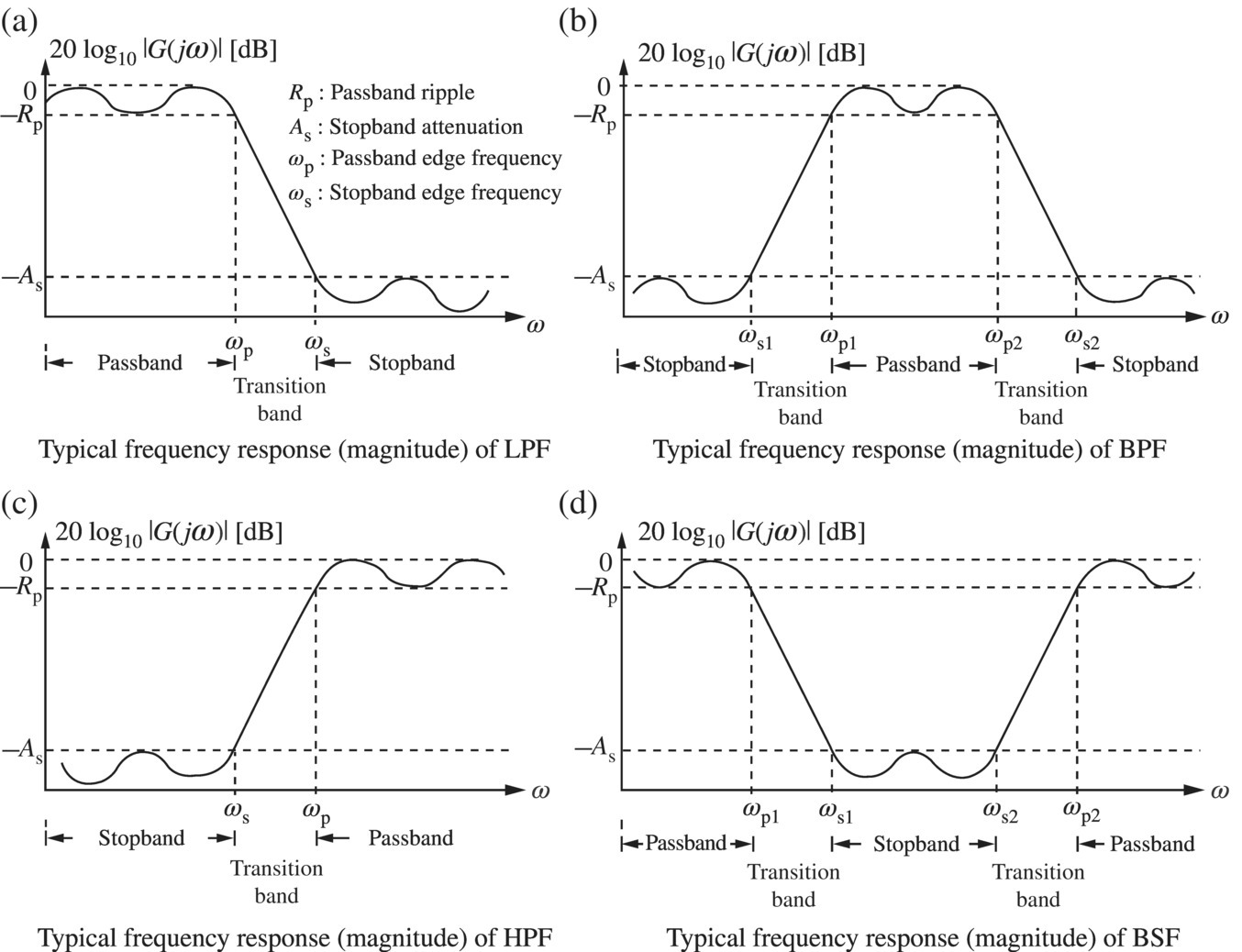
Figure 6.1 Specifications on the log magnitude of analog filter frequency response.
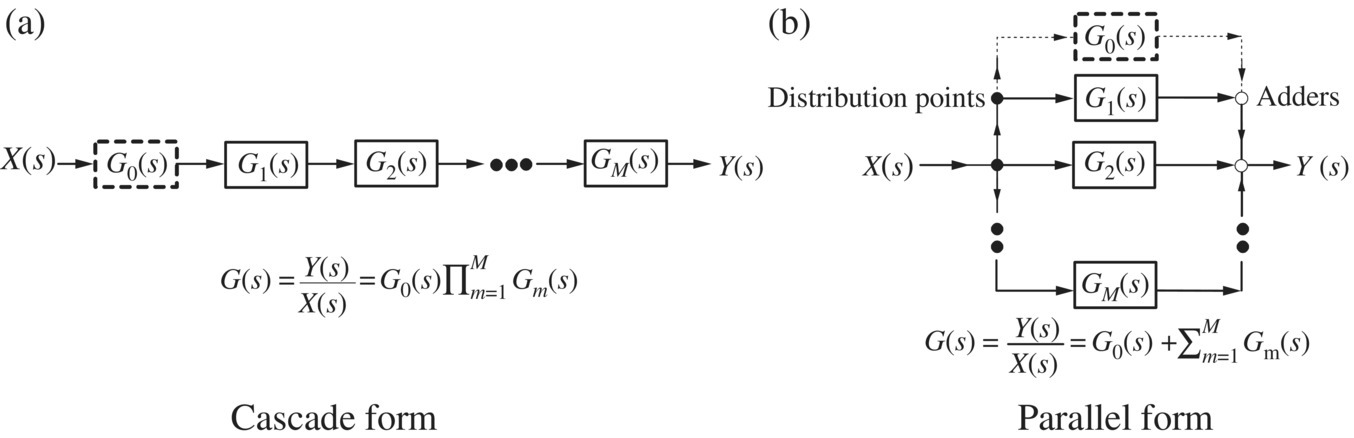
Figure 6.2 Two realizations of analog filter (system or transfer function).
A designed filter transfer function of order N is often factored into the sum or product of SOSs (second‐order sections) called biquads (possibly with an additional first‐order section in the case of an odd filter order) as

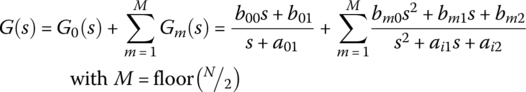
and then realized in cascade or parallel form, respectively, as depicted in Figure 6.2.
Rather than reviewing the design procedures, let us use the MATLAB functions to design a Butterworth low‐pass filter, a Chebyshev I band‐pass filter, a Chebyshev II BSF, and elliptic HPF in the following example.
6.2 Passive Filter
6.2.1 Low‐pass Filter (LPF)
6.2.1.1 Series LR Circuit
Figure 6.4(a) shows a series LR circuit where the voltage vR(t) across the resistor R is taken as the output to the input voltage source vi(t). With VR(s) =  {vR(t)} and Vi(s)=
{vR(t)} and Vi(s)= {vi(t)}, its input‐output relationship can be described by the transfer function and the frequency response as
{vi(t)}, its input‐output relationship can be described by the transfer function and the frequency response as
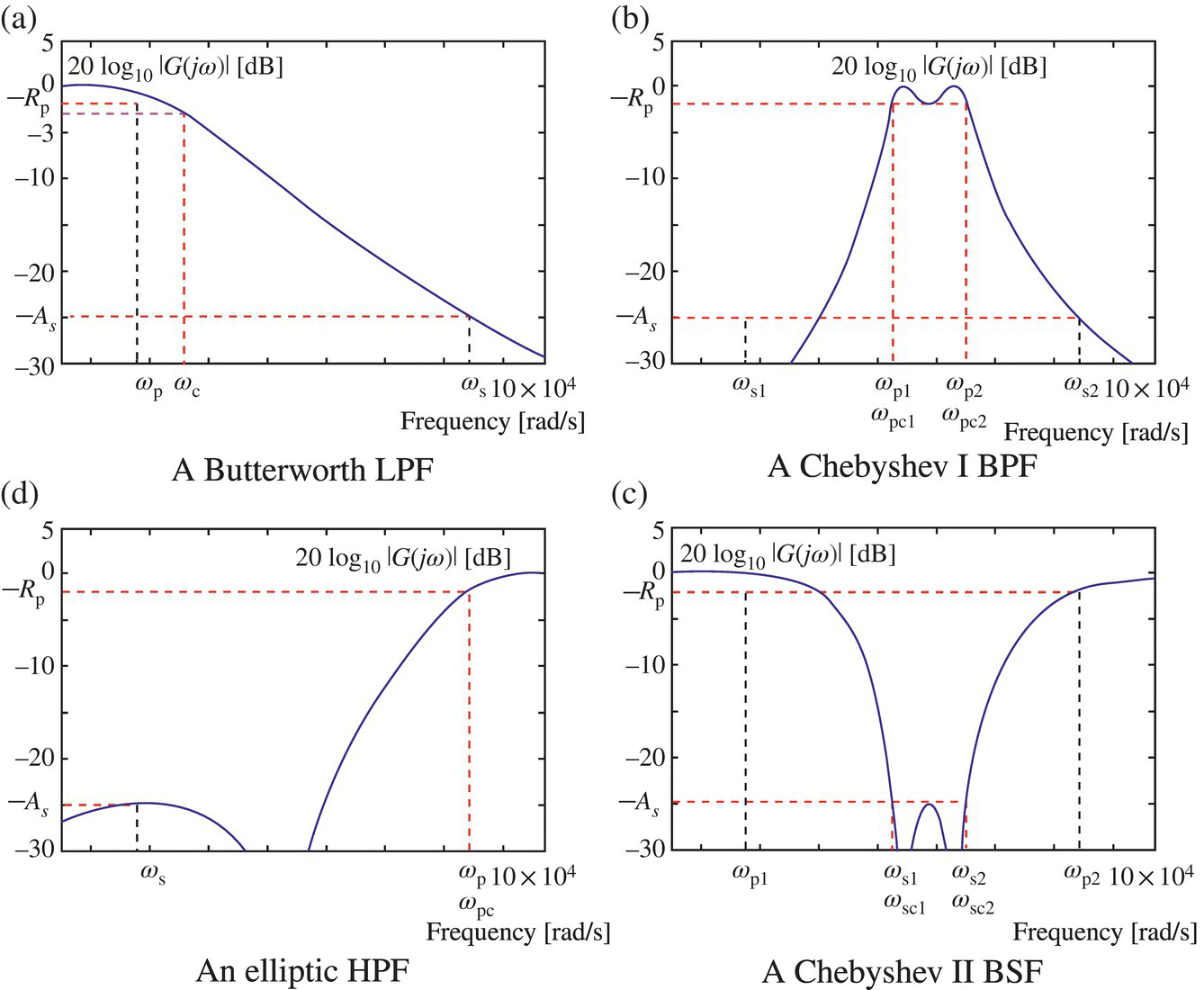
Figure 6.3 Frequency response magnitude curves of the filters designed in Example 8.7.
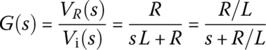

Since the magnitude |G(jω)| of this frequency response becomes smaller as the frequency ω gets higher as depicted in Figure 6.4(b), the circuit is a lowpass filter (LPF) that prefers to have low‐frequency components in its output. Noting that |G(jω)| achieves the maximum Gmax = G(j0) = 1 at ω = 0, we can find the cutoff frequency ωc at which it equals  as
as

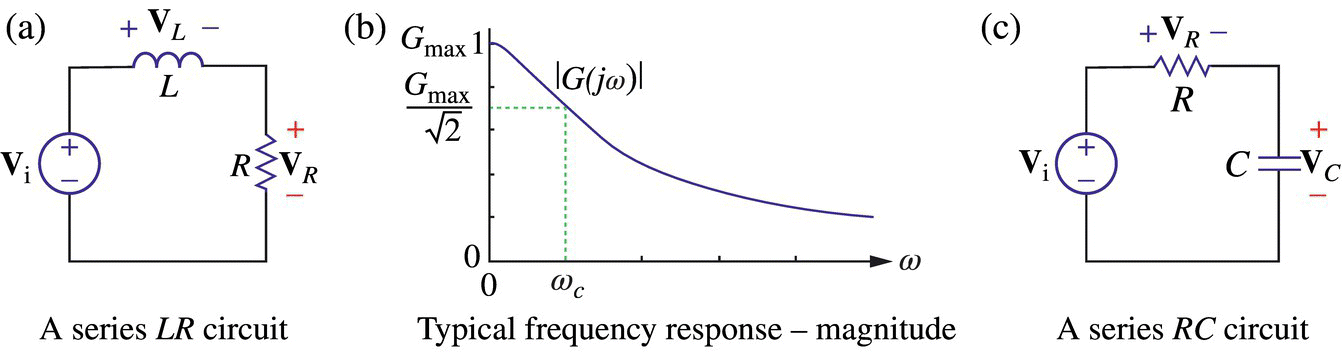
Figure 6.4 Low‐pass filters and their typical frequency response.
The cutoff frequency has a physical meaning as the boundary frequency between the passband and the stopband. Why do we use 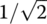 for its definition? In most cases, the transfer function and the frequency response is the ratio of output and input voltages/currents in s‐frequency domain. Since an electric power is proportional to the squared voltage and current, the ratio of
for its definition? In most cases, the transfer function and the frequency response is the ratio of output and input voltages/currents in s‐frequency domain. Since an electric power is proportional to the squared voltage and current, the ratio of 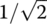 between voltages/currents corresponds to the ratio of 1/2 between powers. For this reason, the cutoff frequency is also referred to as a half‐power frequency or a 3dB frequency on account of that 10log10(1/2) = −3 [dB]. In the case of LPF with cutoff frequency ωc like this circuit, the passband is the range of frequency [0, ωc] and its width is the bandwidth, where the bandwidth means the width of the range of frequency components that pass the filter better than others.
between voltages/currents corresponds to the ratio of 1/2 between powers. For this reason, the cutoff frequency is also referred to as a half‐power frequency or a 3dB frequency on account of that 10log10(1/2) = −3 [dB]. In the case of LPF with cutoff frequency ωc like this circuit, the passband is the range of frequency [0, ωc] and its width is the bandwidth, where the bandwidth means the width of the range of frequency components that pass the filter better than others.
6.2.1.2 Series RC Circuit
Figure 6.4(c) shows a series RC circuit where the voltage vC(t) across the capacitor C is taken as the output to the input voltage source vi(t). With VC(s)= {vC(t)} and Vi(s)=
{vC(t)} and Vi(s)= {vi(t)}, its input‐output relationship can be described by the transfer function and the frequency response as
{vi(t)}, its input‐output relationship can be described by the transfer function and the frequency response as
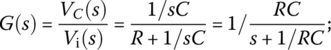
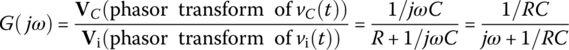
Everything is the same with the series LR circuit in Figure 6.4(a) except for that the cutoff frequency is
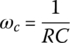
6.2.2 High‐pass Filter (HPF)
6.2.2.1 Series CR Circuit
Figure 6.5(a) shows a series CR circuit where the voltage vR(t) across the resistor R is taken as the output to the input voltage source vi(t). Its input‐output relationship can be described by the transfer function and the frequency response as
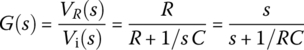

Since the magnitude |G(jω)| of this frequency response becomes larger as the frequency ω gets higher as depicted in Figure 6.5(b), the circuit is a highpass filter (HPF) that prefers to have high‐frequency components in its output. Noting that |G(jω)| achieves the maximum Gmax=G(j∞)=1 at ω=∞, we can find the cutoff frequency ωc at which it equals 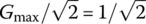 as
as
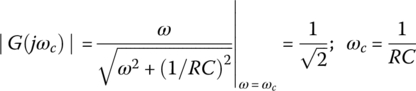
6.2.2.2 Series RL Circuit
Figure 6.5(c) shows a series RL circuit where the voltage vL(t) across the inductor L is taken as the output to the input voltage source vi(t). Its input‐output relationship can be described by the transfer function and the frequency response as

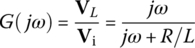
Everything is the same with the series CR circuit in Figure 6.5(a) except for that the cutoff frequency is
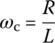

Figure 6.5 High‐pass filters and their typical frequency response.
6.2.3 Band‐pass Filter (BPF)
6.2.3.1 Series Resistor, an Inductor, and a Capacitor (RLC) Circuit and Series Resonance
Let us consider the series resistor, an inductor, and a capacitor (RLC) circuit of Figure 6.6(a) in which the voltage vR(t) across the resistor R is taken as the output to the input voltage source vi(t). Its input‐output relationship can be described by the transfer function and the frequency response as
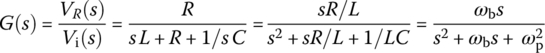
Referring to the typical magnitude curve of the frequency response of a bandpass filter (BPF) shown in Figure 6.6(b), we can find the maximum of the magnitude, |G(jω)|, of the frequency response by setting the derivative of its square |G(jω)|2 w.r.t. frequency ω to zero as
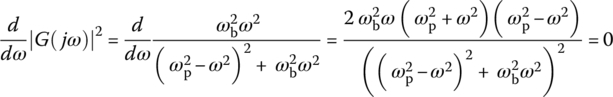
This yields the peak or center frequency
at which the frequency response achieves the maximum magnitude as
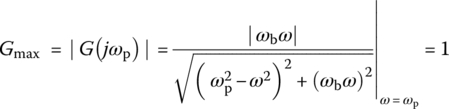
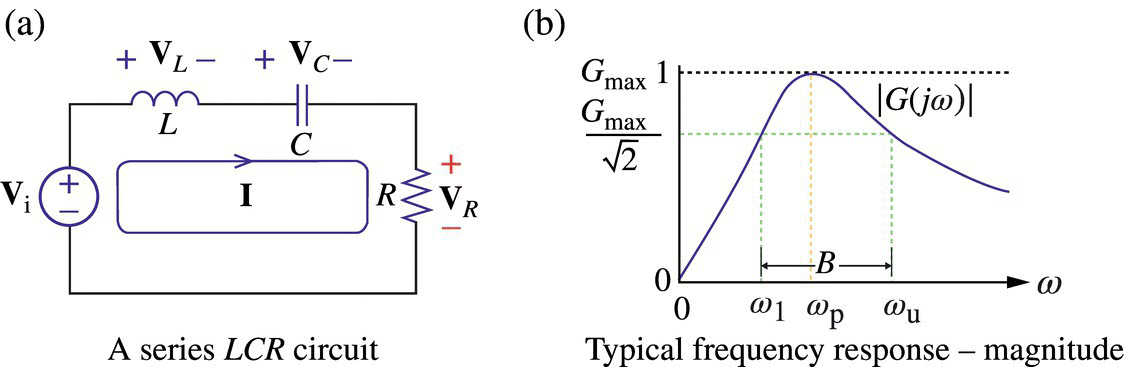
Figure 6.6 A band‐pass filter (BPF) and its typical frequency response.
This frequency happens to coincide with the resonant frequency ωr at which the frequency response is real so that the input and the output are in phase at that frequency. We can also find the lower and upper 3dB frequencies at which the magnitude |G(jω)| of this frequency response is 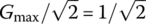 as
as
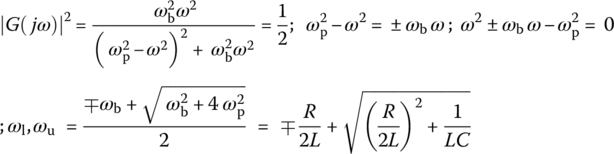
Multiplying these two 3 dB frequencies and taking the square root yields
This implies that the peak frequency ωp is the geometrical mean of two 3 dB frequencies ωl and ωu and also the arithmetical mean of their logarithmic values that is at the midpoint between the two 3 dB frequency points on the log‐frequency (log ω) axis. That is why ωp is also called the center frequency. The frequency band between the two 3 dB frequencies ωl and ωu is the passband and its width is the bandwidth:
Note that the bandwidth for a BPF is the width of the range of frequency components that pass the filter better than others.
For a BPF, we define the quality factor or selectivity (sharpness) as
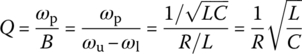
This quality factor is referred to as the selectivity since it is a measure of how selectively the filter responds to the peak frequency and frequencies near it within the passband, discriminating against frequencies outside the passband. It is also referred to as the sharpness in the sense that it describes how sharp the magnitude curve of the frequency response is around the peak frequency. It coincides with the voltage magnification ratio, that is, the ratio of the magnitude of the voltage across the inductor or the capacitor to that of the input voltage at peak frequency as
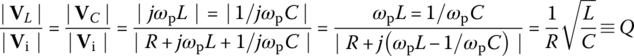
which may be greater than unity. Isn't it interesting that the voltages across some components of a circuit can be higher than the applied voltage?
Now, let us see the following example showing how to determine the parameters of a series RLC circuit so that it can function as a BPF satisfying a design specification on the passband.
Example 6.2 Realization of a BPF with a Series RLC Circuit
Consider a series RLC circuit with the inductor of inductance L = 12.9 mH. Determine the values of the resistance R and capacitance C such that the circuit can function as a BPF with the passband between the two frequencies 691 and 941 Hz.
Noting that the two boundary frequencies are given as the lower/upper 3dB frequencies, we have

First, we substitute these upper/lower 3dB frequencies into Eq. (6.2.12) to get the peak frequency as

Then, we use Eq. (6.2.10) for the peak frequency to find the value of C such that the peak frequency of the circuit will be 5088[rad/s]:
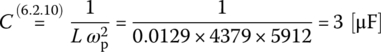
We also use Eq. (6.2.13) for the bandwidth to find the value of R such that the bandwidth of the circuit will be ωu − ωl [rad/s]:

6.2.3.2 Parallel RLC Circuit and Parallel Resonance
Let us consider the parallel RLC circuit of Figure 6.7(a) in which the current iR(t) through the resistor R is taken as the output to the input current source ii(t). Its input‐output relationship can be described by the transfer function and the frequency response as
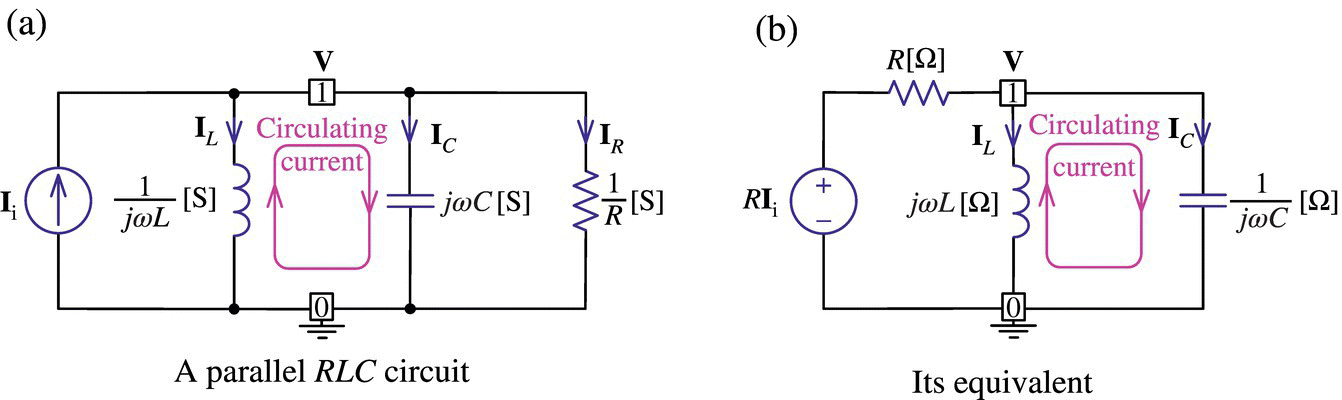
Figure 6.7 A parallel resistor, an inductor, and a capacitor (RLC) circuit and its equivalent.
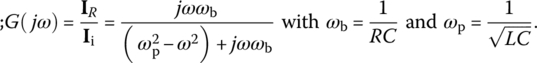
Since this frequency response is the same as that, Eq. (6.2.9b), of the series RLC circuit in Figure 6.6(a) except for ωb, we can obtain the peak or center frequency, the upper/lower 3dB frequencies, the bandwidth, and the quality factor as follows:

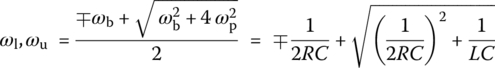
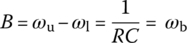
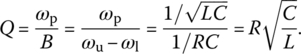
The peak frequency happens to be coinciding with the resonant frequency ωr in the sense that the frequency response is real so that the input and the output are in phase at that frequency. The quality factor coincides with the current magnification ratio, that is, the ratio of the amplitude of the current through the inductor or the capacitor to that of the input current at resonant frequency as
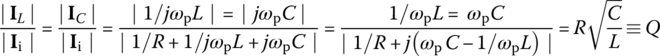
which may be greater than unity. How strange it is that the currents through some components of a circuit can be larger than the applied current!
Let us now consider RLC circuit of Figure 6.7(b) in which the voltage across L‖C (the parallel combination of L and C) is taken as the output to the input voltage source RIi. We can use the voltage divider rule to obtain the transfer function as
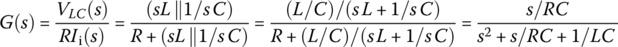
This is the same as Eq. (6.2.16a), which is the transfer function of the parallel RLC circuit of Figure 6.7(a). In fact, the circuit of Figure 6.7(b) is obtained by transforming the current source Ii in parallel with R into a voltage source RIi in series with R in the circuit of Figure 6.7(a).
Remark 6.1 Derivation of Resonance Condition for a BPF
Instead of setting the derivative of the squared magnitude of frequency response to zero, we can derive the resonance condition for a BPF by setting the imaginary part of the impedance or admittance to zero.
Example 6.3 Practical Resonance Condition
As suggested in Remark 6.1, the resonance condition of the circuit of Figure 6.8(a) can be obtained by setting the imaginary part of the impedance or admittance to zero. Since the admittance is easier to find than the impedance for this circuit, we set the imaginary part of the admittance to zero so that the frequency response will be real (see the admittance triangle in Figure 6.8(b)).
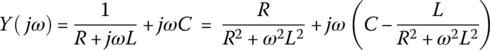

This yields the resonant frequency as

6.2.4 Band‐stop Filter (BSF)
6.2.4.1 Series RLC Circuit
Let us consider the series RLC circuit of Figure 6.9(a) in which the voltage vLC(t) across the series combination of L and C is taken as the output to the input voltage source vi(t). Its input‐output relationship can be described by the transfer function and the frequency response as
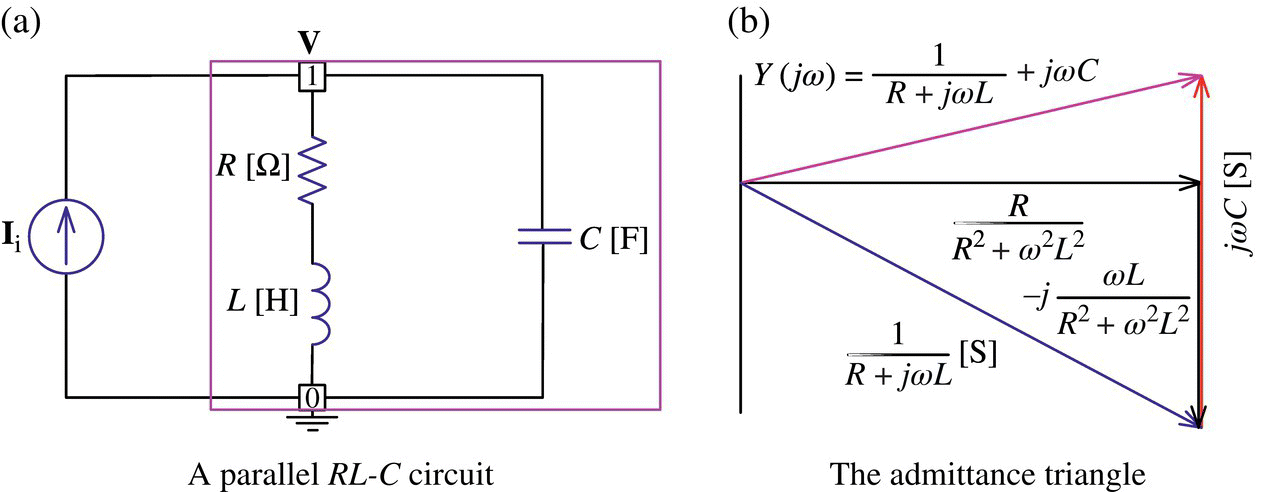
Figure 6.8 A practical parallel resonant circuit and its admittance triangle.
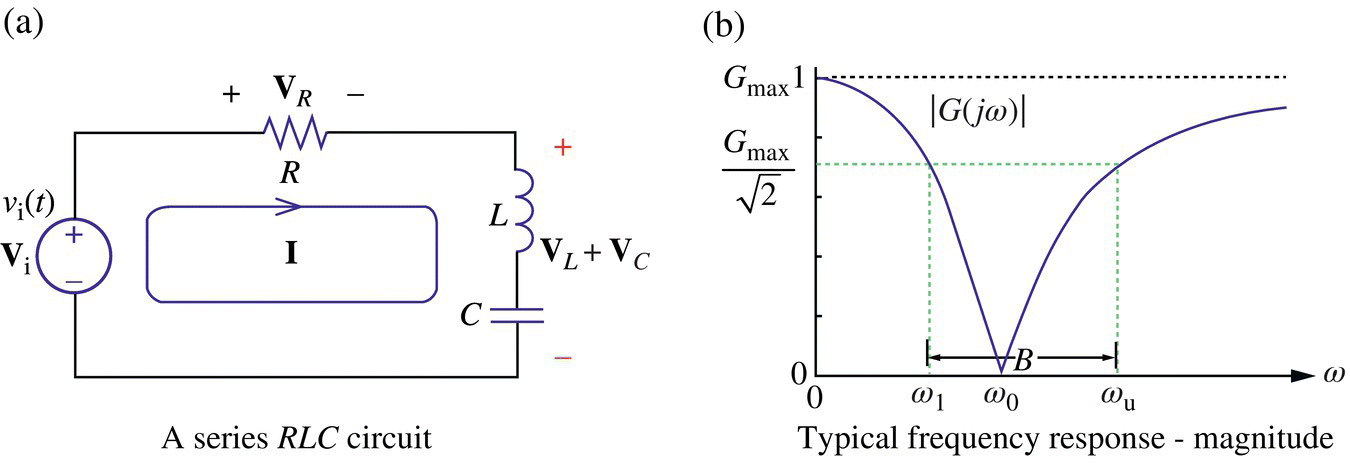
Figure 6.9 A band‐stop filter (BSF) and its typical frequency response.
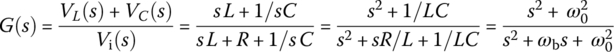
Referring to the typical magnitude curve of the frequency response of a BSF shown in Figure 6.9(b), we can find the minimum of the magnitude of the frequency response by setting the derivative of its square w.r.t. the frequency ω to zero as
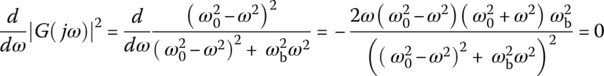
This yields the notch, rejection, or center frequency
at which the frequency response achieves the minimum magnitude as
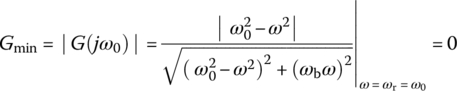
(Note) It is hoped that the readers will enjoy the dual sense of ωr, as the resonant frequency of BPF or the rejection (notch) frequency of BSF (depending on the context), rather than being confused.
Noting that the magnitude of the frequency response achieves its maximum of unity at another extremum frequency ω = 0 or ω = ∞ as
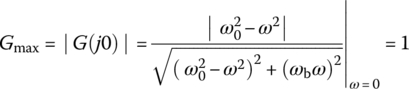
we can find the lower and upper 3 dB frequencies at which the magnitude |G(jω)| of this frequency response is 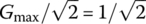 as
as
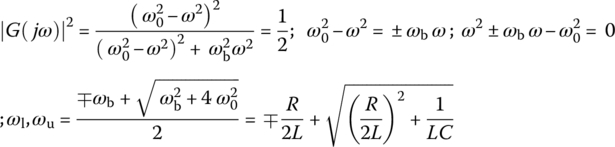
Multiplying these two 3 dB frequencies and taking the square root yields
This implies that the notch frequency ωr is the geometrical mean of two 3 dB frequencies ωl and ωu and also the arithmetical mean of their logarithmic values that is at the midpoint between the two 3 dB frequency points on the log‐frequency (log ω) axis. The band of frequencies between the two 3 dB frequencies ωl and ωu is the stopband and its width is the bandwidth:
Note that the bandwidth for a BSF is the width of the range of frequency components that are relatively more attenuated or rejected by the filter than other frequencies.
For a BSF, we define the quality factor or selectivity (sharpness) as

This quality factor is referred to as the selectivity since it is a measure of how selectively the filter rejects the notch frequency and frequencies near it within the stopband, favoring frequencies outside the stopband. It is also referred to as the sharpness in the sense that it describes how sharp the magnitude curve of the frequency response is around the rejection or notch frequency.
Example 6.4 Realization of a BSF with a Series RLC Circuit
Consider a series RLC circuit with an inductor of inductance L = 13.9 mH. Determine the values of the resistance R and the capacitance C such that the circuit can function as a BSF with the stopband between two frequencies 637 and 1432 Hz.
Noting that the two boundary frequencies are given as the lower/upper 3 dB frequencies, we have
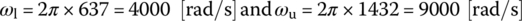
First, we substitute these upper/lower 3 dB frequencies into Eq. (6.2.21) to get the notch frequency as
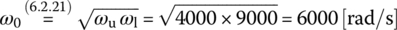
Then, we use Eq. (6.2.20) for the notch frequency to find the value of C such that the notch frequency of the circuit will be 6000 [rad/s]:
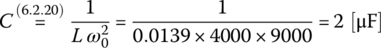
We also use Eq. (6.2.22) for the bandwidth to find the value of R such that the bandwidth of the circuit will be ωu‐ωl[rad/s]:

6.2.4.2 Parallel RLC Circuit
Let us consider the parallel RLC circuit of Figure 6.10(a) in which the current iL(t) + iC(t) through the parallel combination of L and C is taken as the output to the input current source ii(t). Its input‐output relationship can be described by the transfer function and the frequency response as
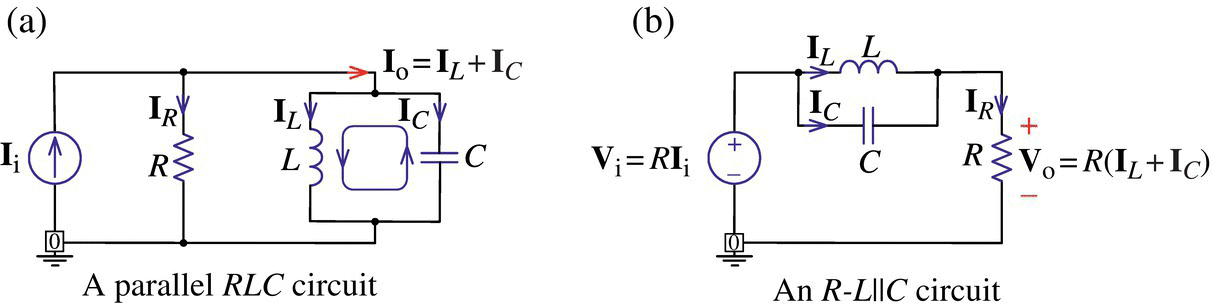
Figure 6.10 Band‐stop filter (BSF).
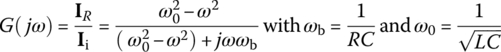
Since this frequency response is the same as that, Eq. (6.2.19b), of the series RLC circuit in Figure 6.9(a) except for ωb, we have the same results for the notch or rejection or center frequency, the upper/lower 3 dB frequencies, the bandwidth, and the quality factor.
Let us now consider the RLC circuit of Figure 6.10(b) in which the voltage across R is taken as the output to the input voltage source RIi. We can use the voltage divider rule to obtain the transfer function as
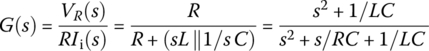
This is exactly the same as Eq. (6.2.24a), which is the transfer function of the parallel RLC circuit of Figure 6.10(a). In fact, this circuit is obtained by transforming the current source Ii in parallel with R into a voltage source RIi in series with R in the circuit of Figure 6.10(a).
6.2.5 Quality Factor
In the previous sections, the quality factors for series and parallel RLC circuits were defined as the ratio of the center frequency ωc to the bandwidth B= ωu ‐ ωl where ωu and ωl are the upper and lower 3 dB frequencies, respectively:
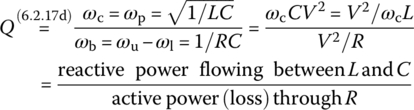
Note that the quality factor Q of a circuit can be viewed as the ratio of the reactive power (i.e. the maximum power stored in L or C) to the active power of the circuit.
Now, let us consider the quality factor of an individual reactive element L or C at the center frequency ωc of the circuit containing the element. It depends on whether the element is modeled as a series or parallel combination with its loss (parasitic) resistance:
where
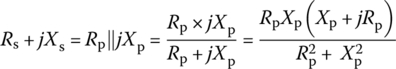
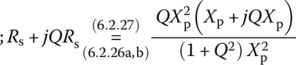

Note that these equivalence conditions between the series and parallel combination models of a reactive element are valid only at a certain frequency since the reactances are frequency dependent. The series‐to‐parallel and parallel‐to‐series conversion processes of L‐R and C‐R circuits have been cast into the following MATLAB functions:
function [Lp,Rp]=ser2par_LR(Ls,Rs,fc)% Series-to-Parallel conversion of Ls-Rs circuit at frequency fc.wc=2*pi*fc; Xs=wc*Ls; Q=Xs/Rs; % Quality factor of Ls-Rs by Eq. (6.2.26a)Xp=(1+Q^2)/Q^2*Xs; Rp=(1+Q^2)*Rs; Lp=Xp/wc; % Eq. (6.2.29a,b)function [Ls,Rs]=par2ser_LR(Lp,Rp,fc)% Parallel-to-Series conversion of Cp|Rp circuit at frequency fc.wc=2*pi*fc; Xp=wc*Lp; Q=Rp/Xp; % Quality factor of Lp|Rp by Eq. (6.2.26b)Xs=Q^2/(1+Q^2)*Xp; Rs=Rp/(1+Q^2); Ls=Xs/wc; % Eq. (6.2.28a,b)function [Cp,Rp]=ser2par_CR(Cs,Rs,fc)% Series-to-Parallel conversion of Cs-Rs circuit at frequency fc.wc=2*pi*fc; Xs=1/wc/Cs; Q=Xs/Rs; % Quality factor of Cs-Rs by Eq. (6.2.26a)Xp=(1+Q^2)/Q^2*Xs; Rp=(1+Q^2)*Rs; Cp=1/Xp/wc; % Eq. (6.2.29a,b)function [Cs,Rs]=par2ser_CR(Cp,Rp,fc)% Parallel-to-Series conversion of Lp|Rp circuit at frequency fc.wc=2*pi*fc; Xp=1/wc/Cp; Q=Rp/Xp; % Quality factor of Cp|Rp by Eq. (6.2.26b)Xs=Q^2/(1+Q^2)*Xp; Rs=Rp/(1+Q^2); Cs=1/Xs/wc; % Eq. (6.2.28a,b)
Example 6.5 Series‐to‐Parallel Conversion of an L‐R Circuit
Make a series‐to‐parallel conversion of the L‐R circuit shown in Figure 6.11(a1) at fc = 100 MHz and plot the AC impedance (magnitude) curves of the series and parallel L‐R circuits for comparison.
We can make and run the MATLAB script “elec06e05.m,” which yields the following conversion results
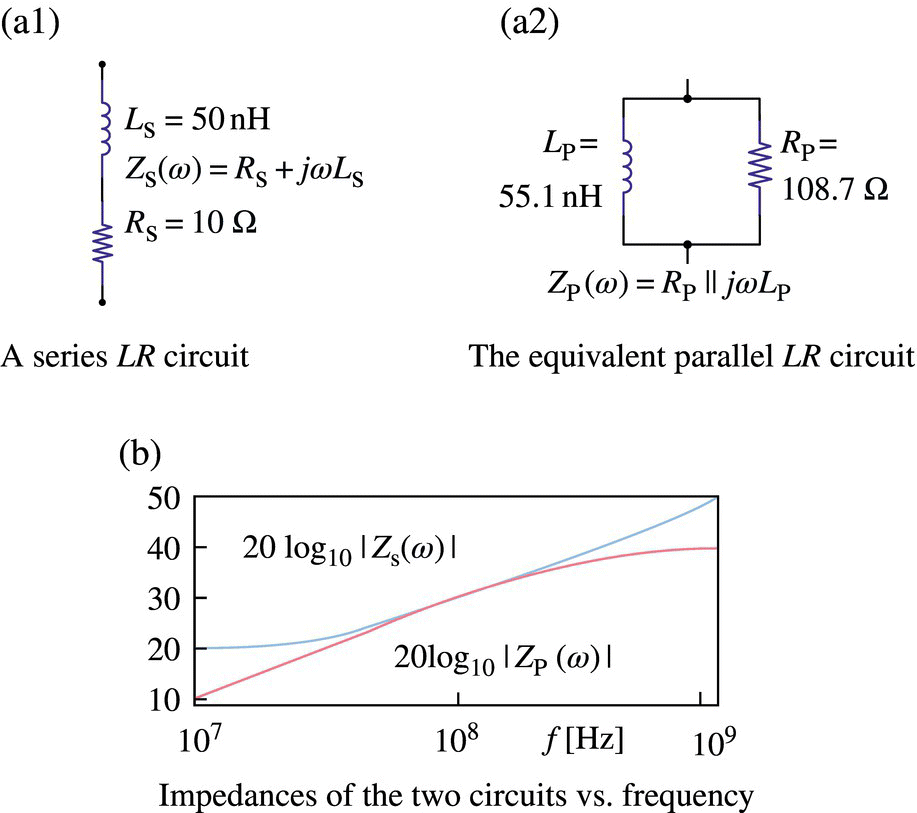
Figure 6.11 Series‐to‐parallel conversion of an L‐R circuit.
Ls = 50 nH – Rs = 10 Ω (Series combination) → Lp = 55.1 nH | Rp = 108.7 Ω (Parallel combination)(as shown in Figure 6.11(a2)) and the AC impedance (magnitude) curves shown in Figure 6.11(b).
%elec06e05.m% Series-to-Parallel conversion of an L-R circuit in Example 6.5.fc=100e6; wc=2*pi*fc; Ls=50e-9; Rs=10;[Lp,Rp]=ser2par_LR(Ls,Rs,fc)% To plot the frequency responseff=logspace(-1,1,601)*fc; w=2*pi*ff;Zsw=Rs+j*w*Ls; Zpw=Rp*j*w*Lp./(Rp+j*w*Lp);ZswdB=20*log10(abs(Zsw)); ZpwdB=20*log10(abs(Zpw));semilogx(ff,ZswdB, ff,ZpwdB,'r')
Now, let us consider the (loaded) quality factor [L-1] QLD of a series RLC circuit with the source resistance Rs and the load resistance RL as shown in Figure 6.12(a). Noting that the circuit is a series connection of (Rs+R+RL)‐L‐C, we can use Eq. (6.2.25a) to write the loaded quality factor QLD as
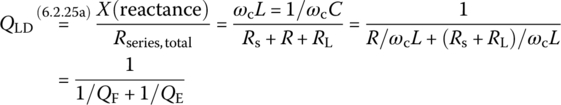
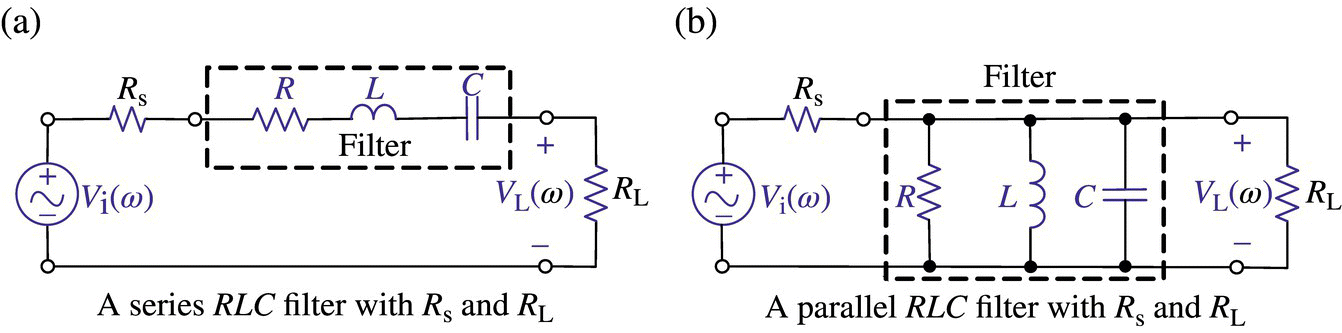
Figure 6.12 Circuits for the definitions of the loaded quality factor QLD.
where the filter quality factor QF and the external quality factor QE are as follows:
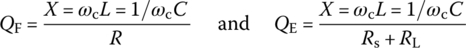
Likewise, the loaded quality factor QLD of a parallel RLC circuit with the source resistance Rs and the load resistance RL as shown in Figure 6.12(b) can be written as

where the filter quality factor QF and the external quality factor QE are as follows:
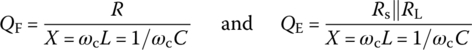
Example 6.6 Design of LC Parallel Resonant Filter
Design an LC parallel resonant filter for a transmission line system with the source/load resistance Rs/RL = 1 kΩ/1 kΩ so that the overall frequency response can have a bandwidth fB = 10 MHz at center frequency fc = 100 MHz where the (element) quality factors of the inductor and capacitor (constituting the LC parallel filter) are QL,p = RL,p/X = 85 and QC,p = RC,p/X = 0, i.e. RC,p = 0 (lossless), respectively, and X = ωcL = 1/ωcC.
Note that this problem amounts to determining such values of L and C in the circuit of Figure 6.12(b) that can yield the loaded quality factor of
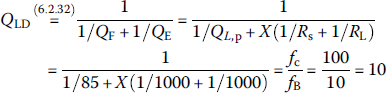
We can solve to get
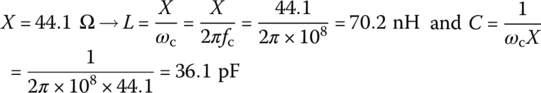
and use Eq. (6.2.26b) to get

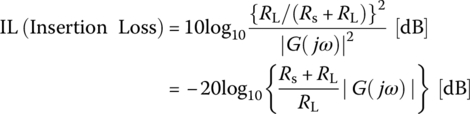
6.2.6 Insertion Loss
When designing a filter to be inserted in a telecommunication system as can be modeled by, say, Figure 6.12(a) or (b), it is important to consider the insertion loss (IL) of the filter, which is defined as the ratio of the power (delivered to the load without the filter) to the power (delivered to the load with the filter inserted):

6.2.7 Frequency Scaling and Transformation
Note the following remarks on frequency scaling and frequency transformation:
Remark 6.2 Frequency Response Scaling on Magnitude and Frequency
- Magnitude Scaling: If the frequency response of a circuit is a kind of AC impedance or admittance as a phasor voltage‐to‐current ratio[V/A] or a phasor current‐to‐voltage ratio[A/V], we can scale its magnitude curve along the vertical (magnitude) axis with the scale factor km by multiplying all resistances/inductances with km and all capacitances with 1/km. For example, we can scale the frequency response of a series RLC circuit by changing its impedance as
(6.2.35)
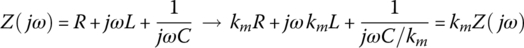
However, if the frequency response is dimensionless as a phasor voltage‐to‐voltage ratio[V/V] or a phasor current‐to‐current ratio[A/A], we cannot scale its magnitude curve along the vertical (magnitude) axis, which implies that all resistances/inductances and capacitances can be multiplied by km and 1/km, respectively, without changing the frequency response.
- Frequency Scaling: We can scale the magnitude/phase curve of frequency response along the horizontal (frequency) axis with the scale factor kf by multiplying all inductances and capacitances with 1/kf and leaving all resistances as they are. This frequency scaling is based on the fact that the reactances of an inductor and a capacitor, ωL and 1/ωC, are not changed when we multiply the frequency variable ω by kf and divide L and C by kf.
Example 6.7 Magnitude and Frequency Scaling of a Series RLC Circuit
Adjust the values of R, L, and C of the RLC filter designed in Example 6.4 by the magnitude scale factor km = 2 and frequency scale factor kf = 10 and plot the frequency response (magnitude) curves of the filter before/after the scalings.
Referring to Remark 6.2, the values of R, L, and C should be adjusted as follows:
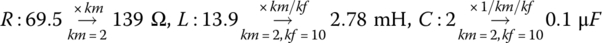
Figure 6.13 shows the frequency response magnitude curves of the filter before/after the magnitude and frequency scalings. Do they agree to your expectation?
Remark 6.3 Transformation of Prototype LPF with Normalized Cutoff Frequency
A prototype LPF with normalized cutoff frequency ωc = 1 [rad/s] can be transformed into other types like LPF, HPF, BPF, and BSF (with another cutoff frequency) by substituting s as listed in Table 6.1 into its transfer function. The following MATLAB function ‘transform_LC()’ finds the values of L's and C's to be determined for such transformations of an LPF.
![Graph illustrating the frequency response magnitudes before/after frequency scaling, with a solid curve for |G(ω)| [dB] and a dashed curve for |G1(ω)| [dB].](Images/c06f013.gif)
Figure 6.13 Frequency response magnitudes before/after frequency scaling.
function [LCs1,LCs1_]=transform_LC(LCs,LCs_,wc,band,Rs)% Frequency transformations (Remark 6.3 and Table 6.1)% Input:% LCs,LCs_ = [C1 L2 C3],{'C(v)','L(h)','C(v)'}% wc = wc/[wl wu] for (LPF|HPF)/(BPF|BSF)% band = 'LPF'/'HPF'/'BPF'/'BSF'% Rs = Line (Sourece) Resistance% Output:% LCs1,LCs1_ = Frequency transformed results% Copyleft: Won Y. Yang, wyyang53@hanmail.net, CAU for academic use onlyif nargin<5, Rs=1; endif nargin<4, band='LPF'; endif nargin<3, wc=1; endif numel(wc)>1, w0=sqrt(wc(1)*wc(2)); wb=abs(wc(2)-wc(1)); endif lower(band(1))=='l' % 'LPF'LCs1=LCs/wc; LCs1_=LCs_; % Eq. (6.2.36)for m=1:numel(LCs_)LC_=LCs_{m};if LC_(1)=='L', LCs1(m)=LCs1(m)*Rs;elseif LC_(1)=='C', LCs1(m)=LCs1(m)/Rs;endendelseLCs1=[]; LCs1_=LCs_;for m=1:numel(LCs_)LC_=LCs_{m};if length(wc)<2 % 'HPF'if LC_(1)=='L', LC_(1)='C'; LCs1_{m}=LC_;LCs1=[LCs1 1/wc/LCs(m)/Rs]; % Eq. (6.2.37b)else LC_(1)='C'; LCs1_{m}=LC_; LCs1=[LCs1 1/wc/LCs(m)*Rs];endelseif numel(wc)<2, error('wc must be [wl wu] for BPF or BSF'); endif lower(band(1:2))=='bp' % 'BPF'if LC_(1)=='L', L=LCs(m);LCs1=[LCs1 L/wb*Rs wb/w0^2/L/Rs]; LCs1_{m}='L-C';%(6.2.38b)else LC_(1)='C'; C=LCs(m);LCs1=[LCs1 wb/w0^2/C*Rs C/wb/Rs]; LCs1_{m}='L|C';%(6.2.38c)endelse % 'BSF'if LC_(1)=='L', L=LCs(m);LCs1=[LCs1 wb/w0^2*L*Rs 1/wb/L/Rs]; LCs1_{m}='L|C';%(6.2.39b)else LC_(1)='C'; C=LCs(m);LCs1=[LCs1 1/wb/C*Rs wb/w0^2*C/Rs]; LCs1_{m}='L-C';%(6.2.39c)endendendendend
Table 6.1 Frequency transformation.
| Frequency transformations | MATLAB function |
| LPF with cutoff frequency ωc: s → s/ωc(6.2.36a) This corresponds to substituting 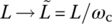 and and 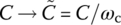 .(6.2.36b) .(6.2.36b) |
lp2lp() |
| HPF with cutoff frequency ωc: s → ωc/s(6.2.37a) This corresponds to substituting 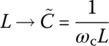 and and 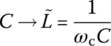 .(6.2.37b) .(6.2.37b) |
lp2hp() |
BPF with upper/lower cutoff frequencies ωu/ωl: 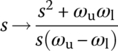 (6.2.38a) (6.2.38a)This corresponds to substituting (  ) )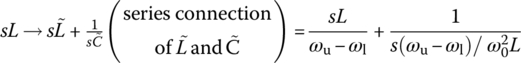 (6.2.38b) (6.2.38b) (6.2.38c) (6.2.38c) |
lp2bp() |
BSF with upper/lower cutoff frequencies ωu/ωl: 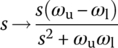 (6.2.39a) (6.2.39a)This corresponds to substituting ( 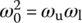 ) ) (6.2.39b) (6.2.39b)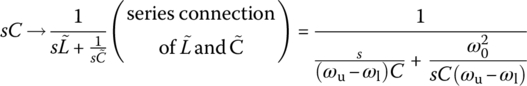 (6.2.39c) (6.2.39c) |
lp2bs() |
Example 6.8 Frequency Transformation of an LPF
Make a frequency transformation of a series RC circuit with cutoff frequency ωc = RC = 1[rad/s] into a BSF with Rs = 69.5[Ω], ωl = 4000[rad/s], and ωu = 9000[rad/s], as specified in Example 6.4.
To this end, we can run the following script “elec06e08.m,” which uses the MATLAB function ‘transform_LC()’ inside, to get
LCs1 = 1.3900e-02 1.9984e-06, LCs1_ = 'L-C'
This means a series connection of L = 0.0139 [H] and C = 2 [μF], as determined in Example 6.4.
%elec06e08.mwl=4000; wu=9000; wc=sqrt(wl*wu); w=logspace(-1,2,600)*wc; jw=j*w;Rs=69.5; LCs=[1]; LCs_={'C'}; wc=[wl wu]; band='BSF';[LCs1,LCs1_]=transform_LC(LCs,LCs_,wc,band,Rs)syms s; L=LCs1(1); C=LCs1(2); Gs1=(s*L+1/s/C)/(Rs+s*L+1/s/C) %Transfer ftn[B1,A1]=numden(simplify(Gs1)); B1=sym2poly(B1); A1=sym2poly(A1);B1=B1/A1(1), A1=A1/A1(1) % Numerator/Denominator of the transfer functionRC=1; b=[0 1]; a=[1 1/RC]; w0=sqrt(wl*wu); wb=wu-wl;[B,A]=lp2bs(b,a,w0,wb) % Using 'lp2hp()' to get just the transfer ftn
6.3 Passive Filter Realization
6.3.1 LC Ladder
Figure 6.14.1(a) and (b) shows the П‐type and T‐type of LC ladder that can be used to realize a prototype LPF where the values of L's, C's, and RL are listed as {g1, g2, … } in Tables 5.2 (Butterworth), 5.3 (linear‐phase), 5.4 (Chebyshev 3 dB), and 5.5 (Chebyshev 0.5 dB) of [L-1] and can also be determined by using the following MATLAB function ‘LPF_ladder_coef()’.
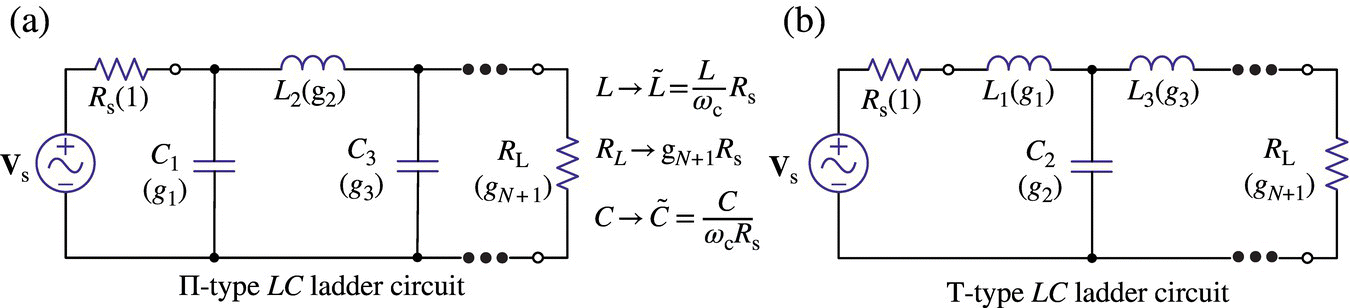
Figure 6.14.1 LC ladders realizing low‐pass filter (LPF).
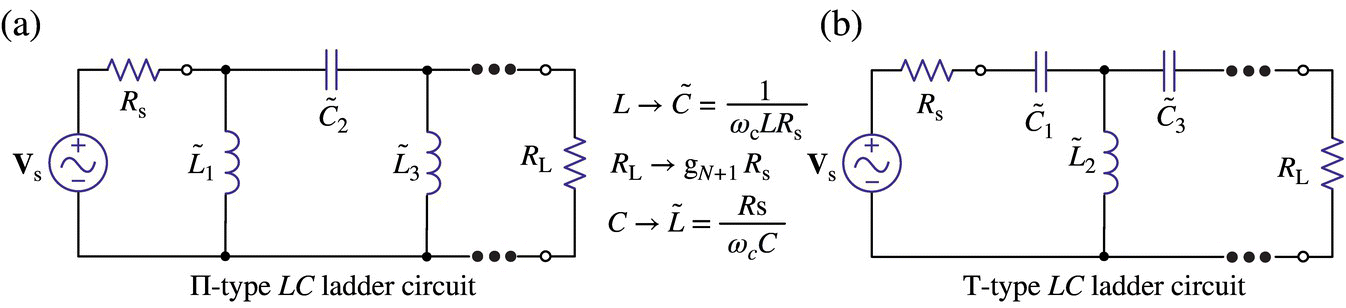
The formulas listed in Table 6.1 can be used to magnitude/frequency scale the LC filter prototypes to make them realize LPF/HPF/BPF/BSF with unnormalized cutoff frequency as depicted in Figures 6.14.1‐6.14.4.

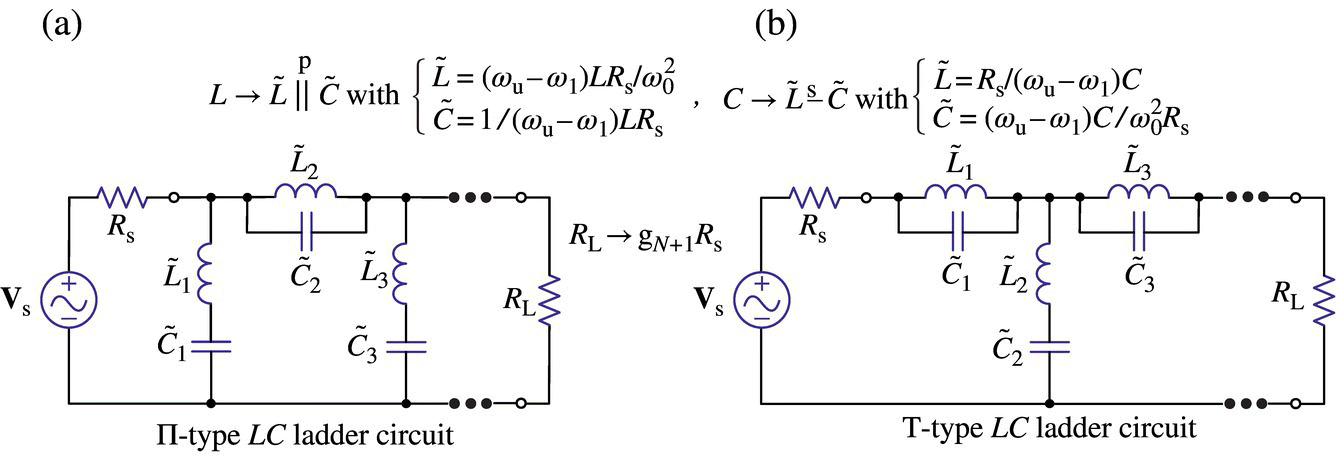
Figure 6.14.4 LC ladders realizing BSF.
Example 6.9 Determining the Values of L's and C's of LC Ladder Realizing a Prototype LPF
To determine the values of L's, C's, and RL of a third‐order Butterworth LPF prototype, we can run the following MATLAB statement:
>>N=3; gg=LPF_ladder_coef(N,'Bu')gg = 1 2 1 1
function [LCRs,LCRs_,Gs]=LC_ladder(Rs,gg,pT,wc,band)% Input:% Rs = Source resistance% gg = Ladder coefficients generated using LPF_ladder_coef()% pT = 'p'/'T' or 1/2 for Pi/T-ladder% wc = wc/[wl wu] for band=('LPF'|'HPF')/('BPF'|'BSF')% band='LPF'/'BPF'/'BSF'/'HPF'% Output:% LCRs,LCRs_=[C1 L2 C3 R],{'C(v)','L(h)','C(v)'} for Pi-ladder Fig. 6.14.1a% LCRs,LCRs_=[L1 C2 L3 R],{'L(h)','C(v)','L(h)'} for T-ladder Fig. 6.14.1b% LCRs,LCRs_=[L1 C1 L2 C2 L3 C3 R],{'L-C(v)','L|C(h)','L-C(v)'} for Pi% LCRs,LCRs_=[L1 C1 L2 C2 L3 C3 R],{'L|C(h)','L-C(v)','L|C(h)'} for T% Gs = G(s): Transfer function% Copyleft: Won Y. Yang, wyyang53@hanmail.net, CAU for academic use onlyif nargin<5, band='LPF'; endif nargin<4, wc=1; endif length(wc)>1, w0=sqrt(wc(1)*wc(2)); wb=wc(2)-wc(1); endsyms sN1=length(gg); N=N1-1;if isnumeric(pT), Kc=pT;else pT=lower(pT); Kc=(pT(1)=='p')+2*(pT(1)=='t'); % Set Kc=1/2 for pi/Tendif mod(Kc+N,2)==1, RL=gg(N1)*Rs; % When gg(N1)=RL/Rselse RL=Rs/gg(N1); % When gg(N1)=Rs/RLendI=1; V=RL; % Set the current through RL to 1 to find the transfer ftn G(s).LCs=[]; % Set LCs as an empty vector.if Kc==1 % Pi-ladderfor n=N:-1:1if mod(n,2)==0, [LCsn,LCs_{n},V]=LC_horizontal(Rs,gg(n),wc,band,V,I);else [LCsn,LCs_{n},I]=LC_vertical(Rs,gg(n),wc,band,V,I);endLCs=[LCsn LCs];endelse % T-ladderfor n=N:-1:1if mod(n,2)==1, [LCsn,LCs_{n},V]=LC_horizontal(Rs,gg(n),wc,band,V,I);else [LCsn,LCs_{n},I]=LC_vertical(Rs,gg(n),wc,band,V,I);endLCs=[LCsn LCs];endendLCRs=[LCs RL]; LCRs_=LCs_; LCRs_{N1}='R(v)';Gs=RL/(V+Rs*I); % Transfer function considering Rs and RL
function [LCsn,LCs_n,V]=LC_horizontal(Rs,ggn,wc,band,V,I)syms sif length(wc)>1, w0=sqrt(wc(1)*wc(2)); wb=wc(2)-wc(1); endswitch upper(band(1:2))case 'LP', L=ggn/wc*Rs; sL=s*L; V=V+sL*I; LCsn=L; LCs_n='L(h)';case 'HP', C=1/ggn/wc/Rs; sC=s*C; V=V+I/sC; LCsn=C; LCs_n='C(h)';case 'BP', L=ggn/wb*Rs; C=1/ggn*wb/w0^2/Rs; sLC=s*L+1/s/C; V=V+sLC*I;LCsn=[L C]; LCs_n='L-C(h)'; % Series L-Cotherwise, L=ggn*wb/w0^2*Rs; C=1/ggn/wb/Rs; sLC=L/C/(s*L+1/s/C);V=V+sLC*I; LCsn=[L C]; LCs_n='L|C(h)'; % Shunt L|Cend
function [LCsn,LCs_n,I]=LC_vertical(Rs,ggn,wc,band,V,I)syms sif length(wc)>1, w0=sqrt(wc(1)*wc(2)); wb=wc(2)-wc(1); endswitch upper(band(1:2))case 'LP', C=ggn/wc/Rs; sC=s*C; I=I+sC*V; LCsn=C; LCs_n='C(v)';case 'HP', L=1/ggn/wc*Rs; sL=s*L; I=I+V/sL; LCsn=L; LCs_n='L(v)';case 'BP', L=1/ggn*wb/w0^2*Rs; C=ggn/wb/Rs; sLC=L/C/(s*L+1/s/C);I=I+V/sLC; LCsn=[L C]; LCs_n='L|C(v)'; % Parallel L-Cotherwise, L=1/ggn/wb*Rs; C=ggn*wb/w0^2/Rs; sLC=s*L+1/s/C; I=I+V/sLC;LCsn=[L C]; LCs_n='L-C(v)'; % Series L-Cendfunction gg=LPF_ladder_coef(N,type,Rp)%returns N+1 L/C values of Butterworth/Linear-phase/Chebyshev 3dB/0.5dB LPF% depending on the order N and type='Bu'/'Li'/'C1'/'C2'% L/C values of LC ladder for normalized linear-phase LPF, Table 5.3, [L-1]if nargin<3, Rp=3; end % Rp is used only for Chebyshev filtersL=[2 1 0 0 0 0 0 0 0 0 0;1.5774 0.4226 1 0 0 0 0 0 0 0 0;1.255 0.5528 0.1922 1 0 0 0 0 0 0 0;1.0598 0.5116 0.3181 0.1104 1 0 0 0 0 0 0;0.9303 0.4577 0.3312 0.209 0.0718 1 0 0 0 0 0;0.8377 0.4116 0.3158 0.2364 0.248 0.0505 1 0 0 0 0;0.7677 0.3744 0.2944 0.2378 0.1778 0.1104 0.0375 1 0 0 0;0.7125 0.3446 0.2735 0.2297 0.1867 0.1387 0.0855 0.0289 1 0 0;0.6678 0.3203 0.2547 0.2184 0.1859 0.1506 0.1111 0.0682 0.023 1 0;0.6305 0.3002 0.2384 0.2066 0.1808 0.1539 0.124 0.0911 0.0557 0.0187 1];% Data by courtesy of L. Weinberg and Journal of the Franklin Institute.k=1:N; T=upper(type(1));if T=='B', gg=[2*sin((2*k-1)*pi/2/N) 1]; % Eq. (6.8) of [C-2]elseif T=='L', gg=L(N,1:N+1);elseif T=='C'beta=log(coth(Rp/17.37)); gamma=sinh(beta/2/N);a=sin((2*k-1)*pi/2/N); b=gamma^2+sin(k*pi/N).^2; % Eq. (6.11) of [C-2]gg(1)=2*a(1)/gamma;for k=2:N, gg(k)=4*a(k-1)*a(k)/b(k-1)/gg(k-1); end % Eq. (6.10) of [C-2]if mod(N,2)==1, gg(N+1)=1; else gg(N+1)=coth(beta/4)^2; endend
This result, returned as the output of the above MATLAB function ‘LPF_ladder_coef()’, means that the two forms of LC ladder depicted in Figure 6.15 can be used as the third‐order Butterworth LPF prototype. For reference, the transfer function of the filter in Figure 6.15(a) can be found as
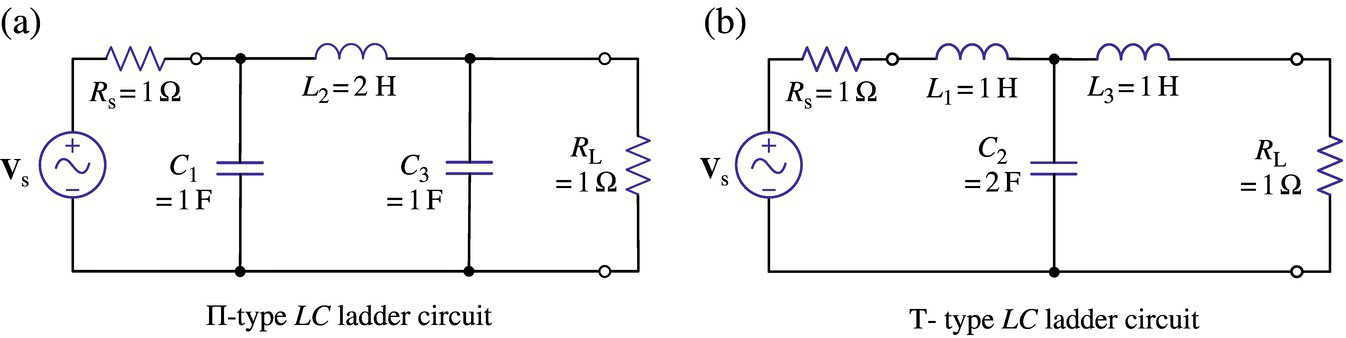
Figure 6.15 A third‐order Butterworth LPF prototype realized with П‐ and T‐type LC ladders.
If you want to get the parameter values for the П‐type LC ladder in Figure 6.15(a) more specifically, run the following MATLAB statements:
>>Rs=1; pT='Pi'; wc=1; [LCRs,LCRs_,Gs]=LC_ladder(Rs,gg,pT,wc);LCRs, LCRs_, pretty(simplify(Gs))
This yields not only the parameter values (LCRs) but also the type and vertical/horizontal orientation of each element:
LCRs = 1.0000e+00 2.0000e+00 1.0000e+00 1.0000e+00LCRs_ = 'C(v)' 'L(h)' 'C(v)' 'R(v)'1- - - - - - - - - - - - - % conforms with Eq. (E6.9.1)3 22 s + 4 s + 4 s + 2
where 'C(v)'/'L(h)' in the cell LCRs_ mean that their corresponding numbers in the vector LCRs are the values of capacitance/inductance to be placed vertically/horizontally, respectively, in the П‐type LC ladder of Figure 6.15(a). If you run the same MATLAB statements, but with pT = 'T',
>>Rs=1; pT='T'; wc=1; [LCRs,LCRs_,Gs]=LC_ladder(Rs,gg,pT,wc);LCRs, LCRs_, pretty(simplify(Gs))
you will get the realization result for the T‐type LC ladder of Figure 6.15(b):
LCRs = 1.0000e+00 2.0000e+00 1.0000e+00 1.0000e+00LCRs_ = 'L(h)' 'C(v)' 'L(h)' 'R(v)'1- - - - - - - - - - - - % conforms with Eq. (E6.9.1)3 22 s + 4 s + 4 s + 2
Example 6.10 Realization of a Fourth‐Order Butterworth LPF by an LC Ladder
Using a П‐type LC ladder circuit, realize a fourth‐order Butterworth LPF with cutoff frequency fc = 10 kHz to be connected to a line or source resistance Rs = 1 kΩ. Then, plot the frequency response magnitude (relative to that without the filter) for two decades around fc, i.e. 0.1fc ≤ f ≤ 10f.
The realization can be determined by running the following MATLAB script “elec06e10.m,” which uses ‘LPF_ladder_coef()’ to get the LC values of the fourth‐order Butterworth LPF prototype and then uses ‘LC_ladder()’ (with pT = ‘pi’) or ‘transform_LC()’ to find a П‐type LC ladder and to plot the magnitude of its frequency response obtained by substituting s = jω into the transfer function (obtained as the third output argument Gs of ‘LC_ladder()’), as shown in Figure 6.16:
%elec06e10.m% To realize a Butterworth LPF by an LC ladder in Example 6.10syms sN=4; pT='pi'; Rs=1e3; % 4th order, Pi-typetype='B'; band='LPF'; fc=1e4; wc=2*pi*fc; % Butterworth LPFgg=LPF_ladder_coef(N,type) % LC values of Nth-order B-LPF prototype[LCRs,LCRs_,Gs]=LC_ladder(Rs,gg,pT,wc,band);format short e; LCRs, LCRs_, RL=LCRs(end)% Another way to determine the LC values using transform_LC():LCs0=gg(1:N); LCs0_={'L(h)','C(v)','L(h)','C(v)'};[LCs1,LCs1_]=transform_LC(LCs0,LCs0_,wc,band,Rs)% To plot the frequency response magnitude (considering Rs and RL)ff=logspace(-1,1,301)*fc; ww=2*pi*ff; % Frequency ranges=j*ww; Gw=eval(Gs); % Frequency responseGwmagdB=20*log10(max(abs(Gw)/(RL/(Rs+RL)),1e-5)); % Freq resp magnitudesemilogx(ff,GwmagdB)
>>elec06e10LCRs = 1.2181e-08 2.9408e-02 2.9408e-08 1.2181e-02 1.0000e+03LCRs_ = 'C(v)' 'L(h)' 'C(v)' 'L(h)' 'R(v)'RL = 1000
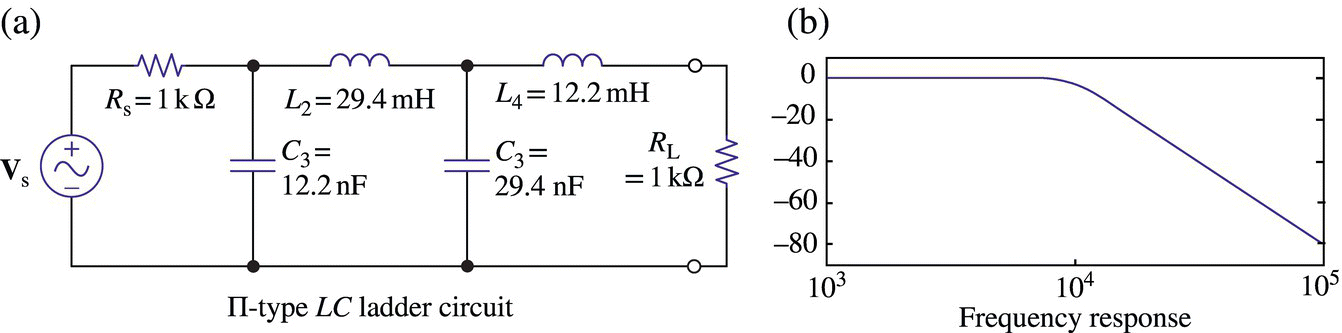
Figure 6.16 Fourth‐order Butterworth LPF realized with a П‐type LC ladder and its frequency response.
Example 6.11 Realization of a Sixth‐Order Chebyshev I BPF with Rp = 3 dB
Using a T‐type LC ladder circuit, realize a sixth‐order Chebyshev I BPF with passband ripple Rp = 3 dB and lower/upper cutoff frequencies fl/fu = 2.16/2.64 [Giga‐Hz] to be connected to a line or source resistance Rs = 50 Ω. Plot its insertion loss (IL), which is defined as the ratio of the power (delivered to the load without the filter) to the power (delivered to the load with the filter inserted):
The filter realization can be obtained by running the following MATLAB script “elec06e11.m,” which uses the MATLAB functions ‘LPF_ladder_coef()’ (with N = 6/2 = 3 for an LPF‐to‐BPF conversion doubling the order) and ‘LC_ladder()’ (with pT = ‘T’) to make the T‐type LC ladder as shown in Figure 6.17(a) and plot its IL as shown in Figure 6.17(b):
%elec06e11.m% Chebyshev I BPF realization in Example 6.11 (Ex 5.4 of [L-1])syms sN=3; pT='T'; Rs=50; type='C'; Rp=3;fl=2.16e9; fu=2.64e9; wl=2*pi*fl; wu=2*pi*fu; w0=sqrt(wl*wu);gg=LPF_ladder_coef(N,type,Rp); % Find the LC values[LCRs,LCRs_,Gs]=LC_ladder(Rs,gg,pT,[wl wu],'BPF');format short e; LCRs, LCRs_, RL=LCRs(end);ww=logspace(-1,1,301)*w0; ff=ww/2/pi; % Frequency rangefor n=1:length(ww), Gw(n)=subs(Gs,s,j*ww(n)); endIL_dB=-20*log10(max((Rs+RL)/RL*abs(Gw),1e-5)); % IL by Eq. (E6.11.1)semilogx(ff,IL_dB)
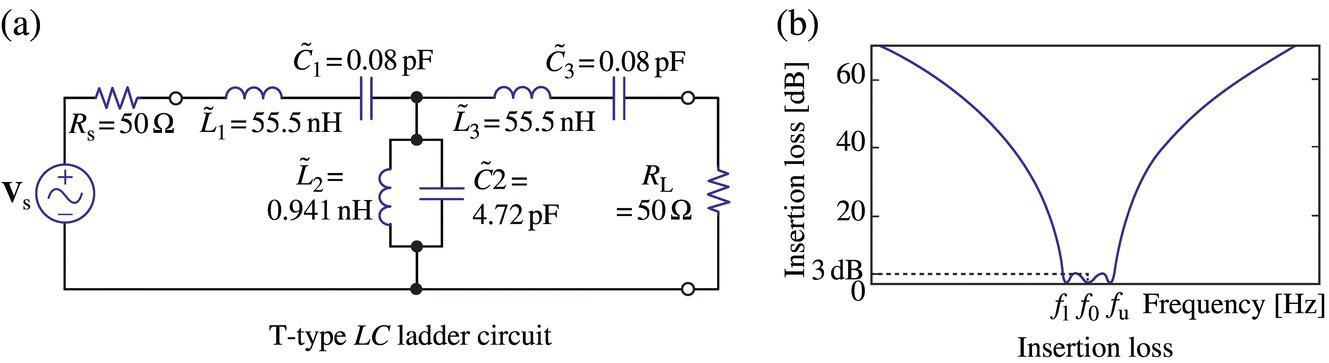
Figure 6.17 Sixth‐order Chebyshev BPF realized with a T‐type LC ladder and its insertion loss.
>>elec06e11LCRs = 5.5521e-08 8.0007e-14 9.4123e-10 4.7194e-125.5521e-08 8.0007e-14 5.0000e+01LCRs_ = 'L-C(h)' 'L|C(v)' 'L-C(h)' 'R(v)'
This describes the circuit (excluding the source‐line part) of Figure 6.17(a) (identical to Figure 5.30 of [L-1]) where the first element of the cell LCRs_, 'L‐C(h)', together with the first two elements of the vector LCRs, means the horizontal LC series connection with L = 0.554 nH and C = 0.08 pF, the second element of the cell LCRs_, 'L|C(v)', together with the next two elements of the vector LCRs, means the vertical LC shunt connection with L = 0.94 nH and C = 4.71 pF, and so on.
The MATLAB function ‘transform_LC()’ can also be used to get the same results:
>>LCs=gg(1:N); % From Table 5-4(a) of [L-1] for N=3Rs=50; LCs_={'L','C','L'}; % For a T-type filter with L firstformat short e[LCs2,LCs2_]=transform_LC(LCs,LCs_,[wl wu],'BPF',Rs) % LC valuesRL=gg(N+1)*Rs % Load resistance
Running these MATLAB statements yields
LCs2 =5.5521e-08 8.0007e-14 9.4123e-10 4.7194e-12 5.5521e-08 8.0007e-14LCs2_ = 'L-C' 'L|C' 'L-C'RL = 50
This describes the circuit (excluding the source‐line part) of Figure 6.17(a) where the first element of the cell LCRs_, 'L‐C', together with the first two elements of the vector LCRs, means the (horizontal) LC series connection with L = 0.554 nH and C = 0.08 pF, the second element of the cell LCRs_, 'L|C', together with the next two elements of the vector LCRs, means the (vertical) LC shunt connection with L = 0.94 nH and C = 4.71 pF, and so on.
If you want to get the numerator and denominator coefficients of the filter transfer function obtained as the third output argument Gs of ‘LC_ladder()’, run the following MATLAB statements:
>>[Ns,Ds]=numden(simplify(Gs)); % Extract the numerator/denominatorB_bpf=sym2poly(Ns); A_bpf=sym2poly(Ds);% To normalize the denominator so that its leading coefficient is 1,B_bpf=B_bpf/A_bpf(1), A_bpf=A_bpf/A_bpf(1)
If you want to get only the numerator and denominator coefficients of the filter transfer function, it is enough to run the following MATLAB statements:
>>[B_bpf1,A_bpf1]=cheby1(N,Rp,[wl wu],'s');B_bpf1=B_bpf1*RL/(Rs+RL), A_bpf1
6.3.2 L‐Type Impedance Matcher
Figure 6.18 shows two L‐types of LC filters (with Zk = jXk = jωLk or Zk = jXk = 1/jωCk) that can be used to accomplish the impedance matching condition [Y-1], (6.38) 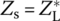 (*: complex conjugate) between the source impedance Zs = Rs + jXs and load impedance ZL = RL + jXL. The impedance matching condition for maximum power transfer of L1‐type filter (Figure 6.18(a)) can be written as
(*: complex conjugate) between the source impedance Zs = Rs + jXs and load impedance ZL = RL + jXL. The impedance matching condition for maximum power transfer of L1‐type filter (Figure 6.18(a)) can be written as
function [X11,X21,X12,X22]=imp_matcher_L(Zs,ZL,fc,type)% If type is not given, find L1&L2-types of LC impedance matcher(s).% If type is given as 1|2, find L1|L2-type of LC impedance matcher(s).% Copyleft: Won Y. Yang, wyyang53@hanmail.net, CAU for academic use onlyX11=inf*[1 1]; X21=[0 0]; X12=[0 0]; X22=inf*[1 1];if nargin<4|type~=2, type=1; endif type==2, tmp=Zs; Zs=ZL; ZL=tmp; end % switch Zs and ZLYs=1/Zs; Gs=real(Ys); Bs=-imag(Ys);RL=real(ZL); XL=imag(ZL);tmp=Gs/RL-Gs^2; B=Bs+sqrt(tmp)*[1 -1]; % Eq. (6.3.1a)if tmp>=0, X11=-1./B; X=RL*(B-Bs)/Gs-XL; X21=X; end % Eq. (6.3.1b)if type==2, tmp=X11; X11=X21; X21=tmp; endexpress_L_filter(X11,X21,2*pi*fc,type);if nargin<4&type==1[X12,X22]=imp_matcher_L(Zs,ZL,fc,2);end% - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -function express_L_filter(X1s,X2s,wc,type)for n=1:length(X1s)X1=X1s(n); X2=X2s(n);if X1==0|X1==inf|X2==0|X2==inf, continue; endif ~(X1==0|X2==0)if X1>0L1=X1/wc*1e6; fprintf(['L' num2str(type) '-type impedance matcher with L1=%8.3e[uH]'],L1);elseC1=-1e9/X1/wc; fprintf(['L' num2str(type) '-type impedance matcher with C1=%8.3e[nF]'],C1);endif X2>0, L2=X2/wc*1e6; fprintf(' and L2=%8.3e[uH]\n',L2);else C2=-1e9/X2/wc; fprintf(' and C2=%8.3e[nF]\n',C2);endendend
Figure 6.18 L‐type impedance matchers.
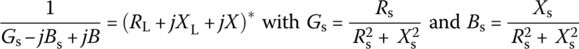
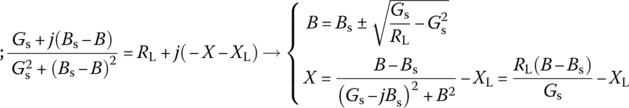
Likewise, noting that the structure of L2‐type filter (Figure 6.18(b)) is just like the reverse of L1‐type filter with Zs and ZL switched, the impedance matching condition of L2‐type filter can be written as
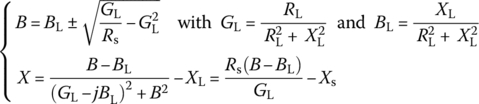
The above MATLAB function ‘imp_matcher_L()’ can be used to find possible L‐type filter(s) for impedance matching between given source/load impedances. Note that the function without the fourth input argument ‘type’ returns all possible L‐type LC filters while with type = 1/2, it returns just L1‐/L2‐type LC filter(s).
Example 6.12 Design of L‐type Impedance Matcher
Design L‐type impedance matchers for maximum power transfer from a transmitter with output impedance Zs = 50 + 1/jωCs (Cs = 9.362 pF) = 50 ‐ j17 to an antenna with input impedance ZL = 40 + jωLL (LL = 7.958 nH) = 40 + j50 at the center frequency fc = 1 GHz. (Visit http://leleivre.com/rf_lcmatch.html for reference.)
To use the above MATLAB function ‘imp_matcher_L()’, we run the MATLAB script “elec06e12.m” below, which uses the MATLAB function ‘imp_matcher_L_and_freq_resp()’:
%elec06e12.m% To design L-type impedance matchers in Example 6.12.clear, clffc=1e9; wc=2*pi*fc; ff=logspace(-1,1,601)*fc; % Center frequencyRs=50; Cs=9.362e-12; RL=40; LL=7.958e-9; % Source and Load impedancesZs=Rs+1/j/wc/Cs % Output impedance of the transmitterZL=RL+j*wc*LL % Input impedance of the load (antenna)[LC,LC_,ff,Gws]=imp_matcher_L_and_freq_resp(Zs,ZL,fc,ff);LC, LC_function [LC,LC_,ff,Gws]=imp_matcher_L_and_freq_resp(Zs,ZL,fc,ff)% LC values and Frequency response of L-type impedance matchersif nargin<4, ff=logspace(-1,1,801)*fc; endwc=2*pi*fc; w=2*pi*ff; jw=j*w; % Frequency vectorsyms sRs=real(Zs); Xs=imag(Zs); Zss=Rs+(Xs>=0)*s*Xs/wc-(Xs<0)*wc*Xs/s;RL=real(ZL); XL=imag(ZL); ZLs=RL+(XL>=0)*s*XL/wc-(XL<0)*wc*XL/s;[X11,X21,X12,X22]=imp_matcher_L(Zs,ZL,fc);Gw1s=[]; Gw2s=[]; LC=[]; gss='bgrmkc';for n=1:numel(X11) % For L1-type,syms s; X1=X11(n); X2=X21(n);if X1==0|X1==inf|X2==0|X2==inf, continue; end% To check if Zs||Z1 and Z2+ZL of L1-type are conjugate,[parallel_comb([Zs j*X1]); j*X2+ZL]if X1>0, LC(n,1)=X1/wc; LC_{n,1}='L(v)';else LC(n,1)=-1/X1/wc; LC_{n,1}='C(v)';endif X2>0, LC(n,2)=X2/wc; LC_{n,2}='L(h)';else LC(n,2)=-1/X2/wc; LC_{n,2}='C(h)';endZ1s=(X1>=0)*s*X1/wc-(X1<0)*wc*X1/s;Z2s=(X2>=0)*s*X2/wc-(X2<0)*wc*X2/s;Z12Ls=Z1s*(Z2s+ZLs)/(Z1s+Z2s+ZLs);G2s=Z12Ls/(Zss+Z12Ls)*RL/(Z2s+ZLs);s=jw; Gw=eval(G2s); Gw1s=[Gw1s; Gw];subplot(233), semilogx(ff,abs(Gw).^2/RL,gss(n))endm=size(LC,1);for n=1:numel(X12) % For L2-type,syms s; X1=X12(n); X2=X22(n);if X1==0|X1==inf|X2==0|X2==inf, continue; end% To check if Zs+Z1 and Z2||ZL of L2-type are conjugate,[Zs+j*X1; parallel_comb([j*X2 ZL])]if X1>0, LC(m+n,1)=X1/wc; LC_{m+n,1}='L(h)';else LC(m+n,1)=-1/X1/wc; LC_{m+n,1}='C(h)';endif X2>0, LC(m+n,2)=X2/wc; LC_{m+n,2}='L(v)';else LC(m+n,2)=-1/X2/wc; LC_{m+n,2}='C(v)';endZ1s=(X1>=0)*s*X1/wc-(X1<0)*wc*X1/s;Z2s=(X2>=0)*s*X2/wc-(X2<0)*wc*X2/s;Z2Ls=Z2s*ZLs/(Z2s+ZLs);G2s=Z2Ls/(Zss+Z1s+Z2Ls)*RL/ZLs;s=jw; Gw=eval(G2s); Gw2s=[Gw2s; Gw];subplot(236), semilogx(ff,abs(Gw).^2/RL,gss(n))endGws=[Gw1s; Gw2s].';
>>eles06e12LC = LC_ =8.2200e-13 6.3975e-12 'C(v)' 'C(h)'9.1702e-09 2.1185e-12 'L(v)' 'C(h)'1.0860e-08 3.5320e-12 'L(h)' 'C(v)'4.6487e-12 3.4983e-13 'C(h)' 'C(v)'
This result implies that there are four L‐type LC circuits that can present impedance matching between the source and load as depicted in Figure 6.19. It can be shown that 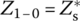 and
and  for all of the LC circuits. Say, for the impedance matcher in Figure 6.19(a1), we have
for all of the LC circuits. Say, for the impedance matcher in Figure 6.19(a1), we have
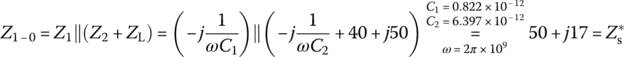
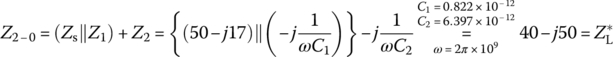
Figure 6.20(a1), (a2), (b1), and (b2) shows the PSpice schematics for the circuits of Figure 6.19. Figure 6.20(c1) and (c2) shows two plots of power (transferred to and dissipated by the load RL) versus frequency, one obtained from PSpice simulation and the other obtained from MATLAB analysis, that conform with each other. It can be seen from the power plots that the four L‐type circuits commonly perform impedance matching so that the power transfer to the load is maximized at the center frequency fc = 1 GHz although their quality factors or selectivities differ.

Figure 6.19 L‐type filters used for impedance matching in Example 6.12.

Figure 6.20 PSpice schematics for the circuits of Figure 6.19 and their plots of power PRL versus frequency.
6.3.3 T‐ and П‐Type Impedance Matchers
Figure 6.21 shows T‐ and П‐type LC ladders (with Zk = jXk = jωLk or Zk = jXk = 1/jωCk) that can be used to accomplish impedance matching between the source impedance Zs = Rs + jXs and load impedance ZL = RL + jXL. The conditions for impedance matching of T‐type filter (Figure 6.21(a)) with quality factor Q can be formulated into the formulas for computing Z3 = jX3, Z2 = jX2, and Z1 = jX1 as
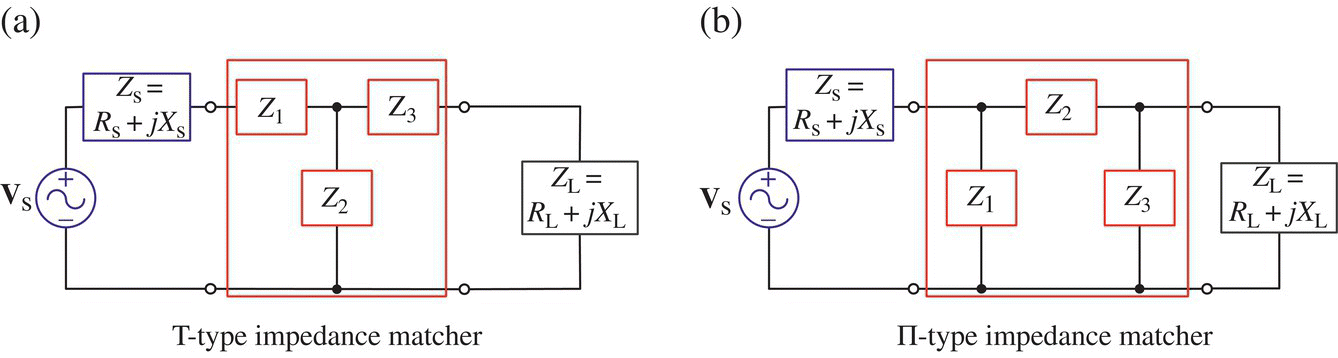
Figure 6.21 T‐ and П‐type impedance matchers.
The Y‐Δ conversion of a T‐type impedance matcher yields its equivalent П‐type impedance matcher (Figure 6.21(b)).
function [X1s,X2s,X3s,Zins]=imp_matcher_T(Zs,ZL,Q,f)% Determine the T-type impedance matcher between Zs and ZL.% Copyleft: Won Y. Yang, wyyang53@hanmail.net, CAU for academic use onlyRs=real(Zs); Xs=imag(Zs); % Source impedanceRL=real(ZL); XL=imag(ZL); % Load impedanceb=2*XL; c=(RL^2+XL^2)-RL*Rs*(1+Q^2); % Eq. (6.3.3a)tmp=b^2-4*c;if tmp<0, error('Rs=real(Zs) must be increased'); endif tmp<=1e-8; X3=-b/2;else X3=(-b+[1 -1]*sqrt(tmp))/2;enda=RL-Rs; b=-2*Rs*(XL+X3); c=-Rs*(RL^2+(XL+X3).^2); % Eq. (6.3.3b)tmp=b.^2-4*a*c; tmp=tmp(1); % Since tmp(1)=tmp(2)if tmp<0, error('Rin=real(Zin) must be increased'); endX3s=[]; X2s=[];for n=1:length(b)if abs(a)<eps, X2n=-c/b; X3n=X3(n); elseif tmp<=1e-8; X2n=-b(n)/2/a; X3n=X3(n);else X2n=(-b(n)+[1 -1]*sqrt(tmp))/2/a; X3n=[X3(n) X3(n)];endendX2s=[X2s X2n]; X3s=[X3s X3n];endZ23Ls=1./(1./(j*X2s)+1./(j*X3s+ZL));ids=find(abs(real(Z23Ls)-Rs)<0.1);X2s=X2s(ids); X3s=X3s(ids); Z23Ls=Z23Ls(ids);X1s=-Xs-imag(Z23Ls); % Eq. (6.3.3c)Zins=j*X1s+Z23Ls;express_T_filter(X1s,X2s,X3s,2*pi*f);function express_T_filter(X1s,X2s,X3s,w)for n=1:length(X1s)X1=X1s(n); X2=X2s(n); X3=X3s(n);if X1>0L1=X1/w*1e6; fprintf('T-type imp matcher: L1=%8.3e[uH]',L1);elseC1=-1e9/X1/w; fprintf('T-type imp matcher: C1=%8.3e[nF]',C1);endif X2>0, L2=X2/w*1e6; fprintf(', L2=%8.3e[uH]',L2);else C2=-1e9/X2/w; fprintf(', C2=%8.3e[nF]',C2);endif X3>0, L3=X3/w*1e6; fprintf(', L3=%8.3e[uH]\n',L3);else C3=-1e9/X3/w; fprintf(', C3=%8.3e[nF]\n',C3);endend
function [X1s,X2s,X3s,Zins]=imp_matcher_pi(Zs,ZL,Q,f)% Determine the pi-type impedance matcher between Zs and ZL.% Copyleft: Won Y. Yang, wyyang53@hanmail.net, CAU for academic use only[Xas,Xbs,Xcs,Zins]=imp_matcher_T(Zs,ZL,Q,f);for i=1:length(Xas)[X1s(i),X3s(i),X2s(i)]=yd_conversion(Xas(i),Xbs(i),Xcs(i));endY23Ls=1./(j*X2s+1./(1./(j*X3s)+1/ZL));Zins=1./(1./(j*X1s)+Y23Ls);express_pi_filter(X1s,X2s,X3s,w);% - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -function express_pi_filter(X1s,X2s,X3s,w)for n=1:length(X1s)X1=X1s(n); X2=X2s(n); X3=X3s(n);if X1>0L1=X1/w*1e6;fprintf('pi-type imp matcher: L1=%8.3e[uH]',L1);elseC1=-1e9/X1/w;fprintf('pi-type imp matcher: C1=%8.3e[nF]',C1);endif X2>0, L2=X2/w*1e6; fprintf(', L2=%8.3e[uH]',L2);else C2=-1e9/X2/w; fprintf(', C2=%8.3e[nF]',C2);endif X3>0, L3=X3/w*1e6; fprintf(', L3=%8.3e[uH]\n',L3);else C3=-1e9/X3/w; fprintf(', C3=%8.3e[nF]\n',C3);endend
function [Zab,Zbc,Zca]=yd_conversion(Za,Zb,Zc)% Wye-Delta Transformationtemp = Za*Zb+Zb*Zc+Zc*Za;Zab=temp/Zc; Zbc=temp/Za; Zca=temp/Zb;function [Za,Zb,Zc]=dy_conversion(Zab,Zbc,Zca)% Delta-Wye Transformationtemp = Zab+Zbc+Zca;Za=Zca*Zab/temp; Zb=Zab*Zbc/temp; Zc=Zbc*Zca/temp;
The above MATLAB functions ‘imp_matcher_T()’/‘imp_matcher_pi()’ can be used to find possible T/П‐type LC filter(s) (with given quality factor Q) tuned for impedance matching between given source and load impedances, respectively.
Example 6.13 Design of T‐type Impedance Matcher
Make as many T‐type ladders as possible, with quality factor Q = 3 for maximum power transfer from a transmitter with output impedance Zs = 10 ‐ j/ωCs (Cs = 7.958 pF) to an antenna with input impedance ZL = 60 ‐ j/ωcCL (CL = 5.305 pF) at the center frequency fc = 1 GHz.
We run the following MATLAB statements:
>>fc=1e9; wc=2*pi*fc; Q=3;Rs=10; Cs=7.958e-12; Zs=Rs-j/(wc*Cs) % Zs=10-20iRL=60; CL=5.305e-12; ZL=RL-j/(wc*CL) % ZL=60-30i[X1s,X2s,X3s,Zins_T]=imp_matcher_T(Zs,ZL,Q,fc);
This yields
T-type imp matcher: C1=1.591e-02[nF], L2=7.289e-03[uH], L3=1.257e-02[uH]T-type imp matcher: L1=7.958e-03[uH], C2=6.074e-03[nF], L3=1.257e-02[uH]T-type imp matcher: C1=1.591e-02[nF], L2=4.170e-03[uH], C3=8.381e-03[nF]T-type imp matcher: L1=7.958e-03[uH], C2=3.475e-03[nF], C3=8.381e-03[nF]
This result implies that there are four T‐types of LC circuits that can present impedance matching between the source and load as depicted in Figure 6.22.
If you want to check if each ladder satisfies the impedance matching condition, it is enough to see that the input impedance (seen from nodes 1‐0) obtained as the fourth output argument Zins_T of ‘imp_matcher_pi()’ is equal to  . If you are still not sure, check if
. If you are still not sure, check if 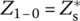 by running the following statements:
by running the following statements:

Figure 6.22 T‐type ladder circuits used for impedance matching in Example 6.13.
>>for n=1:numel(X1s)Z10=j*X1s(n)+parallel_comb([j*X2s(n) j*X3s(n)+ZL]) %Z1+{Z2||(Z3+ZL)}% This is expected to be equal to the conjugate of Zs.end
This yields
Z10 = 10.0000 +19.9994iZ10 = 10.0000 +19.9994iZ10 = 10.0000 +19.9994iZ10 = 10.0000 +19.9994i
That is, for the ladder in Figure 6.22(a), we have
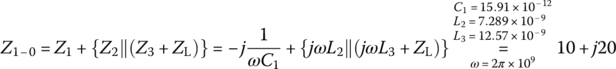
Also, for the ladder in Figure 6.22(b), we have
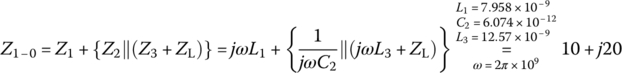
Example 6.14 Design of П‐type Impedance Matcher
Make as many П‐type LC ladders as possible, with quality factor Q = 2 for maximum power transfer from a transmitter with output impedance Zs = 20 − j/ωCs (Cs = 1.658 pF) to an antenna with input impedance ZL = 10 − j/ωcCL (CL = 6.632 pF) at the center frequency fc = 2.4 GHz.
We can run the following MATLAB statements:
>>fc=2.4e9; wc=2*pi*fc; Q=2;Rs=20; Cs=1.658e-12; Zs=Rs-j/(wc*Cs) % Zs=20-40iRL=10; CL=6.632e-12; ZL=RL-j/(wc*CL) % ZL=10-10i[X1s,X2s,X3s,Zins_pi]=imp_matcher_pi(Zs,ZL,Q,fc);
This yields
pi-type imp matcher: C1=6.632e-04[nF], L2=2.652e-03[uH],L3=8.083e+01[uH]pi-type imp matcher: L1=1.326e-03[uH], C2=1.658e-03[nF], L3=6.631e-04[uH]pi-type imp matcher: L1=1.326e-03[uH], C2=3.316e-03[nF],L3=8.084e+00[uH]pi-type imp matcher: C1=3.014e-04[nF], L2=2.918e-03[uH], L3=3.647e-03[uH]
This result implies that there are four П‐type LC ladders that can present impedance matching between the source and load as depicted in Figure 6.23.
If you want to check if each ladder satisfies the impedance matching condition, it is enough to see that the input impedance (seen from nodes 1‐0) obtained as the fourth output argument Zins_pi of ‘imp_matcher_pi()’ is equal to  . If you are still not sure, check if Z1‐0 = (Z2 + Z2‐0)*:
. If you are still not sure, check if Z1‐0 = (Z2 + Z2‐0)*:
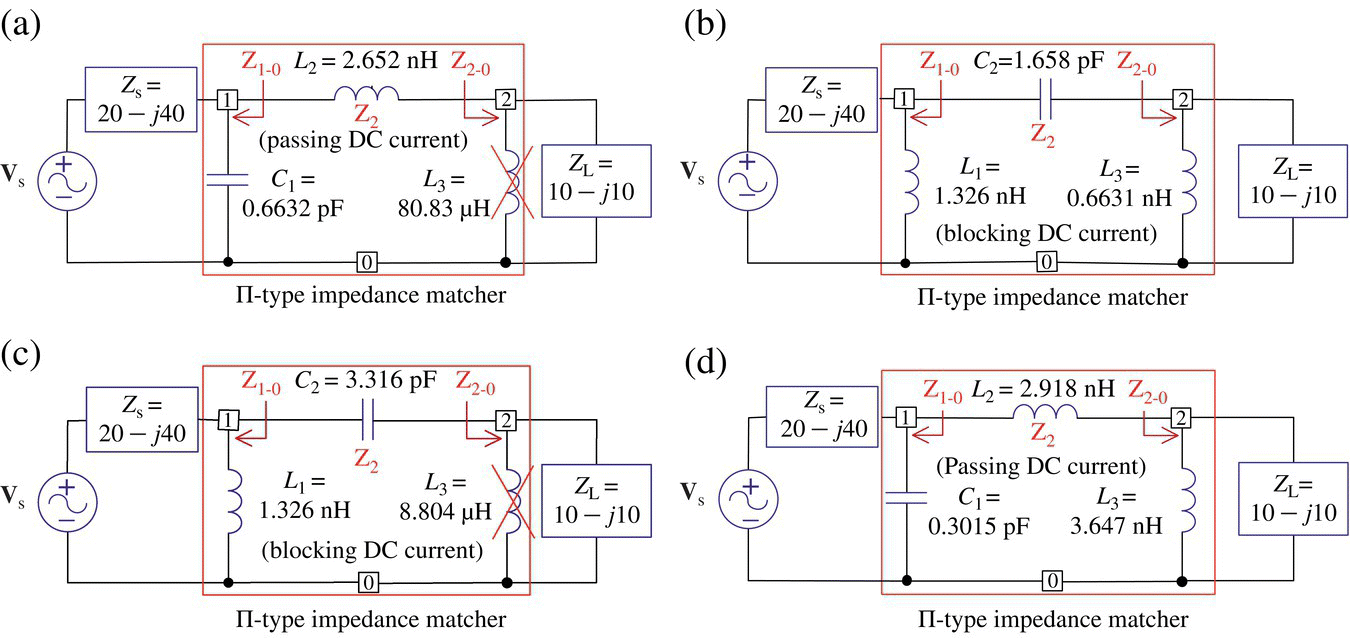
Figure 6.23 П‐type ladder circuits used for impedance matching in Example 6.14.
>>for n=1:numel(X1s)Z10=parallel_comb([Zs j*X1s(n)])Z2=j*X2s(n); Z20=parallel_comb([j*X3s(n) ZL]); Z2+Z20end
However, the values of X3 = ωcL3 of Figure 6.23(a) and (c) are overwhelmingly larger than |ZL| =  , the parallel L3's are not meaningful as can be seen by typing ‘X3s’ at the MATLAB prompt:
, the parallel L3's are not meaningful as can be seen by typing ‘X3s’ at the MATLAB prompt:
>>X3sX3s = 1.0e+06 * 1.21895 0.00001 0.12191 0.00005
This implies that Figure 6.23(a) and (c) is virtually L‐type impedance matcher without L3.
6.3.4 Tapped‐C Impedance Matchers
Figure 6.24(a) shows a tapped‐C(capacitor) impedance matching circuit for a desired quality factor of Q/2 between R1 and R2. Figure 6.24(b) shows the intermediate equivalent circuit where the parallel R1|C2 part (with a target quality factor Qp to be determined) has been transformed into its series equivalent consisting of R1s‐C2s and the parallel L|R2 part (with a quality factor Q given) has been transformed into its series equivalent consisting of Ls‐R2s by applying Eq. (6.2.28a). Figure 6.24(c) shows the final equivalent circuit with the series C1‐C2s part replaced by its series combination where

Figure 6.24 Tapped‐C impedance matching circuit and its equivalents.
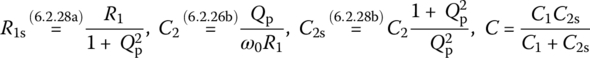
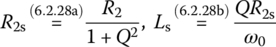
Noting that if the quality factors of the source and load parts from node 2 are equally Q, their composite quality factor will be 1/(1/Q + 1/Q) = Q/2, we write the condition for the quality factor of the load (L|R2) part (i.e. the parallel combination of L and R2) to be Q as
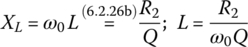
Also, the impedance matching conditions to make the source and load impedances, Z1 and Z2, a complex conjugate pair can be written as
(6.3.8)
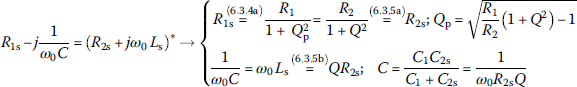
function [L,C1,C2,Qr,Qp,Rp,Z1,Z2]=imp_matcher_tapped_C(R1,R2,f0,Q)% Q : Desired quality factor.w0=2*pi*f0; Q2=2*Q; X2=R2/Q2; % Eq. (6.3.6a)R2s=R2/(1+Q2^2); L=X2/w0; % Eqs. (6.3.5a),(6.3.6b)Qp = sqrt(R1/R2*(1+Q2^2)-1); % Eq. (6.3.7)R1s = R1/(1+Qp^2); % Eq. (6.3.4a)C2 = Qp/w0/R1; C2s = C2*(1+Qp^2)/Qp^2; % Eq. (6.3.4b,c)C = 1/w0/R2s/Q2; % Eq. (6.3.8)C1 = C*C2s/(C2s-C); % Eq. (6.3.9)if C1<0, error('\n How about switching R1 and R2?\n'); endRp=(1+Q2^2)*R1s; % Eq. (6.2.29a): Series-to-parallel conversion of R1sQr = parallel_comb([Rp R2])/X2; % Resulting value of Quality factor% To get the impedance Z1(w) that is expected to be matched to R1,jw0=j*w0; ZC1LRL = 1/jw0/C1 + parallel_comb([jw0*L R2]);Z1 = parallel_comb([1/jw0/C2 ZC1LRL]); % = R1 ?fprintf('\n Z1=%5.0f + j%5.0f matches to R1=%5.0f?',real(Z1),imag(Z1),R1)% To get the impedance Z2(w) that is expected to be matched to R2,ZC1C2Rs = 1/jw0/C1 + parallel_comb([1/jw0/C2 R1]);Z2 = parallel_comb([ZC1C2Rs jw0*L]); % = R2 ?fprintf('\n Z2=%5.0f + j%8.0f matches to R2=%5.0f?\n',real(Z2),imag(Z2),R2)fprintf('\n Design results for given R1=%5.0f[Ohm], R2=%5.0f[Ohm], and Q=%5.0f,',R1,R2,Q)fprintf('\n C1=%11.3e[mF], C2=%11.3e[mF], L=%11.3e[mH]\n', C1*1e3,C2*1e3,L*1e3)
Once the series combination of C1‐C2s part, that is C, is determined from Eq. (6.3.8), we can use the determined value of C2s (Eq. (6.3.4c)) together with Eq. (6.3.8) to find C1:
This process of designing a tapped‐C impedance matcher has been cast into the above MATLAB function ‘imp_matcher_tapped_C()’, in which the resulting value of quality factor Q, in the variable name of ‘Qr’, is computed as
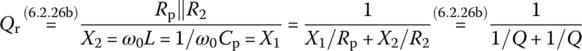
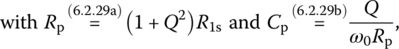
since if the series R1s‐C part (in Figure 6.24(c)) is converted to its parallel equivalent Rp|Cp while the series R2s‐Ls part (in Figure 6.24(c)) is converted back to its parallel equivalent (as shown in Figure 6.24(d)), the resistance in parallel with L and Cp is not just R2 but Rp‖R2.
Example 6.15 Design of Tapped‐C Impedance Matcher
Design a tapped‐C impedance matcher for source/load resistances R1/R2 = 5/50 [Ω] at f0 = 150 MHz such that the loaded quality factor is Q = 10, find the equivalent impedances Z1/Z2 (see Figure 6.25(a)) to check if they match to R1/R2, respectively, and plot its frequency response magnitude G(ω) = Vo(ω)/Vi(ω) to see the resulting value of Q = fp/(fu − fl) where fp is the peak frequency that is expected to conform with the resonant frequency for most BPFs.
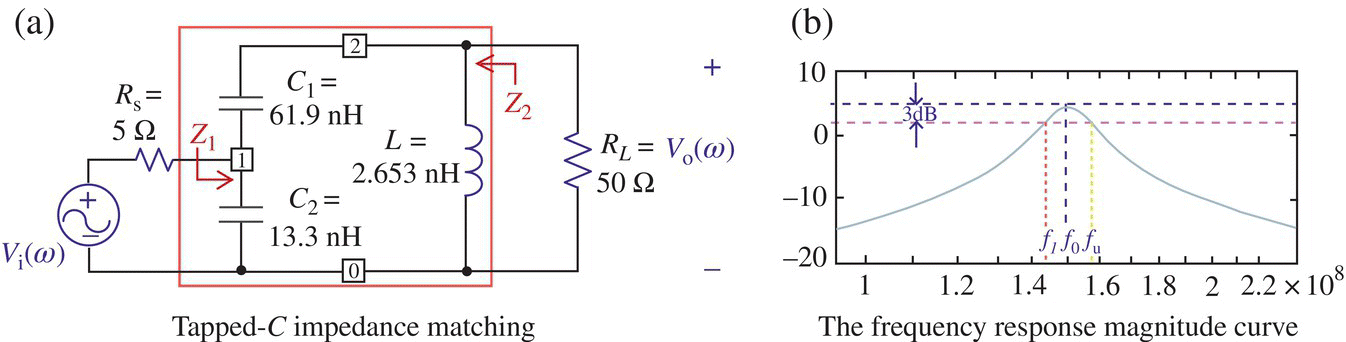
Figure 6.25 Tapped‐C impedance matching circuit for Example 6.15.
%elec06e15.m% Try the tapped-C impedance matching.clear, clfRs=5; RL=50; f0=150e6; w0=2*pi*f0; jw0=j*w0; Q=10;[L,C1,C2,Q_resulting,Qp,Rp,Z1,Z2]=…imp_matcher_tapped_C (Rs,RL,f0,Q);% To get the frequency response,f=logspace(-0.2,0.2,600)*f0; w=2*pi*f; % Frequency rangejw=j*w;ZLRLw = 1./(1./jw/L+1/RL);ZC1LRLw = 1./jw/C1 + ZLRLw;ZC1C2LRLw = 1./(jw*C2 + 1./ZC1LRLw);Gw=ZC1C2LRLw./(Rs+ZC1C2LRLw).*ZLRLw./ZC1LRLw/(RL/(Rs+RL));GwmagdB = 20*log10(abs(Gw)); % Frequency response magnitudesemilogx(f,GwmagdB), hold on[peak,idx]=max(GwmagdB); f0=f(idx) % Peak frequency% To find the lower/upper 3dB frequencies[peaks,idx]=findpeaks(-abs(GwmagdB-peak+3));if numel(idx)>1fl=f(idx(1)), fu=f(idx(2)), Q_loaded_measured = f0/(fu-fl)elsefprintf('\n Q should be larger to get such a concave-down freq.resp. magnitude curve\n that has two 3dB frequenciesfl and fu.\n')end
To this end, we can run the above script “elec06e15.m,” which uses the MATLAB function ‘imp_matcher_tapped_C()’ inside, to get
>>elec06e15Z1= 5 + j 0 matches to R1= 5?Z2= 50 + j 0 matches to R2= 50?Design results for given R1= 5[Ohm], R2= 50[Ohm], and Q= 10C1= 6.190e-07[mF], C2= 1.327e-06[mF], L= 2.653e-06[mH]f0 = 1.5012e+08, fl = 1.4269e+08, fu = 1.5769e+08Q_loaded_measured = 1.0009e+01
This means the tapped‐C impedance matching circuit shown in Figure 6.25(a) where the impedances Z1 and Z2 match R1 = 5 [Ω] and R2 = 50 [Ω], respectively, and the loaded Q = fp/(fu − fl) has turned out to be 10 as required by the design specifications. Figure 6.25(b) shows the frequency response magnitude curve together with the lower and upper 3 dB frequencies.
Note that in case where Rs>RL, the MATLAB function ‘imp_matcher_tapped_C()’ should be used with Rs and RL switched and also the tapped‐C impedance matcher should be flipped horizontally.
6.4 Active Filter Realization
This section introduces some MATLAB functions that can be used to determine the parameters of the circuits depicted in Figures 5.17‐5.20 so that they can implement a given (designed) transfer function.
function [R1,CR2,Gs]=LPF_RC_OPAmp_design(B,A,R2C,KC)% Design a 1st-order LPF with the circuit in Fig. 5.17(a)% R2 1/R2C B A B% G(s) = - -- - - - - - - - = - - - - = - - - - (5.5.1)% R1 s + 1/R2C A s+A s+Aif nargin<4, KC=1; endif KC==1 % Find R1 and C for given R2.R2=R2C; C=1/(A*R2); R1=1/(B*C); CR2=C;else % Find R1 and R2 for given C.C=R2C; R2=1/(A*C); R1=1/(B*C); CR2=R2;endsyms s; Gs = B/(s+A);function [R1,CR2,Gs]=HPF_RC_OPAmp_design(B,A,R2C,KC)% Design a 1st-order HPF with the circuit in Fig. 5.17(b)% R2 s s% G(s) = - - -- - - - - - - = - B - - - (5.5.2)% R1 s + 1/R1C s+Aif nargin<4, KC=1; endif KC==1 % Find R1 and C for given R2.R2=R2C; C=1/(A*R1); R1=R2/B; CR2=C;else % Find R1 and R2 for given C.C=R2C; R1=1/(A*C); R2=R1*B; CR2=R2;endsyms s; Gs = B*s/(s+A);
function [CR1,CR2,Gs]=LPF_Sallen_design(A2,A3,K,RC1,RC2,KC)% Design an LPF with the circuit in Fig. 5.18(a)% KG1G2/C1C2 B3=K*A3% G(s) = - - - - - - - - - - - - - - - - - - - -- - - - - - - - - - = - - - - - - - - - - (5.5.3)% s^2 +((G1+G2)/C1+(1-K)G2/C2)*s +G1G2/C1C2 s^2 + A2*s + A3if K<1, fprintf('Let K=1 since we must have K=(R3+R4)/R3>=1!'); K=1; endif nargin<6, KC=1; endif KC==1 % Find C1 and C2 for given K, R1, and R2.R1= RC1; R2= RC2; G1= 1/R1; G2= 1/R2;a= G1+G2; b= -(K-1)*G2; c= A2; d= A3/G1/G2; tmp = c^2-4*a*b*d;C1= 2*a/(c + sqrt(tmp)); C2= 1/d/C1; CR1= C1; CR2= C2;else % Find R1 and R2 for given K, C1, and C2.C1= RC1; C2= RC2;a= 1/C1; b= 1/C1 - (K-1)/C2; c= A2; d= A3*C1*C2; tmp = c^2-4*a*b*d;if tmp<0, error('Increase C1 and K, or decrease C2'); endG1= (c + sqrt(tmp))/2/a; G2= d/G1; R1= 1/G1; R2= 1/G2; CR1= R1; CR2= R2;endB3= K*A3; A2= (G1+G2)/C1 + (1-K)*G2/C2; A3= G1*G2/C1/C2;syms s; Gs = B3/(s^2+A2*s+A3);
function [CR1,CR2,Gs]=HPF_Sallen_design(A2,A3,K,RC1,RC2,KC)% Design an HPF with the circuit in Fig. 5.18(b)% K*s^2 K*s^2% G(s) = - - - - - - - - - - - - - - - - - - - - - - - - - - - - - = - - - - - - - - - (5.5.4)% s^2 +(G2(1/C1+1/C2)-(K-1)G1/C1)s +G1G2/C1C2 s^2 + A2*s + A3if K<1, fprintf('Let K=1 since we must have K=(R3+R4)/R3>=1!'); K=1; endif nargin<6, KC=1; endif KC==1 % Find C1 and C2 for given K, R1, and R2.R1= RC1; R2= RC2; G1= 1/R1; G2= 1/R2;a= G2+(1-K)*G1; b= G2; c= A2; d= A3/G1/G2; tmp= c^2-4*a*b*d;if tmp<0, error('Try with smaller/greater values of R1/K'); endC1= 2*a/(c + sign(a)*sqrt(tmp)); C2= 1/d/C1; CR1= C1; CR2= C2;else % Find R1 and R2 for given K, C1, and C2.C1=RC1; C2=RC2;a=(1-K)/C1; b=1/C1+1/C2; c=A2; d=A3*C1*C2; tmp=c^2-4*a*b*d;if tmp<0, error('Try with smaller/greater values of C2/K'); endif abs(a)<eps, G2= A2/b; G1= d/G2;else G1= (c + sign(a)*sqrt(tmp))/2/a; G2= d/G1;endR1= 1/G1; R2= 1/G2; CR1= R1; CR2= R2;endB1= K; A2= G2*(1/C1+1/C2) - (K-1)*G1/C1; A3= G1*G2/C1/C2;syms s; Gs = B1*s^2/(s^2+A2*s+A3);
function [R1,C2R3,C5R4,Gs]=LPF_MFB_design(B3,A2,A3,R3C2,R4C5,KC)% Design an LPF with the circuit in Fig. 5.19(a)% -G1G4/C2C5 -B3% G(s) = - - - - - - - - - - - - - - - - - - - - - = - - - - - - - - - (5.5.5)% s^2 + (G1+G3+G4)/C2*s + G3G4/C2C5 s^2 + A2*s + A3if nargin<6, KC=1; endif KC==1 % Find R1, C2 and C5 for given R3 and R4.R3= R3C2; R4= R4C5; G3= 1/R3; G4= 1/R4;G1=G3*B3/A3; C2=(G1+G3+G4)/A2; C5=G3*G4/C2/A3; R1=1/G1; C2R3=C2; C5R4=C5;else % Find R1, R3 and R4 for given C2 and C5.C2=R3C2; C5=R4C5; a=1+B3/A3; b=1; c=A2*C2; d=A3*C2*C5; tmp = c^2-4*a*b*d;if tmp<0, error('Try with greater/smaller values of C2/C5'); endG3= (c + sign(a)*sqrt(tmp))/2/a; G4= d/G3;G1= B3/A3*G3; R3= 1/G3; R4= 1/G4; R1=1/G1; C2R3= R3; C5R4= R4;endB3= G1*G4/C2/C5; A2= (G1+G3+G4)/C2; A3= G3*G4/C2/C5;syms s; Gs = -B3/(s^2+A2*s+A3);function [C1,C3R2,C4R5,Gs]=HPF_MFB_design(B1,A2,A3,R2C3,R5C4,KC)% Design an HPF with the circuit in Fig. 5.19(b)% -(C1/C3)*s^2 -B1*s^2% G(s) = - - - - - - - -- - - - - - - - - - - - - - - - - = - - - - - - - - - (5.5.6)% s^2 + G5(C1+C3+C4)/C3/C4*s + G2G5/C3C4 s^2 + A2*s + A3if nargin<6, KC=1; endif KC==1 % Find C1, C3 and C4 for given R2 and R5.R2= R2C3; R5= R5C4; G2= 1/R2; G5= 1/R5;a= 1; b= 1+B1; c= A2/G5; d= A3/G2/G5; tmp = c^2-4*a*b*d;if tmp<0, error('Try with smaller/greater values of R2/R5'); endC3= 2*a/(c + sqrt(tmp)); C4= 1/d/C3; C1= B1*C3; C3R2= C3; C4R5= C4;else % Find C1, R2 and R5 for given C3 and C4.C3= R2C3; C4= R5C4;C1 = B1*C3; G5= A2/(C1+C3+C4)*C3*C4; G2= A3*C3*C4/G5;R2= 1/G2; R5= 1/G5; C3R2= R2; C4R5= R5;endB1= C1/C3; A2= G5*(C1+C3+C4)/C3/C4; A3= G2*G5/C3/C4;syms s; Gs = -B1*s^2/(s^2+A2*s+A3);
function [C3R1,C4R2,R5,Gs]=BPF_MFBa_design(B2,A2,A3,R1C3,R2C4,KC)% Design a BPF with the circuit in Fig. 5.20(a)% -(G1/C3)*s -B2*s% G(s) = - - - - - - - - - - - - - - - - - - - - - - - - - = - - - - - - - - - (5.5.7)% s^2 + G5(1/C3+1/C4)*s + (G1+G2)G5/C3C4 s^2 + A2*s + A3if nargin<6, KC=(R1C3+R2C4>1)+2*(R1C3+R2C4<1); endif KC==1 % Find C3, C4, and R5 for given R1 and R2.R1=R1C3; R2=R2C4; G1=1/R1; G2=1/R2; C3=G1/B2;G5=(A2-A3*C3/(G1+G2))*C3;if G5<0, error('Try with smaller values of R2'); endC4= G5*(G1+G2)/C3/A3; R5=1/G5;C3R1=C3; C4R2=C4;elseif KC==2 % Find R1, R2 and R5 for given C3 and C4.C3=R1C3; C4=R2C4; G1=B2*C3; G5=A2/(1/C3+1/C4); G2=A3*C3*C4/G5-G1;R5=1/G5; R1=1/G1; R2=1/G2; C3R1=R1; C4R2=R2;elseif KC==3 % Find R1, R5, and C3=C4=C for given R2 and C3=C4.R2=R1C3; G2=1/R2;C=A2*G2/(2*A3-A2*B2); G5=A2/2*C;C3=C; C4=C; G1=B2*C; R1=1/G1; R5=1/G5;C3R1=C3; C4R2=R1;else % Find C3=C4, R5 for given R1 and R2 (not caring about B2).R1=R1C3; R2=R2C4; G1=1/R1; G2=1/R2;C=(G1+G2)*A2/2/A3; C3=C; C4=C; G5=A2/2*C; R5=1/G5;C3R1=C; C4R2=C;endfprintf('\n R1=%8.0f, R2=%8.0f, R5=%8.0f, C3=%10.3e, C4=%10.3e\n', R1,R2,R5,C3,C4)B2=G1/C3; A2=G5*(1/C3+1/C4); A3=(G1+G2)*G5/C3/C4;syms s; Gs = -B2*s/(s^2+A2*s+A3);function [C1,C2R3,C5R4,Gs]=BPF_MFBb_design(B2,A2,A3,R3C5,R4C5,KC)% Design a BPF with the circuit in Fig. 5.20(b)% -(C1G4/(C1+C2)C5)*s -B2*s% G(s)= - - - - - - - - - - - - - - - - - - - - - - - - - - - - = - - - - - - - - - - (5.5.8)% s^2 + ((G3+G4)/(C1+C2))*s + G3G4/(C1+C2)C5 s^2 + A2*s + A3if nargin<6, KC=1; endif KC==1 % Find C1, C2 and C5 for given R3 and R4.R3=R3C5; R4=R4C5; G3=1/R3; G4=1/R4;C1pC2= (G3+G4)/A2; C5= G3*G4/A3/C1pC2; C1=B2*C1pC2*C5/G4; %=B2*G3/A3C2= C1pC2 - C1;if C2<0, error('Try with greater/smaller values of R3/R4'); endC2R3= C2; C5R4= C5;elseif KC==2 % Find C1, R3 and R4 for given C5 and C1=C2.C5=R3C5; G4= 2*C5*B2; G3_2C= A3/G4*C5; %=A3/2/B2: not adjustableC= G4/2/(A2-G3_2C); C1=C; C2=C;if C<0, error('It may work with greater values of B2/A2 and smaller value of A3');endG3= G3_2C*2*C; R3= 1/G3; R4= 1/G4; C2R3= R3; C5R4= R4;else % Find C1=C2, R3=R4 for given C5 (not caring about B2).C5=R3C5; R=A2/2/C5/A3; R3=R; R4=R3; G3=1/R; G4=G3;C=1/R/A2; C1=C; C2=C; C2R3=R; C5R4=C5;endfprintf('R3=%8.0f, R4=%8.0f, C1=%10.3e, C2=%10.3e, C5=%10.3e\n', ...R3,R4,C1,C2,C5)B2= C1*G4/(C1+C2)/C5; A2= (G3+G4)/(C1+C2); A3= G3*G4/(C1+C2)/C5;syms s; Gs = -B2*s/(s^2+A2*s+A3);
function [R1,R2,R3,Gs]=BPF_Sallen_design(B2,A2,A3,K,C1,C2)% Design a BPF with the Sallen-Key circuit in Fig. 5.21% by determining R1, R2, and R3 for given K, C1, and C2.% (KG1/C2) s% G(s) = - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -% s^2 +(G1(1/C1+1/C2)+G2((1-K)/C2+1/C1)+G3/C2)*s +G3(G1+G2)/C1/C2if K<=1, fprintf('Let K=1 since we must have K=(R4+R5)/R4>=1!'); K=1; endG1=B2*C2/K;if G1>0.1, error('Try with smaller C2!'); endD=K-1-C2/C1; E=C2*(A2-G1/C1)-G1;b=(D*G1+E)/D; c=-A3*C1*C2/D; tmp = b^2-4*c;if tmp<0, error('Try with larger K,C1 and/or smaller C2'); endG2 = (-b+sqrt(tmp))/2; G3=D*G2+E;if G3>0.1, error('Try with smaller C1!'); endR1=1/G1; R2=1/G2; R3=1/G3; R4=1e4; R5=(K-1)*R4;B2=K*G1/C2; A2=G1*(1/C1+1/C2)+G2*((1-K)/C2+1/C1)+G3/C2; A3=G3*(G1+G2)/C1/C2;syms s;Gs = B2*s/(s^2+A2*s+A3)fprintf('R1=%8.0f, R2=%8.0f, R3=%8.0f, R4=%8.0f, R5=%8.0f, C1=%10.3e, C2=%10.3e\n', R1,R2,R3,R4,R5,C1,C2)%draw_BPF_Sallen(R1,R2,R3,C1,C2,R4,R5)%K=10; C1=1e-11; C2=1e-11; wr=2e7*pi; Q=0.707; A2=wr/Q; A3=wr^2; B2=A2;%BPF_Sallen_design(B2,A2,A3,K,C1,C2);
For example, we can use the MATLAB function ‘BPF_MFBa_design()’ to tune the parameters of the MFB (multiple feedback) circuit of Figure 5.20(a) so that the circuit realizes the BPF transfer function (E5.3.1) tuned in Example 5.3:

To this end, we have only to run the following statements:
>>B2=100; A2=100; A3=10000; % Desired transfer function B2*s/(s^2+A2*s+A3)>>R2=1e2; KC=3; % With R2=100 and C3=C4 given>>[C3,R1,R5,Gs]=BPF_MFBa_design(B2,A2,A3,R2,0,KC);R1= 100, R2= 100, R5= 200, C3= 1.000e-004, C4= 1.000e-004Gs = -100*s/(s^2+100*s+10000)
For another example, we can use the function ‘LPF_Sallen_design()’ to tune the parameters of the Sallen‐Key circuit of Figure 5.18(a) so that it realizes the following LPF transfer function:

More specifically, suppose we need to determine the values of R1 and R2 of the Sallen‐Key circuit of Figure 5.18(a) with the predetermined values of capacitances C1 = C2 = 100 pF so that it realizes a second‐order LPF with the DC gain K = 1.5, the corner frequency ωr = 2π × 107 [rad/s], and the quality factor Q = 0.707 (for 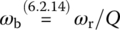 ). To this end, we have only to run the following statements:
). To this end, we have only to run the following statements:
>>K=1.5; C1=1e-10; C2=1e-10; wr=2e7*pi; Q=0.707;% The coefficients of denominator of desired transfer ftn>>A2=wr/Q; A3=wr^2; % G(s)=K*A3/(s^2+A2*s+A3)>>KC=2; [R1,R2,Gs]=LPF_Sallen_design(A2,A3,K,C1,C2,KC);R1= 221, R2= 115, R3= 10000, R4= 5000, C1= 1.000e-010, C2= 1.000e-010Gs = 5921762640653615/(s^2+5964037174912491/67108864*s+7895683520871487/2)
Example 6.16 Fifth‐Order Butterworth LPF Design
%elec06e16.mN=5; fc=1e4; wc=2*pi*fc; % Order and Cutoff frequency of the LPF[B,A]=butter(N,wc,'s') % Butterworth LPF transfer function G(s)=B(s)/A(s)disp('Cascade realization of 5th-order Butterworth LPF')[SOS,K0]= tf2sos(B,A); % Cascade realizationBBc=SOS(:,1:3); AAc=SOS(:,4:6); % Numerator/Denominator of each SOSKC=1; K=1; R1=1e4; R2=1e4; % Predetermined values of R1, R2B1=BBc(1,2)*K0; % Numerator of the 1st-order section initializedfor n=2:ceil(N/2)A2=AAc(n,2); A3=AAc(n,3); B1=B1/A3;LPF_Sallen_design(A2,A3,K,R1,R2,KC);endKC=2; C=1e-9;LPF_RC_OPAmp_design(B1,AAc(1,2),C,KC); % 1st-order section
Find the cascade realization of the fifth‐order Butterworth LPF with cutoff frequency fc = 10 kHz using two Sallen‐Key circuits of Figure 5.18(a) and one first‐order LPF circuit of Figure 5.17(a). To this end, we compose the above MATLAB script “elec06e16.m” and run it to get the C values of the two‐stage Sallen‐Key LPFs (with all the R values fixed at 10 kΩ) and the R values of the first‐order LPF (with C fixed at 1 nF) as follows:
R1= 10000, R2= 10000, R3= 10000, R4= 0, C1=5.150e-009, C2=4.918e-010R1= 10000, R2= 10000, R3= 10000, R4= 0, C1=1.967e-009, C2=1.288e-009R1= 15915, R2= 15915, C=1.000e-009
Note that the voltage dividers consisting of R3 = 10 kΩ and R4 = 0 Ω for the two Sallen‐Key circuits (with K = vo/v‐ = (R3 + R4)/R3 = 1) are not needed and instead, the negative input terminals of the OP Amps should be directly connected (R4 = 0 Ω) to their output terminals with no connection (R3 = ∞ Ω) to the ground as depicted in the PSpice schematic of Figure 6.26(a). Note also that the numerator of the overall transfer function has been divided by the numerator of each SOS (equal to the constant term of its denominator) to yield the numerator of the first‐order section. Figure 6.26(b) shows the frequency response magnitude curve obtained from PSpice simulation (with the analysis type of AC Sweep) where the voltage divider bias (VDB) voltage marker measuring the dB magnitude of the output voltage has been fetched from PSpice > Markers > Advanced > dB magnitude voltage in the top menu bar of the Schematic window.

Figure 6.26 A fifth‐order Butterworth LPF implemented with one first‐order section and two Sallen‐Key LPFs.
Example 6.17 Chebyshev I BPF Design with MFB Circuit
Find the cascade realization of the Chebyshev I BPF using the MFB circuit of Figure 5.20(a) so that it can satisfy the following design specifications:
ωs1 = 2π × 6000, ωp1 = 2π × 10000, ωp2 = 2π × 12000, ωs2 = 2π × 15000 [rad/s],
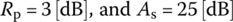
To this end, we compose the following MATLAB script “elec06e17.m” and run it to get the R values of the two‐stage MFB BPFs (with all the C values fixed at 10 nF) as follows:
R1=11241, R2=40, R5=46095, C3=1.000e-008, C4=1.000e-008R1=11241, R2=46, R5=53119, C3=1.000e-008, C4=1.000e-008
%elec06e17.mfs1=6e3; fp1=10e3; fp2=12e3; fs2=15e3; Rp=3; As=25; fp=sqrt(fp1*fp2);ws1=2*pi*fs1; wp1=2*pi*fp1; wp2=2*pi*fp2; ws2=2*pi*fs2;[N,wpc]=cheb1ord([wp1 wp2],[ws1 ws2],Rp,As,'s');[B,A]=cheby1(N,Rp,wpc,'s');f=logspace(-1,1,600)*fp; Gw=freqs(B,A,2*pi*f); % Frequency responsesubplot(221), semilogx(f,20*log10(abs(Gw))), hold on[SOS,K]= tf2sos(B,A);Ns=size(SOS,1); % Number of sectionsGm=K^(1/Ns), BBc=SOS(:,1:3), AAc=SOS(:,4:6)KC=2; % With all the C values fixedfor n=1:NsB2=Gm; A2 = AAc(n,2); A3 = AAc(n,3); C3=1e-8; C4=1e-8;subplot(222+n), BPF_MFBa_design(B2,A2,A3,C3,C4,KC);end
Figure 6.27(a) shows the PSpice schematic with all the parameter values set as suggested by the MATLAB realization functions. Figure 6.27(b1) and (b2) shows the frequency response magnitude curves obtained from PSpice simulation and MATLAB analysis, respectively. Oh, my God! The former seems to have been shifted by −2 kHz compared with the design specification (depicted in Figure 6.27(b2)) although their shapes of having ripples only in the passband look similar. Why is that? The discrepancy may have been caused by the load effect of the second stage on the first stage that was not considered here. Anyway, to make up for this (unexpected) frequency shift, you can try the frequency scaling of the designed filter by a factor of about 6/5 (see Problem 6.9).

Figure 6.27 A fourth‐order Chebyshev I BPF implemented with two cascade‐connected MFB BPFs.
(Note) Multiplying all the resistances/capacitances by the same constant does not change the transfer function and frequency response. This implies that if you want to scale up/down the tuned capacitances/resistances without affecting the transfer function and frequency response, you can scale up/down the predetermined values of resistances/capacitances by the same factor (see Remark 6.2(1)).
(Note) See http://www.analog.com/library/analogdialogue/archives/43‐09/EDCh%208%20filter.pdf; for various configurations of analog filter.

Figure 6.28 A BSF realized by using the BPF of Figure 6.27 (in Example 6.17) and a difference amplifier.
One may wonder why we have no example of BSF design and realization. It is because we may design a BSF satisfying a given frequency response specification as illustrated in Example 6.1(c), but the transfer functions of the SOSs as shown in Eqs. (E6.1.9a,b) do not fit Eq. (6.2.16a), which is the transfer function of the BSF in Figure 5.22. However, a BSF can be realized by the difference amplifier having the input signal and a BPF output as its two inputs as will be illustrated in the next example. Likewise, an HPF can be realized by the difference amplifier having the input signal and an LPF output as its two inputs.
Example 6.18 Realization of a BSF Using a BPF and a Difference Amplifier
Figure 6.28(a) shows the PSpice schematic of a BSF realized by connecting the BPF (in Figure 6.27) and a difference amplifier so that the overall output can be the difference between the input signal and the BPF output:

Figure 6.28(b) shows the frequency response magnitude obtained from the PSpice simulation. Regrettably, it is not a typical shape of BSF frequency response, being contrary to our expectation.
Problems
- 6.1 Design of Passive Filter in the form of LC Ladder Circuit
- Design a Butterworth LPF with cutoff frequency fc = 2 GHz in the form of N = 5‐stage П‐type LC ladder circuit (depicted in Figure 6.14.1(a)) where the source impedance is assumed to be 50 Ω. Plot the frequency response magnitude [dB] (relative to that without the filter) to check the validity of the designed filter.
%elec06p01a.mclear, clf%(a) Butterworth (maximally flat) LPF (Example 8.4 of [P-1] by Pozar)syms sN=5; pT='??'; Rs=50; type='?';fc=2e9; wc=2*pi*fc;gg=LPF_ladder_coef(N,type);[LCRs,LCRs_,Gs]=LC_ladder(Rs,gg,pT,wc,'???');format short e; LCRs, LCRs_, RL=LCRs(end)ff=logspace(-1,1,401)*fc; ww=2*pi*ff; % Frequency ranges=j*ww; Gw=eval(Gs/(RL/(Rs+RL))); % Frequency responseGwmagdB=20*log10(max(abs(Gw),1e-5));subplot(222), semilogx(ff,GwmagdB), hold onplot([ff(1) fc],[-3 -3],'k:', [fc fc],[0 -3],'k:')xlabel('Frequency[Hz]'), ylabel('Relative frequency response[dB]') - Design a Chebyshev BPF with passband ripple Rp = 0.5 dB, peak frequency fp = 1 GHz, and bandwidth 0.1 GHz in the form of N = 3‐stage T‐type LC ladder circuit (depicted in Figure 6.14.1(b)) where the source impedance is assumed to be 50 Ω. Plot the frequency response magnitude or its reciprocal (called the insertion loss) [dB] to check the validity of the designed filter.
%elec06p01b.m% Chebyshev 0.5dB BPF (Example 8.5 of [P-1] by Pozar)syms sN=3; pT='?'; Rs=50; type='?'; Rp=0.5;fp=1e9; wp=2*pi*fp; wb=0.1*wp; sqBw=sqrt(wb^2/4+wp^2); % wb=Bandwidthw12=[-1 1]*wb/2+sqw; fl=w12(1)/2/pi; fu=w12(2)/2/pi;gg=LPF_ladder_coef(N,type,Rp);[LCRs,LCRs_,Gs]=LC_ladder(Rs,gg,pT,w12,'???');format short e; LCRs, LCRs_, RL=LCRs(end)ff=logspace(-0.3,0.3,401)*fp; ww=2*pi*ff; % Frequency ranges=j*ww; Gw=eval(Gs/(RL/(Rs+RL))); % Frequency responseGwmagdB=20*log10(max(abs(Gw),1e-5));subplot(224), semilogx(ff,GwmagdB), hold onplot([fl fl],[-100 -Rp],'k:', [fu fu],[-100 -3],'k:')
- Design a Butterworth LPF with cutoff frequency fc = 2 GHz in the form of N = 5‐stage П‐type LC ladder circuit (depicted in Figure 6.14.1(a)) where the source impedance is assumed to be 50 Ω. Plot the frequency response magnitude [dB] (relative to that without the filter) to check the validity of the designed filter.
- 6.2 Design of Passive Filters in the form of LC Ladder Circuit
- Design a Butterworth LPF with cutoff frequency fc = 10 MHz, passband ripple Rp = 3 dB, and stopband attenuation As = 30 dB at fs = 31.62 MHz where the source and load impedances are equally 50 Ω. Note that the order of the Butterworth LPF can be determined by using the MATLAB function ‘
buttord()’ as>>wp=2*pi*7e6; ws=2*pi*31.62e6; Rp=3; As=30;[N,wc]=buttord(wp,ws,Rp,As,'s'), fc=wc/2/pi%elec06p02a.m%(a) Butterworth LPF (Example 8.6 of [M-2] by Misra)syms sN=3; Rs=50; % % Filter order 3 and Source impedance 50[Ohm]type='B'; band='LPF';fc=1e7; wc=2*pi*fc; % Butterworth LPFgg=LPF_ladder_coef(N,type) %LC values of Nth-order B-LPF prototypeff=logspace(-1,1,401)*fc; ww=2*pi*ff; % Frequency rangefor m=1:2if m==1, pT='T'; else pT='p'; end[LCRs,LCRs_,Gs]=LC_ladder(Rs,gg,pT,wc,????);format short e; LCRs, LCRs_, RL=LCRs(end)subplot(2,2,2*m-1), draw_ladder(LCRs,LCRs_)% To plot the frequency response magnitude (considering Rs,RL)s=j*ww; Gw=eval(Gs); % Frequency responseGwmagdB=20*log10(max(abs(Gw)/(RL/(Rs+RL)),1e-5));subplot(2,2,2*m), semilogx(ff,GwmagdB)end - Design a Chebyshev LPF with cutoff frequency fc = 100 MHz, passband ripple Rp = 0.01 dB, and stopband attenuation As = 5 dB at fs = 40 MHz where the source and load impedances are equally 75 Ω. Note that the minimum order of the Chebyshev LPF can be determined by using the MATLAB function ‘
cheb1ord()’ as>>wp=2*pi*1e8; ws=2*pi*4e8; Rp=0.01; As=5;[N,wc]=cheb1ord(wp,ws,Rp,As,'s')%elec06p02b.m% Chebyshev LPF (Example 8.7 of [M-2] by Misra)clear, clfsyms sN=3; Rs=75; % Filter order 3 and Source impedance 75[Ohm]type='C'; band='LPF';Rp=0.01; fc=1e8; wc=2*pi*fc; % Chebyshev LPFgg=LPF_ladder_coef(N,type,??)%LCs of Nth-order C-LPF prototypeff=logspace(-1,1,401)*fc; ww=2*pi*ff; % Frequency rangefor m=1:2if m==1, pT='T'; else pT='p'; end[LCRs,LCRs_,Gs]=LC_ladder(??,gg,pT,wc,band);format short e; LCRs, LCRs_, RL=LCRs(end)subplot(2,2,2*m-1)draw_ladder(LCRs,LCRs_)s=j*ww; Gw=eval(Gs); % Frequency responseGwmagdB=20*log10(max(abs(Gw)/(RL/(Rs+RL)),1e-5)); subplot(2,2,2*m), semilogx(ff,GwmagdB)end - Design a Chebyshev HPF with cutoff frequency fc = 100 MHz, passband ripple Rp = 0.01 dB, and stopband attenuation As = 5 dB at fs = 25 MHz where the source and load impedances are equally 75 Ω. Note that the minimum order of the Chebyshev HPF can be determined by using the MATLAB function ‘
cheb1ord()’ as>>wp=2*pi*1e8; ws=2*pi*25e6; Rp=0.01; As=5;[N,wc]=cheb1ord(wp,ws,Rp,As,'s')%elec06p02c.m% Chebyshev HPF (Example 8.9 of [M-2] by Misra)N=3; Rs=75; % 3rd ordertype='C'; band='HPF'; Rp=0.01; fc=1e8; wc=2*pi*fc; % Chebyshev HPFgg=LPF_ladder_coef(?,type,Rp) % LCs of Nth-order C-LPF prototypeff=logspace(-1,1,401)*fc; ww=2*pi*ff; % Frequency rangefor m=1:2if m==1, pT='T'; else pT='p'; end[LCRs,LCRs_,Gs]=LC_ladder(Rs,gg,pT,??,band);format short e; LCRs, LCRs_, RL=LCRs(end)subplot(2,2,2*m-1), draw_ladder(LCRs,LCRs_)s=j*ww; Gw=eval(Gs); % Frequency responseGwmagdB=20*log10(max(abs(Gw)/(RL/(Rs+RL)),1e-5));subplot(2,2,2*m), semilogx(ff,GwmagdB, [fc fc],[-100 -Rp],'r:')end - Design a sixth‐order Chebyshev BPF with cutoff frequencies {fc1 = 10 MHz, fc2 = 40 MHz} and passband ripple Rp = 0.01 dB, where the source and load impedances are equally 75 Ω.
%elec06p02d.m% Chebyshev BPF (Example 8.10 of [M-2] by Misra)N=3; Rs=75; % N=6/2=3rd-order LPF prototypetype='C'; band='BPF'; % Chebyshev BPFRp=0.01; fb=[10 40]*1e6; wb=2*pi*fb; fc=sqrt(fb(1)*fb(2));gg=LPF_ladder_coef(N,????,Rp) % LCs of 2Nth-order C-BPF prototypeff=logspace(-1,1,401)*fc; ww=2*pi*ff;for m=1:2if m==1, pT='T'; else pT='p'; end[LCRs,LCRs_,Gs]=LC_ladder(Rs,gg,??,wb,band);format short e; LCRs, LCRs_, RL=LCRs(end)subplot(2,2,2*m-1), draw_ladder(LCRs,LCRs_)s=j*ww; Gw=eval(Gs); % Frequency responseGwmagdB=20*log10(max(abs(Gw)/(RL/(Rs+RL)),1e-5)); subplot(2,2,2*m), semilogx(ff,GwmagdB), hold onsemilogx(fb(1)*[1 1],[-100 -Rp],'r:', fb(2)*[1 1],[-100 -Rp],'r:')end - Design a sixth‐order Butterworth BSF with cutoff frequencies {fc1 = 10 MHz, fc2 = 40 MHz} and passband ripple Rp = 0.1 dB, where the source and load impedances are equally 75 Ω.
%elec06p02e.m% Butterworth BSF (Example 8.11 of [M-2] by Misra)N=3; Rs=75; % N=6/2=3rd-order LPF prototypetype='B'; band='BSF'; % Butterworth BSFRp=0.1; fb=[10 40]*1e6; wb=2*pi*fb; fc=sqrt(fb(1)*fb(2));gg=LPF_ladder_coef(?,type,??) % LCs of 2Nth-order B-LPF prototypeff=logspace(-1,1,401)*fc; ww=2*pi*ff; % Frequency rangefor m=1:2if m==1, pT='T'; else pT='p'; end[LCRs,LCRs_,Gs]=LC_ladder(Rs,??,pT,wb,band);format short e; LCRs, LCRs_, RL=LCRs(end)subplot(2,2,2*m-1), draw_ladder(LCRs,LCRs_)s=j*ww; Gw=eval(Gs); % Frequency responseGwmagdB=20*log10(max(abs(Gw)/(RL/(Rs+RL)),1e-5));subplot(2,2,2*m)semilogx(ff,GwmagdB,[fc fc],[-100 -3],'r:')end
- Design a Butterworth LPF with cutoff frequency fc = 10 MHz, passband ripple Rp = 3 dB, and stopband attenuation As = 30 dB at fs = 31.62 MHz where the source and load impedances are equally 50 Ω. Note that the order of the Butterworth LPF can be determined by using the MATLAB function ‘
- 6.3 Design of L‐Type Impedance Matcher for Maximum Power Transfer
Design as many L‐type impedance matchers as possible for maximum power transfer from a transmitter with output impedance Zs = 50 Ω to an antenna with input impedance ZL = RL + 1/jωCL (RL = 80 Ω, CL = 2.653 pF) at the center frequency fc = 1 GHz. Plot the power delivered to the load RL as shown in Figure 6.20 twice, once by using the MATLAB function ‘
imp_matcher_L_and_freq_resp()’ and once by using PSpice (with AC Sweep analysis type and a power marker on RL in the schematic). Which one of the L‐type filters are you going to use for impedance matching after viewing the power curves? - 6.4 Design of L‐Type Impedance Matcher
- Make as many L‐type impedance matchers as possible to match a load of ZL = 600 Ω to a source of Zs = 50 Ω at a frequency fc = 400 MHz and plot their frequency responses for some frequency band around fc.
%elec06p04a.m% To design L-type impedance matchers (Example 5.6 of [M-2])fc=4e8; wc=2*pi*fc; % Center frequencyZs=50; ZL=600; % Source and Load impedancesff=logspace(-1,1,801)*fc; % Frequency range[LC,LC_]=imp_matcher_L_and_freq_resp(Zs,??,fc,ff); - Make as many two‐stage impedance matchers as possible to match a load of ZL = 600 Ω to a source of Zs = 50 Ω at a frequency fc = 400 MHz where the second stage matches ZL = 600 to 173.2 Ω and the first stage matches 173.2 to Zs = 50 Ω. Use the following MATLAB function ‘
ladder_xfer_ftn()’ to find the frequency responses (for two decades around fc) and the input impedances (Zi(j2πf)'s) of the impedance matchers (with the load impedance ZL = 600 Ω) at fc. Plot the frequency responses to see if they have peaks at fc and check if Zi(j2πf)'s match the source impedance Zs = 50 Ω at fc.function [Gs,Zis]=ladder_xfer_ftn(Rs,LCRs,LCRs_,w)% Input:% Zs = Input impedance% LCRs_ = [C1 L2 C3 RL] for Pi-ladder like Fig. 6.14.1a% LCRs_ = {'C(v)','L(h)','C(v)' 'Z(v)'}% w = (Operation) Frequency[rad/s]% Output:% Gs = G(s) or G(jw) if w is given.% Zis = Input impedance Zi(s) or Zi(jw) if w is given.% Copyleft: Won Y. Yang, wyyang53@hanmail.net, CAU for academic use onlyif nargin>3, s=j*w; else syms s; end[M,N1]=size(LCRs); [M_,N1_]=size(LCRs_); N=N1-1;if M~=M_|N1~=N1, error('LCR and LCR_ are not of the same size!'); endfor m=1:MZL=LCRs(m,N1);I=1; V=ZL; % Set the current through RL to 1 to find G(s)for n=N:-1:1LC=LCRs_{m,n}(1); hv=LCRs_{m,n}(3);if LC=='L', Zs=s*LCRs(m,n); else Zs=1/s/LCRs(m,n); endif hv=='v', I=I+V./Zs; else V=V+Zs.*I; end % Parallel/SeriesendGs(m,:)=ZL./(V+Rs.*I); % Transfer functionZis(m,:)=V./I; % Input impedanceend - Make as many L‐type filters as possible to match a load of YL = 8 − j12 [mS] to a 50 Ω line at a frequency fc = 1 GHz. Use the above MATLAB function ‘
ladder_xfer_ftn()’ to find the input impedances of the impedance matchers (with the load impedance ZL = 1/YL) and check if they match the source impedance Zs = 50 Ω at fc = 1 GHz.%elec06p04b.m% To design L-type impedance matchers (Example 5.7 of [M-2])fc=4e8; wc=2*pi*fc; % Center frequencyZs=50; ZL=600; % Source and Load impedancesff=logspace(-1,1,801)*fc; % Frequency range[LC2,LC2_]=imp_matcher_L_and_freq_resp(?????,ZL,fc,ff); % 2nd stage[LC1,LC1_]=imp_matcher_L_and_freq_resp(??,173.2,fc,ff); % 1st stageLC11=[LC1(1,:) LC2(1,:) ZL], LC11_=[LC1_(1,:) LC2_(?,:) 'RL(v)'][Gss(1,:),Ziws(1)]=ladder_xfer_ftn(Zs,LC11,LC11_); % G(s) and Zi(jw)LC12=[LC1(1,:) LC2(?,:) ZL], LC12_=[LC1_(1,:) LC2_(2,:) 'RL(v)'][Gss(2,:),Ziws(2)]=ladder_xfer_ftn(Zs,LC12,LC12_); % G(s) and Zi(jw)LC21=[LC1(?,:) LC2(1,:) ZL], LC21_=[LC1_(2,:) LC2_(1,:) 'RL(v)'][Gss(3,:),Ziws(3)]=ladder_xfer_ftn(Zs,LC21,LC21_); % G(s) and Zi(jw)LC22=[LC1(2,:) LC2(?,:) ZL], LC22_=[LC1_(2,:) LC2_(2,:) 'RL(v)'][Gss(4,:),Ziws(4)]=ladder_xfer_ftn(Zs,LC22,LC22_); % G(s) and Zi(jw)% To check if the input impedance of each ladder is matched to Zss=j*wc; eval(Ziws) % Input AC impedances at w=wc% To get the frequency responses=j*2*pi*ff;for m=1:4, Gws(:,m)=eval(Gss(m)); endGmagdB=20*log10(abs(Gws)); G3dB=max(GmagdB)-3;semilogx(ff,GmagdB); hold onsemilogx(ff([1 end]),[1;1]*G3dB,'r:', [fc fc],[-100 0],'r:')legend('Gw1','Gw2','Gw3','Gw4')%elec06p04c.m% To design L-type impedance matchers (Example 5.9 of [M-1])clear, clffc=1e9; wc=2*pi*fc; % Center frequencyZs=50; ZL=1e3/(8-12i); % Source and Load impedancesff=logspace(-1,1,801)*fc; % Frequency range[LCs,LCs_,ff,Gws]=imp_matcher_L_and_freq_resp(Zs,ZL,fc,ff);% To check if ZL has been matched to Zs through the LC ladders,[M,N]=size(LCs); N1=N+1;LCRs=[LCs repmat(ZL,M,1)]; LCRs_=LCs_;for m=1:M, LCRs_{m,N1}='Z(v)'; end[Gss,Ziws]=ladder_xfer_ftn(Zs,LCRs,?????); % G(s)'s and Zi(jw)'ss=j*wc; eval(Ziws) % Input AC impedances at w=wc
- Make as many L‐type impedance matchers as possible to match a load of ZL = 600 Ω to a source of Zs = 50 Ω at a frequency fc = 400 MHz and plot their frequency responses for some frequency band around fc.
- 6.5 Design of T‐Type Impedance Matcher
- Use the MATLAB function ‘
imp_matcher_T()’ to make as many T‐type filter(s) as possible matching a load of ZL = 225 Ω to a source of Zs = 15 + j15 Ω with quality factor Q = 5 at a frequency fc = 30MHz. You can visit the website https://www.eeweb.com/tools/t‐match to find two of the designs, one with DC current passed and one with DC current blocked. - Use the MATLAB function ‘
imp_matcher_T()’ to determine just the reactances constituting T‐type filter(s) to match a load of ZL = 50 Ω to a source of Zs = 10 Ω with quality factor Q = 10. (See Example 4.5 of [B-2].)
- Use the MATLAB function ‘
- 6.6 Design of П‐Type Impedance Matcher
Determine just the reactances constituting П‐type filter(s) to match a load of ZL = 1000 Ω to a source of Zs = 100 Ω with quality factor Q = 15. (See Example 4.4 of [B-2].)
- 6.7 Design of Tapped‐C Impedance Matcher
Make a tapped‐C impedance matcher to match a load of ZL = 5 Ω to a source of Zs = 50 Ω with quality factor Q = 5 at f0 = 150 MHz. Plot the frequency response magnitude curve as shown in Figure 6.25(b).
%elec06p07.mRs=50; RL=5; f0=150e6; w0=2*pi*f0; jw0=j*w0; Q=5;[L,C1,C2,Qr,Qp,Rp1,Z1,Z2]=imp_matcher_tapped_C(RL,R?,??,Q);% To get the frequency response,f=logspace(-0.2,0.2,600)*f0; w=2*pi*f; jw=j*w; % Frequency rangeZC2RLw = 1./(jw*C2+1/RL);ZC12RLw = 1./jw/C1 + ZC2RLw;ZLC12RLw = 1./(1./jw/L + 1./ZC12RLw);Gw = ZLC12RLw./(Rs+ZLC12RLw).*ZC2RLw./ZC12RLw; % Frequency responseGwmagdB = 20*log10(abs(Gw));% .. .. .. .. - 6.8 Design, Realization, and Implementation of High‐Order Butterworth Lowpass Filter (LPF)
Given the order, say, N = 4 and cutoff frequency, say, ωc = 2πfc =2π × 104 [rad/s] of an LPF, we can use the following MATLAB statements:
>>format short e; N=4; fc=1e4; wc=2*pi*fc;[B,A]=butter(N,wc,'s')to find the numerator (B) and denominator (A) polynomials in s of the transfer function of the desired fourth‐order Butterworth LPF as
B = 0 0 0 0 1.5585e+019A = 1.0000e+000 1.6419e+005 1.3479e+010 6.4819e+014 1.5585e+019This means the following transfer function:
(P6.8.1)
- Plot the frequency response magnitude 20log10|G(jω)| [dB] of the LPF (for the frequency range of two decades around fc = 104 [Hz]) and show that the transfer function can be realized in cascade form, i.e. as a product of second‐order transfer functions as
(P6.8.2)
%elec06p08a.mclearformat short e% To design a 4th-order Butterworth LPF with fc=1e4N=4; fc=1e4; wc=2*pi*fc;[B,A]=butter(?,??,'s')% To plot the frequency response of G(s)=B(s)/A(s)f=logspace(-1,1,800)*fc; w=2*pi*f; % Frequency of 2 decades around wcGw=freqs(B,A,?); % Frequency response of a system with G(s)=B(s)/A(s)subplot(332), semilogx(f,20*log10(abs(Gw)), fc*[1 1],[0 -3])axis([f(1) f(end) -80 10]), hold ontitle('Designed frequency response')% To find a cascade realization of G(s)=B(s)/A(s)fprintf('\n\nCascade form of realization of G(s):')[SOS,Kc]=tf2sos(B,A); % Cascade realizationNs=size(SOS,1); % Number of sectionsGm=??^(1/??); % (Distributed) gain of each SOS in cascade realizationBBc=Gm*SOS(:,1:3), AAc=SOS(:,4:6) % the numerator/denominator matrix% To find a parallel realization of G(s)=B(s)/A(s)fprintf('\n\nParallel form of realization of G(s):')[BBp,AAp]=tf2par_s(B,A) % the numerator/denominator matrix%elec06p08b.mGw_cas=1; % Initialize the frequency response of cascade realization.R3=1e10; R4=0; K=1+R4/R3; % R3=inf;for m=1:NsA2=AAc(m,2); A3=AAc(m,3); R1=1e4; R2=1e4; KC=1;subplot(333+m), [C3,C4,Gs]=LPF_Sallen_design(A2,A3,K,R1,R2,KC);Gw_cas = Gw_cas.?freqs(BBc(m,:),AAc(m,:),w);endsemilogx(f,20*log10(abs(Gw_cas)),'r:')%elec06p08c.mGw_par=0; % Initialize the frequency response of cascade realization.L=0.01; Rf=BBp(1,2)*L % Common to numerators of SOS 1/2 in Eq. (P6.8.5)for m=1:NsA2=AAp(m,2); A3=AAp(m,3); % Denominators of SOS 1/2 in Eq. (P6.8.5)C=1/A?/L; R=1/A?/C; %Sol of 2 simulataneous eqs: 1/R/C=A2, 1/L/C=A3mc=num2str(m);fprintf(['\n R' mc '=%10.4e, L' mc '=%10.4e, C' mc '=%10.4e\n'], R,L,C)Gw_par = Gw_par ? freqs(BBp(m,:),AAp(m,:),w);endsemilogx(f,20*log10(abs(Gw_par)),'g:')or in parallel form, i.e. as a sum of second‐order transfer functions as
(P6.8.3)
In fact, this implies that the transfer function can be realized as a cascade connection of the two SOSs (second‐order sections), GC1(s) and GC2(s), or a parallel connection of the two SOSs, GP1(s) and GP2(s). You can complete and run the above MATLAB script “elec06p08a.m” to find the cascade and parallel realizations.
- Noting that each SOS of the circuit in Figure P6.8(a) has the following transfer function
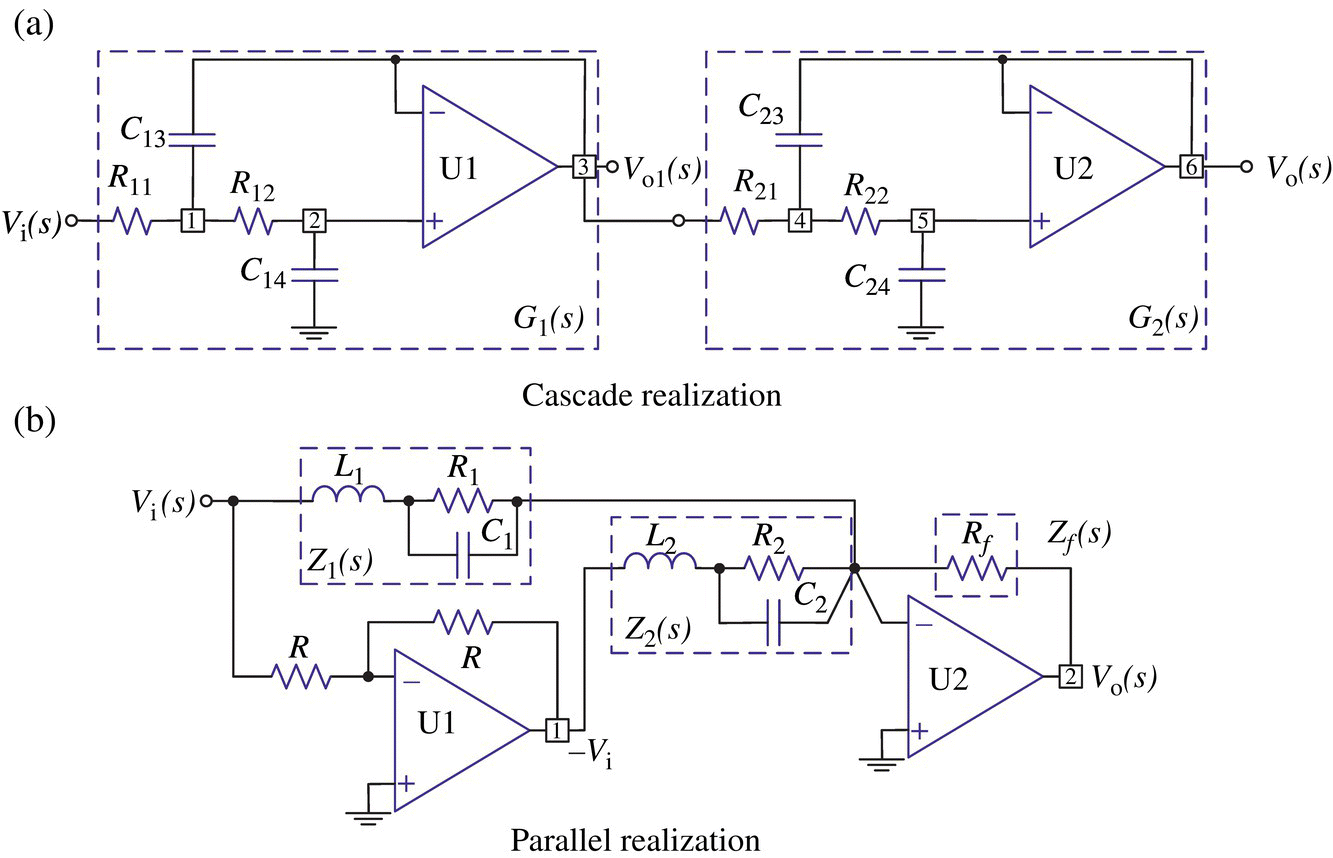
Figure P6.8 Two realizations of a fourth‐order Butterworth LPF.
(P6.8.4)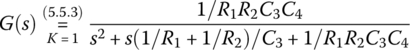
let R11 = R12 = R21 = R22 = 10 kΩ and find the values of C13, C14, C23, and C24 such that the desired transfer function will be implemented. Plot the frequency response of the cascade realization (P6.8.2) to see if it conforms with that of G(s) obtained in (a).
- Noting that the circuit of Figure P6.8(b) has the following transfer function
let L1 = L2 = L = 0.01 H and find the values of R1, C1, R2, C2, and Rf such that the desired transfer function will be implemented. Plot the frequency response of the parallel realization (P6.8.3) to see if it conforms with that of G(s) obtained in (a).
- Perform the PSpice simulation to see that the cutoff frequency of the two circuits, one realized in cascade form and the other in parallel form, is fc = 10 kHz at which the magnitude of the frequency response is
 = 0.7071 =
= 0.7071 = ‐3 dB. You can use the VDB marker (from PSpice > Markers > Advanced) in the Schematic window to measure the frequency response in dB.
- Plot the frequency response magnitude 20log10|G(jω)| [dB] of the LPF (for the frequency range of two decades around fc = 104 [Hz]) and show that the transfer function can be realized in cascade form, i.e. as a product of second‐order transfer functions as
- 6.9 Frequency Scaling
Referring to Remark 6.2(2), try the frequency scaling for Example 6.17 to reduce the discrepancy between the two frequency responses, one obtained from PSpice simulation and the other obtained from MATLAB analysis. Using PSpice, plot the frequency response magnitude of the modified filter to show that you worked properly.
- 6.10 Design and Realization of High‐Order Chebyshev I Bandpass Filter (BPF)
Given the filter order, say, N = 4 and the lower/upper 3 dB frequencies, say, ωl = 2π × 8000 and ωu = 2π × 12500 [rad/s] of a BPF, we can run the following MATLAB statements to find the numerator (B) and denominator (A) polynomials in s of the transfer function of the desired fourth‐order Chebyshev I BPF.
>>format short e; N=4; Rp=3;fl=8000; fu=12500; wl=2*pi*fl; wu=2*pi*fu;[B,A]=cheby1(N/2,Rp,[wl wu],'s')This yields
B = 0 0 4.0067e+008 0 0A = 1.0000e+000 1.8234e+004 8.4616e+009 7.1985e+013 1.5585e+19meaning the following transfer function:
(P6.10.1)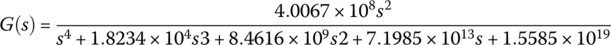
This transfer function can be expressed in the form of product of two second‐order transfer functions as
(P6.10.2)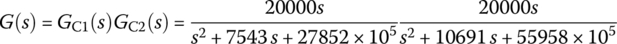
In fact, this implies that the transfer function can be realized as a cascade connection of the two SOSs, GC1(s) and GC2(s).
%elec06p10.mclear, clff=logspace(3,5,801); w=2*pi*f; jw=j*w; % Frequency rangeN=4; % Filter orderfl=8000; fu=12500; wl=2*pi*fl; wu=2*pi*fu; % Lower/upper 3dB freqsRp=3; % Passband ripple[B,A]= cheby1(N/2,Rp,[wl wu],'s') % 4th-order Chebyshev I filter[SOS,K0]= tf2sos(B,A); BBc=SOS(:,1:3); AAc=SOS(:,4:6);K=1; C3=1e-8; C4=1e-8; KC=2; num=1; den=1; N2=floor(N/2);for n=1:N2B2 = K0^(1/N2); A2 = AAc(n,2); A3 = AAc(n,3);num = conv(num,[B2 0]); den = conv(den,[1 A2 A3]);BPF_MFBa_design(B2,??,A3,??,C4,??);endGwd=freqs(B,A,w); Gwd_magdB=20*log10(abs(Gwd));Gw=freqs(num,den,w); Gw_magdB=20*log10(abs(Gw));subplot(2,N2,N2+1)semilogx(f,Gw_magdB, f,Gwd_magdB,'r:'), hold onplot([fl fl],[0 -Rp],'k:', [fu fu],[0 -Rp],'k:')plot(f([1 end]),[-Rp -Rp],'k:'), axis([f(1) f(end) -60 5])- Noting that each SOS of the circuit in Figure P6.10.1 has the following transfer function
(P6.10.3)
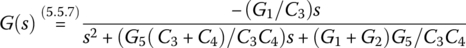
let C13 = C14 = C23 = C24 = 10 nF and find the values of R11, R12, R15, R21, R22, and R25 such that the desired transfer function will be realized. You can complete and run the above script “elec06p10.m,” which uses the MATLAB function ‘
BPF_MFBa_design()’.
Figure P6.10.1 Cascade connection of two second‐order MFB BPFs.
- As depicted in Figure P6.10.2(a), plot the magnitude curve of the frequency response of the filter having the transfer function (P6.10.1) for f = 1–100 kHz. Does it have any ripple in the passband or the stopband? Then perform the PSpice simulation to get the frequency response of the BPF circuit that has been designed in part (a) (as depicted in Figure P6.10.2(b)). Check if the lower and upper 3 dB frequencies of the circuit are close to fl,3 dB = 8000 Hz and fu,3 dB = 12500 Hz, respectively, at which the magnitudes of the frequency response are
 = 0.7071 = −3 dB.
= 0.7071 = −3 dB.

Figure P6.10.2 Frequency response of the circuit in Figure P6.10.1.
- If the PSpice simulation result tells you that the upper/lower 3 dB frequencies are considerably deviated from the expected ones, scale the capacitance values by an appropriate factor for frequency scaling (Remark 6.2(1)) and perform the PSpice simulation again to see if the upper/lower 3 dB frequencies get closer to the expected ones.
- Noting that each SOS of the circuit in Figure P6.10.1 has the following transfer function
- 6.11 Fourier Series Solution of an Active Second‐Order OP Amp Circuit Excited by a Triangular Wave
Consider the active second‐order OP Amp circuit in Figure P6.11(a), which is excited by a triangular wave voltage source of period 0.0004π as depicted in Figure P6.11(b). Find the magnitudes of the leading three frequency components (up to three significant digits) of the input vi(t) and output vo(t) in two ways, one using MATLAB and one using PSpice, and fill in Table P6.11.

Table P6.11 Magnitudes of the leading three frequency components of vi(t) and vo(t).
Order of harmonics k = 1 k = 3 k = 5 MATLAB PSpice MATLAB PSpice MATLAB PSpice Input vi(t) 8.11 0.903 0.324 Output vo(t) 8.16 0.0675 0.0135 - Complete the following MATLAB script “elec06p11.m,” which uses the MATLAB function ‘
Fourier_analysis()’ introduced in Section 1.5.2, together with the MATLAB function ‘elec06p11_f()’ (to be saved in a separate M‐file named “elec06p11_f.m”) and run it to get the waveforms and Fourier spectra of vi(t) and vo(t) as shown in Figure P6.11(c) and (d). - Find the peak (center) frequency ωp and bandwidth ωb of the circuit from its transfer function or frequency response. How is ωp related with the frequency component of the input passing through the filter that can be seen in the input and output spectra shown in Figure P6.11(d)?
- Use the PSpice simulation where the parameters of the periodic voltage source VPULS can be set as follows:
In the Simulation Settings dialog box, set the Analysis type, Run_to_time, and Maximum step as Time Domain (Transient), 20 ms, and 1 u, respectively, and click the Output File Options button to open the Transient Output File Options dialog box, in which the parameters are to be set as

%elec06p11.m : to solve Problem 6.11% Perform Fourier analysis for a BPF with a triangular wave inputclearformat short eglobal T D VmT=0.0004*pi, D=T/2, Vm=10; % Period, Duration, AmplitudeN=5; kk=0:N; % Frequency indices to analyze using Fourier analysisx='elec06p11_f'; % Name of an M-file defining triangular wave functionR1=1e3; R2=20; C3=1e-6; C4=1e-6; R5=???;n= -[1/R1/C3 ?] % Numerator of transfer function G(s) Eq. (5.5.7)d=[? (C3+C4)/R5/C3/C4 ????????????????????] %Denominator of Eq. (5.5.7)[Y,X,THDy,THDx]= ????????????????(n,d,x,T,N);THDx, THDyMagnitude_and_phase_of_input_and_output_spectrum= ...[kk; abs(X); phase(X)*180/pi; abs(Y); angle(Y)*180/pi].'function y=elec06p11_f(t)% defines a triangular wave with period T, duration D, amplitude Vmglobal T D Vmt=mod(t,T); y=Vm*((t<=D).*(1-(2/D)*t) + (t>D).*(-1+(2/D)*(t-D)));
- Complete the following MATLAB script “elec06p11.m,” which uses the MATLAB function ‘