Cumulative distributions

For every probability distribution function f(x), there is a corresponding cumulative distribution function (CDF), denoted by F(x) and defined as:

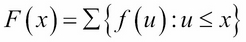
Table 4-3. Dice example

The expression on the right means to sum all the values of f(u) for u ≤ x.

The CDF for the dice example is shown in Table 4-3, and its histogram is shown in Figure 4-6:

x	fX (x)
2	1/36
3	3/36
4	6/36
5	10/36
6	15/36
7	21/36
8	26/36
9	30/36
10	33/36
11	35/36
12	36/36

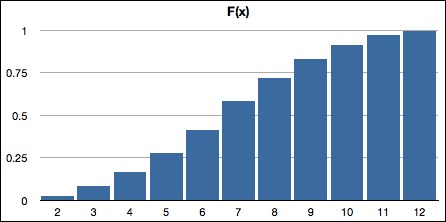
Figure 4-6. Dice cumulative distribution

The properties of a cumulative distribution follow directly from those governing probability distributions. They are:

• 0 ≤ F(x) ≤ 1, for every x ∈ X(S)
• F(x) is monotonically increasing; that is, F(u) ≤ F(v) for u < v
• F(x_max) = 1

Here, x_max is the maximum x value.

The CDF can be used to compute interval probabilities more easily that the PDF. For example, consider the event that 3 < X < 9; that is, that the sum of the two dice is between 3 and 9. Using the PDF, the probability is computed as:

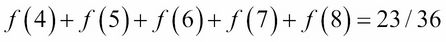
But computing it using the CDF is simpler:

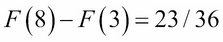
Of course, this assumes that the CDF (in Table 4-3) has already been generated from the PDF.