The conditional probability formula is:
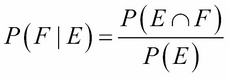
where E and F are any events (that is, sets of outcomes) with positive probabilities. If we swap the names of the two events, we get the equivalent formula:
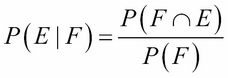
But F ∩ E = E ∩ F, so P(F ∩ E) = P(E ∩ F) = P(F│E) P(E). Thus:
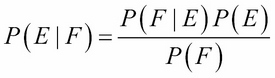
This formula is called Bayes' theorem. The main idea is that it reverses the conditional relationship, allowing one to compute P(E│F) from P(F│E).
To illustrate Bayes' theorem, suppose the records of some Health Department show this data for 1,000 women over the age of 40 who have had a mammogram to test for breast cancer:
- 80 tested positive and had cancer
- 3 tested negative, but had cancer (a Type I error)
- 17 tested positive, but did not have cancer (a Type II error)
- 900 tested negative and did not have cancer
Notice the designations of errors of Type I and II. In general, a Type I error is when a hypothesis or diagnosis is rejected when it should have been accepted (also called a false negative), whereas a Type II error is when a conclusion is accepted when it should have been rejected (also called a false positive).
Here is a contingency table for the data:
|
Positive |
Negative | ||
|---|---|---|---|
|
Cancer |
0.080 |
0.003 |
0.083 |
|
Benign |
0.017 |
0.900 |
0.917 |
|
0.097 |
0.903 |
1.000 |
Table 4-7. Cancer testing
If we think of conditional probability as a measure of a causal relationship, E causing F. Then we can use Bayes' theorem to measure the probability of the cause E.
For example, in the preceding contingency table, if we know what percentage of males are left-handed (P(L│M)), what percentage of people are male (P(M)), and what percentage of people are left-handed (P(L)), then we can compute the percentage of left-handed people that are male:
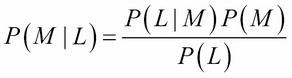
Bayes' theorem is sometimes stated in this more general form:
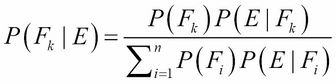
Here, {F1, F2, …, Fn} is a partition of the sample space into n disjoint subsets.