Recall from Chapter 3, Data Visualization, that the normal distribution's probability density function is:
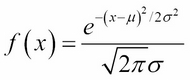
where μ is the population mean and σ is the population standard deviation. Its graph is the well-known bell curve, centered at where x = μ and roughly covering the interval from x = μ–3σ to x = μ+3σ (that is, x = μ±3σ). In theory, the curve is asymptotic to the x axis, never quite touching it, but getting closer as x approaches ±∞.
If a population is normally distributed, then we would expect over 99% of the data points to be within the μ±3σ interval. For example, the American College Board Scholastic Aptitude Test in mathematics (AP math test) was originally set up to have a mean score of μ = 500 and a standard deviation of σ = 100. This would mean that nearly all the scores would fall between μ+3σ = 800 and μ–3σ = 200.
When μ = 0 and σ = 1, we have a special case called the standard normal distribution.
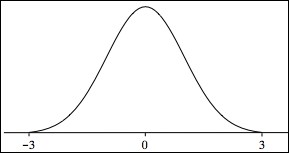
Figure 4-12. The standard normal distribution
Its PDF is:
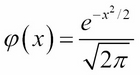
The normal distribution has the same general shape as the binomial distribution: symmetric, highest in the middle, shrinking down to zero at the ends. But there is one fundamental distinction between the two: the normal distribution is continuous, whereas the binomial distribution is discrete.
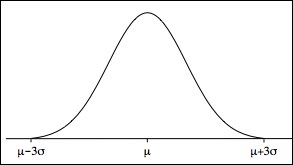
Figure 4-11. The normal distribution
A discrete distribution is one in which the range of the random variable is a finite set of values. A continuous distribution is one in which the range of the random variable is an entire interval of infinitely many values.
The images in Figure 3-22 illustrate this distinction. The top histogram is the graph of the distribution of the number of heads in the flips of four fair coins; its range of values is the finite set {0, 1, 2, 3, 4}. The bottom image is the normal distribution; its range of values is the entire x axis—the interval (–∞, ∞).
When the distribution is discrete, we can compute the probability of an event simply by adding the probabilities of the elementary outcomes that form the event. For example, in the four-coin experiment, the probability of the event E = (X > 2) = {3, 4} is P(X > 2) = f(3) + f(4) = 0.25 + 0.06125 = 0.31125. But when the distribution is continuous, events contain infinitely many values; they cannot be added in the usual way.
To solve this dilemma, look again at Figure 3-22. In each histogram, the height of each rectangle equals the elementary probability of the x-value that it marks. For example, in the top histogram (for the four-coin experiment), the heights of the last two rectangles are 0.25 and 0.06125, representing the probabilities of the outcomes X = 3 and X = 4. But if the width of each rectangle is exactly 1.0, then those elemental probabilities will also equal the areas of the rectangles: the area of the fourth rectangle is A = (width)(height) = (1.0)(0.25) = 0.25.
The histogram in the following figure shows the distribution of the number of heads from flipping 32 coins. That number X can be any integer from 0 to 32:
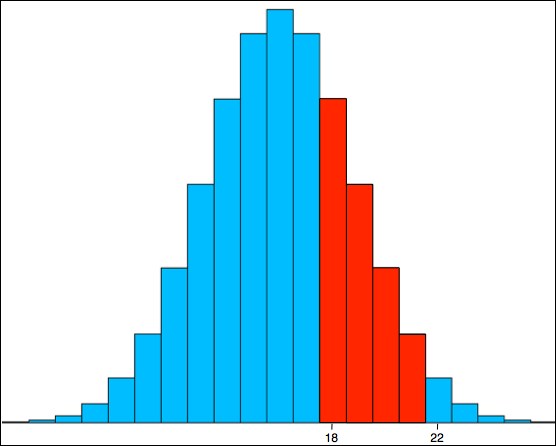
Figure 4-13. Flipping 32 coins
The four red rectangles represent the event E = {x : 17 < x ≤ 21} = {18, 19, 20, 21}. Note that the interval range uses "<" on the left and "≤" on the right. That ensures that the number of values in the range is equal to the difference of the two delimiting values:
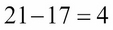
The probability of this event, P(E), is the area of that red region:
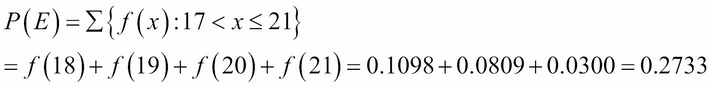
So, the probability of an interval event like this is the area of the region that lies above the event interval and below the PDF curve. When the size of the range of X is small, we have to shift to the right a half unit, as in Figure 4-13, where we used the interval (17.5 ≤ x < 21.5) instead of (17 < x ≤ 21) for the base of the region. But as Figure 3-22 suggests, a continuous random variable is nearly the same as a discrete random variable with a very large number of values in its range.
Instead of adding elementary probabilities to compute the probability of an event E, we can more simply take the difference of two values of the random variables' cumulative distribution function, its CDF. In the preceding example, that would be:
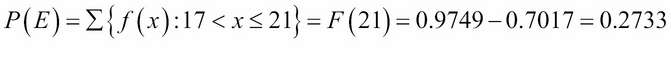
This is how event probabilities are computed for continuous random variables.
The total area under the standard normal curve (Figure 4-12) is exactly 1.0. The cumulative distribution, CDF is denoted by Φ(x) and is computed from the formula:
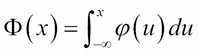
This means the area under the standard normal curve φ and over the interval (– ∞ , x). That area equals the probability that X ≤ x. By subtracting areas, we have the formula for the probability that X is between the given numbers a and b:
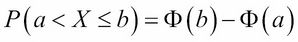
The normal curve in the following figure is the one that best approximates the binomial distribution that is shown in Figure 4-13:
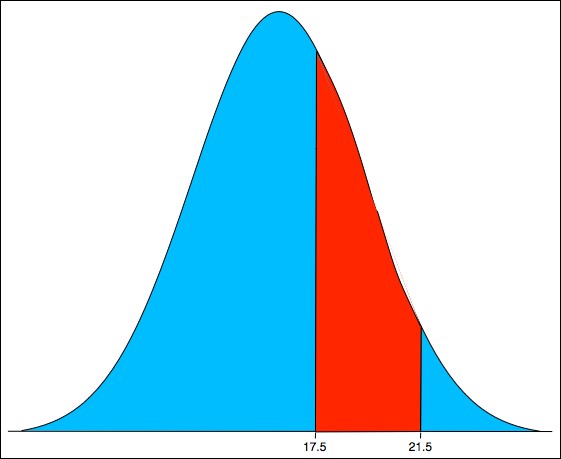
Figure 4-14. Normal probabilities
Its mean is μ = 16.0 and its standard deviation is σ = 2.82. These values are computed from the formulas μ = np and σ2 = np(1-p). For this distribution, the area of the region is P(17.5 < X ≤ 21.5), which is:
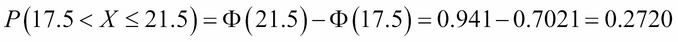
We can see from the calculation for the binomial distribution that this approximation of 0.2720 for 0.2733 is quite good.
The program that computed these probabilities is shown in Listing 4-4:

Listing 4-4. Normal probabilities
It uses the NormalDistribution class from the Apache Commons Math library, as shown at line 8. Its cumulativeProbability() method returns the value of Φ(x).
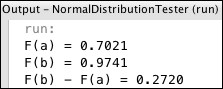
Figure 4-15. Output from Listing 4-4