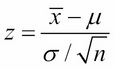A random sample is a set of numbers S = {x1, x2,... , xn}, each of which is a measurement of some unknown value that we seek. We can assume that each xi is a value of a random variable Xi, and that all these random variables X1, X2,…, Xn are independent and have the same distribution with mean μ and standard deviation σ. Let Sn and Z be the random variables:
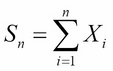
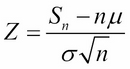
The central limit theorem states that the random variable Z tends to be normally distributed as n gets larger. That means that the PDF of Z will be close to the function φ(x) and the larger n is, the closer it will be.
By dividing numerator and denominator by n, we have this alternative formula for Z:
This isn't any simpler. But if we designate the random variable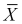 
as:
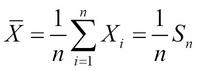
then we can write Z as:
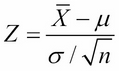
The central limit theorem tells us that this standardization of the random variable 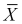is nearly distributed as the standard normal distribution φ(x). So, if we take n measurements x1, x2,…, xn of an unknown quantity that has an unknown distribution, and then compute their sample mean:
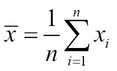
we can expect this value
