The central limit theorem gives us a systematic way to estimate population means, which is essential to the quality control of automated production in many sectors of the economy, from farming to pharmaceuticals.
For example, suppose a manufacturer has an automated machine that produces ball bearings that are supposed to be 0.82 cm in diameter. The quality control department (QCD) takes a random sample of 200 ball bearings and finds that sample mean to be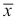 
= 0.824 cm. From long-term previous experience, they have determined that machine's standard deviation s σ = 0.042 cm. Since n = 200 is large enough, we can assume that z is nearly distributed as the standard normal distribution, where:
Suppose that the QCD has a policy of 95% confidence, which can be interpreted as meaning that it tolerates error only 5% of the time. So their objective is to find an interval (a, b) within which we can be 95% confident that the unknown population mean µ lies; that is, P(a ≤ µ ≤ b) = 0.95.
Using code like that in Listing 4-4, or from existing tabulations of the standard normal distribution, or from Table 4-1, we can find the number z95 for which P(-z95≤ z ≤ z95) = 0.95. This constant z95 is called the 95% confidence coefficient. It's value is z95 = 1.96; that is, P(-1.96 ≤ z ≤ 1.96) = 0.95.
In this example, z = 336.7(0.824 - µ), so µ = 0.824 – z/336.7, so -1.96 ≤ z ≤ 1.96 ⟺ 0.818 ≤ µ ≤ 0.830. Thus, P(0.818 ≤ µ ≤ 0.830) = 0.95. That is, we are 95% confident that the unknown population mean µ is between 0.818 cm and 0.830 cm.
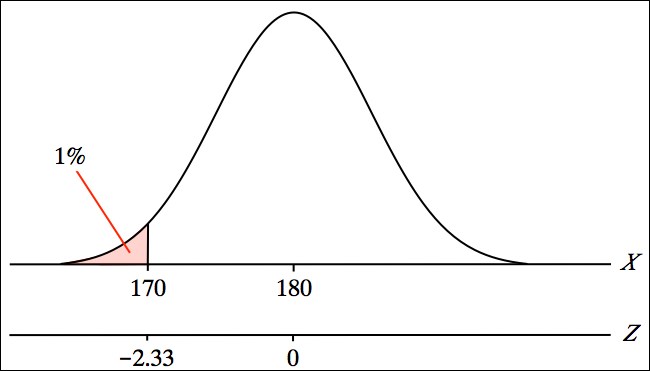
Figure 4-16. One-tailed critical region
Note that the interval bounds a and b were computed by these formulas:
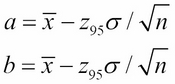
This interval is called a 95% confidence interval.
More generally, we can compute a confidence interval at any level c of confidence, simply by replacing z95 with zc, where zc satisfies the condition P(-zc≤ z ≤ zc) = c. Several values of zc are shown in Table 4-8. For example, z99 = 2.58. So, if the QCD in the preceding example wanted to elevate their quality policy to 99% confidence, they would use 2.58 in place of 1.96 to compute a 99% confidence interval:
So, the 99% confidence interval is (8.16, 8.32), meaning µ = 8.24 ± 0.08. As you would expect, that is less accurate that the 95% confidence interval we computed previously: (8.18, 8.30), meaning µ = 8.24 ± 0.06. The higher the confidence, the larger the confidence interval. The 100% confidence interval is (- ∞ , ∞ ).
|
Confidence Level, c% |
Confidence Coefficient, zc |
|---|---|
|
99% |
2.58 |
|
98% |
2.33 |
|
96% |
2.05 |
|
95% |
1.96 |
|
90% |
1.645 |
|
80% |
1.28 |
|
68.25% |
1.00 |
Table 4-8. Confidence Coefficients