If we think of each column y of the utility matrix as an n-dimensional vector, y = (y1, y2, ..., yn), then we can use the Euclidean dot product (inner product) formula to compute the cosine of the angle θ that the two vectors make at the origin:
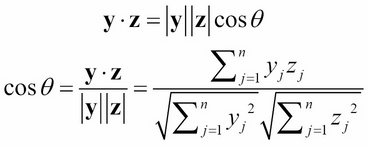
This is called the cosine similarity measure:
For example, if y = (2, 1, 3) and z = (1, 3, 2), then:
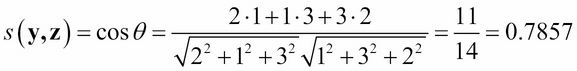
We can see that the cosine similarity measure has the six requisite properties for a similarity measure. If u and v are parallel, then s(y, z) = cos θ = cos 0 = 1. That would be the result in the case where y = (2, 1, 2) and z = (4, 2, 4). On the other hand, if y = (2, 0, 2) and z = (0, 4, 0), then y and z are perpendicular and s(y, z) = cos θ = cos 90º = 0.
We can interpret these extremes in terms of a utility matrix. If y = (2, 1, 2) and z = (4, 2, 4), then z = 2y. They are very similar in that all three of the users rated item z twice as high as item y. But in the second example of (2, 0, 2) and (0, 4, 0), we can detect no similarity at all in this data: item y is rated only by users who didn't rate item z, and vice versa.
That example of u = (2, 0, 2) and v = (0, 4, 0) is not as easy to interpret because the value 0 means no evaluation; that is, the user has no opinion on that item. A better example would be when u = (4, 1, 1) and v = (1, 4, 4). Here, u likes item 1 very much and items 2 and 3 hardly at all, while u has just the opposite opinions. Accordingly, their cosine similarity is low: s(u, v) = 4/11 = 0.3636.