Large sparse matrices

In commercial implementations of these recommender systems, the utility and similarity matrices would be far too large to be stored as internal arrays. Amazon, for example, has millions of items for sale and hundreds of millions of customers. With m = 100,000,000 and n = 1,000,000, the utility matrix would have m·n = 100,000,000,000,000 slots and the similarity matrix would have n2 = 1,000,000,000,000 slots. Moreover, if the average customer buys 100 items, then only 100n = 100,000,000 of the entries of the utility matrix would be non-zero—that's only 0.0001 percent of the entries, making it a very sparse matrix.

A sparse matrix is a matrix in which nearly all the entries are zero. Even if possible, it is very inefficient to store such a matrix as a two-dimensional array. In practice, other data structures are used.

There are several data structures that are good candidates for storing sparse matrices. A map is a data structure that implements a mathematical function y = f(x). With a function, we think of the independent variable x as the input and the dependent variable y as the output. In the context of a map, the input variable x is called the key, and the output variable y is called the value.

With a mathematical function y=f(x), the variables can be integers, real (decimal) numbers, vectors, or even more general mathematical objects. A one-dimensional array is a map where the key x ranges over the set of integers {0, 1, 2, . . . , n-1} (in Java). We write a[i] instead of a(i), but it's the same thing. Similarly, a two-dimensional array is a map where the key x ranges over a set of pairs of integers {(0,0), (0,1), (0,2),..., (1,0), (1,1), (1,2), . . . , (m,0), (m,1), (m,2), . . . , (m-1, n-1)}, and we write a[i][j] instead of a((i, j)).

Java implements the map data structure with the interface java.util.Map<K,V> and a large number of implementing classes (Java 8 provides 19 classes that implement the Map interface). The type parameters K and V stand for key and value. Probably the most commonly used implementations are the HashMap and TreeMap classes. The HashMap class is Java's standard implementation of the hash table data structure. The TreeMap class implements the red-black tree data structure, which maintains the order of the elements as determined by the ordering defined on the V class.

The SparseMatrix class in Listing 9.21 illustrates an elementary implementation for sparse matrices. Its backing store is a Map<Key,Double> object, where Key is defined as an inner class. The advantage of using this SparseMatrix class instead of a two-dimensional array for the utility matrix is that it stores only the data from the Purchases.dat file – each element represents an actual (user, item) purchase.

Note

Recall that in Java, an inner class is a non-static nested class. Our definition of the nested Key class here cannot be static because it accesses the non-static field n in its hashCode() method.

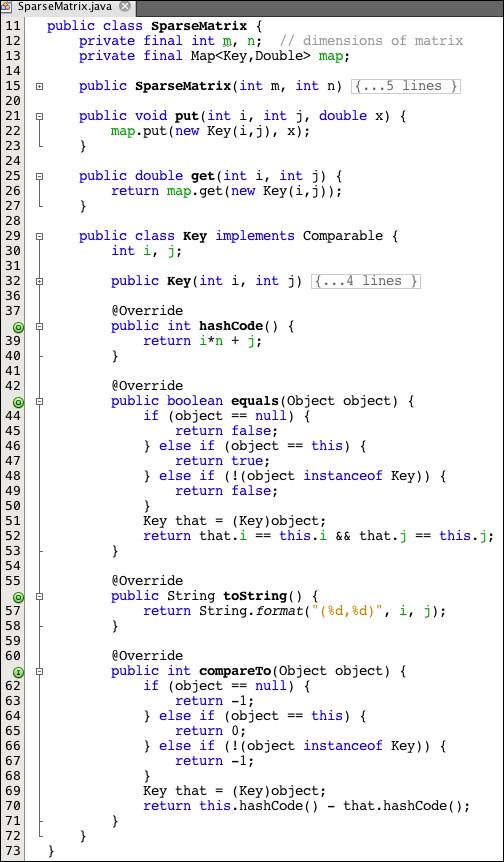
Large sparse matrices

Listing 9.22: A SparseMatrix Class

To use this, we make these changes to the code:

This implementation sacrifices efficiency for simplicity. It is inefficient because it will generate a large number of objects: every entry is an object containing two other objects, and every call to put() and to get() generates another object.

A more efficient implementation would be to use a two-dimensional array of int for the keys and a one-dimensional array of double for the values, like this:

The value key[i][j] would be the index into the u[] array. In other words, uij would be stored as u[key[i][i]]. The key[] array would be maintained in lexicographic order.

Note that this class would not be a good implementation for the similarity matrix, because it is not sparse. But it is symmetric. Consequently, we can halve the work of the computeSimilarityMatrix() method with the improvements shown in Listing 9.22:

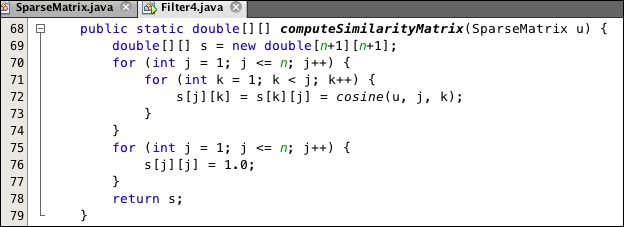
Large sparse matrices

Listing 9.22: A more efficient method for the similarity matrix computation

The double assignment at line 72 eliminates re-computing the duplicate cosine(u, k, j) value. And the loop at lines 75-77 assigns the correct value for all diagonal elements without using the cosine() method.